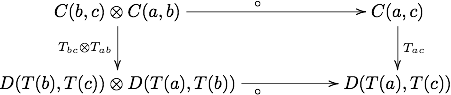समृद्ध श्रेणी
श्रेणी सिद्धांत में, गणित की एक शाखा, एक समृद्ध श्रेणी एक सामान्य मोनोइडल श्रेणी से वस्तुओं के साथ होम सेट को बदलकर एक श्रेणी (गणित) के विचार को सामान्यीकृत करती है। यह अवलोकन से प्रेरित है कि, कई व्यावहारिक अनुप्रयोगों में, होम-सेट में अधिकांशतः अतिरिक्त संरचना होती है जिसका सम्मान किया जाना चाहिए, उदाहरण के लिए, आकारिकी का सदिश स्थान या आकारिकी का एक स्थलीय स्थान होना है। एक समृद्ध श्रेणी में, वस्तुओं की प्रत्येक जोड़ी से जुड़े रूपवाद (होम-सेट) का समुच्चय "होम-ऑब्जेक्ट्स" की कुछ निश्चित मोनोइडल श्रेणी में ऑब्जेक्ट द्वारा प्रतिस्थापित किया जाता है। एक सामान्य श्रेणी में रूपवाद की (सहयोगी) संरचना का अनुकरण करने के लिए, गृह-श्रेणी में होम-ऑब्जेक्ट्स को सहयोगी विधि से बनाने का एक साधन होना चाहिए: अर्थात, हमें कम से कम देने वाली वस्तुओं पर एक बाइनरी ऑपरेशन होना चाहिए एक मोनोइडल श्रेणी की संरचना, चूँकि कुछ संदर्भों में ऑपरेशन को क्रमविनिमेय होने की भी आवश्यकता हो सकती है और संभवतः एक सही आसन्न होने की भी आवश्यकता हो सकती है (अर्थात, श्रेणी को सममित मोनोइडल श्रेणी या यहां तक कि बंद मोनोइडल श्रेणी बनाना)।
समृद्ध श्रेणी सिद्धांत इस प्रकार एक ही ढांचे के अन्दर विभिन्न प्रकार की संरचनाओं को सम्मिलित करता है
- सामान्य श्रेणियां जहां होम-सेट में समुच्चय होने के अतिरिक्त अतिरिक्त संरचना होती है। यही है, आकारिकी के ऐसे संचालन या गुण होते हैं जिन्हें संरचना द्वारा सम्मानित करने की आवश्यकता होती है (उदाहरण के लिए, 2-श्रेणी में रूपवाद और क्षैतिज संरचना के मध्य 2-कोशिकाओं का अस्तित्व, या एबेलियन श्रेणी में रूपवाद पर अतिरिक्त संचालन ) |
- श्रेणी-जैसी संस्थाएँ जिनके पास स्वयं व्यक्तिगत रूपवाद की कोई धारणा नहीं है, किन्तु जिनके होम-ऑब्जेक्ट्स में समान रचना संबंधी पहलू हैं (उदाहरण के लिए, पूर्व-आदेश जहाँ रचना नियम संक्रामकता, या स्यूडोक्वासिआव्यूह स्पेस सुनिश्चित करता है। लॉवर के आव्यूह स्पेस, जहाँ होम-ऑब्जेक्ट्स हैं संख्यात्मक दूरियाँ और रचना नियम त्रिभुज असमानता प्रदान करता है)।
ऐसे स्थिति में जहां होम-ऑब्जेक्ट श्रेणी सामान्य कार्टेशियन उत्पाद के साथ समुच्चय की श्रेणी होती है, समृद्ध श्रेणी की परिभाषाएं, समृद्ध फ़ैक्टर इत्यादि सामान्य श्रेणी सिद्धांत से मूल परिभाषाओं को कम करती हैं।
मोनोइडल श्रेणी M से होम-ऑब्जेक्ट्स के साथ समृद्ध श्रेणी को M से अधिक समृद्ध श्रेणी या M में समृद्ध श्रेणी या केवल M-श्रेणी कहा जाता है। मोनोइडल श्रेणी के संदर्भ में V अक्षर के लिए मैक लेन की वरीयता के कारण, समृद्ध श्रेणियों को कभी-कभी सामान्यतः V-श्रेणियों के रूप में भी संदर्भित किया जाता है।
परिभाषा
(M, ⊗, I, α, λ, ρ) एक मोनोइडल श्रेणी हो। फिर एक समृद्ध श्रेणी C (वैकल्पिक रूप से उन स्थितियों में जहां मोनोइडल श्रेणी की पसंद को स्पष्ट रूप से M, या M-श्रेणी से समृद्ध श्रेणी की आवश्यकता होती है) में सम्मिलित हैं
- 'C' की वस्तुओं का वर्ग (समुच्चय सिद्धांत) OB ('C'),है |
- वस्तु C(a, b) वस्तुओं की प्रत्येक जोड़ी के लिए M का ऑब्जेक्ट a, b C में, तीर को परिभाषित करने के लिए उपयोग किया जाता है | M में तीर के रूप में परिभाषित करने के लिए प्रयोग किया जाता है,|
- तीर ida : I → C(a, a) M में C में प्रत्येक वस्तु a के लिए पहचान निर्दिष्ट करता है,|
- तीर °abc : C(b, c) ⊗ C(a, b) → C(a, c) M C में वस्तुओं के प्रत्येक ट्रिपल a, b, c के लिए रचना को निर्दिष्ट करता है, जिसका उपयोग संरचना को परिभाषित करने के लिए उपयोग किया जाता है और C में साथ तीन आने वाले आरेखों के साथ, नीचे चर्चा की गई।
पहला आरेख रचना की साहचर्यता को व्यक्त करता है:

- यही है, सहयोगी श्रेणी M के सहयोगी द्वारा अब सहयोगीता आवश्यकता को ले लिया गया है। स्थिति के लिए कि M समुच्चय की श्रेणी है और (⊗, I, α, λ, ρ) कार्टेशियन उत्पाद द्वारा दिया गया, मोनोइडल संरचना (×, {•}, …) है | टर्मिनल सिंगल-पॉइंट समुच्चय, और कैनोनिकल आइसोमोर्फिज्म जो वे प्रेरित करते हैं, फिर प्रत्येक C(a, b) ऐसा समुच्चय है जिसके तत्वों को C के अलग-अलग आकारिकी के रूप में माना जा सकता है, जबकि °, जो अब फलन है, यह परिभाषित करता है कि क्रमागत रूप कैसे बनते हैं। इस स्थिति में, पहले आरेख में C(a, d) लगातार तीन अलग-अलग रूपवाद बनाने के दो विधियों में से एक से मेल खाता है | a → b → c → d, अर्थात तत्वों से C(a, b), C(b, c) और C(c, d). आरेख की क्रमविनिमेयता तब केवल यह कथन है कि रचना के दोनों क्रम समान परिणाम देते हैं, जैसा कि सामान्य श्रेणियों के लिए आवश्यक है।
यहाँ जो नया है वह यह है कि उपरोक्त समृद्ध श्रेणी C में अलग-अलग रूपवाद के किसी भी स्पष्ट संदर्भ के बिना सहयोगीता के लिए आवश्यकता व्यक्त करता है - फिर से, ये आरेख मोनोइडल श्रेणी M में रूपवाद के लिए हैं, और C में नहीं - इस प्रकार की सहयोगीता की अवधारणा बना रही है रचना सामान्य स्थिति में सार्थक है जहाँ होम-ऑब्जेक्ट्स C(a, b) अमूर्त हैं, और स्वयं C को व्यक्तिगत रूपवाद की किसी भी धारणा के होने की भी आवश्यकता नहीं है।
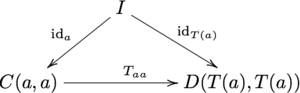
यह धारणा कि सामान्य श्रेणी में पहचान आकारिकी होनी चाहिए, को दूसरे और तीसरे आरेखों द्वारा प्रतिस्थापित किया जाता है, जो बाएँ और दाएँ एककों के संदर्भ में पहचान व्यक्त करते हैं:
 और
और
- उस स्थिति पर वापस लौटना जहां M कार्टेशियन उत्पाद, आकारिकी के साथ समुच्चय की श्रेणी है | एक-बिंदु समुच्चय ida: I → C(a, a) से कार्य बन जाता है और फिर, किसी दिए गए ऑब्जेक्ट के लिए, प्रत्येक समुच्चय के किसी विशेष तत्व C(a, a) की पहचान करता है , कुछ ऐसा जिसे हम 'C' में a के लिए पहचान रूपवाद के रूप में सोच सकते हैं। बाद के दो आरेखों की क्रमविनिमेयता तब कथन है कि 'C' में इन विशिष्ट व्यक्तिगत पहचान रूपवादों को सम्मिलित करने वाली रचनाएँ (जैसा कि कार्यों ° द्वारा परिभाषित है) सामान्य श्रेणियों के लिए पहचान नियमों के अनुसार बिल्कुल व्यवहार करती हैं।
ध्यान दें कि यहां पहचान की कई अलग-अलग धारणाओं को संदर्भित किया जा रहा है:
- M का मोनोइडल पहचान वस्तु केवल मोनॉइड-सैद्धांतिक अर्थ में ⊗ के लिए पहचान होने के सम्बन्ध में , और फिर भी केवल विहित समरूपता (λ, ρ) तक होती है |.
- पहचान रूपवाद 1C(a, b) : C(a, b) → C(a, b) कि M के पास इसकी प्रत्येक वस्तु के लिए (कम से कम) सामान्य श्रेणी होने के कारण है।
- समृद्ध श्रेणी पहचान ida : I → C(a, a) प्रत्येक वस्तु के लिए 'C' में, जो फिर से 'M' का रूपवाद है, यहां तक कि उस स्थिति में भी जहां 'C' को अपने स्वयं के अलग-अलग रूपों के रूप में समझा जाता है, आवश्यक नहीं कि वह किसी विशिष्ट व्यक्ति की पहचान करे।
समृद्ध श्रेणियों के उदाहरण
- साधारण श्रेणियां (समुच्चय, ×, {•}) से समृद्ध श्रेणियां हैं, कार्टेशियन उत्पाद के साथ समुच्चय की श्रेणी मोनोइडल ऑपरेशन के रूप में, जैसा कि ऊपर बताया गया है।
- 2-श्रेणियाँ कैट से अधिक समृद्ध श्रेणियां हैं, छोT श्रेणियों की श्रेणी, जिसमें कार्तीय उत्पाद द्वारा मोनोइडल संरचना दी जा रही है। इस स्थिति में आकारिकी a → b के मध्य 2-कोशिकाएं और उनसे संबंधित लंबवत-रचना नियम सामान्य श्रेणी C(a, ' 'B) और इसका अपना रचना नियम है।
- स्थानीय रूप से छोT श्रेणी (स्मसमुच्चय, ×) पर समृद्ध श्रेणियां हैं, कार्टेशियन उत्पाद के साथ मोनोइडल ऑपरेशन के रूप में छोटे समुच्चय (श्रेणी सिद्धांत) की श्रेणी है। (स्थानीय रूप से छोT श्रेणी वह है जिसकी होम-ऑब्जेक्ट्स छोटे समुच्चय हैं।)
- स्थानीय रूप से परिमित श्रेणी, सादृश्य द्वारा, (फ़िनसमुच्चय, ×) पर समृद्ध श्रेणियां हैं, कार्टेशियन उत्पाद के साथ मोनोइडल ऑपरेशन के रूप में परिमित समुच्चय की श्रेणी है।
- यदि 'C' बंद मोनोइडल श्रेणी है तो 'C' अपने आप में समृद्ध है।
- पूर्व-आदेशित समुच्चय निश्चित मोनोइडल श्रेणी में समृद्ध श्रेणियां हैं, 2, जिसमें दो ऑब्जेक्ट और उनके मध्य गैर-पहचान वाला तीर सम्मिलित है, जिसे हम असत्य → सत्य के रूप में लिख सकते हैं, मोनोइड ऑपरेशन के रूप में संयोजन, और ' 'सत्य इसकी मोनोइडल पहचान के रूप में। होम-ऑब्जेक्ट्स 2(a, b) फिर वस्तुओं की दी गई जोड़ी (a, b) पर एक विशेष द्विआधारी संबंध को अस्वीकार या पुष्टि करते हैं; अधिक परिचित अंकन के लिए हम इस संबंध को इस प्रकार लिख सकते हैं a ≤ b. 2 से अधिक समृद्ध श्रेणी के लिए आवश्यक रचनाओं और पहचान का अस्तित्व क्रमशः निम्नलिखित स्वयंसिद्धों में अनुवाद करता है
- b ≤ c और a ≤ b ⇒ a ≤ c (संक्रमण)
- सत्य ⇒ a ≤ a (रिफ्लेक्सिविT)
- जो ≤ एक पूर्व आदेश होने के स्वयंसिद्ध सिद्धांतों के अतिरिक्त और कोई नहीं हैं। और चूंकि 2 में सभी आरेख लघुकरण करते है, यह 2 से अधिक समृद्ध श्रेणियों के लिए समृद्ध श्रेणी स्वयंसिद्धों की एकमात्र सामग्री है।
- विलियम लॉवरे के सामान्यीकृत आव्यूह रिक्त स्थान, जिन्हें आव्यूह (गणित) स्यूडोक्वासिमेट्रिक्स के रूप में भी जाना जाता है, वे श्रेणियां हैं जो गैर-नकारात्मक विस्तारित वास्तविक संख्याओं R+∞ से समृद्ध हैं , जहां बाद वाले को अपने सामान्य क्रम के व्युत्क्रम के माध्यम से सामान्य श्रेणी की संरचना दी जाती है (अर्थात, आकृतिवाद r → s iff r ≥ s) और जोड़ (+) और शून्य (0) के माध्यम से मोनोइडल संरचना उपस्थित है। होम-ऑब्जेक्ट्स R+∞(a, b) अनिवार्य रूप से दूरी d(a,-b) हैं, और संरचना और पहचान का अस्तित्व अनुवाद करता है
- d(b, c) + d(a, b) ≥ d(a, c) (त्रिकोण असमानता)
- 0 ≥ D(A, A)
- शून्य मोर्फिज्म वाली श्रेणियां ('समुच्चय *', ∧) से समृद्ध श्रेणियां हैं, मोनोइडल ऑपरेशन के रूप में स्मैश उत्पाद के साथ नुकीले समुच्चयों की श्रेणी; होम-ऑब्जेक्ट होम (A,-B) का विशेष बिंदु A से B तक शून्य आकारिकी से मेल खाता है।
- एबेलियन समूह की श्रेणी 'AB' और क्रमविनिमेय रिंग पर मॉड्यूल (गणित) की श्रेणी 'आर-मॉड', और किसी दिए गए क्षेत्र (गणित) पर वेक्टर रिक्त स्थान की श्रेणी 'वेक्ट' स्वयं से समृद्ध होती है, जहां रूपवाद बीजगणितीय संरचना बिंदुवार प्राप्त करते हैं। अधिक सामान्यतः, प्रीएडिटिव श्रेणी वे श्रेणियां होती हैं जो ('AB', ⊗) से अधिक समृद्ध होती हैं, जिसमें मोनोइडल ऑपरेशन के रूप में टेंसर उत्पाद होता है (एबेलियन समूहों को 'जेड'-मॉड्यूल के रूप में सोचना)।
मोनोइडल functors के साथ संबंध
यदि मोनोइडल श्रेणी M से मोनोइडल श्रेणी n तक मोनोइडल फ़ैक्टर है, तो M से अधिक समृद्ध किसी भी श्रेणी को n से समृद्ध श्रेणी के रूप में दोबारा परिभाषित किया जा सकता है। प्रत्येक मोनोइडल श्रेणी M में मोनोइडल फ़ंक्शनर M (I, - ) समुच्चय की श्रेणी में, इसलिए किसी भी समृद्ध श्रेणी में अंतर्निहित सामान्य श्रेणी होती है। कई उदाहरणों में (जैसे ऊपर वाले) यह फ़ैक्टर वफादार फ़ंक्टर है, इसलिए M से समृद्ध श्रेणी को कुछ अतिरिक्त संरचना या गुणों के साथ सामान्य श्रेणी के रूप में वर्णित किया जा सकता है।
समृद्ध कारक
समृद्ध संचालक समृद्ध श्रेणियों के लिए फ़नकार की धारणा का उपयुक्त सामान्यीकरण है। समृद्ध कारक तब समृद्ध श्रेणियों के मध्य मानचित्र होते हैं जो समृद्ध संरचना का सम्मान करते हैं।
अगर C और D M-श्रेणियां हैं (अर्थात, मोनोइडल श्रेणी M पर समृद्ध श्रेणियां), M-समृद्ध फ़ंक्टर T: C → D मानचित्र है जो C की प्रत्येक वस्तु को D की वस्तु प्रदान करता है और C में A और B वस्तुओं की प्रत्येक जोड़ी के लिए M में रूपवाद प्रदान करता है Tab: C (A, B) → D (T (A), T (B)) C और D (जो 'M' में वस्तुएं हैं) के होम-ऑब्जेक्ट्स के मध्य, रोचक के सिद्धांतों के समृद्ध संस्करणों को संतुष्ट करते हैं, जैसे पहचान और संरचना का संरक्षण है।
चूंकि होम-ऑब्जेक्ट्स को समृद्ध श्रेणी में समुच्चय करने की आवश्यकता नहीं है, इसलिए कोई विशेष रूपवाद के बारे में बात नहीं कर सकता है। पहचान रूपवाद की अब कोई धारणा नहीं है, न ही दो आकारिकी के किसी विशेष संयोजन की इसके अतिरिक्त, इकाई से होम-ऑब्जेक्ट के आकारिकी को एक पहचान का चयन करने के बारे में सोचा जाना चाहिए, और मोनोइडल उत्पाद से आकारिकी को संरचना के रूप में सोचा जाना चाहिए। सामान्य क्रियात्मक स्वयंसिद्धों को इन रूपवाद से जुड़े संगत क्रमविनिमेय आरेखों से बदल दिया जाता है।
विस्तार से, किसी के पास वह आरेख है
लघुकरण करता है, जो समीकरण के सामान है
जहां I 'M' की इकाई वस्तु है। यह नियम F(ida) = IDF(a) साधारण कार्यकर्ताओं के लिए। इसके अतिरिक्त, एक मांग करता है कि आरेख
लघुकरण, जो साधारण फ़ैक्टरों के लिए F(fg)=F(f)F(g) नियम के अनुरूप है।
यह भी देखें
- आंतरिक श्रेणी
- इस्बेल संयुग्मन
संदर्भ
- Kelly,G.M. (2005) [1982]. Basic Concepts of Enriched Category Theory. Reprints in Theory and Applications of Categories. Vol. 10.
- Mac Lane, Saunders (September 1998). Categories for the Working Mathematician. Graduate Texts in Mathematics. Vol. 5 (2nd ed.). Springer. ISBN 0-387-98403-8.
- Lawvere, F.W. (2002) [1973]. Metric Spaces, Generalized Logic, and Closed Categories. Reprints in Theory and Applications of Categories. Vol. 1.
- Enriched category at the nLab