जटिल संख्या: Difference between revisions
No edit summary |
No edit summary |
||
| Line 1: | Line 1: | ||
{{Short description|Number with a real and an imaginary part}} | {{Short description|Number with a real and an imaginary part}} | ||
[[File:A plus bi.svg|thumb|upright=1.15|right| | [[File:A plus bi.svg|thumb|upright=1.15|right|सम्मिश्र संख्या को संख्याओं की एक जोड़ी (a, b) के रूप में दृष्टिगत रूप से दर्शाया जा सकता है, जो सम्मिश्र समतल का प्रतिनिधित्व करते हुए, आरगां आरेख नामक आरेख पर एक सदिश बनाता है। Re वास्तविक अक्ष है, Im काल्पनिक अक्ष है, और i "काल्पनिक इकाई" है, जो ''i''<sup>2</sup> = −1 को संतुष्ट करता है।]]गणित में, एक सम्मिश्र संख्या एक [[ संख्या प्रणाली ]] का एक तत्व है जो वास्तविक संख्याओं को एक विशिष्ट तत्व के साथ विस्तारित करता है जिसे {{mvar|i}} कहा जाता है, जिसे काल्पनिक इकाई कहा जाता है और समीकरण <math>i^{2}= -1</math>को संतुष्ट करता है; प्रत्येक सम्मिश्र संख्या को <math>a + bi</math> के रूप में व्यक्त किया जा सकता है, जहां {{mvar|a}} और {{mvar|b}} वास्तविक संख्याएं हैं।क्योंकि कोई भी वास्तविक संख्या उपरोक्त समीकरण को संतुष्ट नहीं करती है, रेने डेसकार्टेस द्वारा {{mvar|i}} एक [[ काल्पनिक संख्या ]] कहा जाता था। सम्मिश्र संख्या <math>a+bi</math> के लिए {{mvar|a}} को वास्तविक भाग और {{mvar|b}} को काल्पनिक भाग कहा जाता है। सम्मिश्र संख्याओं के समुच्चय को <math>\mathbb C</math> या {{math|'''C'''}} प्रतीकों में से किसी एक द्वारा निरूपित किया जाता है। ऐतिहासिक नामकरण काल्पनिक के होते हुए भी, सम्मिश्र संख्याओं को [[ गणितीय विज्ञान ]] में वास्तविक संख्या के समान वास्तविक माना जाता है और प्राकृतिक विश्व के वैज्ञानिक विवरण के कई स्वरूपों में मौलिक हैं।<ref>For an extensive account of the history of "imaginary" numbers, from initial skepticism to ultimate acceptance, see {{cite book |last=Bourbaki |first=Nicolas |author-link=Nicolas Bourbaki |year=1998 |title=Elements of the History of Mathematics |chapter=Foundations of Mathematics § Logic: Set theory |pages=18–24 |publisher=Springer}} | ||
</ref>{{efn| "Complex numbers, as much as reals, and perhaps even more, find a unity with nature that is truly remarkable. It is as though Nature herself is as impressed by the scope and consistency of the complex-number system as we are ourselves, and has entrusted to these numbers the precise operations of her world at its minutest scales." — R. Penrose (2016, <!-- [https://books.google.com/books?id=VWTNCwAAQBAJ&pg=PA73 ] --> p. 73)<ref>{{cite book |first=Roger |last=Penrose |year=2016 |title=The Road to Reality: A complete guide to the laws of the universe |edition=reprint |publisher=Random House |isbn=978-1-4464-1820-8 |pages=72–73 |url=https://books.google.com/books?id=VWTNCwAAQBAJ&pg=PA73}}</ref> }} | </ref>{{efn| "Complex numbers, as much as reals, and perhaps even more, find a unity with nature that is truly remarkable. It is as though Nature herself is as impressed by the scope and consistency of the complex-number system as we are ourselves, and has entrusted to these numbers the precise operations of her world at its minutest scales." — R. Penrose (2016, <!-- [https://books.google.com/books?id=VWTNCwAAQBAJ&pg=PA73 ] --> p. 73)<ref>{{cite book |first=Roger |last=Penrose |year=2016 |title=The Road to Reality: A complete guide to the laws of the universe |edition=reprint |publisher=Random House |isbn=978-1-4464-1820-8 |pages=72–73 |url=https://books.google.com/books?id=VWTNCwAAQBAJ&pg=PA73}}</ref> }} | ||
सम्मिश्र संख्याएं सभी [[ बहुपद समीकरण ]] के समाधान की स्वीकृति देती हैं, यहां तक कि जिनके पास वास्तविक संख्याओं में कोई समाधान नहीं है। अधिक परिशुद्ध रूप से, [[ बीजगणित के मौलिक प्रमेय ]] का दावा है कि वास्तविक या सम्मिश्र गुणांक के साथ प्रत्येक गैर-निरंतर बहुपद समीकरण का एक समाधान होता है जो एक सम्मिश्र संख्या है।उदाहरण के लिए, समीकरण<math>(x+1)^2 = -9</math> कोई वास्तविक समाधान नहीं है, क्योंकि एक वास्तविक संख्या का वर्ग ऋणात्मक नहीं हो सकता है, लेकिन दो गैर -सम्मिश्र सम्मिश्र समाधान हैं <math>-1+3i</math> और <math>-1-3i</math>। | |||
<math>(x+1)^2 = -9</math> | |||
कोई वास्तविक समाधान नहीं है, क्योंकि एक वास्तविक संख्या का वर्ग | |||
जोड़ का उपयोग करके | जोड़ का उपयोग करके सम्मिश्र संख्याओं के जोड़, घटाव और गुणन को स्वाभाविक रूप से परिभाषित किया जा सकता है <math>i^{2}=-1</math> साहचर्य नियम, [[ विनिमेय कानून | विनिमेय नियम]] और वितरण नियम के साथ संयुक्त।प्रत्येक नॉनज़ेरो सम्मिश्र संख्या में एक गुणक उलटा होता है।यह सम्मिश्र संख्याओं को एक [[ क्षेत्र (गणित) ]] बनाता है जिसमें एक उप-क्षेत्र के रूप में वास्तविक संख्या होती है।सम्मिश्र संख्या भी आयाम दो का एक वास्तविक वेक्टर समष्टि बनाती है, {{math|{{mset|1, ''i''}}}} एक [[ मानक आधार ]] के रूप में। | ||
यह मानक आधार | यह मानक आधार सम्मिश्र संख्याओं को एक [[ कार्टेशियन विमान ]] बनाता है, जिसे सम्मिश्र समतल कहा जाता है।यह सम्मिश्र संख्याओं और उनके संचालन की एक ज्यामितीय व्याख्या की स्वीकृति देता है, और इसके विपरीत सम्मिश्र संख्याओं के संदर्भ में कुछ ज्यामितीय गुणों और निर्माणों को व्यक्त करता है।उदाहरण के लिए, वास्तविक संख्या [[ वास्तविक रेखा ]] का निर्माण करती है जिसे सम्मिश्र समतल के क्षैतिज अक्ष के लिए पहचाना जाता है।निरपेक्ष मान की सम्मिश्र संख्या एक [[ एकक व्रत ]] का निर्माण करती है।एक सम्मिश्र संख्या के अतिरिक्त सम्मिश्र समतल में एक [[ अनुवाद ]] (ज्यामिति) है, और एक सम्मिश्र संख्या से गुणा मूल में केंद्रित एक [[ समानता (ज्यामिति) ]] है।[[ जटिल संयुग्मन | सम्मिश्र संयुग्मन]] वास्तविक अक्ष के संबंध में [[ प्रतिबिंब समरूपता ]] है।सम्मिश्र निरपेक्ष मान एक [[ यूक्लिडियन मानदंड ]] है। | ||
सारांश में, | सारांश में, सम्मिश्र संख्या एक समृद्ध संरचना बनाती है जो एक साथ एक बीजगणितीय रूप से संवृत क्षेत्र है, जो वास्तविक पर एक [[ कम्यूटेटिव बीजगणित ]] (संरचना) है, और आयाम दो का एक [[ यूक्लिडियन वेक्टर स्थान | यूक्लिडियन वेक्टर समष्टि]] है। | ||
{{TOC limit|3}} | {{TOC limit|3}} | ||
| Line 19: | Line 15: | ||
== परिभाषा == | == परिभाषा == | ||
[[File:Illustration of a complex number.svg|right|thumb|upright=1.05| | [[File:Illustration of a complex number.svg|right|thumb|upright=1.05|सम्मिश्र संख्या का एक चित्रण {{math|1=''z'' = ''x'' + ''iy''}} वास्तविक भाग x है, और इसका काल्पनिक भाग y है।]]एक सम्मिश्र संख्या फॉर्म की एक संख्या है {{math|1=''a'' + ''bi''}}, कहां {{mvar|a}} और {{mvar|b}} वास्तविक संख्याएं हैं, और {{math|''i''}} एक अनिश्चित संतोषजनक है {{math|1=''i''<sup>2</sup> = −1}}।उदाहरण के लिए, {{math|2 + 3''i''}} एक सम्मिश्र संख्या है।<ref>{{cite book|title=कॉलेज अल्जेबरा|url=https://archive.org/details/collegealgebrawi00axle |url-access=limited |last=Axler |first=Sheldon |page=[https://archive.org/details/collegealgebrawi00axle/page/n285 262]|publisher=Wiley|year=2010|isbn=9780470470770 }}</ref> | ||
इस तरह, एक | इस तरह, एक सम्मिश्र संख्या को एकल अनिश्चितता में वास्तविक गुणांक के साथ एक [[ बहुपद ]] के रूप में परिभाषित किया गया है {{math|''i''}}, जिसके लिए संबंध {{math|''i''<sup>2</sup> + 1 {{=}} 0}} लगाया जाता है।इस परिभाषा के आधार पर, बहुपद के लिए जोड़ और गुणन का उपयोग करके सम्मिश्र संख्याओं को जोड़ा और गुणा किया जा सकता है।रिश्ता {{math|''i''<sup>2</sup> + 1 {{=}} 0}} समानता को प्रेरित करता है {{math|''i''<sup>4''k''</sup> {{=}} 1, ''i''<sup>4''k''+1</sup> {{=}} ''i'', ''i''<sup>4''k''+2</sup> {{=}} −1,}} और {{math|''i''<sup>4''k''+3</sup> {{=}} −''i'',}} जो सभी पूर्णांक के लिए पकड़ है {{mvar|k}};ये किसी भी बहुपद को कम करने की स्वीकृति देते हैं जो सम्मिश्र संख्याओं के जोड़ और गुणन से एक रैखिक बहुपद में परिणाम देता है {{mvar|i}}, फिर से फॉर्म {{math|1=''a'' + ''bi''}} वास्तविक गुणांक के साथ {{mvar|a, b.}} | ||
असली संख्या {{mvar|a}} | असली संख्या {{mvar|a}} सम्मिश्र संख्या का वास्तविक भाग कहा जाता है {{math|''a'' + ''bi''}};असली संख्या {{mvar|b}} इसका काल्पनिक भाग कहा जाता है। जोर देने के लिए, काल्पनिक भाग में एक कारक सम्मिलित नहीं है {{mvar|i}};अर्थात्, काल्पनिक भाग है {{mvar|b}}, नहीं {{math|''bi''}}.<ref>{{cite book |last1=Spiegel |first1= M.R. |last2=Lipschutz |first2= S. |last3= Schiller |first3= J.J. |last4=Spellman |first4=D. |title= जटिल चर|edition=2nd |series=Schaum's Outline Series |publisher= McGraw Hill |isbn= 978-0-07-161569-3|date= 14 April 2009 }}</ref><ref>{{cite book |title=कॉलेज बीजगणित और त्रिकोणमिति|edition=6 |first1=Richard N. |last1=Aufmann |first2=Vernon C. |last2=Barker |first3=Richard D. |last3=Nation |publisher=Cengage Learning |year=2007 |isbn=978-0-618-82515-8 |page=66 |chapter-url=https://books.google.com/books?id=g5j-cT-vg_wC&pg=PA66 |chapter=Chapter P}}</ref> | ||
औपचारिक रूप से, | औपचारिक रूप से, सम्मिश्र संख्याओं को अनिश्चितता में बहुपद वलय के भागफल वलय के रूप में परिभाषित किया गया है {{math|''i''}}, बहुपद द्वारा उत्पन्न आदर्श (वलय थ्योरी) द्वारा {{math|''i''<sup>2</sup> + 1}} ।{{harvnb|Bourbaki|1998|loc=§VIII.1}}</ref> | ||
== संकेतन == | == संकेतन == | ||
एक वास्तविक संख्या {{mvar|a}} एक | एक वास्तविक संख्या {{mvar|a}} एक सम्मिश्र संख्या के रूप में माना जा सकता है {{math|''a'' + 0''i''}}, जिसका काल्पनिक भाग 0. एक विशुद्ध रूप से काल्पनिक संख्या है {{math|''bi''}} एक सम्मिश्र संख्या है {{math|0 + ''bi''}}, जिसका असली भाग शून्य है।बहुपद के साथ, यह लिखना आम है {{mvar|a}} के लिए {{math|''a'' + 0''i''}} और {{math|''bi''}} के लिए {{math|0 + ''bi''}}।इसके अतिरिक्त, जब काल्पनिक भाग ऋणात्मक है, अर्थात्, {{math|1=''b'' = −''{{!}}b{{!}}'' < 0}}, यह लिखना आम है {{math|''a'' − ''{{!}}b{{!}}i''}} के अतिरिक्त {{math|''a'' + (−''{{!}}b{{!}}'')''i''}};उदाहरण के लिए, के लिए {{math|1=''b'' = −4}}, {{math|3 − 4''i''}} के अतिरिक्त लिखा जा सकता है {{math|3 + (−4)''i''}}। | ||
अनिश्चित के गुणन के बाद से {{math|''i''}} और एक वास्तविक वास्तविक गुणांक, बहुपद के साथ बहुपद में कम्यूटेटिव है {{math|''a'' + ''bi''}} के रूप में लिखा जा सकता है {{math|''a'' + ''ib''.}} यह | अनिश्चित के गुणन के बाद से {{math|''i''}} और एक वास्तविक वास्तविक गुणांक, बहुपद के साथ बहुपद में कम्यूटेटिव है {{math|''a'' + ''bi''}} के रूप में लिखा जा सकता है {{math|''a'' + ''ib''.}} यह प्रायः अभिव्यक्तियों द्वारा निरूपित काल्पनिक भागों के लिए समीचीन होता है, उदाहरण के लिए, जब, जब {{mvar|b}} एक कट्टरपंथी है।{{sfn|Ahlfors|1979}} | ||
एक | एक सम्मिश्र संख्या का वास्तविक भाग {{mvar|z}} द्वारा निरूपित किया गया है {{math|Re(''z'')}}, <math>\mathcal{Re}(z)</math>, या <math>\mathfrak{R}(z)</math>;एक सम्मिश्र संख्या का काल्पनिक भाग {{mvar|z}} द्वारा निरूपित किया गया है {{math|Im(''z'')}}, <math>\mathcal{Im}(z)</math>, या <math>\mathfrak{I}(z).</math> उदाहरण के लिए, | ||
<math display=block> \operatorname{Re}(2 + 3i) = 2 \quad \text{ and } \quad \operatorname{Im}(2 + 3i) = 3~.</math> | <math display=block> \operatorname{Re}(2 + 3i) = 2 \quad \text{ and } \quad \operatorname{Im}(2 + 3i) = 3~.</math> | ||
सभी | सभी सम्मिश्र संख्याओं का [[ सेट (गणित) ]] द्वारा निरूपित किया गया है <math>\Complex</math> ([[ ब्लैकबोर्ड बोल्ड ]]) या {{math|'''C'''}} (ईमानदार बोल्ड)। | ||
कुछ विषयों में, विशेष रूप से इलेक्ट्रोमैग्नेटिज्म और [[ [[ विद्युत ]] अभियन्त्रण ]] में, {{mvar|j}} के | कुछ विषयों में, विशेष रूप से इलेक्ट्रोमैग्नेटिज्म और [[ [[ विद्युत ]] अभियन्त्रण ]] में, {{mvar|j}} के अतिरिक्त उपयोग किया जाता है {{mvar|i}} जैसा {{mvar|i}} प्रायः [[ विद्युत प्रवाह ]] का प्रतिनिधित्व करने के लिए उपयोग किया जाता है।<ref>{{cite book |last1=Brown |first1=James Ward |last2=Churchill |first2=Ruel V. |title=जटिल चर और अनुप्रयोग|year=1996 |publisher=McGraw-Hill |location=New York |isbn=978-0-07-912147-9 |edition=6th |page=2 |quote=इलेक्ट्रिकल इंजीनियरिंग में, '' j '' अक्षर का उपयोग '' i '' के बजाय किया जाता है।}}} </ref> इन स्थितियों में, सम्मिश्र संख्याओं को लिखा जाता है {{math|''a'' + ''bj''}}, या {{math|''a'' + ''jb''}}। | ||
== विज़ुअलाइज़ेशन == | == विज़ुअलाइज़ेशन == | ||
{{Main|Complex plane}} | {{Main|Complex plane}} | ||
[[File:Complex number illustration.svg|thumb|right|एक | [[File:Complex number illustration.svg|thumb|right|एक सम्मिश्र संख्या {{mvar|z}}, एक बिंदु (काला) और इसकी स्थिति वेक्टर (नीला) के रूप में]]एक सम्मिश्र संख्या {{mvar|z}} इस प्रकार एक क्रमित जोड़ी के साथ पहचाना जा सकता है <math>(\Re (z),\Im (z))</math> वास्तविक संख्याओं में से, जिसे बदले में दो आयामी समष्टि में एक बिंदु के निर्देशांक के रूप में व्याख्या की जा सकती है। सबसे तत्काल समष्टि उपयुक्त निर्देशांक के साथ यूक्लिडियन विमान है, जिसे तब सम्मिश्र समतल या आर्गन आरेख कहा जाता है,<ref>{{cite book |last=Pedoe |first=Dan |author-link=Daniel Pedoe |title=ज्यामिति: एक व्यापक पाठ्यक्रम|publisher=Dover |year=1988 |isbn=978-0-486-65812-4}}</ref>{{efn| {{harvnb|Solomentsev|2001}}: "The plane <math>\R^2</math> whose points are identified with the elements of <math>\Complex</math> is called the complex plane ... The complete geometric interpretation of complex numbers and operations on them appeared first in the work of C. Wessel (1799). The geometric representation of complex numbers, sometimes called the 'Argand diagram', came into use after the publication in 1806 and 1814 of papers by J.R. Argand, who rediscovered, largely independently, the findings of Wessel".}}<ref name=":2">{{Cite web |last=Weisstein |first=Eric W. |title=जटिल संख्या|url=https://mathworld.wolfram.com/ComplexNumber.html |access-date=2020-08-12 |website=mathworld.wolfram.com}}</ref> [[ जीन-रॉबर्ट फाइट ]] के नाम पर।एक और प्रमुख समष्टि जिस पर निर्देशांक का अनुमान लगाया जा सकता है, वह एक क्षेत्र की दो-आयामी सतह है, जिसे तब रीमैन क्षेत्र कहा जाता है। | ||
=== कार्टेशियन | === कार्टेशियन सम्मिश्र प्लेन === | ||
दो मनमाने वास्तविक मूल्यों को | दो मनमाने वास्तविक मूल्यों को सम्मिलित करने वाली सम्मिश्र संख्याओं की परिभाषा तुरंत सम्मिश्र समतल में कार्टेशियन निर्देशांक के उपयोग का सुझाव देती है।क्षैतिज (वास्तविक) अक्ष का उपयोग सामान्य रूप से वास्तविक भाग को प्रदर्शित करने के लिए किया जाता है, दाईं ओर बढ़ते मूल्यों के साथ, और काल्पनिक भाग ऊर्ध्वाधर (काल्पनिक) अक्ष को चिह्नित करता है, जिसमें मूल्यों को ऊपर की ओर बढ़ता है। | ||
एक चार्टेड संख्या को या तो विक्ट के रूप में देखा जा सकता है: समन्वय बिंदु या इस बिंदु तक मूल से एक [[ वेक्टर (ज्यामितीय) ]] के रूप में।एक | एक चार्टेड संख्या को या तो विक्ट के रूप में देखा जा सकता है: समन्वय बिंदु या इस बिंदु तक मूल से एक [[ वेक्टर (ज्यामितीय) ]] के रूप में।एक सम्मिश्र संख्या के समन्वय मान {{mvar|z}} इसलिए इसके कार्टेशियन, आयताकार या बीजीय रूप में व्यक्त किया जा सकता है। | ||
विशेष रूप से, जोड़ और गुणन के संचालन एक बहुत ही प्राकृतिक ज्यामितीय चरित्र पर ले जाते हैं, जब | विशेष रूप से, जोड़ और गुणन के संचालन एक बहुत ही प्राकृतिक ज्यामितीय चरित्र पर ले जाते हैं, जब सम्मिश्र संख्याओं को स्थिति वैक्टर के रूप में देखा जाता है: इसके अतिरिक्त यूक्लिडियन वेक्टर #जोड़ और घटाव से अनुरूप है, जबकि गुणा (देखें #multiplication और ध्रुवीय रूप में विभाजन) कई गुणा करने से मेल खाती है।उनके परिमाण और वे कोण जो वे वास्तविक अक्ष के साथ बनाते हैं।इस तरह से देखा गया, एक सम्मिश्र संख्या का गुणन {{math|''i''}} मूल के बारे में एक चौथाई मोड़ (ज्यामिति) (ज्यामिति) (सही कोण | 90 °) द्वारा स्थिति वेक्टर ओरिएंटेशन (ज्यामिति) को घुमाने के लिए अनुरूप है - एक तथ्य जिसे बीजगणितीय रूप से इस प्रकार व्यक्त किया जा सकता है: | ||
<math display=block>(a + bi)\cdot i = ai + b(i)^2 = -b + ai .</math> | <math display=block>(a + bi)\cdot i = ai + b(i)^2 = -b + ai .</math> | ||
=== ध्रुवीय | === ध्रुवीय सम्मिश्र समतल === <!-- [[Nth root]] links to this section --> | ||
{{Main|Polar coordinate system}} | {{Main|Polar coordinate system}} | ||
{{Redirect|Polar form|the higher-dimensional analogue|Polar decomposition}} | {{Redirect|Polar form|the higher-dimensional analogue|Polar decomposition}} | ||
[[File:Complex number illustration modarg.svg|right|thumb| | [[File:Complex number illustration modarg.svg|right|thumb|तर्क φ और मापांक r सम्मिश्र तल में एक बिंदु का पता लगाते हैं।]] | ||
==== मापांक और तर्क ==== | ==== मापांक और तर्क ==== | ||
सम्मिश्र समतल में निर्देशांक के लिए एक वैकल्पिक विकल्प ध्रुवीय समन्वय प्रणाली है जो बिंदु की दूरी का उपयोग करता है {{mvar|z}} [[ मूल (गणित) ]] से ({{mvar|O}}), और कोण [[ सकारात्मक वास्तविक अक्ष | धनात्मक वास्तविक अक्ष]] और लाइन खंड के बीच घटाया गया {{mvar|Oz}} एक वामावर्त अर्थों में। यह ध्रुवीय रूप की ओर जाता है | |||
:<math>z=re^{i\varphi}=r(\cos\varphi +i\sin\varphi) </math> | :<math>z=re^{i\varphi}=r(\cos\varphi +i\sin\varphi) </math> | ||
एक | एक सम्मिश्र संख्या का, जहां {{mvar|r}} का पूर्ण मूल्य है {{mvar|z}}, और <math>\varphi</math> का [[ तर्क (जटिल विश्लेषण) | तर्क (सम्मिश्र विश्लेषण)]] है {{mvar|z}}। | ||
एक | एक सम्मिश्र संख्या का निरपेक्ष मान (या मापांक या परिमाण) {{math|1=''z'' = ''x'' + ''yi''}} है{{sfn|Apostol|1981|p=18}} | ||
<math display=block>r=|z|=\sqrt{x^2+y^2}.</math> | <math display=block>r=|z|=\sqrt{x^2+y^2}.</math> | ||
यदि {{mvar|z}} एक वास्तविक संख्या है ( | यदि {{mvar|z}} एक वास्तविक संख्या है (अर्थात, अगर {{math|1=''y'' = 0}}), तब {{math|1=''r'' = {{!}}''x''{{!}}}}।अर्थात्, एक वास्तविक संख्या का निरपेक्ष मान एक सम्मिश्र संख्या के रूप में इसके पूर्ण मान के बराबर है। | ||
पाइथागोरस के प्रमेय द्वारा, एक | पाइथागोरस के प्रमेय द्वारा, एक सम्मिश्र संख्या का निरपेक्ष मान सम्मिश्र समतल में सम्मिश्र संख्या का प्रतिनिधित्व करने वाले बिंदु की उत्पत्ति की दूरी है। | ||
का तर्क {{mvar|z}} (चरण के रूप में संदर्भित कई अनुप्रयोगों में {{mvar|φ}})<ref name=":2" />त्रिज्या का कोण है {{mvar|Oz}} | का तर्क {{mvar|z}} (चरण के रूप में संदर्भित कई अनुप्रयोगों में {{mvar|φ}})<ref name=":2" />त्रिज्या का कोण है {{mvar|Oz}} धनात्मक वास्तविक अक्ष के साथ, और के रूप में लिखा गया है {{math|arg ''z''}}।मापांक के साथ, तर्क आयताकार रूप से पाया जा सकता है {{mvar|x + yi}}<ref>{{cite book | ||
|title=जटिल चर: सिद्धांत और अनुप्रयोग|edition=2nd | |title=जटिल चर: सिद्धांत और अनुप्रयोग|edition=2nd | ||
|chapter=Chapter 1 | |chapter=Chapter 1 | ||
| Line 73: | Line 69: | ||
|isbn=978-81-203-2641-5 | |isbn=978-81-203-2641-5 | ||
|page=14 | |page=14 | ||
|chapter-url=https://books.google.com/books?id=rFhiJqkrALIC&pg=PA14}}</ref>—मैं कालीन-दर-वास्तविक भागों के भागफल के लिए उलटा स्पर्शरेखा को | |chapter-url=https://books.google.com/books?id=rFhiJqkrALIC&pg=PA14}}</ref>—मैं कालीन-दर-वास्तविक भागों के भागफल के लिए उलटा स्पर्शरेखा को प्रयुक्त करना।एक आधा-कोण पहचान का उपयोग करके, आर्कटन की एक एकल शाखा रेंज को कवर करने के लिए पर्याप्त है {{open-closed|−''π'', ''π''}} की {{math|arg}}-फंक्शन, और एक अधिक सूक्ष्म स्थिति-दर-मामला विश्लेषण से बचा जाता है | ||
<math display=block>\varphi = \arg (x+yi) = \begin{cases} | <math display=block>\varphi = \arg (x+yi) = \begin{cases} | ||
| Line 80: | Line 76: | ||
\text{undefined} &\text{if } x = 0 \text{ and } y = 0. | \text{undefined} &\text{if } x = 0 \text{ and } y = 0. | ||
\end{cases}</math> | \end{cases}</math> | ||
सामान्य रूप से, जैसा कि ऊपर दिया गया है, अंतराल में प्रमुख मूल्य {{open-closed|−{{mvar|π}}, {{mvar|π}}}} चुना जाता है।यदि आर्ग मान ऋणात्मक है, तो सीमा में मान {{open-closed|−{{mvar|π}}, {{mvar|π}}}} या {{closed-open|0, 2{{mvar|π}}}} जोड़कर प्राप्त किया जा सकता है {{math|2''π''}}. का मूल्य {{mvar|φ}} इस लेख में [[ कांति ]] में व्यक्त किया गया है।यह किसी भी पूर्णांक से बढ़ सकता है {{math|2''π''}} और अभी भी एक ही कोण दें, धनात्मक वास्तविक अक्ष की किरणों और उत्पत्ति से घटकर सबटेड के रूप में देखा जाता है {{mvar|z}}।इसलिए, ARG फलन को कभी -कभी बहुस्तरीय फलन माना जाता है।सम्मिश्र संख्या 0 के लिए ध्रुवीय कोण अनिश्चित है, लेकिन ध्रुवीय कोण & nbsp; 0 का मनमाना विकल्प आम है। | |||
का मूल्य {{mvar|φ}} ATAN2 के परिणाम के बराबर है: | का मूल्य {{mvar|φ}} ATAN2 के परिणाम के बराबर है: | ||
<math display=block>\varphi = \operatorname{atan2}\left(\operatorname{Im}(z),\operatorname{Re}(z) \right).</math> | <math display=block>\varphi = \operatorname{atan2}\left(\operatorname{Im}(z),\operatorname{Re}(z) \right).</math> | ||
साथ में, {{mvar|r}} और {{mvar|φ}} | साथ में, {{mvar|r}} और {{mvar|φ}} सम्मिश्र संख्याओं का प्रतिनिधित्व करने का एक और तरीका दें, ध्रुवीय रूप, मापांक और तर्क के संयोजन के रूप में विमान पर एक बिंदु की स्थिति को पूरी तरह से निर्दिष्ट करें।ध्रुवीय रूप से मूल आयताकार समन्वय को पुनर्प्राप्त करना त्रिकोणमितीय रूप नामक सूत्र द्वारा किया जाता है | ||
<math display=block> z = r(\cos \varphi + i\sin \varphi ).</math> | <math display=block> z = r(\cos \varphi + i\sin \varphi ).</math> | ||
यूलर के सूत्र का उपयोग करते हुए इसे लिखा जा सकता है | यूलर के सूत्र का उपयोग करते हुए इसे लिखा जा सकता है | ||
<math display=block>z = r e^{i \varphi} \text{ or } z = r \exp i \varphi.</math> | <math display=block>z = r e^{i \varphi} \text{ or } z = r \exp i \varphi.</math> | ||
का उपयोग {{math|[[Cis (mathematics)|cis]]}} | का उपयोग {{math|[[Cis (mathematics)|cis]]}} फलन, यह कभी -कभी संक्षिप्त किया जाता है | ||
<math display=block> z = r \operatorname\mathrm{cis} \varphi. </math> | <math display=block> z = r \operatorname\mathrm{cis} \varphi. </math> | ||
कोण संकेतन में, | कोण संकेतन में, प्रायः [[ इलेक्ट्रानिक्स ]] में एक चरण (साइन तरंगों) का प्रतिनिधित्व करने के लिए उपयोग किया जाता है {{mvar|r}} और चरण {{mvar|φ}}, यह के रूप में लिखा है<ref> | ||
{{cite book | {{cite book | ||
|first1=James William |last1=Nilsson | |first1=James William |last1=Nilsson | ||
| Line 105: | Line 101: | ||
=== | === सम्मिश्र रेखांकन === | ||
{{main|Domain coloring}} | {{main|Domain coloring}} | ||
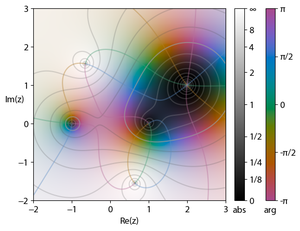
[[File:Complex-plot.png|right|thumb|अभिव्यक्ति का | [[File:Complex-plot.png|right|thumb|अभिव्यक्ति का रंग-चक्र ग्राफ{{math|{{sfrac|(''z''<sup>2</sup> − 1)(''z'' − 2 − ''i'')<sup>2</sup>|''z''<sup>2</sup> + 2 + 2''i''}}}}]][[ जटिल विश्लेषण | सम्मिश्र विश्लेषण]] की कल्पना करते समय, एक सम्मिश्र इनपुट और आउटपुट दोनों की आवश्यकता होती है।क्योंकि प्रत्येक सम्मिश्र संख्या को दो आयामों में दर्शाया जाता है, दृष्टिगत रूप से एक सम्मिश्र फलन को रेखांकन करने के लिए [[ चार आयामी स्थान | चार आयामी समष्टि]] की धारणा की आवश्यकता होगी, जो केवल अनुमानों में संभव है।इस वजह से, सम्मिश्र फलनों को देखने के अन्य तरीकों को डिजाइन किया गया है। | ||
{{math|{{sfrac|(''z''<sup>2</sup> − 1)(''z'' − 2 − ''i'')<sup>2</sup>|''z''<sup>2</sup> + 2 + 2''i''}}}}]][[ जटिल विश्लेषण ]] की कल्पना करते समय, एक | |||
[[ डोमेन रंग ]] में आउटपुट आयामों को क्रमशः रंग और चमक द्वारा दर्शाया जाता | [[ डोमेन रंग | प्रक्षेत्र रंग]] में आउटपुट आयामों को क्रमशः रंग और चमक द्वारा दर्शाया जाता है।प्रक्षेत्र के रूप में सम्मिश्र समतल में प्रत्येक बिंदु को अलंकृत किया जाता है, सामान्य रूप से रंग के साथ सम्मिश्र संख्या के तर्क का प्रतिनिधित्व करते हैं, और चमक का प्रतिनिधित्व करते हुए चमक।डार्क स्पॉट्स मार्क मोडुली शून्य के पास, उज्जवल धब्बे मूल से दूर हैं, ग्रेडेशन संवृत हो सकता है, लेकिन इसे नीरस माना जाता है।रंग प्रायः चरणों में भिन्न होते हैं {{sfrac|{{pi}}|3}} के लिए {{math|0}} को {{math|2{{pi}}}} लाल, पीले, हरे, सियान, नीले, से मैजेंटा तक।इन भूखंडों को प्रक्षेत्र रंग कहा जाता है।यह जानकारी खोए बिना फलनों की कल्पना करने का एक सरल तरीका प्रदान करता है।चित्र के लिए शून्य दिखाता है {{math|±1, (2 + ''i'')}} और पर ध्रुव <math>\pm \sqrt{{-2-2i}}.</math> | ||
== इतिहास == | == इतिहास == | ||
{{See also|Negative number#History}} | {{See also|Negative number#History}} | ||
एक सामान्य क्यूबिक समीकरण के एनटीएच रूट ([[ त्रिकोणमितीय कार्य ]] | एक सामान्य क्यूबिक समीकरण के एनटीएच रूट ([[ त्रिकोणमितीय कार्य | त्रिकोणमितीय]] फलनो के बिना) में समाधान, जब इसकी तीनों जड़ें वास्तविक संख्याएँ होती हैं, तो ऋणात्मक संख्याओं की वर्ग जड़ें होती हैं, एक ऐसी स्थिति जो तर्कसंगत रूट परीक्षण द्वारा सहायता प्राप्त की जा सकती है, यदिक्यूबिक इरेड्यूसिबल बहुपद है;यह तथाकथित कैसस irreducibilis (irreducible मामला) है।इस conundrum ने इतालवी गणितज्ञ [[ Gerolamo Cardano ]] को अपने Ars Magna में लगभग 1545 में सम्मिश्र संख्याओं की कल्पना करने के लिए प्रेरित किया,<ref>{{cite book|first=Morris |last= Kline|title=गणितीय विचार का इतिहास, खंड 1|page=253}}</ref> हालांकि उनकी समझ अल्पविकसित थी;इसके अतिरिक्त उन्होंने बाद में सम्मिश्र संख्याओं को सूक्ष्म रूप से खारिज कर दिया क्योंकि वे बेकार हैं।<ref>{{Cite book|last=Jurij.|first=Kovič|url=http://worldcat.org/oclc/1080410598|title=ट्रिस्टन नीडम, विजुअल कॉम्प्लेक्स एनालिसिस, ऑक्सफोर्ड यूनिवर्सिटी प्रेस इंक।, न्यूयॉर्क, 1998, 592 स्ट्रानी|oclc=1080410598}}</ref> कार्डानो ने काल्पनिक संख्याओं का उपयोग किया, लेकिन उन्हें "मानसिक यातना" के रूप में उपयोग किया गया। <ref>O’Connor and Robertson (2016), “Girolamo Cardano.”</ref> यह ग्राफिकल सम्मिश्र प्लेन के उपयोग से पहले था।कार्डानो और अन्य इतालवी गणितज्ञ, विशेष रूप से [[ स्किपिओन डेल फेरो ]], 1500 के दशक में, क्यूबिक समीकरणों को हल करने के लिए एक एल्गोरिथ्म बनाया गया था जिसमें सामान्य रूप से एक वास्तविक समाधान और दो समाधान थे जिसमें एक काल्पनिक संख्या थी।चूंकि उन्होंने काल्पनिक संख्याओं के साथ उत्तरों को नजरअंदाज कर दिया था, कार्डानो ने उन्हें बेकार पाया।<ref>Nahin, Paul J. An Imaginary Tale: The Story of √-1. Princeton: Princeton University Press, 1998.</ref> | ||
सामान्य बहुपदों की समस्या पर काम करें अंततः बीजगणित के मौलिक प्रमेय का नेतृत्व किया, जो दर्शाता है कि | सामान्य बहुपदों की समस्या पर काम करें अंततः बीजगणित के मौलिक प्रमेय का नेतृत्व किया, जो दर्शाता है कि सम्मिश्र संख्याओं के साथ, एक समाधान डिग्री एक या उच्चतर के प्रत्येक बहुपद समीकरण के लिए मौजूद है।सम्मिश्र संख्या इस प्रकार एक बीजगणितीय रूप से संवृत क्षेत्र का निर्माण करती है, जहां किसी भी बहुपद समीकरण में एक फलन की जड़ होती है। | ||
कई गणितज्ञों ने | कई गणितज्ञों ने सम्मिश्र संख्याओं के विकास में योगदान दिया।इतालवी गणितज्ञ [[ राफेल बॉम्बेली ]] द्वारा सम्मिश्र संख्याओं के जोड़, घटाव, गुणन और रूट निष्कर्षण के नियमों को विकसित किया गया था।<ref>{{cite book |last1=Katz |first1=Victor J. |title=गणित का इतिहास, संक्षिप्त संस्करण|section= 9.1.4 |publisher=[[Addison-Wesley]] |isbn=978-0-321-16193-2 |year=2004}}</ref> सम्मिश्र संख्याओं के लिए एक अधिक अमूर्त औपचारिकता को आयरिश गणितज्ञ [[ विलियम रोवन हैमिल्टन ]] द्वारा विकसित किया गया था, जिन्होंने इस अमूर्तता को चतुर्भुज के सिद्धांत तक बढ़ाया।<ref>{{cite journal |last1=Hamilton |first1=Wm. |title=काल्पनिक मात्रा की एक नई प्रजाति पर चतुर्भुज के सिद्धांत के साथ जुड़ा हुआ है|journal=Proceedings of the Royal Irish Academy |date=1844 |volume=2 |pages=424–434 |url=https://babel.hathitrust.org/cgi/pt?id=njp.32101040410779&view=1up&seq=454}}</ref> | ||
ऋणात्मक संख्याओं की चौकोर जड़ों के लिए जल्द से जल्द क्षणभंगुर संदर्भ शायद पहली शताब्दी ईस्वी में अलेक्जेंड्रिया के [[ हेलेनिस्टिक गणित ]] नायक के काम में होने के लिए कहा जा सकता है, जहां अलेक्जेंड्रिया#ग्रंथ सूची के अपने नायक में उन्होंने माना, जाहिर तौर पर गलती से, की मात्रा, की मात्रा मेंशब्द पर पहुंचने के लिए एक [[ पिरामिड ]] का एक असंभव [[ टुकड़ा ]] <math>\sqrt{81 - 144}</math> उनकी गणना में, जो आज सरल हो जाएगा <math>\sqrt{-63} = 3i\sqrt{7}</math>।ऋणात्मक मात्रा में हेलेनिस्टिक गणित में कल्पना नहीं की गई थी और नायक ने इसे केवल इसके धनात्मक द्वारा प्रतिस्थापित किया था <math>\sqrt{144 - 81} = 3\sqrt{7}.</math><ref>{{cite book |title=एक काल्पनिक कथा: द स्टोरी ऑफ़ -1|last=Nahin |first=Paul J. |year=2007 |publisher=[[Princeton University Press]] |isbn=978-0-691-12798-9 |url=http://mathforum.org/kb/thread.jspa?forumID=149&threadID=383188&messageID=1181284 |access-date=20 April 2011 |archive-url=https://web.archive.org/web/20121012090553/http://mathforum.org/kb/thread.jspa?forumID=149&threadID=383188&messageID=1181284 |archive-date=12 October 2012 |url-status=live }}</ref> | |||
अपने आप में एक विषय के रूप में | अपने आप में एक विषय के रूप में सम्मिश्र संख्याओं का अध्ययन करने के लिए प्रेरणा पहली बार 16 वीं शताब्दी में उत्पन्न हुई जब क्यूबिक समीकरण और [[ चतुर्थक समीकरण ]] बहुपद की जड़ों के लिए बीजगणितीय समाधान इतालवी गणितज्ञों द्वारा खोजे गए (निकोलो फोंटाना टार्टग्लिया, गेरोलमो कार्डो देखें) द्वारा खोजा गया था।यह जल्द ही एहसास हुआ (लेकिन बहुत बाद में साबित हुआ)<ref name=Casus/>ये सूत्र, भले ही कोई केवल वास्तविक समाधानों में रुचि रखता था, कभी -कभी ऋणात्मक संख्याओं की चौकोर जड़ों के हेरफेर की आवश्यकता होती है।एक उदाहरण के रूप में, फॉर्म के क्यूबिक समीकरण के लिए टार्टग्लिया का सूत्र {{math|''x''{{sup|3}} {{=}} ''px'' + ''q''}}{{efn|In modern notation, Tartaglia's solution is based on expanding the cube of the sum of two cube roots: <math>\left(\sqrt[3]{u} + \sqrt[3]{v}\right)^3 = 3 \sqrt[3]{uv} \left(\sqrt[3]{u} + \sqrt[3]{v}\right) + u + v</math> With <math>x = \sqrt[3]{u} + \sqrt[3]{v}</math>, <math>p = 3 \sqrt[3]{uv}</math>, <math>q = u + v</math>, {{mvar|u}} and {{mvar|v}} can be expressed in terms of {{mvar|p}} and {{mvar|q}} as <math>u = q/2 + \sqrt{(q/2)^2-(p/3)^3}</math> and <math>v = q/2 - \sqrt{(q/2)^2-(p/3)^3}</math>, respectively. Therefore, <math>x = \sqrt[3]{q/2 + \sqrt{(q/2)^2-(p/3)^3}} + \ sqrt [3] {q/2 - \ sqrt {(q/2)^2- (p/3)^3}} </math>।कब <math>(q/2)^2-(p/3)^3</math> नकारात्मक है (कैसस irreducibilis), दूसरे क्यूब रूट को पहले एक के जटिल संयुग्म के रूप में माना जाना चाहिए।}} समीकरण को समाधान देता है {{math|1=''x''<sup>3</sup> = ''x''}} जैसा | ||
<math display=block>\tfrac{1}{\sqrt{3}}\left(\left(\sqrt{-1}\right)^{1/3}+\left(\sqrt{-1}\right)^{-1/3}\right).</math> | <math display=block>\tfrac{1}{\sqrt{3}}\left(\left(\sqrt{-1}\right)^{1/3}+\left(\sqrt{-1}\right)^{-1/3}\right).</math> | ||
पहली नज़र में यह बकवास जैसा दिखता है।हालांकि, | पहली नज़र में यह बकवास जैसा दिखता है।हालांकि, सम्मिश्र संख्याओं के साथ औपचारिक गणना बताती है कि समीकरण {{math|1=''z''<sup>3</sup> = ''i''}} तीन समाधान हैं: <math>-i, \frac{\sqrt{3} + i}{2}, \frac{-\sqrt{3}+i}{2}.</math> बदले में इन्हें प्रतिस्थापित करना <math>\sqrt{-1}^{1/3}</math> Tartaglia के क्यूबिक फॉर्मूला और सरलीकरण में, एक को 0, 1 और & माइनस; 1 के समाधान के रूप में मिलता है {{math|1=''x''<sup>3</sup> − ''x'' = 0}}।बेशक इस विशेष समीकरण को दृष्टि में हल किया जा सकता है, लेकिन यह स्पष्ट करता है कि जब सामान्य सूत्रों का उपयोग वास्तविक जड़ों के साथ क्यूबिक समीकरणों को हल करने के लिए किया जाता है, तो बाद में गणितज्ञों ने कठोरता से दिखाया,{{efn|It has been proved that imaginary numbers have necessarily to appear in the cubic formula when the equation has three real, different roots by Pierre Laurent Wantzel in 1843, Vincenzo Mollame in 1890, Otto Hölder in 1891 and Adolf Kneser in 1892. Paolo Ruffini also provided an incomplete proof in 1799. — S. Confalonieri (2015)<ref name=Casus>{{cite book |title=The Unattainable Attempt to Avoid the Casus Irreducibilis for Cubic Equations: Gerolamo Cardano's De Regula Aliza |first=Sara |last=Confalonieri |publisher=Springer |year=2015 |pages=15–16 (note 26) |isbn=978-3658092757 }}</ref>}} सम्मिश्र संख्याओं के कैसस ireducibilis का उपयोग।राफेल बॉम्बेली क्यूबिक समीकरणों के इन प्रतीत होने वाले विरोधाभासी समाधानों को स्पष्ट रूप से संबोधित करने वाले पहले व्यक्ति थे और इन मुद्दों को हल करने के लिए सम्मिश्र अंकगणित के लिए नियमों को विकसित किया। | ||
इन मात्राओं के लिए काल्पनिक शब्द 1637 में रेने डेसकार्टेस द्वारा गढ़ा गया था, जो उनके अवास्तविक प्रकृति पर जोर देने के लिए दर्द में था<ref>{{cite book |title=ला गोमेट्री {{पाइप}} पहले संस्करण के एक चेहरे के साथ रेने डेसकार्टेस की ज्यामिति|last=Descartes |first=René |author-link=René Descartes |year=1954 |orig-year=1637 |publisher=[[Dover Publications]] |isbn=978-0-486-60068-0 |url=https://archive.org/details/geometryofrenede00rend |access-date=20 April 2011 }}</ref> | इन मात्राओं के लिए काल्पनिक शब्द 1637 में रेने डेसकार्टेस द्वारा गढ़ा गया था, जो उनके अवास्तविक प्रकृति पर जोर देने के लिए दर्द में था<ref>{{cite book |title=ला गोमेट्री {{पाइप}} पहले संस्करण के एक चेहरे के साथ रेने डेसकार्टेस की ज्यामिति|last=Descartes |first=René |author-link=René Descartes |year=1954 |orig-year=1637 |publisher=[[Dover Publications]] |isbn=978-0-486-60068-0 |url=https://archive.org/details/geometryofrenede00rend |access-date=20 April 2011 }}</ref> | ||
{{blockquote|... sometimes only imaginary, that is one can imagine as many as I said in each equation, but sometimes there exists no quantity that matches that which we imagine.<br/> | {{blockquote|... sometimes only imaginary, that is one can imagine as many as I said in each equation, but sometimes there exists no quantity that matches that which we imagine.<br/> | ||
[''... quelquefois seulement imaginaires c'est-à-dire que l'on peut toujours en imaginer autant que j'ai dit en chaque équation, mais qu'il n'y a quelquefois aucune quantité qui corresponde à celle qu'on imagine.'']}} | [''... quelquefois seulement imaginaires c'est-à-dire que l'on peut toujours en imaginer autant que j'ai dit en chaque équation, mais qu'il n'y a quelquefois aucune quantité qui corresponde à celle qu'on imagine.'']}} | ||
भ्रम का एक और स्रोत यह था कि समीकरण <math>\sqrt{-1}^2 = \sqrt{-1}\sqrt{-1} = -1</math> बीजीय पहचान के साथ असंगत रूप से असंगत लग रहा था <math>\sqrt{a}\sqrt{b} = \sqrt{ab}</math>, जो गैर- | भ्रम का एक और स्रोत यह था कि समीकरण <math>\sqrt{-1}^2 = \sqrt{-1}\sqrt{-1} = -1</math> बीजीय पहचान के साथ असंगत रूप से असंगत लग रहा था <math>\sqrt{a}\sqrt{b} = \sqrt{ab}</math>, जो गैर-ऋणात्मक वास्तविक संख्याओं के लिए मान्य है {{mvar|a}} और {{mvar|b}}, और जो एक के साथ सम्मिश्र संख्या गणना में भी उपयोग किया गया था {{mvar|a}}, {{mvar|b}} धनात्मक और दूसरा ऋणात्मक।इस पहचान का गलत उपयोग (और संबंधित पहचान <math display=inline>\frac{1}{\sqrt{a}} = \sqrt{\frac{1}{a}}</math>) स्थिति में जब दोनों {{mvar|a}} और {{mvar|b}} ऋणात्मक भी बेडविल्ड [[ लियोनहार्ड यूलर ]] हैं।इस कठिनाई ने अंततः विशेष प्रतीक का उपयोग करने के सम्मेलन को जन्म दिया {{math|''i''}} की जगह में <math>\sqrt{-1}</math> इस गलती से बचाने के लिए।{{Citation needed|date=April 2011}} फिर भी, यूलर ने आज की तुलना में छात्रों को सम्मिश्र संख्याओं से परिचित कराना स्वाभाविक माना।अपनी प्राथमिक बीजगणित पाठ्य पुस्तक, तत्वों के तत्वों में, वह इन नंबरों का परिचय लगभग एक बार में करता है और फिर उन्हें प्राकृतिक तरीके से उपयोग करता है। | ||
18 वीं & nbsp; सेंचुरी | 18 वीं & nbsp; सेंचुरी सम्मिश्र संख्याओं में व्यापक उपयोग प्राप्त हुआ, क्योंकि यह देखा गया था कि त्रिकोणमितीय फलनों से जुड़े गणनाओं को सरल बनाने के लिए सम्मिश्र अभिव्यक्तियों के औपचारिक हेरफेर का उपयोग किया जा सकता है।उदाहरण के लिए, 1730 में [[ अब्राहम डे मोइवर ]] ने उल्लेख किया कि उस कोण के त्रिकोणमितीय फलनों की शक्तियों के लिए एक कोण के एक कोण के त्रिकोणमितीय फलनों से संबंधित पहचान को निम्नलिखित डी मोइवर के सूत्र द्वारा फिर से व्यक्त किया जा सकता है: | ||
<math display=block>(\cos \theta + i\sin \theta)^{n} = \cos n \theta + i\sin n \theta. </math> | <math display=block>(\cos \theta + i\sin \theta)^{n} = \cos n \theta + i\sin n \theta. </math> | ||
1748 में, यूलर ने आगे बढ़कर यूलर के | 1748 में, यूलर ने आगे बढ़कर यूलर के सम्मिश्र विश्लेषण का सूत्र प्राप्त किया:<ref>{{cite book |last1=Euler |first1=Leonard |title=विश्लेषण का परिचय|trans-title=Introduction to the Analysis of the Infinite |date=1748 |publisher=Marc Michel Bosquet & Co. |location=Lucerne, Switzerland |volume=1 |page=104 |url=https://books.google.com/books?id=jQ1bAAAAQAAJ&pg=PA104 |language=la}}</ref> | ||
<math display=block>\cos \theta + i\sin \theta = e ^{i\theta } </math> | <math display=block>\cos \theta + i\sin \theta = e ^{i\theta } </math> | ||
औपचारिक रूप से | औपचारिक रूप से सम्मिश्र बिजली श्रृंखला में हेरफेर करके और देखा गया कि इस सूत्र का उपयोग किसी भी त्रिकोणमितीय पहचान को कम करने के लिए बहुत सरल घातीय पहचान को कम करने के लिए किया जा सकता है। | ||
सम्मिश्र समतल (#complex विमान) में एक बिंदु के रूप में एक सम्मिश्र संख्या का विचार पहली बार [[ डेनमार्क ]] [[ नॉर्वे ]] [[ गणितज्ञ ]] [[ कैस्पर वेसल ]] द्वारा 1799 में वर्णित किया गया था,<ref>{{cite journal |last1=Wessel |first1=Caspar |title=दिशा के विश्लेषणात्मक पदनाम के बारे में, एक वर्तमान, विमान और गोलाकार बहुभुज के उद्घाटन के लिए समझदार है|journal=Nye Samling af det Kongelige Danske Videnskabernes Selskabs Skrifter [New Collection of the Writings of the Royal Danish Science Society] |date=1799 |volume=5 |pages=469–518 |url=https://babel.hathitrust.org/cgi/pt?id=ien.35556000979690&view=1up&seq=527 |trans-title=On the analytic representation of direction, an effort applied in particular to the determination of plane and spherical polygons |language=da}}</ref> हालांकि यह जॉन वालिस में 1685 की शुरुआत में अनुमानित था। वालिस ए ट्रीट ऑफ बीजगणित।<ref>{{cite book |last=Wallis |first=John |date=1685 |title=बीजगणित का एक ग्रंथ, ऐतिहासिक और व्यावहारिक दोनों ...|url=https://echo.mpiwg-berlin.mpg.de/ECHOdocuView?url=/permanent/library/H3GRV5AU/pageimg&start=291&mode=imagepath&pn=291|location=London, England |publisher=printed by John Playford, for Richard Davis |pages=264–273 }}</ref> | |||
वेसेल का संस्मरण [[ कोपेनहेगन एकेडमी ]] की कार्यवाही में दिखाई दिया, लेकिन काफी हद तक किसी का ध्यान नहीं गया।1806 में जीन-रॉबर्ट आर्गंड ने स्वतंत्र रूप से | वेसेल का संस्मरण [[ कोपेनहेगन एकेडमी ]] की कार्यवाही में दिखाई दिया, लेकिन काफी हद तक किसी का ध्यान नहीं गया।1806 में जीन-रॉबर्ट आर्गंड ने स्वतंत्र रूप से सम्मिश्र संख्याओं पर एक पैम्फलेट जारी किया और बीजगणित#इतिहास के मौलिक प्रमेय का एक कठोर प्रमाण प्रदान किया।<ref>{{cite book |last1=Argand |title=ज्यामितीय निर्माणों में काल्पनिक मात्रा का प्रतिनिधित्व करने के तरीके पर निबंध|trans-title=Essay on a way to represent complex quantities by geometric constructions |date=1806 |publisher=Madame Veuve Blanc |location=Paris, France |url=http://www.bibnum.education.fr/mathematiques/geometrie/essai-sur-une-maniere-de-representer-des-quantites-imaginaires-dans-les-cons |language=fr}}</ref> [[ कार्ल फ्रेडरिक गॉस ]] ने पहले 1797 में प्रमेय का एक अनिवार्य रूप से [[ टोपोलॉजी | सांस्थिति]] प्रूफ प्रकाशित किया था, लेकिन उस समय अपने संदेह को व्यक्त किया था, जो कि & माइनस के वर्गमूल के सही तत्वमीमांसा के बारे में है।<ref>Gauss, Carl Friedrich (1799) [https://books.google.com/books?id=g3VaAAAAcAAJ&pg=PP1#v=onepage&q&f=fals ''"Demonstratio nova theorematis omnem functionem algebraicam rationalem integram unius variabilis in factores reales primi vel secundi gradus resolvi posse."''] [New proof of the theorem that any rational integral algebraic function of a single variable can be resolved into real factors of the first or second degree.] Ph.D. thesis, University of Helmstedt, (Germany). (in Latin)</ref> यह 1831 तक नहीं था कि उन्होंने इन संदेहों को पार कर लिया और विमान में बिंदुओं के रूप में सम्मिश्र संख्याओं पर अपने ग्रंथ को प्रकाशित किया,<ref name=Ewald>{{cite book |last=Ewald |first=William B. |date=1996 |title=कांत से हिल्बर्ट: गणित की नींव में एक स्रोत पुस्तक|volume=1 |page=313 |publisher=Oxford University Press |isbn=9780198505358|url=https://books.google.com/books?id=rykSDAAAQBAJ&pg=PA313 |access-date=18 March 2020}}</ref> बड़े पैमाने पर आधुनिक संकेतन और शब्दावली की स्थापना:{{sfn|Gauss|1831|p=638}} | ||
<clockquote> यदि किसी ने पूर्व में इस विषय पर झूठे दृष्टिकोण से चिंतन किया था और इसलिए एक रहस्यमय अंधकार पाया गया, तो यह बड़े हिस्से में अनाड़ी शब्दावली के लिए जिम्मेदार है।एक को +1, -1 नहीं कहा गया था, <math>\sqrt{-1}</math> | <clockquote> यदि किसी ने पूर्व में इस विषय पर झूठे दृष्टिकोण से चिंतन किया था और इसलिए एक रहस्यमय अंधकार पाया गया, तो यह बड़े हिस्से में अनाड़ी शब्दावली के लिए जिम्मेदार है।एक को +1, -1 नहीं कहा गया था, <math>\sqrt{-1}</math> धनात्मक, ऋणात्मक, या काल्पनिक (या असंभव) इकाइयाँ, लेकिन इसके अतिरिक्त, कहते हैं, प्रत्यक्ष, उलटा, या पार्श्व इकाइयाँ, तो इस तरह के अंधेरे की बात कर सकते थे। | ||
19 वीं शताब्दी की शुरुआत में, अन्य गणितज्ञों ने स्वतंत्र रूप से | 19 वीं शताब्दी की शुरुआत में, अन्य गणितज्ञों ने स्वतंत्र रूप से सम्मिश्र संख्याओं के ज्यामितीय प्रतिनिधित्व की खोज की: बुई,<ref>{{cite web| url = https://mathshistory.st-andrews.ac.uk/Biographies/Buee/| title = एड्रियन क्वेंटिन फॉग (1745-1845): मैक्ट्यूएटर}} </fr><ref>{{cite journal |last1=Buée |title=काल्पनिक मात्रा पर स्मृति|journal=Philosophical Transactions of the Royal Society of London |date=1806 |volume=96 |pages=23–88 |doi=10.1098/rstl.1806.0003 |s2cid=110394048 |url=https://royalsocietypublishing.org/doi/pdf/10.1098/rstl.1806.0003 |trans-title=Memoir on imaginary quantities |language=fr}}</ref> सी। वी। मौरी,<ref>{{cite book |last1=Mourey |first1=C.V. |title=नकारात्मक मात्रा और कथित काल्पनिक मात्रा का सच्चा सिद्धांत|trans-title=The true theory of negative quantities and of alleged imaginary quantities |date=1861 |publisher=Mallet-Bachelier |location=Paris, France |url=https://archive.org/details/bub_gb_8YxKAAAAYAAJ |language=fr}} 1861 reprint of 1828 original.</ref> [[ जॉन वॉरेन (गणितज्ञ) ]],<ref>{{cite book |last1=Warren |first1=John |title=नकारात्मक मात्रा के वर्ग जड़ों के ज्यामितीय प्रतिनिधित्व पर एक ग्रंथ|date=1828 |publisher=Cambridge University Press |location=Cambridge, England |url=https://archive.org/details/treatiseongeomet00warrrich}}</ref><ref>{{cite journal |last1=Warren |first1=John |title=नकारात्मक मात्रा की वर्ग जड़ों के ज्यामितीय प्रतिनिधित्व के खिलाफ उठाए गए आपत्तियों पर विचार|journal=Philosophical Transactions of the Royal Society of London |date=1829 |volume=119 |pages=241–254 |s2cid=186211638 |doi=10.1098/rstl.1829.0022 |doi-access=free }}</ref><ref>{{cite journal |last1=Warren |first1=John |title=मात्रा की शक्तियों के ज्यामितीय प्रतिनिधित्व पर, जिनके सूचकांक में नकारात्मक संख्याओं की वर्ग जड़ें शामिल हैं|journal=Philosophical Transactions of the Royal Society of London |date=1829 |volume=119 |pages=339–359 |s2cid=125699726 |doi=10.1098/rstl.1829.0031 |doi-access=free }}</ref> Jacques Frédéric Français | फ्रेंच और उनके भाई, [[ राइट बेल्वाइटिस ]]<ref>{{cite journal |last1=Français |first1=J.F. |title=स्थिति ज्यामिति के नए सिद्धांत, और काल्पनिक प्रतीकों की ज्यामितीय व्याख्या|journal=Annales des mathématiques pures et appliquées |date=1813 |volume=4 |pages=61–71 |url=https://babel.hathitrust.org/cgi/pt?id=uc1.$c126478&view=1up&seq=69 |trans-title=New principles of the geometry of position, and geometric interpretation of complex [number] symbols |language=fr}}</ref><ref>{{cite book |title=दो संस्कृतियाँ|editor= Kim Williams |last1=Caparrini |first1=Sandro |chapter=On the Common Origin of Some of the Works on the Geometrical Interpretation of Complex Numbers |year=2000 |publisher=Birkhäuser |isbn=978-3-7643-7186-9 |page=139 |url=https://books.google.com/books?id=voFsJ1EhCnYC |chapter-url=https://books.google.com/books?id=voFsJ1EhCnYC&pg=PA139}}</ref> | ||
अंग्रेजी गणितज्ञ जी.एच.हार्डी ने टिप्पणी की कि गॉस 'वास्तव में आत्मविश्वास और वैज्ञानिक तरीके' में | अंग्रेजी गणितज्ञ जी.एच.हार्डी ने टिप्पणी की कि गॉस 'वास्तव में आत्मविश्वास और वैज्ञानिक तरीके' में सम्मिश्र संख्याओं का उपयोग करने वाले पहले गणितज्ञ थे, हालांकि नॉर्वे [[ नील्स हेनरिक एबेल ]] और [[ कार्ल गुस्ताव जैकब जैकोबी ]] जैसे गणितज्ञों ने गॉस को 1831 ग्रंथ प्रकाशित करने से पहले उन्हें नियमित रूप से उपयोग किया था।<ref>{{cite book |title=संख्याओं के सिद्धांत का परिचय|last1=Hardy |first1=G.H. |last2=Wright |first2=E.M. |year=2000 |orig-year=1938 |publisher=[[Oxford University Press|OUP Oxford]] |isbn= 978-0-19-921986-5 |page=189 (fourth edition)}}</ref> | ||
[[ ऑगस्टिन-लुइस कॉची ]] और [[ बर्नहार्ड रीमैन ]] ने एक साथ #Complex विश्लेषण के मौलिक विचारों को पूरा करने की एक उच्च स्थिति में लाया, जो कि कॉची के | [[ ऑगस्टिन-लुइस कॉची ]] और [[ बर्नहार्ड रीमैन ]] ने एक साथ #Complex विश्लेषण के मौलिक विचारों को पूरा करने की एक उच्च स्थिति में लाया, जो कि कॉची के स्थिति में 1825 के आसपास शुरू हुआ। | ||
सिद्धांत में उपयोग किए जाने वाले सामान्य शब्द मुख्य रूप से संस्थापकों के कारण हैं।अर्गंड को बुलाया {{math|cos ''φ'' + ''i'' sin ''φ''}} दिशा कारक, और <math>r = \sqrt{a^2 + b^2}</math> मापांक;{{efn| {{harvnb|Argand|1814|p=204}} defines the modulus of a complex number but he doesn't name it:<br/>''"Dans ce qui suit, les accens, indifféremment placés, seront employés pour indiquer la grandeur absolue des quantités qu'ils affectent; ainsi, si <math>a = m + n\sqrt{-1}</math>, <math>m</math> et <math>n</math> étant réels, on devra entendre que <math>a_'</math> ou <math>a' = \sqrt{m^2 + n^2}</math>."''<br/>[In what follows, accent marks, wherever they're placed, will be used to indicate the absolute size of the quantities to which they're assigned; thus if <math>a = m + n\sqrt{-1}</math>, <math>m</math> and <math>n</math> being real, one should understand that <math>a_'</math> or <math>a' = \sqrt{m^2 + n^2}</math>.]<br/> | सिद्धांत में उपयोग किए जाने वाले सामान्य शब्द मुख्य रूप से संस्थापकों के कारण हैं।अर्गंड को बुलाया {{math|cos ''φ'' + ''i'' sin ''φ''}} दिशा कारक, और <math>r = \sqrt{a^2 + b^2}</math> मापांक;{{efn| {{harvnb|Argand|1814|p=204}} defines the modulus of a complex number but he doesn't name it:<br/>''"Dans ce qui suit, les accens, indifféremment placés, seront employés pour indiquer la grandeur absolue des quantités qu'ils affectent; ainsi, si <math>a = m + n\sqrt{-1}</math>, <math>m</math> et <math>n</math> étant réels, on devra entendre que <math>a_'</math> ou <math>a' = \sqrt{m^2 + n^2}</math>."''<br/>[In what follows, accent marks, wherever they're placed, will be used to indicate the absolute size of the quantities to which they're assigned; thus if <math>a = m + n\sqrt{-1}</math>, <math>m</math> and <math>n</math> being real, one should understand that <math>a_'</math> or <math>a' = \sqrt{m^2 + n^2}</math>.]<br/> | ||
{{harvnb|Argand|1814|p=208}} defines and names the ''module'' and the ''direction factor'' of a complex number: ''"... <math>a = \sqrt{m^2 + n^2}</math> pourrait être appelé le ''module'' de <math>a + b \sqrt{-1}</math>, et représenterait la ''grandeur absolue'' de la ligne <math>a + b \sqrt{-1}</math>, tandis que l'autre facteur, dont le module est l'unité, en représenterait la direction."''<br/>[... <math>a = \sqrt{m^2 + n^2}</math> could be called the ''module'' of <math>a + b \sqrt{-1}</math> and would represent the ''absolute size'' of the line <math>a + b \sqrt{-1}\,,</math> (Note that Argand represented complex numbers as vectors.) whereas the other factor [namely, <math>\tfrac{a}{\sqrt{a^2 + b^2}} + \ tfrac {b} {\ sqrt {a^2 + b^2}} \ sqrt {-1} </math>], जिसका मॉड्यूल एकता है [1], इसकी दिशा का प्रतिनिधित्व करेगा।]}}}}}}}}}}}}}}}}}}}}}}}}}}}<ref>{{cite web |author=Jeff Miller |date=Sep 21, 1999 |title=मापांक|url=http://members.aol.com/jeff570/m.html|archive-url=https://web.archive.org/web/19991003034827/http://members.aol.com/jeff570/m.html |work=Earliest Known Uses of Some of the Words of Mathematics (M) |archive-date=1999-10-03 |url-status=usurped}}</ref> Cauchy (1821) को बुलाया {{math|cos ''φ'' + ''i'' sin ''φ''}} कम रूप (कम अभिव्यक्ति)<ref>{{cite book |last=Cauchy |first=Augustin-Louis |date=1821 |title=रॉयल पॉलिटेक्निक स्कूल का विश्लेषण पाठ्यक्रम|url=https://archive.org/details/coursdanalysede00caucgoog/page/n209/mode/2up |location=Paris, France |publisher=L'Imprimerie Royale |volume=1 |page=183 |language=fr }}</ref> और जाहिरा तौर पर शब्द तर्क पेश किया;गॉस का इस्तेमाल किया {{math|''i''}} के लिए <math>\sqrt{-1}</math>,{{efn| Gauss writes:<ref>{{harvnb|Gauss|1831|p=96}}</ref>''"Quemadmodum scilicet arithmetica sublimior in quaestionibus hactenus pertractatis inter solos numeros integros reales versatur, ita theoremata circa residua biquadratica tunc tantum in summa simplicitate ac genuina venustate resplendent, quando campus arithmeticae ad quantitates ''imaginarias'' extenditur, ita ut absque restrictione ipsius obiectum constituant numeri formae ''a + bi'', denotantibus ''i'', pro more quantitatem imaginariam <math>\sqrt{-1}</math>, atque ''a, b'' indefinite omnes numeros reales integros inter -<math>\infty</math> et +<math>\infty</math>."'' [Of course just as the higher arithmetic has been investigated so far in problems only among real integer numbers, so theorems regarding biquadratic residues then shine in greatest simplicity and genuine beauty, when the field of arithmetic is extended to ''imaginary'' quantities, so that, without restrictions on it, numbers of the form ''a + bi'' — ''i'' denoting by convention the imaginary quantity <math>\sqrt{-1}</math>, and the variables ''a, b'' [denoting] all real integer numbers between <math>-\infty</math> and <math>+\infty</math> — constitute an object.]}} के लिए | {{harvnb|Argand|1814|p=208}} defines and names the ''module'' and the ''direction factor'' of a complex number: ''"... <math>a = \sqrt{m^2 + n^2}</math> pourrait être appelé le ''module'' de <math>a + b \sqrt{-1}</math>, et représenterait la ''grandeur absolue'' de la ligne <math>a + b \sqrt{-1}</math>, tandis que l'autre facteur, dont le module est l'unité, en représenterait la direction."''<br/>[... <math>a = \sqrt{m^2 + n^2}</math> could be called the ''module'' of <math>a + b \sqrt{-1}</math> and would represent the ''absolute size'' of the line <math>a + b \sqrt{-1}\,,</math> (Note that Argand represented complex numbers as vectors.) whereas the other factor [namely, <math>\tfrac{a}{\sqrt{a^2 + b^2}} + \ tfrac {b} {\ sqrt {a^2 + b^2}} \ sqrt {-1} </math>], जिसका मॉड्यूल एकता है [1], इसकी दिशा का प्रतिनिधित्व करेगा।]}}}}}}}}}}}}}}}}}}}}}}}}}}}<ref>{{cite web |author=Jeff Miller |date=Sep 21, 1999 |title=मापांक|url=http://members.aol.com/jeff570/m.html|archive-url=https://web.archive.org/web/19991003034827/http://members.aol.com/jeff570/m.html |work=Earliest Known Uses of Some of the Words of Mathematics (M) |archive-date=1999-10-03 |url-status=usurped}}</ref> Cauchy (1821) को बुलाया {{math|cos ''φ'' + ''i'' sin ''φ''}} कम रूप (कम अभिव्यक्ति)<ref>{{cite book |last=Cauchy |first=Augustin-Louis |date=1821 |title=रॉयल पॉलिटेक्निक स्कूल का विश्लेषण पाठ्यक्रम|url=https://archive.org/details/coursdanalysede00caucgoog/page/n209/mode/2up |location=Paris, France |publisher=L'Imprimerie Royale |volume=1 |page=183 |language=fr }}</ref> और जाहिरा तौर पर शब्द तर्क पेश किया;गॉस का इस्तेमाल किया {{math|''i''}} के लिए <math>\sqrt{-1}</math>,{{efn| Gauss writes:<ref>{{harvnb|Gauss|1831|p=96}}</ref>''"Quemadmodum scilicet arithmetica sublimior in quaestionibus hactenus pertractatis inter solos numeros integros reales versatur, ita theoremata circa residua biquadratica tunc tantum in summa simplicitate ac genuina venustate resplendent, quando campus arithmeticae ad quantitates ''imaginarias'' extenditur, ita ut absque restrictione ipsius obiectum constituant numeri formae ''a + bi'', denotantibus ''i'', pro more quantitatem imaginariam <math>\sqrt{-1}</math>, atque ''a, b'' indefinite omnes numeros reales integros inter -<math>\infty</math> et +<math>\infty</math>."'' [Of course just as the higher arithmetic has been investigated so far in problems only among real integer numbers, so theorems regarding biquadratic residues then shine in greatest simplicity and genuine beauty, when the field of arithmetic is extended to ''imaginary'' quantities, so that, without restrictions on it, numbers of the form ''a + bi'' — ''i'' denoting by convention the imaginary quantity <math>\sqrt{-1}</math>, and the variables ''a, b'' [denoting] all real integer numbers between <math>-\infty</math> and <math>+\infty</math> — constitute an object.]}} के लिए सम्मिश्र संख्या शब्द का परिचय दिया {{math|''a'' + ''bi''}},{{efn|Gauss:<ref>{{harvnb|Gauss|1831|p=96}}</ref>''"Tales numeros vocabimus numeros integros complexos, ita quidem, ut reales complexis non opponantur, sed tamquam species sub his contineri censeantur."'' [We will call such numbers [namely, numbers of the form ''a + bi'' ] "complex integer numbers", so that real [numbers] are regarded not as the opposite of complex [numbers] but [as] a type [of number that] is, so to speak, contained within them.]}} और कहा जाता है {{math|''a''<sup>2</sup> + ''b''<sup>2</sup>}} नियम।{{efn|Gauss:<ref>{{harvnb|Gauss|1831|p=98}}</ref> ''"Productum numeri complexi per numerum ipsi conjunctum utriusque ''normam'' vocamus. Pro norma itaque numeri realis, ipsius quadratum habendum est."'' [We call a "norm" the product of a complex number [e.g,. ''a + ib'' ] with its conjugate [''a - ib'' ]. Therefore the square of a real number should be regarded as its norm.]}} अभिव्यक्ति दिशा गुणांक, प्रायः के लिए उपयोग किया जाता है {{math|cos ''φ'' + ''i'' sin ''φ''}}, हैनकेल (1867) के कारण है,<ref>{{cite book |last=Hankel |first=Hermann |date=1867 |title=जटिल संख्याओं और उनके कार्यों के बारे में व्याख्यान|trans-title=Lectures About the Complex Numbers and Their Functions |url=https://books.google.com/books?id=754KAAAAYAAJ&pg=PA71 |location=Leipzig, [Germany] |publisher=Leopold Voss |volume=1 |page=71 |language=de }} From p. 71: ''"Wir werden den Factor (''cos'' φ + i ''sin'' φ) haüfig den ''Richtungscoefficienten'' nennen."'' (We will often call the factor (cos φ + i sin φ) the "coefficient of direction".)</ref> और निरपेक्ष मूल्य, मापांक के लिए, वीरस्ट्रास के कारण है। | ||
बाद में सामान्य सिद्धांत पर शास्त्रीय लेखकों में [[ रिचर्ड डेडेकिंड ]], ओटो होल्डर, [[ फेलिक्स क्लेन ]], हेनरी पोइंकेरे, [[ हरमन श्वार्ज़ ]], [[ कार्ल वीमर स्ट्रैस ]] और कई अन्य | बाद में सामान्य सिद्धांत पर शास्त्रीय लेखकों में [[ रिचर्ड डेडेकिंड ]], ओटो होल्डर, [[ फेलिक्स क्लेन ]], हेनरी पोइंकेरे, [[ हरमन श्वार्ज़ ]], [[ कार्ल वीमर स्ट्रैस ]] और कई अन्य सम्मिलित हैं।20 वीं शताब्दी की शुरुआत में सम्मिश्र बहुभिन्नरूपी पथरी में महत्वपूर्ण फलन (एक व्यवस्थित सहित) शुरू किया गया है।1927 में [[ विल्हेम वर्टिंगर ]] द्वारा महत्वपूर्ण परिणाम प्राप्त किए गए हैं। | ||
== संबंध और संचालन == | == संबंध और संचालन == | ||
=== समानता === | === समानता === | ||
सम्मिश्र संख्याओं में वास्तविक संख्याओं की समानता की एक समान परिभाषा है;दो सम्मिश्र संख्याएँ {{math|''a''<sub>1</sub> + ''b''<sub>1</sub>''i''}} और {{math|''a''<sub>2</sub> + ''b''<sub>2</sub>''i''}} समान हैं यदि और केवल अगर उनके वास्तविक और काल्पनिक दोनों भाग समान हैं, तो, अर्थात् यदि {{math|1=''a''<sub>1</sub> = ''a''<sub>2</sub>}} और {{math|1=''b''<sub>1</sub> = ''b''<sub>2</sub>}}।[[ ध्रुवीय रूप ]] में लिखी नॉनज़ेरो सम्मिश्र नंबर समान हैं यदि और केवल अगर उनके पास समान परिमाण है और उनके तर्क एक पूर्णांक से भिन्न होते हैं {{math|2''π''}}। | |||
=== आदेश === | === आदेश === | ||
वास्तविक संख्याओं के विपरीत, | वास्तविक संख्याओं के विपरीत, सम्मिश्र संख्याओं का कोई प्राकृतिक क्रम नहीं है।विशेष रूप से, सम्मिश्र संख्याओं पर कोई [[ रैखिक आदेश ]] नहीं है जो जोड़ और गुणन के साथ संगत है।इसलिए, सम्मिश्र संख्याओं में एक क्रमित क्षेत्र की संरचना नहीं होती है।इसके लिए एक स्पष्टीकरण यह है कि एक क्रमित क्षेत्र में वर्गों का प्रत्येक गैर-तुच्छ राशि#nontrivialsquaresum nonzero है, और {{math|1=''i''<sup>2</sup> + 1<sup>2</sup> = 0}} वर्गों का एक गैर-तुच्छ योग है।इस प्रकार, सम्मिश्र संख्याओं को स्वाभाविक रूप से दो-आयामी विमान पर मौजूदा माना जाता है। | ||
=== संयुग्म === | === संयुग्म === | ||
{{See also|Complex conjugate}} | {{See also|Complex conjugate}} | ||
[[File:Complex conjugate picture.svg|right|thumb|upright=0.8|ज्यामितीय प्रतिनिधित्व {{mvar|z}} और इसके संयुग्म {{mvar|{{overline|z}}}} | [[File:Complex conjugate picture.svg|right|thumb|upright=0.8|ज्यामितीय प्रतिनिधित्व {{mvar|z}} और इसके संयुग्म {{mvar|{{overline|z}}}} सम्मिश्र समतल में]]सम्मिश्र संख्या का सम्मिश्र संयुग्म {{math|1=''z'' = ''x'' + ''yi''}} द्वारा दिया गया है {{math|''x'' − ''yi''}}।इसे या तो निरूपित किया गया है {{mvar|{{overline|z}}}} या {{math|''z''*}}.<ref>For the former notation, see {{harvnb|Apostol|1981|pp=15–16}}</ref> सम्मिश्र संख्याओं पर यह अनियमित संचालन केवल उनके बुनियादी संचालन जोड़, घटाव, गुणन और विभाजन को प्रयुक्त करके व्यक्त नहीं किया जा सकता है। | ||
ज्यामितीय रूप से, {{mvar|{{overline|z}}}} प्रतिबिंब समरूपता है |प्रतिबिंब {{mvar|z}} असली अक्ष के बारे में।दो बार संयुग्मन मूल | ज्यामितीय रूप से, {{mvar|{{overline|z}}}} प्रतिबिंब समरूपता है |प्रतिबिंब {{mvar|z}} असली अक्ष के बारे में।दो बार संयुग्मन मूल सम्मिश्र संख्या देता है | ||
<math display=block>\overline{\overline{z}}=z,</math> | <math display=block>\overline{\overline{z}}=z,</math> | ||
जो इस | जो इस संक्रिया को एक इनवोल्यूशन (गणित) बनाता है।प्रतिबिंब वास्तविक भाग और परिमाण दोनों को छोड़ देता है {{mvar|z}} अपरिवर्तित, वह है | ||
<math display=block>\operatorname{Re}(\overline{z}) = \operatorname{Re}(z)\quad</math> और <math>\quad |\overline{z}| = |z|.</math> | <math display=block>\operatorname{Re}(\overline{z}) = \operatorname{Re}(z)\quad</math> और <math>\quad |\overline{z}| = |z|.</math> | ||
काल्पनिक | काल्पनिक भाग और एक सम्मिश्र संख्या का तर्क {{mvar|z}} संयुग्मन के तहत उनके संकेत को बदलें | ||
<math display=block>\operatorname{Im}(\overline{z}) = -\operatorname{Im}(z)\quad \text{ and } \quad \operatorname{arg} \overline{z} \equiv -\operatorname{arg} z \pmod {2\pi}.</math> | <math display=block>\operatorname{Im}(\overline{z}) = -\operatorname{Im}(z)\quad \text{ and } \quad \operatorname{arg} \overline{z} \equiv -\operatorname{arg} z \pmod {2\pi}.</math> | ||
तर्क और परिमाण के विवरण के लिए, #Polar फॉर्म पर अनुभाग देखें। | तर्क और परिमाण के विवरण के लिए, #Polar फॉर्म पर अनुभाग देखें। | ||
एक | एक सम्मिश्र संख्या का उत्पाद {{math|''z'' {{=}} ''x'' + ''yi''}} और इसके संयुग्म को [[ निरपेक्ष वर्ग ]] के रूप में जाना जाता है।यह हमेशा एक गैर-ऋणात्मक वास्तविक संख्या होती है और प्रत्येक के परिमाण के वर्ग के बराबर होती है: | ||
<math display=block>z\cdot \overline{z} = x^2 + y^2 = |z|^2 = |\overline{z}|^2.</math> | <math display=block>z\cdot \overline{z} = x^2 + y^2 = |z|^2 = |\overline{z}|^2.</math> | ||
इस संपत्ति का उपयोग एक | इस संपत्ति का उपयोग एक सम्मिश्र भाजक के साथ एक अंश को परिवर्तित करने के लिए किया जा सकता है, जो दिए गए भाजक के संयुग्म द्वारा अंश के अंश और भाजक दोनों का विस्तार करके एक वास्तविक भाजक के साथ एक समान अंश में होता है।इस प्रक्रिया को कभी -कभी भाजक का युक्तिकरण (गणित) कहा जाता है (हालांकि अंतिम अभिव्यक्ति में भाजक एक तर्कहीन वास्तविक संख्या हो सकती है), क्योंकि यह एक भाजक में सरल अभिव्यक्तियों से जड़ों को हटाने के लिए विधि जैसा दिखता है। | ||
एक | एक सम्मिश्र संख्या के वास्तविक और काल्पनिक भागों {{mvar|z}} संयुग्मन का उपयोग करके निकाला जा सकता है: | ||
<math display=block>\operatorname{Re}(z) = \dfrac{z+\overline{z}}{2},\quad \text{ and } \quad \operatorname{Im}(z) = \dfrac{z-\overline{z}}{2i}.</math> | <math display=block>\operatorname{Re}(z) = \dfrac{z+\overline{z}}{2},\quad \text{ and } \quad \operatorname{Im}(z) = \dfrac{z-\overline{z}}{2i}.</math> | ||
इसके | इसके अतिरिक्त, एक सम्मिश्र संख्या वास्तविक है यदि और केवल अगर यह अपने स्वयं के संयुग्म के बराबर है। | ||
संयुग्मन मूल | संयुग्मन मूल सम्मिश्र अंकगणितीय संचालन पर वितरित करता है: | ||
<math display=block>\begin{align} | <math display=block>\begin{align} | ||
\overline{z\pm w} &= \overline{z} \pm \overline{w}, \\ | \overline{z\pm w} &= \overline{z} \pm \overline{w}, \\ | ||
| Line 185: | Line 180: | ||
\overline{z/w} &= \overline{z}/\overline{w}. | \overline{z/w} &= \overline{z}/\overline{w}. | ||
\end{align}</math> | \end{align}</math> | ||
संयुग्मन भी व्युत्क्रम ज्यामिति में नियोजित किया जाता है, ज्यामिति की एक शाखा एक लाइन के बारे में अधिक सामान्य प्रतिबिंबों का अध्ययन करती है।[[ नेटवर्क विश्लेषण ]] (विद्युत सर्किट) में, | संयुग्मन भी व्युत्क्रम ज्यामिति में नियोजित किया जाता है, ज्यामिति की एक शाखा एक लाइन के बारे में अधिक सामान्य प्रतिबिंबों का अध्ययन करती है।[[ नेटवर्क विश्लेषण ]] (विद्युत सर्किट) में, सम्मिश्र संयुग्म का उपयोग समकक्ष प्रतिबाधा को खोजने में किया जाता है जब अधिकतम पावर ट्रांसफर प्रमेय के लिए देखा जाता है। | ||
=== जोड़ और घटाव === | === जोड़ और घटाव === | ||
[[File:Vector Addition.svg|right|thumb|दो | [[File:Vector Addition.svg|right|thumb|समांतर चतुर्भुज की रचना करके दो सम्मिश्र संख्याओं का योग ज्यामितीय रूप से किया जा सकता है।]]दो सम्मिश्र संख्याएँ <math>a =x+yi</math> और <math>b =u+vi</math> अपने वास्तविक और काल्पनिक भागों को अलग से जोड़कर सबसे आसानी से जोड़ रहे हैं।अर्थात: | ||
<math display=block>a + b =(x+yi) + (u+vi) = (x+u) + (y+v)i.</math> | <math display=block>a + b =(x+yi) + (u+vi) = (x+u) + (y+v)i.</math> | ||
इसी तरह, [[ घटाव ]] किया जा सकता है | इसी तरह, [[ घटाव ]] किया जा सकता है | ||
<math display=block>a - b =(x+yi) - (u+vi) = (x-u) + (y-v)i.</math> | <math display=block>a - b =(x+yi) - (u+vi) = (x-u) + (y-v)i.</math> | ||
एक | एक सम्मिश्र संख्या का गुणन <math>a =x+yi</math> और एक वास्तविक संख्या {{mvar|r}} अलग से गुणा करके समान रूप से किया जा सकता है {{mvar|r}} और के वास्तविक और काल्पनिक भागों {{mvar|a}}: | ||
<math display=block>ra=r(x+yi) = rx + ryi.</math> | <math display=block>ra=r(x+yi) = rx + ryi.</math> | ||
विशेष रूप से, घटाव को [[ वियोजक ]] को नकारकर किया जा सकता है (जो इसे गुणा कर रहा है {{math|–1}}) और परिणाम को [[ minuend ]] में जोड़ना: | विशेष रूप से, घटाव को [[ वियोजक ]] को नकारकर किया जा सकता है (जो इसे गुणा कर रहा है {{math|–1}}) और परिणाम को [[ minuend ]] में जोड़ना: | ||
<math display=block>a - b =a + (-1)\,b.</math> | <math display=block>a - b =a + (-1)\,b.</math> | ||
सम्मिश्र समतल में सम्मिश्र संख्याओं के दृश्य का उपयोग करते हुए, इसके अतिरिक्त निम्नलिखित ज्यामितीय व्याख्या है: दो सम्मिश्र संख्याओं का योग {{mvar|a}} और {{mvar|b}}, सम्मिश्र समतल में बिंदुओं के रूप में व्याख्या की गई, तीन वर्टिस से एक [[ समानांतर चतुर्भुज ]] का निर्माण करके प्राप्त बिंदु है {{mvar|O}}, और लेबल वाले तीरों के बिंदु {{mvar|a}} और {{mvar|b}} (परंतु कि वे एक लाइन पर न हों)।समान रूप से, इन बिंदुओं को कॉल करना {{mvar|A}}, {{mvar|B}}, क्रमशः और समांतर चतुर्भुज का चौथा बिंदु {{mvar|X}} [[ त्रिकोण ]] {{mvar|OAB}} और {{mvar|XBA}} [[ बधाई (ज्यामिति) ]] हैं। | |||
=== गुणा और वर्ग{{anchor|Multiplication|Square}}=== | === गुणा और वर्ग{{anchor|Multiplication|Square}}=== | ||
वितरण संपत्ति के नियम, [[ क्रमचयी गुणधर्म ]] (इसके | वितरण संपत्ति के नियम, [[ क्रमचयी गुणधर्म ]] (इसके अतिरिक्त और गुणा), और परिभाषित संपत्ति {{math|1=''i''{{sup|2}} = −1}} सम्मिश्र संख्याओं पर प्रयुक्त करें।यह इस प्रकार है कि | ||
<math display=block>(x+yi)\, (u+vi)= (xu - yv) + (xv + yu)i.</math> | |||
विशेष रूप से, | विशेष रूप से, | ||
<math display=block>(x+yi)^2=x^2-y^2 + 2xyi.</math> | <math display=block>(x+yi)^2=x^2-y^2 + 2xyi.</math> | ||
| Line 207: | Line 202: | ||
=== पारस्परिक और विभाजन === | === पारस्परिक और विभाजन === | ||
संयुग्मन का उपयोग करते हुए, एक नॉनज़ेरो | संयुग्मन का उपयोग करते हुए, एक नॉनज़ेरो सम्मिश्र संख्या का गुणक उलटा {{math|1=''z'' = ''x'' + ''yi''}} हमेशा के लिए टूट सकता है | ||
<math display=block>\frac{1}{z}=\frac{\overline{z}}{z \overline{z}} = \frac{\overline{z}}{|z|^2}=\frac{\overline{z}}{x^2+y^2}=\frac{x}{x^2+y^2} -\frac{y}{x^2+y^2}i,</math> | <math display=block>\frac{1}{z}=\frac{\overline{z}}{z \overline{z}} = \frac{\overline{z}}{|z|^2}=\frac{\overline{z}}{x^2+y^2}=\frac{x}{x^2+y^2} -\frac{y}{x^2+y^2}i,</math> | ||
चूंकि गैर-शून्य का अर्थ है कि {{math|''x''{{sup|2}} + ''y''{{sup|2}}}} शून्य से अधिक है। | चूंकि गैर-शून्य का अर्थ है कि {{math|''x''{{sup|2}} + ''y''{{sup|2}}}} शून्य से अधिक है। | ||
इसका उपयोग एक मनमाना | इसका उपयोग एक मनमाना सम्मिश्र संख्या के एक विभाजन को व्यक्त करने के लिए किया जा सकता है {{math|''w'' {{=}} ''u'' + ''vi''}} एक गैर-शून्य सम्मिश्र संख्या द्वारा {{mvar|z}} जैसा | ||
<math display=block>\frac {w}{z}= w\cdot \frac {1}{z}= (u+vi)\cdot \left(\frac{x}{x^2+y^2} -\frac{y}{x^2+y^2}i\right)= \frac{(ux+vy)+(vx-uy)i} {x^2+y^2}.</math> | <math display=block>\frac {w}{z}= w\cdot \frac {1}{z}= (u+vi)\cdot \left(\frac{x}{x^2+y^2} -\frac{y}{x^2+y^2}i\right)= \frac{(ux+vy)+(vx-uy)i} {x^2+y^2}.</math> | ||
=== गुणा और ध्रुवीय रूप में विभाजन === | === गुणा और ध्रुवीय रूप में विभाजन === | ||
[[File:Complex multi.svg|right|thumb | [[File:Complex multi.svg|right|thumb|2 + i (नीला त्रिभुज) और 3 + i (लाल त्रिभुज) का गुणन। लाल त्रिकोण को नीले त्रिकोण के शीर्ष से मिलाने के लिए घुमाया जाता है (समीकरण में φ1+φ2 के संदर्भ में दोनों कोणों को जोड़कर) और नीले त्रिकोण के कर्ण की लंबाई तक बढ़ाया जाता है(समीकरण में r1r2 पद के अनुसार दोनों त्रिज्याओं का गुणन)।]]गुणन, विभाजन और घातांक के लिए सूत्र कार्टेशियन निर्देशांक में संबंधित सूत्रों की तुलना में ध्रुवीय रूप में सरल हैं।दो सम्मिश्र संख्याओं को देखते हुए {{math|1=''z''<sub>1</sub> = ''r''<sub>1</sub>(cos ''φ''<sub>1</sub> + ''i'' sin ''φ''<sub>1</sub>)}} और {{math|1=''z''<sub>2</sub> = ''r''<sub>2</sub>(cos ''φ''<sub>2</sub> + ''i'' sin ''φ''<sub>2</sub>)}}, [[ त्रिकोणमितीय पहचान ]] के कारण | ||
<math display=block>\begin{alignat}{4} | <math display=block>\begin{alignat}{4} | ||
\cos a \cos b & - \sin a \sin b & {}={} & \cos(a + b) \\ | \cos a \cos b & - \sin a \sin b & {}={} & \cos(a + b) \\ | ||
| Line 228: | Line 223: | ||
चूंकि वास्तविक और काल्पनिक भाग {{math|5 + 5''i''}} समान हैं, उस संख्या का तर्क 45 डिग्री है, या {{math|''π''/4}} (रेडियन में)।दूसरी ओर, यह लाल और नीले रंग के त्रिकोणों की उत्पत्ति में कोणों का योग भी है, क्रमशः [[ आर्कटान ]] (1/3) और आर्कटान (1/2) हैं।इस प्रकार, सूत्र | चूंकि वास्तविक और काल्पनिक भाग {{math|5 + 5''i''}} समान हैं, उस संख्या का तर्क 45 डिग्री है, या {{math|''π''/4}} (रेडियन में)।दूसरी ओर, यह लाल और नीले रंग के त्रिकोणों की उत्पत्ति में कोणों का योग भी है, क्रमशः [[ आर्कटान ]] (1/3) और आर्कटान (1/2) हैं।इस प्रकार, सूत्र | ||
<math display=block>\frac{\pi}{4} = \arctan\left(\frac{1}{2}\right) + \arctan\left(\frac{1}{3}\right) </math> | <math display=block>\frac{\pi}{4} = \arctan\left(\frac{1}{2}\right) + \arctan\left(\frac{1}{3}\right) </math> | ||
होल्ड्स।जैसा कि आर्कटैन | होल्ड्स।जैसा कि आर्कटैन फलन को अत्यधिक कुशलता से अनुमानित किया जा सकता है, इस तरह के सूत्र-माचिन-जैसे सूत्र के रूप में जाना जाता है-का उपयोग पीआई के उच्च-परिशुद्ध सन्निकटन के लिए किया जाता है।{{pi}}। | ||
इसी तरह, विभाजन द्वारा दिया जाता है | इसी तरह, विभाजन द्वारा दिया जाता है | ||
| Line 242: | Line 237: | ||
<math display=block>\delta = (\sgn b)\sqrt{\frac{-a + \sqrt{a^2 + b^2}}{2}},</math> | <math display=block>\delta = (\sgn b)\sqrt{\frac{-a + \sqrt{a^2 + b^2}}{2}},</math> | ||
कहां {{math|sgn}} [[ हस्ताक्षर समारोह ]] | कहां {{math|sgn}} [[ हस्ताक्षर समारोह | हस्ताक्षर फलन]] फलन है।यह वर्ग द्वारा देखा जा सकता है <math> \pm (\gamma + \delta i)</math> प्राप्त करने के लिए {{math|''a'' + ''bi''}}.<ref>{{cite book | ||
|title=सूत्र, रेखांकन और गणितीय तालिकाओं के साथ गणितीय कार्यों की हैंडबुक|first1=Milton | |title=सूत्र, रेखांकन और गणितीय तालिकाओं के साथ गणितीय कार्यों की हैंडबुक|first1=Milton | ||
|last1=Abramowitz | |last1=Abramowitz | ||
| Line 268: | Line 263: | ||
|archive-date=24 April 2016 | |archive-date=24 April 2016 | ||
|url-status=live | |url-status=live | ||
}}, [https://books.google.com/books?id=lUcTsYopfhkC&pg=PA59 Extract: page 59] {{Webarchive|url=https://web.archive.org/web/20160423183239/https://books.google.com/books?id=lUcTsYopfhkC&pg=PA59 |date=23 April 2016 }}</ref> यहां <math>\sqrt{a^2 + b^2}</math> का निरपेक्ष मूल्य कहा जाता है {{math|''a'' + ''bi''}}, और वर्गमूल रूट चिन्ह गैर- | }}, [https://books.google.com/books?id=lUcTsYopfhkC&pg=PA59 Extract: page 59] {{Webarchive|url=https://web.archive.org/web/20160423183239/https://books.google.com/books?id=lUcTsYopfhkC&pg=PA59 |date=23 April 2016 }}</ref> यहां <math>\sqrt{a^2 + b^2}</math> का निरपेक्ष मूल्य कहा जाता है {{math|''a'' + ''bi''}}, और वर्गमूल रूट चिन्ह गैर-ऋणात्मक वास्तविक भाग के साथ वर्गमूल को इंगित करता है, जिसे प्रिंसिपल वर्गमूल कहा जाता है;भी <math>\sqrt{a^2 + b^2}= \sqrt{z\overline{z}},</math> कहां {{math|''z'' {{=}} ''a'' + ''bi''}}.{{sfn|Ahlfors|1979|p=3}} | ||
=== घातीय | === घातीय फलन === | ||
घातीय | घातीय फलन <math>\exp \colon \Complex \to \Complex ; z \mapsto \exp z </math> हर सम्मिश्र संख्या के लिए परिभाषित किया जा सकता है {{mvar|z}} पावर सीरीज़ द्वारा | ||
<math display=block>\exp z= \sum_{n=0}^\infty \frac {z^n}{n!},</math> | <math display=block>\exp z= \sum_{n=0}^\infty \frac {z^n}{n!},</math> | ||
जिसमें अभिसरण का एक अनंत त्रिज्या है। | जिसमें अभिसरण का एक अनंत त्रिज्या है। | ||
पर मूल्य {{math|1}} घातीय | पर मूल्य {{math|1}} घातीय फलन यूलर की संख्या है | ||
<math display=block>e = \exp 1 = \sum_{n=0}^\infty \frac1{n!}\approx 2.71828.</math> | <math display=block>e = \exp 1 = \sum_{n=0}^\infty \frac1{n!}\approx 2.71828.</math> | ||
यदि {{mvar|z}} असली है, एक है | यदि {{mvar|z}} असली है, एक है | ||
<math>\exp z=e^z.</math> | <math>\exp z=e^z.</math> | ||
[[ विश्लेषणात्मक निरंतरता ]] इस समानता को हर | [[ विश्लेषणात्मक निरंतरता ]] इस समानता को हर सम्मिश्र मूल्य के लिए बढ़ाने की स्वीकृति देती है {{mvar|z}}, और इस प्रकार आधार के साथ सम्मिश्र घातांक को परिभाषित करने के लिए {{mvar|e}} जैसा | ||
<math display=block>e^z=\exp z.</math> | <math display=block>e^z=\exp z.</math> | ||
==== [[ कार्यात्मक समीकरण ]] ==== | ==== [[ कार्यात्मक समीकरण ]] ==== | ||
घातीय | घातीय फलन कार्यात्मक समीकरण को संतुष्ट करता है <math>e^{z+t}=e^ze^t.</math> | ||
यह या तो दोनों सदस्यों के बिजली श्रृंखला विस्तार की तुलना करके या समीकरण के प्रतिबंध से वास्तविक तर्कों के लिए विश्लेषणात्मक निरंतरता को | यह या तो दोनों सदस्यों के बिजली श्रृंखला विस्तार की तुलना करके या समीकरण के प्रतिबंध से वास्तविक तर्कों के लिए विश्लेषणात्मक निरंतरता को प्रयुक्त करके साबित किया जा सकता है। | ||
==== यूलर का सूत्र ==== | ==== यूलर का सूत्र ==== | ||
| Line 293: | Line 288: | ||
कार्यात्मक समीकरण का अर्थ है कि, अगर {{mvar|x}} और {{mvar|y}} असली हैं, एक है | कार्यात्मक समीकरण का अर्थ है कि, अगर {{mvar|x}} और {{mvar|y}} असली हैं, एक है | ||
<math display=block>e^{x+iy} = e^x(\cos y + i\sin y) = e^x \cos y + i e^x \sin y ,</math> | <math display=block>e^{x+iy} = e^x(\cos y + i\sin y) = e^x \cos y + i e^x \sin y ,</math> | ||
जो अपने वास्तविक और काल्पनिक भागों में घातीय | जो अपने वास्तविक और काल्पनिक भागों में घातीय फलन का अपघटन है। | ||
=== | === सम्मिश्र लघुगणक === | ||
वास्तविक | वास्तविक स्थिति में, [[ प्राकृतिक ]] लघुगणक को उलटा फलन के रूप में परिभाषित किया जा सकता है | ||
<math>\ln \colon \R^+ \to \R ; x \mapsto \ln x </math> घातीय | <math>\ln \colon \R^+ \to \R ; x \mapsto \ln x </math> घातीय फलन की।इसे सम्मिश्र प्रक्षेत्र में विस्तारित करने के लिए, कोई भी यूलर के सूत्र से शुरू कर सकता है।इसका तात्पर्य है कि, यदि एक सम्मिश्र संख्या <math>z\in \Complex^\times</math> ध्रुवीय रूप में लिखा गया है | ||
<math display=block> z = r(\cos \varphi + i\sin \varphi )</math> | <math display=block> z = r(\cos \varphi + i\sin \varphi )</math> | ||
साथ <math>r, \varphi \in \R ,</math> फिर से | साथ <math>r, \varphi \in \R ,</math> फिर से | ||
<math display=block> \ln z = \ln r + i \varphi </math> | <math display=block> \ln z = \ln r + i \varphi </math> | ||
के रूप में [[ जटिल लघुगणक ]] एक | के रूप में [[ जटिल लघुगणक | सम्मिश्र लघुगणक]] एक उपयुक्त व्युत्क्रम है: | ||
<math display=block> \exp \ln z = \exp(\ln r + i \varphi ) = r \exp i \varphi = r(\cos \varphi + i\sin \varphi ) = z .</math> | <math display=block> \exp \ln z = \exp(\ln r + i \varphi ) = r \exp i \varphi = r(\cos \varphi + i\sin \varphi ) = z .</math> | ||
हालांकि, क्योंकि कोसाइन और साइन आवधिक | हालांकि, क्योंकि कोसाइन और साइन आवधिक फलन हैं, एक पूर्णांक के अतिरिक्त कई {{math|2''π''}} को {{mvar|φ}} नहीं बदलता {{mvar|z}}।उदाहरण के लिए, {{math|1=''e''{{sup|''iπ''}} = ''e''{{sup|3''iπ''}} = −1}} , तो दोनों {{mvar|iπ}} और {{math|3''iπ''}} के प्राकृतिक लघुगणक के लिए संभव मान हैं {{math|−1}}। | ||
इसलिए, यदि | इसलिए, यदि सम्मिश्र लघुगणक को एक बहुउद्देशीय फलन के रूप में परिभाषित नहीं किया जाना है | ||
<math display=block> \ln z = \left\{ \ln r + i (\varphi + 2\pi k) \mid k \in \Z \right\},</math> | <math display=block> \ln z = \left\{ \ln r + i (\varphi + 2\pi k) \mid k \in \Z \right\},</math> | ||
एक को एक शाखा कट का उपयोग करना होगा और [[ संहितात्मक ]] को प्रतिबंधित करना होगा, जिसके परिणामस्वरूप द्विध्रुवीय | एक को एक शाखा कट का उपयोग करना होगा और [[ संहितात्मक ]] को प्रतिबंधित करना होगा, जिसके परिणामस्वरूप द्विध्रुवीय फलन होता है | ||
<math display=block>\ln \colon \; \Complex^\times \; \to \; \; \; \R^+ + \; i \, \left(-\pi, \pi\right] .</math> | <math display=block>\ln \colon \; \Complex^\times \; \to \; \; \; \R^+ + \; i \, \left(-\pi, \pi\right] .</math> | ||
यदि <math>z \in \Complex \setminus \left( -\R_{\ge 0} \right)</math> एक गैर-पॉजिटिव वास्तविक संख्या (एक | यदि <math>z \in \Complex \setminus \left( -\R_{\ge 0} \right)</math> एक गैर-पॉजिटिव वास्तविक संख्या (एक धनात्मक या एक गैर-वास्तविक संख्या) नहीं है, सम्मिश्र लघुगणक का परिणामी प्रमुख मूल्य प्राप्त होता है {{math|−''π'' < ''φ'' < ''π''}}।यह ऋणात्मक वास्तविक संख्याओं के बाहर एक [[ विश्लेषणात्मक कार्य | विश्लेषणात्मक फलन]] है, लेकिन इसे एक ऐसे फलन के लिए लम्बा नहीं किया जा सकता है जो किसी भी ऋणात्मक वास्तविक संख्या पर निरंतर है <math>z \in -\R^+ </math>, जहां प्रमुख मूल्य है {{math|1=ln ''z'' = ln(−''z'') + ''iπ''}}.{{efn|However for another inverse function of the complex exponential function (and not the above defined principal value), the branch cut could be taken at any other [[Line (geometry)#Ray|ray]] thru the origin.}} | ||
=== एक्सपोनेंटेशन === | === एक्सपोनेंटेशन === | ||
यदि {{math|''x'' > 0}} असली है और {{mvar|z}} | यदि {{math|''x'' > 0}} असली है और {{mvar|z}} सम्मिश्र, प्रतिपादक को परिभाषित किया गया है | ||
<math display=block>x^z=e^{z\ln x},</math> | |||
कहां {{math|ln}} प्राकृतिक लघुगणक को दर्शाता है। | कहां {{math|ln}} प्राकृतिक लघुगणक को दर्शाता है। | ||
इस सूत्र को | इस सूत्र को सम्मिश्र मूल्यों तक बढ़ाना स्वाभाविक लगता है {{mvar|x}}, लेकिन इस तथ्य के परिणामस्वरूप कुछ कठिनाइयाँ हैं कि सम्मिश्र लघुगणक वास्तव में एक फलन नहीं है, बल्कि एक बहुस्तरीय फलन है। | ||
यह इस प्रकार है कि अगर {{mvar|z}} ऊपर है, और अगर {{mvar|t}} एक और | यह इस प्रकार है कि अगर {{mvar|z}} ऊपर है, और अगर {{mvar|t}} एक और सम्मिश्र संख्या है, तो घातांक बहुवर्धित फलन है | ||
<math display=block>z^t=\left\{e^{t\ln r}\,(\cos(\varphi t+ 2 \pi kt)+i\sin(\varphi t+ 2 \pi kt))\}\mid k\in \mathbb Z\right\}</math> | <math display=block>z^t=\left\{e^{t\ln r}\,(\cos(\varphi t+ 2 \pi kt)+i\sin(\varphi t+ 2 \pi kt))\}\mid k\in \mathbb Z\right\}</math> | ||
| Line 330: | Line 325: | ||
{{mvar|n}} }} nth रूट |{{mvar|n}}एक जटिल संख्या की जड़ें {{mvar|z}} द्वारा दिए गए हैं | {{mvar|n}} }} nth रूट |{{mvar|n}}एक जटिल संख्या की जड़ें {{mvar|z}} द्वारा दिए गए हैं | ||
<math display=block>z^{1/n} = \sqrt[n]r \left( \cos \left(\frac{\varphi+2k\pi}{n}\right) + i \sin \left(\frac{\varphi+2k\pi}{n}\right)\right)</math> | <math display=block>z^{1/n} = \sqrt[n]r \left( \cos \left(\frac{\varphi+2k\pi}{n}\right) + i \sin \left(\frac{\varphi+2k\pi}{n}\right)\right)</math> | ||
के लिए {{math|0 ≤ ''k'' ≤ ''n'' − 1}}।(यहां <math>\sqrt[n]r</math> सामान्य ( | के लिए {{math|0 ≤ ''k'' ≤ ''n'' − 1}}।(यहां <math>\sqrt[n]r</math> सामान्य (धनात्मक) है {{mvar|n}}धनात्मक वास्तविक संख्या की जड़ {{mvar|r}}।) क्योंकि साइन और कोसाइन आवधिक हैं, अन्य पूर्णांक मान {{mvar|k}} अन्य मूल्य न दें। | ||
जबकि {{mvar|n}}एक | जबकि {{mvar|n}}एक धनात्मक वास्तविक संख्या की जड़ {{mvar|r}} धनात्मक वास्तविक संख्या होने के लिए चुना जाता है {{mvar|c}} संतुष्टि देने वाला {{math|1=''c''<sup>''n''</sup> = ''r''}}, एक विशेष परिसर को अलग करने का कोई प्राकृतिक तरीका नहीं है {{mvar|n}}एक सम्मिश्र संख्या की जड़।इसलिए {{mvar|n}}रूट एक बहुस्तरीय फलन है |{{mvar|n}}का फलन फलन {{mvar|z}}।इसका तात्पर्य है कि, धनात्मक वास्तविक संख्या के स्थिति के विपरीत, एक है | ||
<math display=block>(z^n)^{1/n} \ne z,</math> | |||
चूंकि बाएं हाथ की ओर होता है {{mvar|n}} मान, और दाहिने हाथ की ओर एक ही मूल्य है। | चूंकि बाएं हाथ की ओर होता है {{mvar|n}} मान, और दाहिने हाथ की ओर एक ही मूल्य है। | ||
| Line 339: | Line 334: | ||
=== क्षेत्र संरचना === | === क्षेत्र संरचना === | ||
सेट <math>\Complex</math> | सेट <math>\Complex</math> सम्मिश्र संख्याओं में से एक क्षेत्र (गणित) है।{{sfn|Apostol|1981|pp=15–16}} संक्षेप में, इसका तात्पर्य है कि निम्नलिखित तथ्य हैं: सबसे पहले, किसी भी दो सम्मिश्र संख्याओं को जोड़ा जा सकता है और एक और सम्मिश्र संख्या प्राप्त करने के लिए गुणा किया जा सकता है।दूसरा, किसी भी सम्मिश्र संख्या के लिए {{mvar|z}}, इसके योज्य उलटा {{math|–''z''}} एक सम्मिश्र संख्या भी है;और तीसरा, प्रत्येक नॉनज़ेरो सम्मिश्र संख्या में एक गुणक उलटा सम्मिश्र संख्या होती है।इसके अतिरिक्त, ये संक्रिया कई नियमो को संतुष्ट करते हैं, उदाहरण के लिए किसी भी दो सम्मिश्र संख्याओं के लिए जोड़ और गुणन की [[ संबद्धता ]] का नियम {{math|''z''<sub>1</sub>}} और {{math|''z''<sub>2</sub>}}: | ||
<math display=block>\begin{align} | <math display=block>\begin{align} | ||
z_1 + z_2 & = z_2 + z_1 ,\\ | z_1 + z_2 & = z_2 + z_1 ,\\ | ||
z_1 z_2 & = z_2 z_1 . | z_1 z_2 & = z_2 z_1 . | ||
\end{align}</math> | \end{align}</math> | ||
इन दो | इन दो नियमो और एक क्षेत्र पर अन्य आवश्यकताओं को ऊपर दिए गए सूत्रों द्वारा सिद्ध किया जा सकता है, इस तथ्य का उपयोग करते हुए कि वास्तविक संख्या स्वयं एक क्षेत्र का निर्माण करती है। | ||
रियल के विपरीत, <math>\Complex</math> एक [[ आदेशित क्षेत्र ]] नहीं है, यह कहना है, किसी संबंध को परिभाषित करना संभव नहीं है {{math|''z''<sub>1</sub> < ''z''<sub>2</sub>}} यह जोड़ और गुणन के साथ संगत है।वास्तव में, किसी भी | रियल के विपरीत, <math>\Complex</math> एक [[ आदेशित क्षेत्र | क्रमित क्षेत्र]] नहीं है, यह कहना है, किसी संबंध को परिभाषित करना संभव नहीं है {{math|''z''<sub>1</sub> < ''z''<sub>2</sub>}} यह जोड़ और गुणन के साथ संगत है।वास्तव में, किसी भी क्रमित क्षेत्र में, किसी भी तत्व का वर्ग आवश्यक रूप से धनात्मक है, इसलिए {{math|1=''i''<sup>2</sup> = −1}} [[ कुल आदेश ]] के अस्तित्व को रोकता है <math>\Complex.</math>{{sfn|Apostol|1981|p=25}} जब गणितीय विषय या निर्माण के लिए अंतर्निहित क्षेत्र सम्मिश्र संख्याओं का क्षेत्र होता है, तो विषय का नाम सामान्य रूप से उस तथ्य को प्रतिबिंबित करने के लिए संशोधित किया जाता है।उदाहरण के लिए: सम्मिश्र विश्लेषण, सम्मिश्र [[ मैट्रिक्स (गणित) | आव्यूह (गणित)]] , सम्मिश्र बहुपद और सम्मिश्र [[ झूठ बीजगणित ]]। | ||
जब गणितीय विषय या निर्माण के लिए अंतर्निहित क्षेत्र | |||
=== बहुपद समीकरणों का समाधान === | === बहुपद समीकरणों का समाधान === | ||
किसी भी | किसी भी सम्मिश्र संख्या (गुणांक कहा जाता है) को देखते हुए {{math|''a''<sub>0</sub>, ..., ''a''<sub>''n''</sub>}}, समीकरण | ||
<math display=block>a_n z^n + \dotsb + a_1 z + a_0 = 0</math> | <math display=block>a_n z^n + \dotsb + a_1 z + a_0 = 0</math> | ||
कम से कम एक | कम से कम एक सम्मिश्र समाधान z है, परंतु कि कम से कम उच्च गुणांक में से एक {{math|''a''<sub>1</sub>, ..., ''a''<sub>''n''</sub>}} नॉनज़ेरो है। <रेफ का नाम = बोरबकी 1998 लोकेल = .viiii.1 /> यह कार्ल फ्रेडरिक गॉस और जीन ले रोंड डी'एलबर्ट के बीजगणित के मौलिक प्रमेय का कथन है। इस तथ्य के कारण, <math>\Complex</math> एक बीजगणितीय रूप से संवृत क्षेत्र कहा जाता है।यह संपत्ति [[ तर्कसंगत संख्या ]] के लिए नहीं है <math>\Q</math> (बहुपद {{math|''x''<sup>2</sup> − 2}} एक तर्कसंगत जड़ नहीं है, चूंकि वर्गमूल 2 का वर्गमूल नहीं है। ration2 एक तर्कसंगत संख्या नहीं है) और न ही वास्तविक संख्या <math>\R</math> (बहुपद {{math|''x''<sup>2</sup> + ''a''}} के लिए एक वास्तविक जड़ नहीं है {{math|''a'' > 0}}के बाद से {{mvar|x}} किसी भी वास्तविक संख्या के लिए धनात्मक है {{mvar|x}})। | ||
इस प्रमेय के विभिन्न प्रमाण हैं, या तो एनालिटिक तरीकों जैसे कि लिउविले के प्रमेय ( | इस प्रमेय के विभिन्न प्रमाण हैं, या तो एनालिटिक तरीकों जैसे कि लिउविले के प्रमेय (सम्मिश्र विश्लेषण) | लिउविले के प्रमेय, या सांस्थिति जैसे कि [[ घुमावदार संख्या ]], या एक प्रमाण जो गैलोइस सिद्धांत और इस तथ्य को जोड़ते हैं कि विषम डिग्री का कोई वास्तविक बहुपद हैकम से कम एक वास्तविक जड़। | ||
इस तथ्य के कारण, किसी भी बीजगणितीय रूप से | इस तथ्य के कारण, किसी भी बीजगणितीय रूप से संवृत क्षेत्र के लिए धारण करने वाले प्रमेय प्रयुक्त होते हैं <math>\Complex.</math> उदाहरण के लिए, किसी भी गैर-खाली सम्मिश्र [[ वर्ग मैट्रिक्स | वर्ग आव्यूह]] में कम से कम एक (सम्मिश्र) [[ eigenvalue ]] होता है। | ||
=== बीजीय लक्षण वर्णन === | === बीजीय लक्षण वर्णन === | ||
फील्ड <math>\Complex</math> निम्नलिखित तीन गुण हैं: | फील्ड <math>\Complex</math> निम्नलिखित तीन गुण हैं: | ||
* सबसे पहले, इसकी विशेषता [[ (बीजगणित) ]] 0. है। इसका | * सबसे पहले, इसकी विशेषता [[ (बीजगणित) ]] 0. है। इसका तात्पर्य है कि {{math|1=1 + 1 + ⋯ + 1 ≠ 0}} किसी भी संख्या के लिए (जो सभी के बराबर)। | ||
* दूसरा, इसकी पारगमन की डिग्री खत्म हो गई <math>\Q</math>का मुख्य क्षेत्र <math>\Complex,</math> सातत्य की कार्डिनैलिटी है। | * दूसरा, इसकी पारगमन की डिग्री खत्म हो गई <math>\Q</math>का मुख्य क्षेत्र <math>\Complex,</math> सातत्य की कार्डिनैलिटी है। | ||
* तीसरा, यह बीजगणितीय रूप से | * तीसरा, यह बीजगणितीय रूप से संवृत है (ऊपर देखें)। | ||
यह दिखाया जा सकता है कि इन गुणों वाले किसी भी क्षेत्र में [[ आइसोमॉर्फिक ]] (एक क्षेत्र के रूप में) है <math>\Complex.</math> उदाहरण के लिए, क्षेत्र का बीजगणितीय | यह दिखाया जा सकता है कि इन गुणों वाले किसी भी क्षेत्र में [[ आइसोमॉर्फिक | सममितीय]] (एक क्षेत्र के रूप में) है <math>\Complex.</math> उदाहरण के लिए, क्षेत्र का बीजगणितीय संवृत <math>\Q_p</math> पी-एडिक नंबर का |{{mvar|p}}-एक संख्या भी इन तीन गुणों को संतुष्ट करती है, इसलिए ये दो क्षेत्र सममितीय हैं (क्षेत्र के रूप में, लेकिन संस्थानिक क्षेत्र के रूप में नहीं)।<ref>{{cite book | ||
| last = Marker | first = David | | last = Marker | first = David | ||
| editor1-last = Marker | editor1-first = D. | | editor1-last = Marker | editor1-first = D. | ||
| Line 376: | Line 370: | ||
| series = Lecture Notes in Logic | | series = Lecture Notes in Logic | ||
| title = फ़ील्ड का मॉडल सिद्धांत| volume = 5 | | title = फ़ील्ड का मॉडल सिद्धांत| volume = 5 | ||
| year = 1996}}</ref> भी, <math>\Complex</math> | | year = 1996}}</ref> भी, <math>\Complex</math> सम्मिश्र [[ पुइज़क्स श्रृंखला ]] के क्षेत्र के लिए समरूपीय है।हालांकि, एक आइसोमोर्फिज्म को निर्दिष्ट करने के लिए पसंद के स्वयंसिद्ध की आवश्यकता होती है।इस बीजीय लक्षण वर्णन का एक और परिणाम यह है कि <math>\Complex</math> कई उपयुक्त उपक्षेत्र सम्मिलित हैं जो समरूपीय हैं <math>\Complex</math>। | ||
=== एक | === एक संस्थानिक क्षेत्र के रूप में विशेषता === | ||
के पूर्ववर्ती लक्षण वर्णन <math>\Complex</math> के केवल बीजीय | के पूर्ववर्ती लक्षण वर्णन <math>\Complex</math> के केवल बीजीय स्वरूपों का वर्णन करता है <math>\Complex.</math> यह कहना है, [[ पड़ोस (टोपोलॉजी) | पड़ोस (सांस्थिति)]] और [[ निरंतरता (टोपोलॉजी) | निरंतरता (सांस्थिति)]] के गुण, जो [[ गणितीय विश्लेषण ]] और सांस्थिति जैसे क्षेत्रों में मायने रखते हैं, से निपटा नहीं जाता है।का निम्नलिखित विवरण <math>\Complex</math> एक [[ सामयिक अंगूठी | सामयिक वलय]] के रूप में (अर्थात, एक क्षेत्र जो एक [[ सामयिक स्थान | सामयिक समष्टि]] से लैस है, जो अभिसरण की धारणा की स्वीकृति देता है) संस्थानिक गुणों को ध्यान में रखता है। <math>\Complex</math> एक उप-समुच्चय होता है {{math|''P''}} (अर्थात् धनात्मक वास्तविक संख्याओं कासमुच्चय) नॉनज़ेरो तत्वों के निम्नलिखित तीन स्थितियों को संतुष्ट करते हुए: | ||
* {{math|''P''}} इसके | * {{math|''P''}} इसके अतिरिक्त संवृत है, गुणन और इनवर्स लेना। | ||
* यदि {{mvar|x}} और {{mvar|y}} के अलग -अलग तत्व हैं {{math|''P''}}, तो कोई {{math|''x'' − ''y''}} या {{math|''y'' − ''x''}} में है {{math|''P''}}। | * यदि {{mvar|x}} और {{mvar|y}} के अलग -अलग तत्व हैं {{math|''P''}}, तो कोई {{math|''x'' − ''y''}} या {{math|''y'' − ''x''}} में है {{math|''P''}}। | ||
* यदि {{mvar|S}} का कोई गैर -रिक्त | * यदि {{mvar|S}} का कोई गैर -रिक्त उप-समुच्चय है {{math|''P''}}, तब {{math|1=''S'' + ''P'' = ''x'' + ''P''}} कुछ के लिए {{mvar|x}} में <math>\Complex.</math> | ||
इसके अतिरिक्त, <math>\Complex</math> एक nontrivial invention (गणित) [[ स्वचालितता ]] है {{math|''x'' ↦ ''x''*}} (अर्थात् | इसके अतिरिक्त, <math>\Complex</math> एक nontrivial invention (गणित) [[ स्वचालितता ]] है {{math|''x'' ↦ ''x''*}} (अर्थात् सम्मिश्र संयुग्मन), जैसे कि {{math|''x x''*}} में है {{math|''P''}} किसी भी नॉनज़ेरो के लिए {{mvar|x}} में <math>\Complex.</math> | ||
किसी भी क्षेत्र {{mvar|F}} इन गुणों के साथ सेटों को ले जाकर | किसी भी क्षेत्र {{mvar|F}} इन गुणों के साथ सेटों को ले जाकर सांस्थिति के साथ संपन्न किया जा सकता है {{math|1= ''B''(''x'', ''p'') = { ''y'' {{!}} ''p'' − (''y'' − ''x'')(''y'' − ''x'')* ∈ ''P'' } }} एक [[ आधार (टोपोलॉजी) | आधार (सांस्थिति)]] के रूप में, जहां {{mvar|x}} मैदान पर और {{mvar|p}} पर्वतमाला {{math|''P''}}।इस सांस्थिति के साथ {{mvar|F}} एक संस्थानिक क्षेत्र के रूप में समरूपीय है <math>\Complex.</math> | ||
एकमात्र [[ जुड़ा हुआ स्थान ]] [[ स्थानीय रूप से कॉम्पैक्ट ]] | एकमात्र [[ जुड़ा हुआ स्थान | जुड़ा हुआ समष्टि]] [[ स्थानीय रूप से कॉम्पैक्ट ]] संस्थानिक वलय हैं <math>\R</math> और <math>\Complex.</math> यह एक और लक्षण वर्णन देता है <math>\Complex</math> एक संस्थानिक क्षेत्र के रूप में, जब से <math>\Complex</math> से प्रतिष्ठित किया जा सकता है <math>\R</math> क्योंकि नॉनज़ेरो सम्मिश्र नंबर कनेक्टेड स्पेस हैं, जबकि नॉनज़ेरो रियल नंबर नहीं हैं।{{sfn|Bourbaki|1998|loc=§VIII.4}} | ||
| Line 391: | Line 385: | ||
=== निर्माण के रूप में आदेश जोड़े === | === निर्माण के रूप में आदेश जोड़े === | ||
विलियम रोवन हैमिल्टन | विलियम रोवन हैमिल्टन नेसमुच्चय को परिभाषित करने के लिए दृष्टिकोण पेश किया <math>\Complex</math> सम्मिश्र संख्याओं का<ref>{{cite book|title=संख्याओं का एक संक्षिप्त इतिहास|first=Leo |last=Corry|publisher=Oxford University Press|year=2015|pages=215–16}}</ref>समुच्चय के रूप में <math>\mathbb{R}^2</math> का {{nowrap|[[ordered pair]]s {{math|(''a'', ''b'')}}}} वास्तविक संख्याओं के, जिसमें जोड़ और गुणन के लिए निम्नलिखित नियम प्रयुक्त होते हैं:{{sfn|Apostol|1981|pp=15–16}} | ||
<math display=block>\begin{align} | <math display=block>\begin{align} | ||
| Line 400: | Line 394: | ||
=== एक भागफल क्षेत्र के रूप में निर्माण === | === एक भागफल क्षेत्र के रूप में निर्माण === | ||
यद्यपि यह निम्न-स्तरीय निर्माण | यद्यपि यह निम्न-स्तरीय निर्माण सम्मिश्र संख्याओं की संरचना का सही वर्णन करता है, निम्नलिखित समकक्ष परिभाषा से बीजीय प्रकृति का पता चलता है <math>\Complex</math> अधिक तुरंत।यह लक्षण वर्णन क्षेत्रों और बहुपदों की धारणा पर निर्भर करता है।एक क्षेत्र एकसमुच्चय है जो जोड़, घटाव, गुणा और विभाजन संचालन के साथ संपन्न है, जो कि तर्कसंगत संख्याओं से परिचित है, तर्कसंगत संख्या से परिचित है।उदाहरण के लिए, वितरण नियम | ||
<math display=block>(x+y) z = xz + yz</math> | <math display=block>(x+y) z = xz + yz</math> | ||
किसी भी तीन तत्वों के लिए पकड़ना चाहिए {{mvar|x}}, {{mvar|y}} और {{mvar|z}} एक क्षेत्र का।सेट <math>\R</math> वास्तविक संख्याओं में एक क्षेत्र बनता है।एक बहुपद {{math|''p''(''X'')}} वास्तविक गुणांक के साथ रूप की अभिव्यक्ति है | किसी भी तीन तत्वों के लिए पकड़ना चाहिए {{mvar|x}}, {{mvar|y}} और {{mvar|z}} एक क्षेत्र का।सेट <math>\R</math> वास्तविक संख्याओं में एक क्षेत्र बनता है।एक बहुपद {{math|''p''(''X'')}} वास्तविक गुणांक के साथ रूप की अभिव्यक्ति है | ||
<math display=block>a_nX^n+\dotsb+a_1X+a_0,</math> | <math display=block>a_nX^n+\dotsb+a_1X+a_0,</math> | ||
जहां {{math|''a''<sub>0</sub>, ..., ''a''<sub>''n''</sub>}} वास्तविक संख्याएं हैं।बहुपद का सामान्य जोड़ और | जहां {{math|''a''<sub>0</sub>, ..., ''a''<sub>''n''</sub>}} वास्तविक संख्याएं हैं।बहुपद का सामान्य जोड़ और गुणनसमुच्चय को समाप्त करता है <math>\R[X]</math> एक [[ अंगूठी (गणित) | वलय (गणित)]] संरचना के साथ ऐसे सभी बहुपद।इस वलय को वास्तविक संख्याओं में बहुपद वलय कहा जाता है। | ||
सम्मिश्र संख्याओं केसमुच्चय को भागफल की वलय के रूप में परिभाषित किया गया है <math>\R[X]/(X^2+1).</math><रेफ नाम = bourbaki 1998 loc = §viii.1 /> इस एक्सटेंशन क्षेत्र में दो वर्ग जड़ें हैं {{math|−1}}, अर्थात् (के [[ coset ]]s) {{math|''X''}} और {{math|−''X''}}, क्रमश।(के cosets) {{math|1}} और {{math|''X''}} का आधार बनाना <math>\mathbb{R}[X]/(X^2 + 1)</math> एक वास्तविक [[ सदिश स्थल ]] के रूप में, जिसका अर्थ है कि एक्सटेंशन क्षेत्र के प्रत्येक तत्व को इन दो तत्वों में एक [[ रैखिक संयोजन ]] के रूप में लिखा जा सकता है।समान रूप से, एक्सटेंशन क्षेत्र के तत्वों को ऑर्डर किए गए जोड़े के रूप में लिखा जा सकता है {{math|(''a'', ''b'')}} वास्तविक संख्याओं की।भागफल की वलय एक क्षेत्र है, क्योंकि {{math|''X''<sup>2</sup> + 1}} इरायूबल बहुपद पर है <math>\R,</math> तो यह आदर्श उत्पन्न करता है [[ अधिकतम आदर्श ]] है। | |||
वलय में जोड़ और गुणन के लिए सूत्र <math>\R[X],</math> संबंध को मॉड्यूलो {{math|''X''<sup>2</sup> {{=}} −1}}, क्रमित जोड़े के रूप में परिभाषित सम्मिश्र संख्याओं के जोड़ और गुणन के लिए सूत्रों के अनुरूप।तो क्षेत्र की दो परिभाषाएँ <math>\Complex</math> [[ समाकृतिकता ]] (क्षेत्र के रूप में) हैं। | |||
स्वीकार करते हुए <math>\Complex</math> बीजगणितीय रूप से | स्वीकार करते हुए <math>\Complex</math> बीजगणितीय रूप से संवृत है, क्योंकि यह एक बीजगणितीय विस्तार है <math>\mathbb{R}</math> इस दृष्टिकोण में, <math>\Complex</math> इसलिए बीजगणितीय संवृत है <math>\R.</math> | ||
=== | === आव्यूह सम्मिश्र संख्याओं का प्रतिनिधित्व ===<!-- .This section is linked from [[Cauchy-Riemann equations]] --> | ||
सम्मिश्र आंकड़े {{math|''a'' + ''bi''}} द्वारा भी प्रतिनिधित्व किया जा सकता है {{math|2 × 2}} आव्यूह (गणित) जिसमें रूप है: | |||
<!-- | <!-- | ||
This definition with the minus sign in the upper right corner matches the article [[Rotation matrix]]. Please do not change it. | This definition with the minus sign in the upper right corner matches the article [[Rotation matrix]]. Please do not change it. | ||
| Line 424: | Line 418: | ||
\end{pmatrix} | \end{pmatrix} | ||
</math> | </math> | ||
यहाँ प्रविष्टियाँ {{mvar|a}} और {{mvar|b}} वास्तविक संख्याएं हैं।चूंकि इस तरह के दो मैट्रिस का योग और उत्पाद फिर से इस रूप में है, इसलिए ये मैट्रिस | यहाँ प्रविष्टियाँ {{mvar|a}} और {{mvar|b}} वास्तविक संख्याएं हैं।चूंकि इस तरह के दो मैट्रिस का योग और उत्पाद फिर से इस रूप में है, इसलिए ये मैट्रिस वलय का एक [[ सबरिंग ]] बनाते हैं {{math|2 × 2}} मैट्रिसेस। | ||
एक साधारण गणना से पता चलता है कि नक्शा: | एक साधारण गणना से पता चलता है कि नक्शा: | ||
| Line 431: | Line 425: | ||
b & \;\; a | b & \;\; a | ||
\end{pmatrix}</math> | \end{pmatrix}</math> | ||
एक [[ रिंग आइसोमोर्फिज्म ]] इन मैट्रीस ऑफ इन मैट्रिसेस तक | एक [[ रिंग आइसोमोर्फिज्म | वलय आइसोमोर्फिज्म]] इन मैट्रीस ऑफ इन मैट्रिसेस तक सम्मिश्र संख्याओं के क्षेत्र से है।यह आइसोमोर्फिज्म एक सम्मिश्र संख्या के निरपेक्ष मान के वर्ग को संबंधित आव्यूह के निर्धारक के साथ जोड़ता है, और आव्यूह के [[ पक्षांतरित ]] के साथ एक सम्मिश्र संख्या का संयुग्मित करता है। | ||
सम्मिश्र संख्याओं के गुणन का ज्यामितीय विवरण सम्मिश्र संख्याओं और ऐसे मैट्रिसेस के बीच इस पत्राचार का उपयोग करके [[ रोटेशन मैट्रिक्स | घूर्णन आव्यूह]] के संदर्भ में भी व्यक्त किया जा सकता है।एक वेक्टर पर आव्यूह की कार्रवाई {{math|(''x'', ''y'')}} के गुणन से मेल खाती है {{math|''x'' + ''iy''}} द्वारा {{math|''a'' + ''ib''}}।विशेष रूप से, यदि निर्धारक है {{math|1}}, एक वास्तविक संख्या है {{mvar|t}} इस तरह कि आव्यूह का रूप है: | |||
<math display=block>\begin{pmatrix} | <math display=block>\begin{pmatrix} | ||
\cos t & - \sin t \\ | \cos t & - \sin t \\ | ||
\sin t & \;\; \cos t | \sin t & \;\; \cos t | ||
\end{pmatrix}</math> | \end{pmatrix}</math> | ||
इस | इस स्थिति में, वैक्टर पर आव्यूह की कार्रवाई और सम्मिश्र संख्या से गुणा <math>\cos t+i\sin t</math> दोनों कोण के [[ रोटेशन (गणित) | घूर्णन (गणित)]] दोनों हैं {{mvar|t}}। | ||
== | == सम्मिश्र विश्लेषण == | ||
[[File:Sin1z-cplot.svg|thumb| | [[File:Sin1z-cplot.svg|thumb|प्रक्षेत्र रंग चक्र ग्राफ {{math|sin(1/''z'')}} अंदर के काले भागों में बड़े निरपेक्ष मान वाले संख्याओं को संदर्भित किया जाता है।]] | ||
{{main|Complex analysis}} | {{main|Complex analysis}} | ||
<!-- | <!-- | ||
| Line 461: | Line 455: | ||
--> | --> | ||
एक | एक सम्मिश्र चर के फलनों के अध्ययन को सम्मिश्र विश्लेषण के रूप में जाना जाता है और प्रयुक्त गणित के साथ -साथ गणित की अन्य शाखाओं में भी भारी व्यावहारिक उपयोग होता है।प्रायः, [[ वास्तविक विश्लेषण ]] या यहां तक कि [[ संख्या सिद्धांत ]] में बयानों के लिए सबसे प्राकृतिक प्रमाण सम्मिश्र विश्लेषण से तकनीकों को नियोजित करते हैं (एक उदाहरण के लिए [[ प्रधान संख्या प्रमेय ]] देखें)।वास्तविक फलनों के विपरीत, जिन्हें सामान्य रूप से दो-आयामी ग्राफ़ के रूप में दर्शाया जाता है, [[ जटिल कार्य | सम्मिश्र]] फलनो में चार-आयामी रेखांकन होते हैं और इसे दो चर के एक फलन के एक ग्राफ को रंग-कोडित करके उपयोगी रूप से चित्रित किया जा सकता है। चार आयामों का सुझाव देने के लिए तीन-आयामी ग्राफ, या इसके द्वारा या उसके द्वारा।सम्मिश्र समतल के सम्मिश्र फलन के गतिशील परिवर्तन को एनिमेट करना। | ||
=== | === सम्मिश्र घातीय और संबंधित फलन === | ||
(वास्तविक) विश्लेषण में [[ अभिसरण श्रृंखला ]] और निरंतर | (वास्तविक) विश्लेषण में [[ अभिसरण श्रृंखला ]] और निरंतर फलनों की धारणाओं में सम्मिश्र विश्लेषण में प्राकृतिक एनालॉग्स हैं।एक क्रम सम्मिश्र संख्याओं के रूप में [[ अभिसरण अनुक्रम ]] कहा जाता है यदि और केवल अगर इसके वास्तविक और काल्पनिक भाग करते हैं।यह सीमाओं के (ε, Δ) -Definition के बराबर है, जहां वास्तविक संख्याओं के निरपेक्ष मान को सम्मिश्र संख्याओं में से एक द्वारा प्रतिस्थापित किया जाता है।अधिक अमूर्त दृष्टिकोण से, <math>\mathbb{C}</math>, मीट्रिक (गणित) के साथ संपन्न | ||
<math display=block>\operatorname{d}(z_1, z_2) = |z_1 - z_2|</math> | <math display=block>\operatorname{d}(z_1, z_2) = |z_1 - z_2|</math> | ||
एक पूर्ण [[ मीट्रिक स्थान ]] है, जिसमें विशेष रूप से त्रिभुज असमानता | एक पूर्ण [[ मीट्रिक स्थान | मीट्रिक समष्टि]] है, जिसमें विशेष रूप से त्रिभुज असमानता सम्मिलित है | ||
<math display=block>|z_1 + z_2| \le |z_1| + |z_2|</math> | <math display=block>|z_1 + z_2| \le |z_1| + |z_2|</math> | ||
किसी भी दो | किसी भी दो सम्मिश्र संख्याओं के लिए {{math|''z''<sub>1</sub>}} और {{math|''z''<sub>2</sub>}}। | ||
वास्तविक विश्लेषण की तरह, अभिसरण की इस धारणा का उपयोग कई [[ प्राथमिक कार्य ]] | वास्तविक विश्लेषण की तरह, अभिसरण की इस धारणा का उपयोग कई [[ प्राथमिक कार्य | प्राथमिक]] फलनो के निर्माण के लिए किया जाता है: घातीय फलन {{math|exp ''z''}}, भी लिखा है {{math|''e''<sup>''z''</sup>}}, [[ अनंत श्रृंखला ]] के रूप में परिभाषित किया गया है | ||
<math display=block>\exp z:= 1+z+\frac{z^2}{2\cdot 1}+\frac{z^3}{3\cdot 2\cdot 1}+\cdots = \sum_{n=0}^{\infty} \frac{z^n}{n!}. </math> | <math display=block>\exp z:= 1+z+\frac{z^2}{2\cdot 1}+\frac{z^3}{3\cdot 2\cdot 1}+\cdots = \sum_{n=0}^{\infty} \frac{z^n}{n!}. </math> | ||
वास्तविक त्रिकोणमितीय | वास्तविक त्रिकोणमितीय फलनों को परिभाषित करने वाली श्रृंखला [[ ज्या ]] और [[ कोज्या ]], साथ ही साथ [[ अतिशयोक्ति कार्य | अतिशयोक्ति फलन]] सिंह और कोश भी बिना परिवर्तन के सम्मिश्र तर्कों पर ले जाती है।अन्य त्रिकोणमितीय और अतिपरवयलिक फलनों के लिए, जैसे कि स्पर्शरेखा (फलन), वस्तुए थोड़ी अधिक सम्मिश्र हैं, क्योंकि परिभाषित श्रृंखला सभी सम्मिश्र मूल्यों के लिए अभिसरण नहीं करती है। इसलिए, किसी को उन्हें साइन, कोसाइन और एक्सपोनेंशियल के संदर्भ में परिभाषित करना होगा, या, विश्लेषणात्मक निरंतरता की विधि का उपयोग करके, समकक्ष रूप से। | ||
यूलर के सूत्र में कहा गया है: | यूलर के सूत्र में कहा गया है: | ||
| Line 478: | Line 472: | ||
किसी भी वास्तविक संख्या के लिए {{mvar|φ}}, विशेष रूप से | किसी भी वास्तविक संख्या के लिए {{mvar|φ}}, विशेष रूप से | ||
<math display=block>\exp(i \pi) = -1 </math>, जो यूलर की पहचान है। | <math display=block>\exp(i \pi) = -1 </math>, जो यूलर की पहचान है। | ||
वास्तविक संख्याओं की स्थिति के विपरीत, | वास्तविक संख्याओं की स्थिति के विपरीत, सम्मिश्र समाधानों का एक [[ अनंत सेट | अनंतसमुच्चय]] है {{mvar|z}} समीकरण का | ||
<math display=block>\exp z = w </math> | <math display=block>\exp z = w </math> | ||
किसी भी | किसी भी सम्मिश्र संख्या के लिए {{math|''w'' ≠ 0}}।यह दिखाया जा सकता है कि कोई भी समाधान {{mvar|z}} - का सम्मिश्र लघुगणक कहा जाता है {{mvar|w}} - संतुष्ट करता है | ||
<math display=block>\log w = \ln|w| + i\arg w, </math> | <math display=block>\log w = \ln|w| + i\arg w, </math> | ||
जहां ARG [[ arg (गणित) ]] को परिभाषित किया गया है #polar फॉर्म, और ln (वास्तविक) प्राकृतिक लघुगणक।जैसा कि ARG एक बहुउद्देशीय | जहां ARG [[ arg (गणित) ]] को परिभाषित किया गया है #polar फॉर्म, और ln (वास्तविक) प्राकृतिक लघुगणक।जैसा कि ARG एक बहुउद्देशीय फलन है, केवल एक बहु के लिए अद्वितीय है {{math|2''π''}}, लॉग भी बहुपक्षीय है।लॉग का प्रमुख मूल्य प्रायः [[ अंतराल (गणित) ]] के लिए काल्पनिक भाग को प्रतिबंधित करके लिया जाता है {{open-closed|−''π'', ''π''}}। | ||
सम्मिश्र प्रतिपादन {{math|''z''<sup>''ω''</sup>}} की तरह परिभाषित किया गया है | |||
<math display=block>z^\omega = \exp(\omega \log z), </math> | <math display=block>z^\omega = \exp(\omega \log z), </math> | ||
और बहु-मूल्यवान है, | और बहु-मूल्यवान है, अतिरिक्त कब {{mvar|ω}} एक पूर्णांक है।के लिए {{math|1=''ω'' = 1 / ''n''}}, कुछ प्राकृतिक संख्या के लिए {{mvar|n}}, यह गैर-अवेक्षता को ठीक करता है {{mvar|n}}ऊपर उल्लिखित वें जड़ों। | ||
सम्मिश्र संख्या, वास्तविक संख्याओं के विपरीत, सामान्य रूप से अनमॉडिफाइड पावर और लॉगरिदम पहचान को संतुष्ट नहीं करती है, विशेष कर जब भोले-भाले को एकल-मूल्य वाले फलनों के रूप में माना जाता है;घातांक देखें#शक्ति और लघुगणक पहचान की विफलता।उदाहरण के लिए, वे संतुष्ट नहीं करते हैं | |||
<math display=block>a^{bc} = \left(a^b\right)^c.</math> | <math display=block>a^{bc} = \left(a^b\right)^c.</math> | ||
समीकरण के दोनों पक्षों को यहां दिए गए | समीकरण के दोनों पक्षों को यहां दिए गए सम्मिश्र घातांक की परिभाषा से बहु -कृत किया गया है, और बाईं ओर के मान दाईं ओर उन लोगों का एक उप-समुच्चय हैं। | ||
=== होलोमोर्फिक | === होलोमोर्फिक फलन === | ||
एक | एक फलन F: <math>\mathbb{C}</math> → <math>\mathbb{C}</math> यदि यह Cauchy -riemann समीकरणों को संतुष्ट करता है, तो Holomorphic फलन कहा जाता है।उदाहरण के लिए, किसी भी रैखिक परिवर्तन#परिभाषा और पहले परिणाम |<math>\mathbb{R}</math>-लाइनर मैप <math>\mathbb{C}</math> → <math>\mathbb{C}</math> रूप में लिखा जा सकता है | ||
<math display=block>f(z)=az+b\overline{z}</math> | <math display=block>f(z)=az+b\overline{z}</math> | ||
सम्मिश्र गुणांक के साथ {{mvar|a}} और {{mvar|b}}।यह नक्शा होलोमोर्फिक है अगर और केवल अगर {{math|1=''b'' = 0}}।दूसरा सुमंड <math>b \overline z</math> वास्तविक-विभेद्य है, लेकिन कॉची-अर्मन समीकरणों को संतुष्ट नहीं करता है। | |||
सम्मिश्र विश्लेषण से पता चलता है कि वास्तविक विश्लेषण में कुछ विशेषताएं स्पष्ट नहीं हैं।उदाहरण के लिए, कोई भी दो होलोमोर्फिक फलन करता है {{mvar|f}} और {{mvar|g}} यह एक एकपक्षीय रूप से छोटे विवृत उप-समुच्चय पर सहमत है <math>\mathbb{C}</math> आवश्यक रूप से हर जगह सहमत [[ मेरोमॉर्फिक फ़ंक्शन | मेरोमॉर्फिक फलन]] , फलन जो स्थानीय रूप से लिखे जा सकते हैं {{math|''f''(''z'')/(''z'' − ''z''<sub>0</sub>)<sup>''n''</sup>}} एक होलोमोर्फिक फलन के साथ {{mvar|f}}, अभी भी होलोमोर्फिक फलनों की कुछ विशेषताओं को साझा करें।अन्य फलनों में [[ आवश्यक विलक्षणता ]] है, जैसे {{math|sin(1/''z'')}} पर {{math|1=''z'' = 0}}। | |||
== अनुप्रयोग == | == अनुप्रयोग == | ||
सम्मिश्र संख्याओं में कई वैज्ञानिक क्षेत्रों में अनुप्रयोग होते हैं, जिनमें [[ संकेत प्रसंस्करण ]], [[ नियंत्रण सिद्धांत ]], इलेक्ट्रोमैग्नेटिज्म, [[ द्रव गतिविज्ञान ]], [[ क्वांटम यांत्रिकी ]], [[ नक्शानवीसी ]] और कंपन#कंपन विश्लेषण सम्मिलित हैं।इनमें से कुछ एप्लिकेशन नीचे वर्णित हैं। | |||
=== ज्यामिति === | === ज्यामिति === | ||
==== आकार ==== | ==== आकार ==== | ||
तीन [[ collinearity ]] | गैर-कोलीनियर अंक <math>u, v, w</math> विमान में त्रिभुज के आकार#समानता कक्षाएं निर्धारित करते हैं <math>\{u, v, w\}</math> | तीन [[ collinearity ]] | गैर-कोलीनियर अंक <math>u, v, w</math> विमान में त्रिभुज के आकार#समानता कक्षाएं निर्धारित करते हैं <math>\{u, v, w\}</math>।सम्मिश्र समतल में बिंदुओं का पता लगाना, एक त्रिभुज के इस आकार को सम्मिश्र अंकगणित द्वारा व्यक्त किया जा सकता है | ||
<math display=block>S(u, v, w) = \frac {u - w}{u - v}. </math> | <math display=block>S(u, v, w) = \frac {u - w}{u - v}. </math> | ||
आकार <math>S</math> एक त्रिभुज एक ही रहेगा, जब | आकार <math>S</math> एक त्रिभुज एक ही रहेगा, जब सम्मिश्र समतल अनुवाद या फैलाव (एक affine परिवर्तन द्वारा) द्वारा बदल दिया जाता है, आकार की सहज धारणा के अनुरूप, और समानता (ज्यामिति) का वर्णन करता है।इस प्रकार प्रत्येक त्रिकोण <math>\{u, v, w\}</math> एक ही आकार के साथ त्रिकोणों के एक आकार#समानता वर्गों में है।<ref>{{cite journal |last=Lester |first=J.A. |title=त्रिकोण I: आकार|journal=[[Aequationes Mathematicae]] |volume=52 |pages=30–54 |year=1994 |doi=10.1007/BF01818325 |s2cid=121095307}}</ref> | ||
==== फ्रैक्टल ज्यामिति ==== | ==== फ्रैक्टल ज्यामिति ==== | ||
[[File:Mandelset hires.png|right|thumb|लेबल किए गए वास्तविक और काल्पनिक | [[File:Mandelset hires.png|right|thumb|लेबल किए गए वास्तविक और काल्पनिक अक्षों के साथ मंडेलब्रॉट संस्थापित किया गया।]][[ मंडेलब्रॉट सेट | मंडेलब्रॉटसमुच्चय]] सम्मिश्र समतल पर गठित एक फ्रैक्टल का एक लोकप्रिय उदाहरण है।यह हर समष्टि की साजिश रचकर परिभाषित किया गया है <math>c</math> जहां अनुक्रम को पुनरावृत्ति करना <math>f_c(z)=z^2+c</math> जब पुनरावृति असीम रूप से (स्थिरता सिद्धांत) नहीं होती है।इसी तरह, [[ जूलिया सेट | जूलियासमुच्चय]] के समान नियम हैं, जहां अतिरिक्त इसके <math>c</math> स्थिर रहता है। | ||
==== त्रिकोण ==== | ==== त्रिकोण ==== | ||
हर त्रिभुज में एक अद्वितीय स्टीनर [[ अंडाकार ]] है - त्रिभुज के अंदर एक दीर्घवृत्त और त्रिभुज के तीन पक्षों के मध्य बिंदुओं के लिए स्पर्शरेखा।एक त्रिभुज के [[ स्टेनर इनलिप्स ]] का [[ फोकस (ज्यामिति) ]] मार्डन के प्रमेय के अनुसार, निम्नानुसार पाया जा सकता है:<ref>{{cite journal |last1=Kalman|first1=Dan|title=मार्डन के प्रमेय का एक प्राथमिक प्रमाण|url=http://mathdl.maa.org/mathDL/22/?pa=content&sa=viewDocument&nodeId=3338&pf=1 |journal=[[American Mathematical Monthly]] |volume=115 |issue=4 |pages=330–38 |year=2008a |doi=10.1080/00029890.2008.11920532 |s2cid=13222698 |issn=0002-9890 |access-date=1 January 2012 |archive-url=https://web.archive.org/web/20120308104622/http://mathdl.maa.org/mathDL/22/?pa=content&sa=viewDocument&nodeId=3338&pf=1 |archive-date=8 March 2012|url-status=live}}</ref><ref>{{cite journal |last1=Kalman |first1=Dan |title=गणित में सबसे अद्भुत प्रमेय|url=http://mathdl.maa.org/mathDL/4/?pa=content&sa=viewDocument&nodeId=1663 |journal=[[Journal of Online Mathematics and Its Applications]] |year=2008b |access-date=1 January 2012|archive-url=https://web.archive.org/web/20120208014954/http://mathdl.maa.org/mathDL/4/?pa=content&sa=viewDocument&nodeId=1663 |archive-date=8 February 2012 |url-status=live}}</ref> | हर त्रिभुज में एक अद्वितीय स्टीनर [[ अंडाकार ]] है - त्रिभुज के अंदर एक दीर्घवृत्त और त्रिभुज के तीन पक्षों के मध्य बिंदुओं के लिए स्पर्शरेखा।एक त्रिभुज के [[ स्टेनर इनलिप्स ]] का [[ फोकस (ज्यामिति) ]] मार्डन के प्रमेय के अनुसार, निम्नानुसार पाया जा सकता है:<ref>{{cite journal |last1=Kalman|first1=Dan|title=मार्डन के प्रमेय का एक प्राथमिक प्रमाण|url=http://mathdl.maa.org/mathDL/22/?pa=content&sa=viewDocument&nodeId=3338&pf=1 |journal=[[American Mathematical Monthly]] |volume=115 |issue=4 |pages=330–38 |year=2008a |doi=10.1080/00029890.2008.11920532 |s2cid=13222698 |issn=0002-9890 |access-date=1 January 2012 |archive-url=https://web.archive.org/web/20120308104622/http://mathdl.maa.org/mathDL/22/?pa=content&sa=viewDocument&nodeId=3338&pf=1 |archive-date=8 March 2012|url-status=live}}</ref><ref>{{cite journal |last1=Kalman |first1=Dan |title=गणित में सबसे अद्भुत प्रमेय|url=http://mathdl.maa.org/mathDL/4/?pa=content&sa=viewDocument&nodeId=1663 |journal=[[Journal of Online Mathematics and Its Applications]] |year=2008b |access-date=1 January 2012|archive-url=https://web.archive.org/web/20120208014954/http://mathdl.maa.org/mathDL/4/?pa=content&sa=viewDocument&nodeId=1663 |archive-date=8 February 2012 |url-status=live}}</ref> सम्मिश्र समतल में त्रिभुज के कोने को निरूपित करें {{math|1=''a'' = ''x''<sub>''A''</sub> + ''y''<sub>''A''</sub>''i''}}, {{math|1=''b'' = ''x''<sub>''B''</sub> + ''y''<sub>''B''</sub>''i''}}, और {{math|1=''c'' = ''x''<sub>''C''</sub> + ''y''<sub>''C''</sub>''i''}}।क्यूबिक समीकरण लिखें <math>(x-a)(x-b)(x-c)=0</math>, इसके व्युत्पन्न को लें, और (द्विघात) व्युत्पन्न को शून्य से बराबरी करें।मार्डन के प्रमेय का कहना है कि इस समीकरण के समाधान सम्मिश्र संख्याएं हैं जो स्टीनर इनलिप्स के दो foci के स्थानों को दर्शाती हैं। | ||
=== बीजगणितीय संख्या सिद्धांत === | === बीजगणितीय संख्या सिद्धांत === | ||
[[File:Pentagon construct.gif|right|thumb| | [[File:Pentagon construct.gif|right|thumb|समभुजकोणीय पंचभुज [[ कम्पास और सीधे निर्माण | दिक्सूचक और ऋजु कोर]] का निर्माण।]]जैसा कि ऊपर उल्लेख किया गया है, किसी भी गैर -विरोधी बहुपद समीकरण (सम्मिश्र गुणांक में) में एक समाधान है <math>\mathbb{C}</math>।तर्क एक फोर्टियोरी, वही सच है यदि समीकरण में तर्कसंगत गुणांक हैं।इस तरह के समीकरणों की जड़ों को बीजगणितीय संख्या कहा जाता है - वे बीजगणितीय संख्या सिद्धांत में अध्ययन की एक प्रमुख वस्तु हैं।की तुलना में <math>\overline{\mathbb{Q}}</math>, बीजगणितीय संवृत <math>\mathbb{Q}</math>, जिसमें सभी बीजीय संख्या भी सम्मिलित हैं, <math>\mathbb{C}</math> ज्यामितीय शब्दों में आसानी से समझने योग्य होने का लाभ है।इस तरह, बीजगणितीय तरीकों का उपयोग ज्यामितीय प्रश्नों का अध्ययन करने के लिए किया जा सकता है और इसके विपरीत।बीजगणितीय तरीकों के साथ, अधिक विशेष रूप से [[ क्षेत्र सिद्धांत (गणित) ]] की मशीनरी को [[ एकता की जड़ ]] वाले [[ संख्या क्षेत्र ]] में प्रयुक्त करने के लिए, यह दिखाया जा सकता है कि एक नियमित नॉनगन कम्पास और ऋजु कोर निर्माण - एक विशुद्ध रूप से ज्यामितीय समस्या का निर्माण करना संभव नहीं है। | ||
एक अन्य उदाहरण गॉसियन पूर्णांक है;वह है, फॉर्म की संख्या {{math|''x'' + ''iy''}}, कहां {{mvar|x}} और {{mvar|y}} पूर्णांक हैं, जिसका उपयोग दो वर्गों के रकम पर फ़र्मेट के प्रमेय को वर्गीकृत करने के लिए किया जा सकता है। | एक अन्य उदाहरण गॉसियन पूर्णांक है;वह है, फॉर्म की संख्या {{math|''x'' + ''iy''}}, कहां {{mvar|x}} और {{mvar|y}} पूर्णांक हैं, जिसका उपयोग दो वर्गों के रकम पर फ़र्मेट के प्रमेय को वर्गीकृत करने के लिए किया जा सकता है। | ||
| Line 523: | Line 517: | ||
=== विश्लेषणात्मक संख्या सिद्धांत === | === विश्लेषणात्मक संख्या सिद्धांत === | ||
{{main|Analytic number theory}} | {{main|Analytic number theory}} | ||
विश्लेषणात्मक संख्या सिद्धांत अध्ययन संख्या, | विश्लेषणात्मक संख्या सिद्धांत अध्ययन संख्या, प्रायः पूर्णांक या तर्कसंगत, इस तथ्य का लाभ उठाकर कि उन्हें सम्मिश्र संख्या के रूप में माना जा सकता है, जिसमें विश्लेषणात्मक तरीकों का उपयोग किया जा सकता है।यह सम्मिश्र-मूल्यवान फलनों में संख्या-सिद्धांत संबंधी जानकारी को एन्कोडिंग करके किया जाता है।उदाहरण के लिए, Riemann Zeta फलन {{math|ζ(''s'')}} [[ अभाज्य संख्या ]]ों के वितरण से संबंधित है। | ||
=== अनुचित अभिन्नता === | === अनुचित अभिन्नता === | ||
प्रयुक्त क्षेत्रों में, सम्मिश्र संख्याओं का उपयोग प्रायः सम्मिश्र-मूल्यवान फलनों के माध्यम से कुछ वास्तविक-मूल्यवान अनुचित अभिन्नताओं की गणना करने के लिए किया जाता है।ऐसा करने के लिए कई तरीके मौजूद हैं;[[ समोच्च एकीकरण के तरीके ]] देखें। | |||
=== गतिशील समीकरण === | === गतिशील समीकरण === | ||
[[ अंतर समीकरण ]]ों में, पहले सभी | [[ अंतर समीकरण ]]ों में, पहले सभी सम्मिश्र जड़ों को ढूंढना आम है {{mvar|r}} [[ रैखिक अंतर समीकरण ]]#सजातीय समीकरणों के साथ एक रैखिक अंतर समीकरण या समीकरण प्रणाली के निरंतर गुणांक के साथ और फिर फॉर्म के आधार फलनों के संदर्भ में सिस्टम को हल करने का प्रयास करें {{math|1=''f''(''t'') = ''e''<sup>''rt''</sup>}}।इसी तरह, [[ अंतर समीकरण ]]ों में, सम्मिश्र जड़ें {{mvar|r}} अंतर समीकरण प्रणाली के विशिष्ट समीकरण का उपयोग किया जाता है, फॉर्म के आधार फलनों के संदर्भ में सिस्टम को हल करने का प्रयास करने के लिए {{math|1=''f''(''t'') = ''r''<sup>''t''</sup>}}। | ||
=== रैखिक बीजगणित === | === रैखिक बीजगणित === | ||
[[ एक मैट्रिक्स का eigendecomposition ]] | [[ एक मैट्रिक्स का eigendecomposition | एक आव्यूह का eigendecomposition]] आव्यूह शक्तियों और [[ मैट्रिक्स घातीय | आव्यूह घातीय]] की गणना के लिए एक उपयोगी उपकरण है।हालांकि, इसे प्रायः सम्मिश्र संख्याओं के उपयोग की आवश्यकता होती है, भले ही आव्यूह वास्तविक हो (उदाहरण के लिए, एक घूर्णन आव्यूह)। | ||
सम्मिश्र संख्या प्रायः वास्तविक संख्याओं में मूल रूप से कल्पना की गई अवधारणाओं को सामान्य करती है।उदाहरण के लिए, [[ संयुग्मन संक्रमण ]] ट्रांसपोज़ को सामान्य करता है, [[ हरमिटियन मैट्रिक्स | हरमिटियन आव्यूह]] [[ सममित मैट्रिक्स | सममित आव्यूह]] को सामान्य करता है, और [[ एकात्मक मैट्रिक्स | एकात्मक आव्यूह]] [[ ऑर्थोगोनल मैट्रिक्स | ऑर्थोगोनल आव्यूह]] को सामान्य करता है। | |||
=== | === प्रयुक्त गणित में === | ||
==== नियंत्रण सिद्धांत ==== | ==== नियंत्रण सिद्धांत ==== | ||
{{see also|Complex plane#Use in control theory}} | {{see also|Complex plane#Use in control theory}} | ||
नियंत्रण सिद्धांत में, सिस्टम को | नियंत्रण सिद्धांत में, सिस्टम को प्रायः समय प्रक्षेत्र से [[ लाप्लास रूपांतरण ]] का उपयोग करके सम्मिश्र [[ आवृत्ति डोमेन | आवृत्ति प्रक्षेत्र]] में बदल दिया जाता है।सिस्टम के शून्य और डंडे का विश्लेषण तब सम्मिश्र समतल में किया जाता है।रूट लोकोस, [[ न्यक्विस्ट प्लॉट ]], और [[ निकोल्स प्लॉट ]] तकनीक सभी सम्मिश्र समतल का उपयोग करते हैं। | ||
[[ रूट लोकस ]] विधि में, यह महत्वपूर्ण है कि [[ शून्य और ध्रुव ]] बाएं या दाएं आधे विमानों में हैं, अर्थात, शून्य से अधिक या उससे कम वास्तविक | [[ रूट लोकस ]] विधि में, यह महत्वपूर्ण है कि [[ शून्य और ध्रुव ]] बाएं या दाएं आधे विमानों में हैं, अर्थात, शून्य से अधिक या उससे कम वास्तविक भाग है।यदि एक रैखिक, समय-अपरिवर्तनीय (LTI) प्रणाली में डंडे होते हैं | ||
* सही आधे विमान में, यह [[ अस्थिर ]] होगा, | * सही आधे विमान में, यह [[ अस्थिर ]] होगा, | ||
| Line 551: | Line 545: | ||
==== सिग्नल विश्लेषण ==== | ==== सिग्नल विश्लेषण ==== | ||
समय -समय पर अलग -अलग संकेतों के लिए सुविधाजनक विवरण के लिए सिग्नल विश्लेषण और अन्य क्षेत्रों में | समय -समय पर अलग -अलग संकेतों के लिए सुविधाजनक विवरण के लिए सिग्नल विश्लेषण और अन्य क्षेत्रों में सम्मिश्र संख्याओं का उपयोग किया जाता है।वास्तविक भौतिक मात्राओं का प्रतिनिधित्व करने वाले वास्तविक फलनों के लिए, प्रायः सिन और कोसाइन के संदर्भ में, इसी सम्मिश्र फलनों को माना जाता है जिनके बारे में वास्तविक भाग मूल मात्रा हैं।किसी दिए गए [[ आवृत्ति ]] की [[ साइन लहर ]] के लिए, निरपेक्ष मूल्य {{math|{{!}}''z''{{!}}}} इसी के {{mvar|z}} [[ आयाम ]] और तर्क (सम्मिश्र विश्लेषण) है {{math|arg ''z''}} [[ चरण (तरंगें) ]] है। | ||
यदि [[ फूरियर विश्लेषण ]] किसी दिए गए वास्तविक-मूल्य वाले संकेत को आवधिक | यदि [[ फूरियर विश्लेषण ]] किसी दिए गए वास्तविक-मूल्य वाले संकेत को आवधिक फलनों के योग के रूप में लिखने के लिए नियोजित किया जाता है, तो इन आवधिक फलनों को प्रायः फॉर्म के सम्मिश्र-मूल्यवान फलनों के रूप में लिखा जाता है | ||
<math display=block>x(t) = \operatorname{Re} \{X( t ) \} </math> | <math display=block>x(t) = \operatorname{Re} \{X( t ) \} </math> | ||
| Line 559: | Line 553: | ||
<math display=block>X( t ) = A e^{i\omega t} = a e^{ i \phi } e^{i\omega t} = a e^{i (\omega t + \phi) } </math> | <math display=block>X( t ) = A e^{i\omega t} = a e^{ i \phi } e^{i\omega t} = a e^{i (\omega t + \phi) } </math> | ||
जहां and [[ कोणीय आवृत्ति ]] का प्रतिनिधित्व करता है और | जहां and [[ कोणीय आवृत्ति ]] का प्रतिनिधित्व करता है और सम्मिश्र संख्या ए चरण और आयाम को एन्कोड करता है जैसा कि ऊपर बताया गया है। | ||
इस उपयोग को [[ अंकीय संकेत प्रक्रिया ]] और [[ डिजिटल इमेज प्रोसेसिंग ]] में भी विस्तारित किया जाता है, जो ट्रांसमिट, डेटा संपीड़न, रिस्टोर और अन्यथा [[ डिजिटल डाटा ]] [[ आवाज़ ]] सिग्नल, स्टिल इमेज और [[ वीडियो ]] सिग्नल को प्रसारित करने के लिए फूरियर एनालिसिस (और [[ छोटा लहर ]] एनालिसिस) के डिजिटल संस्करणों का उपयोग करते हैं। | इस उपयोग को [[ अंकीय संकेत प्रक्रिया ]] और [[ डिजिटल इमेज प्रोसेसिंग ]] में भी विस्तारित किया जाता है, जो ट्रांसमिट, डेटा संपीड़न, रिस्टोर और अन्यथा [[ डिजिटल डाटा ]] [[ आवाज़ ]] सिग्नल, स्टिल इमेज और [[ वीडियो ]] सिग्नल को प्रसारित करने के लिए फूरियर एनालिसिस (और [[ छोटा लहर ]] एनालिसिस) के डिजिटल संस्करणों का उपयोग करते हैं। | ||
| Line 579: | Line 573: | ||
==== इलेक्ट्रोमैग्नेटिज्म और इलेक्ट्रिकल इंजीनियरिंग ==== | ==== इलेक्ट्रोमैग्नेटिज्म और इलेक्ट्रिकल इंजीनियरिंग ==== | ||
{{Main|Alternating current}} | {{Main|Alternating current}} | ||
इलेक्ट्रिकल इंजीनियरिंग में, [[ फूरियर रूपांतरण ]] का उपयोग अलग -अलग [[ वोल्टेज ]] और इलेक्ट्रिक करंट का विश्लेषण करने के लिए किया जाता है।प्रतिरोधों, [[ संधारित्र ]], और [[ प्रारंभ करनेवाला ]]ों के उपचार को बाद में दो के लिए काल्पनिक, आवृत्ति-निर्भर प्रतिरोधों को पेश करके और तीनों को एक | इलेक्ट्रिकल इंजीनियरिंग में, [[ फूरियर रूपांतरण ]] का उपयोग अलग -अलग [[ वोल्टेज ]] और इलेक्ट्रिक करंट का विश्लेषण करने के लिए किया जाता है।प्रतिरोधों, [[ संधारित्र ]], और [[ प्रारंभ करनेवाला ]]ों के उपचार को बाद में दो के लिए काल्पनिक, आवृत्ति-निर्भर प्रतिरोधों को पेश करके और तीनों को एक सम्मिश्र संख्या में मिलकर [[ विद्युत प्रतिबाधा ]] नामक एक सम्मिश्र संख्या में एकीकृत किया जा सकता है।इस दृष्टिकोण को [[ फासोर ]] कैलकुलस कहा जाता है। | ||
इलेक्ट्रिकल इंजीनियरिंग में, काल्पनिक इकाई को निरूपित किया जाता है {{mvar|j}}, भ्रम से बचने के लिए {{mvar|I}}, जो | इलेक्ट्रिकल इंजीनियरिंग में, काल्पनिक इकाई को निरूपित किया जाता है {{mvar|j}}, भ्रम से बचने के लिए {{mvar|I}}, जो सामान्य रूप से विद्युत प्रवाह को निरूपित करने के लिए उपयोग में होता है, या, विशेष रूप से, {{mvar|i}}, जो सामान्य रूप से तात्कालिक विद्युत प्रवाह को निरूपित करने के लिए उपयोग में होता है। | ||
चूंकि एक एसी [[ विद्युत परिपथ ]] में वोल्टेज दोलन कर रहा है, इसलिए इसका प्रतिनिधित्व किया जा सकता है | चूंकि एक एसी [[ विद्युत परिपथ ]] में वोल्टेज दोलन कर रहा है, इसलिए इसका प्रतिनिधित्व किया जा सकता है | ||
<math display=block> V(t) = V_0 e^{j \omega t} = V_0 \left (\cos\omega t + j \sin\omega t \right ),</math> | <math display=block> V(t) = V_0 e^{j \omega t} = V_0 \left (\cos\omega t + j \sin\omega t \right ),</math> | ||
औसत दर्जे की मात्रा प्राप्त करने के लिए, वास्तविक | औसत दर्जे की मात्रा प्राप्त करने के लिए, वास्तविक भाग लिया जाता है: | ||
<math display=block> v(t) = \operatorname{Re}(V) = \operatorname{Re}\left [ V_0 e^{j \omega t} \right ] = V_0 \cos \omega t.</math> | <math display=block> v(t) = \operatorname{Re}(V) = \operatorname{Re}\left [ V_0 e^{j \omega t} \right ] = V_0 \cos \omega t.</math> | ||
सम्मिश्र-मूल्यवान संकेत {{math|''V''(''t'')}} वास्तविक-मूल्यवान, औसत दर्जे के संकेत का [[ विश्लेषणात्मक संकेत ]] प्रतिनिधित्व कहा जाता है {{math|''v''(''t'')}}. | |||
<ref>{{cite book |last1=Grant |first1=I.S. |title=विद्युत चुंबकत्व|year=2008|edition=2 |publisher=Manchester Physics Series |isbn=978-0-471-92712-9 |last2=Phillips |first2=W.R.}}</ref> | <ref>{{cite book |last1=Grant |first1=I.S. |title=विद्युत चुंबकत्व|year=2008|edition=2 |publisher=Manchester Physics Series |isbn=978-0-471-92712-9 |last2=Phillips |first2=W.R.}}</ref> | ||
==== द्रव की गतिशीलता ==== | ==== द्रव की गतिशीलता ==== | ||
द्रव की गतिशीलता में, [[ दो आयामों में संभावित प्रवाह ]] का वर्णन करने के लिए | द्रव की गतिशीलता में, [[ दो आयामों में संभावित प्रवाह ]] का वर्णन करने के लिए सम्मिश्र फलनों का उपयोग किया जाता है। | ||
==== क्वांटम यांत्रिकी ==== | ==== क्वांटम यांत्रिकी ==== | ||
सम्मिश्र संख्या क्षेत्र [[ क्वांटम यांत्रिकी के गणितीय योग ]]ों के लिए आंतरिक है, जहां सम्मिश्र [[ हिल्बर्ट स्पेस ]] एक ऐसे सूत्रीकरण के लिए संदर्भ प्रदान करते हैं जो सुविधाजनक और शायद सबसे मानक है।क्वांटम यांत्रिकी के मूल नींव सूत्र - श्रोडिंगर समीकरण और हाइजेनबर्ग के [[ मैट्रिक्स यांत्रिकी | आव्यूह यांत्रिकी]] - सम्मिश्र संख्याओं का उपयोग करते हैं। | |||
==== सापेक्षता ==== | ==== सापेक्षता ==== | ||
[[ विशेष सापेक्षता ]] और [[ सामान्य सापेक्षता ]] में, [[ अंतरिक्ष समय ]] पर मीट्रिक के लिए कुछ सूत्र सरल हो जाते हैं यदि कोई स्पेसटाइम कॉन्टिनम के समय घटक को काल्पनिक होने के लिए लेता है।(यह दृष्टिकोण शास्त्रीय सापेक्षता में अब मानक नहीं है, लेकिन [[ क्वांटम क्षेत्र सिद्धांत ]] में [[ वीक रोटेशन ]] है।) | [[ विशेष सापेक्षता ]] और [[ सामान्य सापेक्षता ]] में, [[ अंतरिक्ष समय ]] पर मीट्रिक के लिए कुछ सूत्र सरल हो जाते हैं यदि कोई स्पेसटाइम कॉन्टिनम के समय घटक को काल्पनिक होने के लिए लेता है।(यह दृष्टिकोण शास्त्रीय सापेक्षता में अब मानक नहीं है, लेकिन [[ क्वांटम क्षेत्र सिद्धांत ]] में [[ वीक रोटेशन | वीक घूर्णन]] है।) सम्मिश्र संख्या [[ स्पिनर ]]ों के लिए आवश्यक हैं, जो सापेक्षता में उपयोग किए जाने वाले [[ टेन्सर ]]्स का एक सामान्यीकरण हैं। | ||
== सामान्यीकरण और संबंधित धारणाएँ == | == सामान्यीकरण और संबंधित धारणाएँ == | ||
[[File:Cayley_Q8_quaternion_multiplication_graph.svg|thumb|upright=1.05 | [[File:Cayley_Q8_quaternion_multiplication_graph.svg|thumb|upright=1.05| केली Q8 चतुष्कोणीय ग्राफ i, j और k द्वारा गुणन के चक्रों को दर्शाता है]]क्षेत्र को विस्तारित करने की प्रक्रिया <math>\mathbb R</math> के लिए <math>\mathbb C</math> केली -डिकसन कंस्ट्रक्शन के रूप में जाना जाता है।इसे और अधिक आयामों तक ले जाया जा सकता है, चतुर्भुजों की उपज <math>\mathbb H</math> और [[ अष्टक ]]्स <math>\mathbb{O}</math> जो (एक वास्तविक वेक्टर अंतरिक्ष के रूप में) क्रमशः आयाम & nbsp; 4 और 8 के हैं। | ||
इस संदर्भ में | इस संदर्भ में सम्मिश्र संख्याओं को बिनरियन कहा गया है।<ref>{{cite book |first=Kevin |last=McCrimmon |year=2004 |title=जॉर्डन बीजगणित का स्वाद|page=64 |series=Universitext |publisher=Springer |isbn=0-387-95447-3}} {{mr|id=2014924}}</ref> | ||
जिस तरह निर्माण को | जिस तरह निर्माण को प्रयुक्त करने से ऑर्डर किए गए क्षेत्र की संपत्ति खो जाती है, वास्तविक और सम्मिश्र संख्याओं से परिचित गुण प्रत्येक एक्सटेंशन के साथ गायब हो जाते हैं।चतुर्भुज कमज़ोरता खो देते हैं, अर्थात्, {{math|''x''·''y'' ≠ ''y''·''x''}} कुछ चतुर्भुजों के लिए {{math|''x'', ''y''}}, और ऑक्टोनियन का गुणन, इसके अतिरिक्त कम्यूटेटिव नहीं होने के कारण, साहचर्य होने में विफल रहता है: {{math|(''x''·''y'')·''z'' ≠ ''x''·(''y''·''z'')}} कुछ पोषण के लिए {{math|''x'', ''y'', ''z''}}। | ||
रियल, | रियल, सम्मिश्र संख्या, चतुर्भुज और ऑक्टोनियन सभी [[ मानदंड विभाजन बीजगणित ]] हैं <math>\mathbb R</math>।हर्विट्ज़ के प्रमेय (मानदंड विभाजन aggebras) द्वारा | हर्विट्ज़ के प्रमेय वे केवल एक ही हैं;[[ धब्बा ]]्स, केली -डिकसन कंस्ट्रक्शन में अगला कदम, इस संरचना में विफल रहता है। | ||
केली -डिकसन निर्माण के [[ नियमित प्रतिनिधित्व ]] से निकटता से संबंधित है <math>\mathbb C,</math> के रूप में सोचा <math>\mathbb R</math>-लगेबरा ( | केली -डिकसन निर्माण के [[ नियमित प्रतिनिधित्व ]] से निकटता से संबंधित है <math>\mathbb C,</math> के रूप में सोचा <math>\mathbb R</math>-लगेबरा (वलय थ्योरी) (ए) <math>\mathbb{R}</math>आधार के संबंध में, एक गुणन के साथ अंतरिक्ष) {{math|(1, ''i'')}}।इसका तात्पर्य है निम्नलिखित: <math>\mathbb R</math>-लाइनर मैप | ||
<math display=block>\begin{align} | <math display=block>\begin{align} | ||
\mathbb{C} &\rightarrow \mathbb{C} \\ | \mathbb{C} &\rightarrow \mathbb{C} \\ | ||
z &\mapsto wz | z &\mapsto wz | ||
\end{align}</math> | \end{align}</math> | ||
कुछ निश्चित | कुछ निश्चित सम्मिश्र संख्या के लिए {{mvar|w}} एक द्वारा प्रतिनिधित्व किया जा सकता है {{math|2 × 2}} आव्यूह (एक बार एक आधार चुना गया है)।आधार के संबंध में {{math|(1, ''i'')}}, यह आव्यूह है | ||
<math display=block>\begin{pmatrix} | <math display=block>\begin{pmatrix} | ||
\operatorname{Re}(w) & -\operatorname{Im}(w) \\ | \operatorname{Re}(w) & -\operatorname{Im}(w) \\ | ||
\operatorname{Im}(w) & \operatorname{Re}(w) | \operatorname{Im}(w) & \operatorname{Re}(w) | ||
\end{pmatrix},</math> | \end{pmatrix},</math> | ||
अर्थात, ऊपर सम्मिश्र संख्याओं के आव्यूह प्रतिनिधित्व पर अनुभाग में उल्लेख किया गया है।जबकि यह एक [[ रैखिक प्रतिनिधित्व ]] है <math>\mathbb C</math> 2 × 2 वास्तविक मैट्रिसेस में, यह केवल एक ही नहीं है।कोई आव्यूह | |||
<math display=block>J = \begin{pmatrix}p & q \\ r & -p \end{pmatrix}, \quad p^2 + qr + 1 = 0</math> | <math display=block>J = \begin{pmatrix}p & q \\ r & -p \end{pmatrix}, \quad p^2 + qr + 1 = 0</math> | ||
क्या संपत्ति है कि इसका वर्ग पहचान | क्या संपत्ति है कि इसका वर्ग पहचान आव्यूह का ऋणात्मक है: {{math|1=''J''<sup>2</sup> = −''I''}}।फिर | ||
<math display=block>\{ z = a I + b J : a,b \in \mathbb{R} \}</math> | <math display=block>\{ z = a I + b J : a,b \in \mathbb{R} \}</math> | ||
क्षेत्र के लिए भी | क्षेत्र के लिए भी समरूपीय है <math>\mathbb C,</math> और एक वैकल्पिक सम्मिश्र संरचना देता है <math>\mathbb R^2.</math> यह एक [[ रैखिक जटिल संरचना | रैखिक सम्मिश्र संरचना]] की धारणा से सामान्यीकृत है। | ||
[[ हाइपरकम्प्लेक्स संख्या ]] भी सामान्यीकरण करती है <math>\mathbb R,</math> <math>\mathbb C,</math> <math>\mathbb H,</math> और <math>\mathbb{O}.</math> उदाहरण के लिए, इस धारणा में [[ विभाजित-संकलन संख्या ]] | [[ हाइपरकम्प्लेक्स संख्या ]] भी सामान्यीकरण करती है <math>\mathbb R,</math> <math>\mathbb C,</math> <math>\mathbb H,</math> और <math>\mathbb{O}.</math> उदाहरण के लिए, इस धारणा में [[ विभाजित-संकलन संख्या ]] सम्मिलित हैं, जो वलय के तत्व हैं <math>\mathbb R[x]/(x^2-1)</math> (विरोध के रूप में <math>\mathbb R[x]/(x^2+1)</math> सम्मिश्र संख्याओं के लिए)।इस वलय में, समीकरण {{math|1=''a''<sup>2</sup> = 1}} चार समाधान हैं। | ||
फील्ड <math>\mathbb R</math> का पूरा होना <math>\mathbb Q,</math> सामान्य निरपेक्ष मूल्य मीट्रिक (गणित) के संबंध में तर्कसंगत संख्याओं का क्षेत्र।मीट्रिक (गणित) के अन्य विकल्प पर <math>\mathbb Q</math> खेतों के लिए नेतृत्व करें <math>\mathbb Q_p</math> पी-एडिक नंबर का |{{mvar|p}}-एक नंबर (किसी भी प्रमुख संख्या के लिए) {{mvar|p}}), जो इस प्रकार अनुरूप हैं <math>\mathbb{R}</math>।पूरा करने के कोई अन्य nontrivial तरीके नहीं हैं <math>\mathbb Q</math> से <math>\mathbb R</math> और <math>\mathbb Q_p,</math> ओस्ट्रोव्स्की के प्रमेय द्वारा।बीजीय | फील्ड <math>\mathbb R</math> का पूरा होना <math>\mathbb Q,</math> सामान्य निरपेक्ष मूल्य मीट्रिक (गणित) के संबंध में तर्कसंगत संख्याओं का क्षेत्र।मीट्रिक (गणित) के अन्य विकल्प पर <math>\mathbb Q</math> खेतों के लिए नेतृत्व करें <math>\mathbb Q_p</math> पी-एडिक नंबर का |{{mvar|p}}-एक नंबर (किसी भी प्रमुख संख्या के लिए) {{mvar|p}}), जो इस प्रकार अनुरूप हैं <math>\mathbb{R}</math>।पूरा करने के कोई अन्य nontrivial तरीके नहीं हैं <math>\mathbb Q</math> से <math>\mathbb R</math> और <math>\mathbb Q_p,</math> ओस्ट्रोव्स्की के प्रमेय द्वारा।बीजीय संवृत हो जाता है <math>\overline {\mathbb{Q}_p}</math> का <math>\mathbb Q_p</math> अभी भी एक आदर्श ले जाता है, लेकिन (इसके विपरीत) <math>\mathbb C</math>) इसके संबंध में पूरा नहीं है।पूर्ण <math>\mathbb{C}_p</math> का <math>\overline {\mathbb{Q}_p}</math> बीजगणित रूप से संवृत हो जाता है।सादृश्य द्वारा, क्षेत्र को कहा जाता है {{mvar|p}}-एक सम्मिश्र संख्या। | ||
खेत <math>\mathbb R,</math> <math>\mathbb Q_p,</math> और उनके परिमित क्षेत्र एक्सटेंशन, सहित <math>\mathbb C,</math> [[ स्थानीय क्षेत्र ]] कहा जाता है। | खेत <math>\mathbb R,</math> <math>\mathbb Q_p,</math> और उनके परिमित क्षेत्र एक्सटेंशन, सहित <math>\mathbb C,</math> [[ स्थानीय क्षेत्र ]] कहा जाता है। | ||
| Line 634: | Line 628: | ||
{{Commons category|Complex numbers}} | {{Commons category|Complex numbers}} | ||
* बीजगणितीय सतह | * बीजगणितीय सतह | ||
* | * सम्मिश्र संख्याओं का उपयोग करते हुए वृत्ताकार गति | ||
* [[ जटिल आधार प्रणाली ]] | * [[ जटिल आधार प्रणाली | सम्मिश्र आधार प्रणाली]] | ||
* [[ जटिल ज्यामिति ]] | * [[ जटिल ज्यामिति | सम्मिश्र ज्यामिति]] | ||
* दोहरी- | * दोहरी-सम्मिश्र संख्या | ||
* | * आइज़ेंस्टीन पूर्णांक | ||
* यूलर की पहचान | * यूलर की पहचान | ||
* ज्यामितीय बीजगणित#यूनिट Pseudoscalars (जिसमें 2-आयामी | * ज्यामितीय बीजगणित#यूनिट Pseudoscalars (जिसमें 2-आयामी संदिश उप-समष्टि <math>\mathcal{G}_2^+</math> के रूप में सम्मिश्र समतल सम्मिलित है) | ||
* [[ एकक जटिल संख्या ]] | * [[ एकक जटिल संख्या | एकक सम्मिश्र संख्या]] | ||
{{Classification of numbers}} | {{Classification of numbers}} | ||
| Line 703: | Line 697: | ||
{{DEFAULTSORT:Complex Number}} | {{DEFAULTSORT:Complex Number}} | ||
श्रेणी: रचना बीजगणित | श्रेणी: रचना बीजगणित | ||
श्रेणी: | श्रेणी: सम्मिश्र संख्याएँ | ||
[[Category: Machine Translated Page]] | [[Category: Machine Translated Page]] | ||
[[Category:Created On 19/12/2022]] | [[Category:Created On 19/12/2022]] | ||
Revision as of 19:25, 19 March 2023
गणित में, एक सम्मिश्र संख्या एक संख्या प्रणाली का एक तत्व है जो वास्तविक संख्याओं को एक विशिष्ट तत्व के साथ विस्तारित करता है जिसे i कहा जाता है, जिसे काल्पनिक इकाई कहा जाता है और समीकरण को संतुष्ट करता है; प्रत्येक सम्मिश्र संख्या को के रूप में व्यक्त किया जा सकता है, जहां a और b वास्तविक संख्याएं हैं।क्योंकि कोई भी वास्तविक संख्या उपरोक्त समीकरण को संतुष्ट नहीं करती है, रेने डेसकार्टेस द्वारा i एक काल्पनिक संख्या कहा जाता था। सम्मिश्र संख्या के लिए a को वास्तविक भाग और b को काल्पनिक भाग कहा जाता है। सम्मिश्र संख्याओं के समुच्चय को या C प्रतीकों में से किसी एक द्वारा निरूपित किया जाता है। ऐतिहासिक नामकरण काल्पनिक के होते हुए भी, सम्मिश्र संख्याओं को गणितीय विज्ञान में वास्तविक संख्या के समान वास्तविक माना जाता है और प्राकृतिक विश्व के वैज्ञानिक विवरण के कई स्वरूपों में मौलिक हैं।[1][lower-alpha 1]
सम्मिश्र संख्याएं सभी बहुपद समीकरण के समाधान की स्वीकृति देती हैं, यहां तक कि जिनके पास वास्तविक संख्याओं में कोई समाधान नहीं है। अधिक परिशुद्ध रूप से, बीजगणित के मौलिक प्रमेय का दावा है कि वास्तविक या सम्मिश्र गुणांक के साथ प्रत्येक गैर-निरंतर बहुपद समीकरण का एक समाधान होता है जो एक सम्मिश्र संख्या है।उदाहरण के लिए, समीकरण कोई वास्तविक समाधान नहीं है, क्योंकि एक वास्तविक संख्या का वर्ग ऋणात्मक नहीं हो सकता है, लेकिन दो गैर -सम्मिश्र सम्मिश्र समाधान हैं और ।
जोड़ का उपयोग करके सम्मिश्र संख्याओं के जोड़, घटाव और गुणन को स्वाभाविक रूप से परिभाषित किया जा सकता है साहचर्य नियम, विनिमेय नियम और वितरण नियम के साथ संयुक्त।प्रत्येक नॉनज़ेरो सम्मिश्र संख्या में एक गुणक उलटा होता है।यह सम्मिश्र संख्याओं को एक क्षेत्र (गणित) बनाता है जिसमें एक उप-क्षेत्र के रूप में वास्तविक संख्या होती है।सम्मिश्र संख्या भी आयाम दो का एक वास्तविक वेक्टर समष्टि बनाती है, {1, i} एक मानक आधार के रूप में।
यह मानक आधार सम्मिश्र संख्याओं को एक कार्टेशियन विमान बनाता है, जिसे सम्मिश्र समतल कहा जाता है।यह सम्मिश्र संख्याओं और उनके संचालन की एक ज्यामितीय व्याख्या की स्वीकृति देता है, और इसके विपरीत सम्मिश्र संख्याओं के संदर्भ में कुछ ज्यामितीय गुणों और निर्माणों को व्यक्त करता है।उदाहरण के लिए, वास्तविक संख्या वास्तविक रेखा का निर्माण करती है जिसे सम्मिश्र समतल के क्षैतिज अक्ष के लिए पहचाना जाता है।निरपेक्ष मान की सम्मिश्र संख्या एक एकक व्रत का निर्माण करती है।एक सम्मिश्र संख्या के अतिरिक्त सम्मिश्र समतल में एक अनुवाद (ज्यामिति) है, और एक सम्मिश्र संख्या से गुणा मूल में केंद्रित एक समानता (ज्यामिति) है। सम्मिश्र संयुग्मन वास्तविक अक्ष के संबंध में प्रतिबिंब समरूपता है।सम्मिश्र निरपेक्ष मान एक यूक्लिडियन मानदंड है।
सारांश में, सम्मिश्र संख्या एक समृद्ध संरचना बनाती है जो एक साथ एक बीजगणितीय रूप से संवृत क्षेत्र है, जो वास्तविक पर एक कम्यूटेटिव बीजगणित (संरचना) है, और आयाम दो का एक यूक्लिडियन वेक्टर समष्टि है।
परिभाषा
एक सम्मिश्र संख्या फॉर्म की एक संख्या है a + bi, कहां a और b वास्तविक संख्याएं हैं, और i एक अनिश्चित संतोषजनक है i2 = −1।उदाहरण के लिए, 2 + 3i एक सम्मिश्र संख्या है।[3]
इस तरह, एक सम्मिश्र संख्या को एकल अनिश्चितता में वास्तविक गुणांक के साथ एक बहुपद के रूप में परिभाषित किया गया है i, जिसके लिए संबंध i2 + 1 = 0 लगाया जाता है।इस परिभाषा के आधार पर, बहुपद के लिए जोड़ और गुणन का उपयोग करके सम्मिश्र संख्याओं को जोड़ा और गुणा किया जा सकता है।रिश्ता i2 + 1 = 0 समानता को प्रेरित करता है i4k = 1, i4k+1 = i, i4k+2 = −1, और i4k+3 = −i, जो सभी पूर्णांक के लिए पकड़ है k;ये किसी भी बहुपद को कम करने की स्वीकृति देते हैं जो सम्मिश्र संख्याओं के जोड़ और गुणन से एक रैखिक बहुपद में परिणाम देता है i, फिर से फॉर्म a + bi वास्तविक गुणांक के साथ a, b. असली संख्या a सम्मिश्र संख्या का वास्तविक भाग कहा जाता है a + bi;असली संख्या b इसका काल्पनिक भाग कहा जाता है। जोर देने के लिए, काल्पनिक भाग में एक कारक सम्मिलित नहीं है i;अर्थात्, काल्पनिक भाग है b, नहीं bi.[4][5] औपचारिक रूप से, सम्मिश्र संख्याओं को अनिश्चितता में बहुपद वलय के भागफल वलय के रूप में परिभाषित किया गया है i, बहुपद द्वारा उत्पन्न आदर्श (वलय थ्योरी) द्वारा i2 + 1 ।Bourbaki 1998, §VIII.1</ref>
संकेतन
एक वास्तविक संख्या a एक सम्मिश्र संख्या के रूप में माना जा सकता है a + 0i, जिसका काल्पनिक भाग 0. एक विशुद्ध रूप से काल्पनिक संख्या है bi एक सम्मिश्र संख्या है 0 + bi, जिसका असली भाग शून्य है।बहुपद के साथ, यह लिखना आम है a के लिए a + 0i और bi के लिए 0 + bi।इसके अतिरिक्त, जब काल्पनिक भाग ऋणात्मक है, अर्थात्, b = −|b| < 0, यह लिखना आम है a − |b|i के अतिरिक्त a + (−|b|)i;उदाहरण के लिए, के लिए b = −4, 3 − 4i के अतिरिक्त लिखा जा सकता है 3 + (−4)i।
अनिश्चित के गुणन के बाद से i और एक वास्तविक वास्तविक गुणांक, बहुपद के साथ बहुपद में कम्यूटेटिव है a + bi के रूप में लिखा जा सकता है a + ib. यह प्रायः अभिव्यक्तियों द्वारा निरूपित काल्पनिक भागों के लिए समीचीन होता है, उदाहरण के लिए, जब, जब b एक कट्टरपंथी है।[6] एक सम्मिश्र संख्या का वास्तविक भाग z द्वारा निरूपित किया गया है Re(z), , या ;एक सम्मिश्र संख्या का काल्पनिक भाग z द्वारा निरूपित किया गया है Im(z), , या उदाहरण के लिए,
कुछ विषयों में, विशेष रूप से इलेक्ट्रोमैग्नेटिज्म और [[ विद्युत अभियन्त्रण ]] में, j के अतिरिक्त उपयोग किया जाता है i जैसा i प्रायः विद्युत प्रवाह का प्रतिनिधित्व करने के लिए उपयोग किया जाता है।[7] इन स्थितियों में, सम्मिश्र संख्याओं को लिखा जाता है a + bj, या a + jb।
विज़ुअलाइज़ेशन
एक सम्मिश्र संख्या z इस प्रकार एक क्रमित जोड़ी के साथ पहचाना जा सकता है वास्तविक संख्याओं में से, जिसे बदले में दो आयामी समष्टि में एक बिंदु के निर्देशांक के रूप में व्याख्या की जा सकती है। सबसे तत्काल समष्टि उपयुक्त निर्देशांक के साथ यूक्लिडियन विमान है, जिसे तब सम्मिश्र समतल या आर्गन आरेख कहा जाता है,[8][lower-alpha 2][9] जीन-रॉबर्ट फाइट के नाम पर।एक और प्रमुख समष्टि जिस पर निर्देशांक का अनुमान लगाया जा सकता है, वह एक क्षेत्र की दो-आयामी सतह है, जिसे तब रीमैन क्षेत्र कहा जाता है।
कार्टेशियन सम्मिश्र प्लेन
दो मनमाने वास्तविक मूल्यों को सम्मिलित करने वाली सम्मिश्र संख्याओं की परिभाषा तुरंत सम्मिश्र समतल में कार्टेशियन निर्देशांक के उपयोग का सुझाव देती है।क्षैतिज (वास्तविक) अक्ष का उपयोग सामान्य रूप से वास्तविक भाग को प्रदर्शित करने के लिए किया जाता है, दाईं ओर बढ़ते मूल्यों के साथ, और काल्पनिक भाग ऊर्ध्वाधर (काल्पनिक) अक्ष को चिह्नित करता है, जिसमें मूल्यों को ऊपर की ओर बढ़ता है।
एक चार्टेड संख्या को या तो विक्ट के रूप में देखा जा सकता है: समन्वय बिंदु या इस बिंदु तक मूल से एक वेक्टर (ज्यामितीय) के रूप में।एक सम्मिश्र संख्या के समन्वय मान z इसलिए इसके कार्टेशियन, आयताकार या बीजीय रूप में व्यक्त किया जा सकता है।
विशेष रूप से, जोड़ और गुणन के संचालन एक बहुत ही प्राकृतिक ज्यामितीय चरित्र पर ले जाते हैं, जब सम्मिश्र संख्याओं को स्थिति वैक्टर के रूप में देखा जाता है: इसके अतिरिक्त यूक्लिडियन वेक्टर #जोड़ और घटाव से अनुरूप है, जबकि गुणा (देखें #multiplication और ध्रुवीय रूप में विभाजन) कई गुणा करने से मेल खाती है।उनके परिमाण और वे कोण जो वे वास्तविक अक्ष के साथ बनाते हैं।इस तरह से देखा गया, एक सम्मिश्र संख्या का गुणन i मूल के बारे में एक चौथाई मोड़ (ज्यामिति) (ज्यामिति) (सही कोण | 90 °) द्वारा स्थिति वेक्टर ओरिएंटेशन (ज्यामिति) को घुमाने के लिए अनुरूप है - एक तथ्य जिसे बीजगणितीय रूप से इस प्रकार व्यक्त किया जा सकता है:
ध्रुवीय सम्मिश्र समतल
मापांक और तर्क
सम्मिश्र समतल में निर्देशांक के लिए एक वैकल्पिक विकल्प ध्रुवीय समन्वय प्रणाली है जो बिंदु की दूरी का उपयोग करता है z मूल (गणित) से (O), और कोण धनात्मक वास्तविक अक्ष और लाइन खंड के बीच घटाया गया Oz एक वामावर्त अर्थों में। यह ध्रुवीय रूप की ओर जाता है
एक सम्मिश्र संख्या का, जहां r का पूर्ण मूल्य है z, और का तर्क (सम्मिश्र विश्लेषण) है z।
एक सम्मिश्र संख्या का निरपेक्ष मान (या मापांक या परिमाण) z = x + yi है[10]
पाइथागोरस के प्रमेय द्वारा, एक सम्मिश्र संख्या का निरपेक्ष मान सम्मिश्र समतल में सम्मिश्र संख्या का प्रतिनिधित्व करने वाले बिंदु की उत्पत्ति की दूरी है।
का तर्क z (चरण के रूप में संदर्भित कई अनुप्रयोगों में φ)[9]त्रिज्या का कोण है Oz धनात्मक वास्तविक अक्ष के साथ, और के रूप में लिखा गया है arg z।मापांक के साथ, तर्क आयताकार रूप से पाया जा सकता है x + yi[11]—मैं कालीन-दर-वास्तविक भागों के भागफल के लिए उलटा स्पर्शरेखा को प्रयुक्त करना।एक आधा-कोण पहचान का उपयोग करके, आर्कटन की एक एकल शाखा रेंज को कवर करने के लिए पर्याप्त है (−π, π] की arg-फंक्शन, और एक अधिक सूक्ष्म स्थिति-दर-मामला विश्लेषण से बचा जाता है
का मूल्य φ ATAN2 के परिणाम के बराबर है:
सम्मिश्र रेखांकन
सम्मिश्र विश्लेषण की कल्पना करते समय, एक सम्मिश्र इनपुट और आउटपुट दोनों की आवश्यकता होती है।क्योंकि प्रत्येक सम्मिश्र संख्या को दो आयामों में दर्शाया जाता है, दृष्टिगत रूप से एक सम्मिश्र फलन को रेखांकन करने के लिए चार आयामी समष्टि की धारणा की आवश्यकता होगी, जो केवल अनुमानों में संभव है।इस वजह से, सम्मिश्र फलनों को देखने के अन्य तरीकों को डिजाइन किया गया है।
प्रक्षेत्र रंग में आउटपुट आयामों को क्रमशः रंग और चमक द्वारा दर्शाया जाता है।प्रक्षेत्र के रूप में सम्मिश्र समतल में प्रत्येक बिंदु को अलंकृत किया जाता है, सामान्य रूप से रंग के साथ सम्मिश्र संख्या के तर्क का प्रतिनिधित्व करते हैं, और चमक का प्रतिनिधित्व करते हुए चमक।डार्क स्पॉट्स मार्क मोडुली शून्य के पास, उज्जवल धब्बे मूल से दूर हैं, ग्रेडेशन संवृत हो सकता है, लेकिन इसे नीरस माना जाता है।रंग प्रायः चरणों में भिन्न होते हैं π/3 के लिए 0 को 2π लाल, पीले, हरे, सियान, नीले, से मैजेंटा तक।इन भूखंडों को प्रक्षेत्र रंग कहा जाता है।यह जानकारी खोए बिना फलनों की कल्पना करने का एक सरल तरीका प्रदान करता है।चित्र के लिए शून्य दिखाता है ±1, (2 + i) और पर ध्रुव
इतिहास
एक सामान्य क्यूबिक समीकरण के एनटीएच रूट ( त्रिकोणमितीय फलनो के बिना) में समाधान, जब इसकी तीनों जड़ें वास्तविक संख्याएँ होती हैं, तो ऋणात्मक संख्याओं की वर्ग जड़ें होती हैं, एक ऐसी स्थिति जो तर्कसंगत रूट परीक्षण द्वारा सहायता प्राप्त की जा सकती है, यदिक्यूबिक इरेड्यूसिबल बहुपद है;यह तथाकथित कैसस irreducibilis (irreducible मामला) है।इस conundrum ने इतालवी गणितज्ञ Gerolamo Cardano को अपने Ars Magna में लगभग 1545 में सम्मिश्र संख्याओं की कल्पना करने के लिए प्रेरित किया,[13] हालांकि उनकी समझ अल्पविकसित थी;इसके अतिरिक्त उन्होंने बाद में सम्मिश्र संख्याओं को सूक्ष्म रूप से खारिज कर दिया क्योंकि वे बेकार हैं।[14] कार्डानो ने काल्पनिक संख्याओं का उपयोग किया, लेकिन उन्हें "मानसिक यातना" के रूप में उपयोग किया गया। [15] यह ग्राफिकल सम्मिश्र प्लेन के उपयोग से पहले था।कार्डानो और अन्य इतालवी गणितज्ञ, विशेष रूप से स्किपिओन डेल फेरो , 1500 के दशक में, क्यूबिक समीकरणों को हल करने के लिए एक एल्गोरिथ्म बनाया गया था जिसमें सामान्य रूप से एक वास्तविक समाधान और दो समाधान थे जिसमें एक काल्पनिक संख्या थी।चूंकि उन्होंने काल्पनिक संख्याओं के साथ उत्तरों को नजरअंदाज कर दिया था, कार्डानो ने उन्हें बेकार पाया।[16] सामान्य बहुपदों की समस्या पर काम करें अंततः बीजगणित के मौलिक प्रमेय का नेतृत्व किया, जो दर्शाता है कि सम्मिश्र संख्याओं के साथ, एक समाधान डिग्री एक या उच्चतर के प्रत्येक बहुपद समीकरण के लिए मौजूद है।सम्मिश्र संख्या इस प्रकार एक बीजगणितीय रूप से संवृत क्षेत्र का निर्माण करती है, जहां किसी भी बहुपद समीकरण में एक फलन की जड़ होती है।
कई गणितज्ञों ने सम्मिश्र संख्याओं के विकास में योगदान दिया।इतालवी गणितज्ञ राफेल बॉम्बेली द्वारा सम्मिश्र संख्याओं के जोड़, घटाव, गुणन और रूट निष्कर्षण के नियमों को विकसित किया गया था।[17] सम्मिश्र संख्याओं के लिए एक अधिक अमूर्त औपचारिकता को आयरिश गणितज्ञ विलियम रोवन हैमिल्टन द्वारा विकसित किया गया था, जिन्होंने इस अमूर्तता को चतुर्भुज के सिद्धांत तक बढ़ाया।[18] ऋणात्मक संख्याओं की चौकोर जड़ों के लिए जल्द से जल्द क्षणभंगुर संदर्भ शायद पहली शताब्दी ईस्वी में अलेक्जेंड्रिया के हेलेनिस्टिक गणित नायक के काम में होने के लिए कहा जा सकता है, जहां अलेक्जेंड्रिया#ग्रंथ सूची के अपने नायक में उन्होंने माना, जाहिर तौर पर गलती से, की मात्रा, की मात्रा मेंशब्द पर पहुंचने के लिए एक पिरामिड का एक असंभव टुकड़ा उनकी गणना में, जो आज सरल हो जाएगा ।ऋणात्मक मात्रा में हेलेनिस्टिक गणित में कल्पना नहीं की गई थी और नायक ने इसे केवल इसके धनात्मक द्वारा प्रतिस्थापित किया था [19] अपने आप में एक विषय के रूप में सम्मिश्र संख्याओं का अध्ययन करने के लिए प्रेरणा पहली बार 16 वीं शताब्दी में उत्पन्न हुई जब क्यूबिक समीकरण और चतुर्थक समीकरण बहुपद की जड़ों के लिए बीजगणितीय समाधान इतालवी गणितज्ञों द्वारा खोजे गए (निकोलो फोंटाना टार्टग्लिया, गेरोलमो कार्डो देखें) द्वारा खोजा गया था।यह जल्द ही एहसास हुआ (लेकिन बहुत बाद में साबित हुआ)[20]ये सूत्र, भले ही कोई केवल वास्तविक समाधानों में रुचि रखता था, कभी -कभी ऋणात्मक संख्याओं की चौकोर जड़ों के हेरफेर की आवश्यकता होती है।एक उदाहरण के रूप में, फॉर्म के क्यूबिक समीकरण के लिए टार्टग्लिया का सूत्र x3 = px + q[lower-alpha 3] समीकरण को समाधान देता है x3 = x जैसा
इन मात्राओं के लिए काल्पनिक शब्द 1637 में रेने डेसकार्टेस द्वारा गढ़ा गया था, जो उनके अवास्तविक प्रकृति पर जोर देने के लिए दर्द में था[21]
... sometimes only imaginary, that is one can imagine as many as I said in each equation, but sometimes there exists no quantity that matches that which we imagine.
[... quelquefois seulement imaginaires c'est-à-dire que l'on peut toujours en imaginer autant que j'ai dit en chaque équation, mais qu'il n'y a quelquefois aucune quantité qui corresponde à celle qu'on imagine.]
भ्रम का एक और स्रोत यह था कि समीकरण बीजीय पहचान के साथ असंगत रूप से असंगत लग रहा था , जो गैर-ऋणात्मक वास्तविक संख्याओं के लिए मान्य है a और b, और जो एक के साथ सम्मिश्र संख्या गणना में भी उपयोग किया गया था a, b धनात्मक और दूसरा ऋणात्मक।इस पहचान का गलत उपयोग (और संबंधित पहचान ) स्थिति में जब दोनों a और b ऋणात्मक भी बेडविल्ड लियोनहार्ड यूलर हैं।इस कठिनाई ने अंततः विशेष प्रतीक का उपयोग करने के सम्मेलन को जन्म दिया i की जगह में इस गलती से बचाने के लिए।[citation needed] फिर भी, यूलर ने आज की तुलना में छात्रों को सम्मिश्र संख्याओं से परिचित कराना स्वाभाविक माना।अपनी प्राथमिक बीजगणित पाठ्य पुस्तक, तत्वों के तत्वों में, वह इन नंबरों का परिचय लगभग एक बार में करता है और फिर उन्हें प्राकृतिक तरीके से उपयोग करता है।
18 वीं & nbsp; सेंचुरी सम्मिश्र संख्याओं में व्यापक उपयोग प्राप्त हुआ, क्योंकि यह देखा गया था कि त्रिकोणमितीय फलनों से जुड़े गणनाओं को सरल बनाने के लिए सम्मिश्र अभिव्यक्तियों के औपचारिक हेरफेर का उपयोग किया जा सकता है।उदाहरण के लिए, 1730 में अब्राहम डे मोइवर ने उल्लेख किया कि उस कोण के त्रिकोणमितीय फलनों की शक्तियों के लिए एक कोण के एक कोण के त्रिकोणमितीय फलनों से संबंधित पहचान को निम्नलिखित डी मोइवर के सूत्र द्वारा फिर से व्यक्त किया जा सकता है:
सम्मिश्र समतल (#complex विमान) में एक बिंदु के रूप में एक सम्मिश्र संख्या का विचार पहली बार डेनमार्क नॉर्वे गणितज्ञ कैस्पर वेसल द्वारा 1799 में वर्णित किया गया था,[23] हालांकि यह जॉन वालिस में 1685 की शुरुआत में अनुमानित था। वालिस ए ट्रीट ऑफ बीजगणित।[24] वेसेल का संस्मरण कोपेनहेगन एकेडमी की कार्यवाही में दिखाई दिया, लेकिन काफी हद तक किसी का ध्यान नहीं गया।1806 में जीन-रॉबर्ट आर्गंड ने स्वतंत्र रूप से सम्मिश्र संख्याओं पर एक पैम्फलेट जारी किया और बीजगणित#इतिहास के मौलिक प्रमेय का एक कठोर प्रमाण प्रदान किया।[25] कार्ल फ्रेडरिक गॉस ने पहले 1797 में प्रमेय का एक अनिवार्य रूप से सांस्थिति प्रूफ प्रकाशित किया था, लेकिन उस समय अपने संदेह को व्यक्त किया था, जो कि & माइनस के वर्गमूल के सही तत्वमीमांसा के बारे में है।[26] यह 1831 तक नहीं था कि उन्होंने इन संदेहों को पार कर लिया और विमान में बिंदुओं के रूप में सम्मिश्र संख्याओं पर अपने ग्रंथ को प्रकाशित किया,[27] बड़े पैमाने पर आधुनिक संकेतन और शब्दावली की स्थापना:[28] <clockquote> यदि किसी ने पूर्व में इस विषय पर झूठे दृष्टिकोण से चिंतन किया था और इसलिए एक रहस्यमय अंधकार पाया गया, तो यह बड़े हिस्से में अनाड़ी शब्दावली के लिए जिम्मेदार है।एक को +1, -1 नहीं कहा गया था, धनात्मक, ऋणात्मक, या काल्पनिक (या असंभव) इकाइयाँ, लेकिन इसके अतिरिक्त, कहते हैं, प्रत्यक्ष, उलटा, या पार्श्व इकाइयाँ, तो इस तरह के अंधेरे की बात कर सकते थे।
19 वीं शताब्दी की शुरुआत में, अन्य गणितज्ञों ने स्वतंत्र रूप से सम्मिश्र संख्याओं के ज्यामितीय प्रतिनिधित्व की खोज की: बुई,Cite error: Closing </ref> missing for <ref> tag सी। वी। मौरी,[29] जॉन वॉरेन (गणितज्ञ) ,[30][31][32] Jacques Frédéric Français | फ्रेंच और उनके भाई, राइट बेल्वाइटिस [33][34]
अंग्रेजी गणितज्ञ जी.एच.हार्डी ने टिप्पणी की कि गॉस 'वास्तव में आत्मविश्वास और वैज्ञानिक तरीके' में सम्मिश्र संख्याओं का उपयोग करने वाले पहले गणितज्ञ थे, हालांकि नॉर्वे नील्स हेनरिक एबेल और कार्ल गुस्ताव जैकब जैकोबी जैसे गणितज्ञों ने गॉस को 1831 ग्रंथ प्रकाशित करने से पहले उन्हें नियमित रूप से उपयोग किया था।[35]
ऑगस्टिन-लुइस कॉची और बर्नहार्ड रीमैन ने एक साथ #Complex विश्लेषण के मौलिक विचारों को पूरा करने की एक उच्च स्थिति में लाया, जो कि कॉची के स्थिति में 1825 के आसपास शुरू हुआ।
सिद्धांत में उपयोग किए जाने वाले सामान्य शब्द मुख्य रूप से संस्थापकों के कारण हैं।अर्गंड को बुलाया cos φ + i sin φ दिशा कारक, और मापांक;[lower-alpha 5]}}}}}}}}}}}}}}}}}}}}}}}}}[36] Cauchy (1821) को बुलाया cos φ + i sin φ कम रूप (कम अभिव्यक्ति)[37] और जाहिरा तौर पर शब्द तर्क पेश किया;गॉस का इस्तेमाल किया i के लिए ,[lower-alpha 6] के लिए सम्मिश्र संख्या शब्द का परिचय दिया a + bi,[lower-alpha 7] और कहा जाता है a2 + b2 नियम।[lower-alpha 8] अभिव्यक्ति दिशा गुणांक, प्रायः के लिए उपयोग किया जाता है cos φ + i sin φ, हैनकेल (1867) के कारण है,[41] और निरपेक्ष मूल्य, मापांक के लिए, वीरस्ट्रास के कारण है।
बाद में सामान्य सिद्धांत पर शास्त्रीय लेखकों में रिचर्ड डेडेकिंड , ओटो होल्डर, फेलिक्स क्लेन , हेनरी पोइंकेरे, हरमन श्वार्ज़ , कार्ल वीमर स्ट्रैस और कई अन्य सम्मिलित हैं।20 वीं शताब्दी की शुरुआत में सम्मिश्र बहुभिन्नरूपी पथरी में महत्वपूर्ण फलन (एक व्यवस्थित सहित) शुरू किया गया है।1927 में विल्हेम वर्टिंगर द्वारा महत्वपूर्ण परिणाम प्राप्त किए गए हैं।
संबंध और संचालन
समानता
सम्मिश्र संख्याओं में वास्तविक संख्याओं की समानता की एक समान परिभाषा है;दो सम्मिश्र संख्याएँ a1 + b1i और a2 + b2i समान हैं यदि और केवल अगर उनके वास्तविक और काल्पनिक दोनों भाग समान हैं, तो, अर्थात् यदि a1 = a2 और b1 = b2।ध्रुवीय रूप में लिखी नॉनज़ेरो सम्मिश्र नंबर समान हैं यदि और केवल अगर उनके पास समान परिमाण है और उनके तर्क एक पूर्णांक से भिन्न होते हैं 2π।
आदेश
वास्तविक संख्याओं के विपरीत, सम्मिश्र संख्याओं का कोई प्राकृतिक क्रम नहीं है।विशेष रूप से, सम्मिश्र संख्याओं पर कोई रैखिक आदेश नहीं है जो जोड़ और गुणन के साथ संगत है।इसलिए, सम्मिश्र संख्याओं में एक क्रमित क्षेत्र की संरचना नहीं होती है।इसके लिए एक स्पष्टीकरण यह है कि एक क्रमित क्षेत्र में वर्गों का प्रत्येक गैर-तुच्छ राशि#nontrivialsquaresum nonzero है, और i2 + 12 = 0 वर्गों का एक गैर-तुच्छ योग है।इस प्रकार, सम्मिश्र संख्याओं को स्वाभाविक रूप से दो-आयामी विमान पर मौजूदा माना जाता है।
संयुग्म
सम्मिश्र संख्या का सम्मिश्र संयुग्म z = x + yi द्वारा दिया गया है x − yi।इसे या तो निरूपित किया गया है z या z*.[42] सम्मिश्र संख्याओं पर यह अनियमित संचालन केवल उनके बुनियादी संचालन जोड़, घटाव, गुणन और विभाजन को प्रयुक्त करके व्यक्त नहीं किया जा सकता है।
ज्यामितीय रूप से, z प्रतिबिंब समरूपता है |प्रतिबिंब z असली अक्ष के बारे में।दो बार संयुग्मन मूल सम्मिश्र संख्या देता है
एक सम्मिश्र संख्या का उत्पाद z = x + yi और इसके संयुग्म को निरपेक्ष वर्ग के रूप में जाना जाता है।यह हमेशा एक गैर-ऋणात्मक वास्तविक संख्या होती है और प्रत्येक के परिमाण के वर्ग के बराबर होती है:
एक सम्मिश्र संख्या के वास्तविक और काल्पनिक भागों z संयुग्मन का उपयोग करके निकाला जा सकता है:
संयुग्मन मूल सम्मिश्र अंकगणितीय संचालन पर वितरित करता है:
जोड़ और घटाव
दो सम्मिश्र संख्याएँ और अपने वास्तविक और काल्पनिक भागों को अलग से जोड़कर सबसे आसानी से जोड़ रहे हैं।अर्थात:
गुणा और वर्ग
वितरण संपत्ति के नियम, क्रमचयी गुणधर्म (इसके अतिरिक्त और गुणा), और परिभाषित संपत्ति i2 = −1 सम्मिश्र संख्याओं पर प्रयुक्त करें।यह इस प्रकार है कि
पारस्परिक और विभाजन
संयुग्मन का उपयोग करते हुए, एक नॉनज़ेरो सम्मिश्र संख्या का गुणक उलटा z = x + yi हमेशा के लिए टूट सकता है
इसका उपयोग एक मनमाना सम्मिश्र संख्या के एक विभाजन को व्यक्त करने के लिए किया जा सकता है w = u + vi एक गैर-शून्य सम्मिश्र संख्या द्वारा z जैसा
गुणा और ध्रुवीय रूप में विभाजन
गुणन, विभाजन और घातांक के लिए सूत्र कार्टेशियन निर्देशांक में संबंधित सूत्रों की तुलना में ध्रुवीय रूप में सरल हैं।दो सम्मिश्र संख्याओं को देखते हुए z1 = r1(cos φ1 + i sin φ1) और z2 = r2(cos φ2 + i sin φ2), त्रिकोणमितीय पहचान के कारण
इसी तरह, विभाजन द्वारा दिया जाता है
वर्गमूल
की चौकोर जड़ें a + bi (साथ b ≠ 0) हैं , कहां
घातीय फलन
घातीय फलन हर सम्मिश्र संख्या के लिए परिभाषित किया जा सकता है z पावर सीरीज़ द्वारा
पर मूल्य 1 घातीय फलन यूलर की संख्या है
विश्लेषणात्मक निरंतरता इस समानता को हर सम्मिश्र मूल्य के लिए बढ़ाने की स्वीकृति देती है z, और इस प्रकार आधार के साथ सम्मिश्र घातांक को परिभाषित करने के लिए e जैसा
कार्यात्मक समीकरण
घातीय फलन कार्यात्मक समीकरण को संतुष्ट करता है यह या तो दोनों सदस्यों के बिजली श्रृंखला विस्तार की तुलना करके या समीकरण के प्रतिबंध से वास्तविक तर्कों के लिए विश्लेषणात्मक निरंतरता को प्रयुक्त करके साबित किया जा सकता है।
यूलर का सूत्र
यूलर के सूत्र में कहा गया है कि, किसी भी वास्तविक संख्या के लिए y,
सम्मिश्र लघुगणक
वास्तविक स्थिति में, प्राकृतिक लघुगणक को उलटा फलन के रूप में परिभाषित किया जा सकता है
घातीय फलन की।इसे सम्मिश्र प्रक्षेत्र में विस्तारित करने के लिए, कोई भी यूलर के सूत्र से शुरू कर सकता है।इसका तात्पर्य है कि, यदि एक सम्मिश्र संख्या ध्रुवीय रूप में लिखा गया है
इसलिए, यदि सम्मिश्र लघुगणक को एक बहुउद्देशीय फलन के रूप में परिभाषित नहीं किया जाना है
एक्सपोनेंटेशन
यदि x > 0 असली है और z सम्मिश्र, प्रतिपादक को परिभाषित किया गया है
इस सूत्र को सम्मिश्र मूल्यों तक बढ़ाना स्वाभाविक लगता है x, लेकिन इस तथ्य के परिणामस्वरूप कुछ कठिनाइयाँ हैं कि सम्मिश्र लघुगणक वास्तव में एक फलन नहीं है, बल्कि एक बहुस्तरीय फलन है।
यह इस प्रकार है कि अगर z ऊपर है, और अगर t एक और सम्मिश्र संख्या है, तो घातांक बहुवर्धित फलन है
पूर्णांक और आंशिक घातांक
यदि, पूर्ववर्ती सूत्र में, t एक पूर्णांक है, तो साइन और कोसाइन स्वतंत्र हैं k।इस प्रकार, यदि प्रतिपादक n एक पूर्णांक है, तो zn}{
n nth रूट |nएक जटिल संख्या की जड़ें z द्वारा दिए गए हैं
जबकि nएक धनात्मक वास्तविक संख्या की जड़ r धनात्मक वास्तविक संख्या होने के लिए चुना जाता है c संतुष्टि देने वाला cn = r, एक विशेष परिसर को अलग करने का कोई प्राकृतिक तरीका नहीं है nएक सम्मिश्र संख्या की जड़।इसलिए nरूट एक बहुस्तरीय फलन है |nका फलन फलन z।इसका तात्पर्य है कि, धनात्मक वास्तविक संख्या के स्थिति के विपरीत, एक है
गुण
क्षेत्र संरचना
सेट सम्मिश्र संख्याओं में से एक क्षेत्र (गणित) है।[46] संक्षेप में, इसका तात्पर्य है कि निम्नलिखित तथ्य हैं: सबसे पहले, किसी भी दो सम्मिश्र संख्याओं को जोड़ा जा सकता है और एक और सम्मिश्र संख्या प्राप्त करने के लिए गुणा किया जा सकता है।दूसरा, किसी भी सम्मिश्र संख्या के लिए z, इसके योज्य उलटा –z एक सम्मिश्र संख्या भी है;और तीसरा, प्रत्येक नॉनज़ेरो सम्मिश्र संख्या में एक गुणक उलटा सम्मिश्र संख्या होती है।इसके अतिरिक्त, ये संक्रिया कई नियमो को संतुष्ट करते हैं, उदाहरण के लिए किसी भी दो सम्मिश्र संख्याओं के लिए जोड़ और गुणन की संबद्धता का नियम z1 और z2:
रियल के विपरीत, एक क्रमित क्षेत्र नहीं है, यह कहना है, किसी संबंध को परिभाषित करना संभव नहीं है z1 < z2 यह जोड़ और गुणन के साथ संगत है।वास्तव में, किसी भी क्रमित क्षेत्र में, किसी भी तत्व का वर्ग आवश्यक रूप से धनात्मक है, इसलिए i2 = −1 कुल आदेश के अस्तित्व को रोकता है [47] जब गणितीय विषय या निर्माण के लिए अंतर्निहित क्षेत्र सम्मिश्र संख्याओं का क्षेत्र होता है, तो विषय का नाम सामान्य रूप से उस तथ्य को प्रतिबिंबित करने के लिए संशोधित किया जाता है।उदाहरण के लिए: सम्मिश्र विश्लेषण, सम्मिश्र आव्यूह (गणित) , सम्मिश्र बहुपद और सम्मिश्र झूठ बीजगणित ।
बहुपद समीकरणों का समाधान
किसी भी सम्मिश्र संख्या (गुणांक कहा जाता है) को देखते हुए a0, ..., an, समीकरण
इस प्रमेय के विभिन्न प्रमाण हैं, या तो एनालिटिक तरीकों जैसे कि लिउविले के प्रमेय (सम्मिश्र विश्लेषण) | लिउविले के प्रमेय, या सांस्थिति जैसे कि घुमावदार संख्या , या एक प्रमाण जो गैलोइस सिद्धांत और इस तथ्य को जोड़ते हैं कि विषम डिग्री का कोई वास्तविक बहुपद हैकम से कम एक वास्तविक जड़।
इस तथ्य के कारण, किसी भी बीजगणितीय रूप से संवृत क्षेत्र के लिए धारण करने वाले प्रमेय प्रयुक्त होते हैं उदाहरण के लिए, किसी भी गैर-खाली सम्मिश्र वर्ग आव्यूह में कम से कम एक (सम्मिश्र) eigenvalue होता है।
बीजीय लक्षण वर्णन
फील्ड निम्नलिखित तीन गुण हैं:
- सबसे पहले, इसकी विशेषता (बीजगणित) 0. है। इसका तात्पर्य है कि 1 + 1 + ⋯ + 1 ≠ 0 किसी भी संख्या के लिए (जो सभी के बराबर)।
- दूसरा, इसकी पारगमन की डिग्री खत्म हो गई का मुख्य क्षेत्र सातत्य की कार्डिनैलिटी है।
- तीसरा, यह बीजगणितीय रूप से संवृत है (ऊपर देखें)।
यह दिखाया जा सकता है कि इन गुणों वाले किसी भी क्षेत्र में सममितीय (एक क्षेत्र के रूप में) है उदाहरण के लिए, क्षेत्र का बीजगणितीय संवृत पी-एडिक नंबर का |p-एक संख्या भी इन तीन गुणों को संतुष्ट करती है, इसलिए ये दो क्षेत्र सममितीय हैं (क्षेत्र के रूप में, लेकिन संस्थानिक क्षेत्र के रूप में नहीं)।[48] भी, सम्मिश्र पुइज़क्स श्रृंखला के क्षेत्र के लिए समरूपीय है।हालांकि, एक आइसोमोर्फिज्म को निर्दिष्ट करने के लिए पसंद के स्वयंसिद्ध की आवश्यकता होती है।इस बीजीय लक्षण वर्णन का एक और परिणाम यह है कि कई उपयुक्त उपक्षेत्र सम्मिलित हैं जो समरूपीय हैं ।
एक संस्थानिक क्षेत्र के रूप में विशेषता
के पूर्ववर्ती लक्षण वर्णन के केवल बीजीय स्वरूपों का वर्णन करता है यह कहना है, पड़ोस (सांस्थिति) और निरंतरता (सांस्थिति) के गुण, जो गणितीय विश्लेषण और सांस्थिति जैसे क्षेत्रों में मायने रखते हैं, से निपटा नहीं जाता है।का निम्नलिखित विवरण एक सामयिक वलय के रूप में (अर्थात, एक क्षेत्र जो एक सामयिक समष्टि से लैस है, जो अभिसरण की धारणा की स्वीकृति देता है) संस्थानिक गुणों को ध्यान में रखता है। एक उप-समुच्चय होता है P (अर्थात् धनात्मक वास्तविक संख्याओं कासमुच्चय) नॉनज़ेरो तत्वों के निम्नलिखित तीन स्थितियों को संतुष्ट करते हुए:
- P इसके अतिरिक्त संवृत है, गुणन और इनवर्स लेना।
- यदि x और y के अलग -अलग तत्व हैं P, तो कोई x − y या y − x में है P।
- यदि S का कोई गैर -रिक्त उप-समुच्चय है P, तब S + P = x + P कुछ के लिए x में
इसके अतिरिक्त, एक nontrivial invention (गणित) स्वचालितता है x ↦ x* (अर्थात् सम्मिश्र संयुग्मन), जैसे कि x x* में है P किसी भी नॉनज़ेरो के लिए x में किसी भी क्षेत्र F इन गुणों के साथ सेटों को ले जाकर सांस्थिति के साथ संपन्न किया जा सकता है B(x, p) = { y | p − (y − x)(y − x)* ∈ P } एक आधार (सांस्थिति) के रूप में, जहां x मैदान पर और p पर्वतमाला P।इस सांस्थिति के साथ F एक संस्थानिक क्षेत्र के रूप में समरूपीय है एकमात्र जुड़ा हुआ समष्टि स्थानीय रूप से कॉम्पैक्ट संस्थानिक वलय हैं और यह एक और लक्षण वर्णन देता है एक संस्थानिक क्षेत्र के रूप में, जब से से प्रतिष्ठित किया जा सकता है क्योंकि नॉनज़ेरो सम्मिश्र नंबर कनेक्टेड स्पेस हैं, जबकि नॉनज़ेरो रियल नंबर नहीं हैं।[49]
औपचारिक निर्माण
निर्माण के रूप में आदेश जोड़े
विलियम रोवन हैमिल्टन नेसमुच्चय को परिभाषित करने के लिए दृष्टिकोण पेश किया सम्मिश्र संख्याओं का[50]समुच्चय के रूप में का ordered pairs (a, b) वास्तविक संख्याओं के, जिसमें जोड़ और गुणन के लिए निम्नलिखित नियम प्रयुक्त होते हैं:[46]
एक भागफल क्षेत्र के रूप में निर्माण
यद्यपि यह निम्न-स्तरीय निर्माण सम्मिश्र संख्याओं की संरचना का सही वर्णन करता है, निम्नलिखित समकक्ष परिभाषा से बीजीय प्रकृति का पता चलता है अधिक तुरंत।यह लक्षण वर्णन क्षेत्रों और बहुपदों की धारणा पर निर्भर करता है।एक क्षेत्र एकसमुच्चय है जो जोड़, घटाव, गुणा और विभाजन संचालन के साथ संपन्न है, जो कि तर्कसंगत संख्याओं से परिचित है, तर्कसंगत संख्या से परिचित है।उदाहरण के लिए, वितरण नियम
सम्मिश्र संख्याओं केसमुच्चय को भागफल की वलय के रूप में परिभाषित किया गया है <रेफ नाम = bourbaki 1998 loc = §viii.1 /> इस एक्सटेंशन क्षेत्र में दो वर्ग जड़ें हैं −1, अर्थात् (के coset s) X और −X, क्रमश।(के cosets) 1 और X का आधार बनाना एक वास्तविक सदिश स्थल के रूप में, जिसका अर्थ है कि एक्सटेंशन क्षेत्र के प्रत्येक तत्व को इन दो तत्वों में एक रैखिक संयोजन के रूप में लिखा जा सकता है।समान रूप से, एक्सटेंशन क्षेत्र के तत्वों को ऑर्डर किए गए जोड़े के रूप में लिखा जा सकता है (a, b) वास्तविक संख्याओं की।भागफल की वलय एक क्षेत्र है, क्योंकि X2 + 1 इरायूबल बहुपद पर है तो यह आदर्श उत्पन्न करता है अधिकतम आदर्श है।
वलय में जोड़ और गुणन के लिए सूत्र संबंध को मॉड्यूलो X2 = −1, क्रमित जोड़े के रूप में परिभाषित सम्मिश्र संख्याओं के जोड़ और गुणन के लिए सूत्रों के अनुरूप।तो क्षेत्र की दो परिभाषाएँ समाकृतिकता (क्षेत्र के रूप में) हैं।
स्वीकार करते हुए बीजगणितीय रूप से संवृत है, क्योंकि यह एक बीजगणितीय विस्तार है इस दृष्टिकोण में, इसलिए बीजगणितीय संवृत है
आव्यूह सम्मिश्र संख्याओं का प्रतिनिधित्व
सम्मिश्र आंकड़े a + bi द्वारा भी प्रतिनिधित्व किया जा सकता है 2 × 2 आव्यूह (गणित) जिसमें रूप है:
एक साधारण गणना से पता चलता है कि नक्शा:
सम्मिश्र संख्याओं के गुणन का ज्यामितीय विवरण सम्मिश्र संख्याओं और ऐसे मैट्रिसेस के बीच इस पत्राचार का उपयोग करके घूर्णन आव्यूह के संदर्भ में भी व्यक्त किया जा सकता है।एक वेक्टर पर आव्यूह की कार्रवाई (x, y) के गुणन से मेल खाती है x + iy द्वारा a + ib।विशेष रूप से, यदि निर्धारक है 1, एक वास्तविक संख्या है t इस तरह कि आव्यूह का रूप है:
सम्मिश्र विश्लेषण
एक सम्मिश्र चर के फलनों के अध्ययन को सम्मिश्र विश्लेषण के रूप में जाना जाता है और प्रयुक्त गणित के साथ -साथ गणित की अन्य शाखाओं में भी भारी व्यावहारिक उपयोग होता है।प्रायः, वास्तविक विश्लेषण या यहां तक कि संख्या सिद्धांत में बयानों के लिए सबसे प्राकृतिक प्रमाण सम्मिश्र विश्लेषण से तकनीकों को नियोजित करते हैं (एक उदाहरण के लिए प्रधान संख्या प्रमेय देखें)।वास्तविक फलनों के विपरीत, जिन्हें सामान्य रूप से दो-आयामी ग्राफ़ के रूप में दर्शाया जाता है, सम्मिश्र फलनो में चार-आयामी रेखांकन होते हैं और इसे दो चर के एक फलन के एक ग्राफ को रंग-कोडित करके उपयोगी रूप से चित्रित किया जा सकता है। चार आयामों का सुझाव देने के लिए तीन-आयामी ग्राफ, या इसके द्वारा या उसके द्वारा।सम्मिश्र समतल के सम्मिश्र फलन के गतिशील परिवर्तन को एनिमेट करना।
सम्मिश्र घातीय और संबंधित फलन
(वास्तविक) विश्लेषण में अभिसरण श्रृंखला और निरंतर फलनों की धारणाओं में सम्मिश्र विश्लेषण में प्राकृतिक एनालॉग्स हैं।एक क्रम सम्मिश्र संख्याओं के रूप में अभिसरण अनुक्रम कहा जाता है यदि और केवल अगर इसके वास्तविक और काल्पनिक भाग करते हैं।यह सीमाओं के (ε, Δ) -Definition के बराबर है, जहां वास्तविक संख्याओं के निरपेक्ष मान को सम्मिश्र संख्याओं में से एक द्वारा प्रतिस्थापित किया जाता है।अधिक अमूर्त दृष्टिकोण से, , मीट्रिक (गणित) के साथ संपन्न
वास्तविक विश्लेषण की तरह, अभिसरण की इस धारणा का उपयोग कई प्राथमिक फलनो के निर्माण के लिए किया जाता है: घातीय फलन exp z, भी लिखा है ez, अनंत श्रृंखला के रूप में परिभाषित किया गया है
यूलर के सूत्र में कहा गया है:
सम्मिश्र प्रतिपादन zω की तरह परिभाषित किया गया है
सम्मिश्र संख्या, वास्तविक संख्याओं के विपरीत, सामान्य रूप से अनमॉडिफाइड पावर और लॉगरिदम पहचान को संतुष्ट नहीं करती है, विशेष कर जब भोले-भाले को एकल-मूल्य वाले फलनों के रूप में माना जाता है;घातांक देखें#शक्ति और लघुगणक पहचान की विफलता।उदाहरण के लिए, वे संतुष्ट नहीं करते हैं
होलोमोर्फिक फलन
एक फलन F: → यदि यह Cauchy -riemann समीकरणों को संतुष्ट करता है, तो Holomorphic फलन कहा जाता है।उदाहरण के लिए, किसी भी रैखिक परिवर्तन#परिभाषा और पहले परिणाम |-लाइनर मैप → रूप में लिखा जा सकता है
सम्मिश्र विश्लेषण से पता चलता है कि वास्तविक विश्लेषण में कुछ विशेषताएं स्पष्ट नहीं हैं।उदाहरण के लिए, कोई भी दो होलोमोर्फिक फलन करता है f और g यह एक एकपक्षीय रूप से छोटे विवृत उप-समुच्चय पर सहमत है आवश्यक रूप से हर जगह सहमत मेरोमॉर्फिक फलन , फलन जो स्थानीय रूप से लिखे जा सकते हैं f(z)/(z − z0)n एक होलोमोर्फिक फलन के साथ f, अभी भी होलोमोर्फिक फलनों की कुछ विशेषताओं को साझा करें।अन्य फलनों में आवश्यक विलक्षणता है, जैसे sin(1/z) पर z = 0।
अनुप्रयोग
सम्मिश्र संख्याओं में कई वैज्ञानिक क्षेत्रों में अनुप्रयोग होते हैं, जिनमें संकेत प्रसंस्करण , नियंत्रण सिद्धांत , इलेक्ट्रोमैग्नेटिज्म, द्रव गतिविज्ञान , क्वांटम यांत्रिकी , नक्शानवीसी और कंपन#कंपन विश्लेषण सम्मिलित हैं।इनमें से कुछ एप्लिकेशन नीचे वर्णित हैं।
ज्यामिति
आकार
तीन collinearity | गैर-कोलीनियर अंक विमान में त्रिभुज के आकार#समानता कक्षाएं निर्धारित करते हैं ।सम्मिश्र समतल में बिंदुओं का पता लगाना, एक त्रिभुज के इस आकार को सम्मिश्र अंकगणित द्वारा व्यक्त किया जा सकता है
फ्रैक्टल ज्यामिति
मंडेलब्रॉटसमुच्चय सम्मिश्र समतल पर गठित एक फ्रैक्टल का एक लोकप्रिय उदाहरण है।यह हर समष्टि की साजिश रचकर परिभाषित किया गया है जहां अनुक्रम को पुनरावृत्ति करना जब पुनरावृति असीम रूप से (स्थिरता सिद्धांत) नहीं होती है।इसी तरह, जूलियासमुच्चय के समान नियम हैं, जहां अतिरिक्त इसके स्थिर रहता है।
त्रिकोण
हर त्रिभुज में एक अद्वितीय स्टीनर अंडाकार है - त्रिभुज के अंदर एक दीर्घवृत्त और त्रिभुज के तीन पक्षों के मध्य बिंदुओं के लिए स्पर्शरेखा।एक त्रिभुज के स्टेनर इनलिप्स का फोकस (ज्यामिति) मार्डन के प्रमेय के अनुसार, निम्नानुसार पाया जा सकता है:[52][53] सम्मिश्र समतल में त्रिभुज के कोने को निरूपित करें a = xA + yAi, b = xB + yBi, और c = xC + yCi।क्यूबिक समीकरण लिखें , इसके व्युत्पन्न को लें, और (द्विघात) व्युत्पन्न को शून्य से बराबरी करें।मार्डन के प्रमेय का कहना है कि इस समीकरण के समाधान सम्मिश्र संख्याएं हैं जो स्टीनर इनलिप्स के दो foci के स्थानों को दर्शाती हैं।
बीजगणितीय संख्या सिद्धांत

जैसा कि ऊपर उल्लेख किया गया है, किसी भी गैर -विरोधी बहुपद समीकरण (सम्मिश्र गुणांक में) में एक समाधान है ।तर्क एक फोर्टियोरी, वही सच है यदि समीकरण में तर्कसंगत गुणांक हैं।इस तरह के समीकरणों की जड़ों को बीजगणितीय संख्या कहा जाता है - वे बीजगणितीय संख्या सिद्धांत में अध्ययन की एक प्रमुख वस्तु हैं।की तुलना में , बीजगणितीय संवृत , जिसमें सभी बीजीय संख्या भी सम्मिलित हैं, ज्यामितीय शब्दों में आसानी से समझने योग्य होने का लाभ है।इस तरह, बीजगणितीय तरीकों का उपयोग ज्यामितीय प्रश्नों का अध्ययन करने के लिए किया जा सकता है और इसके विपरीत।बीजगणितीय तरीकों के साथ, अधिक विशेष रूप से क्षेत्र सिद्धांत (गणित) की मशीनरी को एकता की जड़ वाले संख्या क्षेत्र में प्रयुक्त करने के लिए, यह दिखाया जा सकता है कि एक नियमित नॉनगन कम्पास और ऋजु कोर निर्माण - एक विशुद्ध रूप से ज्यामितीय समस्या का निर्माण करना संभव नहीं है।
एक अन्य उदाहरण गॉसियन पूर्णांक है;वह है, फॉर्म की संख्या x + iy, कहां x और y पूर्णांक हैं, जिसका उपयोग दो वर्गों के रकम पर फ़र्मेट के प्रमेय को वर्गीकृत करने के लिए किया जा सकता है।
विश्लेषणात्मक संख्या सिद्धांत
विश्लेषणात्मक संख्या सिद्धांत अध्ययन संख्या, प्रायः पूर्णांक या तर्कसंगत, इस तथ्य का लाभ उठाकर कि उन्हें सम्मिश्र संख्या के रूप में माना जा सकता है, जिसमें विश्लेषणात्मक तरीकों का उपयोग किया जा सकता है।यह सम्मिश्र-मूल्यवान फलनों में संख्या-सिद्धांत संबंधी जानकारी को एन्कोडिंग करके किया जाता है।उदाहरण के लिए, Riemann Zeta फलन ζ(s) अभाज्य संख्या ों के वितरण से संबंधित है।
अनुचित अभिन्नता
प्रयुक्त क्षेत्रों में, सम्मिश्र संख्याओं का उपयोग प्रायः सम्मिश्र-मूल्यवान फलनों के माध्यम से कुछ वास्तविक-मूल्यवान अनुचित अभिन्नताओं की गणना करने के लिए किया जाता है।ऐसा करने के लिए कई तरीके मौजूद हैं;समोच्च एकीकरण के तरीके देखें।
गतिशील समीकरण
अंतर समीकरण ों में, पहले सभी सम्मिश्र जड़ों को ढूंढना आम है r रैखिक अंतर समीकरण #सजातीय समीकरणों के साथ एक रैखिक अंतर समीकरण या समीकरण प्रणाली के निरंतर गुणांक के साथ और फिर फॉर्म के आधार फलनों के संदर्भ में सिस्टम को हल करने का प्रयास करें f(t) = ert।इसी तरह, अंतर समीकरण ों में, सम्मिश्र जड़ें r अंतर समीकरण प्रणाली के विशिष्ट समीकरण का उपयोग किया जाता है, फॉर्म के आधार फलनों के संदर्भ में सिस्टम को हल करने का प्रयास करने के लिए f(t) = rt।
रैखिक बीजगणित
एक आव्यूह का eigendecomposition आव्यूह शक्तियों और आव्यूह घातीय की गणना के लिए एक उपयोगी उपकरण है।हालांकि, इसे प्रायः सम्मिश्र संख्याओं के उपयोग की आवश्यकता होती है, भले ही आव्यूह वास्तविक हो (उदाहरण के लिए, एक घूर्णन आव्यूह)।
सम्मिश्र संख्या प्रायः वास्तविक संख्याओं में मूल रूप से कल्पना की गई अवधारणाओं को सामान्य करती है।उदाहरण के लिए, संयुग्मन संक्रमण ट्रांसपोज़ को सामान्य करता है, हरमिटियन आव्यूह सममित आव्यूह को सामान्य करता है, और एकात्मक आव्यूह ऑर्थोगोनल आव्यूह को सामान्य करता है।
प्रयुक्त गणित में
नियंत्रण सिद्धांत
नियंत्रण सिद्धांत में, सिस्टम को प्रायः समय प्रक्षेत्र से लाप्लास रूपांतरण का उपयोग करके सम्मिश्र आवृत्ति प्रक्षेत्र में बदल दिया जाता है।सिस्टम के शून्य और डंडे का विश्लेषण तब सम्मिश्र समतल में किया जाता है।रूट लोकोस, न्यक्विस्ट प्लॉट , और निकोल्स प्लॉट तकनीक सभी सम्मिश्र समतल का उपयोग करते हैं।
रूट लोकस विधि में, यह महत्वपूर्ण है कि शून्य और ध्रुव बाएं या दाएं आधे विमानों में हैं, अर्थात, शून्य से अधिक या उससे कम वास्तविक भाग है।यदि एक रैखिक, समय-अपरिवर्तनीय (LTI) प्रणाली में डंडे होते हैं
- सही आधे विमान में, यह अस्थिर होगा,
- सभी बाएं आधे विमान में, यह बिबो स्थिरता होगी,
- काल्पनिक अक्ष पर, इसमें सीमांत स्थिरता होगी।
यदि किसी प्रणाली में दाहिने आधे विमान में शून्य है, तो यह एक गैर -चरण चरण प्रणाली है।
सिग्नल विश्लेषण
समय -समय पर अलग -अलग संकेतों के लिए सुविधाजनक विवरण के लिए सिग्नल विश्लेषण और अन्य क्षेत्रों में सम्मिश्र संख्याओं का उपयोग किया जाता है।वास्तविक भौतिक मात्राओं का प्रतिनिधित्व करने वाले वास्तविक फलनों के लिए, प्रायः सिन और कोसाइन के संदर्भ में, इसी सम्मिश्र फलनों को माना जाता है जिनके बारे में वास्तविक भाग मूल मात्रा हैं।किसी दिए गए आवृत्ति की साइन लहर के लिए, निरपेक्ष मूल्य |z| इसी के z आयाम और तर्क (सम्मिश्र विश्लेषण) है arg z चरण (तरंगें) है।
यदि फूरियर विश्लेषण किसी दिए गए वास्तविक-मूल्य वाले संकेत को आवधिक फलनों के योग के रूप में लिखने के लिए नियोजित किया जाता है, तो इन आवधिक फलनों को प्रायः फॉर्म के सम्मिश्र-मूल्यवान फलनों के रूप में लिखा जाता है
इस उपयोग को अंकीय संकेत प्रक्रिया और डिजिटल इमेज प्रोसेसिंग में भी विस्तारित किया जाता है, जो ट्रांसमिट, डेटा संपीड़न, रिस्टोर और अन्यथा डिजिटल डाटा आवाज़ सिग्नल, स्टिल इमेज और वीडियो सिग्नल को प्रसारित करने के लिए फूरियर एनालिसिस (और छोटा लहर एनालिसिस) के डिजिटल संस्करणों का उपयोग करते हैं।
एक अन्य उदाहरण, एएम रेडियो के आयाम मॉड्यूलेशन के दो साइड बैंड के लिए प्रासंगिक है, है:
भौतिकी में
इलेक्ट्रोमैग्नेटिज्म और इलेक्ट्रिकल इंजीनियरिंग
इलेक्ट्रिकल इंजीनियरिंग में, फूरियर रूपांतरण का उपयोग अलग -अलग वोल्टेज और इलेक्ट्रिक करंट का विश्लेषण करने के लिए किया जाता है।प्रतिरोधों, संधारित्र , और प्रारंभ करनेवाला ों के उपचार को बाद में दो के लिए काल्पनिक, आवृत्ति-निर्भर प्रतिरोधों को पेश करके और तीनों को एक सम्मिश्र संख्या में मिलकर विद्युत प्रतिबाधा नामक एक सम्मिश्र संख्या में एकीकृत किया जा सकता है।इस दृष्टिकोण को फासोर कैलकुलस कहा जाता है।
इलेक्ट्रिकल इंजीनियरिंग में, काल्पनिक इकाई को निरूपित किया जाता है j, भ्रम से बचने के लिए I, जो सामान्य रूप से विद्युत प्रवाह को निरूपित करने के लिए उपयोग में होता है, या, विशेष रूप से, i, जो सामान्य रूप से तात्कालिक विद्युत प्रवाह को निरूपित करने के लिए उपयोग में होता है।
चूंकि एक एसी विद्युत परिपथ में वोल्टेज दोलन कर रहा है, इसलिए इसका प्रतिनिधित्व किया जा सकता है
द्रव की गतिशीलता
द्रव की गतिशीलता में, दो आयामों में संभावित प्रवाह का वर्णन करने के लिए सम्मिश्र फलनों का उपयोग किया जाता है।
क्वांटम यांत्रिकी
सम्मिश्र संख्या क्षेत्र क्वांटम यांत्रिकी के गणितीय योग ों के लिए आंतरिक है, जहां सम्मिश्र हिल्बर्ट स्पेस एक ऐसे सूत्रीकरण के लिए संदर्भ प्रदान करते हैं जो सुविधाजनक और शायद सबसे मानक है।क्वांटम यांत्रिकी के मूल नींव सूत्र - श्रोडिंगर समीकरण और हाइजेनबर्ग के आव्यूह यांत्रिकी - सम्मिश्र संख्याओं का उपयोग करते हैं।
सापेक्षता
विशेष सापेक्षता और सामान्य सापेक्षता में, अंतरिक्ष समय पर मीट्रिक के लिए कुछ सूत्र सरल हो जाते हैं यदि कोई स्पेसटाइम कॉन्टिनम के समय घटक को काल्पनिक होने के लिए लेता है।(यह दृष्टिकोण शास्त्रीय सापेक्षता में अब मानक नहीं है, लेकिन क्वांटम क्षेत्र सिद्धांत में वीक घूर्णन है।) सम्मिश्र संख्या स्पिनर ों के लिए आवश्यक हैं, जो सापेक्षता में उपयोग किए जाने वाले टेन्सर ्स का एक सामान्यीकरण हैं।
सामान्यीकरण और संबंधित धारणाएँ
क्षेत्र को विस्तारित करने की प्रक्रिया के लिए केली -डिकसन कंस्ट्रक्शन के रूप में जाना जाता है।इसे और अधिक आयामों तक ले जाया जा सकता है, चतुर्भुजों की उपज और अष्टक ्स जो (एक वास्तविक वेक्टर अंतरिक्ष के रूप में) क्रमशः आयाम & nbsp; 4 और 8 के हैं।
इस संदर्भ में सम्मिश्र संख्याओं को बिनरियन कहा गया है।[55] जिस तरह निर्माण को प्रयुक्त करने से ऑर्डर किए गए क्षेत्र की संपत्ति खो जाती है, वास्तविक और सम्मिश्र संख्याओं से परिचित गुण प्रत्येक एक्सटेंशन के साथ गायब हो जाते हैं।चतुर्भुज कमज़ोरता खो देते हैं, अर्थात्, x·y ≠ y·x कुछ चतुर्भुजों के लिए x, y, और ऑक्टोनियन का गुणन, इसके अतिरिक्त कम्यूटेटिव नहीं होने के कारण, साहचर्य होने में विफल रहता है: (x·y)·z ≠ x·(y·z) कुछ पोषण के लिए x, y, z।
रियल, सम्मिश्र संख्या, चतुर्भुज और ऑक्टोनियन सभी मानदंड विभाजन बीजगणित हैं ।हर्विट्ज़ के प्रमेय (मानदंड विभाजन aggebras) द्वारा | हर्विट्ज़ के प्रमेय वे केवल एक ही हैं;धब्बा ्स, केली -डिकसन कंस्ट्रक्शन में अगला कदम, इस संरचना में विफल रहता है।
केली -डिकसन निर्माण के नियमित प्रतिनिधित्व से निकटता से संबंधित है के रूप में सोचा -लगेबरा (वलय थ्योरी) (ए) आधार के संबंध में, एक गुणन के साथ अंतरिक्ष) (1, i)।इसका तात्पर्य है निम्नलिखित: -लाइनर मैप
हाइपरकम्प्लेक्स संख्या भी सामान्यीकरण करती है और उदाहरण के लिए, इस धारणा में विभाजित-संकलन संख्या सम्मिलित हैं, जो वलय के तत्व हैं (विरोध के रूप में सम्मिश्र संख्याओं के लिए)।इस वलय में, समीकरण a2 = 1 चार समाधान हैं।
फील्ड का पूरा होना सामान्य निरपेक्ष मूल्य मीट्रिक (गणित) के संबंध में तर्कसंगत संख्याओं का क्षेत्र।मीट्रिक (गणित) के अन्य विकल्प पर खेतों के लिए नेतृत्व करें पी-एडिक नंबर का |p-एक नंबर (किसी भी प्रमुख संख्या के लिए) p), जो इस प्रकार अनुरूप हैं ।पूरा करने के कोई अन्य nontrivial तरीके नहीं हैं से और ओस्ट्रोव्स्की के प्रमेय द्वारा।बीजीय संवृत हो जाता है का अभी भी एक आदर्श ले जाता है, लेकिन (इसके विपरीत) ) इसके संबंध में पूरा नहीं है।पूर्ण का बीजगणित रूप से संवृत हो जाता है।सादृश्य द्वारा, क्षेत्र को कहा जाता है p-एक सम्मिश्र संख्या।
खेत और उनके परिमित क्षेत्र एक्सटेंशन, सहित स्थानीय क्षेत्र कहा जाता है।
यह भी देखें
- बीजगणितीय सतह
- सम्मिश्र संख्याओं का उपयोग करते हुए वृत्ताकार गति
- सम्मिश्र आधार प्रणाली
- सम्मिश्र ज्यामिति
- दोहरी-सम्मिश्र संख्या
- आइज़ेंस्टीन पूर्णांक
- यूलर की पहचान
- ज्यामितीय बीजगणित#यूनिट Pseudoscalars (जिसमें 2-आयामी संदिश उप-समष्टि के रूप में सम्मिश्र समतल सम्मिलित है)
- एकक सम्मिश्र संख्या
टिप्पणियाँ
- ↑ "Complex numbers, as much as reals, and perhaps even more, find a unity with nature that is truly remarkable. It is as though Nature herself is as impressed by the scope and consistency of the complex-number system as we are ourselves, and has entrusted to these numbers the precise operations of her world at its minutest scales." — R. Penrose (2016, p. 73)[2]
- ↑ Solomentsev 2001: "The plane whose points are identified with the elements of is called the complex plane ... The complete geometric interpretation of complex numbers and operations on them appeared first in the work of C. Wessel (1799). The geometric representation of complex numbers, sometimes called the 'Argand diagram', came into use after the publication in 1806 and 1814 of papers by J.R. Argand, who rediscovered, largely independently, the findings of Wessel".
- ↑ In modern notation, Tartaglia's solution is based on expanding the cube of the sum of two cube roots: With , , , u and v can be expressed in terms of p and q as and , respectively. Therefore, ।कब नकारात्मक है (कैसस irreducibilis), दूसरे क्यूब रूट को पहले एक के जटिल संयुग्म के रूप में माना जाना चाहिए।
- ↑ It has been proved that imaginary numbers have necessarily to appear in the cubic formula when the equation has three real, different roots by Pierre Laurent Wantzel in 1843, Vincenzo Mollame in 1890, Otto Hölder in 1891 and Adolf Kneser in 1892. Paolo Ruffini also provided an incomplete proof in 1799. — S. Confalonieri (2015)[20]
- ↑ Argand 1814, p. 204 defines the modulus of a complex number but he doesn't name it:
"Dans ce qui suit, les accens, indifféremment placés, seront employés pour indiquer la grandeur absolue des quantités qu'ils affectent; ainsi, si , et étant réels, on devra entendre que ou ."
[In what follows, accent marks, wherever they're placed, will be used to indicate the absolute size of the quantities to which they're assigned; thus if , and being real, one should understand that or .]
Argand 1814, p. 208 defines and names the module and the direction factor of a complex number: "... pourrait être appelé le module de , et représenterait la grandeur absolue de la ligne , tandis que l'autre facteur, dont le module est l'unité, en représenterait la direction."
[... could be called the module of and would represent the absolute size of the line (Note that Argand represented complex numbers as vectors.) whereas the other factor [namely, ], जिसका मॉड्यूल एकता है [1], इसकी दिशा का प्रतिनिधित्व करेगा।] - ↑ Gauss writes:[38]"Quemadmodum scilicet arithmetica sublimior in quaestionibus hactenus pertractatis inter solos numeros integros reales versatur, ita theoremata circa residua biquadratica tunc tantum in summa simplicitate ac genuina venustate resplendent, quando campus arithmeticae ad quantitates imaginarias extenditur, ita ut absque restrictione ipsius obiectum constituant numeri formae a + bi, denotantibus i, pro more quantitatem imaginariam , atque a, b indefinite omnes numeros reales integros inter - et +." [Of course just as the higher arithmetic has been investigated so far in problems only among real integer numbers, so theorems regarding biquadratic residues then shine in greatest simplicity and genuine beauty, when the field of arithmetic is extended to imaginary quantities, so that, without restrictions on it, numbers of the form a + bi — i denoting by convention the imaginary quantity , and the variables a, b [denoting] all real integer numbers between and — constitute an object.]
- ↑ Gauss:[39]"Tales numeros vocabimus numeros integros complexos, ita quidem, ut reales complexis non opponantur, sed tamquam species sub his contineri censeantur." [We will call such numbers [namely, numbers of the form a + bi ] "complex integer numbers", so that real [numbers] are regarded not as the opposite of complex [numbers] but [as] a type [of number that] is, so to speak, contained within them.]
- ↑ Gauss:[40] "Productum numeri complexi per numerum ipsi conjunctum utriusque normam vocamus. Pro norma itaque numeri realis, ipsius quadratum habendum est." [We call a "norm" the product of a complex number [e.g,. a + ib ] with its conjugate [a - ib ]. Therefore the square of a real number should be regarded as its norm.]
- ↑ However for another inverse function of the complex exponential function (and not the above defined principal value), the branch cut could be taken at any other ray thru the origin.
संदर्भ
- ↑ For an extensive account of the history of "imaginary" numbers, from initial skepticism to ultimate acceptance, see Bourbaki, Nicolas (1998). "Foundations of Mathematics § Logic: Set theory". Elements of the History of Mathematics. Springer. pp. 18–24.
- ↑ Penrose, Roger (2016). The Road to Reality: A complete guide to the laws of the universe (reprint ed.). Random House. pp. 72–73. ISBN 978-1-4464-1820-8.
- ↑ Axler, Sheldon (2010). कॉलेज अल्जेबरा. Wiley. p. 262. ISBN 9780470470770.
- ↑ Spiegel, M.R.; Lipschutz, S.; Schiller, J.J.; Spellman, D. (14 April 2009). जटिल चर. Schaum's Outline Series (2nd ed.). McGraw Hill. ISBN 978-0-07-161569-3.
- ↑ Aufmann, Richard N.; Barker, Vernon C.; Nation, Richard D. (2007). "Chapter P". कॉलेज बीजगणित और त्रिकोणमिति (6 ed.). Cengage Learning. p. 66. ISBN 978-0-618-82515-8.
- ↑ Ahlfors 1979.
- ↑ Brown, James Ward; Churchill, Ruel V. (1996). जटिल चर और अनुप्रयोग (6th ed.). New York: McGraw-Hill. p. 2. ISBN 978-0-07-912147-9.
इलेक्ट्रिकल इंजीनियरिंग में, j अक्षर का उपयोग i के बजाय किया जाता है।
} - ↑ Pedoe, Dan (1988). ज्यामिति: एक व्यापक पाठ्यक्रम. Dover. ISBN 978-0-486-65812-4.
- ↑ 9.0 9.1 Weisstein, Eric W. "जटिल संख्या". mathworld.wolfram.com. Retrieved 2020-08-12.
- ↑ Apostol 1981, p. 18.
- ↑ Kasana, H.S. (2005). "Chapter 1". जटिल चर: सिद्धांत और अनुप्रयोग (2nd ed.). PHI Learning Pvt. Ltd. p. 14. ISBN 978-81-203-2641-5.
- ↑ Nilsson, James William; Riedel, Susan A. (2008). "Chapter 9". Electric circuits (8th ed.). Prentice Hall. p. 338. ISBN 978-0-13-198925-2.
- ↑ Kline, Morris. गणितीय विचार का इतिहास, खंड 1. p. 253.
- ↑ Jurij., Kovič. ट्रिस्टन नीडम, विजुअल कॉम्प्लेक्स एनालिसिस, ऑक्सफोर्ड यूनिवर्सिटी प्रेस इंक।, न्यूयॉर्क, 1998, 592 स्ट्रानी. OCLC 1080410598.
- ↑ O’Connor and Robertson (2016), “Girolamo Cardano.”
- ↑ Nahin, Paul J. An Imaginary Tale: The Story of √-1. Princeton: Princeton University Press, 1998.
- ↑ Katz, Victor J. (2004). "9.1.4". गणित का इतिहास, संक्षिप्त संस्करण. Addison-Wesley. ISBN 978-0-321-16193-2.
- ↑ Hamilton, Wm. (1844). "काल्पनिक मात्रा की एक नई प्रजाति पर चतुर्भुज के सिद्धांत के साथ जुड़ा हुआ है". Proceedings of the Royal Irish Academy. 2: 424–434.
- ↑ Nahin, Paul J. (2007). एक काल्पनिक कथा: द स्टोरी ऑफ़ -1. Princeton University Press. ISBN 978-0-691-12798-9. Archived from the original on 12 October 2012. Retrieved 20 April 2011.
- ↑ 20.0 20.1 Confalonieri, Sara (2015). The Unattainable Attempt to Avoid the Casus Irreducibilis for Cubic Equations: Gerolamo Cardano's De Regula Aliza. Springer. pp. 15–16 (note 26). ISBN 978-3658092757.
- ↑ Descartes, René (1954) [1637]. ला गोमेट्री [[:Template:पाइप]] पहले संस्करण के एक चेहरे के साथ रेने डेसकार्टेस की ज्यामिति. Dover Publications. ISBN 978-0-486-60068-0. Retrieved 20 April 2011.
{{cite book}}: URL–wikilink conflict (help) - ↑ Euler, Leonard (1748). विश्लेषण का परिचय [Introduction to the Analysis of the Infinite] (in Latina). Vol. 1. Lucerne, Switzerland: Marc Michel Bosquet & Co. p. 104.
- ↑ Wessel, Caspar (1799). "दिशा के विश्लेषणात्मक पदनाम के बारे में, एक वर्तमान, विमान और गोलाकार बहुभुज के उद्घाटन के लिए समझदार है" [On the analytic representation of direction, an effort applied in particular to the determination of plane and spherical polygons]. Nye Samling af det Kongelige Danske Videnskabernes Selskabs Skrifter [New Collection of the Writings of the Royal Danish Science Society] (in dansk). 5: 469–518.
- ↑ Wallis, John (1685). बीजगणित का एक ग्रंथ, ऐतिहासिक और व्यावहारिक दोनों ... London, England: printed by John Playford, for Richard Davis. pp. 264–273.
- ↑ Argand (1806). ज्यामितीय निर्माणों में काल्पनिक मात्रा का प्रतिनिधित्व करने के तरीके पर निबंध [Essay on a way to represent complex quantities by geometric constructions] (in français). Paris, France: Madame Veuve Blanc.
- ↑ Gauss, Carl Friedrich (1799) "Demonstratio nova theorematis omnem functionem algebraicam rationalem integram unius variabilis in factores reales primi vel secundi gradus resolvi posse." [New proof of the theorem that any rational integral algebraic function of a single variable can be resolved into real factors of the first or second degree.] Ph.D. thesis, University of Helmstedt, (Germany). (in Latin)
- ↑ Ewald, William B. (1996). कांत से हिल्बर्ट: गणित की नींव में एक स्रोत पुस्तक. Vol. 1. Oxford University Press. p. 313. ISBN 9780198505358. Retrieved 18 March 2020.
- ↑ Gauss 1831, p. 638.
- ↑ Mourey, C.V. (1861). नकारात्मक मात्रा और कथित काल्पनिक मात्रा का सच्चा सिद्धांत [The true theory of negative quantities and of alleged imaginary quantities] (in français). Paris, France: Mallet-Bachelier. 1861 reprint of 1828 original.
- ↑ Warren, John (1828). नकारात्मक मात्रा के वर्ग जड़ों के ज्यामितीय प्रतिनिधित्व पर एक ग्रंथ. Cambridge, England: Cambridge University Press.
- ↑ Warren, John (1829). "नकारात्मक मात्रा की वर्ग जड़ों के ज्यामितीय प्रतिनिधित्व के खिलाफ उठाए गए आपत्तियों पर विचार". Philosophical Transactions of the Royal Society of London. 119: 241–254. doi:10.1098/rstl.1829.0022. S2CID 186211638.
- ↑ Warren, John (1829). "मात्रा की शक्तियों के ज्यामितीय प्रतिनिधित्व पर, जिनके सूचकांक में नकारात्मक संख्याओं की वर्ग जड़ें शामिल हैं". Philosophical Transactions of the Royal Society of London. 119: 339–359. doi:10.1098/rstl.1829.0031. S2CID 125699726.
- ↑ Français, J.F. (1813). "स्थिति ज्यामिति के नए सिद्धांत, और काल्पनिक प्रतीकों की ज्यामितीय व्याख्या" [New principles of the geometry of position, and geometric interpretation of complex [number] symbols]. Annales des mathématiques pures et appliquées (in français). 4: 61–71.
- ↑ Caparrini, Sandro (2000). "On the Common Origin of Some of the Works on the Geometrical Interpretation of Complex Numbers". In Kim Williams (ed.). दो संस्कृतियाँ. Birkhäuser. p. 139. ISBN 978-3-7643-7186-9.
- ↑ Hardy, G.H.; Wright, E.M. (2000) [1938]. संख्याओं के सिद्धांत का परिचय. OUP Oxford. p. 189 (fourth edition). ISBN 978-0-19-921986-5.
- ↑ Jeff Miller (Sep 21, 1999). "मापांक". Earliest Known Uses of Some of the Words of Mathematics (M). Archived from the original on 1999-10-03.
{{cite web}}: CS1 maint: unfit URL (link) - ↑ Cauchy, Augustin-Louis (1821). रॉयल पॉलिटेक्निक स्कूल का विश्लेषण पाठ्यक्रम (in français). Vol. 1. Paris, France: L'Imprimerie Royale. p. 183.
- ↑ Gauss 1831, p. 96
- ↑ Gauss 1831, p. 96
- ↑ Gauss 1831, p. 98
- ↑ Hankel, Hermann (1867). जटिल संख्याओं और उनके कार्यों के बारे में व्याख्यान [Lectures About the Complex Numbers and Their Functions] (in Deutsch). Vol. 1. Leipzig, [Germany]: Leopold Voss. p. 71. From p. 71: "Wir werden den Factor (cos φ + i sin φ) haüfig den Richtungscoefficienten nennen." (We will often call the factor (cos φ + i sin φ) the "coefficient of direction".)
- ↑ For the former notation, see Apostol 1981, pp. 15–16
- ↑ Abramowitz, Milton; Stegun, Irene A. (1964). सूत्र, रेखांकन और गणितीय तालिकाओं के साथ गणितीय कार्यों की हैंडबुक. Courier Dover Publications. p. 17. ISBN 978-0-486-61272-0. Archived from the original on 23 April 2016. Retrieved 16 February 2016., Section 3.7.26, p. 17 Archived 10 September 2009 at the Wayback Machine
- ↑ Cooke, Roger (2008). शास्त्रीय बीजगणित: इसकी प्रकृति, उत्पत्ति और उपयोग. John Wiley and Sons. p. 59. ISBN 978-0-470-25952-8. Archived from the original on 24 April 2016. Retrieved 16 February 2016., Extract: page 59 Archived 23 April 2016 at the Wayback Machine
- ↑ Ahlfors 1979, p. 3.
- ↑ 46.0 46.1 Apostol 1981, pp. 15–16.
- ↑ Apostol 1981, p. 25.
- ↑ Marker, David (1996). "Introduction to the Model Theory of Fields". In Marker, D.; Messmer, M.; Pillay, A. (eds.). फ़ील्ड का मॉडल सिद्धांत. Lecture Notes in Logic. Vol. 5. Berlin: Springer-Verlag. pp. 1–37. ISBN 978-3-540-60741-0. MR 1477154.
- ↑ Bourbaki 1998, §VIII.4.
- ↑ Corry, Leo (2015). संख्याओं का एक संक्षिप्त इतिहास. Oxford University Press. pp. 215–16.
- ↑ Lester, J.A. (1994). "त्रिकोण I: आकार". Aequationes Mathematicae. 52: 30–54. doi:10.1007/BF01818325. S2CID 121095307.
- ↑ Kalman, Dan (2008a). "मार्डन के प्रमेय का एक प्राथमिक प्रमाण". American Mathematical Monthly. 115 (4): 330–38. doi:10.1080/00029890.2008.11920532. ISSN 0002-9890. S2CID 13222698. Archived from the original on 8 March 2012. Retrieved 1 January 2012.
- ↑ Kalman, Dan (2008b). "गणित में सबसे अद्भुत प्रमेय". Journal of Online Mathematics and Its Applications. Archived from the original on 8 February 2012. Retrieved 1 January 2012.
- ↑ Grant, I.S.; Phillips, W.R. (2008). विद्युत चुंबकत्व (2 ed.). Manchester Physics Series. ISBN 978-0-471-92712-9.
- ↑ McCrimmon, Kevin (2004). जॉर्डन बीजगणित का स्वाद. Universitext. Springer. p. 64. ISBN 0-387-95447-3. MR2014924
वर्क्स का हवाला दिया गया
- Ahlfors, Lars (1979). जटिल विश्लेषण (3rd ed.). McGraw-Hill. ISBN 978-0-07-000657-7.
- Apostol, Tom (1981). गणितीय विश्लेषण. Addison-Wesley.
- Argand (1814). "कल्पना के नए सिद्धांत पर विचार, गुदा के एक प्रमेय के प्रदर्शन के लिए एक आवेदन के बाद" [Reflections on the new theory of complex numbers, followed by an application to the proof of a theorem of analysis]. Annales de mathématiques pures et appliquées (in français). 5: 197–209.
- Gauss, C. F. (1831). "Bikadraticorum के अवशेषों का सिद्धांत।दूसरी टिप्पणी।" [Theory of biquadratic residues. Second memoir.]. Commentationes Societatis Regiae Scientiarum Gottingensis Recentiores (in Latina). 7: 89–148.
- Solomentsev, E.D. (2001) [1994], "Complex number", Encyclopedia of Mathematics, EMS Press
आगे की पढाई
- Penrose, Roger (2005). The Road to Reality: A complete guide to the laws of the universe. Alfred A. Knopf. ISBN 978-0-679-45443-4.
- Derbyshire, John (2006). Unknown Quantity: A real and imaginary history of algebra. Joseph Henry Press. ISBN 978-0-309-09657-7.
- Needham, Tristan (1997). Visual Complex Analysis. Clarendon Press. ISBN 978-0-19-853447-1.
गणितीय
- Ahlfors, Lars (1979). जटिल विश्लेषण (3rd ed.). McGraw-Hill. ISBN 978-0-07-000657-7.
- Conway, John B. (1986). एक जटिल चर के कार्य. Springer. ISBN 978-0-387-90328-6.
- Joshi, Kapil D. (1989). असतत गणित की नींव. New York: John Wiley & Sons. ISBN 978-0-470-21152-6.
- Pedoe, Dan (1988). ज्यामिति: एक व्यापक पाठ्यक्रम. Dover. ISBN 978-0-486-65812-4.
- Press, W.H.; Teukolsky, S.A.; Vetterling, W.T.; Flannery, B.P. (2007). "Section 5.5 Complex Arithmetic". संख्यात्मक व्यंजनों: वैज्ञानिक कंप्यूटिंग की कला (3rd ed.). New York: Cambridge University Press. ISBN 978-0-521-88068-8.
- Solomentsev, E.D. (2001) [1994], "Complex number", Encyclopedia of Mathematics, EMS Press
ऐतिहासिक
- Bourbaki, Nicolas (1998). "Foundations of mathematics § logic: set theory". गणित के इतिहास के तत्व. Springer.
- Burton, David M. (1995). गणित का इतिहास (3rd ed.). New York: McGraw-Hill. ISBN 978-0-07-009465-9.
- Katz, Victor J. (2004). गणित का इतिहास, संक्षिप्त संस्करण. Addison-Wesley. ISBN 978-0-321-16193-2.
- Nahin, Paul J. (1998). एक काल्पनिक कहानी: <गणित की कहानी \ scriptstyle \ sqrt {-1} </math>. Princeton University Press. ISBN 978-0-691-02795-1. - जटिल संख्याओं के इतिहास और जटिल विश्लेषण की शुरुआत के लिए एक सौम्य परिचय।
- Ebbinghaus, H. D.; Hermes, H.; Hirzebruch, F.; Koecher, M.; Mainzer, K.; Neukirch, J.; Prestel, A.; Remmert, R. (1991). नंबर (hardcover ed.). Springer. ISBN 978-0-387-97497-2. - संख्या की अवधारणा के ऐतिहासिक विकास पर एक उन्नत परिप्रेक्ष्य।
श्रेणी: रचना बीजगणित श्रेणी: सम्मिश्र संख्याएँ