प्रमुख घटक विश्लेषण: Difference between revisions
No edit summary |
No edit summary |
||
| (14 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
{{Short description|Method of data analysis}} | {{Short description|Method of data analysis}} | ||
'''प्रमुख कंपोनेंट विश्लेषण''' (पीसीए) प्रति अवलोकन उच्च संख्या में आयाम/फीवेरिएबल | '''प्रमुख कंपोनेंट विश्लेषण''' (पीसीए) प्रति अवलोकन उच्च संख्या में आयाम/फीवेरिएबल वाले बड़े डेटासमुच्चय का विश्लेषण करने, अधिकतम मात्रा में सूचना को संरक्षित करते हुए डेटा की व्याख्या को बढ़ाते हैं, और बहुआयामी डेटा के विज़ुअलाइज़ेशन को सक्षम करने के लिए लोकप्रिय तकनीक है औपचारिक रूप से, पीसीए डेटासमुच्चय के आयाम को कम करने के लिए सांख्यिकीय तकनीक है। यह डेटा को रैखिक रूप से नई समन्वय प्रणाली में परिवर्तित करके पूर्ण किया जाता है, जहां (अधिकांश) डेटा में भिन्नता को प्रारंभिक डेटा की तुलना में कम आयामों के साथ वर्णित किया जा सकता है। डेटा को दो आयामों में प्लॉट करने के लिए और निकट से संबंधित डेटा बिंदुओं के समूहों की दृष्टि से पहचान करने के लिए अनेक अध्ययन पहले दो प्रमुख अवयवों का उपयोग करते हैं। यह प्रमुख कंपोनेंट विश्लेषण के अनेक क्षेत्रों में जैसे [[जनसंख्या आनुवंशिकी]], [[माइक्रोबायोम]] अध्ययन और [[वायुमंडलीय विज्ञान]] में अनुप्रयोग होते हैं। <ref>{{Cite journal |last1=Jolliffe |first1=Ian T. |last2=Cadima |first2=Jorge |date=2016-04-13 |title=Principal component analysis: a review and recent developments |journal=Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences |volume=374 |issue=2065 |pages=20150202 |doi=10.1098/rsta.2015.0202 |pmc=4792409 |pmid=26953178}}</ref>[[File:GaussianScatterPCA.svg|300px|thumb|right|सामान्यतः (0.866, 0.5) दिशा में 3 के मानक विचलन और ऑर्थोगोनल दिशा में 1 के मानक विचलन के साथ (1,3) पर केंद्रित बहुभिन्नरूपी गॉसियन वितरण का पीसीए। दिखाए गए सदिश संबंधित आइजेनवैल्यू के वर्गमूल द्वारा स्केल किए गए सहप्रसरण आव्युह के आइजेनवैल्यू और आइजन्वेक्टर हैं, और स्थानांतरित किए गए हैं जिससे उनकी पूंछ माध्य पर हो।]][[वास्तविक समन्वय स्थान]] में बिंदुओं के संग्रह के प्रमुख अवयव <math>p</math> यूनिट सदिश अनुक्रम हैं, जहां <math>i</math>-वें सदिश रेखा की दिशा है जो पहले <math>i-1</math> सदिश के लिए ऑर्थोगोनल होते हुए डेटा को सबसे अच्छी तरह से फिट करता है। यहां, सर्वोत्तम-फिटिंग लाइन को उस रेखा के रूप में परिभाषित किया गया है जो बिंदु से रेखा तक औसत वर्ग [[लंबवत दूरी]] दूरी को कम करता है। यह दिशाएँ अलौकिक आधार का गठन करती हैं जिसमें डेटा के विभिन्न व्यक्तिगत आयाम [[रैखिक सहसंबंध]] होते हैं। प्रमुख अवयव विश्लेषण प्रमुख अवयवों की गणना करने और डेटा के आधार पर परिवर्तन करने के लिए उनका उपयोग करने की प्रक्रिया है, कभी-कभी केवल पहले कुछ प्रमुख अवयवों का उपयोग करके और शेष को अनदेखा करते हुए इसका उपयोग किया जाता है। | ||
डेटा विश्लेषण में, | डेटा विश्लेषण में, <math>p</math> वेरिएबल समुच्चय का पहला प्रमुख अवयव , जिसे संयुक्त रूप से सामान्यतः वितरित माना जाता है, मूल वेरिएबल के रैखिक संयोजन के रूप में गठित व्युत्पन्न वेरिएबल है जो सबसे अधिक विचरण की व्याख्या करता है। दूसरा प्रमुख अवयव पहले अवयव के प्रभाव को हटा दिए जाने के पश्चात जो बचा है उसमें सबसे अधिक भिन्नता की व्याख्या करता है, और हम <math>p</math> पुनरावृत्तियाँ इसके माध्यम से आगे बढ़ सकते हैं जब तक कि सभी विचरण की व्याख्या नहीं की जाती हैं। पीसीए का सबसे अधिक उपयोग तब किया जाता है जब अनेक वेरिएबल दूसरे के साथ अत्यधिक सहसंबद्ध होते हैं और उनकी संख्या को स्वतंत्र समुच्चय में कम करना वांछनीय होता है। | ||
पीसीए का उपयोग खोजपूर्ण डेटा विश्लेषण और | पीसीए का उपयोग खोजपूर्ण डेटा विश्लेषण और [[भविष्य कहनेवाला मॉडलिंग|प्रेडिक्टिव मॉडलिंग]] करने के लिए किया जाता है। यह सामान्यतः प्रत्येक डेटा बिंदु को केवल पहले कुछ प्रमुख अवयवों पर प्रक्षेपित करके [[आयामीता में कमी]] के लिए उपयोग किया जाता है जिससे जितना संभव हो उतना डेटा भिन्नता को संरक्षित करते हुए निम्न-आयामी डेटा प्राप्त किया जा सके। पहले प्रमुख अवयव को समान रूप से दिशा के रूप में परिभाषित किया जा सकता है जो अनुमानित डेटा के विचरण को अधिकतम करता है। यह <math>i</math>वें>-वें प्रमुख अवयव को पहले <math>i-1</math> प्रमुख अवयव के लिए दिशा ऑर्थोगोनल के रूप में लिया जा सकता है जो अनुमानित डेटा के विचरण को अधिकतम करते हैं। | ||
किसी भी उद्देश्य के लिए, यह दिखाया जा सकता है कि प्रमुख अवयव डेटा के सहप्रसरण आव्युह | किसी भी उद्देश्य के लिए, यह दिखाया जा सकता है कि प्रमुख अवयव डेटा के सहप्रसरण आव्युह के आइजन्वेक्टर हैं। इस प्रकार, प्रमुख अवयवों की गणना अधिकतर डेटा सहप्रसरण आव्युह के आइजेनडी कम्पोज़िशन या डेटा आव्युह के एकवचन मान अपघटन द्वारा की जाती है। पीसीए सत्य आइजन्वेक्टर -आधारित बहुभिन्नरूपी विश्लेषणों में सबसे सरल है और [[कारक विश्लेषण]] से निकटता से संबंधित है। कारक विश्लेषण में सामान्यतः अंतर्निहित संरचना के बारे में अधिक डोमेन विशिष्ट मान्यताओं को सम्मिलित किया जाता है और थोड़ा भिन्न आव्युह के आइजन्वेक्टर को हल करता है। पीसीए भी विहित सहसंबंध विहित सहसंबंध विश्लेषण (सीसीए) से संबंधित है। यह सीसीए समन्वय प्रणालियों को परिभाषित करता है जो दो डेटासमुच्चय के मध्य [[क्रॉस सहप्रसरण]] का उत्तम वर्णन करता है जबकि पीसीए नए [[ऑर्थोगोनल समन्वय प्रणाली]] को परिभाषित करता है जो एकल डेटासमुच्चय में भिन्नता का उत्तम वर्णन करता है। <ref>{{Cite journal|author1=Barnett, T. P. |author2=R. Preisendorfer. |name-list-style=amp |title=कैनोनिकल सहसंबंध विश्लेषण द्वारा निर्धारित संयुक्त राज्य सतह हवा के तापमान के लिए मासिक और मौसमी पूर्वानुमान कौशल की उत्पत्ति और स्तर|journal=Monthly Weather Review |volume=115 |issue=9 |pages=1825 |year=1987 |doi=10.1175/1520-0493(1987)115<1825:oaloma>2.0.co;2|bibcode=1987MWRv..115.1825B|doi-access=free }}</ref><ref>{{Cite book |last1=Hsu|first1=Daniel |first2=Sham M.|last2=Kakade |first3=Tong|last3=Zhang |title=छिपे हुए मार्कोव मॉडल सीखने के लिए एक स्पेक्ट्रल एल्गोरिदम|arxiv=0811.4413 |year=2008 |bibcode=2008arXiv0811.4413H}}</ref><ref name="mark2017">{{cite journal|last1=Markopoulos|first1=Panos P.|last2=Kundu|first2=Sandipan|last3=Chamadia|first3=Shubham |last4=Pados|first4=Dimitris A.|title=बिट फ़्लिपिंग के माध्यम से कुशल एल1-नॉर्म प्रिंसिपल-कंपोनेंट विश्लेषण|journal=IEEE Transactions on Signal Processing|date=15 August 2017|volume=65|issue=16|pages=4252–4264|doi=10.1109/TSP.2017.2708023|arxiv=1610.01959|bibcode=2017ITSP...65.4252M|s2cid=7931130}}</ref><ref name="l1tucker">{{cite journal|last1=Chachlakis|first1=Dimitris G.|last2=Prater-Bennette|first2=Ashley|last3=Markopoulos|first3=Panos P.|title=एल1-मानदंड टकर टेन्सर अपघटन|journal=IEEE Access|date=22 November 2019|volume=7|pages=178454–178465|doi=10.1109/ACCESS.2019.2955134|arxiv=1904.06455|doi-access=free}}</ref> शक्तिशाली आंकड़े और [[एलपी स्पेस]] हैं | मानक पीसीए के L1-मानक-आधारित संस्करण भी प्रस्तावित किए गए हैं। <ref name="mark2014">{{cite journal|last1=Markopoulos|first1=Panos P.|last2=Karystinos|first2=George N.|last3=Pados|first3=Dimitris A.|title=एल1-सबस्पेस सिग्नल प्रोसेसिंग के लिए इष्टतम एल्गोरिदम|journal=IEEE Transactions on Signal Processing|date=October 2014|volume=62|issue=19|pages=5046–5058|doi=10.1109/TSP.2014.2338077|arxiv=1405.6785|bibcode=2014ITSP...62.5046M|s2cid=1494171}}</ref><ref>{{cite journal |last1=Zhan |first1=J. |last2=Vaswani |first2=N. |date=2015 |title=आंशिक सबस्पेस ज्ञान के साथ मजबूत पीसीए|url=https://doi.org/10.1109/tsp.2015.2421485 |journal=IEEE Transactions on Signal Processing |volume=63 |issue=13 |pages=3332–3347 | doi=10.1109/tsp.2015.2421485|arxiv=1403.1591 |bibcode=2015ITSP...63.3332Z |s2cid=1516440 }}</ref><ref>{{cite book|last1=Kanade|first1=T.|last2=Ke|first2=Qifa |title=वैकल्पिक उत्तल प्रोग्रामिंग द्वारा बाहरी तत्वों की उपस्थिति और अनुपलब्ध डेटा में मजबूत L1 मानक गुणनखंडन|journal=2005 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR'05)|volume=1|pages=739|date=June 2005|doi=10.1109/CVPR.2005.309|publisher=IEEE|isbn=978-0-7695-2372-9|citeseerx=10.1.1.63.4605|s2cid=17144854}}</ref><ref name="l1tucker" /> | ||
== इतिहास == | == इतिहास == | ||
पीसीए का आविष्कार 1901 में [[कार्ल पियर्सन]] ने किया था।<ref>{{Cite journal|author=Pearson, K. |author-link=Karl Pearson |year=1901 |title=अंतरिक्ष में बिंदुओं के सिस्टम के निकटतम फिट की रेखाओं और विमानों पर|journal=Philosophical Magazine |volume=2 |issue=11 |pages=559–572 |doi=10.1080/14786440109462720|url=https://zenodo.org/record/1430636 }}</ref> यांत्रिकी में [[प्रमुख अक्ष प्रमेय]] के अनुरूप; इसे पश्चात | पीसीए का आविष्कार 1901 में [[कार्ल पियर्सन]] ने किया था। <ref>{{Cite journal|author=Pearson, K. |author-link=Karl Pearson |year=1901 |title=अंतरिक्ष में बिंदुओं के सिस्टम के निकटतम फिट की रेखाओं और विमानों पर|journal=Philosophical Magazine |volume=2 |issue=11 |pages=559–572 |doi=10.1080/14786440109462720|url=https://zenodo.org/record/1430636 }}</ref> यांत्रिकी में [[प्रमुख अक्ष प्रमेय]] के अनुरूप; इसे पश्चात में स्वतंत्र रूप से विकसित किया गया और 1930 के दशक में [[हेरोल्ड होटलिंग]] द्वारा इसका नाम दिया गया है।<ref>Hotelling, H. (1933). Analysis of a complex of statistical variables into principal components. ''[[Journal of Educational Psychology]]'', '''24''', 417–441, and 498–520.<br> {{cite journal |last1=Hotelling |first1=H |year=1936 |title=Relations between two sets of variates |journal=[[Biometrika]] |volume=28 |issue=3/4|pages=321–377 |doi=10.2307/2333955|jstor=2333955}}</ref> अनुप्रयोग के क्षेत्र के आधार पर, इसे असतत करहुनेन-लोएव प्रमेय भी नाम दिया गया है। [[ संकेत आगे बढ़ाना |संकेत आगे बढ़ाना]] में करहुनेन-लोएव रूपांतरण (केएलटी), बहुभिन्नरूपी गुणवत्ता नियंत्रण में हेरोल्ड होटलिंग रूपांतरण, मैकेनिकल इंजीनियरिंग में [[उचित ऑर्थोगोनल अपघटन]] (पीओडी), एकवचन मान X का अपघटन (एसवीडी) (20वीं शताब्दी की अंतिम तिमाही में आविष्कार किया गया <ref> | ||
{{cite journal |last1=Stewart|first1=G. W. |year=1993 |title=On the early history of the singular value decomposition |journal=[[SIAM Review]] |volume=35 |issue=4|pages=551–566|doi=10.1137/1035134|url=http://purl.umn.edu/1868 }}</ref>), | {{cite journal |last1=Stewart|first1=G. W. |year=1993 |title=On the early history of the singular value decomposition |journal=[[SIAM Review]] |volume=35 |issue=4|pages=551–566|doi=10.1137/1035134|url=http://purl.umn.edu/1868 }}</ref>), रेखीय बीजगणित में X<sup>T</sup>X का [[Eigedecomposition|आइजेनडीकम्पोज़िशन]] (ईवीडी) हैं।, कारक विश्लेषण (पीसीए और कारक विश्लेषण के मध्य अंतर की चर्चा के लिए जोलिफ़ प्रमुख कंपोनेंट विश्लेषण का अध्याय 7 देखें),<ref name="Jolliffe2002">{{Cite book |last=Jolliffe |first=I. T. |url=http://link.springer.com/10.1007/b98835 |title=प्रमुख कंपोनेंट विश्लेषण|date=2002 |publisher=Springer-Verlag |isbn=978-0-387-95442-4 |series=Springer Series in Statistics |location=New York |language=en |doi=10.1007/b98835}}</ref> एकार्ट-यंग प्रमेय (हरमन, 1960), या अनुभवजन्य ऑर्थोगोनल फ़ंक्शंस (ईओएफ) मौसम विज्ञान में (लॉरेंज, 1956), अनुभवजन्य ईजेनफंक्शन अपघटन (सिरोविच, 1987), क्वासिहार्मोनिक मोड (ब्रूक्स एट अल।, 1988), [[वर्णक्रमीय प्रमेय]] ध्वनि और कंपन में वर्णक्रमीय अपघटन, और संरचनात्मक गतिशीलता में अनुभवजन्य मोडल विश्लेषण में देखे गये थे। | ||
== अंतर्ज्ञान == | == अंतर्ज्ञान == | ||
पीसीए को डेटा के लिए | पीसीए को डेटा के लिए p-आयामी दीर्घवृत्त के रूप में फिट करने के बारे में सोचा जा सकता है, जहां दीर्घवृत्त का प्रत्येक अक्ष प्रमुख अवयव का प्रतिनिधित्व करता है। यदि [[दीर्घवृत्ताभ]] का कुछ अक्ष लघु है, तब उस अक्ष के साथ विचरण भी लघु होता है। | ||
दीर्घवृत्ताभ के अक्षों को खोजने के लिए, हमें सबसे पहले डेटासमुच्चय | दीर्घवृत्ताभ के अक्षों को खोजने के लिए, हमें सबसे पहले डेटासमुच्चय में प्रत्येक वेरिएबल के मानों को 0 पर केंद्रित करना चाहिए और उनमें से प्रत्येक मान से वेरिएबल के देखे गए मानों का माध्य घटाना चाहिए। प्रत्येक वेरिएबल के लिए मूल देखे गए मानों के अतिरिक्त इन परिवर्तित मानों का उपयोग किया जाता है। पुनः , हम डेटा के सहप्रसरण आव्युह की गणना करते हैं और इस सहसंयोजक आव्युह के आइजेनवैल्यू और संबंधित आइजन्वेक्टर की गणना करते हैं। पुनः हमें प्रत्येक ऑर्थोगोनल आइजन्वेक्टर को यूनिट सदिश में परिवर्तन के लिए [[सामान्यीकरण (सांख्यिकी)]] करना होगा। पुनः यह हो जाने के पश्चात , प्रत्येक परस्पर-ऑर्थोगोनल यूनिट आइजन्वेक्टर को डेटा में फिट किए गए दीर्घवृत्त के अक्ष के रूप में व्याख्या किया जा सकता है। इसके आधार का यह चुनाव सहप्रसरण आव्युह को विकर्ण रूप में परिवर्तित कर देगा, जिसमें विकर्ण अवयव प्रत्येक अक्ष के विचरण का प्रतिनिधित्व करते हैं। प्रत्येक आइजन्वेक्टर द्वारा दर्शाए गए प्रसरण के अनुपात की गणना उस आइजन्वेक्टर के अनुरूप आइजेनवैल्यू को सभी आइजेनवैल्यू के योग से विभाजित करके की जा सकती है। | ||
पीसीए के निष्कर्षों को समझाने के लिए [[बिप्लॉट]] | पीसीए के निष्कर्षों को समझाने के लिए [[बिप्लॉट]]स और [[ मिट्टी - रोढ़ी वाला भूखंड |स्क्री प्लॉट]] (व्याख्या विचरण की डिग्री) का उपयोग किया जाता है। | ||
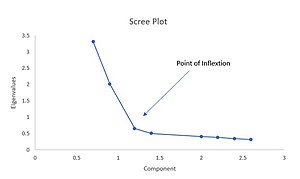
[[File:SCREE_plot.jpg|thumb|ऊपर दी गई तस्वीर डरावने प्लॉट की है जो पीसीए की व्याख्या करने और यह तय करने में | [[File:SCREE_plot.jpg|thumb|ऊपर दी गई तस्वीर डरावने प्लॉट की है जो पीसीए की व्याख्या करने और यह तय करने में सहायता करने के लिए है कि कितने अवयवों को बनाए रखना है। लाइन में मोड़ की प्रारंभ (विभक्ति का बिंदु) इंगित करना चाहिए कि कितने अवयवों को बनाए रखा जाता है, इसलिए इस उदाहरण में, तीन कारकों को बनाए रखा जाना चाहिए।]] | ||
== विवरण == | == विवरण == | ||
पीसीए को [[ऑर्थोगोनल परिवर्तन]] [[रैखिक परिवर्तन]] के रूप में परिभाषित किया गया है जो डेटा को नई समन्वय प्रणाली में | पीसीए को [[ऑर्थोगोनल परिवर्तन]] [[रैखिक परिवर्तन]] के रूप में परिभाषित किया गया है जो डेटा को नई समन्वय प्रणाली में परिवर्तित कर देता है जैसे कि डेटा के कुछ स्केलर प्रक्षेपण द्वारा सबसे बड़ा भिन्नता को पहले समन्वय (जिसे पहला मुख्य अवयव कहा जाता है) पर आती है, तथा दूसरा सबसे बड़ा भिन्नता होती है जैसे कि दूसरा समन्वय, इत्यादि हैं। <ref name="Jolliffe2002"/> | ||
इस पर विचार करें <math>n \times p</math> डेटा [[मैट्रिक्स (गणित)|आव्युह (गणित)]], X, स्तंभ-वार शून्य अनुभवजन्य माध्य के साथ (प्रत्येक स्तंभ का प्रतिरूप माध्य शून्य पर स्थानांतरित कर दिया गया है), जहां प्रत्येक ''n'' पंक्तियाँ प्रयोग की भिन्न पुनरावृत्ति का प्रतिनिधित्व करती हैं, और प्रत्येक ''p'' स्तम्भ विशेष प्रकार की सुविधा देता है ( किसी विशेष सेंसर का परिणाम कहते हैं)। | |||
गणितीय रूप से, परिवर्तन को आकार के समुच्चय | गणितीय रूप से, परिवर्तन को आकार के समुच्चय द्वारा परिभाषित किया जाता है | इसमें <math>l</math> वजन या गुणांक के p-आयामी सदिश <math>\mathbf{w}_{(k)} = (w_1, \dots, w_p)_{(k)} </math> हैं वह प्रत्येक पंक्ति <math>\mathbf{x}_{(i)}</math> सदिश को मानचित्र करता है तथा प्रमुख अवयव स्कोर के नए सदिश के लिए X का <math>\mathbf{t}_{(i)} = (t_1, \dots, t_l)_{(i)}</math>, द्वारा दिए गए होते हैं | | ||
:<math>{t_{k}}_{(i)} = \mathbf{x}_{(i)} \cdot \mathbf{w}_{(k)} \qquad \mathrm{for} \qquad i = 1,\dots,n \qquad k = 1,\dots,l </math> | :<math>{t_{k}}_{(i)} = \mathbf{x}_{(i)} \cdot \mathbf{w}_{(k)} \qquad \mathrm{for} \qquad i = 1,\dots,n \qquad k = 1,\dots,l </math> | ||
इस | इस प्रकार से कि व्यक्तिगत वेरिएबल <math>t_1, \dots, t_l</math> डेटा समुच्चय पर विचार किए गए t के क्रमिक रूप से X से अधिकतम संभव विचरण प्राप्त होता है, प्रत्येक गुणांक सदिश w के साथ इकाई सदिश होने के लिए विवश होता है (जहाँ <math>l</math> सामान्यतः कठोरता से कम होने के लिए चुना जाता है और <math>p</math> आयामीता को कम करने के लिए) चुना जाता है। | ||
=== | === प्रथम अवयव === | ||
प्रसरण को अधिकतम करने के लिए, पहला भार सदिश w<sub>(1)</sub> इस प्रकार संतुष्ट करना पड़ता है | प्रसरण को अधिकतम करने के लिए, पहला भार सदिश w<sub>(1)</sub> इस प्रकार संतुष्ट करना पड़ता है | ||
:<math>\mathbf{w}_{(1)} | :<math>\mathbf{w}_{(1)} | ||
= \arg\max_{\Vert \mathbf{w} \Vert = 1} \,\left\{ \sum_i (t_1)^2_{(i)} \right\} | = \arg\max_{\Vert \mathbf{w} \Vert = 1} \,\left\{ \sum_i (t_1)^2_{(i)} \right\} | ||
= \arg\max_{\Vert \mathbf{w} \Vert = 1} \,\left\{ \sum_i \left(\mathbf{x}_{(i)} \cdot \mathbf{w} \right)^2 \right\}</math> | = \arg\max_{\Vert \mathbf{w} \Vert = 1} \,\left\{ \sum_i \left(\mathbf{x}_{(i)} \cdot \mathbf{w} \right)^2 \right\} </math> | ||
समान रूप से इसे आव्युह | समान रूप से इसे आव्युह रूप में लिखने पर प्राप्त होता है | ||
:<math>\mathbf{w}_{(1)} | :<math>\mathbf{w}_{(1)} | ||
= \arg\max_{\left\| \mathbf{w} \right\| = 1} \left\{ \left\| \mathbf{Xw} \right\|^2 \right\} | = \arg\max_{\left\| \mathbf{w} \right\| = 1} \left\{ \left\| \mathbf{Xw} \right\|^2 \right\} | ||
= \arg\max_{\left\| \mathbf{w} \right\| = 1} \left\{ \mathbf{w}^\mathsf{T} \mathbf{X}^\mathsf{T} \mathbf{X w} \right\}</math> | = \arg\max_{\left\| \mathbf{w} \right\| = 1} \left\{ \mathbf{w}^\mathsf{T} \mathbf{X}^\mathsf{T} \mathbf{X w} \right\} </math> | ||
यह समकक्ष भी संतुष्ट करता है जहाँ w<sub>(1)</sub>के पश्चात से इकाई सदिश के रूप में परिभाषित किया गया है, | |||
:<math>\mathbf{w}_{(1)} = \arg\max \left\{ \frac{\mathbf{w}^\mathsf{T} \mathbf{X}^\mathsf{T} \mathbf{X w}}{\mathbf{w}^\mathsf{T} \mathbf{w}} \right\}</math> | :<math>\mathbf{w}_{(1)} = \arg\max \left\{ \frac{\mathbf{w}^\mathsf{T} \mathbf{X}^\mathsf{T} \mathbf{X w}}{\mathbf{w}^\mathsf{T} \mathbf{w}} \right\} </math> | ||
अधिकतम की जाने वाली मात्रा को [[रेले भागफल]] के रूप में पहचाना जा सकता है। [[सकारात्मक अर्ध निश्चित मैट्रिक्स| | अधिकतम की जाने वाली मात्रा को [[रेले भागफल]] के रूप में पहचाना जा सकता है। [[सकारात्मक अर्ध निश्चित मैट्रिक्स|धनात्मक अर्ध निश्चित आव्युह]] जैसे ''X<sup>T</sup>X'' के लिए मानक परिणाम यह है कि भागफल का अधिकतम संभव मान आव्युह का सबसे बड़ा [[eigenvalue|आइजेनवैल्यू]] है, जो तब होता है जब ''w'' संबंधित [[eigenvector|आइजन्वेक्टर]] होता है। | ||
w<sub>(1)</sub> के साथ मिला, डेटा सदिश ''x<sub>(i)</sub>'' का पहला प्रमुख अवयव रूपांतरित निर्देशांक में पुनः स्कोर ''t<sub>1(i)</sub> = x<sub>(i)</sub> ⋅ w<sub>(1)</sub>'' के रूप में दिया जा सकता है , या मूल वेरिएबल में संबंधित सदिश के रूप में, x<sub>(''i'')</sub> ⋅w<sub>(1)</sub>} w<sub>(1)</sub> होता है | | |||
=== आगे के | === आगे के अवयव === | ||
k-वें अवयव को 'X' से पहले k − 1 प्रमुख अवयवों | k-वें अवयव को 'X' से पहले k − 1 प्रमुख अवयवों को घटाकर प्राप्त किया जा सकता है | | ||
:<math>\mathbf{\hat{X}}_k = \mathbf{X} - \sum_{s = 1}^{k - 1} \mathbf{X} \mathbf{w}_{(s)} \mathbf{w}_{(s)}^{\mathsf{T}} </math> | :<math>\mathbf{\hat{X}}_k = \mathbf{X} - \sum_{s = 1}^{k - 1} \mathbf{X} \mathbf{w}_{(s)} \mathbf{w}_{(s)}^{\mathsf{T}} </math> | ||
और | और पुनः वेट सदिश का पता लगाना जो इस नए डेटा आव्युह से अधिकतम भिन्नता निकालता है | ||
:<math>\mathbf{w}_{(k)} | :<math>\mathbf{w}_{(k)} | ||
= \mathop{\operatorname{arg\,max}}_{\left\| \mathbf{w} \right\| = 1} \left\{ \left\| \mathbf{\hat{X}}_{k} \mathbf{w} \right\|^2 \right\} | = \mathop{\operatorname{arg\,max}}_{\left\| \mathbf{w} \right\| = 1} \left\{ \left\| \mathbf{\hat{X}}_{k} \mathbf{w} \right\|^2 \right\} | ||
= \arg\max \left\{ \tfrac{\mathbf{w}^\mathsf{T} \mathbf{\hat{X}}_{k}^\mathsf{T} \mathbf{\hat{X}}_{k} \mathbf{w}}{\mathbf{w}^T \mathbf{w}} \right\}</math> | = \arg\max \left\{ \tfrac{\mathbf{w}^\mathsf{T} \mathbf{\hat{X}}_{k}^\mathsf{T} \mathbf{\hat{X}}_{k} \mathbf{w}}{\mathbf{w}^T \mathbf{w}} \right\}</math> | ||
यह पता चला है कि यह | यह पता चला है कि यह ''X<sup>T</sup>X'' के शेष आइजन्वेक्टर देता है, कोष्ठकों में मात्रा के लिए उनके संबंधित आइजेनवैल्यू द्वारा दिए गए अधिकतम मानों के साथ हैं। इस प्रकार वजन सदिश ''X<sup>T</sup>X'' के आइजन्वेक्टर हैं। | ||
डेटा सदिश x | डेटा सदिश x<sub>(''i'')</sub> का ''k''-वाँ प्रमुख अवयव रूपांतरित निर्देशांक में, इसलिए स्कोर ''t<sub>k(i)</sub> = x<sub>(i)</sub> ⋅ w<sub>(k)</sub>'' के रूप में दिया जा सकता है या मूल वेरिएबल के स्थान में संबंधित सदिश के रूप में, ''x<sub>(i)</sub> ⋅ w<sub>(k)</sub>} w<sub>(k)</sub>,'' जहां w<sub>(''k'')</sub> ''X<sup>T</sup>X'' का kवां आइजन्वेक्टर है। | ||
इसलिए X का पूर्ण प्रमुख अवयव अपघटन इस प्रकार दिया जा सकता है | इसलिए X का पूर्ण प्रमुख अवयव अपघटन इस प्रकार दिया जा सकता है | ||
:<math>\mathbf{T} = \mathbf{X} \mathbf{W}</math> | :<math>\mathbf{T} = \mathbf{X} \mathbf{W}</math> | ||
जहां W वजन का ''p''- | जहां W वजन का ''p''-द्वारा-''p'' आव्युह है, जिसके स्तम्भ X<sup>T</sup>X के आइजन्वेक्टर हैं। डब्ल्यू के स्थानान्तरण को कभी-कभी श्वेत परिवर्तन कहा जाता है। इसका w के स्तम्भ को इसी आइजेनवैल्यू के वर्गमूल से गुणा किया जाता है, अर्थात, आइजन्वेक्टर को वेरिएंस द्वारा बढ़ाया जाता है, जिन्हें पीसीए या फैक्टर विश्लेषण में 'लोडिंग' कहा जाता है। | ||
=== सहप्रसरण === | === सहप्रसरण === | ||
X<sup>T</sup>X को ही डेटासमुच्चय X<sup>T</sup> के अनुभवजन्य प्रतिरूप सहप्रसरण आव्युह के समानुपाती के रूप में पहचाना जा सकता है |<sup>.<ref name="Jolliffe2002" />{{rp|30–31}}</sup> | |||
डेटासमुच्चय | डेटासमुच्चय पर दो भिन्न -भिन्न प्रमुख अवयवों के मध्य प्रतिरूप सहप्रसरण Q द्वारा दिया गया है: | ||
:<math>\begin{align} | :<math>\begin{align} | ||
| Line 73: | Line 73: | ||
& = \mathbf{w}_{(j)}^\mathsf{T} \lambda_{(k)} \mathbf{w}_{(k)} \\ | & = \mathbf{w}_{(j)}^\mathsf{T} \lambda_{(k)} \mathbf{w}_{(k)} \\ | ||
& = \lambda_{(k)} \mathbf{w}_{(j)}^\mathsf{T} \mathbf{w}_{(k)} | & = \lambda_{(k)} \mathbf{w}_{(j)}^\mathsf{T} \mathbf{w}_{(k)} | ||
\end{align}</math> | \end{align} </math> | ||
जहाँ w | जहाँ w<sub>(''k'')</sub> का आइजेनवैल्यू गुण है लाइन 2 से लाइन 3 पर जाने के लिए उपयोग किया गया है। चूँकि आइजन्वेक्टर w<sub>(''j'')</sub> और w<sub>(''k'')</sub> सममित आव्युह के आइजेनवैल्यू के अनुरूप ओर्थोगोनल हैं (यदि आइजेनवैल्यू भिन्न हैं), या ऑर्थोगोनलाइज़ किया जा सकता है (यदि सदिश समान दोहराया मान साझा करते हैं)। इसलिए अंतिम पंक्ति में गुणनफल शून्य है | यह डेटासमुच्चय पर विभिन्न प्रमुख अवयवों के मध्य कोई प्रतिरूप सहप्रसरण नहीं है। | ||
प्रमुख अवयवों | प्रमुख अवयवों के परिवर्तन को चिह्नित करने का और विधि है, इसलिए समन्वय के परिवर्तन के रूप में जो अनुभवजन्य प्रतिरूप सहप्रसरण आव्युह को विकर्ण करता है। | ||
आव्युह | आव्युह रूप में, मूल वेरिएबल के लिए अनुभवजन्य सहप्रसरण आव्युह लिखा जा सकता है | ||
:<math>\mathbf{Q} \propto \mathbf{X}^\mathsf{T} \mathbf{X} = \mathbf{W} \mathbf{\Lambda} \mathbf{W}^\mathsf{T}</math> | :<math>\mathbf{Q} \propto \mathbf{X}^\mathsf{T} \mathbf{X} = \mathbf{W} \mathbf{\Lambda} \mathbf{W}^\mathsf{T}</math> | ||
प्रमुख अवयवों | प्रमुख अवयवों के मध्य अनुभवजन्य सहप्रसरण आव्युह बन जाता है | ||
:<math>\mathbf{W}^\mathsf{T} \mathbf{Q} \mathbf{W} | :<math>\mathbf{W}^\mathsf{T} \mathbf{Q} \mathbf{W} | ||
\propto \mathbf{W}^\mathsf{T} \mathbf{W} \, \mathbf{\Lambda} \, \mathbf{W}^\mathsf{T} \mathbf{W} | \propto \mathbf{W}^\mathsf{T} \mathbf{W} \, \mathbf{\Lambda} \, \mathbf{W}^\mathsf{T} \mathbf{W} | ||
= \mathbf{\Lambda} </math> | = \mathbf{\Lambda} </math> | ||
जहां Λ | जहां Λ आइजेनवैल्यू ''λ<sub>(k)</sub>'' का ''X<sup>T</sup>X'' का विकर्ण आव्युह है। ''λ<sub>(k)</sub>'' प्रत्येक अवयव k, अर्थात ''λ<sub>(k)</sub>'' से जुड़े डेटासमुच्चय पर ''λ''<sub>(''k'')</sub> = Σ<sub>''i''</sub> ''t<sub>k</sub>''<sup>2</sup><sub>(''i'')</sub> = Σ<sub>''i''</sub> ('''x'''<sub>(''i'')</sub> ⋅ '''w'''<sub>(''k'')</sub>)<sup>2</sup> वर्गों के योग के समान है | ||
=== आयाम में कमी === | === आयाम में कमी === | ||
परिवर्तन T = X W डेटा | परिवर्तन T = X W डेटा सदिश x<sub>(''i'')</sub> को मानचित्र करता है p वेरिएबल्स के मूल स्थान से p वेरिएबल्स के नए स्थान पर जो डेटासमुच्चय पर असंबद्ध हैं। चूँकि , सभी प्रमुख अवयवों को रखने की जरूरत नहीं है। केवल पहले L आइजेन सदिश का उपयोग करके उत्पादित केवल पहले एल प्रमुख अवयवों को बनाए रखना, लघु परिवर्तन देता है | ||
:<math>\mathbf{T}_L = \mathbf{X} \mathbf{W}_L</math> | :<math>\mathbf{T}_L = \mathbf{X} \mathbf{W}_L</math> | ||
जहां आव्युह | जहां आव्युह T<sub>L</sub> अब n पंक्तियाँ हैं किन्तु केवल L स्तम्भ हैं। दूसरे शब्दों में, <math> t = W_L^\mathsf{T} x, x \in \mathbb{R}^p, t \in \mathbb{R}^L,</math> पीसीए रेखीय परिवर्तन सीखता है जहां {{math|''p'' × ''L''}} के स्तम्भ आव्यूह <math>W_L</math> L सुविधाओं (प्रतिनिधित्व t के अवयव ) के लिए ऑर्थोगोनल आधार बनाते हैं जो अलंकृत हैं। <ref>{{Cite journal |author=Bengio, Y.|year=2013|title=Representation Learning: A Review and New Perspectives |journal=IEEE Transactions on Pattern Analysis and Machine Intelligence |volume=35 |issue=8 |pages=1798–1828 |doi=10.1109/TPAMI.2013.50|pmid=23787338|display-authors=etal|arxiv=1206.5538|s2cid=393948}}</ref> यह निर्माण द्वारा, केवल L स्तम्भ के साथ सभी रूपांतरित डेटा मैट्रिसेस में, यह स्कोर आव्युह मूल डेटा में भिन्नता को अधिकतम करता है जिसे संरक्षित किया गया है, जबकि कुल स्क्वायर्ड पुनर्निर्माण <math>\|\mathbf{T}\mathbf{W}^T - \mathbf{T}_L\mathbf{W}^T_L\|_2^2</math> या <math>\|\mathbf{X} - \mathbf{X}_L\|_2^2</math> त्रुटि को कम करता है। | ||
[[File:PCA of Haplogroup J using 37 STRs.png|thumb|right|354 व्यक्तियों से 37 वाई-क्रोमोसोमल एसटीआर मार्करों के लिए रिपीट-काउंट वैल्यू से गणना की गई | [[File:PCA of Haplogroup J using 37 STRs.png|thumb|right|354 व्यक्तियों से 37 वाई-क्रोमोसोमल एसटीआर मार्करों के लिए रिपीट-काउंट वैल्यू से गणना की गई y-एसटीआर [[ haplotype |हैप्लोटाइप]] का प्रमुख अवयव विश्लेषण स्कैटरप्लॉट। व्यक्तियों का वाई-क्रोमोसोमल आनुवंशिक वंश।]]इस तरह की आयामी कमी उच्च-आयामी डेटासमुच्चय को देखने और संसाधित करने के लिए बहुत ही उपयोगी निर्णय हो सकता है, जबकि अभी भी डेटासमुच्चय में जितना संभव हो उतना भिन्नता बनाए रखना हैं। उदाहरण के लिए, L = 2 का चयन करना और केवल पहले दो प्रमुख अवयवों को रखना उच्च-आयामी डेटासमुच्चय के माध्यम से द्वि-आयामी प्लेन को ढूंढता है जिसमें डेटा का सबसे अधिक विस्तार हुआ है, इसलिए यदि डेटा में [[क्लस्टर विश्लेषण]] सम्मिलित है तब यह भी सबसे अधिक फैले हुए हो सकते हैं, और इसलिए द्वि-आयामी आरेख में प्लॉट किए जाने के लिए सबसे अधिक दिखाई देता है; जबकि यदि डेटा के माध्यम से दो दिशाओं (या दो मूल वेरिएबल ) को यादृच्छिक रूप से चुना जाता है, तब क्लस्टर दूसरे से बहुत कम फैल सकते हैं, और वास्तव में दूसरे को अधिक सीमा तक ओवरले करने की संभावना हो सकती है, जिससे वह अप्रभेद्य हो सकते हैं। | ||
इसी तरह, [[प्रतिगमन विश्लेषण]] में, व्याख्यात्मक वेरिएबल | इसी तरह, [[प्रतिगमन विश्लेषण]] में, व्याख्यात्मक वेरिएबल की संख्या जितनी अधिक होगी, मॉडल को ओवरफिट करने की संभावना उतनी ही अधिक होगी, जो अन्य डेटासमुच्चय के सामान्यीकरण में विफल होने वाले निष्कर्ष का उत्पादन करेगा। दृष्टिकोण, विशेष रूप से जब विभिन्न संभावित व्याख्यात्मक वेरिएबल के मध्य शक्तिशाली सहसंबंध होते हैं, तब उन्हें कुछ प्रमुख अवयवों में कम करना और पुनः उनके विरुद्ध प्रतिगमन चलाना है, इस विधि को [[प्रमुख घटक प्रतिगमन|प्रमुख अवयव प्रतिगमन]] कहा जाता है। | ||
जब किसी डेटासमुच्चय | जब किसी डेटासमुच्चय में वेरिएबल्स ध्वनि वाले हों, तब डायमेंशनलिटी रिडक्शन भी उपयुक्त हो सकता है। यदि डेटासमुच्चय के प्रत्येक स्तम्भ में स्वतंत्र समान रूप से वितरित गॉसियन ध्वनि होता है, तब 't' के स्तम्भ में समान रूप से वितरित गॉसियन ध्वनि भी सम्मिलित होगा (ऐसा वितरण आव्युह 'w' के प्रभाव के अनुसार अपरिवर्तनीय है, जिसे इस रूप में सोचा जा सकता है समन्वय अक्षों का उच्च-आयामी घुमाव) हैं। चूँकि, समान ध्वनि भिन्नता की तुलना में पहले कुछ मुख्य अवयवों में केंद्रित कुल भिन्नता के साथ, ध्वनि का आनुपातिक प्रभाव कम होता है | पहले कुछ अवयव उच्च सिग्नल-टू-ध्वनि अनुपात प्राप्त करते हैं। इस प्रकार पीसीए के समीप पहले कुछ प्रमुख अवयवों में सिग्नल को अधिक केंद्रित करने का प्रभाव हो सकता है, जो उपयोगी रूप से आयामीता में कमी द्वारा अधिकृत कर लिया जा सकता है; जबकि पश्चात के प्रमुख अवयवों पर ध्वनि प्रभावी हो सकता है, और इसलिए बिना किसी बड़े हानि से निपटारा किया जा सकता है। यदि डेटासमुच्चय अधिक बड़ा नहीं है, तब बूटस्ट्रैपिंग (सांख्यिकी) या पैरामेट्रिक बूटस्ट्रैप का उपयोग करके प्रमुख अवयवों के महत्व का परीक्षण किया जा सकता है, यह निर्धारित करने में सहायता के रूप में कि कितने प्रमुख अवयवों को बनाए रखना है। <ref>{{Cite journal|author=Forkman J., Josse, J., Piepho, H. P. |year=2019 |title= प्रमुख घटक विश्लेषण के लिए परिकल्पना परीक्षण जब चर मानकीकृत होते हैं|journal= Journal of Agricultural, Biological, and Environmental Statistics|volume=24 |issue=2 |pages= 289–308 |doi=10.1007/s13253-019-00355-5|doi-access=free }}</ref> | ||
=== एकवचन | === एकवचन मान अपघटन === | ||
{{Main| | {{Main|विलक्षण मान अपघटन }} | ||
प्रमुख अवयवों | प्रमुख अवयवों के परिवर्तन को अन्य आव्युह गुणनखंडन के साथ भी जोड़ा जा सकता है, यह X का एकवचन मान अपघटन (एसवीडी) हैं, | ||
:<math>\mathbf{X} = \mathbf{U}\mathbf{\Sigma}\mathbf{W}^T</math> | :<math>\mathbf{X} = \mathbf{U}\mathbf{\Sigma}\mathbf{W}^T</math> | ||
यहाँ Σ ''n''- | यहाँ Σ ''n''-दर-''p'' धनात्मक संख्याओं का [[विकर्ण मैट्रिक्स|विकर्ण आव्युह]] ''σ<sub>(k)</sub>'' है, यह X के विलक्षण मान U कहलाते हैं | यह ''n''-दर-''n'' आव्युह है, जिसके स्तम्भ लंबाई ''n'' के ऑर्थोगोनल यूनिट सदिश हैं जिन्हें X का बायां एकवचन W सदिश कहा जाता है | और ''p''-दर-''p'' आव्युह है जिसके स्तम्भ लंबाई ''p'' केऑर्थोगोनल यूनिट सदिश हैं और X के सही एकवचन सदिश कहलाते हैं। | ||
इस गुणनखंड के संदर्भ में, आव्युह | इस गुणनखंड के संदर्भ में, आव्युह ''X<sup>T</sup>X'' लिखा जा सकता है | ||
:<math>\begin{align} | :<math>\begin{align} | ||
\mathbf{X}^T\mathbf{X} | \mathbf{X}^T\mathbf{X} | ||
| Line 111: | Line 111: | ||
& = \mathbf{W}\mathbf{\Sigma}^\mathsf{T} \mathbf{\Sigma} \mathbf{W}^\mathsf{T} \\ | & = \mathbf{W}\mathbf{\Sigma}^\mathsf{T} \mathbf{\Sigma} \mathbf{W}^\mathsf{T} \\ | ||
& = \mathbf{W}\mathbf{\hat{\Sigma}}^2 \mathbf{W}^\mathsf{T} | & = \mathbf{W}\mathbf{\hat{\Sigma}}^2 \mathbf{W}^\mathsf{T} | ||
\end{align}</math> | \end{align} </math> | ||
जहाँ <math> \mathbf{\hat{\Sigma}} </math>X के एकवचन मानों के साथ वर्ग विकर्ण आव्युह है और अतिरिक्त शून्य काट दिया गया है जो <math> \mathbf{\hat{\Sigma}^2}=\mathbf{\Sigma}^\mathsf{T} \mathbf{\Sigma} </math>. को संतुष्ट करता है | यह ''X<sup>T</sup>X'' के आइजन्वेक्टर गुणनखंडन के साथ तुलना स्थापित करता है कि X का सही एकवचन सदिश W, X<sup>T</sup>X के आइजन्वेक्टर के समतुल्य है, जबकि <math> \mathbf{{X}}</math> एकवचन मान ''σ''<sub>(''k'')</sub> का आइजेनवैल्यू ''λ<sub>(k)</sub>'' के X<sup>T</sup>X का वर्गमूल के समान हैं । | |||
एकवचन | एकवचन मान अपघटन का उपयोग करके स्कोर आव्युह T लिखा जा सकता है | ||
:<math>\begin{align} | :<math>\begin{align} | ||
\mathbf{T} | \mathbf{T} | ||
| Line 120: | Line 120: | ||
& = \mathbf{U}\mathbf{\Sigma}\mathbf{W}^\mathsf{T} \mathbf{W} \\ | & = \mathbf{U}\mathbf{\Sigma}\mathbf{W}^\mathsf{T} \mathbf{W} \\ | ||
& = \mathbf{U}\mathbf{\Sigma} | & = \mathbf{U}\mathbf{\Sigma} | ||
\end{align}</math> | \end{align} </math> | ||
इसलिए T का प्रत्येक स्तंभ X के बाएँ एकवचन सदिशों में से द्वारा संबंधित एकवचन मान से गुणा किया जाता है। यह रूप T का [[ध्रुवीय अपघटन]] भी है। | इसलिए T का प्रत्येक स्तंभ X के बाएँ एकवचन सदिशों में से द्वारा संबंधित एकवचन मान से गुणा किया जाता है। यह रूप T का [[ध्रुवीय अपघटन]] भी है। | ||
आव्युह | आव्युह X<sup>T</sup>X बनाने के बिना X के एसवीडी की गणना करने के लिए कुशल एल्गोरिदम उपस्तिथ हैं, इसलिए एसवीडी की गणना करना अब डेटा आव्युह से प्रमुख अवयव विश्लेषण की गणना करने का मानक विधि है, जब तक कि केवल कुछ ही अवयवों की आवश्यकता नहीं होती है। | ||
आइजन-अपघटन के साथ, | आइजन-अपघटन के साथ, लघु {{math|''n'' × ''L''}} स्कोर आव्युह T<sub>L</sub> केवल पहले L सबसे बड़े एकवचन मान और उनके एकवचन सदिशों पर विचार करके प्राप्त किया जा सकता है: | ||
:<math>\mathbf{T}_L = \mathbf{U}_L\mathbf{\Sigma}_L = \mathbf{X} \mathbf{W}_L </math> | :<math>\mathbf{T}_L = \mathbf{U}_L\mathbf{\Sigma}_L = \mathbf{X} \mathbf{W}_L </math> | ||
इस तरह से काटे गए एकवचन | इस तरह से काटे गए एकवचन मान अपघटन का उपयोग करके आव्युह M या T का कटाव लघु सा आव्युह उत्पन्न करता है जो मूल आव्युह के [[रैंक (रैखिक बीजगणित)]] ''L'' का निकटतम संभव आव्युह है, और इन दोनों के मध्य के अंतर के अर्थ में दो में सबसे लघु संभव [[फ्रोबेनियस मानदंड]] है, इसका परिणाम जिसे एकार्ट-यंग प्रमेय [1936] के रूप में जाना जाता है। | ||
== आगे के विचार == | |||
एकवचन मान (Σ में) आव्युह ''X<sup>T</sup>X'' के आइजेनवैल्यू के वर्गमूल हैं। प्रत्येक आइजेनवैल्यू विचरण के भाग के लिए आनुपातिक है (उनके बहुआयामी माध्य से बिंदुओं की स्क्वायर्ड दूरी के योग का अधिक सही रूप से) जो प्रत्येक आइजन्वेक्टर के साथ जुड़ा हुआ है। सभी आइजेनवैल्यू का योग उनके बहुआयामी माध्य से बिंदुओं की वर्ग दूरी के योग के समान है। पीसीए अनिवार्य रूप से प्रमुख अवयवों के साथ संरेखित करने के लिए उनके माध्य के चारों ओर बिंदुओं के समुच्चय को घुमाता है। यह पहले कुछ आयामों में जितना संभव हो उतना ही भिन्नता (ऑर्थोगोनल परिवर्तन का उपयोग करके) की ओर ले जाता है। इसलिए, शेष आयामों में मान लघु होते हैं और सूचना के न्यूनतम हानि के साथ गिराए जा सकते हैं (सिद्धांत अवयव विश्लेषण या पीसीए और सूचना सिद्धांत देखें)। पीसीए का उपयोग अधिकतर इस तरह से आयाम में कमी के लिए किया जाता है। पीसीए को उप-स्थान रखने के लिए अधिकतम ऑर्थोगोनल परिवर्तन होने का गौरव प्राप्त है जिसमें सबसे बड़ा भिन्नता है (जैसा कि ऊपर परिभाषित किया गया है)। चूँकि, यह लाभ अधिक कम्प्यूटेशनल आवश्यकताओं की मान पर आता है, उदाहरण के लिए, और जब प्रयुक्त हो, तब [[असतत कोसाइन परिवर्तन]] के लिए, और विशेष रूप से डीसीटी-II के लिए होता हैं जिसे केवल डीसीटी के रूप में जाना जाता है। पीसीए की तुलना में [[अरैखिक आयामीता में कमी]] तकनीक की कम्प्यूटेशनल रूप से अधिक मांग होती है। | |||
पीसीए वेरिएबल के स्केलिंग के प्रति संवेदनशील है। यदि हमारे समीप केवल दो वेरिएबल हैं और उनके समीप इसका ही प्रतिरूप भिन्न है और वह पूरी तरह से सहसंबंधित हैं, तब पीसीए 45 डिग्री से घूर्णन करेगा और मुख्य अवयव के संबंध में दो वेरिएबल के लिए वजन (वे घूर्णन के कोसाइन हैं) समान होता हैं। किन्तु यदि हम पहले वेरिएबल के सभी मानों को 100 से गुणा करते हैं, तब पहला प्रमुख अवयव लगभग उसी वेरिएबल के समान होगा, और दूसरे वेरिएबल से लघु से योगदान के साथ होता है , जबकि दूसरा अवयव दूसरे मूल वेरिएबल के साथ लगभग संरेखित होता हैं। इसका कारण यह है कि जब भी भिन्न -भिन्न वेरिएबल की भिन्न -भिन्न इकाइयाँ (जैसे तापमान और द्रव्यमान) होती हैं, तब पीसीए विश्लेषण का कुछ सीमा तक इच्छानुसार विधि होती है। (उदाहरण के लिए सेल्सियस के अतिरिक्त फ़ारेनहाइट का उपयोग करने पर भिन्न -भिन्न परिणाम प्राप्त होंगे।) पियर्सन का मूल पेपर ऑन लाइन्स एंड प्लेन ऑफ़ क्लोजेस्ट फ़िट टू सिस्टम्स ऑफ़ पॉइंट्स इन स्पेस - इन स्पेस का तात्पर्य भौतिक यूक्लिडियन स्पेस से है जहाँ ऐसी चिंताएँ उत्पन्न नहीं होती हैं। पीसीए को कम इच्छानुसार बनाने की विधि यह है कि डेटा को मानकीकृत करके, इकाई विचरण के रूप में स्केल किए गए वेरिएबल का उपयोग किया जाए और इसलिए पीसीए के आधार के रूप में ऑटोकोवरिएंस आव्युह के अतिरिक्त ऑटोकोरिलेशन आव्युह का उपयोग किया जाता हैं। चूँकि, यह सिग्नल स्पेस के सभी आयामों में इकाई विचरण के उतार-चढ़ाव को संकुचित (या विस्तारित) करता है। | |||
पीसीए | मौलिक पीसीए प्रदर्शन करने के लिए मीन घटाव (में मीन सेंटरिंग) आवश्यक है जिससे यह सुनिश्चित किया जा सके कि पहला प्रमुख अवयव अधिकतम विचरण की दिशा का वर्णन करता है। यदि औसत घटाव नहीं किया जाता है, तब पहला प्रमुख अवयव इसके अतिरिक्त डेटा के माध्य से अधिक या कम हो सकता है। आधार खोजने के लिए शून्य का कारण आवश्यक है जो डेटा के अनुमान के [[न्यूनतम औसत वर्ग त्रुटि]] को कम करता है।<ref>A. A. Miranda, Y. A. Le Borgne, and G. Bontempi. [http://www.ulb.ac.be/di/map/yleborgn/pub/NPL_PCA_07.pdf New Routes from Minimal Approximation Error to Principal Components], Volume 27, Number 3 / June, 2008, Neural Processing Letters, Springer</ref> | ||
सहसंबंध आव्युह पर प्रमुख अवयव विश्लेषण करते समय माध्य-केंद्रित अनावश्यक है, क्योंकि सहसंबंधों की गणना के पश्चात डेटा पहले से ही केंद्रित है। सहसंबंध दो मानक स्कोर (जेड-स्कोर) या सांख्यिकीय क्षणों के क्रॉस-उत्पाद से प्राप्त होते हैं (इसलिए नाम: पियर्सन प्रोडक्ट-मोमेंट सहसंबंध)। इसके अतिरिक्त क्रॉम्रे एंड फोस्टर-जॉनसन (1998) का लेख मॉडरेट रिग्रेशन में मीन-सेंटरिंग: मच अडो अबाउट नथिंग पर देख सकते हैं। चूँकि सहप्रसरण आव्युह या सहसंबंध आव्युह से संबंध (मानक स्कोर या गणना हैं | यह (Z- या मानक-स्कोर) 'X' के सहसंबंध आव्युह पर आधारित पीसीए 'Z' के सहप्रसरण आव्युह पर आधारित पीसीए के लिए [[समानता (गणित)]] है। तथा 'X' का मानकीकृत संस्करण होता है। | |||
सहसंबंध आव्युह | |||
पीसीए पैटर्न पहचान में लोकप्रिय प्राथमिक तकनीक है। | पीसीए पैटर्न पहचान में लोकप्रिय प्राथमिक तकनीक है। चूँकि, यह वर्ग पृथक्करण के लिए अनुकूलित नहीं है। <ref>{{Cite book| last=Fukunaga|first=Keinosuke|author-link=Keinosuke Fukunaga | title = सांख्यिकीय पैटर्न पहचान का परिचय|publisher=Elsevier | year = 1990 | url=https://dl.acm.org/doi/book/10.5555/92131| isbn=978-0-12-269851-4}}</ref> चूँकि, इसका उपयोग मुख्य अवयव स्थान में प्रत्येक वर्ग के लिए द्रव्यमान के केंद्र की गणना करके और दो या दो से अधिक वर्गों के द्रव्यमान के केंद्र के मध्य यूक्लिडियन दूरी की रिपोर्ट करके दो या दो से अधिक वर्गों के मध्य की दूरी को मापने के लिए किया गया है। <ref>{{cite journal|last1=Alizadeh|first1=Elaheh|last2=Lyons|first2=Samanthe M|last3=Castle|first3=Jordan M|last4=Prasad|first4=Ashok|title=Zernike मोमेंट्स का उपयोग करके आक्रामक कैंसर सेल आकार में व्यवस्थित परिवर्तनों को मापना|journal=Integrative Biology|date=2016|volume=8|issue=11|pages=1183–1193|doi=10.1039/C6IB00100A|pmid=27735002|url=https://pubs.rsc.org/en/Content/ArticleLanding/2016/IB/C6IB00100A}}</ref> यह [[रैखिक विभेदक विश्लेषण]] विकल्प है जो वर्ग पृथक्करण के लिए अनुकूलित है। | ||
== प्रतीकों और संक्षेपों की तालिका == | == प्रतीकों और संक्षेपों की तालिका == | ||
{| class="wikitable" | {| class="wikitable" | ||
|- | |- | ||
! | ! प्रतीक | ||
! | ! अर्थ | ||
! | ! डाइमेंशन्स | ||
! | ! इंडिसेस | ||
|- | |- | ||
| <math>\mathbf{X} = [ X_{ij} ]</math> | | <math>\mathbf{X} = [ X_{ij} ]</math> | ||
| | | डेटा आव्युह, जिसमें प्रति पंक्ति सदिश सभी डेटा सदिश का समुच्चय सम्मिलित है, | ||
| <math> n \times p</math> | | <math> n \times p</math> | ||
| <math> i = 1 \ldots n </math> <br /> <math> j = 1 \ldots p </math> | | <math> i = 1 \ldots n </math> <br /> <math> j = 1 \ldots p </math> | ||
|- | |- | ||
| <math>n </math> | | <math>n </math> | ||
| | | डेटा समुच्चय में पंक्ति सदिश की संख्या | ||
| <math>1 \times 1</math> | | <math>1 \times 1</math> | ||
| '' | | ''अदिश'' | ||
|- | |- | ||
| <math>p </math> | | <math>p </math> | ||
| | | प्रत्येक पंक्ति सदिश में अवयवों की संख्या (डाइमेंशन्स) | ||
| <math>1 \times 1</math> | | <math>1 \times 1</math> | ||
| '' | | ''अदिश'' | ||
|- | |- | ||
| <math>L </math> | | <math>L </math> | ||
| | | आयामी रूप से कम किए गए उपस्थान में आयामों की संख्या, <math> 1 \le L \le p </math> | ||
| <math>1 \times 1</math> | | <math>1 \times 1</math> | ||
| '' | | ''अदिश'' | ||
|- | |- | ||
| <math>\mathbf{u} = [ u_j ]</math> | | <math>\mathbf{u} = [ u_j ]</math> | ||
| | | अनुभवजन्य साधनों का सदिश , डेटा आव्युह के प्रत्येक स्तम्भ ''j'' के लिए माध्य है | ||
| <math> p \times 1</math> | | <math> p \times 1</math> | ||
| <math> j = 1 \ldots p </math> | | <math> j = 1 \ldots p </math> | ||
|- | |- | ||
| <math>\mathbf{s} = [ s_j ]</math> | | <math>\mathbf{s} = [ s_j ]</math> | ||
| | | अनुभवजन्य मानक विचलन के सदिश , डेटा आव्युह के प्रत्येक स्तम्भ ''j'' के लिए मानक विचलन | ||
| <math> p \times 1</math> | | <math> p \times 1</math> | ||
| <math> j = 1 \ldots p </math> | | <math> j = 1 \ldots p </math> | ||
|- | |- | ||
| <math>\mathbf{h} = [ h_i ]</math> | | <math>\mathbf{h} = [ h_i ]</math> | ||
| | | सभी 1 का सदिश | ||
| <math> 1 \times n</math> | | <math> 1 \times n</math> | ||
| <math> i = 1 \ldots n </math> | | <math> i = 1 \ldots n </math> | ||
|- | |- | ||
| <math>\mathbf{B} = [ B_{ij} ]</math> | | <math>\mathbf{B} = [ B_{ij} ]</math> | ||
| [[Standard deviation| | | [[Standard deviation|विचलन]] डेटा आव्युह के प्रत्येक स्तम्भ j के माध्य से | ||
| <math> n \times p</math> | | <math> n \times p</math> | ||
| <math> i = 1 \ldots n </math> <br /> <math> j = 1 \ldots p </math> | | <math> i = 1 \ldots n </math> <br /> <math> j = 1 \ldots p </math> | ||
|- | |- | ||
| <math>\mathbf{Z} = [ Z_{ij} ] </math> | | <math>\mathbf{Z} = [ Z_{ij} ] </math> | ||
| [[z-score]] | | [[z-score|z-स्कोर]], डेटा आव्युह की प्रत्येक पंक्ति m के लिए माध्य और मानक विचलन का उपयोग करके गणना की जाती है | ||
| <math> n \times p</math> | | <math> n \times p</math> | ||
| <math> i = 1 \ldots n </math> <br /> <math> j = 1 \ldots p </math> | | <math> i = 1 \ldots n </math> <br /> <math> j = 1 \ldots p </math> | ||
|- | |- | ||
| <math>\mathbf{C} = [ C_{jj'} ] </math> | | <math>\mathbf{C} = [ C_{jj'} ] </math> | ||
| [[covariance matrix]] | | [[covariance matrix|सहप्रसरण आव्यूह]] | ||
| <math> p \times p </math> | | <math> p \times p </math> | ||
| <math> j = 1 \ldots p </math> <br /><math> j' = 1 \ldots p </math> | | <math> j = 1 \ldots p </math> <br /><math> j' = 1 \ldots p </math> | ||
|- | |- | ||
| <math>\mathbf{R} = [ R_{jj'} ] </math> | | <math>\mathbf{R} = [ R_{jj'} ] </math> | ||
| [[correlation matrix]] | | [[correlation matrix|सहसम्बंध]] [[covariance matrix|आव्यूह]] | ||
| <math> p \times p </math> | | <math> p \times p </math> | ||
| <math> j = 1 \ldots p </math> <br /><math> j' = 1 \ldots p </math> | | <math> j = 1 \ldots p </math> <br /><math> j' = 1 \ldots p </math> | ||
|- | |- | ||
| <math> \mathbf{V} = [ V_{jj'} ] </math> | | <math> \mathbf{V} = [ V_{jj'} ] </math> | ||
| | | आव्युह जिसमें प्रति स्तम्भ आइजनवेक्टर C के सभी आइजनवेक्टर का समुच्चय सम्मिलित है, | ||
| <math> p \times p </math> | | <math> p \times p </math> | ||
| <math> j = 1 \ldots p </math> <br /><math> j' = 1 \ldots p </math> | | <math> j = 1 \ldots p </math> <br /><math> j' = 1 \ldots p </math> | ||
|- | |- | ||
| <math>\mathbf{D} = [ D_{jj'} ] </math> | | <math>\mathbf{D} = [ D_{jj'} ] </math> | ||
| [[diagonal matrix]] | | [[diagonal matrix|विकर्ण आव्युह]] सभी के समुच्चय से मिलकर [[eigenvalues|आइजेनवैल्यू]] को इसके साथ C का [[principal diagonal|मुख्य विकर्ण]], और अन्य सभी अवयवों के लिए 0 (ध्यान दें 𝛬 ऊपर प्रयुक्त) | ||
| <math> p \times p </math> | | <math> p \times p </math> | ||
| <math> j = 1 \ldots p </math> <br /><math> j' = 1 \ldots p </math> | | <math> j = 1 \ldots p </math> <br /><math> j' = 1 \ldots p </math> | ||
|- | |- | ||
| <math>\mathbf{W} = [ W_{jl} ] </math> | | <math>\mathbf{W} = [ W_{jl} ] </math> | ||
| | | आधार सदिश का आव्युह , प्रति स्तम्भ सदिश है , जहां प्रत्येक आधार सदिश C के आईजनवेक्टर में से है, और जहां W में सदिश V में उन व्यकित का उप-समुच्चय है | ||
| <math> p \times L</math> | | <math> p \times L</math> | ||
| <math> j = 1 \ldots p </math> <br /><math> l = 1 \ldots L</math> | | <math> j = 1 \ldots p </math> <br /><math> l = 1 \ldots L</math> | ||
|- | |- | ||
| <math>\mathbf{T} = [ T_{il} ] </math> | | <math>\mathbf{T} = [ T_{il} ] </math> | ||
| | | आव्युह जिसमें एन पंक्ति सदिश सम्मिलित हैं, जहां प्रत्येक सदिश आव्युह X से संबंधित डेटा सदिश का आव्युह W के स्तम्भ में निहित आधार सदिश पर प्रक्षेपण है। | ||
| <math> n \times L</math> | | <math> n \times L</math> | ||
| <math> i = 1 \ldots n </math> <br /><math> l = 1 \ldots L</math> | | <math> i = 1 \ldots n </math> <br /><math> l = 1 \ldots L</math> | ||
| Line 230: | Line 231: | ||
=== गुण === | === गुण === | ||
पीसीए के कुछ गुणों में सम्मिलित | पीसीए के कुछ गुणों में सम्मिलित हैं <ref name="Jolliffe2002"/> | ||
:<big>'' | :<big>''गुण 1'':</big> किसी भी पूर्णांक ''q'' के लिए, 1 ≤ ''q'' ≤ ''p'', ओर्थोगोनल रैखिक परिवर्तन पर विचार करें | ||
::<math>y =\mathbf{B'}x</math> | ::<math>y =\mathbf{B'}x</math> | ||
: | :जहाँ <math>y</math> q-अवयव सदिश है और <math>\mathbf{B'}</math> (q × p) आव्युह है, और मान लीजिये कि <math>\mathbf{{\Sigma}}_y = \mathbf{B'}\mathbf{\Sigma}\mathbf{B}</math> <math>y</math> के लिए विचरण -[[सहप्रसरण]] आव्युह होते है पुनः <math>\mathbf{\Sigma}_y</math> का संकेत, निरूपित <math>\operatorname{tr} (\mathbf{\Sigma}_y)</math>, <math>\mathbf{B} = \mathbf{A}_q</math> लेने से अधिकतम होता है , जहाँ <math>\mathbf{A}_q</math> के पहले q स्तम्भ सम्मिलित होते हैं | यह <math>\mathbf{A}</math> <math>\mathbf{B'} </math> <math>\mathbf{B} </math> का स्थानान्तरण होता है | | ||
:<big>'' | :<big>''गुण 2'':</big> ओर्थोनॉर्मल परिवर्तन पर पुनः से विचार करें | ||
::<math>y = \mathbf{B'}x</math> | ::<math>y = \mathbf{B'}x</math> | ||
:साथ <math>x, \mathbf{B}, \mathbf{A}</math> और <math>\mathbf{\Sigma}_y</math> पहले की तरह | :इसके साथ <math>x, \mathbf{B}, \mathbf{A}</math> और <math>\mathbf{\Sigma}_y</math> पहले की तरह परिभाषित करता है। तब <math>\operatorname{tr}(\mathbf{\Sigma}_y)</math> <math>\mathbf{B} = \mathbf{A}_q^*,</math> लेने से कम किया जाता है जहाँ <math>\mathbf{A}_q^*</math> के अंतिम q स्तम्भ से मिलकर <math>\mathbf{A}</math> बनता है | | ||
इस संपत्ति का सांख्यिकीय निहितार्थ यह है कि पिछले कुछ पीसी महत्वपूर्ण पीसी को हटाने के पश्चात | इस संपत्ति का सांख्यिकीय निहितार्थ यह है कि पिछले कुछ पीसी महत्वपूर्ण पीसी को हटाने के पश्चात केवल असंरचित बचे हुए भाग नहीं हैं। क्योंकि इन अंतिम पीसी में जितना संभव हो उतना लघु प्रसरण होता है, इसलिए यह अपने आप में उपयोगी होते हैं। वह {{mvar|x}} के अवयवों के मध्य बिना सोचे-समझे निकट-स्थिर रैखिक संबंधों का पता लगाने में सहायता कर सकते हैं , और वह प्रतिगमन विश्लेषण में भी उपयोगी हो सकते हैं, वेरिएबल {{mvar|x}} के उपसमुच्चय का चयन करने में , और आउटलाइयर डिटेक्शन में उपयोग किया जाता है | | ||
:<big>'' | :<big>''गुण 3'':</big> ({{math|'''Σ'''}} का वर्णक्रमीय अपघटन ) | ||
::<math>\mathbf{{\Sigma}} = \lambda_1\alpha_1\alpha_1' + \cdots + \lambda_p\alpha_p\alpha_p'</math> | ::<math>\mathbf{{\Sigma}} = \lambda_1\alpha_1\alpha_1' + \cdots + \lambda_p\alpha_p\alpha_p' </math> | ||
इसके उपयोग को देखने से पहले, हम पहले [[विकर्ण]] | इसके उपयोग को देखने से पहले, हम पहले [[विकर्ण]] अवयवों को देखते हैं, | ||
:<math>\operatorname{Var}(x_j) = \sum_{k=1}^P \lambda_k\alpha_{kj}^2</math> | :<math>\operatorname{Var}(x_j) = \sum_{k=1}^P \lambda_k\alpha_{kj}^2 </math> | ||
पुनः संभवतः परिणाम का मुख्य सांख्यिकीय निहितार्थ यह है कि न केवल हम सभी {{mvar|x}} अवयवों के संयुक्त भिन्नताओं को विघटित कर सकते हैं किंतु प्रत्येक पीसी के कारण घटते योगदान में, हम संपूर्ण सहसंयोजक आव्युह को योगदान <math>\lambda_k\alpha_k\alpha_k'</math> में विघटित भी कर सकते हैं प्रत्येक पीसी से चूँकि कठोरता से कम नहीं हो रहा है, जैसे-जैसे <math>k</math> बढ़ता है <math>\lambda_k\alpha_k\alpha_k'</math> के अवयव तब रूप में लघु हो जाएगा, क्योंकि <math>k</math> बढ़ने के लिए <math>\lambda_k\alpha_k\alpha_k'</math> गैर-बढ़ रहा है , जबकि <math>\alpha_k</math>के अवयव के कारण समान आकार के रहने की प्रवृत्ति रखते हैं | यह सामान्यीकरण बाधाओं <math>\alpha_{k}'\alpha_{k}=1, k=1, \dots, p</math>.होती है | | |||
=== सीमाएं === | === सीमाएं === | ||
जैसा कि ऊपर उल्लेख किया गया है, पीसीए के परिणाम वेरिएबल | जैसा कि ऊपर उल्लेख किया गया है, पीसीए के परिणाम वेरिएबल के स्केलिंग पर निर्भर करते हैं। प्रत्येक विशेषता को उसके मानक विचलन द्वारा स्केल करके इसे सही किया जा सकता है, जिससे इकाई विचरण के साथ आयामहीन सुविधाओं के साथ समाप्त हो जाता हैं। <ref name=Leznik>Leznik, M; Tofallis, C. 2005 [https://uhra.herts.ac.uk/bitstream/handle/2299/715/S56.pdf Estimating Invariant Principal Components Using Diagonal Regression.]</ref> | ||
पीसीए | ऊपर वर्णित पीसीए की प्रयोज्यता कुछ निश्चित (मौन) मान्यताओं द्वारा सीमित है | <ref>Jonathon Shlens, [https://arxiv.org/abs/1404.1100 A Tutorial on Principal Component Analysis.]</ref> यह इसकी व्युत्पत्ति में बनाया गया हैं। विशेष रूप से, पीसीए सुविधाओं के मध्य रैखिक सहसंबंधों को पकड़ सकता है किन्तु जब इस धारणा का उल्लंघन होता है तब यह विफल हो जाता है इसके (संदर्भ में चित्र 6ए देखें)। कुछ स्तिथियों में, समन्वय परिवर्तन रैखिकता धारणा को पुनर्स्थापित कर सकते हैं और पीसीए को तब प्रयुक्त किया जा सकता है | इसके लिए ([[कर्नेल प्रमुख घटक विश्लेषण|कर्नेल प्रमुख अवयव विश्लेषण]] देख) सकते हैं। | ||
पीसीए के लिए सहप्रसरण आव्युह के निर्माण से पहले और सीमा औसत हटाने की प्रक्रिया है। खगोल विज्ञान जैसे क्षेत्रों में, सभी संकेत गैर-ऋणात्मक होते हैं, और माध्य-हटाने की प्रक्रिया कुछ खगोलीय विपत्ति के माध्य को शून्य होने के लिए बाध्य करेगी, जिसके परिणामस्वरूप अभौतिक ऋणात्मक प्रवाह उत्पन्न होता है,<ref name="soummer12" /> और संकेतों की सही परिमाण को पुनर्प्राप्त करने के लिए आगे की मॉडलिंग की जानी चाहिए। <ref name="pueyo16">{{Cite journal|arxiv= 1604.06097 |last1= Pueyo|first1= Laurent |title= Detection and Characterization of Exoplanets using Projections on Karhunen Loeve Eigenimages: Forward Modeling |journal= The Astrophysical Journal |volume= 824|issue= 2|pages= 117|year= 2016|doi= 10.3847/0004-637X/824/2/117|bibcode = 2016ApJ...824..117P|s2cid= 118349503}}</ref> वैकल्पिक पद्धति के रूप में, [[गैर-नकारात्मक मैट्रिक्स गुणनखंड|गैर-ऋणात्मक आव्युह गुणनखंडन]] केवल मेट्रिसेस में गैर-ऋणात्मक अवयवों पर ध्यान केंद्रित करता है, जो खगोल भौतिकीय प्रेक्षणों के लिए अच्छी तरह से अनुकूल है। <ref name="blantonRoweis07" /><ref name="zhu16" /><ref name="ren18" /> यह पीसीए और गैर-ऋणात्मक आव्युह गुणनखंडन के मध्य या गैर-ऋणात्मक आव्युह गुणनखंड संबंध है। | |||
यदि एल्गोरिथम को प्रयुक्त करने से पहले डेटा को मानकीकृत नहीं किया गया है तब पीसीए हानि में है। पीसीए मूल डेटा को उस डेटा में परिवर्तित कर देता है जो उस डेटा के प्रमुख अवयवों के लिए प्रासंगिक होता है, जिसका अर्थ है कि नए डेटा वेरिएबल की उसी तरह से व्याख्या नहीं की जा सकती है जैसे मूल थे। वह मूल वेरिएबलों की रैखिक व्याख्याएँ हैं। इसके अतिरिक्त, यदि पीसीए सही से नहीं किया जाता है, तब सूचना के हानि की उच्च संभावना होती है। <ref>{{cite web | title=What are the Pros and cons of the PCA? | website=i2tutorials | date=September 1, 2019 | url=https://www.i2tutorials.com/what-are-the-pros-and-cons-of-the-pca/ | access-date=June 4, 2021}}</ref> | |||
पीसीए रैखिक मॉडल पर निर्भर करता है। यदि किसी डेटासमुच्चय के अंदर पैटर्न हिडन हुआ है जो कि अरैखिक है, तब पीसीए वास्तव में विश्लेषण को प्रगति की पूर्ण विपरीत दिशा में ले जा सकता है। <ref name="abbott">{{cite book | title=एप्लाइड प्रिडिक्टिव एनालिटिक्स| last=Abbott | first=Dean | isbn=9781118727966 | date=May 2014 | publisher=Wiley}}</ref> कैनसस स्टेट यूनिवर्सिटी के शोधकर्ताओं ने पाया कि उनके प्रयोगों में प्रतिरूप त्रुटि ने पीसीए परिणामों के पूर्वाग्रह को प्रभावित किया जाता हैं। यदि विषयों या ब्लॉकों की संख्या 30 से कम है, और/या शोधकर्ता पीसी में पहले से और अधिक रुचि रखते हैं, तब पीसीए आयोजित करने से पहले सीरियल सहसंबंध के लिए पहले सही करना उत्तम हो सकता है। <ref name="jiang" /> कैनसस स्टेट के शोधकर्ताओं ने यह भी पाया कि यदि डेटा की स्वतःसंबंध संरचना को सही रूप से नियंत्रित नहीं किया जाता है तब पीसीए गंभीर रूप से अनुयायी हो सकता है। <ref name="jiang">{{cite journal| title=सहसंबद्ध प्रेक्षणों के कारण प्रधान घटक विश्लेषण में पक्षपात| url=https://newprairiepress.org/agstatconference/2000/proceedings/13/ |last1=Jiang | first1=Hong| last2=Eskridge | first2=Kent M.| year=2000 | journal=Conference on Applied Statistics in Agriculture |issn=2475-7772| doi=10.4148/2475-7772.1247| doi-access=free}}</ref> | |||
=== पीसीए और सूचना सिद्धांत === | === पीसीए और सूचना सिद्धांत === | ||
आयामीता में कमी के परिणामस्वरूप सामान्यतः | आयामीता में कमी के परिणामस्वरूप सामान्यतः सूचना की हानि होता है। पीसीए-आधारित डायमेंशनलिटी रिडक्शन कुछ सिग्नल और ध्वनि मॉडल के अनुसार उस सूचना हानि को कम करता है। | ||
इस धारणा के | इस धारणा के अनुसार | ||
:<math>\mathbf{x}=\mathbf{s}+\mathbf{n},</math> | :<math>\mathbf{x}=\mathbf{s}+\mathbf{n},</math> | ||
वह डेटा सदिश <math>\mathbf{x}</math> वांछित सूचना-वाहक संकेत का योग <math>\mathbf{s}</math> है और ध्वनि संकेत <math>\mathbf{n}</math> कोई दिखा सकता है कि सूचना-सैद्धांतिक दृष्टिकोण से पीसीए आयामीता में कमी के लिए अधिकतम हो सकता है। | |||
विशेष रूप से, लिंस्कर ने दिखाया कि यदि <math>\mathbf{s}</math> गाऊसी है और <math>\mathbf{n}</math> पहचान आव्युह के आनुपातिक आव्युह के साथ गॉसियन ध्वनि है, पीसीए [[आपसी जानकारी|आपसी सूचना]] <math>I(\mathbf{y};\mathbf{s})</math> को अधिकतम करता है और वांछित सूचना <math>\mathbf{s}</math> और आयामीता-कम उत्पादन <math>\mathbf{y}=\mathbf{W}_L^T\mathbf{x}</math> के मध्य उपयोग किया जाता है | <ref>{{cite journal|last=Linsker|first=Ralph|title=एक अवधारणात्मक नेटवर्क में स्व-संगठन|journal=IEEE Computer|date=March 1988|volume=21|issue=3|pages=105–117|doi=10.1109/2.36|s2cid=1527671}}</ref> | |||
यदि ध्वनि अभी भी गाऊसी है और पहचान आव्युह के समानुपाती सहप्रसरण आव्युह है (अर्थात, सदिश के अवयव <math>\mathbf{n}</math> [[iid]] हैं), किन्तु सूचना देने वाला संकेत <math>\mathbf{s}</math> गैर-गाऊसी है (जो सामान्य परिदृश्य है), पीसीए कम से कम सूचना हानि पर ऊपरी सीमा को कम करता है, जिसे इस रूप में परिभाषित किया गया है | <ref>{{cite book|last=Deco & Obradovic|title=तंत्रिका कम्प्यूटिंग के लिए एक सूचना-सैद्धांतिक दृष्टिकोण|year=1996|publisher=Springer|location=New York, NY|url=https://books.google.com/books?id=z4XTBwAAQBAJ|isbn=9781461240167}}</ref><ref>{{cite book |last=Plumbley|first=Mark|title=सूचना सिद्धांत और अनुपयोगी तंत्रिका नेटवर्क|year=1991}}Tech Note</ref> | |||
यदि | |||
:<math>I(\mathbf{x};\mathbf{s}) - I(\mathbf{y};\mathbf{s}).</math> | :<math>I(\mathbf{x};\mathbf{s}) - I(\mathbf{y};\mathbf{s}).</math> | ||
ध्वनि <math>\mathbf{n}</math> होने पर पीसीए की अधिकतम भी संरक्षित है तथा सूचना देने वाले संकेत की तुलना में iid और कम से कम अधिक गाऊसी (कुल्बैक-लीब्लर विचलन के संदर्भ में) <math>\mathbf{s}</math> है <ref>{{cite journal|last=Geiger|first=Bernhard|author2=Kubin, Gernot|title=प्रासंगिक सूचना हानि को कम करने के रूप में सिग्नल वृद्धि|journal=Proc. ITG Conf. On Systems, Communication and Coding|date=January 2013|arxiv=1205.6935|bibcode=2012arXiv1205.6935G}}</ref> सामान्यतः, तदापि उपरोक्त सिग्नल मॉडल धारण करता है, जैसे ही ध्वनि होती है, पीसीए अपनी सूचना-सैद्धांतिक अधिकतम खो देता है। तथा <math>\mathbf{n}</math> आश्रित हो जाता है। | |||
== सहप्रसरण विधि का उपयोग करके पीसीए की गणना करना == | |||
सहप्रसरण विधि का उपयोग करते हुए पीसीए का विस्तृत विवरण निम्नलिखित है (यह भी देखें [http://www.cs.otago.ac.nz/cosc453/student_tutorials/principal_components.pdf यहां]) सहसंबंध विधि के विपरीत हैं।<ref>{{cite web|title=Engineering Statistics Handbook Section 6.5.5.2|url=http://www.itl.nist.gov/div898/handbook/pmc/section5/pmc552.htm|access-date=19 January 2015}}</ref> | |||
लक्ष्य आयाम ''p'' के दिए गए डेटा समुच्चय X को लघु आयाम ''L'' के वैकल्पिक डेटा समुच्चय Y में परिवर्तित करता है। समतुल्य रूप से, हम आव्युह Y को खोजने का प्रयास कर रहे हैं, जहां Y करहुनेन-लोएव प्रमेय आव्युह X का करहुनेन-लोव ट्रांसफ़ॉर्म (केएलटी) है | | |||
लक्ष्य आयाम ''p'' के दिए गए डेटा समुच्चय | |||
:<math> \mathbf{Y} = \mathbb{KLT} \{ \mathbf{X} \} </math> | :<math> \mathbf{Y} = \mathbb{KLT} \{ \mathbf{X} \} </math> | ||
; डेटा समुच्चय | ; डेटा समुच्चय व्यवस्थित करें | ||
मान लीजिए कि आपके | मान लीजिए कि आपके समीप p वेरिएबलों के प्रेक्षणों के समुच्चय से युक्त डेटा है, और आप डेटा को कम करना चाहते हैं जिससे प्रत्येक प्रेक्षण को केवल L वेरिएबल , L <p के साथ वर्णित किया जा सकता हैं। आगे मान लीजिए कि डेटा को n डेटा सदिश के समुच्चय <math>\mathbf{x}_1 \ldots \mathbf{x}_n</math> के रूप में व्यवस्थित किया जाता है प्रत्येक p के साथ <math>\mathbf{x}_i </math> वेरिएबल्स के एकल समूहीकृत अवलोकन का प्रतिनिधित्व करना हैं। | ||
* | * प्रत्येक p अवयवों के साथ <math>\mathbf{x}_1 \ldots \mathbf{x}_n</math> पंक्ति सदिश के रूप में, लिखना । | ||
* पंक्ति सदिशों को आयाम n × p के एकल आव्यूह 'X' में रखें। | * पंक्ति सदिशों को आयाम n × p के एकल आव्यूह 'X' में रखें। | ||
; अनुभवजन्य माध्य की गणना करें | ; अनुभवजन्य माध्य की गणना करें | ||
* प्रत्येक | * प्रत्येक स्तम्भ j = 1, ..., p के साथ अनुभवजन्य माध्य खोजें। | ||
* परिकलित माध्य मानों को आयाम p × 1 के अनुभवजन्य माध्य सदिश 'u' में रखें। | * परिकलित माध्य मानों को आयाम p × 1 के अनुभवजन्य माध्य सदिश 'u' में रखें। | ||
*:<math>u_j = \frac{1}{n} \sum_{i=1}^n X_{ij} </math> | *:<math>u_j = \frac{1}{n} \sum_{i=1}^n X_{ij} </math> | ||
; माध्य से विचलन की गणना करें | ; माध्य से विचलन की गणना करें | ||
औसत घटाव प्रमुख अवयव आधार खोजने की दिशा में समाधान का अभिन्न अंग है जो डेटा का अनुमान लगाने की औसत वर्ग त्रुटि को कम करता है।<ref>A.A. Miranda, Y.-A. Le Borgne, and G. Bontempi. [http://www.ulb.ac.be/di/map/yleborgn/pub/NPL_PCA_07.pdf New Routes from Minimal Approximation Error to Principal Components], Volume 27, Number 3 / June, 2008, Neural Processing Letters, Springer</ref> इसलिए हम निम्नानुसार डेटा को केंद्रित करके आगे बढ़ते हैं | औसत घटाव प्रमुख अवयव आधार खोजने की दिशा में समाधान का अभिन्न अंग है जो डेटा का अनुमान लगाने की औसत वर्ग त्रुटि को कम करता है।<ref>A.A. Miranda, Y.-A. Le Borgne, and G. Bontempi. [http://www.ulb.ac.be/di/map/yleborgn/pub/NPL_PCA_07.pdf New Routes from Minimal Approximation Error to Principal Components], Volume 27, Number 3 / June, 2008, Neural Processing Letters, Springer</ref> इसलिए हम निम्नानुसार डेटा को केंद्रित करके आगे बढ़ते हैं | ||
* अनुभवजन्य माध्य | * अनुभवजन्य माध्य सदिश घटाएं <math> \mathbf{u}^{T} </math> डेटा आव्युह X की प्रत्येक पंक्ति से हैं। | ||
* माध्य-घटाए गए डेटा को ''n'' × ''p'' आव्युह | * माध्य-घटाए गए डेटा को ''n'' × ''p'' आव्युह B में संग्रहीत करें। | ||
*:<math>\mathbf{B} = \mathbf{X} - \mathbf{h}\mathbf{u}^T </math> | *:<math>\mathbf{B} = \mathbf{X} - \mathbf{h}\mathbf{u}^T </math> | ||
*: जहाँ h है {{math|''n'' × 1}} सभी 1 का | *: जहाँ h है {{math|''n'' × 1}} सभी 1 का स्तम्भ सदिश : | ||
*::<math>h_i = 1 \, \qquad \qquad \text{for } i = 1, \ldots, n </math> | *::<math>h_i = 1 \, \qquad \qquad \text{for } i = 1, \ldots, n </math> | ||
कुछ अनुप्रयोगों में, प्रत्येक वेरिएबल | कुछ अनुप्रयोगों में, प्रत्येक वेरिएबल (B का स्तम्भ ) को 1 के समान भिन्नता के लिए स्केल किया जा सकता है (जेड-स्कोर देखें)।<ref>{{Cite journal|author1=Abdi. H. |author2=Williams, L.J. |name-list-style=amp | author-link=AbdiWilliams | year = 2010 | title = प्रमुख कंपोनेंट विश्लेषण| journal = Wiley Interdisciplinary Reviews: Computational Statistics | volume = 2 | issue=4 | pages = 433–459 | doi = 10.1002/wics.101 |arxiv=1108.4372 |s2cid=122379222 }}</ref> यह निर्णय परिकलित प्रमुख अवयवों को प्रभावित करता है, किन्तु उन्हें विभिन्न वेरिएबलों को मापने के लिए उपयोग की जाने वाली इकाइयों से स्वतंत्र बनाता है। | ||
; सहप्रसरण आव्युह | ; सहप्रसरण आव्युह का पता लगाएं | ||
* आव्युह | * आव्युह 'B' से p × p अनुभवजन्य सहप्रसरण आव्युह 'C' खोजें: <math display="block">\mathbf{C} = { 1 \over {n-1} } \mathbf{B}^{*} \mathbf{B}</math> जहाँ <math> *</math> संयुग्मी स्थानांतरण संकारक है। यदि B में पूरी तरह से वास्तविक संख्याएं होती हैं, जो कि अनेक अनुप्रयोगों में होती है, तब संयुग्म स्थानान्तरण नियमित स्थानान्तरण के समान होता है। | ||
* प्रयोग करने के पीछे तर्क | * प्रयोग करने के पीछे तर्क ''n'' − 1 सहप्रसरण की गणना करने के लिए n के अतिरिक्त बेसेल का सुधार है। | ||
; सहप्रसरण आव्युह | ; सहप्रसरण आव्युह के आइजन्वेक्टर और आइजेनवैल्यू का पता लगाएं | ||
* | * आइजन्वेक्टर के आव्युह 'V' की गणना करें जो सहसंयोजक आव्युह 'C' को विकर्ण करता है: <math display="block">\mathbf{V}^{-1} \mathbf{C} \mathbf{V} = \mathbf{D} </math> जहाँ D, C के आइजेनवैल्यू का विकर्ण आव्युह है। इस चरण में सामान्यतः आव्युह के आइजेनडीकम्पोज़िशन के लिए कंप्यूटर-आधारित एल्गोरिथ्म का उपयोग सम्मिलित होता हैं। यह एल्गोरिदम अधिकांश [[मैट्रिक्स बीजगणित|आव्युह बीजगणित]] प्रणालियों के उप-अवयवों के रूप में सरलता से उपलब्ध हैं, जैसे [[एसएएस (सॉफ्टवेयर)]],<ref>{{Cite web | url=http://support.sas.com/documentation/cdl/en/statug/63962/HTML/default/viewer.htm#statug_princomp_sect001.htm | title=SAS/STAT(R) 9.3 User's Guide}}</ref> [[आर (प्रोग्रामिंग भाषा)]], [[MATLAB|मैटलैब]],<ref>[http://www.mathworks.com/access/helpdesk/help/techdoc/ref/eig.html#998306 eig function] Matlab documentation</ref><ref>{{Cite web|url=https://www.mathworks.com/matlabcentral/fileexchange/24634-face-recognition-system-pca-based|title=चेहरा पहचान प्रणाली-पीसीए आधारित|website=www.mathworks.com}}</ref> गणित,<ref>[http://reference.wolfram.com/mathematica/ref/Eigenvalues.html Eigenvalues function] Mathematica documentation</ref> [[SciPy|साइपी]], आईडीएल (प्रोग्रामिंग लैंग्वेज) ([[इंटरएक्टिव डेटा भाषा]]), या जीएनयू ऑक्टेव और साथ ही [[OpenCV|ओपनसीवी]] होता हैं। | ||
* आव्युह | * आव्युह D ''p'' × ''p'' विकर्ण आव्युह का रूप ले लेगा, जहाँ <math display="block">D_{k\ell} = \lambda_k \qquad \text{for } k = \ell</math> सहप्रसरण आव्युह 'C' का jवां आइजेनवैल्यू है, और <math display="block">D_{k\ell} = 0 \qquad \text{for } k \ne \ell.</math> | ||
* आव्युह | * आव्युह V, आयाम ''p'' × ''p'' का भी, ''p'' स्तम्भ सदिश , प्रत्येक लंबाई ''p'', जो सहप्रसरण आव्युह के ''p'' आइजन्वेक्टर C का प्रतिनिधित्व करता है । | ||
* | * आइजेनवैल्यू और आइजन्वेक्टर को क्रमबद्ध और युग्मित किया जाता है। और ''J''th आइजेनवैल्यू ''j''th आइजन्वेक्टर से मेल खाता है। | ||
* आव्युह | * आव्युह V 'राइट' आइजन्वेक्टर के आव्युह को दर्शाता है ('लेफ्ट' आइजन्वेक्टर के विपरीत) हैं। सामान्यतः , दाएं आइजन्वेक्टर के आव्युह को बाएं आइजन्वेक्टर के आव्युह का नहीं होना चाहिए। | ||
; | ; आइजन्वेक्टर और आइजेनवैल्यू को पुनर्व्यवस्थित करें | ||
* | * आइजन्वेक्टर आव्युह V और आइजेनवैल्यू आव्युह D के स्तम्भ को घटते आइजेनवैल्यू के क्रम में क्रमबद्ध करें। | ||
* प्रत्येक आव्युह | * प्रत्येक आव्युह में स्तंभों के मध्य सही जोड़ियों को बनाए रखना सुनिश्चित करें। | ||
; प्रत्येक | ; प्रत्येक आइजन्वेक्टर के लिए संचयी ऊर्जा सामग्री की गणना करें | ||
* | * आइजेनवैल्यू स्रोत डेटा की ऊर्जा के वितरण का प्रतिनिधित्व करते हैं प्रत्येक आइजन्वेक्टर के मध्य , जहाँ आइजन्वेक्टर डेटा के लिए [[आधार (रैखिक बीजगणित)]] बनाते हैं। जेवें आइजन्वेक्टर के लिए संचयी ऊर्जा सामग्री जी 1 से जे तक सभी ईजेनवैल्यू में ऊर्जा सामग्री का योग है: | ||
*:<math>g_j = \sum_{k=1}^j D_{kk} \qquad \text{for } j = 1,\dots,p </math> | *:<math>g_j = \sum_{k=1}^j D_{kk} \qquad \text{for } j = 1,\dots,p </math> | ||
; आधार सदिश के रूप में | ; आधार सदिश के रूप में आइजन्वेक्टर के सबसमुच्चय का चयन करें | ||
* ' | * 'V' के पहले ''L'' स्तम्भ को ''p × L''आव्युह 'w' के रूप में सहेजें: <math display="block"> W_{kl} = V_{k\ell} \qquad \text{for } k = 1,\dots,p \qquad \ell = 1,\dots,L </math> जहाँ <math display="block">1 \leq L \leq p.</math> | ||
*'L | *'L के लिए उपयुक्त मान चुनने में गाइड के रूप में सदिश g का उपयोग करें। लक्ष्य प्रतिशत के आधार पर g के यथोचित उच्च मान को प्राप्त करते हुए जितना संभव हो सके इसमें L के मान को चुनना है। उदाहरण के लिए, आप L चुन सकते हैं जिससे संचयी ऊर्जा g निश्चित सीमा से ऊपर हो, जैसे 90 प्रतिशत हैं। इस स्तिथियों में, 'L' का सबसे लघु मान चुनें जैसे कि'' <math display="block"> \frac{g_L}{g_p} \ge 0.9 </math>'' | ||
; डेटा को नए आधार पर प्रोजेक्ट करें | ; डेटा को नए आधार पर प्रोजेक्ट करें | ||
* अनुमानित डेटा बिंदु आव्युह | * अनुमानित डेटा बिंदु आव्युह की पंक्तियाँ हैं <math display="block"> \mathbf{T} = \mathbf{B} \cdot \mathbf{W}</math> | ||
अर्थात का पहला स्तम्भ <math>\mathbf{T}</math> पहले प्रमुख अवयव पर डेटा बिंदुओं का प्रक्षेपण है, दूसरा स्तंभ दूसरे प्रमुख अवयव पर प्रक्षेपण आदि है। | |||
== सहप्रसरण विधि का उपयोग करके पीसीए की व्युत्पत्ति == | == सहप्रसरण विधि का उपयोग करके पीसीए की व्युत्पत्ति == | ||
X को स्तम्भ सदिश के रूप में व्यक्त 'D'-आयामी यादृच्छिक सदिश होना चाहिए। व्यापकता के हानि के बिना, मान लें कि X का शून्य माध्य है। | |||
हम खोजना चाहते हैं <math>(\ast)</math> a {{math|''d'' × ''d''}} ऑर्थोनॉर्मल आधार | हम खोजना चाहते हैं कि <math>(\ast)</math> a {{math|''d'' × ''d''}} ऑर्थोनॉर्मल आधार p जिससे पीएक्स में विकर्ण सहप्रसरण आव्युह हो (अर्थात, पीएक्स यादृच्छिक सदिश है जिसके सभी भिन्न -भिन्न अवयव जोड़ीदार असंबद्ध हैं)। | ||
इस प्रकार त्वरित गणना मानते हुए <math>P</math> एकात्मक उपज थे | |||
:<math>\begin{align} | :<math>\begin{align} | ||
| Line 337: | Line 341: | ||
&= P\operatorname{cov}(X)P^{-1}\\ | &= P\operatorname{cov}(X)P^{-1}\\ | ||
\end{align}</math> | \end{align}</math> | ||
इस तरह <math>(\ast)</math> रखती है | इस तरह <math>(\ast)</math> रखती है यदि और केवल यदि <math>\operatorname{cov}(X)</math> <math>P</math> द्वारा विकर्णीय थे . | ||
यह बहुत रचनात्मक है, क्योंकि cov(X) गैर- | यह बहुत रचनात्मक है, क्योंकि cov(X) गैर-ऋणात्मक निश्चित आव्युह होने की गारंटी है और इस प्रकार कुछ एकात्मक आव्युह द्वारा विकर्ण होने की गारंटी है। | ||
== सहप्रसरण-मुक्त संगणना == | == सहप्रसरण-मुक्त संगणना == | ||
व्यावहारिक कार्यान्वयन में, विशेष रूप से [[उच्च आयामी डेटा]] (बड़े {{mvar|p}}), भोली सहप्रसरण विधि का उपयोग | व्यावहारिक कार्यान्वयन में, विशेष रूप से [[उच्च आयामी डेटा]] (बड़े {{mvar|p}}), भोली सहप्रसरण विधि का उपयोग संभवतः ही कभी किया जाता है क्योंकि सहप्रसरण आव्युह को स्पष्ट रूप से निर्धारित करने की उच्च कम्प्यूटेशनल और मेमोरी निवेश के कारण यह कुशल नहीं है। सहप्रसरण-मुक्त दृष्टिकोण {{math|''np''<sup>2</sup>}} से बचा जाता है स्पष्ट रूप से सहप्रसरण आव्युह की गणना और संग्रहण के संचालन {{math|'''X<sup>T</sup>X'''}}, इसके अतिरिक्त आव्युह -मुक्त विधियों में से इसका उपयोग करना हैं, उदाहरण के लिए, उत्पाद का मूल्यांकन करने वाले फलन के आधार पर {{math|'''X<sup>T</sup>(X r)'''}} की मान पर {{math|2''np''}} संचालन किया जाता है। | ||
=== पुनरावृत्ति संगणना === | |||
यह [[शक्ति पुनरावृत्ति]] एल्गोरिथ्म केवल | पहले प्रमुख अवयव की कुशलता से गणना करने की विधि <ref name="roweis">Roweis, Sam. "EM Algorithms for PCA and SPCA." Advances in Neural Information Processing Systems. Ed. Michael I. Jordan, Michael J. Kearns, and [[Sara A. Solla]] The MIT Press, 1998.</ref> शून्य माध्य के साथ, इसके सहप्रसरण आव्युह की गणना किए बिना डेटा आव्युह के लिए निम्नलिखित छद्म कोड {{math|'''X'''}} में दिखाया गया है। <syntaxhighlight lang="abap"> | ||
r = a random vector of length p | |||
r = r / norm(r) | |||
do c times: | |||
s = 0 (a vector of length p) | |||
for each row x in X | |||
s = s + (x ⋅ r) x | |||
λ = rTs // λ is the eigenvalue | |||
error = |λ ⋅ r − s| | |||
r = s / norm(s) | |||
exit if error < tolerance | |||
return λ, r | |||
</syntaxhighlight>यह [[शक्ति पुनरावृत्ति]] एल्गोरिथ्म केवल सदिश {{math|'''X<sup>T</sup>(X r)'''}} की गणना करता है, और परिणाम {{math|'''r'''}} को वापस अंदर रखता है. आइजेनवैल्यू द्वारा {{math|'''r<sup>T</sup> (X<sup>T</sup>X) r'''}} अनुमानित है, जो इकाई सदिश {{math|'''r'''}} पर रेले {{math|'''X<sup>T</sup>X '''}} भागफल है सहप्रसरण आव्युह के लिए . यदि सबसे बड़ा एकवचन मान अगले सबसे बड़े सदिश से अच्छी तरह से {{math|'''r'''}} भिन्न है यह {{math|'''X'''}} के पहले प्रमुख अवयव के समीप {{mvar|c}} हो जाता है पुनरावृत्तियों की संख्या के अंदर, जो {{mvar|p}} के सापेक्ष लघु है, कुल निवेश पर {{math|''2cnp''}}. अधिक उन्नत आव्युह -मुक्त विधियों, जैसे [[लैंक्ज़ोस एल्गोरिथम]] या स्थानीय रूप से अधिकतम ब्लॉक प्रीकंडीशन्ड कंजुगेट ग्रेडिएंट ([[LOBPCG|एलओबीपीसीजी]]) विधि का उपयोग करके प्रति पुनरावृत्ति की छोटी निवेश का त्याग किए बिना शक्ति पुनरावृत्ति अभिसरण को त्वरित किया जा सकता है। | |||
पश्चात | इसके पश्चात के प्रमुख अवयवों की गणना करके अपस्फीति के माध्यम से या साथ ब्लॉक के रूप में की जा सकती है। पूर्व दृष्टिकोण में, पहले से ही गणना किए गए अनुमानित प्रमुख अवयवों में अशुद्धियाँ पश्चात में गणना किए गए प्रमुख अवयवों की स्पष्टता को जोड़ कर प्रभावित करती हैं, इस प्रकार हर नई संगणना के साथ त्रुटि बढ़ जाती है। ब्लॉक पावर पद्धति में पश्चात वाला दृष्टिकोण एकल-सदिश की जगह लेता है {{math|'''r'''}} और {{math|'''s'''}} ब्लॉक-सदिश , मैट्रिसेस के साथ {{math|'''R'''}} और {{math|'''S'''}}. का हर स्तंभ {{math|'''R'''}} प्रमुख प्रमुख अवयवों में से का अनुमान लगाता है, जबकि सभी स्तम्भ साथ पुनरावृत्त होते हैं। मुख्य गणना {{math|'''X<sup>T</sup>(X R)'''}} उत्पाद का मूल्यांकन है कार्यान्वित, उदाहरण के लिए, एलओबीपीसीजी में, कुशल अवरोधन त्रुटियों के संचय को समाप्त करता है, उच्च-स्तरीय [[BLAS|ब्लास]] आव्युह -आव्युह उत्पाद कार्यों का उपयोग करने की अनुमति देता है, और सामान्यतः एकल-सदिश एक-एक-एक तकनीक की तुलना में शीघ्रता से अभिसरण की ओर जाता है। | ||
=== | === निपल्स विधि === | ||
गैर-रैखिक पुनरावृत्त [[आंशिक न्यूनतम वर्ग]] ( | गैर-रैखिक पुनरावृत्त [[आंशिक न्यूनतम वर्ग]] (निपल्स) प्रमुख अवयव या आंशिक कम वर्ग विश्लेषण में पहले कुछ अवयवों की गणना के लिए घटाव द्वारा आव्युह अपस्फीति के साथ मौलिक शक्ति पुनरावृत्ति का प्रकार है। बहुत उच्च-आयामी डेटासमुच्चय के लिए, जैसे कि *ओमिक्स विज्ञान (उदाहरण के लिए, [[जीनोमिक्स]], [[चयापचय]]) में उत्पन्न डेटासमुच्चय के लिए सामान्यतः केवल पहले कुछ पीसी की गणना करना आवश्यक होता है। गैर-रैखिक पुनरावृत्त आंशिक न्यूनतम वर्ग (निपल्स) एल्गोरिथ्म प्रमुख स्कोर और लोडिंग 'T<sub>1</sub> और r<sub>1</sub><sup>T</sup>' के पुनरावृत्त अनुमानों को अद्यतन करता है। शक्ति पुनरावृत्ति द्वारा प्रत्येक पुनरावृत्ति पर X द्वारा बाईं ओर और दाईं ओर गुणा किया जाता है, अर्थात, सहप्रसरण आव्युह की गणना उत्पाद {{math|1='''X<sup>T</sup>(X r)''' = '''((X r)<sup>T</sup>X)<sup>T</sup>'''}} का मूल्यांकन करने वाले फलन के आधार पर, {{math|'''X<sup>T</sup>X'''}} में पावर पुनरावृत्तियों के आव्युह-मुक्त कार्यान्वयन की तरह, टाला जाता है। | ||
घटाव द्वारा आव्युह | घटाव द्वारा आव्युह अपस्फीति बाहरी उत्पाद, T<sub>1</sub>r<sub>1</sub><sup>T</sup> X से घटाकर किया जाता है अवस्फीत अवशिष्ट आव्युह को छोड़ते हुए पश्चात के प्रमुख पीसी की गणना करने के लिए उपयोग किया जाता है।<ref>{{Cite journal | ||
| last1 = Geladi | | last1 = Geladi | ||
| first1 = Paul | | first1 = Paul | ||
| Line 379: | Line 381: | ||
| year = 1986 | | year = 1986 | ||
| doi = 10.1016/0003-2670(86)80028-9 | | doi = 10.1016/0003-2670(86)80028-9 | ||
}}</ref> | }}</ref> बड़े डेटा मेट्रिसेस, या मेट्रिसेस के लिए, जिनमें स्तम्भ कोलीनियरिटी का उच्च स्तर होता है, निपल्स पीसी की ऑर्थोगोनलिटी के हानि से ग्रस्त होता है, क्योंकि प्रत्येक पुनरावृत्ति और आव्युह अपस्फीति में घटाव द्वारा संचित मशीन स्पष्ट [[राउंड-ऑफ त्रुटियां]] होती हैं।<ref>{{cite book |last=Kramer |first=R. |year=1998 |title=मात्रात्मक विश्लेषण के लिए रसायनमितीय तकनीक|publisher=CRC Press |location=New York |isbn= 9780203909805|url=https://books.google.com/books?id=iBpOzwAOfHYC}}</ref> ऑर्थोगोनलिटी के इस हानि को विलुप्त करने के लिए प्रत्येक पुनरावृत्ति चरण पर स्कोर और लोडिंग दोनों के लिए ग्राम-श्मिट री-ऑर्थोगोनलाइज़ेशन एल्गोरिदम प्रयुक्त किया जाता है।<ref>{{cite journal |first=M. |last=Andrecut |title=इटरेटिव पीसीए एल्गोरिदम का समानांतर जीपीयू कार्यान्वयन|journal=Journal of Computational Biology |volume=16 |issue=11 |year=2009 |pages=1593–1599 |doi=10.1089/cmb.2008.0221 |pmid=19772385 |arxiv=0811.1081 |s2cid=1362603 }}</ref> एकल-सदिश गुणन पर निपल्स निर्भरता उच्च-स्तरीय ब्लास का लाभ नहीं उठा सकती है और परिणामस्वरूप क्लस्टर अग्रणी विलक्षण मानों के लिए धीमी गति से अभिसरण होता है इन दोनों कमियों को अधिक परिष्कृत आव्युह -मुक्त ब्लॉक सॉल्वर में हल किया जाता है, जैसे कि स्थानीय रूप से अधिकतम ब्लॉक प्रीकंडिशनेड कंजुगेट ग्रेडिएंट ( एलओबीपीसीजी) विधि होती हैं। | ||
बड़े डेटा मेट्रिसेस, या मेट्रिसेस के लिए, जिनमें | |||
=== ऑनलाइन/अनुक्रमिक अनुमान === | === ऑनलाइन/अनुक्रमिक अनुमान === | ||
ऑनलाइन या स्ट्रीमिंग स्थिति में बैच में संग्रहीत होने के अतिरिक्त अनेक भाग में डेटा आने के साथ, पीसीए प्रोजेक्शन का अनुमान लगाना उपयोगी होता है जिसे क्रमिक रूप से अपडेट किया जा सकता है। यह कुशलता से किया जा सकता है, किन्तु इसके लिए भिन्न -भिन्न एल्गोरिदम की आवश्यकता होती है।<ref>{{Cite journal | |||
| last1 = Warmuth | | last1 = Warmuth | ||
| first1 = M. K. | | first1 = M. K. | ||
| Line 397: | Line 398: | ||
== पीसीए और गुणात्मक वेरिएबल == | == पीसीए और गुणात्मक वेरिएबल == | ||
पीसीए में, यह सामान्य है कि हम गुणात्मक वेरिएबल | पीसीए में, यह सामान्य है कि हम गुणात्मक वेरिएबल को पूरक अवयवों के रूप में प्रस्तुत करना चाहते हैं। उदाहरण के लिए, पौधों पर अनेक मात्रात्मक वेरिएबलों को मापा गया है। इन पौधों के लिए, कुछ गुणात्मक वेरिएबल उपलब्ध हैं, उदाहरण के लिए, वह प्रजाति जिससे पौधे संबंधित हैं। यह डेटा मात्रात्मक वेरिएबल के लिए पीसीए के अधीन थे। परिणामों का विश्लेषण करते समय, प्रमुख अवयवों को गुणात्मक वेरिएबल प्रजातियों से जोड़ना स्वाभाविक है। इसके लिए निम्न परिणाम प्राप्त होते हैं। | ||
इसके लिए निम्न परिणाम प्राप्त होते हैं। | * विभिन्न प्रजातियों की पहचान, तथ्यात्मक प्लेनों पर, उदाहरण के लिए, विभिन्न रंगों का उपयोग करना। | ||
* विभिन्न प्रजातियों की पहचान, तथ्यात्मक | * प्रतिनिधित्व, ही प्रजाति से संबंधित पौधों के गुरुत्वाकर्षण के केंद्रों के तथ्यात्मक प्लेनों पर। | ||
* प्रतिनिधित्व, ही प्रजाति से संबंधित पौधों के गुरुत्वाकर्षण के केंद्रों के तथ्यात्मक | * गुरुत्वाकर्षण के प्रत्येक केंद्र और प्रत्येक अक्ष के लिए, गुरुत्व केंद्र और उत्पत्ति के मध्य के अंतर के महत्व का न्याय करने के लिए पी-मान। | ||
* गुरुत्वाकर्षण के प्रत्येक केंद्र और प्रत्येक अक्ष के लिए, गुरुत्व केंद्र और उत्पत्ति के | |||
इन परिणामों को गुणात्मक वेरिएबल | इन परिणामों को गुणात्मक वेरिएबल को पूरक अवयव के रूप में प्रस्तुत करना कहा जाता है। यह प्रक्रिया हसन, ली और पेज 2009 और पेज 2013 में विस्तृत है।कुछ सॉफ्टवेयर इस विकल्प को स्वचालित विधियों से प्रस्तुत करते हैं। यह [http://www.coheris.com/produits/analytics/logiciel-data-mining/ एसपीएडी] की स्तिथि है, जो ऐतिहासिक रूप से, [[लुडोविक लेबार्ट]] के कार्य के पश्चात , [http://factominer.free.fr/ फैक्टोमाइनर] इस विकल्प और R पैकेज को प्रस्तावित करने वाले प्रथम व्यक्ति थे । | ||
== अनुप्रयोग == | == अनुप्रयोग == | ||
=== बुद्धि === | === बुद्धि === | ||
कारक विश्लेषण का सबसे पहला प्रयोग मानव बुद्धि के अवयवों | कारक विश्लेषण का सबसे पहला प्रयोग मानव बुद्धि के अवयवों का पता लगाने और मापने में था। यह माना जाता था कि बुद्धि में विभिन्न असंबद्ध अवयव होते हैं जैसे कि स्थानिक बुद्धि, मौखिक बुद्धि, आगमन, कटौती आदि और इन पर अंक विभिन्न परीक्षणों के परिणामों से कारक विश्लेषण द्वारा जोड़े जा सकते हैं, जिससे एकल सूचकांक दिया जा सके जिसे इंटेलिजेंस कोशिएंट (IQ) के रूप में जाना जाता है। ). अग्रणी सांख्यिकीय मनोवैज्ञानिक [[चार्ल्स स्पीयरमैन]] ने वास्तव में 1904 में अपने बुद्धि के दो-कारक सिद्धांत दिए हैं | बुद्धि के दो-कारक सिद्धांत के लिए कारक विश्लेषण विकसित किया, जिसमें [[साइकोमेट्रिक्स]] के विज्ञान के लिए औपचारिक तकनीक सम्मिलित थी। 1924 में [[लुई लियोन थर्स्टन]] ने मानसिक आयु की धारणा को विकसित करते हुए बुद्धि के 56 कारकों की खोजने का प्रयास था | मानक IQ परीक्षण आज इसी प्रारंभिक कार्य पर आधारित हैं।<ref name="Kaplan, R.M. 2010">Kaplan, R.M., & Saccuzzo, D.P. (2010). ''Psychological Testing: Principles, Applications, and Issues.'' (8th ed.). Belmont, CA: Wadsworth, Cengage Learning.</ref> | ||
=== आवासीय भेदभाव === | |||
1949 में, शेवकी और विलियम्स ने फैक्टोरियल इकोलॉजी का सिद्धांत प्रस्तुत किया, जो 1950 से 1970 के दशक तक आवासीय भेदभाव के अध्ययन पर प्रभावी था।<ref>{{Cite book |last1=Shevky |first1=Eshref |title=The Social Areas of Los Angeles: Analysis and Typology |last2=Williams |first2=Marilyn |publisher=University of California Press |year=1949}}</ref> यह शहर में निकटतम पहचानने योग्य थे यह विभिन्न विशेषताओं द्वारा दूसरे से भिन्न किए जा सकते थे जिन्हें कारक विश्लेषण द्वारा घटाकर तीन किया जा सकता था। इन्हें 'सामाजिक पद' (व्यावसायिक स्थिति का सूचकांक), 'वर्ग' या समूह का आकार, और 'जातीयता' के रूप में जाना जाता था; क्लस्टर विश्लेषण को तीन प्रमुख कारक वेरिएबल के मानों के अनुसार शहर को क्लस्टर या परिसर में विभाजित करने के लिए प्रयुक्त किया जा सकता है। शहरी भूगोल में फैक्टोरियल इकोलॉजी के आस पास व्यापक साहित्य विकसित हुआ, किन्तु 1980 के पश्चात पद्धतिगत रूप से प्राचीन होने और उत्तर आधुनिक भौगोलिक प्रतिमानों में कम जगह होने के कारण यह दृष्टिकोण फैशन से बाहर हो गया था। | |||
कारक विश्लेषण की समस्याओं में से सदैव विभिन्न कृत्रिम कारकों के लिए ठोस नाम खोजना रहा है। 2000 में, फ्लड ने फैक्टोरियल इकोलॉजी दृष्टिकोण को पुनर्जीवित किया, यह दिखाने के लिए कि प्रमुख अवयव विश्लेषण ने कारक रोटेशन का सहारा लिए बिना वास्तव में सीधे सार्थक उत्तर दिए हैं। प्रमुख अवयव वास्तव में शहरों में व्यकित को साथ या भिन्न करने वाले 'बलों' के दोहरे वेरिएबल या छाया मान थे। पहला अवयव 'पहुंच' था, यात्रा की मांग और अंतरिक्ष की मांग के मध्य क्लासिक व्यापार-संवर्त , जिसके आससमीप मौलिक शहरी अर्थशास्त्र आधारित है। अगले दो अवयव 'हानि ' थे, जो समान स्थिति के व्यकित को भिन्न निकटतम (नियोजन द्वारा मध्यस्थता) में रखता है, और जातीयता, जहां समान जातीय पृष्ठभूमि के लोग सह-पता लगाने की प्रयास करते हैं।<ref>Flood, J (2000). Sydney divided: factorial ecology revisited. Paper to the APA Conference 2000, Melbourne,November and to the 24th ANZRSAI Conference, Hobart, December 2000.[https://www.academia.edu/5135339/Sydney_Divided_Factorial_Ecology_Revisited]</ref> | |||
उसी समय के बारे में, ऑस्ट्रेलियाई सांख्यिकी ब्यूरो ने प्रमुख वेरिएबल के समुच्चय के पहले प्रमुख अवयव को लेते हुए लाभ और हानि के भिन्न -भिन्न सूचकांकों को परिभाषित किया, जिन्हें महत्वपूर्ण माना गया था। यह सेइफ़ा इंडेक्स नियमित रूप से विभिन्न न्यायालयों के लिए प्रकाशित होते हैं, और स्थानिक विश्लेषण में अधिकतर उपयोग किए जाते हैं।<ref>{{Cite web |last= |first= |date=2011 |title=क्षेत्रों के लिए सामाजिक-आर्थिक सूचकांक|url=https://www.abs.gov.au/websitedbs/censushome.nsf/home/seifa |access-date=2022-05-05 |website=Australian Bureau of Statistics |language=en}}</ref> | |||
=== विकास सूचकांक === | === विकास सूचकांक === | ||
पीसीए इंडेक्स के विकास के लिए उपलब्ध एकमात्र औपचारिक | पीसीए इंडेक्स के विकास के लिए उपलब्ध एकमात्र औपचारिक विधि रहा है, जो अन्यथा हिट-या-मिस तदर्थ उपक्रम है। | ||
[[नगर विकास सूचकांक]] पीसीए द्वारा 1996 में 254 वैश्विक शहरों के सर्वेक्षण में शहर के परिणामों के लगभग 200 संकेतकों से विकसित किया गया था। पहला प्रमुख अवयव पुनरावृत्त प्रतिगमन के अधीन था, मूल वेरिएबल | [[नगर विकास सूचकांक]] पीसीए द्वारा 1996 में 254 वैश्विक शहरों के सर्वेक्षण में शहर के परिणामों के लगभग 200 संकेतकों से विकसित किया गया था। पहला प्रमुख अवयव पुनरावृत्त प्रतिगमन के अधीन था, मूल वेरिएबल को तब तक जोड़ा गया जब तक कि इसकी लगभग 90% भिन्नता की गणना नहीं की जस सकती हैं। इंडेक्स ने अंततः लगभग 15 संकेतकों का उपयोग किया किन्तु अनेक और वेरिएबलों का अच्छा भविष्यवक्ता था। इसका तुलनात्मक मान प्रत्येक शहर की स्थिति के व्यक्तिपरक मूल्यांकन के साथ बहुत अच्छी तरह से मेल खाता है। मूलभूत फ्रेम की वस्तुओं पर गुणांक अंतर्निहित सेवाएं प्रदान करने की औसत निवेश के लगभग आनुपातिक थे, यह सुझाव देते हुए कि सूचकांक वास्तव में शहर में प्रभावी भौतिक और सामाजिक निवेश का उपाय था। | ||
संयुक्त राष्ट्र विकास कार्यक्रम से देश-स्तरीय [[मानव विकास सूचकांक]] (एचडीआई), जो 1990 से प्रकाशित हुआ है और विकास अध्ययनों में बहुत व्यापक रूप से उपयोग किया जाता है,<ref>{{Cite web |last=Human Development Reports |title=मानव विकास सूचकांक|url=https://hdr.undp.org/en/content/human-development-index-hdi |access-date=2022-05-06 |website=United Nations Development Programme}}</ref> समान संकेतकों पर बहुत समान गुणांक हैं, यह दृढ़ता से सुझाव देते हैं कि यह मूल रूप से पीसीए का उपयोग करके बनाया गया था। | संयुक्त राष्ट्र विकास कार्यक्रम से देश-स्तरीय [[मानव विकास सूचकांक]] (एचडीआई), जो 1990 से प्रकाशित हुआ है और विकास अध्ययनों में बहुत व्यापक रूप से उपयोग किया जाता है,<ref>{{Cite web |last=Human Development Reports |title=मानव विकास सूचकांक|url=https://hdr.undp.org/en/content/human-development-index-hdi |access-date=2022-05-06 |website=United Nations Development Programme}}</ref> यह समान संकेतकों पर बहुत समान गुणांक हैं, यह दृढ़ता से सुझाव देते हैं कि यह मूल रूप से पीसीए का उपयोग करके बनाया गया था। | ||
=== जनसंख्या आनुवंशिकी === | === जनसंख्या आनुवंशिकी === | ||
1978 में [[लुइगी लुका कवेली-स्फोर्ज़ा]] | 1978 में [[लुइगी लुका कवेली-स्फोर्ज़ा]] कैवली-स्फोर्ज़ा और अन्य ने क्षेत्रों में मानव जीन आवृत्तियों में भिन्नता पर डेटा को सारांशित करने के लिए प्रमुख अवयव विश्लेषण (पीसीए) के उपयोग उत्तरदायित्व उठाया हैं। अवयवों ने विशिष्ट पैटर्न दिखाए, जिनमें ग्रेडियेंट और साइनसॉइडल तरंगें सम्मिलित हैं। उन्होंने विशिष्ट प्राचीन प्रवासन घटनाओं के परिणामस्वरूप इन प्रतिमानों की व्याख्या की हैं। | ||
तब से, पीसीए प्रदर्शन तंत्र के रूप में पीसीए का उपयोग करने वाले हजारों पेपरों के साथ जनसंख्या आनुवंशिकी में सर्वव्यापी रहा है। इसमें निकटता के अनुसार आनुवंशिकी अधिक सीमा तक भिन्न होती है, इसलिए पहले दो प्रमुख अवयव वास्तव में स्थानिक वितरण दिखाते हैं और इसका उपयोग विभिन्न जनसंख्या समूहों के सापेक्ष भौगोलिक स्थान को मानचित्र करने के लिए किया जा सकता है, जिससे ऐसे व्यक्तियों को दिखाया जा सकता है जो अपने मूल स्थानों से भटक गए हैं।<ref>{{Cite journal |last1=Novembre |first1=John |last2=Stephens |first2=Matthew |date=2008 |title=स्थानिक जनसंख्या आनुवंशिक भिन्नता के प्रमुख घटक विश्लेषण की व्याख्या करना|journal=Nat Genet |volume=40 |issue=5 |pages=646–49 |doi=10.1038/ng.139 |pmid=18425127 |pmc=3989108 }}</ref> | |||
जेनेटिक्स में पीसीए तकनीकी रूप से विवादास्पद रहा है, जिसमें तकनीक असतत गैर-सामान्य वेरिएबल और अधिकतर बाइनरी एलील मार्करों पर की गई है। पीसीए में मानक त्रुटि के किसी भी उपाय की कमी भी अधिक सुसंगत उपयोग के लिए बाधा है। अगस्त 2022 में, आणविक जीवविज्ञानी [[ईरान जोड़ा गया]] ने 12 पीसीए अनुप्रयोगों का विश्लेषण करते हुए [[वैज्ञानिक रिपोर्ट]] में सैद्धांतिक पेपर प्रकाशित किया। उन्होंने यह निष्कर्ष निकाला कि इस विधि में परिवर्रतन करना सरल था, जो, उनके विचार में, 'त्रुटी, विरोधाभासी और व्यर्थ' परिणाम उत्पन्न करता था। विशेष रूप से, उन्होंने तर्क दिया, जनसंख्या आनुवंशिकी में प्राप्त परिणाम चेरी-पिकिंग और सर्कुलर तर्क द्वारा विशेषता थे।<ref>{{cite journal | first = Eran | last = Elhaik | author-link = Eran Elhaik | doi = 10.1038/s41598-022-14395-4 | title = Principal Component Analyses (PCA)‑based findings in population genetic studies are highly biased and must be reevaluated | journal = [[Scientific Reports]] | volume = 12 | at = 14683 | year = 2022| issue = 1 | pmid = 36038559 | pmc = 9424212 | s2cid = 251932226 | doi-access = free }}</ref> | |||
=== मार्केट अनुसंधान और दृष्टिकोण के सूचकांक === | |||
मार्केट अनुसंधान पीसीए का व्यापक उपयोगकर्ता रहा है। इसका उपयोग उत्पादों के लिए क्लाइंट की संतुष्टि या ग्राहक निष्ठा स्कोर विकसित करने के लिए किया जाता है, और क्लस्टरिंग के साथ, मार्केट खंडों को विकसित करने के लिए विज्ञापन अभियानों के साथ लक्षित किया जा सकता है, उसी प्रकार जैसे फैक्टोरियल इकोलॉजी समान विशेषताओं वाले भौगोलिक क्षेत्रों का पता लगा सकते हैं। <ref>{{Cite journal |last1=DeSarbo |first1=Wayne |last2=Hausmann |first2=Robert |last3=Kukitz |first3=Jeffrey |date=2007 |title=विपणन अनुसंधान के लिए प्रतिबंधित प्रमुख घटक विश्लेषण|url=https://www.researchgate.net/publication/247623679 |journal=Journal of Marketing in Management |volume=2 |pages=305–328 |via=Researchgate}}</ref> | |||
पीसीए शीघ्रता से बड़ी मात्रा में डेटा को लघु, सरलता से पचने वाले वेरिएबल में परिवर्तित कर देता है जिसे अधिक शीघ्रता से और सरलता से विश्लेषण किया जा सकता है। किसी भी उपभोक्ता प्रश्नावली में, उपभोक्ता के दृष्टिकोण को जानने के लिए डिज़ाइन किए गए प्रश्नों की श्रृंखला होती है, और प्रमुख अवयव इन दृष्टिकोणों के अंतर्निहित अव्यक्त वेरिएबल की खोज करते हैं। उदाहरण के लिए, 2013 में ऑक्सफोर्ड इंटरनेट सर्वेक्षण ने 2000 व्यकित से उनके दृष्टिकोण और विश्वासों के बारे में पूछा, और इन विश्लेषकों से चार प्रमुख अवयव आयाम निकाले, जिन्हें उन्होंने 'एस्केप', 'सोशल नेटवर्किंग', 'दक्षता' और 'समस्या उत्पन्न करने' के रूप में पहचाना जाता हैं। .<ref>{{Cite book |last1=Dutton |first1=William H |url=http://oxis.oii.ox.ac.uk/wp-content/uploads/2014/11/OxIS-2013.pdf |title=Cultures of the Internet: The Internet in Britain |last2=Blank |first2=Grant |publisher=Oxford Internet Institute |year=2013 |pages=6}}</ref> | |||
2008 में जो फ्लड (नीति विश्लेषक) के अन्य उदाहरण ने ऑस्ट्रेलिया में 2697 समूहों के राष्ट्रीय सर्वेक्षण में 28 दृष्टिकोण प्रश्नों से आवास के प्रति व्यवहारिक सूचकांक निकाला जाता हैं। पहला प्रमुख अवयव संपत्ति और घर के स्वामित्व के प्रति सामान्य दृष्टिकोण का प्रतिनिधित्व करता है। अनुक्रमणिका, या इसके सन्निहित अभिवृत्ति प्रश्न, कार्यकाल पसंद के सामान्य रेखीय मॉडल में डाले जा सकते हैं। यह आय, वैवाहिक स्थिति या सामान्य प्रकार के अतिरिक्त अब तक निजी किराये का सबसे शक्तिशाली निर्धारक विधि सूचकांक था।<ref>{{Cite journal |last=Flood |first=Joe |date=2008 |title=हाउसिंग करियर सर्वे के लिए बहुराष्ट्रीय विश्लेषण|url=https://www.academia.edu/33218811 |access-date=6 May 2022 |website=Paper to the European Network for Housing Research Conference, Dublin}}</ref> | |||
=== मात्रात्मक वित्त === | === मात्रात्मक वित्त === | ||
{{See also| | {{See also|पोर्टफोलियो अनुकूलन }} | ||
[[मात्रात्मक वित्त]] में, प्रमुख अवयव विश्लेषण सीधे ब्याज दर डेरिवेटिव पोर्टफोलियो के [[जोखिम प्रबंधन]] पर | [[मात्रात्मक वित्त]] में, प्रमुख अवयव विश्लेषण सीधे ब्याज दर डेरिवेटिव पोर्टफोलियो के [[जोखिम प्रबंधन|विपत्ति प्रबंधन]] पर प्रयुक्त किया जा सकता है।<ref name=PHIRS>[http://www.tradinginterestrates.com The Pricing and Hedging of Interest Rate Derivatives: A Practical Guide to Swaps], J H M Darbyshire, 2016, {{isbn|978-0995455511}}</ref> ट्रेडिंग मल्टीपल स्वैप (वित्त) जो सामान्यतः 30-500 अन्य मार्केट उद्धृत योग्य स्वैप उपकरणों का कार्य है, इसको सामान्यतः 3 या 4 प्रमुख अवयवों तक कम करने की मांग की जाती है, जो मैक्रो आधार पर ब्याज दरों के मार्ग का प्रतिनिधित्व करते हैं। फैक्टर लोडिंग (या मल्टीप्लायर) के रूप में प्रतिनिधित्व किए जाने वाले विपत्ति को परिवर्तित करना व्यक्तिगत 30–500 बकेट के विपत्ति को सामूहिक रूप से देखने के लिए उपलब्ध से विपरीत आकलन और समझ प्रदान करता है। | ||
पीसीए को [[ भंडार | | पीसीए को [[ भंडार |संग्रहण]] पर भी इसी तरह से प्रयुक्त किया गया है,<ref>Giorgia Pasini (2017); [https://ijpam.eu/contents/2017-115-1/12/12.pdf Principal Component Analysis for Stock Portfolio Management]. ''International Journal of Pure and Applied Mathematics''. Volume 115 No. 1 2017, 153–167</ref> [[जोखिम वापसी अनुपात|विपत्ति वापसी अनुपात]] और विपत्ति -प्रतिफल स्पेक्ट्रम दोनों के लिए हैं। आवेदन पोर्टफोलियो विपत्ति को कम करना है, जहां [[परिसंपत्ति आवंटन|संपत्ति आवंटन]] अंतर्निहित शेयरों के अतिरिक्त प्रमुख पोर्टफोलियो पर प्रयुक्त होता है।<ref>Libin Yang. [https://ir.canterbury.ac.nz/bitstream/handle/10092/10293/thesis.pdf?sequence=1 ''An Application of Principal Component Analysis to Stock Portfolio Management'']. Department of Economics and Finance, [[University of Canterbury]], January 2015.</ref> दूसरा, पोर्टफोलियो रिटर्न को बढ़ाने के लिए प्रमुख अवयवों का उपयोग [[स्टॉक चयन मानदंड]] के साथ ऊपर की क्षमता के साथ करना है। | ||
=== [[तंत्रिका विज्ञान]] === | === [[तंत्रिका विज्ञान]] === | ||
प्रमुख अवयव विश्लेषण के प्रकार का उपयोग तंत्रिका विज्ञान में उत्तेजना के विशिष्ट गुणों की पहचान करने के लिए किया जाता है जो [[न्यूरॉन]] की क्रिया क्षमता उत्पन्न करने की संभावना को बढ़ाता है।<ref>{{cite journal|last1=Chapin|first1=John|last2=Nicolelis |first2=Miguel|title=न्यूरोनल पहनावा गतिविधि के प्रधान घटक विश्लेषण से बहुआयामी सोमाटोसेंसरी अभ्यावेदन का पता चलता है|journal=Journal of Neuroscience Methods|date=1999|volume=94|issue=1|pages=121-140|doi=10.1016/S0165-0270(99)00130-2|pmid=10638820}}</ref><ref name="brenner00">Brenner, N., Bialek, W., & de Ruyter van Steveninck, R.R. (2000).</ref> इस तकनीक को [[स्पाइक-ट्रिगर सहप्रसरण]] | प्रमुख अवयव विश्लेषण के प्रकार का उपयोग तंत्रिका विज्ञान में उत्तेजना के विशिष्ट गुणों की पहचान करने के लिए किया जाता है जो [[न्यूरॉन]] की क्रिया क्षमता उत्पन्न करने की संभावना को बढ़ाता है।<ref>{{cite journal|last1=Chapin|first1=John|last2=Nicolelis |first2=Miguel|title=न्यूरोनल पहनावा गतिविधि के प्रधान घटक विश्लेषण से बहुआयामी सोमाटोसेंसरी अभ्यावेदन का पता चलता है|journal=Journal of Neuroscience Methods|date=1999|volume=94|issue=1|pages=121-140|doi=10.1016/S0165-0270(99)00130-2|pmid=10638820}}</ref><ref name="brenner00">Brenner, N., Bialek, W., & de Ruyter van Steveninck, R.R. (2000).</ref> इस तकनीक को [[स्पाइक-ट्रिगर सहप्रसरण]] स्पाइक-ट्रिगर सहप्रसरण विश्लेषण के रूप में जाना जाता है। विशिष्ट अनुप्रयोग में प्रयोगकर्ता सफेद ध्वनि प्रक्रिया को उत्तेजना के रूप में प्रस्तुत करता है (सामान्यतः यह तब परीक्षण विषय के लिए संवेदी इनपुट के रूप में, या [[विद्युत प्रवाह]] के रूप में सीधे न्यूरॉन में इंजेक्ट किया जाता है) और एक्शन पोटेंशिअल या स्पाइक्स की ट्रेन रिकॉर्ड करता है, जो परिणामस्वरूप न्यूरॉन उत्पादित होता है। । संभवतः, उत्तेजना की कुछ विशेषताएं न्यूरॉन को स्पाइक करने की अधिक संभावना बनाती हैं। इन सुविधाओं को निकालने के लिए, प्रयोगकर्ता स्पाइक-ट्रिगर किए गए आर्टिस्ट की भाग के सहप्रसरण आव्युह की गणना करता है, सभी उत्तेजनाओं का समुच्चय (सामान्यतः 100 एमएस के क्रम में परिमित समय खिड़की पर परिभाषित और विघटित) जो तुरंत स्पाइक से पहले होता है। स्पाइक-ट्रिगर सहप्रसरण आव्युह और पूर्व उत्तेजना पहनावा के सहप्रसरण आव्युह के मध्य अंतर के आइजन्वेक्टर और ईगेनवेल्यूज़ (सभी उत्तेजनाओं का समुच्चय , समान लंबाई समय विंडो पर परिभाषित) पुनः उत्तेजनाओं के सदिश स्थान में दिशाओं का संकेत देते हैं जिसके साथ स्पाइक-ट्रिगर पहनावा का विचरण पूर्व प्रोत्साहन पहनावा से सबसे भिन्न था। विशेष रूप से, सबसे बड़े धनात्मक आइजेनवैल्यू वाले आइजन्वेक्टर उन दिशाओं के अनुरूप होते हैं जिनके साथ स्पाइक-ट्रिगर पहनावा के विचरण ने पूर्व के विचरण की तुलना में सबसे बड़ा धनात्मक परिवर्तन दिखाया हैं। चूँकि यह वह दिशाएँ थीं जिनमें भिन्न -भिन्न उत्तेजनाओं ने स्पाइक का नेतृत्व किया, वह अधिकतर प्रासंगिक उत्तेजना सुविधाओं के पश्चात की मांग के अच्छे अनुमान हैं। | ||
तंत्रिका विज्ञान में, पीसीए का उपयोग न्यूरॉन की पहचान को उसकी क्रिया क्षमता के आकार से पहचानने के लिए भी किया जाता है। [[स्पाइक छँटाई]] महत्वपूर्ण प्रक्रिया है क्योंकि इलेक्ट्रोफिजियोलॉजी | तंत्रिका विज्ञान में, पीसीए का उपयोग न्यूरॉन की पहचान को उसकी क्रिया क्षमता के आकार से पहचानने के लिए भी किया जाता है। [[स्पाइक छँटाई|स्पाइक सॉर्टिंग]] महत्वपूर्ण प्रक्रिया है क्योंकि इलेक्ट्रोफिजियोलॉजी या बाह्यकोशिकीय रिकॉर्डिंग तकनीकें अधिकतर से अधिक न्यूरॉन से संकेत लेती हैं। स्पाइक इसमें, पहले पीसीए का उपयोग एक्शन पोटेंशियल वेवफॉर्म के स्थान की गतिशीलता को कम करने के लिए किया जाता है, और पुनः व्यक्तिगत न्यूरॉन्स के साथ विशिष्ट एक्शन पोटेंशिअल को जोड़ने के लिए क्लस्टर विश्लेषण किया जाता है। | ||
पीसीए आयाम कमी तकनीक के रूप में विशेष रूप से बड़े न्यूरोनल पहनावा की समन्वित गतिविधियों का पता लगाने के लिए अनुकूल है। यह मस्तिष्क में [[चरण संक्रमण|वेरिएबल | पीसीए आयाम कमी तकनीक के रूप में विशेष रूप से बड़े न्यूरोनल पहनावा की समन्वित गतिविधियों का पता लगाने के लिए अनुकूल है। यह मस्तिष्क में [[चरण संक्रमण|वेरिएबल संक्रमण]] के समय सामूहिक वेरिएबल , अर्थात [[ आदेश पैरामीटर |आदेश पैरामीटर]] निर्धारित करने में उपयोग किया गया है। <ref>{{cite journal|last1=Jirsa|first1=Victor|last2=Friedrich|first2=R|last3=Haken|first3=Herman|last4=Kelso|first4=Scott|title=मानव मस्तिष्क में चरण संक्रमण का एक सैद्धांतिक मॉडल|journal=Biological Cybernetics|date=1994|volume=71|issue=1|pages=27–35|doi=10.1007/bf00198909|pmid=8054384|s2cid=5155075}}</ref> | ||
== अन्य विधियों के साथ संबंध == | == अन्य विधियों के साथ संबंध == | ||
=== [[पत्राचार विश्लेषण]] === | === [[पत्राचार विश्लेषण|कॉरेस्पोंडेंस विश्लेषण]] === | ||
कॉरेस्पोंडेंस विश्लेषण (सीए) जीन-पॉल बेंजेक्री द्वारा विकसित किया गया था <ref>{{Cite book | |||
जीन-पॉल बेंजेक्री द्वारा विकसित किया गया था<ref>{{Cite book | |||
| author = Benzécri, J.-P. | | author = Benzécri, J.-P. | ||
| publisher=Dunod |location= Paris, France | | publisher=Dunod |location= Paris, France | ||
| year = 1973 | | year = 1973 | ||
| title = L'Analyse des Données. Volume II. L'Analyse des Correspondances | | title = L'Analyse des Données. Volume II. L'Analyse des Correspondances | ||
}}</ref> | }}</ref>और वैचारिक रूप से पीसीए के समान है, किन्तु डेटा को मापता है (जो गैर-ऋणात्मक होना चाहिए) जिससे पंक्तियों और स्तंभों को समान रूप से व्यवहार किया जा सके। यह परंपरागत रूप से आकस्मिक तालिकाओं पर प्रयुक्त होता है। सीए इस तालिका से जुड़े ची-स्क्वायर आँकड़ों को ऑर्थोगोनल कारकों में विघटित करता है।<ref>{{Cite book | ||
और वैचारिक रूप से पीसीए के समान है, | |||
| author = Greenacre, Michael | | author = Greenacre, Michael | ||
| publisher=Academic Press |location= London | | publisher=Academic Press |location= London | ||
| Line 471: | Line 474: | ||
| title = Theory and Applications of Correspondence Analysis | | title = Theory and Applications of Correspondence Analysis | ||
| isbn = 978-0-12-299050-2 | | isbn = 978-0-12-299050-2 | ||
}}</ref> | }}</ref> क्योंकि सीए वर्णनात्मक तकनीक है, इसे उन तालिकाओं पर प्रयुक्त किया जा सकता है जिनके लिए ची-स्क्वेर्ड आँकड़ा उपयुक्त है या नहीं हैं। सीए के अनेक प्रकार उपलब्ध हैं जिनमें डिट्रेंडेड कॉरेस्पोंडेंस विश्लेषण और कैनोनिकल कॉरेस्पोंडेंस विश्लेषण सम्मिलित हैं। विशेष विस्तार [[एकाधिक पत्राचार विश्लेषण|एकाधिक कॉरेस्पोंडेंस विश्लेषण]] है, जिसे श्रेणीबद्ध डेटा के लिए प्रमुख अवयव विश्लेषण के समकक्ष के रूप में देखा जा सकता है।<ref>{{Cite book | ||
क्योंकि | |||
सीए के अनेक | |||
|author1=Le Roux |author2=Brigitte and Henry Rouanet | publisher=Kluwer|location= Dordrecht | |author1=Le Roux |author2=Brigitte and Henry Rouanet | publisher=Kluwer|location= Dordrecht | ||
| year = 2004 | | year = 2004 | ||
| Line 482: | Line 483: | ||
=== कारक विश्लेषण === | === कारक विश्लेषण === | ||
[[File:PCA_versus_Factor_Analysis.jpg|thumb|ऊपर दी गई तस्वीर पीसीए और फैक्टर विश्लेषण | [[File:PCA_versus_Factor_Analysis.jpg|thumb|ऊपर दी गई तस्वीर पीसीए और फैक्टर विश्लेषण के मध्य अंतर का उदाहरण है। शीर्ष आरेख में कारक (जैसे, कैरियर पथ) तीन देखे गए वेरिएबल (जैसे, डॉक्टर, वकील, शिक्षक) का प्रतिनिधित्व करता है, जबकि नीचे के आरेख में देखे गए वेरिएबल (जैसे, पूर्व-विद्यालय शिक्षक, मध्य विद्यालय शिक्षक, उच्च विद्यालय शिक्षक) ब्याज के अवयव में कम हो जाते हैं (जैसे, शिक्षक)।]]प्रमुख कंपोनेंट विश्लेषण वेरिएबल्स बनाता है जो मूल वेरिएबल्स के रैखिक संयोजन हैं। नए वेरिएबल्स में यह संपत्ति है कि वेरिएबल्स सभी ऑर्थोगोनल हैं। पीसीए परिवर्तन क्लस्टरिंग से पहले प्री-प्रोसेसिंग चरण के रूप में सहायक हो सकता है। पीसीए भिन्नता-केंद्रित दृष्टिकोण है जो कुल परिवर्तनीय भिन्नता को पुन: उत्पन्न करने की मांग करता है, जिसमें अवयव वेरिएबल के सामान्य और अद्वितीय भिन्नता दोनों को दर्शाते हैं। पीसीए को सामान्यतः डेटा में कमी के प्रयोजनों के लिए पसंद किया जाता है (अर्थात, वेरिएबल स्थान को अधिकतम कारक स्थान में अनुवाद करना) हैं किन्तु तब नहीं जब लक्ष्य अव्यक्त निर्माण या कारकों का पता लगाना होता हैं। | ||
=== गैर- | कारक विश्लेषण प्रमुख अवयव विश्लेषण के समान है, उस कारक विश्लेषण में वेरिएबल के रैखिक संयोजन भी सम्मिलित हैं। पीसीए से भिन्न , कारक विश्लेषण सहसंबंध-केंद्रित दृष्टिकोण है जो वेरिएबल के मध्य अंतर-सहसंबंधों को पुन: उत्पन्न करने की मांग करता है, जिसमें कारक वेरिएबल के सामान्य भिन्नता अद्वितीय भिन्नता को छोड़कर इसका प्रतिनिधित्व करते हैं।<ref>Timothy A. Brown. [https://books.google.com/books?id=JDb3BQAAQBAJ&printsec=frontcover#v=onepage&q&f=false Confirmatory Factor Analysis for Applied Research Methodology in the social sciences]. Guilford Press, 2006</ref> सहसंबंध आव्युह के संदर्भ में, यह ऑफ-डायगोनल नियमों (अर्थात , साझा सह-विचरण ) को समझाने पर ध्यान केंद्रित करने के अनुरूप है, जबकि पीसीए विकर्ण पर बैठने वाली नियमों को समझाने पर ध्यान केंद्रित करता है। चूँकि , साइड परिणाम के रूप में, ऑन-डायगोनल नियमों को पुन: प्रस्तुत करने की प्रयास करते समय, पीसीए भी ऑफ-डायगोनल सहसंबंधों को अपेक्षाकृत अच्छी तरह से फिट करने की प्रयास करता है।<ref name="Jolliffe2002" />{{rp|158}} पीसीए और कारक विश्लेषण द्वारा दिए गए परिणाम ज्यादातर स्थितियों में बहुत समान होते हैं, किन्तु सदैव ऐसा नहीं होता है, और कुछ समस्याएं ऐसी होती हैं जहां परिणाम महत्वपूर्ण रूप से भिन्न होते हैं। कारक विश्लेषण का सामान्यतः उपयोग तब किया जाता है जब अनुसंधान उद्देश्य डेटा संरचना (अर्थात, अव्यक्त निर्माण या कारक) या [[कारण मॉडलिंग]] का पता लगा रहा हो। यदि कारक मॉडल त्रुटी विधियों से तैयार किया गया है या मान्यताओं को पूर्ण नहीं किया गया है, तब कारक विश्लेषण त्रुटी परिणाम देता हैं।<ref>{{cite journal |last1=Meglen|first1=R.R. |title=Examining Large Databases: A Chemometric Approach Using Principal Component Analysis|journal=Journal of Chemometrics |volume=5 |issue=3|pages=163–179 |date=1991 |doi=10.1002/cem.1180050305 |s2cid=120886184 }}</ref> | ||
=== {{math|<var>K</var>}}-कारण क्लस्टरिंग === | |||
यह प्रमाण किया गया है कि {{math|<var>k</var>}}-कारण क्लस्टरिंग का सरल समाधान {{math|<var>k</var>}}-कारण क्लस्टरिंग, क्लस्टर संकेतक द्वारा निर्दिष्ट, प्रमुख अवयवों द्वारा दिया जाता है, और मुख्य दिशाओं द्वारा विस्तार हुआ पीसीए सबस्पेस क्लस्टर सेंट्रोइड सबस्पेस के समान है।<ref>{{cite journal|author=H. Zha |author2=C. Ding |author3=M. Gu |author4=X. He |author5=H.D. Simon|title=K- साधन क्लस्टरिंग के लिए वर्णक्रमीय विश्राम|journal=Neural Information Processing Systems Vol.14 (NIPS 2001)|pages=1057–1064|date=Dec 2001|url=http://ranger.uta.edu/~chqding/papers/Zha-Kmeans.pdf}}</ref><ref>{{cite journal|author=Chris Ding |author2=Xiaofeng He|title=K- साधन प्रमुख घटक विश्लेषण के माध्यम से क्लस्टरिंग|journal=Proc. Of Int'l Conf. Machine Learning (ICML 2004)|pages=225–232|date=July 2004|url=http://ranger.uta.edu/~chqding/papers/KmeansPCA1.pdf}}</ref> चूँकि , वह पीसीए की उपयोगी छूट है यह {{math|<var>k</var>}}-कारण क्लस्टरिंग नया परिणाम नहीं था,<ref>{{cite journal | title = एकवचन मूल्य अपघटन के माध्यम से बड़े रेखांकन को क्लस्टर करना| journal = Machine Learning | year = 2004 | first = P. | last = Drineas |author2=A. Frieze |author3=R. Kannan |author4=S. Vempala |author5=V. Vinay | volume = 56 | issue = 1–3 | pages = 9–33| url = http://www.cc.gatech.edu/~vempala/papers/dfkvv.pdf | access-date = 2012-08-02 | doi=10.1023/b:mach.0000033113.59016.96| s2cid = 5892850 | doi-access = free }}</ref> और इस कथन के प्रति उदाहरणों को उजागर करना सीधा है कि क्लस्टर सेंट्रोइड उप-स्थान प्रमुख दिशाओं द्वारा विस्तार हुआ है।<ref>{{cite book | title = के-मीन्स क्लस्टरिंग और निम्न रैंक सन्निकटन के लिए आयाम में कमी (परिशिष्ट बी)| year = 2014 | first = M. | last = Cohen |author2=S. Elder |author3=C. Musco |author4=C. Musco |author5=M. Persu | arxiv = 1410.6801|bibcode=2014arXiv1410.6801C}}</ref> | |||
=== गैर-ऋणात्मक आव्युह गुणन === | |||
आंशिक अवशिष्ट भिन्नता तुलना, पीसीए और एनएमएफ पीसीए और एनएमएफ के लिए आंशिक अवशिष्ट भिन्नता (एफआरवी) भूखंड;<ref name="ren18"/> पीसीए के लिए, सैद्धांतिक मान अवशिष्ट आइजेनवैल्यू से योगदान है। इसकी तुलना में, पीसीए के लिए एफआरवी घटता और इसको यह तक पहुंचता है जहां कोई संकेत प्रभावी रूप से नहीं पकड़ा जाता है; जबकि एनएमएफ एफआरवी घटता निरंतर गिर रहा है, जो संकेत पकड़ने की उत्तम क्षमता का संकेत देता है। एनएमएफ के लिए एफआरवी घटता भी पीसीए की तुलना में उच्च स्तर पर परिवर्तित होता है, जो एनएमएफ की कम-ओवरफिटिंग संपत्ति को दर्शाता है। गैर-ऋणात्मक आव्युह कारककरण (एनएमएफ) आयाम कमी विधि है जहां आव्युह में केवल गैर-ऋणात्मक अवयवों का उपयोग किया जाता है, जो कि खगोल विज्ञान में आशाजनक विधि है,<ref name="blantonRoweis07">{{Cite journal|arxiv=astro-ph/0606170|last1= Blanton|first1= Michael R.|title= के-सुधार और पराबैंगनी, ऑप्टिकल और निकट अवरक्त में परिवर्तन|journal= The Astronomical Journal|volume= 133|issue= 2|pages= 734–754|last2= Roweis|first2= Sam |year= 2007|doi= 10.1086/510127|bibcode = 2007AJ....133..734B|s2cid= 18561804}}</ref><ref name="zhu16"/><ref name="ren18"/> इस अर्थ में कि ज्योतिषीय संकेत गैर-ऋणात्मक हैं। पीसीए अवयव दूसरे के लिए ओर्थोगोनल हैं, जबकि एनएमएफ अवयव सभी गैर-ऋणात्मक हैं और इसलिए गैर-ऑर्थोगोनल आधार बनाते हैं। | |||
पीसीए में, प्रत्येक अवयव के योगदान को उसके संबंधित | पीसीए में, प्रत्येक अवयव के योगदान को उसके संबंधित आइजेनवैल्यू के परिमाण के आधार पर रैंक किया जाता है, जो कि अनुभवजन्य डेटा का विश्लेषण करने में भिन्नात्मक अवशिष्ट विचरण (एफआरवी) के समान है।<ref name = "soummer12">{{Cite journal|arxiv=1207.4197|last1= Soummer|first1= Rémi |title= Detection and Characterization of Exoplanets and Disks Using Projections on Karhunen-Loève Eigenimages|journal= The Astrophysical Journal Letters |volume= 755|issue= 2|pages= L28|last2= Pueyo|first2= Laurent|last3= Larkin | first3 = James|year= 2012|doi= 10.1088/2041-8205/755/2/L28|bibcode = 2012ApJ...755L..28S |s2cid= 51088743}}</ref> एनएमएफ के लिए, इसके अवयवों को केवल अनुभवजन्य एफआरवी वक्रों के आधार पर रैंक किया गया है।<ref name = "ren18">{{Cite journal|arxiv=1712.10317|last1= Ren|first1= Bin |title= Non-negative Matrix Factorization: Robust Extraction of Extended Structures|journal= The Astrophysical Journal|volume= 852|issue= 2|pages= 104|last2= Pueyo|first2= Laurent|last3= Zhu | first3 = Guangtun B.|last4= Duchêne|first4= Gaspard |year= 2018|doi= 10.3847/1538-4357/aaa1f2|bibcode = 2018ApJ...852..104R |s2cid= 3966513}}</ref> अवशिष्ट भिन्नात्मक आइजेनवैल्यू भूखंड, अर्थात, <math> 1-\sum_{i=1}^k \lambda_i\Big/\sum_{j=1}^n \lambda_j</math> अवयव संख्या के फंक्सन के रूप में <math>k</math> कुल दिया <math>n</math> अवयव , पीसीए के लिए समतल पठार है, जहां अर्ध-स्थैतिक ध्वनि को दूर करने के लिए कोई डेटा कैप्वेरिएबल नहीं किया जाता है, पुनः ओवर-फिटिंग के संकेत के रूप में घटता शीघ्रता से गिर जाता है और यादृच्छिक ध्वनि को पकड़ लेता है।<ref name="soummer12"/> एनएमएफ के लिए एफआरवी घटता निरंतर घट रहा है<ref name="ren18"/> जब एनएमएफ अवयवों का निर्माण किया जाता है तब गैर-ऋणात्मक आव्युह गुणन या अनुक्रमिक एनएमएफ ,<ref name="zhu16">{{Cite arXiv|last=Zhu|first=Guangtun B.|date=2016-12-19|title=गैर-ऋणात्मक मैट्रिक्स गुणनखंडन (NMF) विषमलैंगिक अनिश्चितताओं और लापता डेटा के साथ|eprint=1612.06037|class=astro-ph.IM}}</ref> अर्ध-स्थैतिक ध्वनि के निरंतर कैप्वेरिएबल का संकेत; पुनः पीसीए की तुलना में उच्च स्तर पर अभिसरण करें,<ref name="ren18"/> एनएमएफ की कम ओवरफिटिंग संपत्ति का संकेत दिया है । | ||
=== सहसंबंधों की प्रतीकात्मकता === | === सहसंबंधों की प्रतीकात्मकता === | ||
मुख्य अवयवों | मुख्य अवयवों की व्याख्या करना अधिकतर मुश्किल होता है जब डेटा में विभिन्न उत्पत्ति के अनेक वेरिएबल सम्मिलित होते हैं, या जब कुछ वेरिएबल गुणात्मक होते हैं। यह पीसीए उपयोगकर्ता को अनेक वेरिएबलों के नाजुक उन्मूलन की ओर ले जाता है। यदि टिप्पणियों या वेरिएबल का अक्षों की दिशा पर अत्यधिक प्रभाव पड़ता है, तब उन्हें हटा दिया जाना चाहिए और पुनः पूरक अवयवों के रूप में प्रक्षेपित किया जाना चाहिए। इसके अतिरिक्त , फैक्टोरियल प्लेन के केंद्र के समीप बिंदुओं के मध्य की निकटता की व्याख्या करने से बचना आवश्यक है। | ||
[[File:AirMerIconographyCorrelation.jpg|thumb|सहसंबंधों की आइकनोग्राफी - समुद्री एरोसोल की भू-रसायन]]इसके विपरीत, सहसंबंधों की प्रतिमा, जो कुल्हाड़ियों की प्रणाली पर प्रक्षेपण नहीं है, में | [[File:AirMerIconographyCorrelation.jpg|thumb|सहसंबंधों की आइकनोग्राफी - समुद्री एरोसोल की भू-रसायन]]इसके विपरीत, सहसंबंधों की प्रतिमा, जो कुल्हाड़ियों की प्रणाली पर प्रक्षेपण नहीं है, में यह कमियां नहीं हैं। इसलिए हम सभी वेरिएबल रख सकते हैं। | ||
आरेख का सिद्धांत ठोस रेखा ( | आरेख का सिद्धांत ठोस रेखा (धनात्मक सहसंबंध) या बिंदीदार रेखा (ऋणात्मक सहसंबंध) द्वारा सहसंबंध आव्युह के उल्लेखनीय सहसंबंधों को रेखांकित करना है। | ||
शक्तिशाली सहसंबंध उल्लेखनीय नहीं है यदि यह प्रत्यक्ष नहीं है, किन्तु तीसरे वेरिएबल के प्रभाव के कारण होता है। इसके विपरीत, अशक्त सहसंबंध उल्लेखनीय हो सकते हैं। उदाहरण के लिए, यदि वेरिएबल Y अनेक स्वतंत्र वेरिएबलों पर निर्भर करता है, तब उनमें से प्रत्येक के साथ Y का सहसंबंध अशक्त और पुनः भी उल्लेखनीय है। | |||
== सामान्यीकरण == | == सामान्यीकरण == | ||
=== विरल पीसीए === | === विरल पीसीए === | ||
{{main| | {{main|विरल पीसीए }} | ||
पीसीए का विशेष | पीसीए का विशेष हानि यह है कि प्रमुख अवयव सामान्यतः सभी इनपुट वेरिएबलों के रैखिक संयोजन होते हैं। [[विरल पीसीए]] केवल कुछ इनपुट वेरिएबल वाले रैखिक संयोजनों को ढूंढकर इस हानि को दूर करता है। यह इनपुट वेरिएबल्स पर स्पार्सिटी बाधा जोड़कर डेटा की डायमेंशनलिटी को कम करने के लिए प्रमुख कंपोनेंट विश्लेषण (पीसीए) की क्लासिक पद्धति का विस्तार करता है। इसके साथ अनेक दृष्टिकोण प्रस्तावित किए गए हैं | ||
* प्रतिगमन फ्रेम,<ref> | |||
* | |||
{{cite journal | {{cite journal | ||
|author1=Hui Zou | |author1=Hui Zou | ||
| Line 526: | Line 522: | ||
|s2cid=5730904 | |s2cid=5730904 | ||
}}</ref> | }}</ref> | ||
* | * उत्तल छूट / अर्ध-परिमित प्रोग्रामिंग फ्रेम,<ref name="SDP"> | ||
{{cite journal | {{cite journal | ||
|author1=Alexandre d'Aspremont | |author1=Alexandre d'Aspremont | ||
| Line 541: | Line 537: | ||
|s2cid=5490061 | |s2cid=5490061 | ||
}}</ref> | }}</ref> | ||
* | * सामान्यीकृत शक्ति विधि फ्रेम<ref> | ||
{{cite journal | {{cite journal | ||
|author1=Michel Journee | |author1=Michel Journee | ||
| Line 556: | Line 552: | ||
|bibcode=2008arXiv0811.4724J | |bibcode=2008arXiv0811.4724J | ||
}}</ref> | }}</ref> | ||
* | * वैकल्पिक अधिकतमकरण फ्रेम<ref> | ||
{{cite arXiv | {{cite arXiv | ||
|author1=Peter Richtarik | |author1=Peter Richtarik | ||
| Line 566: | Line 562: | ||
|class=stat.ML | |class=stat.ML | ||
}}</ref> | }}</ref> | ||
* शाखा-और-बाध्य तकनीकों का उपयोग करके आगे-पीछे | * शाखा-और-बाध्य तकनीकों का उपयोग करके आगे-पीछे ग्रीडी खोज और स्पष्ट विधियाँ ,<ref> | ||
{{cite conference | {{cite conference | ||
|author1=Baback Moghaddam | |author1=Baback Moghaddam | ||
| Line 603: | Line 599: | ||
=== नॉनलाइनियर पीसीए === | === नॉनलाइनियर पीसीए === | ||
[[File:Elmap breastcancer wiki.png|thumb|300px| रैखिक पीसीए बनाम नॉनलाइनियर प्रमुख | [[File:Elmap breastcancer wiki.png|thumb|300px| रैखिक पीसीए बनाम नॉनलाइनियर प्रमुख मैनिफोल्ड्स<ref>[[Alexander Nikolaevich Gorban|A. N. Gorban]], A. Y. Zinovyev, [https://arxiv.org/abs/0809.0490 "Principal Graphs and Manifolds"], In: ''Handbook of Research on Machine Learning Applications and Trends: Algorithms, Methods and Techniques'', Olivas E.S. et al Eds. Information Science Reference, IGI Global: Hershey, PA, USA, 2009. 28–59.</ref> [[स्तन कैंसर]] [[माइक्रोएरे]] डेटा के वैज्ञानिक विज़ुअलाइज़ेशन के लिए: a) 3D पीसीए लीनियर मैनिफोल्ड में नोड्स और 2D प्रमुख सरफेस का कॉन्फिगरेशन। डेटासमुच्चय वृत्ताकार है और इसे 2D प्रमुख प्लेन पर पर्याप्त रूप से मानचित्र नहीं किया जा सकता है; बी) बिंदुओं के घनत्व के अनुमान के साथ आंतरिक 2डी गैर-रेखीय प्रमुख सतह निर्देशांक (ईएलमैप2D) में वितरण; c) b के समान), किन्तु रैखिक 2D पीसीए मैनिफोल्ड (पीसीए 2D) के लिए। बेसल स्तन कैंसर उपप्रकार को ईएलमैप2D के साथ अधिक पर्याप्त रूप से देखा जाता है और पीसीए 2D की तुलना में वितरण की कुछ विशेषताएं उत्तम रूप से हल हो जाती हैं। प्रमुख मैनिफोल्ड्स [[ लोचदार नक्शा |लोचदार मानचित्र]] एल्गोरिथम द्वारा निर्मित होते हैं। डेटा सार्वजनिक प्रतियोगिता के लिए उपलब्ध हैं।<ref>{{cite journal |last1=Wang |first1=Y. |last2=Klijn |first2=J. G. |last3=Zhang |first3=Y. |last4=Sieuwerts |first4=A. M. |last5=Look |first5=M. P. |last6=Yang |first6=F. |last7=Talantov |first7=D. |last8=Timmermans |first8=M. |last9=Meijer-van Gelder |first9=M. E. |last10=Yu |first10=J. |title=लिम्फ-नोड-नकारात्मक प्राथमिक स्तन कैंसर के दूर के मेटास्टेसिस की भविष्यवाणी करने के लिए जीन अभिव्यक्ति प्रोफाइल|journal=[[The Lancet]] |volume=365 |issue=9460 |pages=671–679 |year=2005 |doi=10.1016/S0140-6736(05)17947-1 |pmid=15721472 |s2cid=16358549 |display-authors=etal}} [https://www.ihes.fr/~zinovyev/princmanif2006/ Data online]</ref> सॉफ्टवेयर मुफ्त गैर-व्यावसायिक उपयोग के लिए उपलब्ध है।<ref>{{cite web |first=A. |last=Zinovyev |url=http://bioinfo-out.curie.fr/projects/vidaexpert/ |title=ViDaExpert – Multidimensional Data Visualization Tool |work=[[Curie Institute (Paris)|Institut Curie]] |location=Paris }} (free for non-commercial use)</ref>]]गैर-रैखिक आयामीता में कमी के अधिकांश आधुनिक विधियों पीसीए या K-साधनों में अपनी सैद्धांतिक और एल्गोरिथम जड़ें पाते हैं। पियर्सन का मूल विचार सीधी रेखा (या समतल) लेना था जो डेटा बिंदुओं के समुच्चय के लिए सबसे उपयुक्त होगा। ट्रेवर हैस्टी ने प्रमुख [[ वक्र |वक्र]] ्स को प्रस्तावित करके इस अवधारणा पर विस्तार किया<ref>{{cite journal|author1-last=Hastie|author1-first=T. |author1-link=Trevor Hastie|author2-last=Stuetzle|author2-first=W. |title=प्रधान वक्र|journal=[[Journal of the American Statistical Association]]|date=June 1989|volume=84|issue=406|pages=502–506|doi=10.1080/01621459.1989.10478797 |url=https://web.stanford.edu/~hastie/Papers/Principal_Curves.pdf}}</ref> पीसीए की ज्यामितीय व्याख्या के लिए प्राकृतिक विस्तार के रूप में, जो स्पष्ट रूप से [[प्रोजेक्शन (गणित)]] के पश्चात डेटा [[सन्निकटन]] के लिए अनेक गुना निर्माण करता है, जैसा कि अंजीर में दिखाया गया है। | ||
इलास्टिक | इलास्टिक मानचित्र एल्गोरिथम [[प्रमुख जियोडेसिक विश्लेषण]] विश्लेषण भी देखें।<ref>A.N. Gorban, B. Kegl, D.C. Wunsch, A. Zinovyev (Eds.), [https://www.researchgate.net/publication/271642170_Principal_Manifolds_for_Data_Visualisation_and_Dimension_Reduction_LNCSE_58 Principal Manifolds for Data Visualisation and Dimension Reduction], | ||
LNCSE 58, Springer, Berlin – Heidelberg – New York, 2007. {{isbn|978-3-540-73749-0}}</ref> अन्य लोकप्रिय सामान्यीकरण [[कर्नेल पीसीए]] है, जो | LNCSE 58, Springer, Berlin – Heidelberg – New York, 2007. {{isbn|978-3-540-73749-0}}</ref> अन्य लोकप्रिय सामान्यीकरण [[कर्नेल पीसीए]] है, जो धनात्मक निश्चित कर्नेल से जुड़े प्रजनन कर्नेल हिल्बर्ट स्पेस में किए गए पीसीए से मेल खाता है। | ||
[[बहुरेखीय उप-स्थान सीखना]] में,<ref name="Vasilescu2003">{{cite conference | [[बहुरेखीय उप-स्थान सीखना]] में,<ref name="Vasilescu2003">{{cite conference | ||
| Line 634: | Line 630: | ||
|date=June 2005 | |date=June 2005 | ||
|volume=1 | |volume=1 | ||
|pages=547–553}}</ref> पीसीए को [[ बहुरेखीय प्रमुख घटक विश्लेषण |बहुरेखीय प्रमुख अवयव विश्लेषण]] (एमपीसीए) के लिए सामान्यीकृत किया गया है जो सीधे टेंसर प्रस्तुतियों से सुविधाओं को निकालता है। Mपीसीए | |pages=547–553}}</ref> पीसीए को [[ बहुरेखीय प्रमुख घटक विश्लेषण |बहुरेखीय प्रमुख अवयव विश्लेषण]] (एमपीसीए) के लिए सामान्यीकृत किया गया है जो सीधे टेंसर प्रस्तुतियों से सुविधाओं को निकालता है। Mपीसीए को टेंसर के प्रत्येक मोड में पुनरावृत्त रूप से पीसीए करके हल किया जाता है। एमपीसीए को चेहरे की पहचान, चाल की पहचान आदि के लिए प्रयुक्त किया गया है। एमपीसीए को आगे असंबद्ध एमपीसीए, गैर-ऋणात्मक एमपीसीए और शक्तिशाली एमपीसीए तक बढ़ाया गया है। | ||
टकर अपघटन, [[PARAFAC]], बहु-कारक विश्लेषण, सह-जड़ता विश्लेषण, | टकर अपघटन, [[PARAFAC|पैराफैक]], बहु-कारक विश्लेषण, सह-जड़ता विश्लेषण, स्टेटिस और डिस्टैटिस जैसे मॉडलों के साथ n-वे प्रमुख अवयव विश्लेषण किया जा सकता है। | ||
=== | === शक्तिशाली पीसीए === | ||
जबकि पीसीए गणितीय रूप से | जबकि पीसीए गणितीय रूप से अधिकतम विधि (स्क्वायर्ड त्रुटि को कम करने के रूप में) पाता है, यह अभी भी डेटा में [[ग़ैर]] के प्रति संवेदनशील है जो बड़ी त्रुटियां उत्पन्न करता है, कुछ ऐसा जो विधि पहले स्थान से बचने की प्रयास करती है। इसलिए पीसीए की गणना करने से पहले आउटलेयर को हटाना आम बात है। चूँकि, कुछ संदर्भों में, आउटलेयर को पहचानना मुश्किल हो सकता है। उदाहरण के लिए, [[डेटा खनन]] एल्गोरिदम जैसे [[सहसंबंध क्लस्टरिंग]] में, क्लस्टर और आउटलेयर को पॉइंट्स का असाइनमेंट पहले से ज्ञात नहीं है। | ||
पीसीए का हाल ही में प्रस्तावित सामान्यीकरण<ref>{{Cite book | doi = 10.1007/978-3-540-69497-7_27 | title = पीसीए-आधारित सहसंबंध क्लस्टरिंग एल्गोरिदम की मजबूती बढ़ाने के लिए एक सामान्य ढांचा| isbn = 978-3-540-69476-2 | series = Lecture Notes in Computer Science | journal = Scientific and Statistical Database Management| year = 2008 | last1 = Kriegel | first1 = H. P. | last2 = Kröger | first2 = P. | last3 = Schubert | first3 = E. | last4 = Zimek | first4 = A. | volume = 5069 | pages = 418–435 | citeseerx = 10.1.1.144.4864 }}</ref> भारित पीसीए के आधार पर डेटा ऑब्जेक्ट्स को उनकी अनुमानित प्रासंगिकता के आधार पर भिन्न -भिन्न | पीसीए का हाल ही में प्रस्तावित सामान्यीकरण<ref>{{Cite book | doi = 10.1007/978-3-540-69497-7_27 | title = पीसीए-आधारित सहसंबंध क्लस्टरिंग एल्गोरिदम की मजबूती बढ़ाने के लिए एक सामान्य ढांचा| isbn = 978-3-540-69476-2 | series = Lecture Notes in Computer Science | journal = Scientific and Statistical Database Management| year = 2008 | last1 = Kriegel | first1 = H. P. | last2 = Kröger | first2 = P. | last3 = Schubert | first3 = E. | last4 = Zimek | first4 = A. | volume = 5069 | pages = 418–435 | citeseerx = 10.1.1.144.4864 }}</ref> भारित पीसीए के आधार पर डेटा ऑब्जेक्ट्स को उनकी अनुमानित प्रासंगिकता के आधार पर भिन्न -भिन्न भार देकर शक्तिशाली बढ़ जाती है। | ||
L1-नॉर्म फॉर्मूलेशन ([[L1-मानक प्रमुख घटक विश्लेषण|L1-मानक प्रमुख अवयव विश्लेषण]] | L1-पीसीए) के आधार पर पीसीए के बाहरी-प्रतिरोधी वेरिएंट भी प्रस्तावित किए गए हैं।<ref name="mark2014"/><ref name="mark2017" /> | |||
[[ मजबूत प्रमुख घटक विश्लेषण | | [[ मजबूत प्रमुख घटक विश्लेषण | शक्तिशाली प्रमुख अवयव विश्लेषण]] (आरपीसीए ) निम्न-श्रेणी और विरल मैट्रिसेस में अपघटन के माध्यम से पीसीए का संशोधन है जो व्यापक रूप से दूषित टिप्पणियों के संबंध में अच्छी तरह से काम करता है।<ref name=RPCA>{{cite journal|last=Emmanuel J. Candes|author2=Xiaodong Li |author3=Yi Ma |author4=John Wright |title=Robust Principal Component Analysis?|journal=Journal of the ACM|volume=58|issue=3|pages=11 |doi=10.1145/1970392.1970395|arxiv=0912.3599|year=2011 |s2cid=7128002 }}</ref><ref name=RPCA-BOUWMANS>{{cite journal|last=T. Bouwmans|author2= E. Zahzah|title=Robust PCA via Principal Component Pursuit: A Review for a Comparative Evaluation in Video Surveillance|journal=Computer Vision and Image Understanding|volume= 122|pages= 22–34|year=2014|doi= 10.1016/j.cviu.2013.11.009}}</ref><ref name=RPCA-BOUWMANS-COSREV>{{Cite journal|last=T. Bouwmans|author2= A. Sobral|author3= S. Javed|author4= S. Jung|author5= E. Zahzah|title=Decomposition into Low-rank plus Additive Matrices for Background/Foreground Separation: A Review for a Comparative Evaluation with a Large-Scale Dataset |journal= Computer Science Review|volume= 23|pages= 1–71|arxiv=1511.01245|year=2015|doi= 10.1016/j.cosrev.2016.11.001|bibcode= 2015arXiv151101245B|s2cid= 10420698}}</ref> | ||
| Line 650: | Line 646: | ||
=== [[स्वतंत्र घटक विश्लेषण|स्वतंत्र अवयव विश्लेषण]] === | === [[स्वतंत्र घटक विश्लेषण|स्वतंत्र अवयव विश्लेषण]] === | ||
स्वतंत्र अवयव विश्लेषण (आईसीए) को प्रमुख अवयव विश्लेषण के समान समस्याओं के लिए निर्देशित किया जाता है, | स्वतंत्र अवयव विश्लेषण (आईसीए) को प्रमुख अवयव विश्लेषण के समान समस्याओं के लिए निर्देशित किया जाता है, किन्तु क्रमिक अनुमानों के अतिरिक्त योगात्मक रूप से वियोज्य अवयवों को ढूंढता है। | ||
=== नेटवर्क अवयव विश्लेषण === | === नेटवर्क अवयव विश्लेषण === | ||
आव्युह <math>E</math> दिया, यह इसे दो मैट्रिसेस <math>E=AP | |||
</math>. पीसीए और आईसीए जैसी तकनीकों से महत्वपूर्ण अंतर यह है कि कुछ प्रविष्टियां <math>A</math> 0. यहाँ विवश हैं <math>P</math> नियामक परत कहा जाता है। जबकि | </math> में विघटित करने की प्रयास करता है . पीसीए और आईसीए जैसी तकनीकों से महत्वपूर्ण अंतर यह है कि कुछ प्रविष्टियां <math>A</math> 0. यहाँ विवश हैं और <math>P</math> नियामक परत कहा जाता है। जबकि सामान्यतः इस तरह के अपघटन के अनेक समाधान हो सकते हैं, वह सिद्ध करते हैं कि यदि निम्नलिखित नियम में पूर्ण होती हैं: | ||
# <math>A</math> पूर्ण स्तंभ रैंक है | # <math>A</math> पूर्ण स्तंभ रैंक है | ||
# | # <math>A</math> का प्रत्येक स्तंभ कम से कम होना चाहिए <math>L-1</math> शून्य जहाँ <math>L</math> के स्तंभों की संख्या <math>A</math> है (या वैकल्पिक रूप से पंक्तियों की संख्या <math>P</math>). इस मानदंड के लिए औचित्य यह है कि यदि नोड को विनियामक परत से हटा दिया जाता है, साथ ही इससे जुड़े सभी आउटपुट नोड्स के साथ, परिणाम अभी भी पूर्ण स्तंभ रैंक के साथ कनेक्टिविटी आव्युह द्वारा विशेषता होना चाहिए। | ||
# <math>P</math> पूरी पंक्ति रैंक होनी चाहिए। | # <math>P</math> पूरी पंक्ति रैंक होनी चाहिए। | ||
तब अपघटन अदिश द्वारा गुणन तक अद्वितीय होता है।<ref>{{Cite journal|title = Network component analysis: Reconstruction of regulatory signals in biological systems|last1=Liao|first1=J. C.|last2=Boscolo|first2=R.|last3=Yang|first3=Y.-L.|last4=Tran|first4=L. M.|last5=Sabatti|first5=C.|author5-link=Chiara Sabatti|last6=Roychowdhury|first6=V. P.|journal=Proceedings of the National Academy of Sciences|volume=100|issue=26|date=2003|pages=15522–15527|doi=10.1073/pnas.2136632100|pmid = 14673099|pmc = 307600|bibcode = 2003PNAS..10015522L|doi-access=free}}</ref> | तब अपघटन अदिश द्वारा गुणन तक अद्वितीय होता है।<ref>{{Cite journal|title = Network component analysis: Reconstruction of regulatory signals in biological systems|last1=Liao|first1=J. C.|last2=Boscolo|first2=R.|last3=Yang|first3=Y.-L.|last4=Tran|first4=L. M.|last5=Sabatti|first5=C.|author5-link=Chiara Sabatti|last6=Roychowdhury|first6=V. P.|journal=Proceedings of the National Academy of Sciences|volume=100|issue=26|date=2003|pages=15522–15527|doi=10.1073/pnas.2136632100|pmid = 14673099|pmc = 307600|bibcode = 2003PNAS..10015522L|doi-access=free}}</ref> | ||
=== प्रमुख अवयवों | === प्रमुख अवयवों का विभेदक विश्लेषण === | ||
प्रमुख | प्रमुख कंपोनेंट्स (डीएपीसी) का डिस्क्रिमिनेंट विश्लेषण बहुभिन्नरूपी विधि है जिसका उपयोग आनुवंशिक रूप से संबंधित व्यक्तियों के समूहों की पहचान करने और उनका वर्णन करने के लिए किया जाता है। आनुवंशिक भिन्नता को दो अवयवों में विभाजित किया गया है: समूहों के मध्य और समूहों के अंदर भिन्नता, और यह पूर्व को अधिकतम करती है। रेखीय विभेदक युग्मविकल्पी के रेखीय संयोजन होते हैं जो गुच्छों को सर्वोत्तम रूप से भिन्न करते हैं। एलील्स जो इस भेदभाव में सबसे अधिक योगदान करते हैं, इसलिए वह हैं जो समूहों में सबसे अधिक स्पष्ट रूप से भिन्न हैं। डीएपीसी द्वारा पहचाने गए समूहों में एलील्स का योगदान समूहों के मध्य आनुवंशिक विचलन को चलाने वाले जीनोम के क्षेत्रों की पहचान करने की अनुमति दे सकता है।<ref>{{Cite journal|title = Discriminant analysis of principal components: a new method for the analysis of genetically structured populations.|last1=Liao|first1=T.|last2=Jombart|first2=S.|last3=Devillard|first3=F.|last4=Balloux|journal=BMC Genetics|date=2010|volume=11|pages=11:94|doi=10.1186/1471-2156-11-94|pmid = 20950446|pmc=2973851}}</ref> डीएपीसी में, डेटा को पहले प्रमुख अवयव विश्लेषण (पीसीए ) का उपयोग करके रूपांतरित किया जाता है और इसके पश्चात इसमें विभेदक विश्लेषण (डीए) का उपयोग करके समूहों की पहचान की जाती है। | ||
एडिजनेट पैकेज का उपयोग करके R पर डीएपीसी से (अधिक सूचना: [https://adegenet.r-forge.r-project.org/ एडिजनेट वेब पर]) प्राप्त किया जा सकता है | |||
=== [[दिशात्मक घटक विश्लेषण|दिशात्मक अवयव विश्लेषण]] === | === [[दिशात्मक घटक विश्लेषण|दिशात्मक अवयव विश्लेषण]] === | ||
दिशात्मक अवयव विश्लेषण ( | दिशात्मक अवयव विश्लेषण (डीसीए ) बहुभिन्नरूपी डेटासमुच्चय के विश्लेषण के लिए वायुमंडलीय विज्ञान में उपयोग की जाने वाली विधि है।<ref name="jewson"/> पीसीए की तरह, यह आयाम में कमी, उत्तम विज़ुअलाइज़ेशन और बड़े डेटा-समुच्चय की उत्तम व्याख्या करने की अनुमति देता है। पीसीए की तरह, यह इनपुट डेटासमुच्चय से प्राप्त सहप्रसरण आव्युह पर आधारित है। पीसीए और डीसीए के मध्य अंतर यह है कि डीसीए को सदिश दिशा के इनपुट की अतिरिक्त आवश्यकता होती है, जिसे प्रभाव कहा जाता है। जबकि पीसीए स्पष्ट विचरण को अधिकतम करता है, डीसीए प्रभाव को देखते हुए संभाव्यता घनत्व को अधिकतम करता है। डीसीए के लिए प्रेरणा बहुभिन्नरूपी डेटासमुच्चय के अवयवों को खोजना है जो संभावित (संभाव्यता घनत्व का उपयोग करके मापा गया) और महत्वपूर्ण (प्रभाव का उपयोग करके मापा गया) दोनों हैं। डीसीए का उपयोग मौसम पूर्वानुमान समूहों में सबसे संभावित और सबसे गंभीर हीट-वेव पैटर्न खोजने के लिए किया गया है<ref name="scheretal"/> और जलवायु परिवर्तन के कारण वर्षा में सबसे संभावित और सबसे प्रभावशाली परिवर्तन होता हैं |<ref name="jewsonetal"/> | ||
पीसीए की तरह, यह इनपुट डेटासमुच्चय | |||
पीसीए और डीसीए के | |||
जबकि पीसीए स्पष्ट विचरण | |||
== सॉफ्टवेयर/स्रोत कोड == | == सॉफ्टवेयर/स्रोत कोड == | ||
* [[ALGLIB]] - C++ और C | * [[ALGLIB|अल्ग्लिब]] - C++ और C लाइब्रेरी जो पीसीए को प्रयुक्त करती है और पीसीए को लघु करती है | ||
* [[एनालिटिका (सॉफ्टवेयर)]] - बिल्ट-इन | * [[एनालिटिका (सॉफ्टवेयर)]] - बिल्ट-इन ईजेनडेकॉम्प फलन प्रमुख अवयवों की गणना करता है। | ||
* ईएलकेआई - प्रक्षेपण के लिए पीसीए सम्मिलित | * ईएलकेआई - प्रक्षेपण के लिए पीसीए सम्मिलित है, जिसमें पीसीए के शक्तिशाली वेरिएंट, साथ ही पीसीए-आधारित क्लस्टर विश्लेषण सम्मिलित हैं। | ||
* [[ग्रेटल]] - प्रमुख अवयव विश्लेषण या | * [[ग्रेटल]] - प्रमुख अवयव विश्लेषण या तब के माध्यम से किया जा सकता है <code>pca</code> कमांड या के माध्यम से <code>princomp()</code> फंक्सन हैं। | ||
* [[जूलिया भाषा]] - के साथ पीसीए का समर्थन करता है <code>pca</code> | * [[जूलिया भाषा]] - के साथ पीसीए का समर्थन करता है <code>pca</code> मल्टीवेरिएटस्टैट्स पैकेज में कार्य करता है | ||
* [[KNIME]] - विश्लेषण के लिए जावा आधारित नोडल व्यवस्था सॉफ्टवेयर, इसमें पीसीए, पीसीए कंप्यूट, पीसीए अप्लाई, पीसीए इनवर्स नामक नोड्स इसे | * [[KNIME|नाइमे]] - विश्लेषण के लिए जावा आधारित नोडल व्यवस्था सॉफ्टवेयर, इसमें पीसीए, पीसीए कंप्यूट, पीसीए अप्लाई, पीसीए इनवर्स नामक नोड्स इसे सरलता से बनाते हैं। | ||
* [[मेपल (सॉफ्टवेयर)]] - पीसीए कमांड का उपयोग डेटा के समुच्चय | * [[मेपल (सॉफ्टवेयर)]] - पीसीए कमांड का उपयोग डेटा के समुच्चय पर प्रमुख अवयव विश्लेषण करने के लिए किया जाता है। | ||
* मेथेमेटिका - सहप्रसरण और सहसंबंध विधियों दोनों का उपयोग करके प्रमुख कंपोनेंट्स कमांड के साथ प्रमुख | * मेथेमेटिका - सहप्रसरण और सहसंबंध विधियों दोनों का उपयोग करके प्रमुख कंपोनेंट्स कमांड के साथ प्रमुख कंपोनेंट विश्लेषण प्रयुक्त करता है। | ||
* | * गणितपीएचपी - पीसीए के समर्थन के साथ [[पीएचपी]] गणित पुस्तकालय हैं। | ||
* | * मैटलैब - एसवीडी फलन मूल प्रणाली का हिस्सा है। सांख्यिकी टूलबॉक्स में, कार्य <code>princomp</code> और <code>pca</code> (R2012b) प्रमुख अवयव देते हैं, जबकि कार्य <code>pcares</code> निम्न-रैंक पीसीए सन्निकटन के लिए अवशिष्ट और पुनर्निर्मित आव्युह देता है। | ||
* [[Matplotlib]] – | * [[Matplotlib|माटप्लोटलिब]] – पायथन (प्रोग्रामिंग लैंग्वेज) लाइब्रेरी में .एमएलएबी मॉड्यूल में पीसीए पैकेज है। | ||
* [[ mypack | | * [[ mypack | माइपैक]] - [[सी ++|C++]] में प्रमुख अवयव विश्लेषण का कार्यान्वयन प्रदान करता है। | ||
* [https://github.com/mikerabat/mrmath | * [https://github.com/mikerabat/mrmath मर्मठ] - [[डेल्फी (सॉफ्टवेयर)]] और [[ फ़्री पास्कल |फ़्री समीप्कल]] के लिए उच्च प्रदर्शन गणित पुस्तकालय पीसीए शक्तिशाली वेरिएंट सहित कर सकता है। | ||
* [[एनएजी न्यूमेरिकल लाइब्रेरी]] - प्रधान अवयव विश्लेषण के माध्यम से कार्यान्वित किया जाता है <code>g03aa</code> | * [[एनएजी न्यूमेरिकल लाइब्रेरी]] - प्रधान अवयव विश्लेषण के माध्यम से कार्यान्वित किया जाता है जो <code>g03aa</code> दिनचर्या (पुस्तकालय के दोनों फोरट्रान संस्करणों में उपलब्ध) हैं। | ||
* [[NMath]] - . | * [[NMath|एनमैथ]] - .नेट फ्रेमवर्क के लिए पीसीए युक्त प्रोप्राइटरी संख्यात्मक पुस्तकालय हैं। | ||
* जीएनयू ऑक्टेव - मुफ्त सॉफ्टवेयर कम्प्यूटेशनल वातावरण ज्यादातर | * जीएनयू ऑक्टेव - मुफ्त सॉफ्टवेयर कम्प्यूटेशनल वातावरण ज्यादातर मैटलैब, फलन के साथ संगत है <code>princomp</code> प्रमुख अवयव देता है। | ||
* ओपनसीवी | * ओपनसीवी | ||
* | * ओरेकल डाटाबेस 12c - के माध्यम से प्रयुक्त किया गया <code>DBMS_DATA_MINING.SVDS_SCORING_MODE</code> सेटिंग मान निर्दिष्ट करके <code>SVDS_SCORING_पीसीए</code> हैं | | ||
* ऑरेंज (सॉफ्टवेयर) - अपने दृश्य प्रोग्रामिंग वातावरण में पीसीए को एकीकृत करता है। पीसीए स्क्री प्लॉट (व्याख्या विचरण | *ऑरेंज (सॉफ्टवेयर) - अपने दृश्य प्रोग्रामिंग वातावरण में पीसीए को एकीकृत करता है। पीसीए स्क्री प्लॉट (व्याख्या विचरण की डिग्री) प्रदर्शित करता है जहां उपयोगकर्ता प्रमुख अवयवों की संख्या को अंतःक्रियात्मक रूप से चुन सकता है। | ||
* [[उत्पत्ति (डेटा विश्लेषण सॉफ्टवेयर)]] - इसके प्रो संस्करण में पीसीए सम्मिलित | * [[उत्पत्ति (डेटा विश्लेषण सॉफ्टवेयर)]] - इसके प्रो संस्करण में पीसीए सम्मिलित है। | ||
* [[क्लोकोर]] - पीसीए का उपयोग करके त्वरित प्रतिक्रिया के साथ बहुभिन्नरूपी डेटा का विश्लेषण करने के लिए वाणिज्यिक | * [[क्लोकोर]] - पीसीए का उपयोग करके त्वरित प्रतिक्रिया के साथ बहुभिन्नरूपी डेटा का विश्लेषण करने के लिए वाणिज्यिक सॉफ्टवेयर हैं। | ||
* आर (प्रोग्रामिंग भाषा) - [[मुफ्त सॉफ्टवेयर]] सांख्यिकीय पैकेज, कार्य <code>princomp</code> और <code>prcomp</code> प्रमुख अवयव विश्लेषण के लिए | * आर (प्रोग्रामिंग भाषा) - [[मुफ्त सॉफ्टवेयर]] सांख्यिकीय पैकेज, कार्य <code>princomp</code> और <code>prcomp</code> प्रमुख अवयव विश्लेषण के लिए उपयोग किया जा सकता है; <code>prcomp</code> एकवचन मान अपघटन का उपयोग करता है जो सामान्यतः उत्तम संख्यात्मक स्पष्टता देता है। आर में पीसीए को प्रयुक्त करने वाले कुछ पैकेजों में सम्मिलित हैं, किन्तु यह इन तक सीमित नहीं हैं: <code>ade4</code>, <code>vegan</code>, <code>ExPosition</code>, <code>dimRed</code>, और <code>FactoMineR</code>. हैं | | ||
* एसएएस (सॉफ्टवेयर) - | * एसएएस (सॉफ्टवेयर) - प्रोप्राइटरी सॉफ्टवेयर; उदाहरण के लिए देखें <ref>{{cite web|title=प्रमुख घटक विश्लेषण|url=https://stats.idre.ucla.edu/sas/output/principal-components-analysis/|website=Institute for Digital Research and Education|publisher=UCLA|access-date=29 May 2018}}</ref> | ||
* [[scikit-सीखें]] - मशीन लर्निंग के लिए पायथन लाइब्रेरी जिसमें अपघटन मॉड्यूल में पीसीए, प्रोबेबिलिस्टिक पीसीए, कर्नेल पीसीए, स्पार्स पीसीए और अन्य तकनीकें सम्मिलित | * [[scikit-सीखें|स्किकिट-सीखें]] - मशीन लर्निंग के लिए पायथन लाइब्रेरी जिसमें अपघटन मॉड्यूल में पीसीए, प्रोबेबिलिस्टिक पीसीए, कर्नेल पीसीए, स्पार्स पीसीए और अन्य तकनीकें सम्मिलित हैं। | ||
* [[साइलैब]] - फ्री और ओपन-सोर्स, क्रॉस-प्लेटफॉर्म न्यूमेरिकल कम्प्यूटेशनल पैकेज, फंक्शन <code>princomp</code> प्रमुख अवयव विश्लेषण, | * [[साइलैब]] - फ्री और ओपन-सोर्स, क्रॉस-प्लेटफॉर्म न्यूमेरिकल कम्प्यूटेशनल पैकेज, फंक्शन <code>princomp</code> प्रमुख अवयव विश्लेषण, फलन की गणना करता है <code>pca</code> मानकीकृत वेरिएबलों के साथ प्रमुख अवयव विश्लेषण की गणना करता है। | ||
* [[एसपीएसएस]] - पीसीए, कारक विश्लेषण और संबंधित क्लस्टर विश्लेषण के लिए सामाजिक वैज्ञानिकों द्वारा सामान्यतः | * [[एसपीएसएस]] - पीसीए, कारक विश्लेषण और संबंधित क्लस्टर विश्लेषण के लिए सामाजिक वैज्ञानिकों द्वारा सामान्यतः उपयोग किया जाने वाला प्रोप्राइटरी सॉफ्टवेयर हैं। | ||
* वीका (मशीन लर्निंग) - मशीन लर्निंग के लिए जावा लाइब्रेरी जिसमें प्रमुख अवयवों | * वीका (मशीन लर्निंग) - मशीन लर्निंग के लिए जावा लाइब्रेरी जिसमें प्रमुख अवयवों की गणना के लिए मॉड्यूल होते हैं। | ||
== यह भी देखें == | == यह भी देखें == | ||
{{Div col|colwidth=22em}} | {{Div col|colwidth=22em}} | ||
* | * कॉरेस्पोंडेंस विश्लेषण (आकस्मिक तालिकाओं के लिए) | ||
* एकाधिक | * एकाधिक कॉरेस्पोंडेंस विश्लेषण (गुणात्मक वेरिएबल के लिए) | ||
* [[मिश्रित डेटा का कारक विश्लेषण]] (मात्रात्मक और गुणात्मक | * [[मिश्रित डेटा का कारक विश्लेषण]] (मात्रात्मक और गुणात्मक वेरिएबल के लिए) | ||
* कैननिकल सहसंबंध | * कैननिकल सहसंबंध | ||
* [[ | * [[सी.यू.आर आव्युह सन्निकटन]] (निम्न-रैंक एस वी डी सन्निकटन की जगह ले सकता है) | ||
* | * डिट्रेंडेड कॉरेस्पोंडेंस विश्लेषण | ||
* दिशात्मक | * दिशात्मक अवयव विश्लेषण | ||
* [[गतिशील मोड अपघटन]] | * [[गतिशील मोड अपघटन]] | ||
* [[ | * [[आइजेनफेस]] | ||
* अपेक्षा-अधिकतमकरण एल्गोरिथम | * अपेक्षा-अधिकतमकरण एल्गोरिथम | ||
* v: अन्वेषी कारक विश्लेषण (विकिविश्वविद्यालय) | * v: अन्वेषी कारक विश्लेषण (विकिविश्वविद्यालय) | ||
* [[क्रमगुणित कोड]] | * [[क्रमगुणित कोड]] | ||
* [[कार्यात्मक प्रमुख | * [[कार्यात्मक प्रमुख अवयव विश्लेषण]] | ||
* [[ज्यामितीय डेटा विश्लेषण]] | * [[ज्यामितीय डेटा विश्लेषण]] | ||
* स्वतंत्र घटक विश्लेषण | * स्वतंत्र घटक विश्लेषण | ||
* कर्नेल पीसीए | * कर्नेल पीसीए | ||
* | * L1-मानक प्रमुख घटक विश्लेषण | ||
* [[निम्न-श्रेणी सन्निकटन]] | * [[निम्न-श्रेणी सन्निकटन]] | ||
* [[ | * [[आव्युह अपघटन]] | ||
* गैर- | * गैर-ऋणात्मक आव्युह गुणनखंड | ||
* गैर रेखीय आयामीता में कमी | * गैर रेखीय आयामीता में कमी | ||
* ओजा | * ओजा रुल | ||
* [[बिंदु वितरण मॉडल]] (पीसीए मॉर्फोमेट्री और कंप्यूटर विजन पर | * [[बिंदु वितरण मॉडल]] (पीसीए मॉर्फोमेट्री और कंप्यूटर विजन पर प्रयुक्त होता है) | ||
* बी: सांख्यिकी/बहुभिन्नरूपी डेटा विश्लेषण/प्रमुख | * बी: सांख्यिकी/बहुभिन्नरूपी डेटा विश्लेषण/प्रमुख अवयव विश्लेषण (विकिपुस्तक) | ||
* प्रधान | * प्रधान अवयव प्रतिगमन | ||
* [[एकवचन स्पेक्ट्रम विश्लेषण]] | * [[एकवचन स्पेक्ट्रम विश्लेषण]] | ||
* विलक्षण मान अपघटन | * विलक्षण मान अपघटन | ||
* विरल पीसीए | * विरल पीसीए | ||
* रूपांतरण कोडिंग | * रूपांतरण कोडिंग | ||
* | * भारित न्यूनतम वर्ग | ||
{{div col end}} | {{div col end}} | ||
| Line 827: | Line 815: | ||
{{Statistics|analysis|state=collapsed}} | {{Statistics|analysis|state=collapsed}} | ||
{{Authority control}} | {{Authority control}} | ||
[[Category: | [[Category:Articles with hatnote templates targeting a nonexistent page]] | ||
[[Category:CS1 English-language sources (en)]] | |||
[[Category:CS1 maint]] | |||
[[Category:Collapse templates]] | |||
[[Category:Commons category link is the pagename]] | |||
[[Category:Created On 28/02/2023]] | [[Category:Created On 28/02/2023]] | ||
[[Category:Lua-based templates]] | |||
[[Category:Machine Translated Page]] | |||
[[Category:Multi-column templates]] | |||
[[Category:Navigational boxes| ]] | |||
[[Category:Navigational boxes without horizontal lists]] | |||
[[Category:Pages using div col with small parameter]] | |||
[[Category:Pages with empty portal template]] | |||
[[Category:Pages with script errors]] | |||
[[Category:Portal-inline template with redlinked portals]] | |||
[[Category:Short description with empty Wikidata description]] | |||
[[Category:Sidebars with styles needing conversion]] | |||
[[Category:Template documentation pages|Documentation/doc]] | |||
[[Category:Templates Vigyan Ready]] | |||
[[Category:Templates generating microformats]] | |||
[[Category:Templates that add a tracking category]] | |||
[[Category:Templates that are not mobile friendly]] | |||
[[Category:Templates that generate short descriptions]] | |||
[[Category:Templates using TemplateData]] | |||
[[Category:Templates using under-protected Lua modules]] | |||
[[Category:Wikipedia fully protected templates|Div col]] | |||
[[Category:Wikipedia metatemplates]] | |||
[[Category:आयाम में कमी]] | |||
[[Category:मैट्रिक्स अपघटन]] | |||
Latest revision as of 11:05, 14 August 2023
प्रमुख कंपोनेंट विश्लेषण (पीसीए) प्रति अवलोकन उच्च संख्या में आयाम/फीवेरिएबल वाले बड़े डेटासमुच्चय का विश्लेषण करने, अधिकतम मात्रा में सूचना को संरक्षित करते हुए डेटा की व्याख्या को बढ़ाते हैं, और बहुआयामी डेटा के विज़ुअलाइज़ेशन को सक्षम करने के लिए लोकप्रिय तकनीक है औपचारिक रूप से, पीसीए डेटासमुच्चय के आयाम को कम करने के लिए सांख्यिकीय तकनीक है। यह डेटा को रैखिक रूप से नई समन्वय प्रणाली में परिवर्तित करके पूर्ण किया जाता है, जहां (अधिकांश) डेटा में भिन्नता को प्रारंभिक डेटा की तुलना में कम आयामों के साथ वर्णित किया जा सकता है। डेटा को दो आयामों में प्लॉट करने के लिए और निकट से संबंधित डेटा बिंदुओं के समूहों की दृष्टि से पहचान करने के लिए अनेक अध्ययन पहले दो प्रमुख अवयवों का उपयोग करते हैं। यह प्रमुख कंपोनेंट विश्लेषण के अनेक क्षेत्रों में जैसे जनसंख्या आनुवंशिकी, माइक्रोबायोम अध्ययन और वायुमंडलीय विज्ञान में अनुप्रयोग होते हैं। [1]

वास्तविक समन्वय स्थान में बिंदुओं के संग्रह के प्रमुख अवयव यूनिट सदिश अनुक्रम हैं, जहां -वें सदिश रेखा की दिशा है जो पहले सदिश के लिए ऑर्थोगोनल होते हुए डेटा को सबसे अच्छी तरह से फिट करता है। यहां, सर्वोत्तम-फिटिंग लाइन को उस रेखा के रूप में परिभाषित किया गया है जो बिंदु से रेखा तक औसत वर्ग लंबवत दूरी दूरी को कम करता है। यह दिशाएँ अलौकिक आधार का गठन करती हैं जिसमें डेटा के विभिन्न व्यक्तिगत आयाम रैखिक सहसंबंध होते हैं। प्रमुख अवयव विश्लेषण प्रमुख अवयवों की गणना करने और डेटा के आधार पर परिवर्तन करने के लिए उनका उपयोग करने की प्रक्रिया है, कभी-कभी केवल पहले कुछ प्रमुख अवयवों का उपयोग करके और शेष को अनदेखा करते हुए इसका उपयोग किया जाता है।
डेटा विश्लेषण में, वेरिएबल समुच्चय का पहला प्रमुख अवयव , जिसे संयुक्त रूप से सामान्यतः वितरित माना जाता है, मूल वेरिएबल के रैखिक संयोजन के रूप में गठित व्युत्पन्न वेरिएबल है जो सबसे अधिक विचरण की व्याख्या करता है। दूसरा प्रमुख अवयव पहले अवयव के प्रभाव को हटा दिए जाने के पश्चात जो बचा है उसमें सबसे अधिक भिन्नता की व्याख्या करता है, और हम पुनरावृत्तियाँ इसके माध्यम से आगे बढ़ सकते हैं जब तक कि सभी विचरण की व्याख्या नहीं की जाती हैं। पीसीए का सबसे अधिक उपयोग तब किया जाता है जब अनेक वेरिएबल दूसरे के साथ अत्यधिक सहसंबद्ध होते हैं और उनकी संख्या को स्वतंत्र समुच्चय में कम करना वांछनीय होता है।
पीसीए का उपयोग खोजपूर्ण डेटा विश्लेषण और प्रेडिक्टिव मॉडलिंग करने के लिए किया जाता है। यह सामान्यतः प्रत्येक डेटा बिंदु को केवल पहले कुछ प्रमुख अवयवों पर प्रक्षेपित करके आयामीता में कमी के लिए उपयोग किया जाता है जिससे जितना संभव हो उतना डेटा भिन्नता को संरक्षित करते हुए निम्न-आयामी डेटा प्राप्त किया जा सके। पहले प्रमुख अवयव को समान रूप से दिशा के रूप में परिभाषित किया जा सकता है जो अनुमानित डेटा के विचरण को अधिकतम करता है। यह वें>-वें प्रमुख अवयव को पहले प्रमुख अवयव के लिए दिशा ऑर्थोगोनल के रूप में लिया जा सकता है जो अनुमानित डेटा के विचरण को अधिकतम करते हैं।
किसी भी उद्देश्य के लिए, यह दिखाया जा सकता है कि प्रमुख अवयव डेटा के सहप्रसरण आव्युह के आइजन्वेक्टर हैं। इस प्रकार, प्रमुख अवयवों की गणना अधिकतर डेटा सहप्रसरण आव्युह के आइजेनडी कम्पोज़िशन या डेटा आव्युह के एकवचन मान अपघटन द्वारा की जाती है। पीसीए सत्य आइजन्वेक्टर -आधारित बहुभिन्नरूपी विश्लेषणों में सबसे सरल है और कारक विश्लेषण से निकटता से संबंधित है। कारक विश्लेषण में सामान्यतः अंतर्निहित संरचना के बारे में अधिक डोमेन विशिष्ट मान्यताओं को सम्मिलित किया जाता है और थोड़ा भिन्न आव्युह के आइजन्वेक्टर को हल करता है। पीसीए भी विहित सहसंबंध विहित सहसंबंध विश्लेषण (सीसीए) से संबंधित है। यह सीसीए समन्वय प्रणालियों को परिभाषित करता है जो दो डेटासमुच्चय के मध्य क्रॉस सहप्रसरण का उत्तम वर्णन करता है जबकि पीसीए नए ऑर्थोगोनल समन्वय प्रणाली को परिभाषित करता है जो एकल डेटासमुच्चय में भिन्नता का उत्तम वर्णन करता है। [2][3][4][5] शक्तिशाली आंकड़े और एलपी स्पेस हैं | मानक पीसीए के L1-मानक-आधारित संस्करण भी प्रस्तावित किए गए हैं। [6][7][8][5]
इतिहास
पीसीए का आविष्कार 1901 में कार्ल पियर्सन ने किया था। [9] यांत्रिकी में प्रमुख अक्ष प्रमेय के अनुरूप; इसे पश्चात में स्वतंत्र रूप से विकसित किया गया और 1930 के दशक में हेरोल्ड होटलिंग द्वारा इसका नाम दिया गया है।[10] अनुप्रयोग के क्षेत्र के आधार पर, इसे असतत करहुनेन-लोएव प्रमेय भी नाम दिया गया है। संकेत आगे बढ़ाना में करहुनेन-लोएव रूपांतरण (केएलटी), बहुभिन्नरूपी गुणवत्ता नियंत्रण में हेरोल्ड होटलिंग रूपांतरण, मैकेनिकल इंजीनियरिंग में उचित ऑर्थोगोनल अपघटन (पीओडी), एकवचन मान X का अपघटन (एसवीडी) (20वीं शताब्दी की अंतिम तिमाही में आविष्कार किया गया [11]), रेखीय बीजगणित में XTX का आइजेनडीकम्पोज़िशन (ईवीडी) हैं।, कारक विश्लेषण (पीसीए और कारक विश्लेषण के मध्य अंतर की चर्चा के लिए जोलिफ़ प्रमुख कंपोनेंट विश्लेषण का अध्याय 7 देखें),[12] एकार्ट-यंग प्रमेय (हरमन, 1960), या अनुभवजन्य ऑर्थोगोनल फ़ंक्शंस (ईओएफ) मौसम विज्ञान में (लॉरेंज, 1956), अनुभवजन्य ईजेनफंक्शन अपघटन (सिरोविच, 1987), क्वासिहार्मोनिक मोड (ब्रूक्स एट अल।, 1988), वर्णक्रमीय प्रमेय ध्वनि और कंपन में वर्णक्रमीय अपघटन, और संरचनात्मक गतिशीलता में अनुभवजन्य मोडल विश्लेषण में देखे गये थे।
अंतर्ज्ञान
पीसीए को डेटा के लिए p-आयामी दीर्घवृत्त के रूप में फिट करने के बारे में सोचा जा सकता है, जहां दीर्घवृत्त का प्रत्येक अक्ष प्रमुख अवयव का प्रतिनिधित्व करता है। यदि दीर्घवृत्ताभ का कुछ अक्ष लघु है, तब उस अक्ष के साथ विचरण भी लघु होता है।
दीर्घवृत्ताभ के अक्षों को खोजने के लिए, हमें सबसे पहले डेटासमुच्चय में प्रत्येक वेरिएबल के मानों को 0 पर केंद्रित करना चाहिए और उनमें से प्रत्येक मान से वेरिएबल के देखे गए मानों का माध्य घटाना चाहिए। प्रत्येक वेरिएबल के लिए मूल देखे गए मानों के अतिरिक्त इन परिवर्तित मानों का उपयोग किया जाता है। पुनः , हम डेटा के सहप्रसरण आव्युह की गणना करते हैं और इस सहसंयोजक आव्युह के आइजेनवैल्यू और संबंधित आइजन्वेक्टर की गणना करते हैं। पुनः हमें प्रत्येक ऑर्थोगोनल आइजन्वेक्टर को यूनिट सदिश में परिवर्तन के लिए सामान्यीकरण (सांख्यिकी) करना होगा। पुनः यह हो जाने के पश्चात , प्रत्येक परस्पर-ऑर्थोगोनल यूनिट आइजन्वेक्टर को डेटा में फिट किए गए दीर्घवृत्त के अक्ष के रूप में व्याख्या किया जा सकता है। इसके आधार का यह चुनाव सहप्रसरण आव्युह को विकर्ण रूप में परिवर्तित कर देगा, जिसमें विकर्ण अवयव प्रत्येक अक्ष के विचरण का प्रतिनिधित्व करते हैं। प्रत्येक आइजन्वेक्टर द्वारा दर्शाए गए प्रसरण के अनुपात की गणना उस आइजन्वेक्टर के अनुरूप आइजेनवैल्यू को सभी आइजेनवैल्यू के योग से विभाजित करके की जा सकती है।
पीसीए के निष्कर्षों को समझाने के लिए बिप्लॉटस और स्क्री प्लॉट (व्याख्या विचरण की डिग्री) का उपयोग किया जाता है।
विवरण
पीसीए को ऑर्थोगोनल परिवर्तन रैखिक परिवर्तन के रूप में परिभाषित किया गया है जो डेटा को नई समन्वय प्रणाली में परिवर्तित कर देता है जैसे कि डेटा के कुछ स्केलर प्रक्षेपण द्वारा सबसे बड़ा भिन्नता को पहले समन्वय (जिसे पहला मुख्य अवयव कहा जाता है) पर आती है, तथा दूसरा सबसे बड़ा भिन्नता होती है जैसे कि दूसरा समन्वय, इत्यादि हैं। [12]
इस पर विचार करें डेटा आव्युह (गणित), X, स्तंभ-वार शून्य अनुभवजन्य माध्य के साथ (प्रत्येक स्तंभ का प्रतिरूप माध्य शून्य पर स्थानांतरित कर दिया गया है), जहां प्रत्येक n पंक्तियाँ प्रयोग की भिन्न पुनरावृत्ति का प्रतिनिधित्व करती हैं, और प्रत्येक p स्तम्भ विशेष प्रकार की सुविधा देता है ( किसी विशेष सेंसर का परिणाम कहते हैं)।
गणितीय रूप से, परिवर्तन को आकार के समुच्चय द्वारा परिभाषित किया जाता है | इसमें वजन या गुणांक के p-आयामी सदिश हैं वह प्रत्येक पंक्ति सदिश को मानचित्र करता है तथा प्रमुख अवयव स्कोर के नए सदिश के लिए X का , द्वारा दिए गए होते हैं |
इस प्रकार से कि व्यक्तिगत वेरिएबल डेटा समुच्चय पर विचार किए गए t के क्रमिक रूप से X से अधिकतम संभव विचरण प्राप्त होता है, प्रत्येक गुणांक सदिश w के साथ इकाई सदिश होने के लिए विवश होता है (जहाँ सामान्यतः कठोरता से कम होने के लिए चुना जाता है और आयामीता को कम करने के लिए) चुना जाता है।
प्रथम अवयव
प्रसरण को अधिकतम करने के लिए, पहला भार सदिश w(1) इस प्रकार संतुष्ट करना पड़ता है
समान रूप से इसे आव्युह रूप में लिखने पर प्राप्त होता है
यह समकक्ष भी संतुष्ट करता है जहाँ w(1)के पश्चात से इकाई सदिश के रूप में परिभाषित किया गया है,
अधिकतम की जाने वाली मात्रा को रेले भागफल के रूप में पहचाना जा सकता है। धनात्मक अर्ध निश्चित आव्युह जैसे XTX के लिए मानक परिणाम यह है कि भागफल का अधिकतम संभव मान आव्युह का सबसे बड़ा आइजेनवैल्यू है, जो तब होता है जब w संबंधित आइजन्वेक्टर होता है।
w(1) के साथ मिला, डेटा सदिश x(i) का पहला प्रमुख अवयव रूपांतरित निर्देशांक में पुनः स्कोर t1(i) = x(i) ⋅ w(1) के रूप में दिया जा सकता है , या मूल वेरिएबल में संबंधित सदिश के रूप में, x(i) ⋅w(1)} w(1) होता है |
आगे के अवयव
k-वें अवयव को 'X' से पहले k − 1 प्रमुख अवयवों को घटाकर प्राप्त किया जा सकता है |
और पुनः वेट सदिश का पता लगाना जो इस नए डेटा आव्युह से अधिकतम भिन्नता निकालता है
यह पता चला है कि यह XTX के शेष आइजन्वेक्टर देता है, कोष्ठकों में मात्रा के लिए उनके संबंधित आइजेनवैल्यू द्वारा दिए गए अधिकतम मानों के साथ हैं। इस प्रकार वजन सदिश XTX के आइजन्वेक्टर हैं।
डेटा सदिश x(i) का k-वाँ प्रमुख अवयव रूपांतरित निर्देशांक में, इसलिए स्कोर tk(i) = x(i) ⋅ w(k) के रूप में दिया जा सकता है या मूल वेरिएबल के स्थान में संबंधित सदिश के रूप में, x(i) ⋅ w(k)} w(k), जहां w(k) XTX का kवां आइजन्वेक्टर है।
इसलिए X का पूर्ण प्रमुख अवयव अपघटन इस प्रकार दिया जा सकता है
जहां W वजन का p-द्वारा-p आव्युह है, जिसके स्तम्भ XTX के आइजन्वेक्टर हैं। डब्ल्यू के स्थानान्तरण को कभी-कभी श्वेत परिवर्तन कहा जाता है। इसका w के स्तम्भ को इसी आइजेनवैल्यू के वर्गमूल से गुणा किया जाता है, अर्थात, आइजन्वेक्टर को वेरिएंस द्वारा बढ़ाया जाता है, जिन्हें पीसीए या फैक्टर विश्लेषण में 'लोडिंग' कहा जाता है।
सहप्रसरण
XTX को ही डेटासमुच्चय XT के अनुभवजन्य प्रतिरूप सहप्रसरण आव्युह के समानुपाती के रूप में पहचाना जा सकता है |.[12]: 30–31
डेटासमुच्चय पर दो भिन्न -भिन्न प्रमुख अवयवों के मध्य प्रतिरूप सहप्रसरण Q द्वारा दिया गया है:
जहाँ w(k) का आइजेनवैल्यू गुण है लाइन 2 से लाइन 3 पर जाने के लिए उपयोग किया गया है। चूँकि आइजन्वेक्टर w(j) और w(k) सममित आव्युह के आइजेनवैल्यू के अनुरूप ओर्थोगोनल हैं (यदि आइजेनवैल्यू भिन्न हैं), या ऑर्थोगोनलाइज़ किया जा सकता है (यदि सदिश समान दोहराया मान साझा करते हैं)। इसलिए अंतिम पंक्ति में गुणनफल शून्य है | यह डेटासमुच्चय पर विभिन्न प्रमुख अवयवों के मध्य कोई प्रतिरूप सहप्रसरण नहीं है।
प्रमुख अवयवों के परिवर्तन को चिह्नित करने का और विधि है, इसलिए समन्वय के परिवर्तन के रूप में जो अनुभवजन्य प्रतिरूप सहप्रसरण आव्युह को विकर्ण करता है।
आव्युह रूप में, मूल वेरिएबल के लिए अनुभवजन्य सहप्रसरण आव्युह लिखा जा सकता है
प्रमुख अवयवों के मध्य अनुभवजन्य सहप्रसरण आव्युह बन जाता है
जहां Λ आइजेनवैल्यू λ(k) का XTX का विकर्ण आव्युह है। λ(k) प्रत्येक अवयव k, अर्थात λ(k) से जुड़े डेटासमुच्चय पर λ(k) = Σi tk2(i) = Σi (x(i) ⋅ w(k))2 वर्गों के योग के समान है
आयाम में कमी
परिवर्तन T = X W डेटा सदिश x(i) को मानचित्र करता है p वेरिएबल्स के मूल स्थान से p वेरिएबल्स के नए स्थान पर जो डेटासमुच्चय पर असंबद्ध हैं। चूँकि , सभी प्रमुख अवयवों को रखने की जरूरत नहीं है। केवल पहले L आइजेन सदिश का उपयोग करके उत्पादित केवल पहले एल प्रमुख अवयवों को बनाए रखना, लघु परिवर्तन देता है
जहां आव्युह TL अब n पंक्तियाँ हैं किन्तु केवल L स्तम्भ हैं। दूसरे शब्दों में, पीसीए रेखीय परिवर्तन सीखता है जहां p × L के स्तम्भ आव्यूह L सुविधाओं (प्रतिनिधित्व t के अवयव ) के लिए ऑर्थोगोनल आधार बनाते हैं जो अलंकृत हैं। [13] यह निर्माण द्वारा, केवल L स्तम्भ के साथ सभी रूपांतरित डेटा मैट्रिसेस में, यह स्कोर आव्युह मूल डेटा में भिन्नता को अधिकतम करता है जिसे संरक्षित किया गया है, जबकि कुल स्क्वायर्ड पुनर्निर्माण या त्रुटि को कम करता है।

इस तरह की आयामी कमी उच्च-आयामी डेटासमुच्चय को देखने और संसाधित करने के लिए बहुत ही उपयोगी निर्णय हो सकता है, जबकि अभी भी डेटासमुच्चय में जितना संभव हो उतना भिन्नता बनाए रखना हैं। उदाहरण के लिए, L = 2 का चयन करना और केवल पहले दो प्रमुख अवयवों को रखना उच्च-आयामी डेटासमुच्चय के माध्यम से द्वि-आयामी प्लेन को ढूंढता है जिसमें डेटा का सबसे अधिक विस्तार हुआ है, इसलिए यदि डेटा में क्लस्टर विश्लेषण सम्मिलित है तब यह भी सबसे अधिक फैले हुए हो सकते हैं, और इसलिए द्वि-आयामी आरेख में प्लॉट किए जाने के लिए सबसे अधिक दिखाई देता है; जबकि यदि डेटा के माध्यम से दो दिशाओं (या दो मूल वेरिएबल ) को यादृच्छिक रूप से चुना जाता है, तब क्लस्टर दूसरे से बहुत कम फैल सकते हैं, और वास्तव में दूसरे को अधिक सीमा तक ओवरले करने की संभावना हो सकती है, जिससे वह अप्रभेद्य हो सकते हैं।
इसी तरह, प्रतिगमन विश्लेषण में, व्याख्यात्मक वेरिएबल की संख्या जितनी अधिक होगी, मॉडल को ओवरफिट करने की संभावना उतनी ही अधिक होगी, जो अन्य डेटासमुच्चय के सामान्यीकरण में विफल होने वाले निष्कर्ष का उत्पादन करेगा। दृष्टिकोण, विशेष रूप से जब विभिन्न संभावित व्याख्यात्मक वेरिएबल के मध्य शक्तिशाली सहसंबंध होते हैं, तब उन्हें कुछ प्रमुख अवयवों में कम करना और पुनः उनके विरुद्ध प्रतिगमन चलाना है, इस विधि को प्रमुख अवयव प्रतिगमन कहा जाता है।
जब किसी डेटासमुच्चय में वेरिएबल्स ध्वनि वाले हों, तब डायमेंशनलिटी रिडक्शन भी उपयुक्त हो सकता है। यदि डेटासमुच्चय के प्रत्येक स्तम्भ में स्वतंत्र समान रूप से वितरित गॉसियन ध्वनि होता है, तब 't' के स्तम्भ में समान रूप से वितरित गॉसियन ध्वनि भी सम्मिलित होगा (ऐसा वितरण आव्युह 'w' के प्रभाव के अनुसार अपरिवर्तनीय है, जिसे इस रूप में सोचा जा सकता है समन्वय अक्षों का उच्च-आयामी घुमाव) हैं। चूँकि, समान ध्वनि भिन्नता की तुलना में पहले कुछ मुख्य अवयवों में केंद्रित कुल भिन्नता के साथ, ध्वनि का आनुपातिक प्रभाव कम होता है | पहले कुछ अवयव उच्च सिग्नल-टू-ध्वनि अनुपात प्राप्त करते हैं। इस प्रकार पीसीए के समीप पहले कुछ प्रमुख अवयवों में सिग्नल को अधिक केंद्रित करने का प्रभाव हो सकता है, जो उपयोगी रूप से आयामीता में कमी द्वारा अधिकृत कर लिया जा सकता है; जबकि पश्चात के प्रमुख अवयवों पर ध्वनि प्रभावी हो सकता है, और इसलिए बिना किसी बड़े हानि से निपटारा किया जा सकता है। यदि डेटासमुच्चय अधिक बड़ा नहीं है, तब बूटस्ट्रैपिंग (सांख्यिकी) या पैरामेट्रिक बूटस्ट्रैप का उपयोग करके प्रमुख अवयवों के महत्व का परीक्षण किया जा सकता है, यह निर्धारित करने में सहायता के रूप में कि कितने प्रमुख अवयवों को बनाए रखना है। [14]
एकवचन मान अपघटन
प्रमुख अवयवों के परिवर्तन को अन्य आव्युह गुणनखंडन के साथ भी जोड़ा जा सकता है, यह X का एकवचन मान अपघटन (एसवीडी) हैं,
यहाँ Σ n-दर-p धनात्मक संख्याओं का विकर्ण आव्युह σ(k) है, यह X के विलक्षण मान U कहलाते हैं | यह n-दर-n आव्युह है, जिसके स्तम्भ लंबाई n के ऑर्थोगोनल यूनिट सदिश हैं जिन्हें X का बायां एकवचन W सदिश कहा जाता है | और p-दर-p आव्युह है जिसके स्तम्भ लंबाई p केऑर्थोगोनल यूनिट सदिश हैं और X के सही एकवचन सदिश कहलाते हैं।
इस गुणनखंड के संदर्भ में, आव्युह XTX लिखा जा सकता है
जहाँ X के एकवचन मानों के साथ वर्ग विकर्ण आव्युह है और अतिरिक्त शून्य काट दिया गया है जो . को संतुष्ट करता है | यह XTX के आइजन्वेक्टर गुणनखंडन के साथ तुलना स्थापित करता है कि X का सही एकवचन सदिश W, XTX के आइजन्वेक्टर के समतुल्य है, जबकि एकवचन मान σ(k) का आइजेनवैल्यू λ(k) के XTX का वर्गमूल के समान हैं ।
एकवचन मान अपघटन का उपयोग करके स्कोर आव्युह T लिखा जा सकता है
इसलिए T का प्रत्येक स्तंभ X के बाएँ एकवचन सदिशों में से द्वारा संबंधित एकवचन मान से गुणा किया जाता है। यह रूप T का ध्रुवीय अपघटन भी है।
आव्युह XTX बनाने के बिना X के एसवीडी की गणना करने के लिए कुशल एल्गोरिदम उपस्तिथ हैं, इसलिए एसवीडी की गणना करना अब डेटा आव्युह से प्रमुख अवयव विश्लेषण की गणना करने का मानक विधि है, जब तक कि केवल कुछ ही अवयवों की आवश्यकता नहीं होती है।
आइजन-अपघटन के साथ, लघु n × L स्कोर आव्युह TL केवल पहले L सबसे बड़े एकवचन मान और उनके एकवचन सदिशों पर विचार करके प्राप्त किया जा सकता है:
इस तरह से काटे गए एकवचन मान अपघटन का उपयोग करके आव्युह M या T का कटाव लघु सा आव्युह उत्पन्न करता है जो मूल आव्युह के रैंक (रैखिक बीजगणित) L का निकटतम संभव आव्युह है, और इन दोनों के मध्य के अंतर के अर्थ में दो में सबसे लघु संभव फ्रोबेनियस मानदंड है, इसका परिणाम जिसे एकार्ट-यंग प्रमेय [1936] के रूप में जाना जाता है।
आगे के विचार
एकवचन मान (Σ में) आव्युह XTX के आइजेनवैल्यू के वर्गमूल हैं। प्रत्येक आइजेनवैल्यू विचरण के भाग के लिए आनुपातिक है (उनके बहुआयामी माध्य से बिंदुओं की स्क्वायर्ड दूरी के योग का अधिक सही रूप से) जो प्रत्येक आइजन्वेक्टर के साथ जुड़ा हुआ है। सभी आइजेनवैल्यू का योग उनके बहुआयामी माध्य से बिंदुओं की वर्ग दूरी के योग के समान है। पीसीए अनिवार्य रूप से प्रमुख अवयवों के साथ संरेखित करने के लिए उनके माध्य के चारों ओर बिंदुओं के समुच्चय को घुमाता है। यह पहले कुछ आयामों में जितना संभव हो उतना ही भिन्नता (ऑर्थोगोनल परिवर्तन का उपयोग करके) की ओर ले जाता है। इसलिए, शेष आयामों में मान लघु होते हैं और सूचना के न्यूनतम हानि के साथ गिराए जा सकते हैं (सिद्धांत अवयव विश्लेषण या पीसीए और सूचना सिद्धांत देखें)। पीसीए का उपयोग अधिकतर इस तरह से आयाम में कमी के लिए किया जाता है। पीसीए को उप-स्थान रखने के लिए अधिकतम ऑर्थोगोनल परिवर्तन होने का गौरव प्राप्त है जिसमें सबसे बड़ा भिन्नता है (जैसा कि ऊपर परिभाषित किया गया है)। चूँकि, यह लाभ अधिक कम्प्यूटेशनल आवश्यकताओं की मान पर आता है, उदाहरण के लिए, और जब प्रयुक्त हो, तब असतत कोसाइन परिवर्तन के लिए, और विशेष रूप से डीसीटी-II के लिए होता हैं जिसे केवल डीसीटी के रूप में जाना जाता है। पीसीए की तुलना में अरैखिक आयामीता में कमी तकनीक की कम्प्यूटेशनल रूप से अधिक मांग होती है।
पीसीए वेरिएबल के स्केलिंग के प्रति संवेदनशील है। यदि हमारे समीप केवल दो वेरिएबल हैं और उनके समीप इसका ही प्रतिरूप भिन्न है और वह पूरी तरह से सहसंबंधित हैं, तब पीसीए 45 डिग्री से घूर्णन करेगा और मुख्य अवयव के संबंध में दो वेरिएबल के लिए वजन (वे घूर्णन के कोसाइन हैं) समान होता हैं। किन्तु यदि हम पहले वेरिएबल के सभी मानों को 100 से गुणा करते हैं, तब पहला प्रमुख अवयव लगभग उसी वेरिएबल के समान होगा, और दूसरे वेरिएबल से लघु से योगदान के साथ होता है , जबकि दूसरा अवयव दूसरे मूल वेरिएबल के साथ लगभग संरेखित होता हैं। इसका कारण यह है कि जब भी भिन्न -भिन्न वेरिएबल की भिन्न -भिन्न इकाइयाँ (जैसे तापमान और द्रव्यमान) होती हैं, तब पीसीए विश्लेषण का कुछ सीमा तक इच्छानुसार विधि होती है। (उदाहरण के लिए सेल्सियस के अतिरिक्त फ़ारेनहाइट का उपयोग करने पर भिन्न -भिन्न परिणाम प्राप्त होंगे।) पियर्सन का मूल पेपर ऑन लाइन्स एंड प्लेन ऑफ़ क्लोजेस्ट फ़िट टू सिस्टम्स ऑफ़ पॉइंट्स इन स्पेस - इन स्पेस का तात्पर्य भौतिक यूक्लिडियन स्पेस से है जहाँ ऐसी चिंताएँ उत्पन्न नहीं होती हैं। पीसीए को कम इच्छानुसार बनाने की विधि यह है कि डेटा को मानकीकृत करके, इकाई विचरण के रूप में स्केल किए गए वेरिएबल का उपयोग किया जाए और इसलिए पीसीए के आधार के रूप में ऑटोकोवरिएंस आव्युह के अतिरिक्त ऑटोकोरिलेशन आव्युह का उपयोग किया जाता हैं। चूँकि, यह सिग्नल स्पेस के सभी आयामों में इकाई विचरण के उतार-चढ़ाव को संकुचित (या विस्तारित) करता है।
मौलिक पीसीए प्रदर्शन करने के लिए मीन घटाव (में मीन सेंटरिंग) आवश्यक है जिससे यह सुनिश्चित किया जा सके कि पहला प्रमुख अवयव अधिकतम विचरण की दिशा का वर्णन करता है। यदि औसत घटाव नहीं किया जाता है, तब पहला प्रमुख अवयव इसके अतिरिक्त डेटा के माध्य से अधिक या कम हो सकता है। आधार खोजने के लिए शून्य का कारण आवश्यक है जो डेटा के अनुमान के न्यूनतम औसत वर्ग त्रुटि को कम करता है।[15]
सहसंबंध आव्युह पर प्रमुख अवयव विश्लेषण करते समय माध्य-केंद्रित अनावश्यक है, क्योंकि सहसंबंधों की गणना के पश्चात डेटा पहले से ही केंद्रित है। सहसंबंध दो मानक स्कोर (जेड-स्कोर) या सांख्यिकीय क्षणों के क्रॉस-उत्पाद से प्राप्त होते हैं (इसलिए नाम: पियर्सन प्रोडक्ट-मोमेंट सहसंबंध)। इसके अतिरिक्त क्रॉम्रे एंड फोस्टर-जॉनसन (1998) का लेख मॉडरेट रिग्रेशन में मीन-सेंटरिंग: मच अडो अबाउट नथिंग पर देख सकते हैं। चूँकि सहप्रसरण आव्युह या सहसंबंध आव्युह से संबंध (मानक स्कोर या गणना हैं | यह (Z- या मानक-स्कोर) 'X' के सहसंबंध आव्युह पर आधारित पीसीए 'Z' के सहप्रसरण आव्युह पर आधारित पीसीए के लिए समानता (गणित) है। तथा 'X' का मानकीकृत संस्करण होता है।
पीसीए पैटर्न पहचान में लोकप्रिय प्राथमिक तकनीक है। चूँकि, यह वर्ग पृथक्करण के लिए अनुकूलित नहीं है। [16] चूँकि, इसका उपयोग मुख्य अवयव स्थान में प्रत्येक वर्ग के लिए द्रव्यमान के केंद्र की गणना करके और दो या दो से अधिक वर्गों के द्रव्यमान के केंद्र के मध्य यूक्लिडियन दूरी की रिपोर्ट करके दो या दो से अधिक वर्गों के मध्य की दूरी को मापने के लिए किया गया है। [17] यह रैखिक विभेदक विश्लेषण विकल्प है जो वर्ग पृथक्करण के लिए अनुकूलित है।
प्रतीकों और संक्षेपों की तालिका
| प्रतीक | अर्थ | डाइमेंशन्स | इंडिसेस |
|---|---|---|---|
| डेटा आव्युह, जिसमें प्रति पंक्ति सदिश सभी डेटा सदिश का समुच्चय सम्मिलित है, | | ||
| डेटा समुच्चय में पंक्ति सदिश की संख्या | अदिश | ||
| प्रत्येक पंक्ति सदिश में अवयवों की संख्या (डाइमेंशन्स) | अदिश | ||
| आयामी रूप से कम किए गए उपस्थान में आयामों की संख्या, | अदिश | ||
| अनुभवजन्य साधनों का सदिश , डेटा आव्युह के प्रत्येक स्तम्भ j के लिए माध्य है | |||
| अनुभवजन्य मानक विचलन के सदिश , डेटा आव्युह के प्रत्येक स्तम्भ j के लिए मानक विचलन | |||
| सभी 1 का सदिश | |||
| विचलन डेटा आव्युह के प्रत्येक स्तम्भ j के माध्य से | | ||
| z-स्कोर, डेटा आव्युह की प्रत्येक पंक्ति m के लिए माध्य और मानक विचलन का उपयोग करके गणना की जाती है | | ||
| सहप्रसरण आव्यूह | | ||
| सहसम्बंध आव्यूह | | ||
| आव्युह जिसमें प्रति स्तम्भ आइजनवेक्टर C के सभी आइजनवेक्टर का समुच्चय सम्मिलित है, | | ||
| विकर्ण आव्युह सभी के समुच्चय से मिलकर आइजेनवैल्यू को इसके साथ C का मुख्य विकर्ण, और अन्य सभी अवयवों के लिए 0 (ध्यान दें 𝛬 ऊपर प्रयुक्त) | | ||
| आधार सदिश का आव्युह , प्रति स्तम्भ सदिश है , जहां प्रत्येक आधार सदिश C के आईजनवेक्टर में से है, और जहां W में सदिश V में उन व्यकित का उप-समुच्चय है | | ||
| आव्युह जिसमें एन पंक्ति सदिश सम्मिलित हैं, जहां प्रत्येक सदिश आव्युह X से संबंधित डेटा सदिश का आव्युह W के स्तम्भ में निहित आधार सदिश पर प्रक्षेपण है। | |
पीसीए के गुण और सीमाएं
गुण
पीसीए के कुछ गुणों में सम्मिलित हैं [12]
- गुण 1: किसी भी पूर्णांक q के लिए, 1 ≤ q ≤ p, ओर्थोगोनल रैखिक परिवर्तन पर विचार करें
- जहाँ q-अवयव सदिश है और (q × p) आव्युह है, और मान लीजिये कि के लिए विचरण -सहप्रसरण आव्युह होते है पुनः का संकेत, निरूपित , लेने से अधिकतम होता है , जहाँ के पहले q स्तम्भ सम्मिलित होते हैं | यह का स्थानान्तरण होता है |
- गुण 2: ओर्थोनॉर्मल परिवर्तन पर पुनः से विचार करें
- इसके साथ और पहले की तरह परिभाषित करता है। तब लेने से कम किया जाता है जहाँ के अंतिम q स्तम्भ से मिलकर बनता है |
इस संपत्ति का सांख्यिकीय निहितार्थ यह है कि पिछले कुछ पीसी महत्वपूर्ण पीसी को हटाने के पश्चात केवल असंरचित बचे हुए भाग नहीं हैं। क्योंकि इन अंतिम पीसी में जितना संभव हो उतना लघु प्रसरण होता है, इसलिए यह अपने आप में उपयोगी होते हैं। वह x के अवयवों के मध्य बिना सोचे-समझे निकट-स्थिर रैखिक संबंधों का पता लगाने में सहायता कर सकते हैं , और वह प्रतिगमन विश्लेषण में भी उपयोगी हो सकते हैं, वेरिएबल x के उपसमुच्चय का चयन करने में , और आउटलाइयर डिटेक्शन में उपयोग किया जाता है |
- गुण 3: (Σ का वर्णक्रमीय अपघटन )
इसके उपयोग को देखने से पहले, हम पहले विकर्ण अवयवों को देखते हैं,
पुनः संभवतः परिणाम का मुख्य सांख्यिकीय निहितार्थ यह है कि न केवल हम सभी x अवयवों के संयुक्त भिन्नताओं को विघटित कर सकते हैं किंतु प्रत्येक पीसी के कारण घटते योगदान में, हम संपूर्ण सहसंयोजक आव्युह को योगदान में विघटित भी कर सकते हैं प्रत्येक पीसी से चूँकि कठोरता से कम नहीं हो रहा है, जैसे-जैसे बढ़ता है के अवयव तब रूप में लघु हो जाएगा, क्योंकि बढ़ने के लिए गैर-बढ़ रहा है , जबकि के अवयव के कारण समान आकार के रहने की प्रवृत्ति रखते हैं | यह सामान्यीकरण बाधाओं .होती है |
सीमाएं
जैसा कि ऊपर उल्लेख किया गया है, पीसीए के परिणाम वेरिएबल के स्केलिंग पर निर्भर करते हैं। प्रत्येक विशेषता को उसके मानक विचलन द्वारा स्केल करके इसे सही किया जा सकता है, जिससे इकाई विचरण के साथ आयामहीन सुविधाओं के साथ समाप्त हो जाता हैं। [18]
ऊपर वर्णित पीसीए की प्रयोज्यता कुछ निश्चित (मौन) मान्यताओं द्वारा सीमित है | [19] यह इसकी व्युत्पत्ति में बनाया गया हैं। विशेष रूप से, पीसीए सुविधाओं के मध्य रैखिक सहसंबंधों को पकड़ सकता है किन्तु जब इस धारणा का उल्लंघन होता है तब यह विफल हो जाता है इसके (संदर्भ में चित्र 6ए देखें)। कुछ स्तिथियों में, समन्वय परिवर्तन रैखिकता धारणा को पुनर्स्थापित कर सकते हैं और पीसीए को तब प्रयुक्त किया जा सकता है | इसके लिए (कर्नेल प्रमुख अवयव विश्लेषण देख) सकते हैं।
पीसीए के लिए सहप्रसरण आव्युह के निर्माण से पहले और सीमा औसत हटाने की प्रक्रिया है। खगोल विज्ञान जैसे क्षेत्रों में, सभी संकेत गैर-ऋणात्मक होते हैं, और माध्य-हटाने की प्रक्रिया कुछ खगोलीय विपत्ति के माध्य को शून्य होने के लिए बाध्य करेगी, जिसके परिणामस्वरूप अभौतिक ऋणात्मक प्रवाह उत्पन्न होता है,[20] और संकेतों की सही परिमाण को पुनर्प्राप्त करने के लिए आगे की मॉडलिंग की जानी चाहिए। [21] वैकल्पिक पद्धति के रूप में, गैर-ऋणात्मक आव्युह गुणनखंडन केवल मेट्रिसेस में गैर-ऋणात्मक अवयवों पर ध्यान केंद्रित करता है, जो खगोल भौतिकीय प्रेक्षणों के लिए अच्छी तरह से अनुकूल है। [22][23][24] यह पीसीए और गैर-ऋणात्मक आव्युह गुणनखंडन के मध्य या गैर-ऋणात्मक आव्युह गुणनखंड संबंध है।
यदि एल्गोरिथम को प्रयुक्त करने से पहले डेटा को मानकीकृत नहीं किया गया है तब पीसीए हानि में है। पीसीए मूल डेटा को उस डेटा में परिवर्तित कर देता है जो उस डेटा के प्रमुख अवयवों के लिए प्रासंगिक होता है, जिसका अर्थ है कि नए डेटा वेरिएबल की उसी तरह से व्याख्या नहीं की जा सकती है जैसे मूल थे। वह मूल वेरिएबलों की रैखिक व्याख्याएँ हैं। इसके अतिरिक्त, यदि पीसीए सही से नहीं किया जाता है, तब सूचना के हानि की उच्च संभावना होती है। [25]
पीसीए रैखिक मॉडल पर निर्भर करता है। यदि किसी डेटासमुच्चय के अंदर पैटर्न हिडन हुआ है जो कि अरैखिक है, तब पीसीए वास्तव में विश्लेषण को प्रगति की पूर्ण विपरीत दिशा में ले जा सकता है। [26] कैनसस स्टेट यूनिवर्सिटी के शोधकर्ताओं ने पाया कि उनके प्रयोगों में प्रतिरूप त्रुटि ने पीसीए परिणामों के पूर्वाग्रह को प्रभावित किया जाता हैं। यदि विषयों या ब्लॉकों की संख्या 30 से कम है, और/या शोधकर्ता पीसी में पहले से और अधिक रुचि रखते हैं, तब पीसीए आयोजित करने से पहले सीरियल सहसंबंध के लिए पहले सही करना उत्तम हो सकता है। [27] कैनसस स्टेट के शोधकर्ताओं ने यह भी पाया कि यदि डेटा की स्वतःसंबंध संरचना को सही रूप से नियंत्रित नहीं किया जाता है तब पीसीए गंभीर रूप से अनुयायी हो सकता है। [27]
पीसीए और सूचना सिद्धांत
आयामीता में कमी के परिणामस्वरूप सामान्यतः सूचना की हानि होता है। पीसीए-आधारित डायमेंशनलिटी रिडक्शन कुछ सिग्नल और ध्वनि मॉडल के अनुसार उस सूचना हानि को कम करता है।
इस धारणा के अनुसार
वह डेटा सदिश वांछित सूचना-वाहक संकेत का योग है और ध्वनि संकेत कोई दिखा सकता है कि सूचना-सैद्धांतिक दृष्टिकोण से पीसीए आयामीता में कमी के लिए अधिकतम हो सकता है।
विशेष रूप से, लिंस्कर ने दिखाया कि यदि गाऊसी है और पहचान आव्युह के आनुपातिक आव्युह के साथ गॉसियन ध्वनि है, पीसीए आपसी सूचना को अधिकतम करता है और वांछित सूचना और आयामीता-कम उत्पादन के मध्य उपयोग किया जाता है | [28]
यदि ध्वनि अभी भी गाऊसी है और पहचान आव्युह के समानुपाती सहप्रसरण आव्युह है (अर्थात, सदिश के अवयव iid हैं), किन्तु सूचना देने वाला संकेत गैर-गाऊसी है (जो सामान्य परिदृश्य है), पीसीए कम से कम सूचना हानि पर ऊपरी सीमा को कम करता है, जिसे इस रूप में परिभाषित किया गया है | [29][30]
ध्वनि होने पर पीसीए की अधिकतम भी संरक्षित है तथा सूचना देने वाले संकेत की तुलना में iid और कम से कम अधिक गाऊसी (कुल्बैक-लीब्लर विचलन के संदर्भ में) है [31] सामान्यतः, तदापि उपरोक्त सिग्नल मॉडल धारण करता है, जैसे ही ध्वनि होती है, पीसीए अपनी सूचना-सैद्धांतिक अधिकतम खो देता है। तथा आश्रित हो जाता है।
सहप्रसरण विधि का उपयोग करके पीसीए की गणना करना
सहप्रसरण विधि का उपयोग करते हुए पीसीए का विस्तृत विवरण निम्नलिखित है (यह भी देखें यहां) सहसंबंध विधि के विपरीत हैं।[32]
लक्ष्य आयाम p के दिए गए डेटा समुच्चय X को लघु आयाम L के वैकल्पिक डेटा समुच्चय Y में परिवर्तित करता है। समतुल्य रूप से, हम आव्युह Y को खोजने का प्रयास कर रहे हैं, जहां Y करहुनेन-लोएव प्रमेय आव्युह X का करहुनेन-लोव ट्रांसफ़ॉर्म (केएलटी) है |
- डेटा समुच्चय व्यवस्थित करें
मान लीजिए कि आपके समीप p वेरिएबलों के प्रेक्षणों के समुच्चय से युक्त डेटा है, और आप डेटा को कम करना चाहते हैं जिससे प्रत्येक प्रेक्षण को केवल L वेरिएबल , L <p के साथ वर्णित किया जा सकता हैं। आगे मान लीजिए कि डेटा को n डेटा सदिश के समुच्चय के रूप में व्यवस्थित किया जाता है प्रत्येक p के साथ वेरिएबल्स के एकल समूहीकृत अवलोकन का प्रतिनिधित्व करना हैं।
- प्रत्येक p अवयवों के साथ पंक्ति सदिश के रूप में, लिखना ।
- पंक्ति सदिशों को आयाम n × p के एकल आव्यूह 'X' में रखें।
- अनुभवजन्य माध्य की गणना करें
- प्रत्येक स्तम्भ j = 1, ..., p के साथ अनुभवजन्य माध्य खोजें।
- परिकलित माध्य मानों को आयाम p × 1 के अनुभवजन्य माध्य सदिश 'u' में रखें।
- माध्य से विचलन की गणना करें
औसत घटाव प्रमुख अवयव आधार खोजने की दिशा में समाधान का अभिन्न अंग है जो डेटा का अनुमान लगाने की औसत वर्ग त्रुटि को कम करता है।[33] इसलिए हम निम्नानुसार डेटा को केंद्रित करके आगे बढ़ते हैं
- अनुभवजन्य माध्य सदिश घटाएं डेटा आव्युह X की प्रत्येक पंक्ति से हैं।
- माध्य-घटाए गए डेटा को n × p आव्युह B में संग्रहीत करें।
- जहाँ h है n × 1 सभी 1 का स्तम्भ सदिश :
कुछ अनुप्रयोगों में, प्रत्येक वेरिएबल (B का स्तम्भ ) को 1 के समान भिन्नता के लिए स्केल किया जा सकता है (जेड-स्कोर देखें)।[34] यह निर्णय परिकलित प्रमुख अवयवों को प्रभावित करता है, किन्तु उन्हें विभिन्न वेरिएबलों को मापने के लिए उपयोग की जाने वाली इकाइयों से स्वतंत्र बनाता है।
- सहप्रसरण आव्युह का पता लगाएं
- आव्युह 'B' से p × p अनुभवजन्य सहप्रसरण आव्युह 'C' खोजें: जहाँ संयुग्मी स्थानांतरण संकारक है। यदि B में पूरी तरह से वास्तविक संख्याएं होती हैं, जो कि अनेक अनुप्रयोगों में होती है, तब संयुग्म स्थानान्तरण नियमित स्थानान्तरण के समान होता है।
- प्रयोग करने के पीछे तर्क n − 1 सहप्रसरण की गणना करने के लिए n के अतिरिक्त बेसेल का सुधार है।
- सहप्रसरण आव्युह के आइजन्वेक्टर और आइजेनवैल्यू का पता लगाएं
- आइजन्वेक्टर के आव्युह 'V' की गणना करें जो सहसंयोजक आव्युह 'C' को विकर्ण करता है: जहाँ D, C के आइजेनवैल्यू का विकर्ण आव्युह है। इस चरण में सामान्यतः आव्युह के आइजेनडीकम्पोज़िशन के लिए कंप्यूटर-आधारित एल्गोरिथ्म का उपयोग सम्मिलित होता हैं। यह एल्गोरिदम अधिकांश आव्युह बीजगणित प्रणालियों के उप-अवयवों के रूप में सरलता से उपलब्ध हैं, जैसे एसएएस (सॉफ्टवेयर),[35] आर (प्रोग्रामिंग भाषा), मैटलैब,[36][37] गणित,[38] साइपी, आईडीएल (प्रोग्रामिंग लैंग्वेज) (इंटरएक्टिव डेटा भाषा), या जीएनयू ऑक्टेव और साथ ही ओपनसीवी होता हैं।
- आव्युह D p × p विकर्ण आव्युह का रूप ले लेगा, जहाँ सहप्रसरण आव्युह 'C' का jवां आइजेनवैल्यू है, और
- आव्युह V, आयाम p × p का भी, p स्तम्भ सदिश , प्रत्येक लंबाई p, जो सहप्रसरण आव्युह के p आइजन्वेक्टर C का प्रतिनिधित्व करता है ।
- आइजेनवैल्यू और आइजन्वेक्टर को क्रमबद्ध और युग्मित किया जाता है। और Jth आइजेनवैल्यू jth आइजन्वेक्टर से मेल खाता है।
- आव्युह V 'राइट' आइजन्वेक्टर के आव्युह को दर्शाता है ('लेफ्ट' आइजन्वेक्टर के विपरीत) हैं। सामान्यतः , दाएं आइजन्वेक्टर के आव्युह को बाएं आइजन्वेक्टर के आव्युह का नहीं होना चाहिए।
- आइजन्वेक्टर और आइजेनवैल्यू को पुनर्व्यवस्थित करें
- आइजन्वेक्टर आव्युह V और आइजेनवैल्यू आव्युह D के स्तम्भ को घटते आइजेनवैल्यू के क्रम में क्रमबद्ध करें।
- प्रत्येक आव्युह में स्तंभों के मध्य सही जोड़ियों को बनाए रखना सुनिश्चित करें।
- प्रत्येक आइजन्वेक्टर के लिए संचयी ऊर्जा सामग्री की गणना करें
- आइजेनवैल्यू स्रोत डेटा की ऊर्जा के वितरण का प्रतिनिधित्व करते हैं प्रत्येक आइजन्वेक्टर के मध्य , जहाँ आइजन्वेक्टर डेटा के लिए आधार (रैखिक बीजगणित) बनाते हैं। जेवें आइजन्वेक्टर के लिए संचयी ऊर्जा सामग्री जी 1 से जे तक सभी ईजेनवैल्यू में ऊर्जा सामग्री का योग है:
- आधार सदिश के रूप में आइजन्वेक्टर के सबसमुच्चय का चयन करें
- 'V' के पहले L स्तम्भ को p × Lआव्युह 'w' के रूप में सहेजें: जहाँ
- 'L के लिए उपयुक्त मान चुनने में गाइड के रूप में सदिश g का उपयोग करें। लक्ष्य प्रतिशत के आधार पर g के यथोचित उच्च मान को प्राप्त करते हुए जितना संभव हो सके इसमें L के मान को चुनना है। उदाहरण के लिए, आप L चुन सकते हैं जिससे संचयी ऊर्जा g निश्चित सीमा से ऊपर हो, जैसे 90 प्रतिशत हैं। इस स्तिथियों में, 'L' का सबसे लघु मान चुनें जैसे कि
- डेटा को नए आधार पर प्रोजेक्ट करें
- अनुमानित डेटा बिंदु आव्युह की पंक्तियाँ हैं
अर्थात का पहला स्तम्भ पहले प्रमुख अवयव पर डेटा बिंदुओं का प्रक्षेपण है, दूसरा स्तंभ दूसरे प्रमुख अवयव पर प्रक्षेपण आदि है।
सहप्रसरण विधि का उपयोग करके पीसीए की व्युत्पत्ति
X को स्तम्भ सदिश के रूप में व्यक्त 'D'-आयामी यादृच्छिक सदिश होना चाहिए। व्यापकता के हानि के बिना, मान लें कि X का शून्य माध्य है।
हम खोजना चाहते हैं कि a d × d ऑर्थोनॉर्मल आधार p जिससे पीएक्स में विकर्ण सहप्रसरण आव्युह हो (अर्थात, पीएक्स यादृच्छिक सदिश है जिसके सभी भिन्न -भिन्न अवयव जोड़ीदार असंबद्ध हैं)।
इस प्रकार त्वरित गणना मानते हुए एकात्मक उपज थे
इस तरह रखती है यदि और केवल यदि द्वारा विकर्णीय थे .
यह बहुत रचनात्मक है, क्योंकि cov(X) गैर-ऋणात्मक निश्चित आव्युह होने की गारंटी है और इस प्रकार कुछ एकात्मक आव्युह द्वारा विकर्ण होने की गारंटी है।
सहप्रसरण-मुक्त संगणना
व्यावहारिक कार्यान्वयन में, विशेष रूप से उच्च आयामी डेटा (बड़े p), भोली सहप्रसरण विधि का उपयोग संभवतः ही कभी किया जाता है क्योंकि सहप्रसरण आव्युह को स्पष्ट रूप से निर्धारित करने की उच्च कम्प्यूटेशनल और मेमोरी निवेश के कारण यह कुशल नहीं है। सहप्रसरण-मुक्त दृष्टिकोण np2 से बचा जाता है स्पष्ट रूप से सहप्रसरण आव्युह की गणना और संग्रहण के संचालन XTX, इसके अतिरिक्त आव्युह -मुक्त विधियों में से इसका उपयोग करना हैं, उदाहरण के लिए, उत्पाद का मूल्यांकन करने वाले फलन के आधार पर XT(X r) की मान पर 2np संचालन किया जाता है।
पुनरावृत्ति संगणना
पहले प्रमुख अवयव की कुशलता से गणना करने की विधि [39] शून्य माध्य के साथ, इसके सहप्रसरण आव्युह की गणना किए बिना डेटा आव्युह के लिए निम्नलिखित छद्म कोड X में दिखाया गया है।
r = a random vector of length p
r = r / norm(r)
do c times:
s = 0 (a vector of length p)
for each row x in X
s = s + (x ⋅ r) x
λ = rTs // λ is the eigenvalue
error = |λ ⋅ r − s|
r = s / norm(s)
exit if error < tolerance
return λ, r
यह शक्ति पुनरावृत्ति एल्गोरिथ्म केवल सदिश XT(X r) की गणना करता है, और परिणाम r को वापस अंदर रखता है. आइजेनवैल्यू द्वारा rT (XTX) r अनुमानित है, जो इकाई सदिश r पर रेले XTX भागफल है सहप्रसरण आव्युह के लिए . यदि सबसे बड़ा एकवचन मान अगले सबसे बड़े सदिश से अच्छी तरह से r भिन्न है यह X के पहले प्रमुख अवयव के समीप c हो जाता है पुनरावृत्तियों की संख्या के अंदर, जो p के सापेक्ष लघु है, कुल निवेश पर 2cnp. अधिक उन्नत आव्युह -मुक्त विधियों, जैसे लैंक्ज़ोस एल्गोरिथम या स्थानीय रूप से अधिकतम ब्लॉक प्रीकंडीशन्ड कंजुगेट ग्रेडिएंट (एलओबीपीसीजी) विधि का उपयोग करके प्रति पुनरावृत्ति की छोटी निवेश का त्याग किए बिना शक्ति पुनरावृत्ति अभिसरण को त्वरित किया जा सकता है।
इसके पश्चात के प्रमुख अवयवों की गणना करके अपस्फीति के माध्यम से या साथ ब्लॉक के रूप में की जा सकती है। पूर्व दृष्टिकोण में, पहले से ही गणना किए गए अनुमानित प्रमुख अवयवों में अशुद्धियाँ पश्चात में गणना किए गए प्रमुख अवयवों की स्पष्टता को जोड़ कर प्रभावित करती हैं, इस प्रकार हर नई संगणना के साथ त्रुटि बढ़ जाती है। ब्लॉक पावर पद्धति में पश्चात वाला दृष्टिकोण एकल-सदिश की जगह लेता है r और s ब्लॉक-सदिश , मैट्रिसेस के साथ R और S. का हर स्तंभ R प्रमुख प्रमुख अवयवों में से का अनुमान लगाता है, जबकि सभी स्तम्भ साथ पुनरावृत्त होते हैं। मुख्य गणना XT(X R) उत्पाद का मूल्यांकन है कार्यान्वित, उदाहरण के लिए, एलओबीपीसीजी में, कुशल अवरोधन त्रुटियों के संचय को समाप्त करता है, उच्च-स्तरीय ब्लास आव्युह -आव्युह उत्पाद कार्यों का उपयोग करने की अनुमति देता है, और सामान्यतः एकल-सदिश एक-एक-एक तकनीक की तुलना में शीघ्रता से अभिसरण की ओर जाता है।
निपल्स विधि
गैर-रैखिक पुनरावृत्त आंशिक न्यूनतम वर्ग (निपल्स) प्रमुख अवयव या आंशिक कम वर्ग विश्लेषण में पहले कुछ अवयवों की गणना के लिए घटाव द्वारा आव्युह अपस्फीति के साथ मौलिक शक्ति पुनरावृत्ति का प्रकार है। बहुत उच्च-आयामी डेटासमुच्चय के लिए, जैसे कि *ओमिक्स विज्ञान (उदाहरण के लिए, जीनोमिक्स, चयापचय) में उत्पन्न डेटासमुच्चय के लिए सामान्यतः केवल पहले कुछ पीसी की गणना करना आवश्यक होता है। गैर-रैखिक पुनरावृत्त आंशिक न्यूनतम वर्ग (निपल्स) एल्गोरिथ्म प्रमुख स्कोर और लोडिंग 'T1 और r1T' के पुनरावृत्त अनुमानों को अद्यतन करता है। शक्ति पुनरावृत्ति द्वारा प्रत्येक पुनरावृत्ति पर X द्वारा बाईं ओर और दाईं ओर गुणा किया जाता है, अर्थात, सहप्रसरण आव्युह की गणना उत्पाद XT(X r) = ((X r)TX)T का मूल्यांकन करने वाले फलन के आधार पर, XTX में पावर पुनरावृत्तियों के आव्युह-मुक्त कार्यान्वयन की तरह, टाला जाता है।
घटाव द्वारा आव्युह अपस्फीति बाहरी उत्पाद, T1r1T X से घटाकर किया जाता है अवस्फीत अवशिष्ट आव्युह को छोड़ते हुए पश्चात के प्रमुख पीसी की गणना करने के लिए उपयोग किया जाता है।[40] बड़े डेटा मेट्रिसेस, या मेट्रिसेस के लिए, जिनमें स्तम्भ कोलीनियरिटी का उच्च स्तर होता है, निपल्स पीसी की ऑर्थोगोनलिटी के हानि से ग्रस्त होता है, क्योंकि प्रत्येक पुनरावृत्ति और आव्युह अपस्फीति में घटाव द्वारा संचित मशीन स्पष्ट राउंड-ऑफ त्रुटियां होती हैं।[41] ऑर्थोगोनलिटी के इस हानि को विलुप्त करने के लिए प्रत्येक पुनरावृत्ति चरण पर स्कोर और लोडिंग दोनों के लिए ग्राम-श्मिट री-ऑर्थोगोनलाइज़ेशन एल्गोरिदम प्रयुक्त किया जाता है।[42] एकल-सदिश गुणन पर निपल्स निर्भरता उच्च-स्तरीय ब्लास का लाभ नहीं उठा सकती है और परिणामस्वरूप क्लस्टर अग्रणी विलक्षण मानों के लिए धीमी गति से अभिसरण होता है इन दोनों कमियों को अधिक परिष्कृत आव्युह -मुक्त ब्लॉक सॉल्वर में हल किया जाता है, जैसे कि स्थानीय रूप से अधिकतम ब्लॉक प्रीकंडिशनेड कंजुगेट ग्रेडिएंट ( एलओबीपीसीजी) विधि होती हैं।
ऑनलाइन/अनुक्रमिक अनुमान
ऑनलाइन या स्ट्रीमिंग स्थिति में बैच में संग्रहीत होने के अतिरिक्त अनेक भाग में डेटा आने के साथ, पीसीए प्रोजेक्शन का अनुमान लगाना उपयोगी होता है जिसे क्रमिक रूप से अपडेट किया जा सकता है। यह कुशलता से किया जा सकता है, किन्तु इसके लिए भिन्न -भिन्न एल्गोरिदम की आवश्यकता होती है।[43]
पीसीए और गुणात्मक वेरिएबल
पीसीए में, यह सामान्य है कि हम गुणात्मक वेरिएबल को पूरक अवयवों के रूप में प्रस्तुत करना चाहते हैं। उदाहरण के लिए, पौधों पर अनेक मात्रात्मक वेरिएबलों को मापा गया है। इन पौधों के लिए, कुछ गुणात्मक वेरिएबल उपलब्ध हैं, उदाहरण के लिए, वह प्रजाति जिससे पौधे संबंधित हैं। यह डेटा मात्रात्मक वेरिएबल के लिए पीसीए के अधीन थे। परिणामों का विश्लेषण करते समय, प्रमुख अवयवों को गुणात्मक वेरिएबल प्रजातियों से जोड़ना स्वाभाविक है। इसके लिए निम्न परिणाम प्राप्त होते हैं।
- विभिन्न प्रजातियों की पहचान, तथ्यात्मक प्लेनों पर, उदाहरण के लिए, विभिन्न रंगों का उपयोग करना।
- प्रतिनिधित्व, ही प्रजाति से संबंधित पौधों के गुरुत्वाकर्षण के केंद्रों के तथ्यात्मक प्लेनों पर।
- गुरुत्वाकर्षण के प्रत्येक केंद्र और प्रत्येक अक्ष के लिए, गुरुत्व केंद्र और उत्पत्ति के मध्य के अंतर के महत्व का न्याय करने के लिए पी-मान।
इन परिणामों को गुणात्मक वेरिएबल को पूरक अवयव के रूप में प्रस्तुत करना कहा जाता है। यह प्रक्रिया हसन, ली और पेज 2009 और पेज 2013 में विस्तृत है।कुछ सॉफ्टवेयर इस विकल्प को स्वचालित विधियों से प्रस्तुत करते हैं। यह एसपीएडी की स्तिथि है, जो ऐतिहासिक रूप से, लुडोविक लेबार्ट के कार्य के पश्चात , फैक्टोमाइनर इस विकल्प और R पैकेज को प्रस्तावित करने वाले प्रथम व्यक्ति थे ।
अनुप्रयोग
बुद्धि
कारक विश्लेषण का सबसे पहला प्रयोग मानव बुद्धि के अवयवों का पता लगाने और मापने में था। यह माना जाता था कि बुद्धि में विभिन्न असंबद्ध अवयव होते हैं जैसे कि स्थानिक बुद्धि, मौखिक बुद्धि, आगमन, कटौती आदि और इन पर अंक विभिन्न परीक्षणों के परिणामों से कारक विश्लेषण द्वारा जोड़े जा सकते हैं, जिससे एकल सूचकांक दिया जा सके जिसे इंटेलिजेंस कोशिएंट (IQ) के रूप में जाना जाता है। ). अग्रणी सांख्यिकीय मनोवैज्ञानिक चार्ल्स स्पीयरमैन ने वास्तव में 1904 में अपने बुद्धि के दो-कारक सिद्धांत दिए हैं | बुद्धि के दो-कारक सिद्धांत के लिए कारक विश्लेषण विकसित किया, जिसमें साइकोमेट्रिक्स के विज्ञान के लिए औपचारिक तकनीक सम्मिलित थी। 1924 में लुई लियोन थर्स्टन ने मानसिक आयु की धारणा को विकसित करते हुए बुद्धि के 56 कारकों की खोजने का प्रयास था | मानक IQ परीक्षण आज इसी प्रारंभिक कार्य पर आधारित हैं।[44]
आवासीय भेदभाव
1949 में, शेवकी और विलियम्स ने फैक्टोरियल इकोलॉजी का सिद्धांत प्रस्तुत किया, जो 1950 से 1970 के दशक तक आवासीय भेदभाव के अध्ययन पर प्रभावी था।[45] यह शहर में निकटतम पहचानने योग्य थे यह विभिन्न विशेषताओं द्वारा दूसरे से भिन्न किए जा सकते थे जिन्हें कारक विश्लेषण द्वारा घटाकर तीन किया जा सकता था। इन्हें 'सामाजिक पद' (व्यावसायिक स्थिति का सूचकांक), 'वर्ग' या समूह का आकार, और 'जातीयता' के रूप में जाना जाता था; क्लस्टर विश्लेषण को तीन प्रमुख कारक वेरिएबल के मानों के अनुसार शहर को क्लस्टर या परिसर में विभाजित करने के लिए प्रयुक्त किया जा सकता है। शहरी भूगोल में फैक्टोरियल इकोलॉजी के आस पास व्यापक साहित्य विकसित हुआ, किन्तु 1980 के पश्चात पद्धतिगत रूप से प्राचीन होने और उत्तर आधुनिक भौगोलिक प्रतिमानों में कम जगह होने के कारण यह दृष्टिकोण फैशन से बाहर हो गया था।
कारक विश्लेषण की समस्याओं में से सदैव विभिन्न कृत्रिम कारकों के लिए ठोस नाम खोजना रहा है। 2000 में, फ्लड ने फैक्टोरियल इकोलॉजी दृष्टिकोण को पुनर्जीवित किया, यह दिखाने के लिए कि प्रमुख अवयव विश्लेषण ने कारक रोटेशन का सहारा लिए बिना वास्तव में सीधे सार्थक उत्तर दिए हैं। प्रमुख अवयव वास्तव में शहरों में व्यकित को साथ या भिन्न करने वाले 'बलों' के दोहरे वेरिएबल या छाया मान थे। पहला अवयव 'पहुंच' था, यात्रा की मांग और अंतरिक्ष की मांग के मध्य क्लासिक व्यापार-संवर्त , जिसके आससमीप मौलिक शहरी अर्थशास्त्र आधारित है। अगले दो अवयव 'हानि ' थे, जो समान स्थिति के व्यकित को भिन्न निकटतम (नियोजन द्वारा मध्यस्थता) में रखता है, और जातीयता, जहां समान जातीय पृष्ठभूमि के लोग सह-पता लगाने की प्रयास करते हैं।[46]
उसी समय के बारे में, ऑस्ट्रेलियाई सांख्यिकी ब्यूरो ने प्रमुख वेरिएबल के समुच्चय के पहले प्रमुख अवयव को लेते हुए लाभ और हानि के भिन्न -भिन्न सूचकांकों को परिभाषित किया, जिन्हें महत्वपूर्ण माना गया था। यह सेइफ़ा इंडेक्स नियमित रूप से विभिन्न न्यायालयों के लिए प्रकाशित होते हैं, और स्थानिक विश्लेषण में अधिकतर उपयोग किए जाते हैं।[47]
विकास सूचकांक
पीसीए इंडेक्स के विकास के लिए उपलब्ध एकमात्र औपचारिक विधि रहा है, जो अन्यथा हिट-या-मिस तदर्थ उपक्रम है।
नगर विकास सूचकांक पीसीए द्वारा 1996 में 254 वैश्विक शहरों के सर्वेक्षण में शहर के परिणामों के लगभग 200 संकेतकों से विकसित किया गया था। पहला प्रमुख अवयव पुनरावृत्त प्रतिगमन के अधीन था, मूल वेरिएबल को तब तक जोड़ा गया जब तक कि इसकी लगभग 90% भिन्नता की गणना नहीं की जस सकती हैं। इंडेक्स ने अंततः लगभग 15 संकेतकों का उपयोग किया किन्तु अनेक और वेरिएबलों का अच्छा भविष्यवक्ता था। इसका तुलनात्मक मान प्रत्येक शहर की स्थिति के व्यक्तिपरक मूल्यांकन के साथ बहुत अच्छी तरह से मेल खाता है। मूलभूत फ्रेम की वस्तुओं पर गुणांक अंतर्निहित सेवाएं प्रदान करने की औसत निवेश के लगभग आनुपातिक थे, यह सुझाव देते हुए कि सूचकांक वास्तव में शहर में प्रभावी भौतिक और सामाजिक निवेश का उपाय था।
संयुक्त राष्ट्र विकास कार्यक्रम से देश-स्तरीय मानव विकास सूचकांक (एचडीआई), जो 1990 से प्रकाशित हुआ है और विकास अध्ययनों में बहुत व्यापक रूप से उपयोग किया जाता है,[48] यह समान संकेतकों पर बहुत समान गुणांक हैं, यह दृढ़ता से सुझाव देते हैं कि यह मूल रूप से पीसीए का उपयोग करके बनाया गया था।
जनसंख्या आनुवंशिकी
1978 में लुइगी लुका कवेली-स्फोर्ज़ा कैवली-स्फोर्ज़ा और अन्य ने क्षेत्रों में मानव जीन आवृत्तियों में भिन्नता पर डेटा को सारांशित करने के लिए प्रमुख अवयव विश्लेषण (पीसीए) के उपयोग उत्तरदायित्व उठाया हैं। अवयवों ने विशिष्ट पैटर्न दिखाए, जिनमें ग्रेडियेंट और साइनसॉइडल तरंगें सम्मिलित हैं। उन्होंने विशिष्ट प्राचीन प्रवासन घटनाओं के परिणामस्वरूप इन प्रतिमानों की व्याख्या की हैं।
तब से, पीसीए प्रदर्शन तंत्र के रूप में पीसीए का उपयोग करने वाले हजारों पेपरों के साथ जनसंख्या आनुवंशिकी में सर्वव्यापी रहा है। इसमें निकटता के अनुसार आनुवंशिकी अधिक सीमा तक भिन्न होती है, इसलिए पहले दो प्रमुख अवयव वास्तव में स्थानिक वितरण दिखाते हैं और इसका उपयोग विभिन्न जनसंख्या समूहों के सापेक्ष भौगोलिक स्थान को मानचित्र करने के लिए किया जा सकता है, जिससे ऐसे व्यक्तियों को दिखाया जा सकता है जो अपने मूल स्थानों से भटक गए हैं।[49]
जेनेटिक्स में पीसीए तकनीकी रूप से विवादास्पद रहा है, जिसमें तकनीक असतत गैर-सामान्य वेरिएबल और अधिकतर बाइनरी एलील मार्करों पर की गई है। पीसीए में मानक त्रुटि के किसी भी उपाय की कमी भी अधिक सुसंगत उपयोग के लिए बाधा है। अगस्त 2022 में, आणविक जीवविज्ञानी ईरान जोड़ा गया ने 12 पीसीए अनुप्रयोगों का विश्लेषण करते हुए वैज्ञानिक रिपोर्ट में सैद्धांतिक पेपर प्रकाशित किया। उन्होंने यह निष्कर्ष निकाला कि इस विधि में परिवर्रतन करना सरल था, जो, उनके विचार में, 'त्रुटी, विरोधाभासी और व्यर्थ' परिणाम उत्पन्न करता था। विशेष रूप से, उन्होंने तर्क दिया, जनसंख्या आनुवंशिकी में प्राप्त परिणाम चेरी-पिकिंग और सर्कुलर तर्क द्वारा विशेषता थे।[50]
मार्केट अनुसंधान और दृष्टिकोण के सूचकांक
मार्केट अनुसंधान पीसीए का व्यापक उपयोगकर्ता रहा है। इसका उपयोग उत्पादों के लिए क्लाइंट की संतुष्टि या ग्राहक निष्ठा स्कोर विकसित करने के लिए किया जाता है, और क्लस्टरिंग के साथ, मार्केट खंडों को विकसित करने के लिए विज्ञापन अभियानों के साथ लक्षित किया जा सकता है, उसी प्रकार जैसे फैक्टोरियल इकोलॉजी समान विशेषताओं वाले भौगोलिक क्षेत्रों का पता लगा सकते हैं। [51]
पीसीए शीघ्रता से बड़ी मात्रा में डेटा को लघु, सरलता से पचने वाले वेरिएबल में परिवर्तित कर देता है जिसे अधिक शीघ्रता से और सरलता से विश्लेषण किया जा सकता है। किसी भी उपभोक्ता प्रश्नावली में, उपभोक्ता के दृष्टिकोण को जानने के लिए डिज़ाइन किए गए प्रश्नों की श्रृंखला होती है, और प्रमुख अवयव इन दृष्टिकोणों के अंतर्निहित अव्यक्त वेरिएबल की खोज करते हैं। उदाहरण के लिए, 2013 में ऑक्सफोर्ड इंटरनेट सर्वेक्षण ने 2000 व्यकित से उनके दृष्टिकोण और विश्वासों के बारे में पूछा, और इन विश्लेषकों से चार प्रमुख अवयव आयाम निकाले, जिन्हें उन्होंने 'एस्केप', 'सोशल नेटवर्किंग', 'दक्षता' और 'समस्या उत्पन्न करने' के रूप में पहचाना जाता हैं। .[52]
2008 में जो फ्लड (नीति विश्लेषक) के अन्य उदाहरण ने ऑस्ट्रेलिया में 2697 समूहों के राष्ट्रीय सर्वेक्षण में 28 दृष्टिकोण प्रश्नों से आवास के प्रति व्यवहारिक सूचकांक निकाला जाता हैं। पहला प्रमुख अवयव संपत्ति और घर के स्वामित्व के प्रति सामान्य दृष्टिकोण का प्रतिनिधित्व करता है। अनुक्रमणिका, या इसके सन्निहित अभिवृत्ति प्रश्न, कार्यकाल पसंद के सामान्य रेखीय मॉडल में डाले जा सकते हैं। यह आय, वैवाहिक स्थिति या सामान्य प्रकार के अतिरिक्त अब तक निजी किराये का सबसे शक्तिशाली निर्धारक विधि सूचकांक था।[53]
मात्रात्मक वित्त
मात्रात्मक वित्त में, प्रमुख अवयव विश्लेषण सीधे ब्याज दर डेरिवेटिव पोर्टफोलियो के विपत्ति प्रबंधन पर प्रयुक्त किया जा सकता है।[54] ट्रेडिंग मल्टीपल स्वैप (वित्त) जो सामान्यतः 30-500 अन्य मार्केट उद्धृत योग्य स्वैप उपकरणों का कार्य है, इसको सामान्यतः 3 या 4 प्रमुख अवयवों तक कम करने की मांग की जाती है, जो मैक्रो आधार पर ब्याज दरों के मार्ग का प्रतिनिधित्व करते हैं। फैक्टर लोडिंग (या मल्टीप्लायर) के रूप में प्रतिनिधित्व किए जाने वाले विपत्ति को परिवर्तित करना व्यक्तिगत 30–500 बकेट के विपत्ति को सामूहिक रूप से देखने के लिए उपलब्ध से विपरीत आकलन और समझ प्रदान करता है।
पीसीए को संग्रहण पर भी इसी तरह से प्रयुक्त किया गया है,[55] विपत्ति वापसी अनुपात और विपत्ति -प्रतिफल स्पेक्ट्रम दोनों के लिए हैं। आवेदन पोर्टफोलियो विपत्ति को कम करना है, जहां संपत्ति आवंटन अंतर्निहित शेयरों के अतिरिक्त प्रमुख पोर्टफोलियो पर प्रयुक्त होता है।[56] दूसरा, पोर्टफोलियो रिटर्न को बढ़ाने के लिए प्रमुख अवयवों का उपयोग स्टॉक चयन मानदंड के साथ ऊपर की क्षमता के साथ करना है।
तंत्रिका विज्ञान
प्रमुख अवयव विश्लेषण के प्रकार का उपयोग तंत्रिका विज्ञान में उत्तेजना के विशिष्ट गुणों की पहचान करने के लिए किया जाता है जो न्यूरॉन की क्रिया क्षमता उत्पन्न करने की संभावना को बढ़ाता है।[57][58] इस तकनीक को स्पाइक-ट्रिगर सहप्रसरण स्पाइक-ट्रिगर सहप्रसरण विश्लेषण के रूप में जाना जाता है। विशिष्ट अनुप्रयोग में प्रयोगकर्ता सफेद ध्वनि प्रक्रिया को उत्तेजना के रूप में प्रस्तुत करता है (सामान्यतः यह तब परीक्षण विषय के लिए संवेदी इनपुट के रूप में, या विद्युत प्रवाह के रूप में सीधे न्यूरॉन में इंजेक्ट किया जाता है) और एक्शन पोटेंशिअल या स्पाइक्स की ट्रेन रिकॉर्ड करता है, जो परिणामस्वरूप न्यूरॉन उत्पादित होता है। । संभवतः, उत्तेजना की कुछ विशेषताएं न्यूरॉन को स्पाइक करने की अधिक संभावना बनाती हैं। इन सुविधाओं को निकालने के लिए, प्रयोगकर्ता स्पाइक-ट्रिगर किए गए आर्टिस्ट की भाग के सहप्रसरण आव्युह की गणना करता है, सभी उत्तेजनाओं का समुच्चय (सामान्यतः 100 एमएस के क्रम में परिमित समय खिड़की पर परिभाषित और विघटित) जो तुरंत स्पाइक से पहले होता है। स्पाइक-ट्रिगर सहप्रसरण आव्युह और पूर्व उत्तेजना पहनावा के सहप्रसरण आव्युह के मध्य अंतर के आइजन्वेक्टर और ईगेनवेल्यूज़ (सभी उत्तेजनाओं का समुच्चय , समान लंबाई समय विंडो पर परिभाषित) पुनः उत्तेजनाओं के सदिश स्थान में दिशाओं का संकेत देते हैं जिसके साथ स्पाइक-ट्रिगर पहनावा का विचरण पूर्व प्रोत्साहन पहनावा से सबसे भिन्न था। विशेष रूप से, सबसे बड़े धनात्मक आइजेनवैल्यू वाले आइजन्वेक्टर उन दिशाओं के अनुरूप होते हैं जिनके साथ स्पाइक-ट्रिगर पहनावा के विचरण ने पूर्व के विचरण की तुलना में सबसे बड़ा धनात्मक परिवर्तन दिखाया हैं। चूँकि यह वह दिशाएँ थीं जिनमें भिन्न -भिन्न उत्तेजनाओं ने स्पाइक का नेतृत्व किया, वह अधिकतर प्रासंगिक उत्तेजना सुविधाओं के पश्चात की मांग के अच्छे अनुमान हैं।
तंत्रिका विज्ञान में, पीसीए का उपयोग न्यूरॉन की पहचान को उसकी क्रिया क्षमता के आकार से पहचानने के लिए भी किया जाता है। स्पाइक सॉर्टिंग महत्वपूर्ण प्रक्रिया है क्योंकि इलेक्ट्रोफिजियोलॉजी या बाह्यकोशिकीय रिकॉर्डिंग तकनीकें अधिकतर से अधिक न्यूरॉन से संकेत लेती हैं। स्पाइक इसमें, पहले पीसीए का उपयोग एक्शन पोटेंशियल वेवफॉर्म के स्थान की गतिशीलता को कम करने के लिए किया जाता है, और पुनः व्यक्तिगत न्यूरॉन्स के साथ विशिष्ट एक्शन पोटेंशिअल को जोड़ने के लिए क्लस्टर विश्लेषण किया जाता है।
पीसीए आयाम कमी तकनीक के रूप में विशेष रूप से बड़े न्यूरोनल पहनावा की समन्वित गतिविधियों का पता लगाने के लिए अनुकूल है। यह मस्तिष्क में वेरिएबल संक्रमण के समय सामूहिक वेरिएबल , अर्थात आदेश पैरामीटर निर्धारित करने में उपयोग किया गया है। [59]
अन्य विधियों के साथ संबंध
कॉरेस्पोंडेंस विश्लेषण
कॉरेस्पोंडेंस विश्लेषण (सीए) जीन-पॉल बेंजेक्री द्वारा विकसित किया गया था [60]और वैचारिक रूप से पीसीए के समान है, किन्तु डेटा को मापता है (जो गैर-ऋणात्मक होना चाहिए) जिससे पंक्तियों और स्तंभों को समान रूप से व्यवहार किया जा सके। यह परंपरागत रूप से आकस्मिक तालिकाओं पर प्रयुक्त होता है। सीए इस तालिका से जुड़े ची-स्क्वायर आँकड़ों को ऑर्थोगोनल कारकों में विघटित करता है।[61] क्योंकि सीए वर्णनात्मक तकनीक है, इसे उन तालिकाओं पर प्रयुक्त किया जा सकता है जिनके लिए ची-स्क्वेर्ड आँकड़ा उपयुक्त है या नहीं हैं। सीए के अनेक प्रकार उपलब्ध हैं जिनमें डिट्रेंडेड कॉरेस्पोंडेंस विश्लेषण और कैनोनिकल कॉरेस्पोंडेंस विश्लेषण सम्मिलित हैं। विशेष विस्तार एकाधिक कॉरेस्पोंडेंस विश्लेषण है, जिसे श्रेणीबद्ध डेटा के लिए प्रमुख अवयव विश्लेषण के समकक्ष के रूप में देखा जा सकता है।[62]
कारक विश्लेषण

प्रमुख कंपोनेंट विश्लेषण वेरिएबल्स बनाता है जो मूल वेरिएबल्स के रैखिक संयोजन हैं। नए वेरिएबल्स में यह संपत्ति है कि वेरिएबल्स सभी ऑर्थोगोनल हैं। पीसीए परिवर्तन क्लस्टरिंग से पहले प्री-प्रोसेसिंग चरण के रूप में सहायक हो सकता है। पीसीए भिन्नता-केंद्रित दृष्टिकोण है जो कुल परिवर्तनीय भिन्नता को पुन: उत्पन्न करने की मांग करता है, जिसमें अवयव वेरिएबल के सामान्य और अद्वितीय भिन्नता दोनों को दर्शाते हैं। पीसीए को सामान्यतः डेटा में कमी के प्रयोजनों के लिए पसंद किया जाता है (अर्थात, वेरिएबल स्थान को अधिकतम कारक स्थान में अनुवाद करना) हैं किन्तु तब नहीं जब लक्ष्य अव्यक्त निर्माण या कारकों का पता लगाना होता हैं।
कारक विश्लेषण प्रमुख अवयव विश्लेषण के समान है, उस कारक विश्लेषण में वेरिएबल के रैखिक संयोजन भी सम्मिलित हैं। पीसीए से भिन्न , कारक विश्लेषण सहसंबंध-केंद्रित दृष्टिकोण है जो वेरिएबल के मध्य अंतर-सहसंबंधों को पुन: उत्पन्न करने की मांग करता है, जिसमें कारक वेरिएबल के सामान्य भिन्नता अद्वितीय भिन्नता को छोड़कर इसका प्रतिनिधित्व करते हैं।[63] सहसंबंध आव्युह के संदर्भ में, यह ऑफ-डायगोनल नियमों (अर्थात , साझा सह-विचरण ) को समझाने पर ध्यान केंद्रित करने के अनुरूप है, जबकि पीसीए विकर्ण पर बैठने वाली नियमों को समझाने पर ध्यान केंद्रित करता है। चूँकि , साइड परिणाम के रूप में, ऑन-डायगोनल नियमों को पुन: प्रस्तुत करने की प्रयास करते समय, पीसीए भी ऑफ-डायगोनल सहसंबंधों को अपेक्षाकृत अच्छी तरह से फिट करने की प्रयास करता है।[12]: 158 पीसीए और कारक विश्लेषण द्वारा दिए गए परिणाम ज्यादातर स्थितियों में बहुत समान होते हैं, किन्तु सदैव ऐसा नहीं होता है, और कुछ समस्याएं ऐसी होती हैं जहां परिणाम महत्वपूर्ण रूप से भिन्न होते हैं। कारक विश्लेषण का सामान्यतः उपयोग तब किया जाता है जब अनुसंधान उद्देश्य डेटा संरचना (अर्थात, अव्यक्त निर्माण या कारक) या कारण मॉडलिंग का पता लगा रहा हो। यदि कारक मॉडल त्रुटी विधियों से तैयार किया गया है या मान्यताओं को पूर्ण नहीं किया गया है, तब कारक विश्लेषण त्रुटी परिणाम देता हैं।[64]
K-कारण क्लस्टरिंग
यह प्रमाण किया गया है कि k-कारण क्लस्टरिंग का सरल समाधान k-कारण क्लस्टरिंग, क्लस्टर संकेतक द्वारा निर्दिष्ट, प्रमुख अवयवों द्वारा दिया जाता है, और मुख्य दिशाओं द्वारा विस्तार हुआ पीसीए सबस्पेस क्लस्टर सेंट्रोइड सबस्पेस के समान है।[65][66] चूँकि , वह पीसीए की उपयोगी छूट है यह k-कारण क्लस्टरिंग नया परिणाम नहीं था,[67] और इस कथन के प्रति उदाहरणों को उजागर करना सीधा है कि क्लस्टर सेंट्रोइड उप-स्थान प्रमुख दिशाओं द्वारा विस्तार हुआ है।[68]
गैर-ऋणात्मक आव्युह गुणन
आंशिक अवशिष्ट भिन्नता तुलना, पीसीए और एनएमएफ पीसीए और एनएमएफ के लिए आंशिक अवशिष्ट भिन्नता (एफआरवी) भूखंड;[24] पीसीए के लिए, सैद्धांतिक मान अवशिष्ट आइजेनवैल्यू से योगदान है। इसकी तुलना में, पीसीए के लिए एफआरवी घटता और इसको यह तक पहुंचता है जहां कोई संकेत प्रभावी रूप से नहीं पकड़ा जाता है; जबकि एनएमएफ एफआरवी घटता निरंतर गिर रहा है, जो संकेत पकड़ने की उत्तम क्षमता का संकेत देता है। एनएमएफ के लिए एफआरवी घटता भी पीसीए की तुलना में उच्च स्तर पर परिवर्तित होता है, जो एनएमएफ की कम-ओवरफिटिंग संपत्ति को दर्शाता है। गैर-ऋणात्मक आव्युह कारककरण (एनएमएफ) आयाम कमी विधि है जहां आव्युह में केवल गैर-ऋणात्मक अवयवों का उपयोग किया जाता है, जो कि खगोल विज्ञान में आशाजनक विधि है,[22][23][24] इस अर्थ में कि ज्योतिषीय संकेत गैर-ऋणात्मक हैं। पीसीए अवयव दूसरे के लिए ओर्थोगोनल हैं, जबकि एनएमएफ अवयव सभी गैर-ऋणात्मक हैं और इसलिए गैर-ऑर्थोगोनल आधार बनाते हैं।
पीसीए में, प्रत्येक अवयव के योगदान को उसके संबंधित आइजेनवैल्यू के परिमाण के आधार पर रैंक किया जाता है, जो कि अनुभवजन्य डेटा का विश्लेषण करने में भिन्नात्मक अवशिष्ट विचरण (एफआरवी) के समान है।[20] एनएमएफ के लिए, इसके अवयवों को केवल अनुभवजन्य एफआरवी वक्रों के आधार पर रैंक किया गया है।[24] अवशिष्ट भिन्नात्मक आइजेनवैल्यू भूखंड, अर्थात, अवयव संख्या के फंक्सन के रूप में कुल दिया अवयव , पीसीए के लिए समतल पठार है, जहां अर्ध-स्थैतिक ध्वनि को दूर करने के लिए कोई डेटा कैप्वेरिएबल नहीं किया जाता है, पुनः ओवर-फिटिंग के संकेत के रूप में घटता शीघ्रता से गिर जाता है और यादृच्छिक ध्वनि को पकड़ लेता है।[20] एनएमएफ के लिए एफआरवी घटता निरंतर घट रहा है[24] जब एनएमएफ अवयवों का निर्माण किया जाता है तब गैर-ऋणात्मक आव्युह गुणन या अनुक्रमिक एनएमएफ ,[23] अर्ध-स्थैतिक ध्वनि के निरंतर कैप्वेरिएबल का संकेत; पुनः पीसीए की तुलना में उच्च स्तर पर अभिसरण करें,[24] एनएमएफ की कम ओवरफिटिंग संपत्ति का संकेत दिया है ।
सहसंबंधों की प्रतीकात्मकता
मुख्य अवयवों की व्याख्या करना अधिकतर मुश्किल होता है जब डेटा में विभिन्न उत्पत्ति के अनेक वेरिएबल सम्मिलित होते हैं, या जब कुछ वेरिएबल गुणात्मक होते हैं। यह पीसीए उपयोगकर्ता को अनेक वेरिएबलों के नाजुक उन्मूलन की ओर ले जाता है। यदि टिप्पणियों या वेरिएबल का अक्षों की दिशा पर अत्यधिक प्रभाव पड़ता है, तब उन्हें हटा दिया जाना चाहिए और पुनः पूरक अवयवों के रूप में प्रक्षेपित किया जाना चाहिए। इसके अतिरिक्त , फैक्टोरियल प्लेन के केंद्र के समीप बिंदुओं के मध्य की निकटता की व्याख्या करने से बचना आवश्यक है।
इसके विपरीत, सहसंबंधों की प्रतिमा, जो कुल्हाड़ियों की प्रणाली पर प्रक्षेपण नहीं है, में यह कमियां नहीं हैं। इसलिए हम सभी वेरिएबल रख सकते हैं।
आरेख का सिद्धांत ठोस रेखा (धनात्मक सहसंबंध) या बिंदीदार रेखा (ऋणात्मक सहसंबंध) द्वारा सहसंबंध आव्युह के उल्लेखनीय सहसंबंधों को रेखांकित करना है।
शक्तिशाली सहसंबंध उल्लेखनीय नहीं है यदि यह प्रत्यक्ष नहीं है, किन्तु तीसरे वेरिएबल के प्रभाव के कारण होता है। इसके विपरीत, अशक्त सहसंबंध उल्लेखनीय हो सकते हैं। उदाहरण के लिए, यदि वेरिएबल Y अनेक स्वतंत्र वेरिएबलों पर निर्भर करता है, तब उनमें से प्रत्येक के साथ Y का सहसंबंध अशक्त और पुनः भी उल्लेखनीय है।
सामान्यीकरण
विरल पीसीए
पीसीए का विशेष हानि यह है कि प्रमुख अवयव सामान्यतः सभी इनपुट वेरिएबलों के रैखिक संयोजन होते हैं। विरल पीसीए केवल कुछ इनपुट वेरिएबल वाले रैखिक संयोजनों को ढूंढकर इस हानि को दूर करता है। यह इनपुट वेरिएबल्स पर स्पार्सिटी बाधा जोड़कर डेटा की डायमेंशनलिटी को कम करने के लिए प्रमुख कंपोनेंट विश्लेषण (पीसीए) की क्लासिक पद्धति का विस्तार करता है। इसके साथ अनेक दृष्टिकोण प्रस्तावित किए गए हैं
- प्रतिगमन फ्रेम,[69]
- उत्तल छूट / अर्ध-परिमित प्रोग्रामिंग फ्रेम,[70]
- सामान्यीकृत शक्ति विधि फ्रेम[71]
- वैकल्पिक अधिकतमकरण फ्रेम[72]
- शाखा-और-बाध्य तकनीकों का उपयोग करके आगे-पीछे ग्रीडी खोज और स्पष्ट विधियाँ ,[73]
- बायेसियन फॉर्मूलेशन फ्रेमवर्क।[74]
स्पार्स पीसीए के पद्धतिगत और सैद्धांतिक विकास के साथ-साथ वैज्ञानिक अध्ययनों में इसके अनुप्रयोगों की हाल ही में सर्वेक्षण पत्र में समीक्षा की गई थी।[75]
नॉनलाइनियर पीसीए

गैर-रैखिक आयामीता में कमी के अधिकांश आधुनिक विधियों पीसीए या K-साधनों में अपनी सैद्धांतिक और एल्गोरिथम जड़ें पाते हैं। पियर्सन का मूल विचार सीधी रेखा (या समतल) लेना था जो डेटा बिंदुओं के समुच्चय के लिए सबसे उपयुक्त होगा। ट्रेवर हैस्टी ने प्रमुख वक्र ्स को प्रस्तावित करके इस अवधारणा पर विस्तार किया[79] पीसीए की ज्यामितीय व्याख्या के लिए प्राकृतिक विस्तार के रूप में, जो स्पष्ट रूप से प्रोजेक्शन (गणित) के पश्चात डेटा सन्निकटन के लिए अनेक गुना निर्माण करता है, जैसा कि अंजीर में दिखाया गया है।
इलास्टिक मानचित्र एल्गोरिथम प्रमुख जियोडेसिक विश्लेषण विश्लेषण भी देखें।[80] अन्य लोकप्रिय सामान्यीकरण कर्नेल पीसीए है, जो धनात्मक निश्चित कर्नेल से जुड़े प्रजनन कर्नेल हिल्बर्ट स्पेस में किए गए पीसीए से मेल खाता है।
बहुरेखीय उप-स्थान सीखना में,[81][82][83] पीसीए को बहुरेखीय प्रमुख अवयव विश्लेषण (एमपीसीए) के लिए सामान्यीकृत किया गया है जो सीधे टेंसर प्रस्तुतियों से सुविधाओं को निकालता है। Mपीसीए को टेंसर के प्रत्येक मोड में पुनरावृत्त रूप से पीसीए करके हल किया जाता है। एमपीसीए को चेहरे की पहचान, चाल की पहचान आदि के लिए प्रयुक्त किया गया है। एमपीसीए को आगे असंबद्ध एमपीसीए, गैर-ऋणात्मक एमपीसीए और शक्तिशाली एमपीसीए तक बढ़ाया गया है।
टकर अपघटन, पैराफैक, बहु-कारक विश्लेषण, सह-जड़ता विश्लेषण, स्टेटिस और डिस्टैटिस जैसे मॉडलों के साथ n-वे प्रमुख अवयव विश्लेषण किया जा सकता है।
शक्तिशाली पीसीए
जबकि पीसीए गणितीय रूप से अधिकतम विधि (स्क्वायर्ड त्रुटि को कम करने के रूप में) पाता है, यह अभी भी डेटा में ग़ैर के प्रति संवेदनशील है जो बड़ी त्रुटियां उत्पन्न करता है, कुछ ऐसा जो विधि पहले स्थान से बचने की प्रयास करती है। इसलिए पीसीए की गणना करने से पहले आउटलेयर को हटाना आम बात है। चूँकि, कुछ संदर्भों में, आउटलेयर को पहचानना मुश्किल हो सकता है। उदाहरण के लिए, डेटा खनन एल्गोरिदम जैसे सहसंबंध क्लस्टरिंग में, क्लस्टर और आउटलेयर को पॉइंट्स का असाइनमेंट पहले से ज्ञात नहीं है। पीसीए का हाल ही में प्रस्तावित सामान्यीकरण[84] भारित पीसीए के आधार पर डेटा ऑब्जेक्ट्स को उनकी अनुमानित प्रासंगिकता के आधार पर भिन्न -भिन्न भार देकर शक्तिशाली बढ़ जाती है।
L1-नॉर्म फॉर्मूलेशन (L1-मानक प्रमुख अवयव विश्लेषण | L1-पीसीए) के आधार पर पीसीए के बाहरी-प्रतिरोधी वेरिएंट भी प्रस्तावित किए गए हैं।[6][4]
शक्तिशाली प्रमुख अवयव विश्लेषण (आरपीसीए ) निम्न-श्रेणी और विरल मैट्रिसेस में अपघटन के माध्यम से पीसीए का संशोधन है जो व्यापक रूप से दूषित टिप्पणियों के संबंध में अच्छी तरह से काम करता है।[85][86][87]
समान तकनीकें
स्वतंत्र अवयव विश्लेषण
स्वतंत्र अवयव विश्लेषण (आईसीए) को प्रमुख अवयव विश्लेषण के समान समस्याओं के लिए निर्देशित किया जाता है, किन्तु क्रमिक अनुमानों के अतिरिक्त योगात्मक रूप से वियोज्य अवयवों को ढूंढता है।
नेटवर्क अवयव विश्लेषण
आव्युह दिया, यह इसे दो मैट्रिसेस में विघटित करने की प्रयास करता है . पीसीए और आईसीए जैसी तकनीकों से महत्वपूर्ण अंतर यह है कि कुछ प्रविष्टियां 0. यहाँ विवश हैं और नियामक परत कहा जाता है। जबकि सामान्यतः इस तरह के अपघटन के अनेक समाधान हो सकते हैं, वह सिद्ध करते हैं कि यदि निम्नलिखित नियम में पूर्ण होती हैं:
- पूर्ण स्तंभ रैंक है
- का प्रत्येक स्तंभ कम से कम होना चाहिए शून्य जहाँ के स्तंभों की संख्या है (या वैकल्पिक रूप से पंक्तियों की संख्या ). इस मानदंड के लिए औचित्य यह है कि यदि नोड को विनियामक परत से हटा दिया जाता है, साथ ही इससे जुड़े सभी आउटपुट नोड्स के साथ, परिणाम अभी भी पूर्ण स्तंभ रैंक के साथ कनेक्टिविटी आव्युह द्वारा विशेषता होना चाहिए।
- पूरी पंक्ति रैंक होनी चाहिए।
तब अपघटन अदिश द्वारा गुणन तक अद्वितीय होता है।[88]
प्रमुख अवयवों का विभेदक विश्लेषण
प्रमुख कंपोनेंट्स (डीएपीसी) का डिस्क्रिमिनेंट विश्लेषण बहुभिन्नरूपी विधि है जिसका उपयोग आनुवंशिक रूप से संबंधित व्यक्तियों के समूहों की पहचान करने और उनका वर्णन करने के लिए किया जाता है। आनुवंशिक भिन्नता को दो अवयवों में विभाजित किया गया है: समूहों के मध्य और समूहों के अंदर भिन्नता, और यह पूर्व को अधिकतम करती है। रेखीय विभेदक युग्मविकल्पी के रेखीय संयोजन होते हैं जो गुच्छों को सर्वोत्तम रूप से भिन्न करते हैं। एलील्स जो इस भेदभाव में सबसे अधिक योगदान करते हैं, इसलिए वह हैं जो समूहों में सबसे अधिक स्पष्ट रूप से भिन्न हैं। डीएपीसी द्वारा पहचाने गए समूहों में एलील्स का योगदान समूहों के मध्य आनुवंशिक विचलन को चलाने वाले जीनोम के क्षेत्रों की पहचान करने की अनुमति दे सकता है।[89] डीएपीसी में, डेटा को पहले प्रमुख अवयव विश्लेषण (पीसीए ) का उपयोग करके रूपांतरित किया जाता है और इसके पश्चात इसमें विभेदक विश्लेषण (डीए) का उपयोग करके समूहों की पहचान की जाती है।
एडिजनेट पैकेज का उपयोग करके R पर डीएपीसी से (अधिक सूचना: एडिजनेट वेब पर) प्राप्त किया जा सकता है
दिशात्मक अवयव विश्लेषण
दिशात्मक अवयव विश्लेषण (डीसीए ) बहुभिन्नरूपी डेटासमुच्चय के विश्लेषण के लिए वायुमंडलीय विज्ञान में उपयोग की जाने वाली विधि है।[90] पीसीए की तरह, यह आयाम में कमी, उत्तम विज़ुअलाइज़ेशन और बड़े डेटा-समुच्चय की उत्तम व्याख्या करने की अनुमति देता है। पीसीए की तरह, यह इनपुट डेटासमुच्चय से प्राप्त सहप्रसरण आव्युह पर आधारित है। पीसीए और डीसीए के मध्य अंतर यह है कि डीसीए को सदिश दिशा के इनपुट की अतिरिक्त आवश्यकता होती है, जिसे प्रभाव कहा जाता है। जबकि पीसीए स्पष्ट विचरण को अधिकतम करता है, डीसीए प्रभाव को देखते हुए संभाव्यता घनत्व को अधिकतम करता है। डीसीए के लिए प्रेरणा बहुभिन्नरूपी डेटासमुच्चय के अवयवों को खोजना है जो संभावित (संभाव्यता घनत्व का उपयोग करके मापा गया) और महत्वपूर्ण (प्रभाव का उपयोग करके मापा गया) दोनों हैं। डीसीए का उपयोग मौसम पूर्वानुमान समूहों में सबसे संभावित और सबसे गंभीर हीट-वेव पैटर्न खोजने के लिए किया गया है[91] और जलवायु परिवर्तन के कारण वर्षा में सबसे संभावित और सबसे प्रभावशाली परिवर्तन होता हैं |[92]
सॉफ्टवेयर/स्रोत कोड
- अल्ग्लिब - C++ और C लाइब्रेरी जो पीसीए को प्रयुक्त करती है और पीसीए को लघु करती है
- एनालिटिका (सॉफ्टवेयर) - बिल्ट-इन ईजेनडेकॉम्प फलन प्रमुख अवयवों की गणना करता है।
- ईएलकेआई - प्रक्षेपण के लिए पीसीए सम्मिलित है, जिसमें पीसीए के शक्तिशाली वेरिएंट, साथ ही पीसीए-आधारित क्लस्टर विश्लेषण सम्मिलित हैं।
- ग्रेटल - प्रमुख अवयव विश्लेषण या तब के माध्यम से किया जा सकता है
pcaकमांड या के माध्यम सेprincomp()फंक्सन हैं। - जूलिया भाषा - के साथ पीसीए का समर्थन करता है
pcaमल्टीवेरिएटस्टैट्स पैकेज में कार्य करता है - नाइमे - विश्लेषण के लिए जावा आधारित नोडल व्यवस्था सॉफ्टवेयर, इसमें पीसीए, पीसीए कंप्यूट, पीसीए अप्लाई, पीसीए इनवर्स नामक नोड्स इसे सरलता से बनाते हैं।
- मेपल (सॉफ्टवेयर) - पीसीए कमांड का उपयोग डेटा के समुच्चय पर प्रमुख अवयव विश्लेषण करने के लिए किया जाता है।
- मेथेमेटिका - सहप्रसरण और सहसंबंध विधियों दोनों का उपयोग करके प्रमुख कंपोनेंट्स कमांड के साथ प्रमुख कंपोनेंट विश्लेषण प्रयुक्त करता है।
- गणितपीएचपी - पीसीए के समर्थन के साथ पीएचपी गणित पुस्तकालय हैं।
- मैटलैब - एसवीडी फलन मूल प्रणाली का हिस्सा है। सांख्यिकी टूलबॉक्स में, कार्य
princompऔरpca(R2012b) प्रमुख अवयव देते हैं, जबकि कार्यpcaresनिम्न-रैंक पीसीए सन्निकटन के लिए अवशिष्ट और पुनर्निर्मित आव्युह देता है। - माटप्लोटलिब – पायथन (प्रोग्रामिंग लैंग्वेज) लाइब्रेरी में .एमएलएबी मॉड्यूल में पीसीए पैकेज है।
- माइपैक - C++ में प्रमुख अवयव विश्लेषण का कार्यान्वयन प्रदान करता है।
- मर्मठ - डेल्फी (सॉफ्टवेयर) और फ़्री समीप्कल के लिए उच्च प्रदर्शन गणित पुस्तकालय पीसीए शक्तिशाली वेरिएंट सहित कर सकता है।
- एनएजी न्यूमेरिकल लाइब्रेरी - प्रधान अवयव विश्लेषण के माध्यम से कार्यान्वित किया जाता है जो
g03aaदिनचर्या (पुस्तकालय के दोनों फोरट्रान संस्करणों में उपलब्ध) हैं। - एनमैथ - .नेट फ्रेमवर्क के लिए पीसीए युक्त प्रोप्राइटरी संख्यात्मक पुस्तकालय हैं।
- जीएनयू ऑक्टेव - मुफ्त सॉफ्टवेयर कम्प्यूटेशनल वातावरण ज्यादातर मैटलैब, फलन के साथ संगत है
princompप्रमुख अवयव देता है। - ओपनसीवी
- ओरेकल डाटाबेस 12c - के माध्यम से प्रयुक्त किया गया
DBMS_DATA_MINING.SVDS_SCORING_MODEसेटिंग मान निर्दिष्ट करकेSVDS_SCORING_पीसीएहैं | - ऑरेंज (सॉफ्टवेयर) - अपने दृश्य प्रोग्रामिंग वातावरण में पीसीए को एकीकृत करता है। पीसीए स्क्री प्लॉट (व्याख्या विचरण की डिग्री) प्रदर्शित करता है जहां उपयोगकर्ता प्रमुख अवयवों की संख्या को अंतःक्रियात्मक रूप से चुन सकता है।
- उत्पत्ति (डेटा विश्लेषण सॉफ्टवेयर) - इसके प्रो संस्करण में पीसीए सम्मिलित है।
- क्लोकोर - पीसीए का उपयोग करके त्वरित प्रतिक्रिया के साथ बहुभिन्नरूपी डेटा का विश्लेषण करने के लिए वाणिज्यिक सॉफ्टवेयर हैं।
- आर (प्रोग्रामिंग भाषा) - मुफ्त सॉफ्टवेयर सांख्यिकीय पैकेज, कार्य
princompऔरprcompप्रमुख अवयव विश्लेषण के लिए उपयोग किया जा सकता है;prcompएकवचन मान अपघटन का उपयोग करता है जो सामान्यतः उत्तम संख्यात्मक स्पष्टता देता है। आर में पीसीए को प्रयुक्त करने वाले कुछ पैकेजों में सम्मिलित हैं, किन्तु यह इन तक सीमित नहीं हैं:ade4,vegan,ExPosition,dimRed, औरFactoMineR. हैं | - एसएएस (सॉफ्टवेयर) - प्रोप्राइटरी सॉफ्टवेयर; उदाहरण के लिए देखें [93]
- स्किकिट-सीखें - मशीन लर्निंग के लिए पायथन लाइब्रेरी जिसमें अपघटन मॉड्यूल में पीसीए, प्रोबेबिलिस्टिक पीसीए, कर्नेल पीसीए, स्पार्स पीसीए और अन्य तकनीकें सम्मिलित हैं।
- साइलैब - फ्री और ओपन-सोर्स, क्रॉस-प्लेटफॉर्म न्यूमेरिकल कम्प्यूटेशनल पैकेज, फंक्शन
princompप्रमुख अवयव विश्लेषण, फलन की गणना करता हैpcaमानकीकृत वेरिएबलों के साथ प्रमुख अवयव विश्लेषण की गणना करता है। - एसपीएसएस - पीसीए, कारक विश्लेषण और संबंधित क्लस्टर विश्लेषण के लिए सामाजिक वैज्ञानिकों द्वारा सामान्यतः उपयोग किया जाने वाला प्रोप्राइटरी सॉफ्टवेयर हैं।
- वीका (मशीन लर्निंग) - मशीन लर्निंग के लिए जावा लाइब्रेरी जिसमें प्रमुख अवयवों की गणना के लिए मॉड्यूल होते हैं।
यह भी देखें
- कॉरेस्पोंडेंस विश्लेषण (आकस्मिक तालिकाओं के लिए)
- एकाधिक कॉरेस्पोंडेंस विश्लेषण (गुणात्मक वेरिएबल के लिए)
- मिश्रित डेटा का कारक विश्लेषण (मात्रात्मक और गुणात्मक वेरिएबल के लिए)
- कैननिकल सहसंबंध
- सी.यू.आर आव्युह सन्निकटन (निम्न-रैंक एस वी डी सन्निकटन की जगह ले सकता है)
- डिट्रेंडेड कॉरेस्पोंडेंस विश्लेषण
- दिशात्मक अवयव विश्लेषण
- गतिशील मोड अपघटन
- आइजेनफेस
- अपेक्षा-अधिकतमकरण एल्गोरिथम
- v: अन्वेषी कारक विश्लेषण (विकिविश्वविद्यालय)
- क्रमगुणित कोड
- कार्यात्मक प्रमुख अवयव विश्लेषण
- ज्यामितीय डेटा विश्लेषण
- स्वतंत्र घटक विश्लेषण
- कर्नेल पीसीए
- L1-मानक प्रमुख घटक विश्लेषण
- निम्न-श्रेणी सन्निकटन
- आव्युह अपघटन
- गैर-ऋणात्मक आव्युह गुणनखंड
- गैर रेखीय आयामीता में कमी
- ओजा रुल
- बिंदु वितरण मॉडल (पीसीए मॉर्फोमेट्री और कंप्यूटर विजन पर प्रयुक्त होता है)
- बी: सांख्यिकी/बहुभिन्नरूपी डेटा विश्लेषण/प्रमुख अवयव विश्लेषण (विकिपुस्तक)
- प्रधान अवयव प्रतिगमन
- एकवचन स्पेक्ट्रम विश्लेषण
- विलक्षण मान अपघटन
- विरल पीसीए
- रूपांतरण कोडिंग
- भारित न्यूनतम वर्ग
संदर्भ
- ↑ Jolliffe, Ian T.; Cadima, Jorge (2016-04-13). "Principal component analysis: a review and recent developments". Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences. 374 (2065): 20150202. doi:10.1098/rsta.2015.0202. PMC 4792409. PMID 26953178.
- ↑ Barnett, T. P. & R. Preisendorfer. (1987). "कैनोनिकल सहसंबंध विश्लेषण द्वारा निर्धारित संयुक्त राज्य सतह हवा के तापमान के लिए मासिक और मौसमी पूर्वानुमान कौशल की उत्पत्ति और स्तर". Monthly Weather Review. 115 (9): 1825. Bibcode:1987MWRv..115.1825B. doi:10.1175/1520-0493(1987)115<1825:oaloma>2.0.co;2.
- ↑ Hsu, Daniel; Kakade, Sham M.; Zhang, Tong (2008). छिपे हुए मार्कोव मॉडल सीखने के लिए एक स्पेक्ट्रल एल्गोरिदम. arXiv:0811.4413. Bibcode:2008arXiv0811.4413H.
- ↑ 4.0 4.1 Markopoulos, Panos P.; Kundu, Sandipan; Chamadia, Shubham; Pados, Dimitris A. (15 August 2017). "बिट फ़्लिपिंग के माध्यम से कुशल एल1-नॉर्म प्रिंसिपल-कंपोनेंट विश्लेषण". IEEE Transactions on Signal Processing. 65 (16): 4252–4264. arXiv:1610.01959. Bibcode:2017ITSP...65.4252M. doi:10.1109/TSP.2017.2708023. S2CID 7931130.
- ↑ 5.0 5.1 Chachlakis, Dimitris G.; Prater-Bennette, Ashley; Markopoulos, Panos P. (22 November 2019). "एल1-मानदंड टकर टेन्सर अपघटन". IEEE Access. 7: 178454–178465. arXiv:1904.06455. doi:10.1109/ACCESS.2019.2955134.
- ↑ 6.0 6.1 Markopoulos, Panos P.; Karystinos, George N.; Pados, Dimitris A. (October 2014). "एल1-सबस्पेस सिग्नल प्रोसेसिंग के लिए इष्टतम एल्गोरिदम". IEEE Transactions on Signal Processing. 62 (19): 5046–5058. arXiv:1405.6785. Bibcode:2014ITSP...62.5046M. doi:10.1109/TSP.2014.2338077. S2CID 1494171.
- ↑ Zhan, J.; Vaswani, N. (2015). "आंशिक सबस्पेस ज्ञान के साथ मजबूत पीसीए". IEEE Transactions on Signal Processing. 63 (13): 3332–3347. arXiv:1403.1591. Bibcode:2015ITSP...63.3332Z. doi:10.1109/tsp.2015.2421485. S2CID 1516440.
- ↑ Kanade, T.; Ke, Qifa (June 2005). वैकल्पिक उत्तल प्रोग्रामिंग द्वारा बाहरी तत्वों की उपस्थिति और अनुपलब्ध डेटा में मजबूत L1 मानक गुणनखंडन. p. 739. CiteSeerX 10.1.1.63.4605. doi:10.1109/CVPR.2005.309. ISBN 978-0-7695-2372-9. S2CID 17144854.
{{cite book}}:|journal=ignored (help) - ↑ Pearson, K. (1901). "अंतरिक्ष में बिंदुओं के सिस्टम के निकटतम फिट की रेखाओं और विमानों पर". Philosophical Magazine. 2 (11): 559–572. doi:10.1080/14786440109462720.
- ↑ Hotelling, H. (1933). Analysis of a complex of statistical variables into principal components. Journal of Educational Psychology, 24, 417–441, and 498–520.
Hotelling, H (1936). "Relations between two sets of variates". Biometrika. 28 (3/4): 321–377. doi:10.2307/2333955. JSTOR 2333955. - ↑ Stewart, G. W. (1993). "On the early history of the singular value decomposition". SIAM Review. 35 (4): 551–566. doi:10.1137/1035134.
- ↑ 12.0 12.1 12.2 12.3 12.4 Jolliffe, I. T. (2002). प्रमुख कंपोनेंट विश्लेषण. Springer Series in Statistics (in English). New York: Springer-Verlag. doi:10.1007/b98835. ISBN 978-0-387-95442-4.
- ↑ Bengio, Y.; et al. (2013). "Representation Learning: A Review and New Perspectives". IEEE Transactions on Pattern Analysis and Machine Intelligence. 35 (8): 1798–1828. arXiv:1206.5538. doi:10.1109/TPAMI.2013.50. PMID 23787338. S2CID 393948.
- ↑ Forkman J., Josse, J., Piepho, H. P. (2019). "प्रमुख घटक विश्लेषण के लिए परिकल्पना परीक्षण जब चर मानकीकृत होते हैं". Journal of Agricultural, Biological, and Environmental Statistics. 24 (2): 289–308. doi:10.1007/s13253-019-00355-5.
{{cite journal}}: CS1 maint: multiple names: authors list (link) - ↑ A. A. Miranda, Y. A. Le Borgne, and G. Bontempi. New Routes from Minimal Approximation Error to Principal Components, Volume 27, Number 3 / June, 2008, Neural Processing Letters, Springer
- ↑ Fukunaga, Keinosuke (1990). सांख्यिकीय पैटर्न पहचान का परिचय. Elsevier. ISBN 978-0-12-269851-4.
- ↑ Alizadeh, Elaheh; Lyons, Samanthe M; Castle, Jordan M; Prasad, Ashok (2016). "Zernike मोमेंट्स का उपयोग करके आक्रामक कैंसर सेल आकार में व्यवस्थित परिवर्तनों को मापना". Integrative Biology. 8 (11): 1183–1193. doi:10.1039/C6IB00100A. PMID 27735002.
- ↑ Leznik, M; Tofallis, C. 2005 Estimating Invariant Principal Components Using Diagonal Regression.
- ↑ Jonathon Shlens, A Tutorial on Principal Component Analysis.
- ↑ 20.0 20.1 20.2 Soummer, Rémi; Pueyo, Laurent; Larkin, James (2012). "Detection and Characterization of Exoplanets and Disks Using Projections on Karhunen-Loève Eigenimages". The Astrophysical Journal Letters. 755 (2): L28. arXiv:1207.4197. Bibcode:2012ApJ...755L..28S. doi:10.1088/2041-8205/755/2/L28. S2CID 51088743.
- ↑ Pueyo, Laurent (2016). "Detection and Characterization of Exoplanets using Projections on Karhunen Loeve Eigenimages: Forward Modeling". The Astrophysical Journal. 824 (2): 117. arXiv:1604.06097. Bibcode:2016ApJ...824..117P. doi:10.3847/0004-637X/824/2/117. S2CID 118349503.
- ↑ 22.0 22.1 Blanton, Michael R.; Roweis, Sam (2007). "के-सुधार और पराबैंगनी, ऑप्टिकल और निकट अवरक्त में परिवर्तन". The Astronomical Journal. 133 (2): 734–754. arXiv:astro-ph/0606170. Bibcode:2007AJ....133..734B. doi:10.1086/510127. S2CID 18561804.
- ↑ 23.0 23.1 23.2 Zhu, Guangtun B. (2016-12-19). "गैर-ऋणात्मक मैट्रिक्स गुणनखंडन (NMF) विषमलैंगिक अनिश्चितताओं और लापता डेटा के साथ". arXiv:1612.06037 [astro-ph.IM].
- ↑ 24.0 24.1 24.2 24.3 24.4 24.5 Ren, Bin; Pueyo, Laurent; Zhu, Guangtun B.; Duchêne, Gaspard (2018). "Non-negative Matrix Factorization: Robust Extraction of Extended Structures". The Astrophysical Journal. 852 (2): 104. arXiv:1712.10317. Bibcode:2018ApJ...852..104R. doi:10.3847/1538-4357/aaa1f2. S2CID 3966513.
- ↑ "What are the Pros and cons of the PCA?". i2tutorials. September 1, 2019. Retrieved June 4, 2021.
- ↑ Abbott, Dean (May 2014). एप्लाइड प्रिडिक्टिव एनालिटिक्स. Wiley. ISBN 9781118727966.
- ↑ 27.0 27.1 Jiang, Hong; Eskridge, Kent M. (2000). "सहसंबद्ध प्रेक्षणों के कारण प्रधान घटक विश्लेषण में पक्षपात". Conference on Applied Statistics in Agriculture. doi:10.4148/2475-7772.1247. ISSN 2475-7772.
- ↑ Linsker, Ralph (March 1988). "एक अवधारणात्मक नेटवर्क में स्व-संगठन". IEEE Computer. 21 (3): 105–117. doi:10.1109/2.36. S2CID 1527671.
- ↑ Deco & Obradovic (1996). तंत्रिका कम्प्यूटिंग के लिए एक सूचना-सैद्धांतिक दृष्टिकोण. New York, NY: Springer. ISBN 9781461240167.
- ↑ Plumbley, Mark (1991). सूचना सिद्धांत और अनुपयोगी तंत्रिका नेटवर्क.Tech Note
- ↑ Geiger, Bernhard; Kubin, Gernot (January 2013). "प्रासंगिक सूचना हानि को कम करने के रूप में सिग्नल वृद्धि". Proc. ITG Conf. On Systems, Communication and Coding. arXiv:1205.6935. Bibcode:2012arXiv1205.6935G.
- ↑ "Engineering Statistics Handbook Section 6.5.5.2". Retrieved 19 January 2015.
- ↑ A.A. Miranda, Y.-A. Le Borgne, and G. Bontempi. New Routes from Minimal Approximation Error to Principal Components, Volume 27, Number 3 / June, 2008, Neural Processing Letters, Springer
- ↑ Abdi. H. & Williams, L.J. (2010). "प्रमुख कंपोनेंट विश्लेषण". Wiley Interdisciplinary Reviews: Computational Statistics. 2 (4): 433–459. arXiv:1108.4372. doi:10.1002/wics.101. S2CID 122379222.
- ↑ "SAS/STAT(R) 9.3 User's Guide".
- ↑ eig function Matlab documentation
- ↑ "चेहरा पहचान प्रणाली-पीसीए आधारित". www.mathworks.com.
- ↑ Eigenvalues function Mathematica documentation
- ↑ Roweis, Sam. "EM Algorithms for PCA and SPCA." Advances in Neural Information Processing Systems. Ed. Michael I. Jordan, Michael J. Kearns, and Sara A. Solla The MIT Press, 1998.
- ↑ Geladi, Paul; Kowalski, Bruce (1986). "Partial Least Squares Regression:A Tutorial". Analytica Chimica Acta. 185: 1–17. doi:10.1016/0003-2670(86)80028-9.
- ↑ Kramer, R. (1998). मात्रात्मक विश्लेषण के लिए रसायनमितीय तकनीक. New York: CRC Press. ISBN 9780203909805.
- ↑ Andrecut, M. (2009). "इटरेटिव पीसीए एल्गोरिदम का समानांतर जीपीयू कार्यान्वयन". Journal of Computational Biology. 16 (11): 1593–1599. arXiv:0811.1081. doi:10.1089/cmb.2008.0221. PMID 19772385. S2CID 1362603.
- ↑ Warmuth, M. K.; Kuzmin, D. (2008). "Randomized online PCA algorithms with regret bounds that are logarithmic in the dimension" (PDF). Journal of Machine Learning Research. 9: 2287–2320.
- ↑ Kaplan, R.M., & Saccuzzo, D.P. (2010). Psychological Testing: Principles, Applications, and Issues. (8th ed.). Belmont, CA: Wadsworth, Cengage Learning.
- ↑ Shevky, Eshref; Williams, Marilyn (1949). The Social Areas of Los Angeles: Analysis and Typology. University of California Press.
- ↑ Flood, J (2000). Sydney divided: factorial ecology revisited. Paper to the APA Conference 2000, Melbourne,November and to the 24th ANZRSAI Conference, Hobart, December 2000.[1]
- ↑ "क्षेत्रों के लिए सामाजिक-आर्थिक सूचकांक". Australian Bureau of Statistics (in English). 2011. Retrieved 2022-05-05.
- ↑ Human Development Reports. "मानव विकास सूचकांक". United Nations Development Programme. Retrieved 2022-05-06.
- ↑ Novembre, John; Stephens, Matthew (2008). "स्थानिक जनसंख्या आनुवंशिक भिन्नता के प्रमुख घटक विश्लेषण की व्याख्या करना". Nat Genet. 40 (5): 646–49. doi:10.1038/ng.139. PMC 3989108. PMID 18425127.
- ↑ Elhaik, Eran (2022). "Principal Component Analyses (PCA)‑based findings in population genetic studies are highly biased and must be reevaluated". Scientific Reports. 12 (1). 14683. doi:10.1038/s41598-022-14395-4. PMC 9424212. PMID 36038559. S2CID 251932226.
- ↑ DeSarbo, Wayne; Hausmann, Robert; Kukitz, Jeffrey (2007). "विपणन अनुसंधान के लिए प्रतिबंधित प्रमुख घटक विश्लेषण". Journal of Marketing in Management. 2: 305–328 – via Researchgate.
- ↑ Dutton, William H; Blank, Grant (2013). Cultures of the Internet: The Internet in Britain (PDF). Oxford Internet Institute. p. 6.
- ↑ Flood, Joe (2008). "हाउसिंग करियर सर्वे के लिए बहुराष्ट्रीय विश्लेषण". Paper to the European Network for Housing Research Conference, Dublin. Retrieved 6 May 2022.
- ↑ The Pricing and Hedging of Interest Rate Derivatives: A Practical Guide to Swaps, J H M Darbyshire, 2016, ISBN 978-0995455511
- ↑ Giorgia Pasini (2017); Principal Component Analysis for Stock Portfolio Management. International Journal of Pure and Applied Mathematics. Volume 115 No. 1 2017, 153–167
- ↑ Libin Yang. An Application of Principal Component Analysis to Stock Portfolio Management. Department of Economics and Finance, University of Canterbury, January 2015.
- ↑ Chapin, John; Nicolelis, Miguel (1999). "न्यूरोनल पहनावा गतिविधि के प्रधान घटक विश्लेषण से बहुआयामी सोमाटोसेंसरी अभ्यावेदन का पता चलता है". Journal of Neuroscience Methods. 94 (1): 121–140. doi:10.1016/S0165-0270(99)00130-2. PMID 10638820.
- ↑ Brenner, N., Bialek, W., & de Ruyter van Steveninck, R.R. (2000).
- ↑ Jirsa, Victor; Friedrich, R; Haken, Herman; Kelso, Scott (1994). "मानव मस्तिष्क में चरण संक्रमण का एक सैद्धांतिक मॉडल". Biological Cybernetics. 71 (1): 27–35. doi:10.1007/bf00198909. PMID 8054384. S2CID 5155075.
- ↑ Benzécri, J.-P. (1973). L'Analyse des Données. Volume II. L'Analyse des Correspondances. Paris, France: Dunod.
- ↑ Greenacre, Michael (1983). Theory and Applications of Correspondence Analysis. London: Academic Press. ISBN 978-0-12-299050-2.
- ↑ Le Roux; Brigitte and Henry Rouanet (2004). Geometric Data Analysis, From Correspondence Analysis to Structured Data Analysis. Dordrecht: Kluwer. ISBN 9781402022357.
- ↑ Timothy A. Brown. Confirmatory Factor Analysis for Applied Research Methodology in the social sciences. Guilford Press, 2006
- ↑ Meglen, R.R. (1991). "Examining Large Databases: A Chemometric Approach Using Principal Component Analysis". Journal of Chemometrics. 5 (3): 163–179. doi:10.1002/cem.1180050305. S2CID 120886184.
- ↑ H. Zha; C. Ding; M. Gu; X. He; H.D. Simon (Dec 2001). "K- साधन क्लस्टरिंग के लिए वर्णक्रमीय विश्राम" (PDF). Neural Information Processing Systems Vol.14 (NIPS 2001): 1057–1064.
- ↑ Chris Ding; Xiaofeng He (July 2004). "K- साधन प्रमुख घटक विश्लेषण के माध्यम से क्लस्टरिंग" (PDF). Proc. Of Int'l Conf. Machine Learning (ICML 2004): 225–232.
- ↑ Drineas, P.; A. Frieze; R. Kannan; S. Vempala; V. Vinay (2004). "एकवचन मूल्य अपघटन के माध्यम से बड़े रेखांकन को क्लस्टर करना" (PDF). Machine Learning. 56 (1–3): 9–33. doi:10.1023/b:mach.0000033113.59016.96. S2CID 5892850. Retrieved 2012-08-02.
- ↑ Cohen, M.; S. Elder; C. Musco; C. Musco; M. Persu (2014). के-मीन्स क्लस्टरिंग और निम्न रैंक सन्निकटन के लिए आयाम में कमी (परिशिष्ट बी). arXiv:1410.6801. Bibcode:2014arXiv1410.6801C.
- ↑ Hui Zou; Trevor Hastie; Robert Tibshirani (2006). "Sparse principal component analysis" (PDF). Journal of Computational and Graphical Statistics. 15 (2): 262–286. CiteSeerX 10.1.1.62.580. doi:10.1198/106186006x113430. S2CID 5730904.
- ↑ Alexandre d'Aspremont; Laurent El Ghaoui; Michael I. Jordan; Gert R. G. Lanckriet (2007). "A Direct Formulation for Sparse PCA Using Semidefinite Programming" (PDF). SIAM Review. 49 (3): 434–448. arXiv:cs/0406021. doi:10.1137/050645506. S2CID 5490061.
- ↑ Michel Journee; Yurii Nesterov; Peter Richtarik; Rodolphe Sepulchre (2010). "Generalized Power Method for Sparse Principal Component Analysis" (PDF). Journal of Machine Learning Research. 11: 517–553. arXiv:0811.4724. Bibcode:2008arXiv0811.4724J. CORE Discussion Paper 2008/70.
- ↑ Peter Richtarik; Martin Takac; S. Damla Ahipasaoglu (2012). "Alternating Maximization: Unifying Framework for 8 Sparse PCA Formulations and Efficient Parallel Codes". arXiv:1212.4137 [stat.ML].
- ↑ Baback Moghaddam; Yair Weiss; Shai Avidan (2005). "Spectral Bounds for Sparse PCA: Exact and Greedy Algorithms" (PDF). Advances in Neural Information Processing Systems. Vol. 18. MIT Press.
- ↑ Yue Guan; Jennifer Dy (2009). "Sparse Probabilistic Principal Component Analysis" (PDF). Journal of Machine Learning Research Workshop and Conference Proceedings. 5: 185.
- ↑ Hui Zou; Lingzhou Xue (2018). "A Selective Overview of Sparse Principal Component Analysis". Proceedings of the IEEE. 106 (8): 1311–1320. doi:10.1109/JPROC.2018.2846588.
- ↑ A. N. Gorban, A. Y. Zinovyev, "Principal Graphs and Manifolds", In: Handbook of Research on Machine Learning Applications and Trends: Algorithms, Methods and Techniques, Olivas E.S. et al Eds. Information Science Reference, IGI Global: Hershey, PA, USA, 2009. 28–59.
- ↑ Wang, Y.; Klijn, J. G.; Zhang, Y.; Sieuwerts, A. M.; Look, M. P.; Yang, F.; Talantov, D.; Timmermans, M.; Meijer-van Gelder, M. E.; Yu, J.; et al. (2005). "लिम्फ-नोड-नकारात्मक प्राथमिक स्तन कैंसर के दूर के मेटास्टेसिस की भविष्यवाणी करने के लिए जीन अभिव्यक्ति प्रोफाइल". The Lancet. 365 (9460): 671–679. doi:10.1016/S0140-6736(05)17947-1. PMID 15721472. S2CID 16358549. Data online
- ↑ Zinovyev, A. "ViDaExpert – Multidimensional Data Visualization Tool". Institut Curie. Paris. (free for non-commercial use)
- ↑ Hastie, T.; Stuetzle, W. (June 1989). "प्रधान वक्र" (PDF). Journal of the American Statistical Association. 84 (406): 502–506. doi:10.1080/01621459.1989.10478797.
- ↑ A.N. Gorban, B. Kegl, D.C. Wunsch, A. Zinovyev (Eds.), Principal Manifolds for Data Visualisation and Dimension Reduction, LNCSE 58, Springer, Berlin – Heidelberg – New York, 2007. ISBN 978-3-540-73749-0
- ↑ Vasilescu, M.A.O.; Terzopoulos, D. (2003). Multilinear Subspace Analysis of Image Ensembles (PDF). Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR’03). Madison, WI.
- ↑ Vasilescu, M.A.O.; Terzopoulos, D. (2002). Multilinear Analysis of Image Ensembles: TensorFaces (PDF). Lecture Notes in Computer Science 2350; (Presented at Proc. 7th European Conference on Computer Vision (ECCV'02), Copenhagen, Denmark). Springer, Berlin, Heidelberg. doi:10.1007/3-540-47969-4_30. ISBN 978-3-540-43745-1.
- ↑ Vasilescu, M.A.O.; Terzopoulos, D. (June 2005). Multilinear Independent Component Analysis (PDF). Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR’05). Vol. 1. San Diego, CA. pp. 547–553.
- ↑ Kriegel, H. P.; Kröger, P.; Schubert, E.; Zimek, A. (2008). पीसीए-आधारित सहसंबंध क्लस्टरिंग एल्गोरिदम की मजबूती बढ़ाने के लिए एक सामान्य ढांचा. pp. 418–435. CiteSeerX 10.1.1.144.4864. doi:10.1007/978-3-540-69497-7_27. ISBN 978-3-540-69476-2.
{{cite book}}:|journal=ignored (help) - ↑ Emmanuel J. Candes; Xiaodong Li; Yi Ma; John Wright (2011). "Robust Principal Component Analysis?". Journal of the ACM. 58 (3): 11. arXiv:0912.3599. doi:10.1145/1970392.1970395. S2CID 7128002.
- ↑ T. Bouwmans; E. Zahzah (2014). "Robust PCA via Principal Component Pursuit: A Review for a Comparative Evaluation in Video Surveillance". Computer Vision and Image Understanding. 122: 22–34. doi:10.1016/j.cviu.2013.11.009.
- ↑ T. Bouwmans; A. Sobral; S. Javed; S. Jung; E. Zahzah (2015). "Decomposition into Low-rank plus Additive Matrices for Background/Foreground Separation: A Review for a Comparative Evaluation with a Large-Scale Dataset". Computer Science Review. 23: 1–71. arXiv:1511.01245. Bibcode:2015arXiv151101245B. doi:10.1016/j.cosrev.2016.11.001. S2CID 10420698.
- ↑ Liao, J. C.; Boscolo, R.; Yang, Y.-L.; Tran, L. M.; Sabatti, C.; Roychowdhury, V. P. (2003). "Network component analysis: Reconstruction of regulatory signals in biological systems". Proceedings of the National Academy of Sciences. 100 (26): 15522–15527. Bibcode:2003PNAS..10015522L. doi:10.1073/pnas.2136632100. PMC 307600. PMID 14673099.
- ↑ Liao, T.; Jombart, S.; Devillard, F.; Balloux (2010). "Discriminant analysis of principal components: a new method for the analysis of genetically structured populations". BMC Genetics. 11: 11:94. doi:10.1186/1471-2156-11-94. PMC 2973851. PMID 20950446.
- ↑ Jewson, S. (2020). "An Alternative to PCA for Estimating Dominant Patterns of Climate Variability and Extremes, with Application to U.S. and China Seasonal Rainfall". Atmosphere. 11 (4): 354. Bibcode:2020Atmos..11..354J. doi:10.3390/atmos11040354.
- ↑ Scher, S.; Jewson, S.; Messori, G. (2021). "Robust Worst-Case Scenarios from Ensemble Forecasts". Weather and Forecasting. 36 (4): 1357–1373. Bibcode:2021WtFor..36.1357S. doi:10.1175/WAF-D-20-0219.1. S2CID 236300040.
- ↑ Jewson, S.; Messori, G.; Barbato, G.; Mercogliano, P.; Mysiak, J.; Sassi, M. (2022). "Developing Representative Impact Scenarios From Climate Projection Ensembles, With Application to UKCP18 and EURO-CORDEX Precipitation". Journal of Advances in Modeling Earth Systems. 15 (1). doi:10.1029/2022MS003038. S2CID 254965361.
- ↑ "प्रमुख घटक विश्लेषण". Institute for Digital Research and Education. UCLA. Retrieved 29 May 2018.
अग्रिम पठन
- Jackson, J.E. (1991). A User's Guide to Principal Components (Wiley).
- Jolliffe, I. T. (1986). Principal Component Analysis. Springer Series in Statistics. Springer-Verlag. pp. 487. CiteSeerX 10.1.1.149.8828. doi:10.1007/b98835. ISBN 978-0-387-95442-4.
- Jolliffe, I. T. (2002). Principal Component Analysis. Springer Series in Statistics (in English). New York: Springer-Verlag. doi:10.1007/b98835. ISBN 978-0-387-95442-4.
- Husson François, Lê Sébastien & Pagès Jérôme (2009). Exploratory Multivariate Analysis by Example Using R. Chapman & Hall/CRC The R Series, London. 224p. ISBN 978-2-7535-0938-2
- Pagès Jérôme (2014). Multiple Factor Analysis by Example Using R. Chapman & Hall/CRC The R Series London 272 p
बाहरी संबंध
- University of Copenhagen video by Rasmus Bro on YouTube
- Stanford University video by Andrew Ng on YouTube
- A Tutorial on Principal Component Analysis
- A layman's introduction to principal component analysis on YouTube (a video of less than 100 seconds.)
- StatQuest: StatQuest: Principal Component Analysis (PCA), Step-by-Step on YouTube
- See also the list of Software implementations