यूक्लिडियन ज्यामिति: Difference between revisions

Latest revision as of 11:44, 18 August 2023

236px द स्कूल ऑफ़ एथेंस में एक यूनानी गणितज्ञ की विशेषता है - शायद यूक्लिड या आर्किमिडीज का प्रतिनिधित्व करते हुए - एक ज्यामितीय निर्माण को आकर्षित करने के लिए कम्पास (ड्राफ्टिंग) का उपयोग करना।

यूक्लिडियन ज्यामिति एक गणितीय प्रणाली होती है जिसका श्रेय प्राचीन यूनानी गणित यूक्लिड को जाता है, जिसका वर्णन उन्होंने ज्यामिति, एलिमेंट्स पर अपनी पाठ्यपुस्तक में किया है। यूक्लिड के दृष्टिकोण में सहज रूप से आकर्षक एक्सिओम्सों(अभिधारणाओं) के एक छोटे से समूह को ग्रहण करना और इनमें से कई अन्य प्रस्तावों (प्रमेय) को निकालने में सम्मिलित होता है। यद्यपि यूक्लिड के कई परिणाम पहले बताए जा चुके थे,^[1] यूक्लिड ने सर्वप्रथम इन प्रस्तावों को एक लॉजिक में व्यवस्थित किया।लॉजिकल प्रणाली जिसमें प्रत्येक परिणाम एक्सिओम्स और पहले सिद्ध प्रमेयों से गणितीय प्रमाण है।^[2]

तत्वों का प्रारम्भ प्लेन ज्योमेट्री से होता है, अभी भी माध्यमिक विद्यालय (हाई स्कूल) में पहली एक्सिओम्स प्रणाली और गणितीय प्रमाणों के पहले उदाहरण के रूप में पढ़ाया जाता है। यह तीन आयामों की ठोस ज्यामिति पर जाता है। अधिकांश तत्व उन परिणामों को बताते हैं जिन्हें अब बीजगणित और संख्या सिद्धांत कहा जाता है, जिन्हें ज्यामितीय भाषा में समझाया गया है।^[1]

दो हजार से अधिक वर्षों के लिए, विशेषण यूक्लिडियन अनावश्यक था क्योंकि किसी अन्य प्रकार की ज्यामिति की कल्पना नहीं की गई थी। यूक्लिड के एक्सिओम्स इतने सहज रूप से स्पष्ट थे ( समानांतर अभिधारणा के संभावित अपवाद के साथ) कि उनसे सिद्ध कोई भी प्रमेय एक निरपेक्ष, अधिकांशतः आध्यात्मिक, अर्थ में सत्य माना जाता था। आज, यद्यपि, कई अन्य स्व-संगत गैर-यूक्लिडियन ज्यामिति ज्ञात हैं, जो सर्वप्रथम 19वीं शताब्दी के प्रारम्भ में अन्वेषण की गई थीं। अल्बर्ट आइंस्टीन के सामान्य सापेक्षता के सिद्धांत का एक निहितार्थ यह है कि भौतिक स्थान स्वयं यूक्लिडियन नहीं होते है, और त्रि-आयामी स्पेस मात्र छोटी दूरी ( गुरुत्वाकर्षण की ताकत के सापेक्ष) पर इसके लिए एक अच्छा सन्निकटन होता है।^[3]

यूक्लिडियन ज्यामिति सिंथेटिक ज्यामिति का एक उदाहरण है, जिसमें यह उन वस्तुओं के बारे में प्रस्तावों के लिए बिंदुओं और रेखाओं जैसे ज्यामितीय वस्तुओं के मूल गुणों का वर्णन करने वाले एक्सिओम्स से लॉजिकल रूप से आगे बढ़ता है। यह विश्लेषणात्मक ज्यामिति के विपरीत है, जिसे लगभग 2,000 साल पश्चात् रेने डेसकार्टेस द्वारा प्रस्तुत किया गया था, जो बीजगणितीय सूत्रों के रूप में ज्यामितीय गुणों को व्यक्त करने के लिए निर्देशांक का उपयोग करता है।

तत्व

तत्व मुख्य रूप से ज्यामिति के पहले के ज्ञान का एक व्यवस्थितकरण होता है। पहले के उपचारों पर इसके सुधार को शीघ्रता से पहचाना गया, जिसके परिणामस्वरूप पहले वाले उपचारों को संरक्षित करने में कोई रुचि नहीं थी, और वे अब न्यूनाधिक सभी गायब हो चुके हैं।

तत्वों में 13 पुस्तकें हैं:

पुस्तकें I-IV और VI समतल ज्यामिति पर चर्चा करती हैं। समतल आकृतियों के बारे में कई परिणाम सिद्ध होते हैं, उदाहरण के लिए, किसी भी त्रिभुज में, किसी भी तरह से एक साथ लिए गए दो कोण दो समकोण से कम होते हैं। (पुस्तक I प्रस्ताव 17) और पायथागॉरियन प्रमेय समकोण त्रिभुजों में समकोण को अंतरित करने वाली भुजा का वर्ग समकोण वाले पक्षों के वर्गों के समान होता है। (पुस्तक I, प्रस्ताव 47)

पुस्तकें V और VII-X संख्या सिद्धांत से संबंधित हैं, संख्याओं को ज्यामितीय रूप से रेखा खंडों या सतह क्षेत्रों के क्षेत्रों की लंबाई के रूप में माना जाता है। अभाज्य संख्याएँ और परिमेय संख्या एँ और अपरिमेय संख्या एँ जैसी धारणाएँ प्रस्तुत की जाती हैं। यह सिद्ध हो गया है कि अपरिमित रूप से अनेक अभाज्य संख्याएँ होती हैं।

पुस्तकें XI-XIII ठोस ज्यामिति से संबंधित होती हैं। एक विशिष्ट परिणाम शंकु के आयतन और समान ऊँचाई और आधार वाले बेलन के मध्य 1:3 का अनुपात होता है। प्लेटोनिक ठोस का निर्माण किया जाता है।

एक्सिओम्स

समांतर अभिधारणा (अभिधारणा 5): यदि दो रेखाएं एक तिहाई को इस प्रकार प्रतिच्छेद करती हैं कि एक तरफ के आंतरिक कोणों का योग दो समकोणों से कम है, तो दो रेखाएं अनिवार्य रूप से एक दूसरे को उस तरफ एक दूसरे को काटती हैं यदि इसे दूर तक बढ़ाया जाए।

यूक्लिडियन ज्यामिति एक एक्सिओम्स प्रणाली है, जिसमें सभी प्रमेय (सच्चे कथन) कम संख्या में सरल एक्सिओम्स से प्राप्त होते हैं। गैर-यूक्लिडियन ज्यामिति के आगमन तक, इन एक्सिओम्सों को भौतिक दुनिया में स्पष्ट रूप से सच माना जाता था, जिससे सभी प्रमेय समान रूप से सत्य हों। यद्यपि, यूक्लिड की मान्यताओं से लेकर निष्कर्ष तक के लॉजिक उनकी भौतिक वास्तविकता से स्वतंत्र रूप से मान्य होते हैं।^[4]

तत्वों की पहली पुस्तक की प्रारम्भ के समीप, यूक्लिड विमान ज्यामिति के लिए पांच अभिगृहीत (एक्सिओम्स) देता है, जिसे निर्माण के संदर्भ में कहा गया है (जैसा कि थॉमस हीथ द्वारा अनुवादित किया गया है):^[5]

निम्नलिखित को अभिधारणा दें:

किसी भी बिंदु (ज्यामिति) से किसी भी बिंदु तक एक सीधी रेखा खींचना।
एक सीधी रेखा में निरंतर एक रेखा खंड का निर्माण (विस्तार) करना।
किसी भी केंद्र और दूरी (त्रिज्या) वाले वृत्त का वर्णन करना।
कि सभी समकोण एक दूसरे के समान हैं।
[समानांतर अभिधारणा]: कि, यदि दो सीधी रेखाओं पर गिरने वाली एक सीधी रेखा एक ही तरफ के आंतरिक कोणों को दो समकोण से कम बनाती है, तो दो सीधी रेखाएँ, यदि अनिश्चित काल तक उत्पन्न होती हैं, तो उस तरफ मिलती हैं जिस पर कोण होते हैं दो समकोण से कम।

यद्यपि यूक्लिड स्पष्ट रूप से मात्र निर्मित वस्तुओं के अस्तित्व पर अधिक महत्व देता है, अपने लॉजिक में वह यह भी मानता है कि वे अद्वितीय हैं।

तत्वों में निम्नलिखित पाँच सामान्य धारणाएँ भी सम्मिलित हैं:

चीजें जो एक ही चीज के समान होती हैं वे भी एक दूसरे के समान होती हैं ( यूक्लिडियन संबंध की सकर्मक गुण)।
यदि समान में समान जोड़ दिया जाए, तो पूर्ण समान होते हैं (समानता का योग गुण)।
यदि समान में से समान घटाया जाए, तो अंतर समान (समानता का घटाव गुण) होता है।
एक दूसरे के साथ समरूप वाली चीजें एक दूसरे के समान होती हैं (रिफ्लेक्सिव गुण)।
पूरा भाग से बड़ा होता है।

आधुनिक विद्वान इस बात से सहमत हैं कि यूक्लिड की अभिधारणाएँ पूर्ण लॉजिकल आधार प्रदान नहीं करती हैं जो यूक्लिड को अपनी प्रस्तुति के लिए आवश्यक थी।^[6] ज्यामिति की आधुनिक नींव एक्सिओम्सों के अधिक व्यापक और पूर्ण समुच्चय का उपयोग करती है।

समानांतर अभिधारणा

पूर्वजों को, समानांतर अभिधारणा दूसरों की तुलना में कम स्पष्ट लगती थी। वे बिल्कुल निश्चित प्रस्तावों की एक प्रणाली बनाने की इच्छा रखते थे, और उनके लिए, ऐसा लगता था जैसे समानांतर रेखा सरल कथनों से आवश्यक प्रमाण प्रदान करती है। अब यह ज्ञात है कि ऐसा प्रमाण असंभव है क्योंकि कोई भी ज्यामिति की सुसंगत प्रणाली (अन्य एक्सिओम्सों का पालन करते हुए) का निर्माण कर सकता है जिसमें समानांतर अभिधारणा सत्य है, और अन्य जिसमें यह गलत है।^[7] ऐसा लगता है कि यूक्लिड ने इसे दूसरों से गुणात्मक रूप से भिन्न माना है, जैसा कि तत्वों के संगठन द्वारा प्रमाणित किया गया है: उनके पहले 28 प्रस्ताव वे हैं जिन्हें इसके बिना सिद्ध किया जा सकता है।

कई वैकल्पिक अभिगृहीत निर्मितर किए जा सकते हैं जो समानांतर अभिधारणा (अन्य एक्सिओम्सों के संदर्भ में) के लॉजिकल समकक्ष हैं। उदाहरण के लिए, प्लेफेयर का एक्सिओम्स कहता है:

एक समतल (ज्यामिति) में, एक बिंदु से होकर जो दी गई सीधी रेखा पर नहीं होती है, अधिक से अधिक एक ऐसी रेखा खींची जा सकती है जो दी गई रेखा से कभी नहीं मिलती।

"अधिकतम" खंड वह है जिसकी आवश्यकता है क्योंकि शेष एक्सिओम्सों से यह सिद्ध किया जा सकता है कि कम से कम एक समानांतर रेखा उपस्थित होती है।

यूक्लिड के तत्वों से एक प्रमाण है कि, एक रेखा खंड दिया गया है, कोई एक समबाहु त्रिभुज का निर्माण कर सकता है जिसमें खंड को इसके पक्षों में से एक के रूप में सम्मिलित किया गया है: एक समबाहु त्रिभुज को और बिंदुओं पर केंद्रित वृत्त बनाकर बनाया जाता है, और त्रिभुज के तीसरे शीर्ष के रूप में वृत्तों का एक प्रतिच्छेदन होता है।

प्रमाण की विधियाँ

यूक्लिडियन ज्यामिति रचनात्मक प्रमाण है। 1, 2, 3, और 5 कुछ ज्यामितीय आकृतियों के अस्तित्व और विशिष्टता पर महत्व देते हैं, और ये दावे एक रचनात्मक प्रकृति के हैं: अर्थात्, हमें मात्र न बताया जाता है कि कुछ चीजें उपस्थित हैं, जबकि उन्हें उन्हें कम्पास और एक अचिह्नित सीधे किनारे से अधिक कुछ नहीं बनाने की विधियां भी दी जाती हैं।^[8] इस अर्थ में, यूक्लिडियन ज्यामिति कई आधुनिक एक्सिओम्स प्रणालियों की तुलना में अधिक ठोस है, जैसे कि समुच्चय सिद्धांत, जो अधिकांशतः वस्तुओं के अस्तित्व पर यह कहे बिना कि उन्हें कैसे बनाया जाए, या यहां तक कि उन वस्तुओं के अस्तित्व पर महत्व देते हैं जिन्हें सिद्धांत के भीतर निर्मित नहीं किया जा सकता है।^[9]

यूक्लिड ने अधिकांशतः विरोधाभास द्वारा प्रमाण का प्रयोग किया। यूक्लिडियन ज्यामिति भी सुपरपोजिशन की विधि की अनुमति देती है, जिसमें एक आकृति को स्पेस में दूसरे बिंदु पर स्थानांतरित किया जाता है। उदाहरण के लिए, प्रस्ताव I.4, त्रिभुजों की भुजा-कोण-भुजा सर्वांगसमता, दो त्रिभुजों में से एक को इस प्रकार घुमाकर सिद्ध किया जाता है कि इसकी एक भुजा दूसरे त्रिभुज की समान भुजा के साथ समरूप होती है, और फिर यह सिद्ध करती है कि अन्य भुजाएँ भी संपाती हैं। कुछ आधुनिक उपचारों में एक छठी अभिधारणा, त्रिभुज की कठोरता को जोड़ा जाता है, जिसे अध्यारोपण के विकल्प के रूप में प्रयोग किया जा सकता है।

संकेतन और शब्दावली

अंकों और अंकों का नामकरण

अंक सामान्यतः वर्णमाला के बड़े अक्षरों का उपयोग करके नामित किए जाते हैं। अन्य आंकड़े, जैसे कि रेखाएं, त्रिकोण, या मंडल, को प्रासंगिक आंकड़े से स्पष्ट रूप से चुनने के लिए पर्याप्त संख्या में बिंदुओं को सूचीबद्ध करके नामित किया गया है, उदाहरण के लिए, त्रिभुज एबीसी सामान्यतः बिंदु ए, बी और सी पर शिखर के साथ एक त्रिकोण होगा।

पूरक और पूरक कोण

वे कोण जिनका योग समकोण होता है, पूरक कोण कहलाते हैं। पूरक कोण तब बनते हैं जब एक किरण एक ही शीर्ष को साझा करती है और उस दिशा में इंगित की जाती है जो समकोण बनाने वाली दो मूल किरणों के मध्य होती है। दो मूल किरणों के मध्य किरणों की संख्या अनंत है।

जिन कोणों का योग एक सरल कोण होता है वे पूरक कोण होते हैं। पूरक कोण तब बनते हैं जब एक किरण एक ही शीर्ष को साझा करती है और एक दिशा में इंगित की जाती है जो दो मूल किरणों के मध्य होती है जो सीधा कोण (180 डिग्री कोण) बनाती है। दो मूल किरणों के मध्य किरणों की संख्या अनंत है।

यूक्लिड के संकेतन के आधुनिक संस्करण

आधुनिक शब्दावली में, कोणों को सामान्यतः डिग्री (कोण) या रेडियंस में मापा जाता है।

आधुनिक स्कूल की पाठ्यपुस्तकें अधिकांशतः भिन्न-भिन्न आकृतियों को परिभाषित करती हैं जिन्हें रेखा (ज्यामिति) s (अनंत), रेखा (गणित), किरण (अर्ध-अनंत), और रेखा खंड (परिमित लंबाई का) कहा जाता है। यूक्लिड, एक किरण को एक ऐसी वस्तु के रूप में चर्चा करने के अतिरिक्त जो एक दिशा में अनंत तक फैली हुई है, सामान्यतः ऐसे स्थानों का उपयोग करती है जैसे कि रेखा को पर्याप्त लंबाई तक बढ़ाया जाता है, यद्यपि वह कभी-कभी अनंत रेखाओं को संदर्भित करता है। यूक्लिड में एक रेखा या तो सीधी या घुमावदार हो सकती है, और जब आवश्यक हो तो उसने अधिक विशिष्ट शब्द सीधी रेखा का उपयोग करती है।

कुछ महत्वपूर्ण या प्रसिद्ध परिणाम

The pons asinorum or bridge of asses theorem states that in an isosceles triangle, α = β and γ = δ.
The triangle angle sum theorem states that the sum of the three angles of any triangle, in this case angles α, β, and γ, will always equal 180 degrees.
The Pythagorean theorem states that the sum of the areas of the two squares on the legs (a and b) of a right triangle equals the area of the square on the hypotenuse (c).
Thales' theorem states that if AC is a diameter, then the angle at B is a right angle.

पोंस एसिनोरम

पोन्स एसिनोरम (का पुल) बताता है कि समद्विबाहु त्रिभुज में आधार पर कोण एक दूसरे के समान होते हैं, और, यदि समान सीधी रेखाएँ आगे उत्पन्न होती हैं, तो आधार के नीचे के कोण एक दूसरे के समान होते हैं।^[10] इसका नाम पाठक की बुद्धि के तत्वों में पहली वास्तविक परीक्षा के रूप में और उसके पश्चात् आने वाले कठिन प्रस्तावों के पुल के रूप में इसकी निरंतर भूमिका के लिए जिम्मेदार ठहराया जा सकता है। इसका नाम इसलिए भी रखा जा सकता है क्योंकि ज्यामितीय आकृति एक खड़ी पुल से मिलती-जुलती है जिसे मात्र एक स्योर फूटेड डंकी ही पार कर सकता है।^[11]

त्रिभुजों की सर्वांगसमता

त्रिभुजों की सर्वांगसमता दो भुजाओं और उनके मध्य के कोण (SAS), दो कोणों और उनके मध्य की भुजा (ASA) या दो कोणों और संबंधित आसन्न भुजा (AAS) को निर्दिष्ट करके निर्धारित की जाती है। दो पक्षों और एक आसन्न कोण (एसएसए) को निर्दिष्ट करना, यद्यपि, दो भिन्न-भिन्न संभावित त्रिकोण उत्पन्न कर सकते हैं जब तक कि निर्दिष्ट कोण सही कोण न हो।

त्रिभुज सर्वांगसम होते हैं यदि उनकी तीनों भुजाएँ समान (SSS), दो भुजाएँ और उनके मध्य का कोण समान (SAS), या दो कोण और एक भुजा समान (ASA) (पुस्तक I, प्रस्ताव 4, 8, और 26) हो। तीन समान कोणों (AAA) वाले त्रिभुज समरूप होते हैं, परन्तु आवश्यक नहीं कि सर्वांगसम हों। साथ ही, दो समान भुजाओं वाले और एक आसन्न कोण वाले त्रिभुज आवश्यक रूप से समान या सर्वांगसम नहीं होते हैं।

त्रिभुज कोण योग

त्रिभुज के कोणों का योग एक सरल कोण (180 डिग्री) के समान होता है।^[12] इसके कारण एक समबाहु त्रिभुज में 60 डिग्री के तीन आंतरिक कोण होते हैं। इसके अतिरिक्त, यह प्रत्येक त्रिभुज में कम से कम दो न्यून कोण और एक अधिक कोण या समकोण होने का कारण बनता है।

पाइथागोरस प्रमेय

प्रसिद्ध पायथागॉरियन प्रमेय (पुस्तक I, प्रस्ताव 47) में कहा गया है कि किसी भी समकोण त्रिभुज में, वर्ग का क्षेत्रफल जिसकी भुजा कर्ण (समकोण के विपरीत भुजा) होती है, उन वर्गों के क्षेत्रफलों के योग के समान होती है जिनकी भुजाएँ होती हैं दो पैर (दो भुजाएँ जो समकोण पर मिलती हैं)।

थेल्स प्रमेय

थेल्स के प्रमेय, जिसका नाम थेल्स ऑफ मिलेटस के नाम पर रखा गया है, में कहा गया है कि यदि ए, बी और सी एक वृत्त पर बिंदु हैं जहां रेखा एसी वृत्त का व्यास है, तो कोण एबीसी एक समकोण है। कैंटर का मानना था कि थेल्स ने यूक्लिड बुक I, प्रस्ताव 32 के माध्यम से यूक्लिड बुक III, प्रस्ताव 31 के विधियाँ से अपने प्रमेय को सिद्ध किया।^[13]^[14]

क्षेत्रफल और आयतन का मापन

आधुनिक शब्दावली में, एक समतल आकृति का क्षेत्रफल उसके किसी भी रैखिक आयाम के वर्ग के समानुपाती होता है, $A\propto L^{2}$ , और घन में ठोस का आयतन, $V\propto L^{3}$ . यूक्लिड ने इन परिणामों को विभिन्न विशेष स्थितियों में सिद्ध किया जैसे कि एक वृत्त का क्षेत्रफल^[15] और एक समानांतर चतुर्भुज ठोस का आयतन।^[16] यूक्लिड ने आनुपातिकता के प्रासंगिक स्थिरांक के कुछ, परन्तु सभी को निर्धारित नहीं किया। उदाहरण के लिए, यह उनके उत्तराधिकारी आर्किमिडीज थे जिन्होंने यह सिद्ध किया कि एक गोले में परिक्रमण बेलन का आयतन 2/3 होता है।^[17]

माप और अंकगणित की प्रणाली

यूक्लिडियन ज्यामिति में दो मूलभूत प्रकार के माप होते हैं: कोण और यूक्लिडियन दूरी। कोण का मापदंड निरपेक्ष होता है, और यूक्लिड अपनी मूल इकाई के रूप में समकोण का उपयोग करता है, इसलिए, उदाहरण के लिए, 45-डिग्री (कोण) कोण को समकोण के आधे के रूप में संदर्भित किया जाएगा। दूरी का मापदंड सापेक्ष है; एक इकाई के रूप में एक निश्चित गैर-शून्य लंबाई के साथ एक रेखा खंड को इच्छानुसार चयन करता है, और अन्य दूरियां इसके संबंध में व्यक्त की जाती हैं। दूरियों के जोड़ को एक निर्माण द्वारा प्रदर्शित जाता है जिसमें एक लाइन सेगमेंट को दूसरे लाइन सेगमेंट के अंत में उसकी लंबाई बढ़ाने के लिए कॉपी किया जाता है, और इसी तरह घटाव के लिए भी किया जाता है।

क्षेत्रफल (ज्यामिति) और आयत न का मापन दूरियों से किया जाता है। उदाहरण के लिए, 3 की चौड़ाई और 4 की लंबाई वाले एक आयत में एक क्षेत्र होता है जो उत्पाद का प्रतिनिधित्व करता है, 12. क्योंकि गुणन की यह ज्यामितीय व्याख्या तीन आयामों तक सीमित थी, चार या अधिक के उत्पाद की व्याख्या करने का कोई सीधा विधि नहीं थी। संख्या, और यूक्लिड ने ऐसे उत्पादों से बचाव किया, यद्यपि वे निहित हैं, उदाहरण के लिए पुस्तक IX, प्रस्ताव 20 के प्रमाण में।

एकरूपता का एक उदाहरण। बाईं ओर की दो आकृतियाँ सर्वांगसम हैं, जबकि तीसरी उनसे समानता (ज्यामिति) है। अंतिम आंकड़ा न तो है। सर्वांगसमताएं कुछ गुणों को बदल देती हैं, जैसे कि स्थान और अभिविन्यास, परन्तु अन्य को अपरिवर्तित छोड़ देते हैं, जैसे दूरी और कोण । पश्चात् के गुणों को अपरिवर्तनीय (गणित) कहा जाता है और उनका अध्ययन करना ज्यामिति का सार है।

यूक्लिड रेखाओं की एक जोड़ी, या तलीय या ठोस आकृतियों की एक जोड़ी को समान (ἴσος) के रूप में संदर्भित करता है यदि उनकी लंबाई, क्षेत्रफल या आयतन क्रमशः समान हैं, और इसी तरह कोणों के लिए मजबूत शब्द सर्वांगसमता (ज्यामिति) इस विचार को संदर्भित करता है कि एक संपूर्ण आकृति एक ही आकार और आकृति के समान होती है। वैकल्पिक रूप से, दो आंकड़े सर्वांगसम होते हैं यदि एक को दूसरे के ऊपर ले जाया जा सकता है जिससे यह ठीक से समरूप होता हो। (इसे पलटने की अनुमति है।) इस प्रकार, उदाहरण के लिए, एक 2x6 आयत और एक 3x4 आयत समान हैं परन्तु सर्वांगसम नहीं हैं, और अक्षर R इसकी दर्पण छवि के सर्वांगसम है। भिन्न-भिन्न आकारों को छोड़कर जो आंकड़े सर्वांगसम होंगे, उन्हें समानता (ज्यामिति) कहा जाता है। समान आकृतियों के युग्म में संगत भुजाएँ और संगत कोण सर्वांगसम होते हैं और संगत भुजाएँ एक-दूसरे के समानुपाती होती हैं।

आवेदन

गणित में यूक्लिडियन ज्यामिति की मौलिक स्थिति के कारण, यहां अनुप्रयोगों के प्रतिनिधि नमूने से अधिक देना अव्यावहारिक है।

A surveyor uses a level
Sphere packing applies to a stack of oranges.
A parabolic mirror brings parallel rays of light to a focus.

जैसा कि शब्द की व्युत्पत्ति द्वारा सुझाया गया है, रुचि के प्रारम्भी कारणों में से एक और ज्यामिति के सबसे आम वर्तमान उपयोग में से एक सर्वेक्षण है,^[18] और यूक्लिडियन ज्यामिति के कुछ व्यावहारिक परिणाम, जैसे कि 3-4-5 त्रिभुज का समकोण गुण, औपचारिक रूप से सिद्ध होने से बहुत पहले उपयोग किए गए थे।^[19] यूक्लिडियन ज्यामिति में माप के मूलभूत प्रकार दूरी और कोण हैं, दोनों को सीधे एक सर्वेक्षक द्वारा मापा जा सकता है। ऐतिहासिक रूप से, दूरियों को अधिकांशतः जंजीरों द्वारा मापा जाता था, जैसे कि गुंटर की श्रृंखला, और कोणों को स्नातक किए गए हलकों और पश्चात् में, थियोडोलाइट का उपयोग करके।

यूक्लिडियन ठोस ज्यामिति का एक अनुप्रयोग पैकिंग समस्या है, जैसे कि n आयामों में सबसे कुशल गोलाकार पैकिंग अन्वेषण की समस्या। इस समस्या में त्रुटि का पता लगाने और सुधार में अनुप्रयोग हैं।

ज्यामितीय प्रकाशिकी लेंस और दर्पण द्वारा प्रकाश के फोकस का विश्लेषण करने के लिए यूक्लिडियन ज्यामिति का उपयोग करती है।

Geometry is used in art and architecture.
The water tower consists of a cone, a cylinder, and a hemisphere. Its volume can be calculated using solid geometry.
Geometry can be used to design origami.

वास्तुकला में ज्यामिति का व्यापक रूप से उपयोग किया जाता है।

ओरिगेमी को डिजाइन करने के लिए ज्यामिति का उपयोग किया जा सकता है। कुछ कंपास और स्ट्रेटएज कंस्ट्रक्श कंपास और स्ट्रेटेज का उपयोग करके असंभव निर्माण असंभव हैं, परन्तु पेपर फोल्डिंग का गणित हो सकता है।^[20]

अधिकांश कंप्यूटर एडेड डिजाइन सीएडी (कंप्यूटर एडेड डिजाइन) और कंप्यूटर कंप्यूटर सहायतायुक्त विनिर्माण सीएएम (कंप्यूटर एडेड मैन्युफैक्चरिंग) यूक्लिडियन ज्योमेट्री पर आधारित है। डिज़ाइन ज्यामिति में सामान्यतः प्लेन, सिलेंडरों, शंकुओं, तोरी और अन्य समान आकृतियों से घिरी आकृतियाँ होती हैं। वर्तमान समय में, कार, हवाई जहाज, जहाज और स्मार्टफोन सहित न्यूनाधिक हर चीज के डिजाइन में CAD/CAM आवश्यक है। कुछ दशक पहले, परिष्कृत ड्राफ्ट्समैन अत्यधिक उन्नत यूक्लिडियन ज्यामिति सीखेंगे, जिसमें पास्कल के प्रमेय और ब्रायनचॉन के प्रमेय जैसी चीजें सम्मिलित हैं, परन्तु आधुनिक समय में यह अब आवश्यक नहीं है।

पश्चात् में काम

आर्किमिडीज और अपोलोनियस

एक गोले का आयतन और सतह क्षेत्रफल उसके परिचालित बेलन का 2/3 है। उनके अनुरोध पर आर्किमिडीज़ की कब्र पर एक गोला और सिलेंडर रखा गया था।

आर्किमिडीज (सी। 287 ईसा पूर्व - सी। 212 ईसा पूर्व), एक रंगीन आकृति जिसके बारे में कई ऐतिहासिक उपाख्यानों को दर्ज किया गया है, को यूक्लिड के साथ प्राचीन गणितज्ञों में से एक के रूप में याद किया जाता है। यद्यपि उनके काम की नींव यूक्लिड द्वारा रखी गई थी, उनका काम, यूक्लिड के विपरीत, पूरी तरह से मौलिक माना जाता है।^[21] उन्होंने दो और तीन आयामों में विभिन्न आकृतियों के आयतन और क्षेत्रफल के समीकरणों को सिद्ध किया और परिमित संख्याओं के आर्किमिडीयन गुण को प्रतिपादित किया।

पेर्गा का अपोलोनियस (सी। 262 ईसा पूर्व - सी। 190 ईसा पूर्व) मुख्य रूप से शंकु वर्गों की जांच के लिए जाना जाता है।

रेने डेस्कर्टेस। फ़्रांसिस हल्स , 1648 के पश्चात् पोर्ट्रेट।

17वीं सदी: डेसकार्टेस

रेने डेसकार्टेस (1596-1650) ने विश्लेषणात्मक ज्यामिति विकसित की, ज्यामिति को औपचारिक रूप देने के लिए एक वैकल्पिक विधि जो ज्यामिति को बीजगणित में बदलने पर केंद्रित थी।^[22]

इस दृष्टिकोण में, एक समतल पर एक बिंदु को उसके कार्टेशियन निर्देशांक प्रणाली (x, y) निर्देशांक द्वारा प्रदर्शित जाता है, एक रेखा को उसके समीकरण द्वारा प्रदर्शित जाता है।

यूक्लिड के मूल दृष्टिकोण में, पाइथागोरस प्रमेय यूक्लिड के अभिगृहीतों का अनुसरण करता है। कार्टेशियन दृष्टिकोण में, एक्सिओम्स बीजगणित के एक्सिओम्स हैं, और पाइथागोरस प्रमेय को व्यक्त करने वाला समीकरण तब यूक्लिड के एक्सिओम्स शब्दों में से एक की परिभाषा है, जिसे अब प्रमेय माना जाता है।

समीकरण

|PQ|={\sqrt {(p_{x}-q_{x})^{2}+(p_{y}-q_{y})^{2}}}\,

दो बिंदुओं के मध्य की दूरी को परिभाषित करना P = (p_x, p_y) और Q = (q_x, q_y) को तब यूक्लिडियन मीट्रिक स्थान के रूप में जाना जाता है, और अन्य मीट्रिक गैर-यूक्लिडियन ज्यामिति ज्यामिति को परिभाषित करते हैं।

विश्लेषणात्मक ज्यामिति के संदर्भ में, मौलिक ज्यामिति के कंपास और सीधा निर्माण पर प्रतिबंध का अर्थ है पहले और दूसरे क्रम के समीकरणों पर प्रतिबंध, उदाहरण के लिए, y = 2x + 1 (एक रेखा), or x² + y² = 7 (एक वृत्त)।

इसके अतिरिक्त 17वीं शताब्दी में, गिरार्ड डिसारगुएस, परिप्रेक्ष्य के सिद्धांत (ग्राफिकल) से प्रेरित होकर, अनंत पर आदर्श बिंदुओं, रेखाओं और प्लेन की अवधारणा की प्रारम्भ की। परिणाम को एक प्रकार की सामान्यीकृत ज्यामिति, प्रक्षेपी ज्यामिति के रूप में माना जा सकता है, परन्तु इसका उपयोग साधारण यूक्लिडियन ज्यामिति में प्रमाण निर्मितर करने के लिए भी किया जा सकता है जिसमें विशेष स्थितियों की संख्या कम हो जाती है।^[23]

वृत्त का वर्ग बनाना: इस वर्ग और इस वृत्त के क्षेत्रफल समान होते हैं। 1882 में, यह सिद्ध हो गया था कि इस आकृति का निर्माण एक आदर्श कंपास और स्ट्रेटेज के साथ सीमित चरणों में नहीं किया जा सकता है।

18वीं सदी

18 वीं शताब्दी के जियोमीटर ने यूक्लिडियन प्रणाली की सीमाओं को परिभाषित करने के लिए संघर्ष किया। बहुतों ने पहले चार में से पाँचवीं अभिधारणा को सिद्ध करने का व्यर्थ प्रयास किया। 1763 तक, कम से कम 28 विभिन्न प्रमाण प्रकाशित हो चुके थे, परन्तु सभी गलत पाए गए।^[24]

इस अवधि तक अग्रणी, जियोमीटर ने यह निर्धारित करने का भी प्रयास किया कि यूक्लिडियन ज्यामिति में कौन से निर्माण किए जा सकते हैं। उदाहरण के लिए, एक कम्पास और स्ट्रेटेज के साथ एक कोण को ट्राइसेक्ट करने की समस्या वह है जो स्वाभाविक रूप से सिद्धांत के भीतर होती है, क्योंकि एक्सिओम्स रचनात्मक कार्यों को संदर्भित करते हैं जिन्हें उन उपकरणों के साथ किया जा सकता है। यद्यपि, इस समस्या का समाधान अन्वेषण में सदियों के प्रयास विफल रहे, जब तक कि पियरे वांट्ज़ेल ने 1837 में एक प्रमाण प्रकाशित नहीं किया कि ऐसा निर्माण असंभव था। अन्य निर्माण जो असंभव सिद्ध हुए, उनमें घन को दोगुना करना और वृत्त का वर्ग करना सम्मिलित है। घन को दोगुना करने के स्थिति में, निर्माण की असंभवता इस तथ्य से उत्पन्न होती है कि कंपास और सीधी विधि में समीकरण सम्मिलित होते हैं जिनका क्रम दो की अभिन्न शक्ति है,^[25] घन को दोगुना करते समय तीसरे क्रम के समीकरण के समाधान की आवश्यकता होती है।

लियोनहार्ड यूलर ने यूक्लिडियन ज्यामिति के एक सामान्यीकरण पर चर्चा की, जिसे एफ़िन ज्यामिति कहा जाता है, जो तीन और चार को कम महत्व करते हुए पांचवीं अभिधारणा को अपरिवर्तित रखता है, जिससे कोण (जहां सही त्रिकोण अर्थहीन हो जाते हैं) और सामान्य रूप से रेखा खंडों की लंबाई की समानता को समाप्त कर देता है। (जहां से वृत्त अर्थहीन हो जाते हैं) समानांतरता की धारणा को रेखाओं के मध्य एक तुल्यता संबंध के रूप में बनाए रखते हुए, और समानांतर रेखा खंडों की लंबाई की समानता (इसलिए रेखा खंडों का मध्य बिंदु बना रहता है)।

19वीं सदी

Comparison of elliptic, Euclidean and hyperbolic geometries in two dimensions

19वीं शताब्दी की प्रारम्भ में, लज़ारे कार्नो और अगस्त फर्डिनेंड मोबियस ने परिणामों को सरल और एकीकृत करने के विधियाँ के रूप में व्यवस्थित रूप से हस्ताक्षरित कोणों और रेखा खंडों के उपयोग को विकसित किया।^[26]

उच्च आयाम

1840 के दशक में विलियम रोवन हैमिल्टन ने चतुर्भुज विकसित किए, और जॉन टी। ग्रेव्स और आर्थर केली ने ऑक्टोनियन विकसित किए। ये सामान्य बीजगणित हैं जो सम्मिश्र संख्याओं का विस्तार करते हैं। पश्चात् में यह समझा गया कि चतुर्भुज भी चार लॉजिकसंगत कार्टेशियन निर्देशांक के साथ एक यूक्लिडियन ज्यामितीय प्रणाली हैं। केली ने 4-आयामी यूक्लिडियन स्पेस में घूर्णन का अध्ययन करने के लिए चतुर्भुज का उपयोग किया।

मध्य शताब्दी में लुडविग श्लाफली ने यूक्लिडियन स्पेस की सामान्य अवधारणा विकसित की, यूक्लिडियन ज्यामिति को लुडविग श्लाफली उच्च आयामों तक विस्तारित किया। उन्होंने पॉलीस्कीम्स को परिभाषित किया, जिसे पश्चात् में पॉलीटोप कहा जाता है, जो बहुभुज और पॉलीहेड्रा के उच्च-आयामी एनालॉग हैं। |उन्होंने अपने सिद्धांत को विकसित किया और सभी नियमित पॉलीटोप्स की खोज की, अर्थात् $n$ नियमित बहुभुज और प्लेटोनिक ठोस के -आयामी अनुरूप। उन्होंने पाया कि छह नियमित 4-पॉलीटॉप हैं, और तीन सभी उच्च आयामों में हैं।

Regular convex 4-polytopes
Symmetry group	A₄	B₄		F₄	H₄
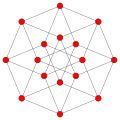
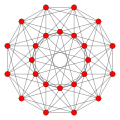
Name	5-cell Hyper-tetrahedron 5-point	16-cell Hyper-octahedron 8-point	8-cell Hyper-cube 16-point	24-cell 24-point	600-cell Hyper-icosahedron 120-point	120-cell Hyper-dodecahedron 600-point
Schläfli symbol	{3, 3, 3}	{3, 3, 4}	{4, 3, 3}	{3, 4, 3}	{3, 3, 5}	{5, 3, 3}
Coxeter mirrors
Mirror dihedrals	𝝅/3 𝝅/3 𝝅/3 𝝅/2 𝝅/2 𝝅/2	𝝅/3 𝝅/3 𝝅/4 𝝅/2 𝝅/2 𝝅/2	𝝅/4 𝝅/3 𝝅/3 𝝅/2 𝝅/2 𝝅/2	𝝅/3 𝝅/4 𝝅/3 𝝅/2 𝝅/2 𝝅/2	𝝅/3 𝝅/3 𝝅/5 𝝅/2 𝝅/2 𝝅/2	𝝅/5 𝝅/3 𝝅/3 𝝅/2 𝝅/2 𝝅/2
Graph
Vertices	5 tetrahedral	8 octahedral	16 tetrahedral	24 cubical	120 icosahedral	600 tetrahedral
Edges	10 triangular	24 square	32 triangular	96 triangular	720 pentagonal	1200 triangular
Faces	10 triangles	32 triangles	24 squares	96 triangles	1200 triangles	720 pentagons
Cells	5 tetrahedra	16 tetrahedra	8 cubes	24 octahedra	600 tetrahedra	120 dodecahedra
Tori	1 5-tetrahedron	2 8-tetrahedron	2 4-cube	4 6-octahedron	20 30-tetrahedron	12 10-dodecahedron
Inscribed	120 in 120-cell	675 in 120-cell	2 16-cells	3 8-cells	25 24-cells	10 600-cells
Great polygons		2 squares x 3	4 rectangles x 4	4 hexagons x 4	12 decagons x 6	100 irregular hexagons x 4
Petrie polygons	1 pentagon	1 octagon	2 octagons	2 dodecagons	4 30-gons	20 30-gons
Long radius	$1$	$1$	$1$	$1$	$1$	$1$
Edge length	${\sqrt {\tfrac {5}{2}}}\approx 1.581$	${\sqrt {2}}\approx 1.414$	$1$	$1$	${\tfrac {1}{\phi }}\approx 0.618$	${\tfrac {1}{\phi ^{2}{\sqrt {2}}}}\approx 0.270$
Short radius	${\tfrac {1}{4}}$	${\tfrac {1}{2}}$	${\tfrac {1}{2}}$	${\sqrt {\tfrac {1}{2}}}\approx 0.707$	${\sqrt {\tfrac {\phi ^{4}}{8}}}\approx 0.926$	${\sqrt {\tfrac {\phi ^{4}}{8}}}\approx 0.926$
Area	$10\left({\tfrac {5{\sqrt {3}}}{8}}\right)\approx 10.825$	$32\left({\sqrt {\tfrac {3}{4}}}\right)\approx 27.713$	$24$	$96\left({\sqrt {\tfrac {3}{16}}}\right)\approx 41.569$	$1200\left({\tfrac {\sqrt {3}}{4\phi ^{2}}}\right)\approx 198.48$	$720\left({\tfrac {\sqrt {25+10{\sqrt {5}}}}{8\phi ^{4}}}\right)\approx 90.366$
Volume	$5\left({\tfrac {5{\sqrt {5}}}{24}}\right)\approx 2.329$	$16\left({\tfrac {1}{3}}\right)\approx 5.333$	$8$	$24\left({\tfrac {\sqrt {2}}{3}}\right)\approx 11.314$	$600\left({\tfrac {\sqrt {2}}{12\phi ^{3}}}\right)\approx 16.693$	$120\left({\tfrac {15+7{\sqrt {5}}}{4\phi ^{6}{\sqrt {8}}}}\right)\approx 18.118$
4-Content	${\tfrac {\sqrt {5}}{24}}\left({\tfrac {\sqrt {5}}{2}}\right)^{4}\approx 0.146$	${\tfrac {2}{3}}\approx 0.667$	$1$	$2$	${\tfrac {{\text{Short}}\times {\text{Vol}}}{4}}\approx 3.863$	${\tfrac {{\text{Short}}\times {\text{Vol}}}{4}}\approx 4.193$

श्लाफलीने सापेक्ष अस्पष्टता में यह काम किया और इसे मात्र मरणोपरांत 1901 में पूर्ण रूप से प्रकाशित किया गया था। जब तक इसे फिर से अन्वेषण नहीं किया गया और H.S.M द्वारा नियमित पॉलीटोप्स (पुस्तक) तब तक इसका बहुत कम प्रभाव था।

1878 में विलियम किंगडन क्लिफोर्ड ने प्रस्तुत किया जिसे अब ज्यामितीय बीजगणित कहा जाता है, हरमन ग्रासमैन के बीजगणित के साथ हैमिल्टन के चतुर्भुज को एकीकृत करता है और इन प्रणालियों की ज्यामितीय प्रकृति को प्रकट करता है, विशेषकर चार आयामों में। ज्यामितीय बीजगणित के संचालन में उन ज्यामितीय वस्तुओं को प्रतिबिंबित करने, घुमाने, अनुवाद करने और मानचित्रण करने का प्रभाव होता है जिन्हें नए पदों पर मॉडलिंग किया जा रहा है। 3-क्षेत्र की सतह पर क्लिफोर्ड टोरस दो सर्किलों के कार्टेशियन उत्पाद का सबसे सरल और सबसे सममित फ्लैट एम्बेडिंग है (उसी अर्थ में एक सिलेंडर की सतह फ्लैट है)।

गैर-यूक्लिडियन ज्यामिति

ज्यामिति में सदी का सबसे प्रभावशाली विकास तब हुआ, जब 1830 के आसपास, जेनोस बोल्याई और निकोलाई इवानोविच लोबचेव्स्की ने गैर-यूक्लिडियन ज्यामिति पर भिन्न-भिन्न काम प्रकाशित किया, जिसमें समानांतर अभिधारणा मान्य नहीं है।^[27] चूंकि गैर-यूक्लिडियन ज्यामिति यूक्लिडियन ज्यामिति के साथ अपेक्षाकृत रूप से संगत है, समानांतर अभिधारणा को अन्य अभिधारणाओं से सिद्ध नहीं किया जा सकता है।

19वीं शताब्दी में, यह भी महसूस किया गया कि यूक्लिड के दस एक्सिओम्स और सामान्य विचार तत्वों में बताए गए सभी प्रमेयों को सिद्ध करने के लिए पर्याप्त नहीं हैं। उदाहरण के लिए, यूक्लिड ने परोक्ष रूप से माना कि किसी भी रेखा में कम से कम दो बिंदु होते हैं, परन्तु इस धारणा को अन्य एक्सिओम्सों से सिद्ध नहीं किया जा सकता है, और इसलिए स्वयं एक एक्सिओम्स होना चाहिए। ऊपर की आकृति में दिखाए गए तत्वों में सबसे पहला ज्यामितीय प्रमाण यह है कि कोई भी रेखा खंड त्रिभुज का हिस्सा होता है; यूक्लिड दोनों समापन बिंदुओं के चारों ओर वृत्त खींचकर और उनके प्रतिच्छेदन को तीसरे बिंदु के रूप में लेते हुए सामान्य विधियाँ से इसकी रचना करता है: शीर्ष। यद्यपि, उनके एक्सिओम्स, इस बात की गारंटी नहीं देते हैं कि वृत्त वास्तव में प्रतिच्छेद करते हैं, क्योंकि वे निरंतरता की ज्यामितीय गुण पर महत्व नहीं देते हैं, जो कि कार्टेशियन शब्दों में वास्तविक संख्या # वास्तविक संख्याओं की पूर्णता गुण के समान है। 1882 में मोरित्ज़ पास्च से शुरू होकर, ज्यामिति के लिए कई उन्नत एक्सिओम्स प्रणालियों का प्रस्ताव किया गया है, जिनमें से सबसे प्रसिद्ध हिल्बर्ट के एक्सिओम्स हैं,^[28] बिरखॉफ के एक्सिओम्स,^[29] और टार्स्की के एक्सिओम्स थे।^[30]

20वीं सदी और सापेक्षता

भौतिक स्थान के विवरण के रूप में यूक्लिडियन ज्यामिति का एक खंडन। 1919 में सापेक्षता के सामान्य सिद्धांत के परीक्षण में, सूर्य ग्रहण के दौरान सितारों (छोटी क्षैतिज रेखाओं के साथ चिह्नित) की तस्वीरें खींची गईं। सूर्य के गुरुत्वाकर्षण द्वारा पृथ्वी की ओर जाते समय तारों की किरणें मुड़ी हुई थीं। इसकी व्याख्या आइंस्टीन की भविष्यवाणी के पक्ष में प्रमाण के रूप में की जाती है कि गुरुत्वाकर्षण यूक्लिडियन ज्यामिति से विचलन का कारण बनेगा।

अल्बर्ट आइंस्टीन के विशेष सापेक्षता के सिद्धांत में चार-आयामी स्पेस-समय, मिंकोव्स्की स्पेस सम्मिलित है, जो गैर-यूक्लिडियन ज्यामिति है। इससे पता चलता है कि गैर-यूक्लिडियन ज्यामिति, जिन्हें कुछ साल पहले यह दिखाने के लिए प्रस्तुत किया गया था कि समानांतर अभिधारणा को सिद्ध नहीं किया जा सकता है, भौतिक दुनिया का वर्णन करने के लिए भी उपयोगी हैं।

यद्यपि, मिंकोव्स्की स्पेस का त्रि-आयामी स्पेस भाग यूक्लिडियन ज्यामिति का स्थान बना हुआ है। सामान्य सापेक्षता के स्थिति में ऐसा नहीं है, जिसके लिए स्पेस-समय के स्पेस भाग की ज्यामिति यूक्लिडियन ज्यामिति नहीं है।^[31] उदाहरण के लिए, यदि त्रिभुज का निर्माण प्रकाश की तीन किरणों से किया जाता है, तो सामान्य तौर पर गुरुत्वाकर्षण के कारण आंतरिक कोण 180 डिग्री तक नहीं जुड़ते हैं। एक अपेक्षाकृत कममहत्व गुरुत्वाकर्षण क्षेत्र, जैसे कि पृथ्वी या सूर्य का, एक मीट्रिक द्वारा प्रदर्शित जाता है जो यूक्लिडियन के लगभग, परन्तु बिल्कुल नहीं है। 20वीं शताब्दी तक, यूक्लिडियन ज्यामिति से प्रकाश की किरणों में इन विचलन का पता लगाने में सक्षम कोई तकनीक नहीं थी, परन्तु आइंस्टीन ने भविष्यवाणी की थी कि ऐसे विचलन उपस्थित होंगे। पश्चात् में 1919 में सूर्य ग्रहण के दौरान सूर्य द्वारा तारों का हल्का सा झुकना जैसे अवलोकनों द्वारा उन्हें सत्यापित किया गया था, और इस तरह के विचार अब ग्लोबल पोजिशनिंग सिस्टम सिस्टम को चलाने वाले सॉफ़्टवेयर का एक अभिन्न अंग हैं।^[32]

स्पेस की संरचना के विवरण के रूप में

यूक्लिड का मानना था कि उनके एक्सिओम्स भौतिक वास्तविकता के बारे में स्व-स्पष्ट कथन थे। यूक्लिड के प्रमाण उन मान्यताओं पर निर्भर करते हैं जो यूक्लिड के मौलिक एक्सिओम्सों में स्पष्ट नहीं हैं,^[33] विशेष रूप से कि आकृतियों के कुछ संचलन उनके ज्यामितीय गुणों को नहीं बदलते हैं जैसे कि पक्षों की लंबाई और आंतरिक कोण, तथाकथित यूक्लिडियन गति, जिसमें अनुवाद, प्रतिबिंब और आंकड़ों के घुमाव सम्मिलित हैं।^[34] स्पेस के भौतिक विवरण के रूप में लिया गया, अभिधारणा 2 (एक पंक्ति का विस्तार करना) का दावा है कि स्पेस में छेद या सीमाएँ नहीं हैं; अभिधारणा 4 (समकोण की समानता) कहती है कि स्पेस समदैशिक है और सर्वांगसमता (ज्यामिति) बनाए रखते हुए आंकड़ों को किसी भी स्थान पर ले जाया जा सकता है; और 5 (समानांतर अभिधारणा) को अभिगृहीत करें कि स्पेस समतल है (इसमें कोई आंतरिक वक्रता नहीं है)।

जैसा कि ऊपर चर्चा की गई है, अल्बर्ट आइंस्टीन का सापेक्षता का सिद्धांत इस दृष्टिकोण को महत्वपूर्ण रूप से संशोधित करता है।

मूल रूप से यूक्लिड द्वारा निर्मितर किए गए एक्सिओम्सों का अस्पष्ट चरित्र स्पेस की संरचना के लिए उनके कुछ अन्य निहितार्थों के बारे में विभिन्न टिप्पणीकारों के लिए असहमत होना संभव बनाता है, जैसे कि यह अनंत है या नहीं हीथ, पृ. 200.</ref> (नीचे देखें) और इसकी टोपोलॉजी क्या है। प्रणाली के आधुनिक, अधिक कठोर सुधार उदाहरण के लिए, टार्स्की (1951)। का लक्ष्य सामान्यतः इन उद्देशों को साफ-सुथरा विधियाँ से भिन्न करना है। इस अधिक आधुनिक दृष्टिकोण की भावना में यूक्लिड के एक्सिओम्सों की व्याख्या करते हए, एक्सिओम्स 1-4 अनंत या परिमित स्थान ( अण्डाकार ज्यामिति के रूप में) के अनुरूप हैं, और सभी पांच एक्सिओम्स विभिन्न प्रकार के टोपोलॉजी (जैसे, एक विमान, एक सिलेंडर) या द्वि-आयामी यूक्लिडियन ज्यामिति के लिए एक टोरस) के अनुरूप हैं।

अनंत ट्रीटमेंट

अनंत वस्तुएं

यूक्लिड को कभी-कभी परिमित रेखाओं (जैसे, अभिधारणा 2) और अनंत रेखाओं (पुस्तक I, प्रस्ताव 12) के मध्य स्पष्ट रूप से पहचाना जाता है। यद्यपि, उन्होंने सामान्यतः ऐसे भेद नहीं किए, जब तक कि वे आवश्यक न हों। अभिधारणाएं स्पष्ट रूप से अनंत रेखाओं का उल्लेख नहीं करती हैं, यद्यपि उदाहरण के लिए कुछ टिप्पणीकार अभिधारणा 3 की व्याख्या करते हैं, किसी भी त्रिज्या के साथ एक वृत्त का अस्तित्व, जिसका अर्थ है कि स्पेस अनंत है।

अतिसूक्ष्मजीव की धारणा पर पहले एलीटिक स्कूल द्वारा व्यापक रूप से चर्चा की गई थी, परन्तु कोई भी उन्हें एक ठोस लॉजिकल आधार पर रखने में सक्षम नहीं था, जिसमें ज़ेनो के विरोधाभास जैसे विरोधाभास थे जो सार्वभौमिक संतुष्टि के लिए हल नहीं हुए थे। यूक्लिड ने इनफिनिटिमल्स के अतिरिक्त एग्जॉस्ट की विधि का प्रयोग किया।^[35]

पश्चात् के प्राचीन टिप्पणीकारों, जैसे कि प्रोक्लुस (410-485 सीई) ने अनंत के बारे में कई सवालों को प्रमाण की मांग के उद्देशों के रूप में माना और, उदाहरण के लिए, प्रोक्लस ने एक लाइन की अनंत विभाज्यता को सिद्ध करने का दावा किया, जो कि विरोधाभास के प्रमाण के आधार पर था जिसमें उन्होंने स्थितियों पर विचार किया था। इसे बनाने वाले सम और विषम अंकों की संख्या।^[36]

20 वीं शताब्दी के मोड़ पर, ओटो स्टोल्ज़ , पॉल डू बोइस-रेमंड , ग्यूसेप वेरोनीज़ , और अन्य ने आर्किमिडीज़ गुण पर विवादास्पद काम का निर्माण किया। यूक्लिडियन ज्यामिति के गैर-आर्किमिडियन मॉडल, जिसमें दो बिंदुओं के मध्य की दूरी अनंत या असीम हो सकती है, आइजैक न्यूटन -गॉटफ्राइड लाइबनिज अर्थ में।^[37] पचास साल पश्चात्, अब्राहम रॉबिन्सन ने वेरोनीज़ के काम के लिए एक कठोर लॉजिकल आधार प्रदान किया।^[38]

अनंत प्रक्रियाएं

एक कारण यह है कि पूर्वजों ने समानांतर अभिधारणा को दूसरों की तुलना में कम निश्चित माना है कि इसे भौतिक रूप से सत्यापित करने के लिए हमें दो पंक्तियों का निरीक्षण करने की आवश्यकता होगी जिससे यह जांचा जा सके कि वे कभी भी बहुत दूर बिंदु पर प्रतिच्छेद नहीं करते हैं, और यह निरीक्षण संभावित रूप से एक अनंत राशि ले सकता है समय की।^[39]

प्रेरण द्वारा प्रमाण का आधुनिक सूत्रीकरण 17वीं शताब्दी तक विकसित नहीं हुआ था, परन्तु कुछ पश्चात् के टिप्पणीकारों ने इसे यूक्लिड के कुछ प्रमाणों में निहित माना है, उदाहरण के लिए, अपराधों की अनंतता का प्रमाण।^[40] अनंत श्रृंखला से जुड़े कथित विरोधाभास, जैसे कि ज़ेनो का विरोधाभास, यूक्लिड से पहले का था। यूक्लिड ने इस तरह की चर्चाओं से परहेज किया, उदाहरण के लिए, IX.35 में ज्यामितीय श्रृंखला के आंशिक योग के लिए व्यंजक, शब्दों की संख्या को अनंत होने देने की संभावना पर टिप्पणी किए बिना।

लॉजिकल आधार

मौलिक लॉजिक

यूक्लिड ने अधिकांशतः विरोधाभास द्वारा प्रमाण की विधि का प्रयोग किया, और इसलिए यूक्लिडियन ज्यामिति की पारंपरिक प्रस्तुति मौलिक लॉजिक मानती है, जिसमें प्रत्येक प्रस्ताव या तो सत्य या गलत होता है, यानी, किसी भी प्रस्ताव पी के लिए, प्रस्ताव पी या नहीं पी स्वचालित रूप से सत्य है।

कठोरता के आधुनिक मानक

यूक्लिडियन ज्यामिति को ठोस स्वयंसिद्ध आधार पर रखना सदियों से गणितज्ञों का काम था।^[41] 1900 के पेरिस सम्मेलन में ग्यूसेप पीनो प्रतिनिधिमंडल के एलेसेंड्रो पडोआ द्वारा आदिम धारणा ओं, या अपरिभाषित अवधारणाओं की भूमिका को स्पष्ट रूप से सामने रखा गया था:^[41]^[42]

....जब हम सिद्धांत निर्मित करना प्रारम्भ करते हैं, तो हम कल्पना कर सकते हैं कि अपरिभाषित प्रतीक पूरी तरह से अर्थ से रहित हैं और अप्रमाणित प्रस्ताव केवल अपरिभाषित प्रतीकों पर दिए गये उद्देश्य हैं।
फिर, विचारों की जिस प्रणाली को हमने प्रारम्भ में चयन किया है वह अपरिभाषित प्रतीकों की मात्र एक व्याख्या है; परन्तु..इस व्याख्या को पाठक द्वारा अनदेखा किया जा सकता है, जो इसे अपने दिमाग में किसी अन्य व्याख्या से परिवर्तित करने के लिए स्वतंत्र है.. जो उद्देशों को पूरा करती हो...
इस प्रकार लॉजिकल प्रश्न अनुभवजन्य या मनोवैज्ञानिक प्रश्नों से पूरी तरह स्वतंत्र हो जाते हैं...
अपरिभाषित प्रतीकों की प्रणाली को विशिष्ट सिद्धांतों से प्राप्त अमूर्तता के रूप में माना जा सकता है, जिसके परिणामस्वरूप... अपरिभाषित प्रतीकों की प्रणाली को प्रत्येक व्याख्या द्वारा क्रमिक रूप से प्रतिस्थापित किया जाता है...
— पडोआ, एस्से डी'यून थ्योरी अल्जेब्रिक डेस नॉम्ब्रे एंटियर्स, एवेक यून इंट्रोडक्शन लॉजिक ए यूने थ्योरी डिडक्टिव क्वेल्कोनक

अर्थात्, गणित एक पदानुक्रमित ढांचे के भीतर संदर्भ-स्वतंत्र ज्ञान है। जैसा कि बर्ट्रेंड रसेल ने कहा है:^[43]

यदि हमारी परिकल्पना किसी एक या अधिक विशेष चीज़ों के बारे में नहीं, जबकि किसी चीज़ के बारे में है, तो हमारे निष्कर्ष गणित का गठन करते हैं। इस प्रकार, गणित को उस विषय के रूप में परिभाषित किया जा सकता है जिसमें हम कभी नहीं जानते कि हम किस बारे में बात कर रहे हैं, न ही यह कि हम जो कह रहे हैं वह सच है या नहीं।
— बर्ट्रेंड रसेल, गणित और तत्वमीमांसा

इस तरह के मूलभूत दृष्टिकोण नींववाद और औपचारिकता (गणित) के मध्य होते हैं।

एक्सिओम्स सूत्र

यूक्लिड के अभिगृहीत: कैम्ब्रिज के ट्रिनिटी कॉलेज में अपने शोध प्रबंध में, बर्ट्रेंड रसेल ने उस समय तक के दार्शनिकों के दिमाग में यूक्लिड की ज्यामिति की बदलती भूमिका को संक्षेप में प्रस्तुत किया।^[44] यह कुछ ज्ञान, प्रयोग से स्वतंत्र, और अनुभववाद के मध्य एक संघर्ष था, जिसमें प्रयोगात्मक इनपुट की आवश्यकता थी। यह मुद्दा स्पष्ट हो गया क्योंकि यह पाया गया कि समानांतर अभिधारणा आवश्यक रूप से मान्य नहीं थी और इसकी प्रयोज्यता एक अनुभवजन्य मामला था, यह तय करते हुए कि प्रयुक्त ज्यामिति यूक्लिडियन थी या गैर-यूक्लिडियन ज्यामिति ।
हिल्बर्ट के एक्सिओम्स: हिल्बर्ट के एक्सिओम्सों का लक्ष्य स्वतंत्र एक्सिओम्सों के एक सरल और पूर्ण समुच्चय की पहचान करना था जिससे सबसे महत्वपूर्ण ज्यामितीय प्रमेयों को निकाला जा सके। उत्कृष्ट उद्देश्य यूक्लिडियन ज्यामिति को कठोर बनाना (छिपी हुई धारणाओं से बचना) और समानांतर अभिधारणा के प्रभाव को स्पष्ट करना था।
बीरखॉफ के अभिगृहीत: बिरखॉफ ने यूक्लिडियन ज्यामिति के लिए चार अभिधारणाओं का प्रस्ताव रखा, जिनकी पुष्टि पैमाने और चांदा के साथ प्रयोगात्मक रूप से की जा सकती है। यह प्रणाली वास्तविक संख्या ओं के गुणों पर बहुत अधिक निर्भर करती है।^[45]^[46]^[47] कोण और दूरी की धारणाएँ आदिम अवधारणाएँ बन जाती हैं।^[48]
टार्स्की के एक्सिओम्स: अल्फ्रेड टार्स्किक (1902-1983) और उनके छात्रों ने प्राथमिक यूक्लिडियन ज्यामिति को ज्यामिति के रूप में परिभाषित किया, जिसे प्रथम-क्रम लॉजिक में व्यक्त किया जा सकता है और इसके लॉजिकल आधार के लिए समुच्चय सिद्धांत पर निर्भर नहीं करता है,^[49] हिल्बर्ट के एक्सिओम्सों के विपरीत, जिसमें बिंदु समुच्चय सम्मिलित हैं।^[50] टार्स्की ने सिद्ध किया कि प्राथमिक यूक्लिडियन ज्यामिति का उनका एक्सिओम्स सूत्रीकरण एक निश्चित निर्णायकता (लॉजिक) में सुसंगत और पूर्ण है: एक कलन विधि होती है, जो प्रत्येक प्रस्ताव के लिए, या तो सही या गलत दिखाया जा सकता है।^[30](यह गोडेल की अपूर्णता प्रमेयों का उल्लंघन नहीं करता है | (यह गोडेल के प्रमेय का उल्लंघन नहीं करता है, क्योंकि यूक्लिडियन ज्यामिति प्रमेय को प्रयुक्त करने के लिए पर्याप्त मात्रा में अंकगणित का वर्णन नहीं कर सकती है।) यह वास्तविक संवृत क्षेत्र की निर्णायकता के बराबर है, जिसमें से प्राथमिक यूक्लिडियन ज्यामिति एक मॉडल है।^[51]

यह भी देखें

निरपेक्ष ज्यामिति
विश्लेषणात्मक ज्यामिति
बीरखोफ के अभिगृहीत
कार्तीय समन्वय प्रणाली
हिल्बर्ट के अभिगृहीत
घटना ज्यामिति
इंटरैक्टिव ज्यामिति सॉफ्टवेयर की सूची
मीट्रिक स्पेस
गैर-यूक्लिडियन ज्यामिति
आदेशित ज्यामिति
समानांतर अभिधारणा
प्रकार सिद्धांत

मौलिक प्रमेय

कोण द्विभाजक प्रमेय
बटरफ्लाई प्रमेय
सीवा का प्रमेय
हीरोन का सूत्र
मेनेलॉस प्रमेय
नौ-बिंदु वृत्त
पाइथागोरस प्रमेय

↑ ^1.0 ^1.1 Eves 1963, p. 19.
↑ Eves 1963, p. 10.
↑ Misner, Thorne, and Wheeler (1973), p. 47.
↑ The assumptions of Euclid are discussed from a modern perspective in Harold E. Wolfe (2007). Introduction to Non-Euclidean Geometry. Mill Press. p. 9. ISBN 978-1-4067-1852-2.
↑ tr. Heath, pp. 195–202.
↑ Venema, Gerard A. (2006), Foundations of Geometry, Prentice-Hall, p. 8, ISBN 978-0-13-143700-5.
↑ Florence P. Lewis (Jan 1920), "History of the Parallel Postulate", The American Mathematical Monthly, The American Mathematical Monthly, Vol. 27, No. 1, 27 (1): 16–23, doi:10.2307/2973238, JSTOR 2973238.
↑ Ball, p. 56.
↑ यूक्लिड की मान्यताओं के भीतर, त्रिभुजों और वर्गों के क्षेत्रफल के लिए एक सूत्र देना काफी आसान है। हालांकि, सेट थ्योरी जैसे अधिक सामान्य संदर्भ में, यह साबित करना उतना आसान नहीं है कि एक वर्ग का क्षेत्रफल उसके टुकड़ों के क्षेत्रों का योग है, उदाहरण के लिए। Lebesgue माप और Banach-Tarski विरोधाभास देखें। कड़ाई से बोलते हुए, कागज पर रेखाएं उन वस्तुओं के उदाहरणों के बजाय औपचारिक प्रणाली के भीतर परिभाषित वस्तुओं के वैज्ञानिक मॉडलिंग हैं। उदाहरण के लिए, एक यूक्लिडियन सीधी रेखा की कोई चौड़ाई नहीं होती है, लेकिन कोई भी वास्तविक खींची गई रेखा होगी। हालांकि लगभग सभी आधुनिक गणितज्ञ अस्तित्व प्रमेय को रचनात्मक मानते हैं, यूक्लिड के रचनात्मक प्रमाणों ने अक्सर भ्रामक गैर-रचनात्मक लोगों की जगह ले ली है - उदाहरण के लिए, पाइथागोरस के कुछ प्रमाण जिनमें अपरिमेय संख्याएँ शामिल हैं, जिन्हें आमतौर पर एक बयान की आवश्यकता होती है जैसे कि सबसे बड़ा सामान्य उपाय खोजें ... रेफरी>Daniel Shanks (2002). संख्या सिद्धांत में हल और अनसुलझी समस्याएं. American Mathematical Society.
↑ Euclid, book I, proposition 5, tr. Heath, p. 251.
↑ Ignoring the alleged difficulty of Book I, Proposition 5, Sir Thomas L. Heath mentions another interpretation. This rests on the resemblance of the figure's lower straight lines to a steeply inclined bridge that could be crossed by an ass but not by a horse: "But there is another view (as I have learnt lately) which is more complimentary to the ass. It is that, the figure of the proposition being like that of a trestle bridge, with a ramp at each end which is more practicable the flatter the figure is drawn, the bridge is such that, while a horse could not surmount the ramp, an ass could; in other words, the term is meant to refer to the sure-footedness of the ass rather than to any want of intelligence on his part." (in "Excursis II", volume 1 of Heath's translation of The Thirteen Books of the Elements).
↑ Euclid, book I, proposition 32.
↑ Heath, p. 135. Extract of page 135.
↑ Heath, p. 318.
↑ Euclid, book XII, proposition 2.
↑ Euclid, book XI, proposition 33.
↑ Ball, p. 66.
↑ Ball, p. 5.
↑ Eves, vol. 1, p. 5; Mlodinow, p. 7.
↑ Tom Hull. "ओरिगेमी और ज्यामितीय निर्माण".
↑ Eves, p. 27.
↑ Ball, pp. 268ff.
↑ Eves (1963).
↑ Hofstadter 1979, p. 91.
↑ Theorem 120, Elements of Abstract Algebra, Allan Clark, Dover, ISBN 0-486-64725-0.
↑ Eves (1963), p. 64.
↑ Ball, p. 485.
↑ * Howard Eves, 1997 (1958). Foundations and Fundamental Concepts of Mathematics. Dover.
↑ Birkhoff, G. D., 1932, "A Set of Postulates for Plane Geometry (Based on Scale and Protractors)", Annals of Mathematics 33.
↑ ^30.0 ^30.1 Tarski (1951).
↑ Misner, Thorne, and Wheeler (1973), p. 191.
↑ Rizos, Chris. University of New South Wales. GPS Satellite Signals Archived 2010-06-12 at the Wayback Machine. 1999.
↑ Richard J. Trudeau (2008). "Euclid's axioms". गैर-यूक्लिडियन क्रांति. Birkhäuser. pp. 39 ff. ISBN 978-0-8176-4782-7.
↑ देखें, उदाहरण के लिए: Luciano da Fontoura Costa; Roberto Marcondes Cesar (2001). आकार विश्लेषण और वर्गीकरण: सिद्धांत और व्यवहार. CRC Press. p. 314. ISBN 0-8493-3493-4. तथा Helmut Pottmann; Johannes Wallner (2010). कम्प्यूटेशनल लाइन ज्यामिति. Springer. p. 60. ISBN 978-3-642-04017-7. गतियों का समूह ज्यामिति की मीट्रिक धारणाओं को रेखांकित करता है। देखना Felix Klein (2004). एक उन्नत दृष्टिकोण से प्राथमिक गणित: ज्यामिति (Reprint of 1939 Macmillan Company ed.). Courier Dover. p. 167. ISBN 0-486-43481-8.
↑ Ball, p. 31.
↑ Heath, p. 268.
↑ Giuseppe Veronese, On Non-Archimedean Geometry, 1908. English translation in Real Numbers, Generalizations of the Reals, and Theories of Continua, ed. Philip Ehrlich, Kluwer, 1994.
↑ Robinson, Abraham (1966). Non-standard analysis.
↑ For the assertion that this was the historical reason for the ancients considering the parallel postulate less obvious than the others, see Nagel and Newman 1958, p. 9.
↑ Cajori (1918), p. 197.
↑ ^41.0 ^41.1 A detailed discussion can be found in James T. Smith (2000). "Chapter 2: Foundations". Methods of geometry. Wiley. pp. 19 ff. ISBN 0-471-25183-6.
↑ Société française de philosophie (1900). तत्वमीमांसा और नैतिकता के जर्नल, खंड 8. Hachette. p. 592.
↑ Bertrand Russell (2000). "Mathematics and the metaphysicians". In James Roy Newman (ed.). गणित की दुनिया. Vol. 3 (Reprint of Simon and Schuster 1956 ed.). Courier Dover Publications. p. 1577. ISBN 0-486-41151-6.
↑ Bertrand Russell (1897). "Introduction". ज्यामिति की नींव पर एक निबंध. Cambridge University Press.
↑ George David Birkhoff; Ralph Beatley (1999). "Chapter 2: The five fundamental principles". मूल ज्यामिति (3rd ed.). AMS Bookstore. pp. 38 ff. ISBN 0-8218-2101-6.
↑ James T. Smith (10 January 2000). "Chapter 3: Elementary Euclidean Geometry". उद्धृत कार्य. pp. 84 ff. ISBN 9780471251835.
↑ Edwin E. Moise (1990). एक उन्नत दृष्टिकोण से प्राथमिक ज्यामिति (3rd ed.). Addison–Wesley. ISBN 0-201-50867-2.
↑ John R. Silvester (2001). "§1.4 Hilbert and Birkhoff". ज्यामिति: प्राचीन और आधुनिक. Oxford University Press. ISBN 0-19-850825-5.
↑ Alfred Tarski (2007). "What is elementary geometry". In Leon Henkin; Patrick Suppes; Alfred Tarski (eds.). तर्कशास्त्र और गणित की नींव में अध्ययन - ज्यामिति और भौतिकी के विशेष संदर्भ के साथ स्वयंसिद्ध विधि (Proceedings of International Symposium at Berkeley 1957–8; Reprint ed.). Brouwer Press. p. 16. ISBN 978-1-4067-5355-4. हम यूक्लिडियन ज्यामिति के उस हिस्से को प्राथमिक मानते हैं जिसे किसी भी सेट-सैद्धांतिक उपकरणों की सहायता के बिना तैयार और स्थापित किया जा सकता है
↑ Keith Simmons (2009). "Tarski's logic". In Dov M. Gabbay; John Woods (eds.). रसेल से चर्च तक तर्क. Elsevier. p. 574. ISBN 978-0-444-51620-6.
↑ Franzén, Torkel (2005). Gödel's Theorem: An Incomplete Guide to its Use and Abuse. AK Peters. ISBN 1-56881-238-8. Pp. 25–26.

संदर्भ

Ball, W. W. Rouse (1960). A Short Account of the History of Mathematics (4th ed. [Reprint. Original publication: London: Macmillan & Co., 1908] ed.). New York: Dover Publications. pp. 50–62. ISBN 0-486-20630-0.
Coxeter, H. S. M. (1961). Introduction to Geometry. New York: Wiley.
Eves, Howard (1963). A Survey of Geometry (Volume One). Allyn and Bacon.
Heath, Thomas L. (1956). The Thirteen Books of Euclid's Elements (2nd ed. [Facsimile. Original publication: Cambridge University Press, 1925] ed.). New York: Dover Publications. In 3 vols.: vol. 1 ISBN 0-486-60088-2, vol. 2 ISBN 0-486-60089-0, vol. 3 ISBN 0-486-60090-4. Heath's authoritative translation of Euclid's Elements, plus his extensive historical research and detailed commentary throughout the text.
Misner, Charles W.; Thorne, Kip S.; Wheeler, John Archibald (1973). Gravitation. W. H. Freeman.
Mlodinow (2001). Euclid's Window. The Free Press. ISBN 9780684865232.
Nagel, E.; Newman, J. R. (1958). Gödel's Proof. New York University Press.
Tarski, Alfred (1951). A Decision Method for Elementary Algebra and Geometry. Univ. of California Press.

इस पृष्ठ में अनुपलब्ध आंतरिक कड़ियों की सूची

कम्पास (प्रारूपण)
रफएल
ग्रीक गणित
घन ज्यामिति
माध्यमिक स्कूल
आत्म-संगत
बीजीय सूत्र
COORDINATES
पाइथागोरस प्रमेय
अभाज्य सँख्या
मांगना
घेरा
ज्यामिति की नींव
समतल ज्यामिति)
लॉजिकल तुल्यता
समुच्चय सिद्धान्त
लेबेस्गु उपाय
संपूरक कोण
अधिक कोण
क्षेत्र (ज्यामिति)
संगत पक्ष
भूमि की नाप
पैकिंग की समस्या
कागज तह का गणित
आर्किमिडीज गुण
कार्तीय समन्वय प्रणाली
परिप्रेक्ष्य (ग्राफिकल)
प्रक्षेप्य ज्यामिति
घन दुगना
वृत्त को चौकोर करना
एफाइन ज्यामिति
चार का समुदाय
जटिल आंकड़े
यूक्लिडियन स्पेस
नियमित 4-पॉलीटोप्स
मोरित्ज़ पास्चो
मिंकोव्स्की स्पेस
स्पेस समय
सूक्तियों
अनंतता
थकावट का विधि
गॉटफ्राइड लाइबनिज़ो
प्रेरण द्वारा प्रमाण
जियोमीट्रिक श्रंखला
निर्णयशीलता (लॉजिक)

बाहरी संबंध

"Euclidean geometry", Encyclopedia of Mathematics, EMS Press, 2001 [1994]
"Plane trigonometry", Encyclopedia of Mathematics, EMS Press, 2001 [1994]
Kiran Kedlaya, Geometry Unbound (a treatment using analytic geometry; PDF format, GFDL licensed)

[eves1_19-1] 1.0 ^1.1 Eves 1963, p. 19.

[2] Eves 1963, p. 10.

[3] Misner, Thorne, and Wheeler (1973), p. 47.

[Wolfe-4] The assumptions of Euclid are discussed from a modern perspective in Harold E. Wolfe (2007). Introduction to Non-Euclidean Geometry. Mill Press. p. 9. ISBN 978-1-4067-1852-2.

[5] tr. Heath, pp. 195–202.

[6] Venema, Gerard A. (2006), Foundations of Geometry, Prentice-Hall, p. 8, ISBN 978-0-13-143700-5.

[7] Florence P. Lewis (Jan 1920), "History of the Parallel Postulate", The American Mathematical Monthly, The American Mathematical Monthly, Vol. 27, No. 1, 27 (1): 16–23, doi:10.2307/2973238, JSTOR 2973238.

[8] Ball, p. 56.

[set_theory-9] यूक्लिड की मान्यताओं के भीतर, त्रिभुजों और वर्गों के क्षेत्रफल के लिए एक सूत्र देना काफी आसान है। हालांकि, सेट थ्योरी जैसे अधिक सामान्य संदर्भ में, यह साबित करना उतना आसान नहीं है कि एक वर्ग का क्षेत्रफल उसके टुकड़ों के क्षेत्रों का योग है, उदाहरण के लिए। Lebesgue माप और Banach-Tarski विरोधाभास देखें। कड़ाई से बोलते हुए, कागज पर रेखाएं उन वस्तुओं के उदाहरणों के बजाय औपचारिक प्रणाली के भीतर परिभाषित वस्तुओं के वैज्ञानिक मॉडलिंग हैं। उदाहरण के लिए, एक यूक्लिडियन सीधी रेखा की कोई चौड़ाई नहीं होती है, लेकिन कोई भी वास्तविक खींची गई रेखा होगी। हालांकि लगभग सभी आधुनिक गणितज्ञ अस्तित्व प्रमेय को रचनात्मक मानते हैं, यूक्लिड के रचनात्मक प्रमाणों ने अक्सर भ्रामक गैर-रचनात्मक लोगों की जगह ले ली है - उदाहरण के लिए, पाइथागोरस के कुछ प्रमाण जिनमें अपरिमेय संख्याएँ शामिल हैं, जिन्हें आमतौर पर एक बयान की आवश्यकता होती है जैसे कि सबसे बड़ा सामान्य उपाय खोजें ... रेफरी>Daniel Shanks (2002). संख्या सिद्धांत में हल और अनसुलझी समस्याएं. American Mathematical Society.

[10] Euclid, book I, proposition 5, tr. Heath, p. 251.

[11] Ignoring the alleged difficulty of Book I, Proposition 5, Sir Thomas L. Heath mentions another interpretation. This rests on the resemblance of the figure's lower straight lines to a steeply inclined bridge that could be crossed by an ass but not by a horse: "But there is another view (as I have learnt lately) which is more complimentary to the ass. It is that, the figure of the proposition being like that of a trestle bridge, with a ramp at each end which is more practicable the flatter the figure is drawn, the bridge is such that, while a horse could not surmount the ramp, an ass could; in other words, the term is meant to refer to the sure-footedness of the ass rather than to any want of intelligence on his part." (in "Excursis II", volume 1 of Heath's translation of The Thirteen Books of the Elements).

[12] Euclid, book I, proposition 32.

[13] Heath, p. 135. Extract of page 135.

[14] Heath, p. 318.

[15] Euclid, book XII, proposition 2.

[16] Euclid, book XI, proposition 33.

[17] Ball, p. 66.

[18] Ball, p. 5.

[19] Eves, vol. 1, p. 5; Mlodinow, p. 7.

[20] Tom Hull. "ओरिगेमी और ज्यामितीय निर्माण".

[21] Eves, p. 27.

[22] Ball, pp. 268ff.

[23] Eves (1963).

[24] Hofstadter 1979, p. 91.

[25] Theorem 120, Elements of Abstract Algebra, Allan Clark, Dover, ISBN 0-486-64725-0.

[26] Eves (1963), p. 64.

[27] Ball, p. 485.

[28] * Howard Eves, 1997 (1958). Foundations and Fundamental Concepts of Mathematics. Dover.

[29] Birkhoff, G. D., 1932, "A Set of Postulates for Plane Geometry (Based on Scale and Protractors)", Annals of Mathematics 33.

[Tarski_1951-30] 30.0 ^30.1 Tarski (1951).

[31] Misner, Thorne, and Wheeler (1973), p. 191.

[32] Rizos, Chris. University of New South Wales. GPS Satellite Signals Archived 2010-06-12 at the Wayback Machine. 1999.

[Trudeau-33] Richard J. Trudeau (2008). "Euclid's axioms". गैर-यूक्लिडियन क्रांति. Birkhäuser. pp. 39 ff. ISBN 978-0-8176-4782-7.

[Euclidean_Motion-34] देखें, उदाहरण के लिए: Luciano da Fontoura Costa; Roberto Marcondes Cesar (2001). आकार विश्लेषण और वर्गीकरण: सिद्धांत और व्यवहार. CRC Press. p. 314. ISBN 0-8493-3493-4. तथा Helmut Pottmann; Johannes Wallner (2010). कम्प्यूटेशनल लाइन ज्यामिति. Springer. p. 60. ISBN 978-3-642-04017-7. गतियों का समूह ज्यामिति की मीट्रिक धारणाओं को रेखांकित करता है। देखना Felix Klein (2004). एक उन्नत दृष्टिकोण से प्राथमिक गणित: ज्यामिति (Reprint of 1939 Macmillan Company ed.). Courier Dover. p. 167. ISBN 0-486-43481-8.

[35] Ball, p. 31.

[36] Heath, p. 268.

[37] Giuseppe Veronese, On Non-Archimedean Geometry, 1908. English translation in Real Numbers, Generalizations of the Reals, and Theories of Continua, ed. Philip Ehrlich, Kluwer, 1994.

[38] Robinson, Abraham (1966). Non-standard analysis.

[39] For the assertion that this was the historical reason for the ancients considering the parallel postulate less obvious than the others, see Nagel and Newman 1958, p. 9.

[40] Cajori (1918), p. 197.

[Smith-41] 41.0 ^41.1 A detailed discussion can be found in James T. Smith (2000). "Chapter 2: Foundations". Methods of geometry. Wiley. pp. 19 ff. ISBN 0-471-25183-6.

[revue-42] Société française de philosophie (1900). तत्वमीमांसा और नैतिकता के जर्नल, खंड 8. Hachette. p. 592.

[Newman-43] Bertrand Russell (2000). "Mathematics and the metaphysicians". In James Roy Newman (ed.). गणित की दुनिया. Vol. 3 (Reprint of Simon and Schuster 1956 ed.). Courier Dover Publications. p. 1577. ISBN 0-486-41151-6.

[Russell-44] Bertrand Russell (1897). "Introduction". ज्यामिति की नींव पर एक निबंध. Cambridge University Press.

[Brikhoff-45] George David Birkhoff; Ralph Beatley (1999). "Chapter 2: The five fundamental principles". मूल ज्यामिति (3rd ed.). AMS Bookstore. pp. 38 ff. ISBN 0-8218-2101-6.

[Smith2-46] James T. Smith (10 January 2000). "Chapter 3: Elementary Euclidean Geometry". उद्धृत कार्य. pp. 84 ff. ISBN 9780471251835.

[Moise-47] Edwin E. Moise (1990). एक उन्नत दृष्टिकोण से प्राथमिक ज्यामिति (3rd ed.). Addison–Wesley. ISBN 0-201-50867-2.

[Silvester-48] John R. Silvester (2001). "§1.4 Hilbert and Birkhoff". ज्यामिति: प्राचीन और आधुनिक. Oxford University Press. ISBN 0-19-850825-5.

[Tarski0-49] Alfred Tarski (2007). "What is elementary geometry". In Leon Henkin; Patrick Suppes; Alfred Tarski (eds.). तर्कशास्त्र और गणित की नींव में अध्ययन - ज्यामिति और भौतिकी के विशेष संदर्भ के साथ स्वयंसिद्ध विधि (Proceedings of International Symposium at Berkeley 1957–8; Reprint ed.). Brouwer Press. p. 16. ISBN 978-1-4067-5355-4. हम यूक्लिडियन ज्यामिति के उस हिस्से को प्राथमिक मानते हैं जिसे किसी भी सेट-सैद्धांतिक उपकरणों की सहायता के बिना तैयार और स्थापित किया जा सकता है

[Simmons-50] Keith Simmons (2009). "Tarski's logic". In Dov M. Gabbay; John Woods (eds.). रसेल से चर्च तक तर्क. Elsevier. p. 574. ISBN 978-0-444-51620-6.

[51] Franzén, Torkel (2005). Gödel's Theorem: An Incomplete Guide to its Use and Abuse. AK Peters. ISBN 1-56881-238-8. Pp. 25–26.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[20]

[21]

[22]

[23]

[24]

[25]

[26]

[27]

[28]

[29]

[30]

[31]

[32]

[33]

[34]

[35]

[36]

[37]

[38]

[39]

[40]

[41]

[42]

[43]

[44]

[45]

[46]

[47]

[48]

[49]

[50]

[51]

@@ Line 373: / Line 373: @@
 [[Category:Commons category link is the pagename|Euclidean Geometry]]
 [[Category:Created On 10/11/2022|Euclidean Geometry]]
+[[Category:Lua-based templates|Euclidean Geometry]]
 [[Category:Machine Translated Page|Euclidean Geometry]]
 [[Category:Mathematics sidebar templates|Euclidean Geometry]]
@@ Line 379: / Line 380: @@
 [[Category:Pages with broken file links|Euclidean Geometry]]
 [[Category:Pages with empty portal template|Euclidean Geometry]]
-[[Category:Vigyan Ready]]
+[[Category:Pages with script errors|Euclidean Geometry]]
+[[Category:Physics sidebar templates|Euclidean Geometry]]
+[[Category:Portal-inline template with redlinked portals|Euclidean Geometry]]
+[[Category:Short description with empty Wikidata description|Euclidean Geometry]]
+[[Category:Sidebars with styles needing conversion|Euclidean Geometry]]
+[[Category:Template documentation pages|Documentation/doc]]
+[[Category:Templates Translated in Hindi|Euclidean Geometry]]
+[[Category:Templates Vigyan Ready|Euclidean Geometry]]
+[[Category:Templates generating microformats|Euclidean Geometry]]
+[[Category:Templates that add a tracking category|Euclidean Geometry]]
+[[Category:Templates that are not mobile friendly|Euclidean Geometry]]
+[[Category:Templates that generate short descriptions|Euclidean Geometry]]
+[[Category:Templates using TemplateData|Euclidean Geometry]]
+[[Category:Webarchive template wayback links]]
+[[Category:Wikipedia metatemplates|Euclidean Geometry]]

v t e Major topics in Geometry
Euclidean geometry	Combinatorial Convex Discrete Plane geometry Polygon Solid geometry
Non-Euclidean geometry	Elliptic Hyperbolic Symplectic Spherical Affine Projective Riemannian
Other	Trigonometry Lie group Algebraic geometry Differential geometry
Lists	Shape Lists List of geometry topics List of differential geometry topics

Anonymous

Search