अनुकूलता (यांत्रिकी): Difference between revisions

Latest revision as of 07:03, 23 September 2023

सातत्य यांत्रिकी में, निकाय में अनुकूलता परिमित विरूपण टेंसर (या तनाव टेंसर) क्षेत्र वह अद्वितीय टेंसर क्षेत्र होता है जो तब प्राप्त होता है जब निकाय निरंतर कार्य, एकल-मूल्यवान, विस्थापन क्षेत्र (यांत्रिकी) के अधीन होता है। अनुकूलता उन परिस्थितियों का अध्ययन है जिनके अनुसार ऐसे विस्थापन क्षेत्र की गारंटी दी जा सकती है। इस प्रकार अनुकूलता स्थितियाँ अभिन्नता स्थितियों के विशेष स्थिति हैं और इन्हें पहली बार 1864 में बैरे डी सेंट-वेनेंट द्वारा रैखिक लोच के लिए प्राप्त किया गया था और 1886 में यूजेनियो बेल्ट्रामी द्वारा कठोरता से सिद्ध किया गया था।^[1]

ठोस पिंड के सातत्य विवरण में हम कल्पना करते हैं कि यह पिंड अनंत छोटे आयतनों या भौतिक बिंदुओं के समूह से बना है। प्रत्येक वॉल्यूम को बिना किसी अंतराल या ओवरलैप के अपने निकट से जुड़ा हुआ माना जाता है। इस प्रकार यह सुनिश्चित करने के लिए कुछ गणितीय नियमो को पूरा करना होगा कि सातत्य निकाय के विकृत होने पर अंतराल/ओवरलैप विकसित नही होते है। ऐसा निकाय जो बिना किसी अंतराल/ओवरलैप के विकृत हो जाता है, उसे अनुकूल निकाय कहा जाता है। इस प्रकार अनुकूलता स्थितियाँ गणितीय स्थितियाँ हैं जो यह निर्धारित करती हैं कि कोई विशेष विकृति किसी निकाय को अनुकूल स्थिति में छोड़ देगी या नहीं छोडती है।^[2]

अपरिमित तनाव सिद्धांत के संदर्भ में, ये स्थितियाँ यह बताने के समान हैं कि किसी पिंड में विस्थापन अपरिमित तनाव सिद्धांतों को एकीकृत करके प्राप्त किया जा सकता है। ऐसा एकीकरण संभव है यदि सेंट-वेनैंट का टेंसर (या असंगति टेंसर) ${\boldsymbol {R}}({\boldsymbol {\varepsilon }})$ सरलता से जुड़े हुए निकाय में लुप्त हो जाता है^[3] जहाँ ${\boldsymbol {\varepsilon }}$ इनफिनिटसिमल तनाव सिद्धांत है और

{\boldsymbol {R}}:={\boldsymbol {\nabla }}\times ({\boldsymbol {\nabla }}\times {\boldsymbol {\varepsilon }})^{T}={\boldsymbol {0}}~.

परिमित विकृतियों सिद्धांत के लिए अनुकूलता स्थितियाँ रूप लेती हैं

{\boldsymbol {R}}:={\boldsymbol {\nabla }}\times {\boldsymbol {F}}={\boldsymbol {0}}

जहाँ ${\boldsymbol {F}}$ विरूपण प्रवणता है.

अत्यंत सूक्ष्म तनाव के लिए अनुकूलता की स्थितियाँ

रैखिक लोच में अनुकूलता स्थितियाँ यह देखकर प्राप्त की जाती हैं कि छह तनाव-विस्थापन संबंध हैं जो केवल तीन अज्ञात विस्थापनों के कार्य हैं। इससे पता चलता है कि तीन विस्थापनों को सूचना की हानि के बिना समीकरणों की प्रणाली से हटाया जा सकता है। इस प्रकार केवल तनाव के संदर्भ में परिणामी अभिव्यक्तियाँ तनाव क्षेत्र के संभावित रूपों पर बाधाएं प्रदान करती हैं।

2-आयाम

द्वि-आयामी, समतल तनाव समस्याओं के लिए तनाव-विस्थापन संबंध हैं

\varepsilon _{11}={\cfrac {\partial u_{1}}{\partial x_{1}}}~;~~\varepsilon _{12}={\cfrac {1}{2}}\left[{\cfrac {\partial u_{1}}{\partial x_{2}}}+{\cfrac {\partial u_{2}}{\partial x_{1}}}\right]~;~~\varepsilon _{22}={\cfrac {\partial u_{2}}{\partial x_{2}}}

विस्थापन $u_{1}$ और $u_{2}$ को दूर करने के लिए इन संबंधों का बार-बार विभेदन होता है, इस प्रकार हमें तनाव के लिए द्वि-आयामी अनुकूलता स्थिति प्रदान करता है

{\cfrac {\partial ^{2}\varepsilon _{11}}{\partial x_{2}^{2}}}-2{\cfrac {\partial ^{2}\varepsilon _{12}}{\partial x_{1}\partial x_{2}}}+{\cfrac {\partial ^{2}\varepsilon _{22}}{\partial x_{1}^{2}}}=0

एकमात्र विस्थापन क्षेत्र जिसे अनुकूल समतल तनाव क्षेत्र द्वारा अनुमति दी जाती है, वह समतल विस्थापन क्षेत्र है, अर्थात, $\mathbf {u} =\mathbf {u} (x_{1},x_{2})$ .

3-आयाम

तीन आयामों में, दो आयामों के लिए देखे गए स्वरूप के दो और समीकरणों के अतिरिक्त स्वरूप के तीन और समीकरण हैं

{\cfrac {\partial ^{2}\varepsilon _{33}}{\partial x_{1}\partial x_{2}}}={\cfrac {\partial }{\partial x_{3}}}\left[{\cfrac {\partial \varepsilon _{23}}{\partial x_{1}}}+{\cfrac {\partial \varepsilon _{31}}{\partial x_{2}}}-{\cfrac {\partial \varepsilon _{12}}{\partial x_{3}}}\right]

इसलिए 3⁴=81 आंशिक अंतर समीकरण हैं, चूंकि समरूपता स्थितियों के कारण यह संख्या छह भिन्न-भिन्न अनुकूलता स्थितियों तक कम हो जाती है। इस प्रकार हम इन नियमो को सूचकांक में इस प्रकार लिख सकते हैं ^[4]

e_{ikr}~e_{jls}~\varepsilon _{ij,kl}=0

जहाँ $e_{ijk}$ क्रमपरिवर्तन प्रतीक है. प्रत्यक्ष टेंसर सूचकांक में

{\boldsymbol {\nabla }}\times ({\boldsymbol {\nabla }}\times {\boldsymbol {\varepsilon }})^{T}={\boldsymbol {0}}

जहां कर्ल ऑपरेटर को ऑर्थोनॉर्मल समन्वय प्रणाली ${\boldsymbol {\nabla }}\times {\boldsymbol {\varepsilon }}=e_{ijk}\varepsilon _{rj,i}\mathbf {e} _{k}\otimes \mathbf {e} _{r}$ के रूप में व्यक्त किया जा सकता है .

दूसरे क्रम का टेंसर

{\boldsymbol {R}}:={\boldsymbol {\nabla }}\times ({\boldsymbol {\nabla }}\times {\boldsymbol {\varepsilon }})^{T}~;~~R_{rs}:=e_{ikr}~e_{jls}~\varepsilon _{ij,kl}

असंगति टेंसर के रूप में जाना जाता है, और यह सेंट-वेनैंट की अनुकूलता स्थिति या क्रम 2 टेंसर क्षेत्र्स या सेंट-वेनैंट अनुकूलता टेंसर के समान है

परिमित तनाव के लिए अनुकूलता की स्थिति

उन ठोस पदार्थों के लिए जिनमें विकृतियों का छोटा होना आवश्यक नहीं है, अनुकूलता की स्थितियाँ रूप ले लेती हैं

{\boldsymbol {\nabla }}\times {\boldsymbol {F}}={\boldsymbol {0}}

जहाँ ${\boldsymbol {F}}$ विरूपण प्रवणता है. इस प्रकार कार्टेशियन समन्वय प्रणाली के संबंध में अवयवो के संदर्भ में हम इन अनुकूलता संबंधों को इस प्रकार लिख सकते हैं

e_{ABC}~{\cfrac {\partial F_{iB}}{\partial X_{A}}}=0

यदि विरूपण निरंतर होना है और मानचित्रण $\mathbf {x} ={\boldsymbol {\chi }}(\mathbf {X} ,t)$ से प्राप्त होना है तो यह नियम आवश्यक है (परिमित तनाव सिद्धांत देखें)। यही स्थिति सरल रूप से जुड़े निकाय में अनुकूलता सुनिश्चित करने के लिए भी पर्याप्त है।

सही कॉची-ग्रीन विरूपण टेंसर के लिए अनुकूलता स्थिति

परिमित तनाव सिद्धांत के लिए अनुकूलता की स्थिति या सही कॉची-ग्रीन विरूपण टेंसर को इस प्रकार व्यक्त किया जा सकता है

R_{\alpha \beta \rho }^{\gamma }:={\frac {\partial }{\partial X^{\rho }}}[\Gamma _{\alpha \beta }^{\gamma }]-{\frac {\partial }{\partial X^{\beta }}}[\Gamma _{\alpha \rho }^{\gamma }]+\Gamma _{\mu \rho }^{\gamma }~\Gamma _{\alpha \beta }^{\mu }-\Gamma _{\mu \beta }^{\gamma }~\Gamma _{\alpha \rho }^{\mu }=0

जहाँ $\Gamma _{ij}^{k}$ वक्ररेखीय निर्देशांक है. इस प्रकार मात्रा $R_{ijk}^{m}$ रीमैन-क्रिस्टोफ़ेल वक्रता टेंसर के मिश्रित अवयवो का प्रतिनिधित्व करता है।

सामान्य अनुकूलता समस्या

सातत्य यांत्रिकी में अनुकूलता की समस्या में सरल रूप से जुड़े निकायों पर स्वीकार्य एकल-मूल्य वाले निरंतर क्षेत्रों का निर्धारण सम्मिलित है। अधिक स्पष्ट रूप से, समस्या को निम्नलिखित विधि से बताया जा सकता है।^[5]

चित्र 1. सातत्य पिंड की गति।

चित्र 1 में दिखाए गए किसी पिंड के विरूपण पर विचार करें। यदि हम सभी सदिश को संदर्भ समन्वय प्रणाली के संदर्भ में व्यक्त करते हैं इस प्रकार $\{(\mathbf {E} _{1},\mathbf {E} _{2},\mathbf {E} _{3}),O\}$ , निकाय में बिंदु का विस्थापन द्वारा दिया जाता है

\mathbf {u} =\mathbf {x} -\mathbf {X} ~;~~u_{i}=x_{i}-X_{i}

भी

{\boldsymbol {\nabla }}\mathbf {u} ={\frac {\partial \mathbf {u} }{\partial \mathbf {X} }}~;~~{\boldsymbol {\nabla }}\mathbf {x} ={\frac {\partial \mathbf {x} }{\partial \mathbf {X} }}

किसी निकाय पर दिए गए दूसरे क्रम के टेंसर क्षेत्र ${\boldsymbol {A}}(\mathbf {X} )$ पर कौन सी स्थितियाँ आवश्यक और पर्याप्त हैं जिससे एक अद्वितीय सदिश क्षेत्र $\mathbf {v} (\mathbf {X} )$ उपस्थितहो जो संतुष्ट हो

{\boldsymbol {\nabla }}\mathbf {v} ={\boldsymbol {A}}\quad \equiv \quad v_{i,j}=A_{ij}

आवश्यक नियम

आवश्यक नियमो के लिए हम मानते हैं कि क्षेत्र $\mathbf {v}$ उपस्थितहै और $v_{i,j}=A_{ij}$ को संतुष्ट करता है, तब

v_{i,jk}=A_{ij,k}~;~~v_{i,kj}=A_{ik,j}

चूँकि विभेदन का क्रम परिवर्तन से हमारे प्राप्त परिणाम पर कोई प्रभाव नहीं पड़ता है

v_{i,jk}=v_{i,kj}

इस तरह

A_{ij,k}=A_{ik,j}

टेंसर व्युत्पन्न (सातत्य यांत्रिकी) के लिए प्रसिद्ध पहचान से हमें आवश्यक नियम मिलती है

{\boldsymbol {\nabla }}\times {\boldsymbol {A}}={\boldsymbol {0}}

पर्याप्त स्थितियाँ

चित्र 2. अनुकूलता के लिए पर्याप्तता नियमो को सिद्ध करने में उपयोग किए जाने वाले एकीकरण पथ।

यह सिद्ध करने के लिए कि यह स्थिति अनुकूल दूसरे क्रम के टेंसर क्षेत्र के अस्तित्व की गारंटी देने के लिए पर्याप्त है, हम इस धारणा से नियम करते हैं कि क्षेत्र ${\boldsymbol {A}}$ ऐसा उपस्थित है

${\boldsymbol {\nabla }}\times {\boldsymbol {A}}={\boldsymbol {0}}$

हम सदिश क्षेत्र खोजने के लिए इस क्षेत्र को एकीकृत करेंगे $\mathbf {v}$ बिंदुओं के मध्य रेखा के साथ $A$ और $B$ (चित्र 2 देखें), अर्थात,

\mathbf {v} (\mathbf {X} _{B})-\mathbf {v} (\mathbf {X} _{A})=\int _{\mathbf {X} _{A}}^{\mathbf {X} _{B}}{\boldsymbol {\nabla }}\mathbf {v} \cdot ~d\mathbf {X} =\int _{\mathbf {X} _{A}}^{\mathbf {X} _{B}}{\boldsymbol {A}}(\mathbf {X} )\cdot d\mathbf {X}

यदि सदिश क्षेत्र $\mathbf {v}$ एकल-मूल्यवान होना है तो अभिन्न का मूल्य आगे बढ़ने के लिए अपनाए गए पथ से स्वतंत्र होना चाहिए इस प्रकार $A$ को $B$ .

स्टोक्स के प्रमेय से, संवृत पथ के साथ दूसरे क्रम के टेंसर का अभिन्न अंग दिया जाता है

\oint _{\partial \Omega }{\boldsymbol {A}}\cdot d\mathbf {s} =\int _{\Omega }\mathbf {n} \cdot ({\boldsymbol {\nabla }}\times {\boldsymbol {A}})~da

इस धारणा का उपयोग करते हुए कि कर्ल ${\boldsymbol {A}}$ शून्य है, हमें मिलता है

\oint _{\partial \Omega }{\boldsymbol {A}}\cdot d\mathbf {s} =0\quad \implies \quad \int _{AB}{\boldsymbol {A}}\cdot d\mathbf {X} +\int _{BA}{\boldsymbol {A}}\cdot d\mathbf {X} =0

इसलिए इंटीग्रल पथ स्वतंत्र है और अद्वितीयता सुनिश्चित करने के लिए अनुकूलता स्थिति $\mathbf {v}$ क्षेत्र पर्याप्त है, परंतु निकाय केवल जुड़ा हुआ होता है।

विरूपण प्रवणता की अनुकूलता

विरूपण प्रवणता के लिए अनुकूलता की स्थिति उपरोक्त प्रमाण से सीधे अवलोकन करके प्राप्त की जाती है

{\boldsymbol {F}}={\cfrac {\partial \mathbf {x} }{\partial \mathbf {X} }}={\boldsymbol {\nabla }}\mathbf {x}

फिर अनुकूल के अस्तित्व के लिए आवश्यक और पर्याप्त नियम ${\boldsymbol {F}}$ साधारण रूप से जुड़े हुए निकाय पर क्षेत्र हैं

{\boldsymbol {\nabla }}\times {\boldsymbol {F}}={\boldsymbol {0}}

अतिसूक्ष्म तनाव की अनुकूलता

छोटे तनाव के लिए अनुकूलता समस्या को निम्नानुसार बताया जा सकता है।

एक सममित दूसरे क्रम के टेंसर क्षेत्र ${\boldsymbol {\epsilon }}$ को देखते हुए एक सदिश क्षेत्र $\mathbf {u}$ का निर्माण करना जब संभव है जैसे कि

{\boldsymbol {\epsilon }}={\frac {1}{2}}[{\boldsymbol {\nabla }}\mathbf {u} +({\boldsymbol {\nabla }}\mathbf {u} )^{T}]

आवश्यक नियम

मान लीजिए कि $\mathbf {u}$ का अस्तित्व इस प्रकार है कि ${\boldsymbol {\epsilon }}$ के लिए अभिव्यक्ति धारण है। अब

{\boldsymbol {\nabla }}\mathbf {u} ={\boldsymbol {\epsilon }}+{\boldsymbol {\omega }}

जहाँ

{\boldsymbol {\omega }}:={\frac {1}{2}}[{\boldsymbol {\nabla }}\mathbf {u} -({\boldsymbol {\nabla }}\mathbf {u} )^{T}]

इसलिए, सूचकांक संकेतन में,

{\boldsymbol {\nabla }}{\boldsymbol {\omega }}\equiv \omega _{ij,k}={\frac {1}{2}}(u_{i,jk}-u_{j,ik})={\frac {1}{2}}(u_{i,jk}+u_{k,ji}-u_{j,ik}-u_{k,ji})=\varepsilon _{ik,j}-\varepsilon _{jk,i}

यदि ${\boldsymbol {\omega }}$ निरंतर अवकलनीय है तो हमारे निकट $\omega _{ij,kl}=\omega _{ij,lk}$ इसलिए है

\varepsilon _{ik,jl}-\varepsilon _{jk,il}-\varepsilon _{il,jk}+\varepsilon _{jl,ik}=0

प्रत्यक्ष टेंसर सूचकांक में

{\boldsymbol {\nabla }}\times ({\boldsymbol {\nabla }}\times {\boldsymbol {\epsilon }})^{T}={\boldsymbol {0}}

उपरोक्त आवश्यक नियम हैं. यदि $\mathbf {w}$ तो यह अनन्तसूक्ष्म तनाव ${\boldsymbol {\nabla }}\times {\boldsymbol {\epsilon }}={\boldsymbol {\nabla }}\mathbf {w} +{\boldsymbol {\nabla }}\mathbf {w} ^{T}$ सिद्धांत है अतः आवश्यक नियम को इस प्रकार भी लिखा जा सकता है ${\boldsymbol {\nabla }}\times ({\boldsymbol {\nabla }}\mathbf {w} +{\boldsymbol {\nabla }}\mathbf {w} ^{T})^{T}={\boldsymbol {0}}$ .

पर्याप्त स्थितियाँ

आइए अब मान लें कि स्थिति ${\boldsymbol {\nabla }}\times ({\boldsymbol {\nabla }}\times {\boldsymbol {\epsilon }})^{T}={\boldsymbol {0}}$ निकाय के भाग में संतुष्ट है. क्या यह स्थिति निरंतर, एकल-मूल्य वाले विस्थापन क्षेत्र $\mathbf {u}$ के अस्तित्व की गारंटी देने के लिए पर्याप्त है ?

इस प्रक्रिया में पहला चरण यह दिखाना है कि इस स्थिति का तात्पर्य यह है कि अपरिमित घूर्णन टेंसर ${\boldsymbol {\omega }}$ विशिष्ट रूप से परिभाषित है। ऐसा करने के लिए हम ${\boldsymbol {\nabla }}\mathbf {w}$ को $\mathbf {X} _{A}$ को $\mathbf {X} _{B}$ पथ के साथ एकीकृत करते हैं, अर्थात,

\mathbf {w} (\mathbf {X} _{B})-\mathbf {w} (\mathbf {X} _{A})=\int _{\mathbf {X} _{A}}^{\mathbf {X} _{B}}{\boldsymbol {\nabla }}\mathbf {w} \cdot d\mathbf {X} =\int _{\mathbf {X} _{A}}^{\mathbf {X} _{B}}({\boldsymbol {\nabla }}\times {\boldsymbol {\epsilon }})\cdot d\mathbf {X}

ध्यान दें कि कठोर निकाय के घूर्णन को ठीक करने के लिए हमें एक संदर्भ $\mathbf {w} (\mathbf {X} _{A})$ जानने की आवश्यकता है। जो की क्षेत्र $\mathbf {w} (\mathbf {X} )$ विशिष्ट रूप से केवल तभी निर्धारित होता है जब रूपरेखा संवृत रूपरेखा के साथ अभिन्न होता है इस प्रकार $\mathbf {X} _{A}$ और $\mathbf {X} _{b}$ शून्य है, अर्थात,

\oint _{\mathbf {X} _{A}}^{\mathbf {X} _{B}}({\boldsymbol {\nabla }}\times {\boldsymbol {\epsilon }})\cdot d\mathbf {X} ={\boldsymbol {0}}

किन्तु स्टोक्स के प्रमेय से सरल रूप से जुड़े निकाय और अनुकूलता के लिए आवश्यक नियम के लिए

\oint _{\mathbf {X} _{A}}^{\mathbf {X} _{B}}({\boldsymbol {\nabla }}\times {\boldsymbol {\epsilon }})\cdot d\mathbf {X} =\int _{\Omega _{AB}}\mathbf {n} \cdot ({\boldsymbol {\nabla }}\times {\boldsymbol {\nabla }}\times {\boldsymbol {\epsilon }})~da={\boldsymbol {0}}

इसलिए, क्षेत्र $\mathbf {w}$ विशिष्ट रूप से परिभाषित किया गया है जिसका अर्थ है कि अनंत लघु घूर्णन टेंसर ${\boldsymbol {\omega }}$ इसे भी विशिष्ट रूप से परिभाषित किया गया है, परंतु निकाय सामान्यतः जुड़ा हुआ होन चाहिए।

प्रक्रिया के अगले चरण में हम विस्थापन क्षेत्र $\mathbf {u}$ की विशिष्टता पर विचार करेंगे, पहले की तरह हम विस्थापन प्रवणता को एकीकृत करते हैं

\mathbf {u} (\mathbf {X} _{B})-\mathbf {u} (\mathbf {X} _{A})=\int _{\mathbf {X} _{A}}^{\mathbf {X} _{B}}{\boldsymbol {\nabla }}\mathbf {u} \cdot d\mathbf {X} =\int _{\mathbf {X} _{A}}^{\mathbf {X} _{B}}({\boldsymbol {\epsilon }}+{\boldsymbol {\omega }})\cdot d\mathbf {X}

स्टोक्स के प्रमेय से और हमारे निकट उपस्थित संबंध ${\boldsymbol {\nabla }}\times {\boldsymbol {\epsilon }}={\boldsymbol {\nabla }}\mathbf {w} =-{\boldsymbol {\nabla }}\times \omega$ का उपयोग करके

\oint _{\mathbf {X} _{A}}^{\mathbf {X} _{B}}({\boldsymbol {\epsilon }}+{\boldsymbol {\omega }})\cdot d\mathbf {X} =\int _{\Omega _{AB}}\mathbf {n} \cdot ({\boldsymbol {\nabla }}\times {\boldsymbol {\epsilon }}+{\boldsymbol {\nabla }}\times {\boldsymbol {\omega }})~da={\boldsymbol {0}}

इसलिए विस्थापन क्षेत्र $\mathbf {u}$ भी विशिष्ट रूप से निर्धारित किया जाता है। इसलिए अनुकूलता स्थितियाँ सरलता से जुड़े निकाय में अद्वितीय विस्थापन क्षेत्र $\mathbf {u}$ के अस्तित्व की गारंटी के लिए पर्याप्त हैं .

राइट कॉची-ग्रीन विरूपण क्षेत्र के लिए अनुकूलता

राइट कॉची-ग्रीन विरूपण क्षेत्र के लिए अनुकूलता समस्या को निम्नानुसार प्रस्तुत किया जा सकता है।

समस्या: मान लीजिए

{\boldsymbol {C}}(\mathbf {X} )

संदर्भ विन्यास पर परिभाषित एक धनात्मक निश्चित सममित टेंसर क्षेत्र है। इस प्रकार

{\boldsymbol {C}}

पर किन परिस्थितियों में स्थिति क्षेत्र

\mathbf {x} (\mathbf {X} )

द्वारा चिह्नित विकृत विन्यास उपस्थित है जैसे कि

(1)\quad \left({\frac {\partial \mathbf {x} }{\partial \mathbf {X} }}\right)^{T}\left({\frac {\partial \mathbf {x} }{\partial \mathbf {X} }}\right)={\boldsymbol {C}}

आवश्यक नियम

मान लीजिए कि क्षेत्र $\mathbf {x} (\mathbf {X} )$ उपस्थित है जो नियम (1) को संतुष्ट करता है। इस प्रकार आयताकार कार्टेशियन आधार के संबंध में अवयवो के संदर्भ में

{\frac {\partial x^{i}}{\partial X^{\alpha }}}{\frac {\partial x^{i}}{\partial X^{\beta }}}=C_{\alpha \beta }

परिमित तनाव सिद्धांत से हम यह जानते हैं कि $C_{\alpha \beta }=g_{\alpha \beta }$ . इसलिए हम लिख सकते हैं

\delta _{ij}~{\frac {\partial x^{i}}{\partial X^{\alpha }}}~{\frac {\partial x^{j}}{\partial X^{\beta }}}=g_{\alpha \beta }

दो सममित द्वितीय-क्रम टेंसर क्षेत्र के लिए जिन्हें एक-से-एक मैप किया जाता है, हमारे निकट परिमित तनाव सिद्धांत भी है इस प्रकार विरूपण उपायों और क्रिस्टोफ़ेल प्रतीकों के मध्य कुछ संबंध

G_{ij}={\frac {\partial X^{\alpha }}{\partial x^{i}}}~{\frac {\partial X^{\beta }}{\partial x^{j}}}~g_{\alpha \beta }

$G_{ij}$ और $g_{\alpha \beta }$ के मध्य के संबंध से जो $\delta _{ij}=G_{ij}$ हमारे पास है

_{(x)}\Gamma _{ij}^{k}=0

फिर, सम्बन्ध से

{\frac {\partial ^{2}x^{m}}{\partial X^{\alpha }\partial X^{\beta }}}={\frac {\partial x^{m}}{\partial X^{\mu }}}\,_{(X)}\Gamma _{\alpha \beta }^{\mu }-{\frac {\partial x^{i}}{\partial X^{\alpha }}}~{\frac {\partial x^{j}}{\partial X^{\beta }}}\,_{(x)}\Gamma _{ij}^{m}

हमारे निकट है

{\frac {\partial F_{~\alpha }^{m}}{\partial X^{\beta }}}=F_{~\mu }^{m}\,_{(X)}\Gamma _{\alpha \beta }^{\mu }\qquad ;~~F_{~\alpha }^{i}:={\frac {\partial x^{i}}{\partial X^{\alpha }}}

परिमित तनाव सिद्धांत से विरूपण उपायों और क्रिस्टोफ़ेल प्रतीकों के मध्य कुछ संबंध भी हमारे निकट हैं

_{(X)}\Gamma _{\alpha \beta \gamma }={\frac {1}{2}}\left({\frac {\partial g_{\alpha \gamma }}{\partial X^{\beta }}}+{\frac {\partial g_{\beta \gamma }}{\partial X^{\alpha }}}-{\frac {\partial g_{\alpha \beta }}{\partial X^{\gamma }}}\right)~;~~_{(X)}\Gamma _{\alpha \beta }^{\nu }=g^{\nu \gamma }\,_{(X)}\Gamma _{\alpha \beta \gamma }~;~~g_{\alpha \beta }=C_{\alpha \beta }~;~~g^{\alpha \beta }=C^{\alpha \beta }

इसलिए,

\,_{(X)}\Gamma _{\alpha \beta }^{\mu }={\cfrac {C^{\mu \gamma }}{2}}\left({\frac {\partial C_{\alpha \gamma }}{\partial X^{\beta }}}+{\frac {\partial C_{\beta \gamma }}{\partial X^{\alpha }}}-{\frac {\partial C_{\alpha \beta }}{\partial X^{\gamma }}}\right)

और हमारे निकट है

{\frac {\partial F_{~\alpha }^{m}}{\partial X^{\beta }}}=F_{~\mu }^{m}~{\cfrac {C^{\mu \gamma }}{2}}\left({\frac {\partial C_{\alpha \gamma }}{\partial X^{\beta }}}+{\frac {\partial C_{\beta \gamma }}{\partial X^{\alpha }}}-{\frac {\partial C_{\alpha \beta }}{\partial X^{\gamma }}}\right)

फिर से, विभेदन के क्रम की क्रमविनिमेय प्रकृति का उपयोग करते हुए, हमारे निकट है

{\frac {\partial ^{2}F_{~\alpha }^{m}}{\partial X^{\beta }\partial X^{\rho }}}={\frac {\partial ^{2}F_{~\alpha }^{m}}{\partial X^{\rho }\partial X^{\beta }}}\implies {\frac {\partial F_{~\mu }^{m}}{\partial X^{\rho }}}\,_{(X)}\Gamma _{\alpha \beta }^{\mu }+F_{~\mu }^{m}~{\frac {\partial }{\partial X^{\rho }}}[\,_{(X)}\Gamma _{\alpha \beta }^{\mu }]={\frac {\partial F_{~\mu }^{m}}{\partial X^{\beta }}}\,_{(X)}\Gamma _{\alpha \rho }^{\mu }+F_{~\mu }^{m}~{\frac {\partial }{\partial X^{\beta }}}[\,_{(X)}\Gamma _{\alpha \rho }^{\mu }]

या

F_{~\gamma }^{m}\,_{(X)}\Gamma _{\mu \rho }^{\gamma }\,_{(X)}\Gamma _{\alpha \beta }^{\mu }+F_{~\mu }^{m}~{\frac {\partial }{\partial X^{\rho }}}[\,_{(X)}\Gamma _{\alpha \beta }^{\mu }]=F_{~\gamma }^{m}\,_{(X)}\Gamma _{\mu \beta }^{\gamma }\,_{(X)}\Gamma _{\alpha \rho }^{\mu }+F_{~\mu }^{m}~{\frac {\partial }{\partial X^{\beta }}}[\,_{(X)}\Gamma _{\alpha \rho }^{\mu }]

नियमो को एकत्रित करने के पश्चात् हमें मिलता है

F_{~\gamma }^{m}\left(\,_{(X)}\Gamma _{\mu \rho }^{\gamma }\,_{(X)}\Gamma _{\alpha \beta }^{\mu }+{\frac {\partial }{\partial X^{\rho }}}[\,_{(X)}\Gamma _{\alpha \beta }^{\gamma }]-\,_{(X)}\Gamma _{\mu \beta }^{\gamma }\,_{(X)}\Gamma _{\alpha \rho }^{\mu }-{\frac {\partial }{\partial X^{\beta }}}[\,_{(X)}\Gamma _{\alpha \rho }^{\gamma }]\right)=0

$F_{\gamma }^{m}$ की परिभाषा से हम पाते हैं कि यह विपरीत है और इसलिए शून्य नहीं हो सकता है। इसलिए,

R_{\alpha \beta \rho }^{\gamma }:={\frac {\partial }{\partial X^{\rho }}}[\,_{(X)}\Gamma _{\alpha \beta }^{\gamma }]-{\frac {\partial }{\partial X^{\beta }}}[\,_{(X)}\Gamma _{\alpha \rho }^{\gamma }]+\,_{(X)}\Gamma _{\mu \rho }^{\gamma }\,_{(X)}\Gamma _{\alpha \beta }^{\mu }-\,_{(X)}\Gamma _{\mu \beta }^{\gamma }\,_{(X)}\Gamma _{\alpha \rho }^{\mu }=0

हम दिखा सकते हैं कि यह रीमैन-क्रिस्टोफ़ेल वक्रता टेंसर के मिश्रित अवयव हैं। इसलिए, के लिए आवश्यक नियम ${\boldsymbol {C}}$ -अनुकूलता यह है कि विरूपण की रीमैन-क्रिस्टोफ़ेल वक्रता शून्य है।

पर्याप्त स्थितियाँ

पर्याप्तता का प्रमाण थोड़ा अधिक सम्मिलित है।^[5]^[6] हम इस धारणा से नियम करते हैं कि

R_{\alpha \beta \rho }^{\gamma }=0~;~~g_{\alpha \beta }=C_{\alpha \beta }

हमें यह दिखाना होगा कि $\mathbf {x}$ और $\mathbf {X}$ ऐसे उपस्थित हैं

{\frac {\partial x^{i}}{\partial X^{\alpha }}}{\frac {\partial x^{i}}{\partial X^{\beta }}}=C_{\alpha \beta }

टी.वाई.थॉमस के प्रमेय से ^[7] हम जानते हैं कि समीकरणों की प्रणाली

{\frac {\partial F_{~\alpha }^{i}}{\partial X^{\beta }}}=F_{~\gamma }^{i}~\,_{(X)}\Gamma _{\alpha \beta }^{\gamma }

सरल रूप से जुड़े डोमेन पर अद्वितीय समाधान $F_{~\alpha }^{i}$ है

_{(X)}\Gamma _{\alpha \beta }^{\gamma }=_{(X)}\Gamma _{\beta \alpha }^{\gamma }~;~~R_{\alpha \beta \rho }^{\gamma }=0

इनमें से पहला $\Gamma _{jk}^{i}$ की परिभाषा से सत्य है और दूसरा मान लिया गया है। इसलिए स्वीकृत स्थिति हमें एक अद्वितीय $F_{~\alpha }^{i}$ देती है जो कि $C^{2}$ निरंतर है।

आगे समीकरणों की प्रणाली पर विचार करें

{\frac {\partial x^{i}}{\partial X^{\alpha }}}=F_{~\alpha }^{i}

चूँकि $F_{~\alpha }^{i}$ $C^{2}$ है और निकाय सामान्यतः जुड़ा हुआ है, इसलिए उपरोक्त समीकरणों के लिए कुछ समाधान $x^{i}(X^{\alpha })$ उपस्थित है। इस प्रकार हम दिखा सकते हैं कि $x^{i}$ उस गुण को भी संतुष्ट करता है

\det \left|{\frac {\partial x^{i}}{\partial X^{\alpha }}}\right|\neq 0

हम वह सम्बन्ध भी दिखा सकते हैं

{\frac {\partial x^{i}}{\partial X^{\alpha }}}~g^{\alpha \beta }~{\frac {\partial x^{j}}{\partial X^{\beta }}}=\delta ^{ij}

तात्पर्य यह है

g_{\alpha \beta }=C_{\alpha \beta }={\frac {\partial x^{k}}{\partial X^{\alpha }}}~{\frac {\partial x^{k}}{\partial X^{\beta }}}

यदि हम इन मात्राओं को टेंसर क्षेत्र के साथ जोड़ते हैं तो हम यह दिखा सकते हैं कि ${\frac {\partial \mathbf {x} }{\partial \mathbf {X} }}$ विपरीत है और निर्मित टेंसर क्षेत्र ${\boldsymbol {C}}$ के लिए अभिव्यक्ति को संतुष्ट करता है

यह भी देखें

सेंट-वेनैंट की अनुकूलता स्थिति
रेखीय लोच
विरूपण (यांत्रिकी)
अनंतिम तनाव सिद्धांत
परिमित तनाव सिद्धांत
टेंसर व्युत्पन्न (सातत्य यांत्रिकी)
वक्ररेखीय निर्देशांक

संदर्भ

↑ C Amrouche, PG Ciarlet, L Gratie, S Kesavan, On Saint Venant's compatibility conditions and Poincaré's lemma, C. R. Acad. Sci. Paris, Ser. I, 342 (2006), 887-891. doi:10.1016/j.crma.2006.03.026
↑ Barber, J. R., 2002, Elasticity - 2nd Ed., Kluwer Academic Publications.
↑ N.I. Muskhelishvili, Some Basic Problems of the Mathematical Theory of Elasticity. Leyden: Noordhoff Intern. Publ., 1975.
↑ Slaughter, W. S., 2003, The linearized theory of elasticity, Birkhauser
↑ ^5.0 ^5.1 Acharya, A., 1999, On Compatibility Conditions for the Left Cauchy–Green Deformation Field in Three Dimensions, Journal of Elasticity, Volume 56, Number 2 , 95-105
↑ Blume, J. A., 1989, "Compatibility conditions for a left Cauchy-Green strain field", J. Elasticity, v. 21, p. 271-308.
↑ Thomas, T. Y., 1934, "Systems of total differential equations defined over simply connected domains", Annals of Mathematics, 35(4), p. 930-734

बाहरी संबंध

[Amrouche-1] C Amrouche, PG Ciarlet, L Gratie, S Kesavan, On Saint Venant's compatibility conditions and Poincaré's lemma, C. R. Acad. Sci. Paris, Ser. I, 342 (2006), 887-891. doi:10.1016/j.crma.2006.03.026

[Barber-2] Barber, J. R., 2002, Elasticity - 2nd Ed., Kluwer Academic Publications.

[3] N.I. Muskhelishvili, Some Basic Problems of the Mathematical Theory of Elasticity. Leyden: Noordhoff Intern. Publ., 1975.

[Slaughter-4] Slaughter, W. S., 2003, The linearized theory of elasticity, Birkhauser

[acharya-5] 5.0 ^5.1 Acharya, A., 1999, On Compatibility Conditions for the Left Cauchy–Green Deformation Field in Three Dimensions, Journal of Elasticity, Volume 56, Number 2 , 95-105

[Blume-6] Blume, J. A., 1989, "Compatibility conditions for a left Cauchy-Green strain field", J. Elasticity, v. 21, p. 271-308.

[Thomas-7] Thomas, T. Y., 1934, "Systems of total differential equations defined over simply connected domains", Annals of Mathematics, 35(4), p. 930-734

[1]

[2]

[3]

[4]

[5]

[6]

[7]

Anonymous

Search

अनुकूलता (यांत्रिकी): Difference between revisions

Namespaces

More

Page actions

Latest revision as of 07:03, 23 September 2023

Contents

अत्यंत सूक्ष्म तनाव के लिए अनुकूलता की स्थितियाँ

2-आयाम

3-आयाम

परिमित तनाव के लिए अनुकूलता की स्थिति

सही कॉची-ग्रीन विरूपण टेंसर के लिए अनुकूलता स्थिति

सामान्य अनुकूलता समस्या

आवश्यक नियम

पर्याप्त स्थितियाँ

विरूपण प्रवणता की अनुकूलता

अतिसूक्ष्म तनाव की अनुकूलता

आवश्यक नियम

पर्याप्त स्थितियाँ

राइट कॉची-ग्रीन विरूपण क्षेत्र के लिए अनुकूलता

आवश्यक नियम

पर्याप्त स्थितियाँ

यह भी देखें

संदर्भ

बाहरी संबंध

Navigation

Navigation

Wiki tools

Wiki tools

@@ Line 1: / Line 1: @@
-{{Continuum mechanics|cTopic=solid}}
+{{Continuum mechanics|cTopic=ठोस}}
-सातत्य यांत्रिकी में, शरीर में संगत [[परिमित विरूपण टेंसर]] (या [[ तनाव टेंसर |तनाव टेंसर]] ) टेंसर क्षेत्र वह ''अद्वितीय'' टेंसर क्षेत्र होता है जो तब प्राप्त होता है जब शरीर निरंतर कार्य, एकल-मूल्यवान, [[विस्थापन क्षेत्र (यांत्रिकी)]] के अधीन होता है। . अनुकूलता उन परिस्थितियों का अध्ययन है जिनके तहत ऐसे विस्थापन क्षेत्र की गारंटी दी जा सकती है। संगतता स्थितियाँ अभिन्नता स्थितियों के विशेष मामले हैं और पहली बार 1864 में अधेमर जीन क्लाउड बर्रे डी सेंट-वेनेंट द्वारा [[रैखिक लोच]] के लिए प्राप्त की गई थीं और 1886 में [[यूजेनियो बेल्ट्रामी]] द्वारा कठोरता से साबित की गईं।<ref name="Amrouche">C Amrouche, [[Philippe G. Ciarlet|PG Ciarlet]], L Gratie, S Kesavan,  On Saint Venant's compatibility conditions and Poincaré's lemma, C. R. Acad. Sci. Paris, Ser. I, 342 (2006), 887-891.  {{doi|10.1016/j.crma.2006.03.026}}</ref>
-ठोस पिंड के सातत्य विवरण में हम कल्पना करते हैं कि यह पिंड अनंत छोटे आयतनों या भौतिक बिंदुओं के समूह से बना है। प्रत्येक वॉल्यूम को बिना किसी अंतराल या ओवरलैप के अपने पड़ोसियों से जुड़ा हुआ माना जाता है। यह सुनिश्चित करने के लिए कुछ गणितीय शर्तों को पूरा करना होगा कि सातत्य शरीर के विकृत होने पर अंतराल/ओवरलैप विकसित न हो। ऐसा शरीर जो बिना किसी अंतराल/ओवरलैप के विकृत हो जाता है, उसे संगत शरीर कहा जाता है। संगतता स्थितियाँ गणितीय स्थितियाँ हैं जो यह निर्धारित करती हैं कि कोई विशेष विकृति किसी शरीर को संगत स्थिति में छोड़ देगी या नहीं।<ref name=Barber>Barber, J. R., 2002, Elasticity - 2nd Ed., Kluwer Academic Publications.</ref>
+सातत्य यांत्रिकी में, निकाय में '''अनुकूलता''' परिमित विरूपण टेंसर (या तनाव टेंसर) क्षेत्र वह ''अद्वितीय'' टेंसर क्षेत्र होता है जो तब प्राप्त होता है जब निकाय निरंतर कार्य, एकल-मूल्यवान, [[विस्थापन क्षेत्र (यांत्रिकी)]] के अधीन होता है। अनुकूलता उन परिस्थितियों का अध्ययन है जिनके अनुसार ऐसे विस्थापन क्षेत्र की गारंटी दी जा सकती है। इस प्रकार अनुकूलता स्थितियाँ अभिन्नता स्थितियों के विशेष स्थिति हैं और इन्हें पहली बार 1864 में बैरे डी सेंट-वेनेंट द्वारा रैखिक लोच के लिए प्राप्त किया गया था और 1886 में [[यूजेनियो बेल्ट्रामी]] द्वारा कठोरता से सिद्ध किया गया था।<ref name="Amrouche">C Amrouche, [[Philippe G. Ciarlet|PG Ciarlet]], L Gratie, S Kesavan,  On Saint Venant's compatibility conditions and Poincaré's lemma, C. R. Acad. Sci. Paris, Ser. I, 342 (2006), 887-891.  {{doi|10.1016/j.crma.2006.03.026}}</ref>
-इनफिनिटिमल स्ट्रेन सिद्धांत के संदर्भ में, ये स्थितियाँ यह बताने के बराबर हैं कि किसी पिंड में विस्थापन इनफिनिटिमल स्ट्रेन सिद्धांतों को एकीकृत करके प्राप्त किया जा सकता है। ऐसा एकीकरण संभव है यदि सेंट-वेनैंट का टेंसर (या असंगति टेंसर) <math>\boldsymbol{R}(\boldsymbol{\varepsilon})</math> सरलता से जुड़े हुए शरीर में लुप्त हो जाता है<ref>N.I. Muskhelishvili,   Some Basic Problems of the Mathematical Theory of Elasticity. Leyden: Noordhoff Intern. Publ., 1975.</ref> कहाँ <math>\boldsymbol{\varepsilon}</math> इनफिनिटसिमल स्ट्रेन सिद्धांत है और
+ठोस पिंड के सातत्य विवरण में हम कल्पना करते हैं कि यह पिंड अनंत छोटे आयतनों या भौतिक बिंदुओं के समूह से बना है। प्रत्येक वॉल्यूम को बिना किसी अंतराल या ओवरलैप के अपने निकट से जुड़ा हुआ माना जाता है। इस प्रकार यह सुनिश्चित करने के लिए कुछ गणितीय नियमो को पूरा करना होगा कि सातत्य निकाय के विकृत होने पर अंतराल/ओवरलैप विकसित नही होते है। ऐसा निकाय जो बिना किसी अंतराल/ओवरलैप के विकृत हो जाता है, उसे अनुकूल निकाय कहा जाता है। इस प्रकार अनुकूलता स्थितियाँ गणितीय स्थितियाँ हैं जो यह निर्धारित करती हैं कि कोई विशेष विकृति किसी निकाय को अनुकूल स्थिति में छोड़ देगी या नहीं छोडती है।<ref name="Barber">Barber, J. R., 2002, Elasticity - 2nd Ed., Kluwer Academic Publications.</ref>
+अपरिमित तनाव सिद्धांत के संदर्भ में, ये स्थितियाँ यह बताने के समान हैं कि किसी पिंड में विस्थापन अपरिमित तनाव सिद्धांतों को एकीकृत करके प्राप्त किया जा सकता है। ऐसा एकीकरण संभव है यदि सेंट-वेनैंट का टेंसर (या असंगति टेंसर) <math>\boldsymbol{R}(\boldsymbol{\varepsilon})</math> सरलता से जुड़े हुए निकाय में लुप्त हो जाता है<ref>N.I. Muskhelishvili,   Some Basic Problems of the Mathematical Theory of Elasticity. Leyden: Noordhoff Intern. Publ., 1975.</ref> जहाँ <math>\boldsymbol{\varepsilon}</math> इनफिनिटसिमल तनाव सिद्धांत है और
 :<math>
    \boldsymbol{R} := \boldsymbol{\nabla}\times(\boldsymbol{\nabla}\times\boldsymbol{\varepsilon})^T = \boldsymbol{0} ~.
 </math>
-[[परिमित तनाव सिद्धांत]] के लिए अनुकूलता स्थितियाँ रूप लेती हैं
+[[परिमित तनाव सिद्धांत|परिमित विकृतियों सिद्धांत]] के लिए अनुकूलता स्थितियाँ रूप लेती हैं
 :<math>
     \boldsymbol{R} :=\boldsymbol{\nabla}\times\boldsymbol{F} = \boldsymbol{0}
   </math>
-कहाँ <math>\boldsymbol{F}</math> [[विरूपण प्रवणता]] है.
+जहाँ <math>\boldsymbol{F}</math> विरूपण प्रवणता है.
-==अतिसूक्ष्म उपभेदों के लिए अनुकूलता की स्थितियाँ ==
+==अत्यंत सूक्ष्म तनाव के लिए अनुकूलता की स्थितियाँ ==
-रैखिक लोच में अनुकूलता स्थितियाँ यह देखकर प्राप्त की जाती हैं कि छह तनाव-विस्थापन संबंध हैं जो केवल तीन अज्ञात विस्थापनों के कार्य हैं। इससे पता चलता है कि तीन विस्थापनों को सूचना की हानि के बिना समीकरणों की प्रणाली से हटाया जा सकता है। केवल उपभेदों के संदर्भ में परिणामी अभिव्यक्तियाँ तनाव क्षेत्र के संभावित रूपों पर बाधाएं प्रदान करती हैं।
+रैखिक लोच में अनुकूलता स्थितियाँ यह देखकर प्राप्त की जाती हैं कि छह तनाव-विस्थापन संबंध हैं जो केवल तीन अज्ञात विस्थापनों के कार्य हैं। इससे पता चलता है कि तीन विस्थापनों को सूचना की हानि के बिना समीकरणों की प्रणाली से हटाया जा सकता है। इस प्रकार केवल तनाव के संदर्भ में परिणामी अभिव्यक्तियाँ तनाव क्षेत्र के संभावित रूपों पर बाधाएं प्रदान करती हैं।
 === 2-आयाम ===
@@ Line 22: / Line 26: @@
     \varepsilon_{22} = \cfrac{\partial u_{2}}{\partial x_2}
   </math>
-विस्थापन को दूर करने के लिए इन संबंधों का बार-बार विभेदन करना <math>u_1</math> और <math>u_2</math>, हमें उपभेदों के लिए द्वि-आयामी अनुकूलता स्थिति प्रदान करता है
+विस्थापन <math>u_1</math> और <math>u_2</math> को दूर करने के लिए इन संबंधों का बार-बार विभेदन होता है, इस प्रकार हमें तनाव के लिए द्वि-आयामी अनुकूलता स्थिति प्रदान करता है
 :<math>
     \cfrac{\partial^2 \varepsilon_{11}}{\partial x_2^2}
@@ Line 28: / Line 33: @@
     + \cfrac{\partial^2 \varepsilon_{22}}{\partial x_1^2} = 0
 </math>
-एकमात्र विस्थापन क्षेत्र जिसे संगत समतल तनाव क्षेत्र द्वारा अनुमति दी जाती है, वह समतल विस्थापन क्षेत्र है, अर्थात, <math> \mathbf{u} = \mathbf{u}(x_1, x_2) </math>.
+एकमात्र विस्थापन क्षेत्र जिसे अनुकूल समतल तनाव क्षेत्र द्वारा अनुमति दी जाती है, वह समतल विस्थापन क्षेत्र है, अर्थात, <math> \mathbf{u} = \mathbf{u}(x_1, x_2) </math>.
 === 3-आयाम ===
-तीन आयामों में दो आयामों के लिए देखे गए स्वरूप के दो और समीकरण भी हैं
+तीन आयामों में, दो आयामों के लिए देखे गए स्वरूप के दो और समीकरणों के अतिरिक्त स्वरूप के तीन और समीकरण हैं
-प्रपत्र के तीन और समीकरण
 :<math>
     \cfrac{\partial^2 \varepsilon_{33}}{\partial x_1 \partial x_2} = \cfrac{\partial}{\partial x_3}\left[
@@ Line 38: / Line 42: @@
     \cfrac{\partial \varepsilon_{12}}{\partial x_3}\right]
   </math>
-इसलिए, 3 हैं<sup>4</sup>=81 आंशिक अंतर समीकरण, हालांकि समरूपता स्थितियों के कारण, यह संख्या छह अलग-अलग संगतता स्थितियों तक कम हो जाती है। हम इन शर्तों को इंडेक्स नोटेशन में इस प्रकार लिख सकते हैं<ref name=Slaughter>Slaughter, W. S., 2003, ''The linearized theory of elasticity'', Birkhauser</ref>
+इसलिए 3<sup>4</sup>=81 आंशिक अंतर समीकरण हैं, चूंकि समरूपता स्थितियों के कारण यह संख्या छह भिन्न-भिन्न अनुकूलता स्थितियों तक कम हो जाती है। इस प्रकार हम इन नियमो को सूचकांक में इस प्रकार लिख सकते हैं <ref name="Slaughter">Slaughter, W. S., 2003, ''The linearized theory of elasticity'', Birkhauser</ref>
 :<math>
     e_{ikr}~e_{jls}~\varepsilon_{ij,kl} = 0
   </math>
-कहाँ <math>e_{ijk}</math> [[क्रमपरिवर्तन प्रतीक]] है. प्रत्यक्ष टेंसर नोटेशन में
+जहाँ <math>e_{ijk}</math> क्रमपरिवर्तन प्रतीक है. प्रत्यक्ष टेंसर सूचकांक में
 :<math>
     \boldsymbol{\nabla}\times(\boldsymbol{\nabla}\times\boldsymbol{\varepsilon})^T = \boldsymbol{0}
   </math>
-जहां कर्ल ऑपरेटर को ऑर्थोनॉर्मल समन्वय प्रणाली में व्यक्त किया जा सकता है <math>\boldsymbol{\nabla}\times\boldsymbol{\varepsilon} = e_{ijk}\varepsilon_{rj,i}\mathbf{e}_k\otimes\mathbf{e}_r </math>.
+जहां कर्ल ऑपरेटर को ऑर्थोनॉर्मल समन्वय प्रणाली <math>\boldsymbol{\nabla}\times\boldsymbol{\varepsilon} = e_{ijk}\varepsilon_{rj,i}\mathbf{e}_k\otimes\mathbf{e}_r </math> के रूप में व्यक्त किया जा सकता है .
 दूसरे क्रम का टेंसर
@@ Line 52: / Line 58: @@
     \boldsymbol{R} := \boldsymbol{\nabla}\times(\boldsymbol{\nabla}\times\boldsymbol{\varepsilon})^T ~;~~ R_{rs} := e_{ikr}~e_{jls}~\varepsilon_{ij,kl}
   </math>
-असंगति टेंसर के रूप में जाना जाता है, और यह सेंट-वेनैंट की अनुकूलता स्थिति#रैंक 2 टेंसर फ़ील्ड्स|सेंट-वेनैंट संगतता टेंसर के बराबर है
+असंगति टेंसर के रूप में जाना जाता है, और यह सेंट-वेनैंट की अनुकूलता स्थिति या क्रम 2 टेंसर क्षेत्र्स या सेंट-वेनैंट अनुकूलता टेंसर के समान है
-== परिमित उपभेदों के लिए अनुकूलता की स्थिति ==
+== परिमित तनाव के लिए अनुकूलता की स्थिति ==
 उन ठोस पदार्थों के लिए जिनमें विकृतियों का छोटा होना आवश्यक नहीं है, अनुकूलता की स्थितियाँ रूप ले लेती हैं
 :<math>
     \boldsymbol{\nabla}\times\boldsymbol{F} = \boldsymbol{0}
   </math>
-कहाँ <math>\boldsymbol{F}</math> विरूपण प्रवणता है. कार्टेशियन समन्वय प्रणाली के संबंध में घटकों के संदर्भ में हम इन संगतता संबंधों को इस प्रकार लिख सकते हैं
+जहाँ <math>\boldsymbol{F}</math> विरूपण प्रवणता है. इस प्रकार कार्टेशियन समन्वय प्रणाली के संबंध में अवयवो के संदर्भ में हम इन अनुकूलता संबंधों को इस प्रकार लिख सकते हैं
 :<math>
     e_{ABC}~\cfrac{\partial F_{iB}}{\partial X_A} = 0
   </math>
-यदि विरूपण निरंतर होना है और मानचित्रण से प्राप्त होना है तो यह शर्त आवश्यक है <math>\mathbf{x} = \boldsymbol{\chi}(\mathbf{X},t)</math> (परिमित तनाव सिद्धांत देखें)। यही स्थिति सरल रूप से जुड़े निकाय में अनुकूलता सुनिश्चित करने के लिए भी पर्याप्त है।
+यदि विरूपण निरंतर होना है और मानचित्रण <math>\mathbf{x} = \boldsymbol{\chi}(\mathbf{X},t)</math> से प्राप्त होना है तो यह नियम आवश्यक है (परिमित तनाव सिद्धांत देखें)। यही स्थिति सरल रूप से जुड़े निकाय में अनुकूलता सुनिश्चित करने के लिए भी पर्याप्त है।
-=== सही कॉची-ग्रीन विरूपण टेंसर के लिए संगतता स्थिति ===
+=== सही कॉची-ग्रीन विरूपण टेंसर के लिए अनुकूलता स्थिति ===
-परिमित तनाव सिद्धांत के लिए अनुकूलता की स्थिति | सही कॉची-ग्रीन विरूपण टेंसर को इस प्रकार व्यक्त किया जा सकता है
+परिमित तनाव सिद्धांत के लिए अनुकूलता की स्थिति या सही कॉची-ग्रीन विरूपण टेंसर को इस प्रकार व्यक्त किया जा सकता है
 :<math>
    R^\gamma_{\alpha\beta\rho} :=
@@ Line 74: / Line 80: @@
    \Gamma^\gamma_{\mu\beta}~\Gamma^\mu_{\alpha\rho} = 0
 </math>
-कहाँ <math>\Gamma^k_{ij}</math> [[वक्ररेखीय निर्देशांक]] है. मात्रा <math>R^m_{ijk}</math> [[रीमैन-क्रिस्टोफ़ेल वक्रता टेंसर]] के मिश्रित घटकों का प्रतिनिधित्व करता है।
+जहाँ <math>\Gamma^k_{ij}</math> [[वक्ररेखीय निर्देशांक]] है. इस प्रकार मात्रा <math>R^m_{ijk}</math> रीमैन-क्रिस्टोफ़ेल वक्रता टेंसर के मिश्रित अवयवो का प्रतिनिधित्व करता है।
 == सामान्य अनुकूलता समस्या ==
-सातत्य यांत्रिकी में अनुकूलता की समस्या में सरल रूप से जुड़े निकायों पर स्वीकार्य एकल-मूल्य वाले निरंतर क्षेत्रों का निर्धारण शामिल है। अधिक सटीक रूप से, समस्या को निम्नलिखित तरीके से बताया जा सकता है।<ref name=acharya>Acharya, A., 1999, '' On Compatibility Conditions for the Left Cauchy–Green Deformation Field in Three Dimensions'',	Journal of Elasticity, 	Volume 56, Number 2 , 95-105</ref>
+सातत्य यांत्रिकी में अनुकूलता की समस्या में सरल रूप से जुड़े निकायों पर स्वीकार्य एकल-मूल्य वाले निरंतर क्षेत्रों का निर्धारण सम्मिलित है। अधिक स्पष्ट रूप से, समस्या को निम्नलिखित विधि से बताया जा सकता है।<ref name=acharya>Acharya, A., 1999, '' On Compatibility Conditions for the Left Cauchy–Green Deformation Field in Three Dimensions'',	Journal of Elasticity, 	Volume 56, Number 2 , 95-105</ref>
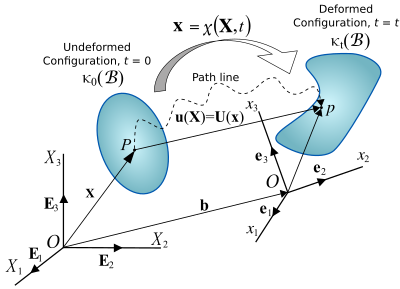
-[[Image:Displacement of a continuum.svg|400px|right|thumb|चित्र 1. सातत्य पिंड की गति।]]चित्र 1 में दिखाए गए किसी पिंड के विरूपण पर विचार करें। यदि हम सभी वैक्टर को संदर्भ समन्वय प्रणाली के संदर्भ में व्यक्त करते हैं <math>\{(\mathbf{E}_1, \mathbf{E}_2, \mathbf{E}_3), O\}</math>, शरीर में बिंदु का विस्थापन द्वारा दिया जाता है
+[[Image:Displacement of a continuum.svg|400px|right|thumb|चित्र 1. सातत्य पिंड की गति।]]चित्र 1 में दिखाए गए किसी पिंड के विरूपण पर विचार करें। यदि हम सभी सदिश को संदर्भ समन्वय प्रणाली के संदर्भ में व्यक्त करते हैं इस प्रकार <math>\{(\mathbf{E}_1, \mathbf{E}_2, \mathbf{E}_3), O\}</math>, निकाय में बिंदु का विस्थापन द्वारा दिया जाता है
 :<math>
    \mathbf{u} = \mathbf{x} - \mathbf{X} ~;~~ u_i = x_i - X_i
@@ Line 88: / Line 94: @@
    \boldsymbol{\nabla} \mathbf{x} = \frac{\partial \mathbf{x}}{\partial \mathbf{X}}
 </math>
-किसी दिए गए दूसरे क्रम के टेंसर फ़ील्ड पर क्या स्थितियाँ हैं <math>\boldsymbol{A}(\mathbf{X})</math> किसी पिंड पर अद्वितीय वेक्टर क्षेत्र मौजूद होने के लिए आवश्यक और पर्याप्त हैं <math>\mathbf{v}(\mathbf{X})</math> जो संतुष्ट करता है
+किसी निकाय पर दिए गए दूसरे क्रम के टेंसर क्षेत्र <math>\boldsymbol{A}(\mathbf{X})</math> पर कौन सी स्थितियाँ आवश्यक और पर्याप्त हैं जिससे एक अद्वितीय सदिश क्षेत्र <math>\mathbf{v}(\mathbf{X})</math> उपस्थितहो जो संतुष्ट हो
 :<math>
    \boldsymbol{\nabla} \mathbf{v} = \boldsymbol{A} \quad \equiv \quad v_{i,j} = A_{ij}
 </math>
+===आवश्यक नियम===
-===आवश्यक शर्तें===
+आवश्यक नियमो के लिए हम मानते हैं कि क्षेत्र <math>\mathbf{v}</math> उपस्थितहै और <math>v_{i,j} = A_{ij}</math> को संतुष्ट करता है, तब
-आवश्यक शर्तों के लिए हम यह मान लेते हैं कि फ़ील्ड <math>\mathbf{v}</math> मौजूद है और संतुष्ट करता है
-<math>v_{i,j} = A_{ij}</math>. तब
 :<math>
    v_{i,jk} = A_{ij,k} ~;~~ v_{i,kj} = A_{ik,j}
 </math>
-चूँकि विभेदन का क्रम बदलने से हमारे प्राप्त परिणाम पर कोई प्रभाव नहीं पड़ता है
+चूँकि विभेदन का क्रम परिवर्तन से हमारे प्राप्त परिणाम पर कोई प्रभाव नहीं पड़ता है
 :<math>
    v_{i,jk} = v_{i,kj}
@@ Line 108: / Line 113: @@
    A_{ij,k} = A_{ik,j}
 </math>
-[[टेंसर व्युत्पन्न (सातत्य यांत्रिकी)]] के लिए प्रसिद्ध पहचान से हमें आवश्यक शर्त मिलती है
+[[टेंसर व्युत्पन्न (सातत्य यांत्रिकी)]] के लिए प्रसिद्ध पहचान से हमें आवश्यक नियम मिलती है
 :<math>
    \boldsymbol{\nabla} \times \boldsymbol{A} = \boldsymbol{0}
@@ Line 115: / Line 120: @@
 ===पर्याप्त स्थितियाँ===
-[[Image:Compatibility mechanics.png|200px|right|thumb|चित्र 2. अनुकूलता के लिए पर्याप्तता शर्तों को साबित करने में उपयोग किए जाने वाले एकीकरण पथ।]]यह साबित करने के लिए कि यह स्थिति संगत दूसरे क्रम के टेंसर फ़ील्ड के अस्तित्व की गारंटी देने के लिए पर्याप्त है, हम इस धारणा से शुरू करते हैं कि फ़ील्ड <math>\boldsymbol{A}</math> ऐसा मौजूद है
+[[Image:Compatibility mechanics.png|200px|right|thumb|चित्र 2. अनुकूलता के लिए पर्याप्तता नियमो को सिद्ध करने में उपयोग किए जाने वाले एकीकरण पथ।]]यह सिद्ध करने के लिए कि यह स्थिति अनुकूल दूसरे क्रम के टेंसर क्षेत्र के अस्तित्व की गारंटी देने के लिए पर्याप्त है, हम इस धारणा से नियम करते हैं कि क्षेत्र <math>\boldsymbol{A}</math> ऐसा उपस्थित है
-<math> \boldsymbol{\nabla} \times \boldsymbol{A} = \boldsymbol{0} </math>. हम वेक्टर फ़ील्ड खोजने के लिए इस फ़ील्ड को एकीकृत करेंगे <math>\mathbf{v}</math> बिंदुओं के बीच रेखा के साथ <math>A</math> और <math>B</math> (चित्र 2 देखें), यानी,
+<math> \boldsymbol{\nabla} \times \boldsymbol{A} = \boldsymbol{0} </math>
+हम सदिश क्षेत्र खोजने के लिए इस क्षेत्र को एकीकृत करेंगे <math>\mathbf{v}</math> बिंदुओं के मध्य रेखा के साथ <math>A</math> और <math>B</math> (चित्र 2 देखें), अर्थात,
 :<math>
    \mathbf{v}(\mathbf{X}_B) - \mathbf{v}(\mathbf{X}_A) = \int_{\mathbf{X}_A}^{\mathbf{X}_B} \boldsymbol{\nabla} \mathbf{v}\cdot~d\mathbf{X}
     = \int_{\mathbf{X}_A}^{\mathbf{X}_B} \boldsymbol{A}(\mathbf{X})\cdot d\mathbf{X}
 </math>
-यदि वेक्टर फ़ील्ड <math>\mathbf{v}</math> एकल-मूल्यवान होना है तो अभिन्न का मूल्य आगे बढ़ने के लिए अपनाए गए पथ से स्वतंत्र होना चाहिए <math>A</math> को <math>B</math>.
+यदि सदिश क्षेत्र <math>\mathbf{v}</math> एकल-मूल्यवान होना है तो अभिन्न का मूल्य आगे बढ़ने के लिए अपनाए गए पथ से स्वतंत्र होना चाहिए इस प्रकार <math>A</math> को <math>B</math>.
-स्टोक्स के प्रमेय से, बंद पथ के साथ दूसरे क्रम के टेंसर का अभिन्न अंग दिया जाता है
+स्टोक्स के प्रमेय से, संवृत पथ के साथ दूसरे क्रम के टेंसर का अभिन्न अंग दिया जाता है
 :<math>
     \oint_{\partial\Omega} \boldsymbol{A}\cdot d\mathbf{s} = \int_{\Omega} \mathbf{n}\cdot(\boldsymbol{\nabla} \times \boldsymbol{A})~da
@@ Line 132: / Line 139: @@
     \int_{AB} \boldsymbol{A}\cdot d\mathbf{X} + \int_{BA} \boldsymbol{A}\cdot d\mathbf{X} = 0
 </math>
-इसलिए इंटीग्रल पथ स्वतंत्र है और अद्वितीयता सुनिश्चित करने के लिए संगतता स्थिति पर्याप्त है <math>\mathbf{v}</math> फ़ील्ड, बशर्ते कि शरीर बस जुड़ा हुआ हो।
+इसलिए इंटीग्रल पथ स्वतंत्र है और अद्वितीयता सुनिश्चित करने के लिए अनुकूलता स्थिति <math>\mathbf{v}</math> क्षेत्र पर्याप्त है, परंतु निकाय केवल जुड़ा हुआ होता है।
 == विरूपण प्रवणता की अनुकूलता ==
@@ Line 139: / Line 146: @@
     \boldsymbol{F} = \cfrac{\partial \mathbf{x}}{\partial \mathbf{X}} = \boldsymbol{\nabla}\mathbf{x}
   </math>
-फिर संगत के अस्तित्व के लिए आवश्यक और पर्याप्त शर्तें <math>\boldsymbol{F}</math> साधारण रूप से जुड़े हुए निकाय पर फ़ील्ड हैं
+फिर अनुकूल के अस्तित्व के लिए आवश्यक और पर्याप्त नियम <math>\boldsymbol{F}</math> साधारण रूप से जुड़े हुए निकाय पर क्षेत्र हैं
 :<math>
     \boldsymbol{\nabla}\times\boldsymbol{F} = \boldsymbol{0}
   </math>
+==अतिसूक्ष्म तनाव की अनुकूलता==
+छोटे तनाव के लिए अनुकूलता समस्या को निम्नानुसार बताया जा सकता है।
-==अतिसूक्ष्म उपभेदों की अनुकूलता==
+एक सममित दूसरे क्रम के टेंसर क्षेत्र <math>\boldsymbol{\epsilon}</math> को देखते हुए एक सदिश क्षेत्र <math>\mathbf{u}</math> का निर्माण करना जब संभव है जैसे कि
-छोटे उपभेदों के लिए अनुकूलता समस्या को निम्नानुसार बताया जा सकता है।
-सममित द्वितीय क्रम टेंसर फ़ील्ड दिया गया है <math>\boldsymbol{\epsilon}</math> वेक्टर फ़ील्ड का निर्माण कब संभव है <math>\mathbf{u}</math> ऐसा है कि
 :<math>
     \boldsymbol{\epsilon} = \frac{1}{2} [\boldsymbol{\nabla}\mathbf{u} + (\boldsymbol{\nabla}\mathbf{u})^T]
 </math>
+===आवश्यक नियम===
-===आवश्यक शर्तें===
+मान लीजिए कि <math>\mathbf{u}</math> का अस्तित्व इस प्रकार है कि <math>\boldsymbol{\epsilon}</math> के लिए अभिव्यक्ति धारण है। अब
-मान लीजिए कि वहाँ मौजूद है <math>\mathbf{u}</math> इस तरह कि अभिव्यक्ति के लिए <math>\boldsymbol{\epsilon}</math> धारण करता है. अब
 :<math>
     \boldsymbol{\nabla}\mathbf{u} = \boldsymbol{\epsilon} + \boldsymbol{\omega}
 </math>
-कहाँ
+जहाँ
 :<math>
     \boldsymbol{\omega} := \frac{1}{2} [\boldsymbol{\nabla}\mathbf{u} - (\boldsymbol{\nabla}\mathbf{u})^T]
@@ Line 167: / Line 172: @@
    \boldsymbol{\nabla} \boldsymbol{\omega} \equiv \omega_{ij,k} = \frac{1}{2} (u_{i,jk} - u_{j,ik}) = \frac{1}{2} (u_{i,jk} + u_{k,ji} - u_{j,ik} - u_{k,ji}) = \varepsilon_{ik,j} - \varepsilon_{jk,i}
 </math>
-अगर <math>\boldsymbol{\omega}</math> हमारे पास निरंतर भिन्नता है <math>\omega_{ij,kl} = \omega_{ij,lk}</math>. इस तरह,
+यदि <math>\boldsymbol{\omega}</math> निरंतर अवकलनीय है तो हमारे निकट <math>\omega_{ij,kl} = \omega_{ij,lk}</math> इसलिए है
 :<math>
    \varepsilon_{ik,jl} - \varepsilon_{jk,il} - \varepsilon_{il,jk} + \varepsilon_{jl,ik} = 0
 </math>
-प्रत्यक्ष टेंसर नोटेशन में
+प्रत्यक्ष टेंसर सूचकांक में
 :<math>
    \boldsymbol{\nabla} \times (\boldsymbol{\nabla} \times\boldsymbol{\epsilon})^T = \boldsymbol{0}
 </math>
-उपरोक्त आवश्यक शर्तें हैं. अगर <math>\mathbf{w}</math> तो यह अनन्तसूक्ष्म तनाव सिद्धांत है <math>\boldsymbol{\nabla} \times \boldsymbol{\epsilon} = \boldsymbol{\nabla} \mathbf{w}+\boldsymbol{\nabla} \mathbf{w}^T</math>. अतः आवश्यक शर्त को इस प्रकार भी लिखा जा सकता है <math>\boldsymbol{\nabla}
+उपरोक्त आवश्यक नियम हैं. यदि <math>\mathbf{w}</math> तो यह अनन्तसूक्ष्म तनाव <math>\boldsymbol{\nabla} \times \boldsymbol{\epsilon} = \boldsymbol{\nabla} \mathbf{w}+\boldsymbol{\nabla} \mathbf{w}^T</math> सिद्धांत है अतः आवश्यक नियम को इस प्रकार भी लिखा जा सकता है <math>\boldsymbol{\nabla}
   \times
 ( \boldsymbol{\nabla} \mathbf{w}+\boldsymbol{\nabla} \mathbf{w}^T)^T
@@ Line 182: / Line 188: @@
 ===पर्याप्त स्थितियाँ===
-आइए अब मान लें कि स्थिति <math>\boldsymbol{\nabla} \times (\boldsymbol{\nabla} \times\boldsymbol{\epsilon})^T = \boldsymbol{0}</math> शरीर के हिस्से में संतुष्ट है. क्या यह स्थिति निरंतर, एकल-मूल्य वाले विस्थापन क्षेत्र के अस्तित्व की गारंटी देने के लिए पर्याप्त है <math>\mathbf{u}</math>?
+आइए अब मान लें कि स्थिति <math>\boldsymbol{\nabla} \times (\boldsymbol{\nabla} \times\boldsymbol{\epsilon})^T = \boldsymbol{0}</math> निकाय के भाग में संतुष्ट है. क्या यह स्थिति निरंतर, एकल-मूल्य वाले विस्थापन क्षेत्र <math>\mathbf{u}</math> के अस्तित्व की गारंटी देने के लिए पर्याप्त है ?
-इस प्रक्रिया में पहला कदम यह दिखाना है कि यह स्थिति इनफिनिटसिमल स्ट्रेन सिद्धांत का तात्पर्य है <math>\boldsymbol{\omega}</math> विशिष्ट रूप से परिभाषित किया गया है। ऐसा करने के लिए हम एकीकृत करते हैं <math>\boldsymbol{\nabla} \mathbf{w}</math> रास्ते के साथ साथ <math>\mathbf{X}_A</math> को <math>\mathbf{X}_B</math>, अर्थात।,
+इस प्रक्रिया में पहला चरण यह दिखाना है कि इस स्थिति का तात्पर्य यह है कि अपरिमित घूर्णन टेंसर <math>\boldsymbol{\omega}</math> विशिष्ट रूप से परिभाषित है। ऐसा करने के लिए हम <math>\boldsymbol{\nabla} \mathbf{w}</math> को <math>\mathbf{X}_A</math> को <math>\mathbf{X}_B</math> पथ के साथ एकीकृत करते हैं, अर्थात,
 :<math>
     \mathbf{w}(\mathbf{X}_B) - \mathbf{w}(\mathbf{X}_A) = \int_{\mathbf{X}_A}^{\mathbf{X}_B} \boldsymbol{\nabla} \mathbf{w}\cdot d\mathbf{X}
      = \int_{\mathbf{X}_A}^{\mathbf{X}_B} (\boldsymbol{\nabla} \times \boldsymbol{\epsilon})\cdot d\mathbf{X}
 </math>
-ध्यान दें कि हमें संदर्भ जानने की आवश्यकता है <math>\mathbf{w}(\mathbf{X}_A)</math> कठोर शरीर के घुमाव को ठीक करने के लिए। फील्ड <math>\mathbf{w}(\mathbf{X})</math> विशिष्ट रूप से केवल तभी निर्धारित होता है जब समोच्च बंद समोच्च के साथ अभिन्न होता है <math>\mathbf{X}_A</math> और <math>\mathbf{X}_b</math> शून्य है, अर्थात,
+ध्यान दें कि कठोर निकाय के घूर्णन को ठीक करने के लिए हमें एक संदर्भ <math>\mathbf{w}(\mathbf{X}_A)</math> जानने की आवश्यकता है। जो की क्षेत्र <math>\mathbf{w}(\mathbf{X})</math> विशिष्ट रूप से केवल तभी निर्धारित होता है जब रूपरेखा संवृत रूपरेखा के साथ अभिन्न होता है इस प्रकार <math>\mathbf{X}_A</math> और <math>\mathbf{X}_b</math> शून्य है, अर्थात,
 :<math>
     \oint_{\mathbf{X}_A}^{\mathbf{X}_B} (\boldsymbol{\nabla} \times \boldsymbol{\epsilon})\cdot d\mathbf{X}  = \boldsymbol{0}
 </math>
-लेकिन स्टोक्स के प्रमेय से सरल रूप से जुड़े शरीर और अनुकूलता के लिए आवश्यक शर्त के लिए
+किन्तु स्टोक्स के प्रमेय से सरल रूप से जुड़े निकाय और अनुकूलता के लिए आवश्यक नियम के लिए
 :<math>
     \oint_{\mathbf{X}_A}^{\mathbf{X}_B} (\boldsymbol{\nabla} \times \boldsymbol{\epsilon})\cdot d\mathbf{X}  = \int_{\Omega_{AB}} \mathbf{n}\cdot(\boldsymbol{\nabla} \times \boldsymbol{\nabla}\times\boldsymbol{\epsilon})~da
      = \boldsymbol{0}
 </math>
-इसलिए, क्षेत्र <math>\mathbf{w}</math> विशिष्ट रूप से परिभाषित किया गया है जिसका अर्थ है कि अनंत लघु घूर्णन टेंसर <math>\boldsymbol{\omega}</math> इसे भी विशिष्ट रूप से परिभाषित किया गया है, बशर्ते शरीर बस जुड़ा हुआ हो।
+इसलिए, क्षेत्र <math>\mathbf{w}</math> विशिष्ट रूप से परिभाषित किया गया है जिसका अर्थ है कि अनंत लघु घूर्णन टेंसर <math>\boldsymbol{\omega}</math> इसे भी विशिष्ट रूप से परिभाषित किया गया है, परंतु निकाय सामान्यतः जुड़ा हुआ होन चाहिए।
+प्रक्रिया के अगले चरण में हम विस्थापन क्षेत्र <math>\mathbf{u}</math> की विशिष्टता पर विचार करेंगे, पहले की तरह हम विस्थापन प्रवणता को एकीकृत करते हैं
-प्रक्रिया के अगले चरण में हम विस्थापन क्षेत्र की विशिष्टता पर विचार करेंगे <math>\mathbf{u}</math>. पहले की तरह हम विस्थापन प्रवणता को एकीकृत करते हैं
 :<math>
     \mathbf{u}(\mathbf{X}_B) - \mathbf{u}(\mathbf{X}_A) = \int_{\mathbf{X}_A}^{\mathbf{X}_B} \boldsymbol{\nabla} \mathbf{u}\cdot d\mathbf{X}
       = \int_{\mathbf{X}_A}^{\mathbf{X}_B} (\boldsymbol{\epsilon} + \boldsymbol{\omega})\cdot d\mathbf{X}
 </math>
-स्टोक्स के प्रमेय से और संबंधों का उपयोग करते हुए <math>\boldsymbol{\nabla} \times \boldsymbol{\epsilon} = \boldsymbol{\nabla} \mathbf{w} = -\boldsymbol{\nabla} \times \omega</math> हमारे पास है
+स्टोक्स के प्रमेय से और हमारे निकट उपस्थित संबंध <math>\boldsymbol{\nabla} \times \boldsymbol{\epsilon} = \boldsymbol{\nabla} \mathbf{w} = -\boldsymbol{\nabla} \times \omega</math> का उपयोग करके
 :<math>
     \oint_{\mathbf{X}_A}^{\mathbf{X}_B} (\boldsymbol{\epsilon} + \boldsymbol{\omega})\cdot d\mathbf{X} = \int_{\Omega_{AB}} \mathbf{n}\cdot(\boldsymbol{\nabla} \times \boldsymbol{\epsilon}+\boldsymbol{\nabla} \times \boldsymbol{\omega})~da = \boldsymbol{0}
 </math>
-इसलिए विस्थापन क्षेत्र <math>\mathbf{u}</math> भी विशिष्ट रूप से निर्धारित किया जाता है। इसलिए अनुकूलता स्थितियाँ अद्वितीय विस्थापन क्षेत्र के अस्तित्व की गारंटी के लिए पर्याप्त हैं <math>\mathbf{u}</math> सरलता से जुड़े शरीर में.
+इसलिए विस्थापन क्षेत्र <math>\mathbf{u}</math> भी विशिष्ट रूप से निर्धारित किया जाता है। इसलिए अनुकूलता स्थितियाँ सरलता से जुड़े निकाय में अद्वितीय विस्थापन क्षेत्र <math>\mathbf{u}</math> के अस्तित्व की गारंटी के लिए पर्याप्त हैं .
 ==राइट कॉची-ग्रीन विरूपण क्षेत्र के लिए अनुकूलता==
-राइट कॉची-ग्रीन विरूपण क्षेत्र के लिए संगतता समस्या को निम्नानुसार प्रस्तुत किया जा सकता है।
+राइट कॉची-ग्रीन विरूपण क्षेत्र के लिए अनुकूलता समस्या को निम्नानुसार प्रस्तुत किया जा सकता है।
+:समस्या: मान लीजिए <math>\boldsymbol{C}(\mathbf{X})</math> संदर्भ विन्यास पर परिभाषित एक धनात्मक निश्चित सममित टेंसर क्षेत्र है। इस प्रकार <math>\boldsymbol{C}</math> पर किन परिस्थितियों में स्थिति क्षेत्र <math>\mathbf{x}(\mathbf{X})</math> द्वारा चिह्नित विकृत विन्यास उपस्थित है जैसे कि
- समस्या: चलो <math>\boldsymbol{C}(\mathbf{X})</math> संदर्भ विन्यास पर परिभाषित सकारात्मक निश्चित सममित टेंसर फ़ील्ड बनें। किन शर्तों पर <math>\boldsymbol{C}</math> क्या स्थिति फ़ील्ड द्वारा चिह्नित कोई विकृत कॉन्फ़िगरेशन मौजूद है <math>\mathbf{x}(\mathbf{X})</math> ऐसा है कि
 :<math>
     (1)\quad\left(\frac{\partial \mathbf{x}}{\partial \mathbf{X}}\right)^T \left(\frac{\partial \mathbf{x}}{\partial \mathbf{X}}\right) = \boldsymbol{C}
@@ Line 220: / Line 227: @@
-===आवश्यक शर्तें===
+===आवश्यक नियम===
-मान लीजिए कि फ़ील्ड <math>\mathbf{x}(\mathbf{X})</math> मौजूद है जो शर्त (1) को संतुष्ट करता है। आयताकार कार्टेशियन आधार के संबंध में घटकों के संदर्भ में
+मान लीजिए कि क्षेत्र <math>\mathbf{x}(\mathbf{X})</math> उपस्थित है जो नियम (1) को संतुष्ट करता है। इस प्रकार आयताकार कार्टेशियन आधार के संबंध में अवयवो के संदर्भ में
 :<math>
     \frac{\partial x^i}{\partial X^\alpha}\frac{\partial x^i}{\partial X^\beta} = C_{\alpha\beta}
 </math>
-परिमित तनाव सिद्धांत से हम यह जानते हैं <math>C_{\alpha\beta} = g_{\alpha\beta}</math>. इसलिए हम लिख सकते हैं
+परिमित तनाव सिद्धांत से हम यह जानते हैं कि <math>C_{\alpha\beta} = g_{\alpha\beta}</math>. इसलिए हम लिख सकते हैं
 :<math>
     \delta_{ij}~\frac{\partial x^i}{\partial X^\alpha}~\frac{\partial x^j}{\partial X^\beta} = g_{\alpha\beta}
 </math>
-दो सममित द्वितीय-क्रम टेंसर फ़ील्ड के लिए जिन्हें एक-से-एक मैप किया जाता है, हमारे पास परिमित तनाव सिद्धांत भी है #विरूपण उपायों और क्रिस्टोफ़ेल प्रतीकों के बीच कुछ संबंध
+दो सममित द्वितीय-क्रम टेंसर क्षेत्र के लिए जिन्हें एक-से-एक मैप किया जाता है, हमारे निकट परिमित तनाव सिद्धांत भी है इस प्रकार विरूपण उपायों और क्रिस्टोफ़ेल प्रतीकों के मध्य कुछ संबंध
 :<math>
     G_{ij} = \frac{\partial X^\alpha}{\partial x^i}~\frac{\partial X^\beta}{\partial x^j}~g_{\alpha\beta}
 </math>
-के बीच के संबंध से <math>G_{ij}</math> और <math>g_{\alpha\beta}</math> वह <math>\delta_{ij} = G_{ij}</math>, हमारे पास है
+<math>G_{ij}</math> और <math>g_{\alpha\beta}</math> के मध्य के संबंध से जो <math>\delta_{ij} = G_{ij}</math> हमारे पास है
 :<math>
    _{(x)}\Gamma_{ij}^k = 0
 </math>
-फिर, रिश्ते से
+फिर, सम्बन्ध से
 :<math>
 \frac{\partial^2 x^m}{\partial X^\alpha \partial X^\beta}  = \frac{\partial x^m}{\partial X^\mu}\,_{(X)}\Gamma^\mu_{\alpha\beta} - \frac{\partial x^i}{\partial X^\alpha}~\frac{\partial x^j}{\partial X^\beta} \,_{(x)}\Gamma^m_{ij}
 </math>
-हमारे पास है
+हमारे निकट है
 :<math>
 \frac{\partial F^m_{~\alpha}}{\partial X^\beta}  = F^m_{~\mu}\,_{(X)}\Gamma^\mu_{\alpha\beta} \qquad; ~~
    F^i_{~\alpha} := \frac{\partial x^i}{\partial X^\alpha}
 </math>
-परिमित तनाव सिद्धांत से#विरूपण उपायों और क्रिस्टोफ़ेल प्रतीकों के बीच कुछ संबंध भी हमारे पास हैं
+परिमित तनाव सिद्धांत से विरूपण उपायों और क्रिस्टोफ़ेल प्रतीकों के मध्य कुछ संबंध भी हमारे निकट हैं
 :<math>
     _{(X)}\Gamma_{\alpha\beta\gamma} = \frac{1}{2}\left(\frac{\partial g_{\alpha\gamma}}{\partial X^\beta} + \frac{\partial g_{\beta\gamma}}{\partial X^\alpha} - \frac{\partial g_{\alpha\beta}}{\partial X^\gamma}\right) ~;~~
@@ Line 256: / Line 264: @@
   \,_{(X)}\Gamma^\mu_{\alpha\beta} = \cfrac{C^{\mu\gamma}}{2}\left(\frac{\partial C_{\alpha\gamma}}{\partial X^\beta} + \frac{\partial C_{\beta\gamma}}{\partial X^\alpha} - \frac{\partial C_{\alpha\beta}}{\partial X^\gamma}\right)
 </math>
-और हमारे पास है
+और हमारे निकट है
 :<math>
 \frac{\partial F^m_{~\alpha}}{\partial X^\beta}  = F^m_{~\mu}~\cfrac{C^{\mu\gamma}}{2}\left(\frac{\partial C_{\alpha\gamma}}{\partial X^\beta} + \frac{\partial C_{\beta\gamma}}{\partial X^\alpha} - \frac{\partial C_{\alpha\beta}}{\partial X^\gamma}\right)
 </math>
-फिर से, विभेदन के क्रम की क्रमविनिमेय प्रकृति का उपयोग करते हुए, हमारे पास है
+फिर से, विभेदन के क्रम की क्रमविनिमेय प्रकृति का उपयोग करते हुए, हमारे निकट है
 :<math>
 \frac{\partial^2 F^m_{~\alpha}}{\partial X^\beta \partial X^\rho} = \frac{\partial^2 F^m_{~\alpha}}{\partial X^\rho \partial X^\beta}
@@ Line 276: / Line 284: @@
     F^m_{~\mu}~\frac{\partial }{\partial X^\beta}[\,_{(X)}\Gamma^\mu_{\alpha\rho}]
 </math>
-शर्तों को एकत्रित करने के बाद हमें मिलता है
+नियमो को एकत्रित करने के पश्चात् हमें मिलता है
 :<math>
    F^m_{~\gamma}\left(\,_{(X)}\Gamma^\gamma_{\mu\rho}\,_{(X)}\Gamma^\mu_{\alpha\beta} +
@@ Line 283: / Line 291: @@
     \frac{\partial }{\partial X^\beta}[\,_{(X)}\Gamma^\gamma_{\alpha\rho}]\right) = 0
 </math>
-की परिभाषा से <math>F^m_{\gamma}</math> हम देखते हैं कि यह उलटा है और इसलिए शून्य नहीं हो सकता। इसलिए,
+<math>F^m_{\gamma}</math> की परिभाषा से हम पाते हैं कि यह विपरीत है और इसलिए शून्य नहीं हो सकता है। इसलिए,
 :<math>
    R^\gamma_{\alpha\beta\rho} :=
@@ Line 291: / Line 300: @@
    \,_{(X)}\Gamma^\gamma_{\mu\beta}\,_{(X)}\Gamma^\mu_{\alpha\rho} = 0
 </math>
-हम दिखा सकते हैं कि ये रीमैन-क्रिस्टोफ़ेल वक्रता टेंसर के मिश्रित घटक हैं। इसलिए, के लिए आवश्यक शर्तें <math>\boldsymbol{C}</math>-संगतता यह है कि विरूपण की रीमैन-क्रिस्टोफ़ेल वक्रता शून्य है।
+हम दिखा सकते हैं कि यह रीमैन-क्रिस्टोफ़ेल वक्रता टेंसर के मिश्रित अवयव हैं। इसलिए, के लिए आवश्यक नियम <math>\boldsymbol{C}</math>-अनुकूलता यह है कि विरूपण की रीमैन-क्रिस्टोफ़ेल वक्रता शून्य है।
 ===पर्याप्त स्थितियाँ===
-पर्याप्तता का प्रमाण थोड़ा अधिक शामिल है।<ref name="acharya"/><ref name=Blume>Blume, J. A., 1989, "Compatibility conditions for a left Cauchy-Green strain field", J. Elasticity, v. 21, p. 271-308.</ref> हम इस धारणा से शुरू करते हैं कि
+पर्याप्तता का प्रमाण थोड़ा अधिक सम्मिलित है।<ref name="acharya"/><ref name=Blume>Blume, J. A., 1989, "Compatibility conditions for a left Cauchy-Green strain field", J. Elasticity, v. 21, p. 271-308.</ref> हम इस धारणा से नियम करते हैं कि
 :<math>
    R^\gamma_{\alpha\beta\rho} = 0 ~;~~ g_{\alpha\beta} = C_{\alpha\beta}
 </math>
-हमें यह दिखाना होगा कि अस्तित्व है <math>\mathbf{x}</math> और <math>\mathbf{X}</math> ऐसा है कि
+हमें यह दिखाना होगा कि <math>\mathbf{x}</math> और <math>\mathbf{X}</math> ऐसे उपस्थित हैं
 :<math>
     \frac{\partial x^i}{\partial X^\alpha}\frac{\partial x^i}{\partial X^\beta} = C_{\alpha\beta}
@@ Line 306: / Line 316: @@
     \frac{\partial F^i_{~\alpha}}{\partial X^\beta} = F^i_{~\gamma}~\,_{(X)}\Gamma^\gamma_{\alpha\beta}
 </math>
-अद्वितीय समाधान हैं <math>F^i_{~\alpha}</math> यदि सरलता से जुड़े डोमेन पर
+सरल रूप से जुड़े डोमेन पर अद्वितीय समाधान <math>F^i_{~\alpha}</math> है
 :<math>
    _{(X)}\Gamma^\gamma_{\alpha\beta} = _{(X)}\Gamma^\gamma_{\beta\alpha} ~;~~
    R^\gamma_{\alpha\beta\rho} = 0
 </math>
-इनमें से पहला की परिभाषा से सत्य है <math>\Gamma^i_{jk}</math> और दूसरा मान लिया गया है. इसलिए कल्पित स्थिति हमें अद्वितीयता प्रदान करती है <math>F^i_{~\alpha}</math> वह है <math>C^2</math> निरंतर।
+इनमें से पहला <math>\Gamma^i_{jk}</math> की परिभाषा से सत्य है और दूसरा मान लिया गया है। इसलिए स्वीकृत स्थिति हमें एक अद्वितीय <math>F^i_{~\alpha}</math> देती है जो कि <math>C^2</math> निरंतर है।
 आगे समीकरणों की प्रणाली पर विचार करें
@@ Line 317: / Line 330: @@
     \frac{\partial x^i}{\partial X^\alpha} = F^i_{~\alpha}
 </math>
-तब से <math>F^i_{~\alpha}</math> है <math>C^2</math> और शरीर बस जुड़ा हुआ है, वहां कुछ समाधान मौजूद है <math>x^i(X^\alpha)</math> उपरोक्त समीकरणों के लिए. हम दिखा सकते हैं कि <math>x^i</math> उस संपत्ति को भी संतुष्ट करें
+चूँकि <math>F^i_{~\alpha}</math> <math>C^2</math> है और निकाय सामान्यतः जुड़ा हुआ है, इसलिए उपरोक्त समीकरणों के लिए कुछ समाधान <math>x^i(X^\alpha)</math> उपस्थित है। इस प्रकार हम दिखा सकते हैं कि <math>x^i</math> उस गुण को भी संतुष्ट करता है
 :<math>
    \det\left|\frac{\partial x^i}{\partial X^\alpha}\right| \ne 0
 </math>
-हम वह रिश्ता भी दिखा सकते हैं
+हम वह सम्बन्ध भी दिखा सकते हैं
 :<math>
     \frac{\partial x^i}{\partial X^\alpha}~g^{\alpha\beta}~\frac{\partial x^j}{\partial X^\beta} = \delta^{ij}
 </math>
-इसका आशय है
+तात्पर्य यह है
 :<math>
     g_{\alpha\beta} = C_{\alpha\beta} = \frac{\partial x^k}{\partial X^\alpha}~\frac{\partial x^k}{\partial X^\beta}
 </math>
-यदि हम इन मात्राओं को टेंसर फ़ील्ड के साथ जोड़ते हैं तो हम इसे दिखा सकते हैं <math>\frac{\partial \mathbf{x}}{\partial \mathbf{X}}</math> उलटा है और निर्मित टेंसर फ़ील्ड अभिव्यक्ति को संतुष्ट करता है <math>\boldsymbol{C}</math>.
+यदि हम इन मात्राओं को टेंसर क्षेत्र के साथ जोड़ते हैं तो हम यह दिखा सकते हैं कि <math>\frac{\partial \mathbf{x}}{\partial \mathbf{X}}</math> विपरीत है और निर्मित टेंसर क्षेत्र <math>\boldsymbol{C}</math> के लिए अभिव्यक्ति को संतुष्ट करता है
 == यह भी देखें ==
 * सेंट-वेनैंट की अनुकूलता स्थिति
 *रेखीय लोच
-* [[विरूपण (यांत्रिकी)]]
+* विरूपण (यांत्रिकी)
 * अनंतिम तनाव सिद्धांत
 * परिमित तनाव सिद्धांत
@@ Line 353: / Line 366: @@
 [[Category: Machine Translated Page]]
 [[Category:Created On 11/08/2023]]
+[[Category:Vigyan Ready]]

Anonymous

Search

अनुकूलता (यांत्रिकी): Difference between revisions

Latest revision as of 07:03, 23 September 2023

अत्यंत सूक्ष्म तनाव के लिए अनुकूलता की स्थितियाँ

2-आयाम

3-आयाम

परिमित तनाव के लिए अनुकूलता की स्थिति

सही कॉची-ग्रीन विरूपण टेंसर के लिए अनुकूलता स्थिति

सामान्य अनुकूलता समस्या

आवश्यक नियम

पर्याप्त स्थितियाँ

विरूपण प्रवणता की अनुकूलता

अतिसूक्ष्म तनाव की अनुकूलता

आवश्यक नियम

पर्याप्त स्थितियाँ

राइट कॉची-ग्रीन विरूपण क्षेत्र के लिए अनुकूलता

आवश्यक नियम

पर्याप्त स्थितियाँ

यह भी देखें

संदर्भ

बाहरी संबंध

Navigation

Wiki tools

Page tools

Other projects

Categories