स्थितिज ऊर्जा: Difference between revisions
No edit summary |
No edit summary |
||
| (9 intermediate revisions by 4 users not shown) | |||
| Line 1: | Line 1: | ||
{{Short description|Energy held by an object because of its position relative to other objects}} | {{Short description|Energy held by an object because of its position relative to other objects}} | ||
{{Classical mechanics}} | {{Classical mechanics}} | ||
भौतिक विज्ञान में, स्थितिज [[ ऊर्जा ]] वह ऊर्जा है जो किसी वस्तु द्वारा अन्य वस्तुओं के सापेक्ष उसकी स्थिति, स्वयं के भीतर तनाव, उसके बिजली आवेश या अन्य कारकों के कारण धारण की जाती है।<ref>{{cite book|author=Jain, Mahesh C.|chapter=Fundamental forces and laws: a brief review|title=इंजीनियरिंग भौतिकी की पाठ्यपुस्तक, भाग 1|publisher=PHI Learning Pvt. Ltd.|isbn= 978-81-203-3862-3|page=10|chapter-url=https://books.google.com/books?id=DqZlU3RJTywC&pg=PA10|year=2009}}</ref><ref>{{cite book|author=McCall, Robert P.|chapter=Energy, Work and Metabolism|title=मानव शरीर का भौतिकी|publisher=JHU Press|date=2010|isbn=978-0-8018-9455-8|page=[https://archive.org/details/physicsofhumanbo0000mcca/page/74 74]|chapter-url=https://books.google.com/books?id=LSyC41h6CG8C&pg=PA74|url=https://archive.org/details/physicsofhumanbo0000mcca/page/74}}</ref> | भौतिक विज्ञान में, '''स्थितिज [[ऊर्जा]]''' वह ऊर्जा है जो किसी वस्तु द्वारा अन्य वस्तुओं के सापेक्ष उसकी स्थिति, स्वयं के भीतर तनाव, उसके बिजली आवेश या अन्य कारकों के कारण धारण की जाती है।<ref>{{cite book|author=Jain, Mahesh C.|chapter=Fundamental forces and laws: a brief review|title=इंजीनियरिंग भौतिकी की पाठ्यपुस्तक, भाग 1|publisher=PHI Learning Pvt. Ltd.|isbn= 978-81-203-3862-3|page=10|chapter-url=https://books.google.com/books?id=DqZlU3RJTywC&pg=PA10|year=2009}}</ref><ref>{{cite book|author=McCall, Robert P.|chapter=Energy, Work and Metabolism|title=मानव शरीर का भौतिकी|publisher=JHU Press|date=2010|isbn=978-0-8018-9455-8|page=[https://archive.org/details/physicsofhumanbo0000mcca/page/74 74]|chapter-url=https://books.google.com/books?id=LSyC41h6CG8C&pg=PA74|url=https://archive.org/details/physicsofhumanbo0000mcca/page/74}}</ref> | ||
संभावित ऊर्जा | सामान्य प्रकार की संभावित ऊर्जा में किसी वस्तु की गुरुत्वाकर्षण संभावित ऊर्जा, विस्तारित वसंत की लोचदार संभावित ऊर्जा, और [[ विद्युत क्षेत्र |बिजली क्षेत्र]] में बिजली आवेश की [[ विद्युत संभावित ऊर्जा |बिजली संभावित ऊर्जा]] सम्मिलित होती है। [[ इकाइयों की अंतर्राष्ट्रीय प्रणाली |इकाइयों की अंतर्राष्ट्रीय प्रणाली]] (SI) में ऊर्जा की इकाई जूल है, जिसका प्रतीक J है। | ||
संभावित ऊर्जा शब्द की प्रारंभिक 19वीं सदी के स्कॉटिश इंजीनियर और भौतिक विज्ञानी [[ विलियम रैंकिन |विलियम रैंकिन]] ने की थी।<ref>William John Macquorn Rankine (1853) "On the general law of the transformation of energy," ''Proceedings of the Philosophical Society of Glasgow'', vol. 3, no. 5, pages 276–280; reprinted in: '''(1)''' ''Philosophical Magazine'', series 4, vol. 5, no. 30, [https://books.google.com/books?id=3Ov22-gFMnEC&pg=PA106 pp. 106–117] (February 1853); and '''(2)''' W. J. Millar, ed., ''Miscellaneous Scientific Papers: by W. J. Macquorn Rankine'', ... (London, England: Charles Griffin and Co., 1881), part II, [https://books.google.com/books?id=-kRB9v6KRvsC&pg=PA203 pp. 203–208].</ref><ref>{{Cite book| last = Smith | first = Crosbie | title = ऊर्जा का विज्ञान - विक्टोरियन ब्रिटेन में ऊर्जा भौतिकी का एक सांस्कृतिक इतिहास| publisher = The University of Chicago Press | date = 1998 | isbn = 0-226-76420-6}}</ref> चूंकि इसका संबंध यूनानी दार्शनिक [[ अरस्तू |अरस्तू]] की सामर्थ्य और वास्तविकता की अवधारणा से है। संभावित ऊर्जा उन बलों से जुड़ी होती है जो किसी पिंड पर इस तरह कार्य करते हैं कि इन बलों द्वारा पिंड पर किया गया कुल कार्य केवल अंतरिक्ष में पिंड की प्रारंभिक और अंतिम स्थिति पर निर्भर करता है। इन बलों, जिन्हें कंजर्वेटिव बल कहा जाता है, को अंतरिक्ष में हर बिंदु पर निश्चित स्केलर फ़ंक्शन के ग्रेडियेंट के रूप में व्यक्त वैक्टर द्वारादिखाया गया है किया जा सकता है जिसे संभावित कहा जाता है। | |||
चूँकि किसी पिंड पर कार्य करने वाली संभावित शक्तियों का कार्य जो प्रारंभ से अंत की स्थिति तक जाता है, केवल इन दो स्थितियों से निर्धारित होता है, और यह शरीर के प्रक्षेपवक्र पर निर्भर नहीं करता है, जिसे क्षमता के रूप में जाना जाता है जिसका मूल्यांकन किया जा सकता है इस कार्य को निर्धारित करने के लिए दो पद है । | |||
एक क्षमता से व्युत्पन्न बलों को संरक्षी बल भी कहा जाता है। | == अवलोकन == | ||
विभिन्न प्रकार की संभावित ऊर्जा होती है, प्रत्येक विशेष प्रकार के बल से जुड़ी होती है। उदाहरण के लिए, [[ लोच (भौतिकी) |लोच (भौतिकी)]] बल के कार्य को लोचदार संभावित ऊर्जा कहा जाता है; गुरुत्वाकर्षण बल के कार्य को गुरुत्वाकर्षण स्थितिज ऊर्जा कहा जाता है; [[ कूलम्ब बल |कूलम्ब बल]] के कार्य को बिजली स्थितिज ऊर्जा कहा जाता है; [[ बेरिऑन |बेरिऑन]] आवेश (भौतिकी) पर कार्यरत प्रबल नाभिकीय बल या दुर्बल नाभिकीय बल के कार्य को नाभिकीय स्थितिज ऊर्जा कहते हैं; अन्तराअणुक बलों के कार्य को अन्तराअणुक स्थितिज ऊर्जा कहते हैं। रासायनिक संभावित ऊर्जा, जैसे कि [[ जीवाश्म ईंधन |जीवाश्म ईंधन]] में संग्रहीत ऊर्जा, परमाणुओं और अणुओं में इलेक्ट्रॉनों और नाभिकों के विन्यास की पुनर्व्यवस्था के समयकूलम्ब बल का कार्य है। ऊष्मीय ऊर्जा में सामान्यतः दो घटक होते हैं: कणों की यादृच्छिक गति की गतिज ऊर्जा और उनके विन्यास की संभावित ऊर्जा। | |||
एक क्षमता से व्युत्पन्न बलों को संरक्षी बल भी कहा जाता है। [[ रूढ़िवादी बल |रूढ़िवादी बल]] द्वारा किया गया कार्य है | |||
<math display="block">W = -\Delta U</math> | <math display="block">W = -\Delta U</math> | ||
कहां <math>\Delta U</math> बल से जुड़ी संभावित ऊर्जा में परिवर्तन है। ऋणात्मक चिह्न यह परिपाटी प्रदान करता है कि बल क्षेत्र के विरुद्ध किया गया कार्य स्थितिज ऊर्जा को बढ़ाता है, जबकि बल क्षेत्र द्वारा किया गया कार्य स्थितिज ऊर्जा को घटाता है। संभावित ऊर्जा के लिए सामान्य संकेत PE, U, V और E | कहां <math>\Delta U</math> बल से जुड़ी संभावित ऊर्जा में परिवर्तन है। ऋणात्मक चिह्न यह परिपाटी प्रदान करता है कि बल क्षेत्र के विरुद्ध किया गया कार्य स्थितिज ऊर्जा को बढ़ाता है, जबकि बल क्षेत्र द्वारा किया गया कार्य स्थितिज ऊर्जा को घटाता है। संभावित ऊर्जा के लिए सामान्य संकेत PE, U, V और E<sub>p</sub> हैं. | ||
संभावित ऊर्जा अन्य वस्तुओं के सापेक्ष किसी वस्तु की स्थिति के आधार पर ऊर्जा है।<ref name=":0">{{Cite book|title = रसायन विज्ञान केंद्रीय विज्ञान|last = Brown|first = Theodore L.|publisher = Pearson Education, Inc.|year = 2006|isbn = 0-13-109686-9|location = Upper Saddle River, New Jersey|pages = [https://archive.org/details/chemistry00theo_0/page/168 168]|url = https://archive.org/details/chemistry00theo_0/page/168}}</ref> संभावित ऊर्जा अधिकांशतः [[ वसंत (उपकरण) ]] या [[ गुरुत्वाकर्षण ]] बल जैसे बहाल करने वाली शक्तियों से जुड़ी | संभावित ऊर्जा अन्य वस्तुओं के सापेक्ष किसी वस्तु की स्थिति के आधार पर ऊर्जा है।<ref name=":0">{{Cite book|title = रसायन विज्ञान केंद्रीय विज्ञान|last = Brown|first = Theodore L.|publisher = Pearson Education, Inc.|year = 2006|isbn = 0-13-109686-9|location = Upper Saddle River, New Jersey|pages = [https://archive.org/details/chemistry00theo_0/page/168 168]|url = https://archive.org/details/chemistry00theo_0/page/168}}</ref> संभावित ऊर्जा अधिकांशतः [[ वसंत (उपकरण) |वसंत (उपकरण)]] या [[ गुरुत्वाकर्षण |गुरुत्वाकर्षण]] बल जैसे बहाल करने वाली शक्तियों से जुड़ी होत है। किसी स्प्रिंग को खींचने या किसी द्रव्यमान को उठाने की क्रिया बाहरी बल द्वारा की जाती है जो क्षमता के बल क्षेत्र के विरुद्ध कार्य करता है। यह कार्य बल क्षेत्र में संग्रहित होता है, जिसे स्थितिज ऊर्जा के रूप में संग्रहित कहा जाता है। यदि बाहरी बल को हटा दिया जाता है तो बल क्षेत्र कार्य करने के लिए शरीर पर कार्य करता है क्योंकि यह शरीर को प्रारंभिक स्थिति में वापस ले जाता है, वसंत के खिंचाव को कम करता है या शरीर को गिरने का कारण बनता है। | ||
एक गेंद पर विचार करें जिसका द्रव्यमान है {{math|''m''}} और किसकी ऊंचाई है {{math|''h''}}. त्वरण {{math|''g''}} फ्री फॉल लगभग स्थिर है, इसलिए गेंद का वजन बल {{math|''mg''}} स्थिर है। बल और विस्थापन के गुणनफल से किया गया कार्य प्राप्त होता है, जो इस प्रकार गुरुत्वीय स्थितिज ऊर्जा के बराबर होता है | एक गेंद पर विचार करें जिसका द्रव्यमान है {{math|''m''}} और किसकी ऊंचाई है {{math|''h''}}. त्वरण {{math|''g''}} फ्री फॉल लगभग स्थिर है, इसलिए गेंद का वजन बल {{math|''mg''}} स्थिर है। बल और विस्थापन के गुणनफल से किया गया कार्य प्राप्त होता है, जो इस प्रकार गुरुत्वीय स्थितिज ऊर्जा के बराबर होता है | ||
| Line 37: | Line 23: | ||
अधिक औपचारिक परिभाषा यह है कि संभावित ऊर्जा किसी दिए गए स्थान पर किसी वस्तु की ऊर्जा और किसी संदर्भ स्थिति में उसकी ऊर्जा के बीच का अंतर है। | अधिक औपचारिक परिभाषा यह है कि संभावित ऊर्जा किसी दिए गए स्थान पर किसी वस्तु की ऊर्जा और किसी संदर्भ स्थिति में उसकी ऊर्जा के बीच का अंतर है। | ||
== | == काम और संभावित ऊर्जा == | ||
संभावित ऊर्जा [[ बल (भौतिकी) ]] से निकटता से जुड़ी हुई है। यदि किसी पिंड पर बल द्वारा किया गया कार्य जो A से B तक जाता है, इन बिंदुओं के बीच के पथ पर निर्भर नहीं करता है (यदि कार्य | संभावित ऊर्जा [[ बल (भौतिकी) |बल (भौतिकी)]] से निकटता से जुड़ी हुई है। यदि किसी पिंड पर बल द्वारा किया गया कार्य जो A से B तक जाता है, इन बिंदुओं के बीच के पथ पर निर्भर नहीं करता है (यदि कार्य रूढ़िवादी बल द्वारा किया जाता है), तो A से मापे गए इस बल का कार्य अदिश मान प्रदान करता है अंतरिक्ष में हर दूसरे बिंदु पर और स्केलर संभावित क्षेत्र को परिभाषित करता है। इस स्थिति में, बल को संभावित क्षेत्र के [[ ढाल |कवच]] के ऋणात्मक के रूप में परिभाषित किया जा सकता है। | ||
यदि लागू बल के लिए कार्य पथ से स्वतंत्र है, तो बल द्वारा किए गए कार्य का मूल्यांकन अनुप्रयोग बिंदु के प्रक्षेपवक्र के प्रारंभ से अंत तक किया जाता है। इसका मतलब यह है कि फ़ंक्शन U('x') है, जिसे संभावित कहा जाता है, जिसका मूल्यांकन दो बिंदुओं 'x'<sub>''A''</sub> पर किया जा सकता है और x<sub>''B''</sub> इन दो बिंदुओं के बीच किसी भी प्रक्षेपवक्र पर कार्य प्राप्त करने के लिए। इस कार्य को नकारात्मक संकेत के साथ परिभाषित करने का क्रम है जिससे सकारात्मक कार्य क्षमता में कमी हो, अर्थात | |||
यदि लागू बल के लिए कार्य पथ से स्वतंत्र है, तो बल द्वारा किए गए कार्य का मूल्यांकन अनुप्रयोग बिंदु के प्रक्षेपवक्र के प्रारंभ से अंत तक किया जाता है। इसका मतलब यह है कि | |||
<math display="block">W =\int_{C} \mathbf{F} \cdot d\mathbf{x} = U(\mathbf{x}_A)-U(\mathbf{x}_B)</math> | <math display="block">W =\int_{C} \mathbf{F} \cdot d\mathbf{x} = U(\mathbf{x}_A)-U(\mathbf{x}_B)</math> | ||
जहाँ C, A से B तक लिया गया प्रक्षेपवक्र है। क्योंकि किया गया कार्य लिए गए पथ से स्वतंत्र है, तो यह अभिव्यक्ति A से B तक किसी भी प्रक्षेपवक्र C के लिए सत्य है। | जहाँ C, A से B तक लिया गया प्रक्षेपवक्र है। क्योंकि किया गया कार्य लिए गए पथ से स्वतंत्र है, तो यह अभिव्यक्ति A से B तक किसी भी प्रक्षेपवक्र C के लिए सत्य है। | ||
| Line 47: | Line 32: | ||
फलन U('x') आरोपित बल से संबद्ध स्थितिज ऊर्जा कहलाती है। संभावित ऊर्जा वाले बलों के उदाहरण गुरुत्वाकर्षण और वसंत बल हैं। | फलन U('x') आरोपित बल से संबद्ध स्थितिज ऊर्जा कहलाती है। संभावित ऊर्जा वाले बलों के उदाहरण गुरुत्वाकर्षण और वसंत बल हैं। | ||
=== संभावित === | ==== संभावित से व्युत्पन्न ==== | ||
इस खंड में कार्य और स्थितिज ऊर्जा के बीच संबंध को अधिक विस्तार से प्रस्तुत किया गया है। रेखा समाकल जो वक्र C के साथ कार्य को परिभाषित करता है, | इस खंड में कार्य और स्थितिज ऊर्जा के बीच संबंध को अधिक विस्तार से प्रस्तुत किया गया है। रेखा समाकल जो वक्र C के साथ कार्य को परिभाषित करता है, विशेष रूप लेता है यदि बल 'F' अदिश क्षेत्र U'('x') से संबंधित है जिससे | ||
<math display="block"> \mathbf{F}={\nabla U'} = \left ( \frac{\partial U'}{\partial x}, \frac{\partial U'}{\partial y}, \frac{\partial U'}{\partial z} \right ). </math> | <math display="block"> \mathbf{F}={\nabla U'} = \left ( \frac{\partial U'}{\partial x}, \frac{\partial U'}{\partial y}, \frac{\partial U'}{\partial z} \right ). </math> | ||
इसका मतलब यह है कि | इसका मतलब यह है कि U' की इकाइयां इस स्थिति में होनी चाहिए, वक्र के साथ काम द्वारा दिया गया है | ||
<math display="block">W = \int_{C} \mathbf{F} \cdot d\mathbf{x} | <math display="block">W = \int_{C} \mathbf{F} \cdot d\mathbf{x} | ||
= \int_{C} \nabla U'\cdot d\mathbf{x},</math> | = \int_{C} \nabla U'\cdot d\mathbf{x},</math> | ||
जिसे प्राप्त करने के लिए [[ ढाल प्रमेय | कवच प्रमेय]] का उपयोग करके मूल्यांकन किया जा सकता है | जिसे प्राप्त करने के लिए [[ ढाल प्रमेय |कवच प्रमेय]] का उपयोग करके मूल्यांकन किया जा सकता है | ||
<math display="block"> W= U'(\mathbf{x}_B) - U'(\mathbf{x}_A).</math> | <math display="block"> W= U'(\mathbf{x}_B) - U'(\mathbf{x}_A).</math> | ||
इससे पता चलता है कि जब बल | इससे पता चलता है कि जब बल अदिश क्षेत्र से व्युत्पन्न होते हैं, तो वक्र C के साथ उन बलों के कार्य की गणना प्रारंभ बिंदु A और वक्र के अंतिम बिंदु B पर अदिश क्षेत्र का मूल्यांकन करके की जाती है। इसका अर्थ है कि कार्य समाकलन A और B के बीच के पथ पर निर्भर नहीं करता है और इसे पथ से स्वतंत्र कहा जाता है। | ||
संभावित ऊर्जा {{math|1=''U'' = - ''U'''('''x''')}} पारंपरिक रूप से इस अदिश क्षेत्र के ऋणात्मक के रूप में परिभाषित किया जाता है जिससे बल क्षेत्र द्वारा कार्य संभावित ऊर्जा को कम कर दे, अर्थात | संभावित ऊर्जा {{math|1=''U'' = - ''U'''('''x''')}} पारंपरिक रूप से इस अदिश क्षेत्र के ऋणात्मक के रूप में परिभाषित किया जाता है जिससे बल क्षेत्र द्वारा कार्य संभावित ऊर्जा को कम कर दे, अर्थात | ||
<math display="block"> W = U(\mathbf{x}_A) - U(\mathbf{x}_B).</math> | <math display="block"> W = U(\mathbf{x}_A) - U(\mathbf{x}_B).</math> | ||
इस | इस स्थिति में, डेल [[ ऑपरेटर |ऑपरेटर]] के कार्य फ़ंक्शन प्रमाणित के लिए आवेदन, | ||
<math display="block"> {\nabla W} = -{\nabla U} = -\left ( \frac{\partial U}{\partial x}, \frac{\partial U}{\partial y}, \frac{\partial U}{\partial z} \right ) = \mathbf{F},</math> | <math display="block"> {\nabla W} = -{\nabla U} = -\left ( \frac{\partial U}{\partial x}, \frac{\partial U}{\partial y}, \frac{\partial U}{\partial z} \right ) = \mathbf{F},</math> | ||
और बल F को विभव से व्युत्पन्न कहा जाता है।<ref>{{cite book|author=John Robert Taylor|title=शास्त्रीय यांत्रिकी|url=https://books.google.com/books?id=P1kCtNr-pJsC&pg=PA117|date=2005|publisher=University Science Books|isbn=978-1-891389-22-1|page=117}}</ref> इसका अर्थ यह भी है कि F | और बल F को विभव से व्युत्पन्न कहा जाता है।<ref>{{cite book|author=John Robert Taylor|title=शास्त्रीय यांत्रिकी|url=https://books.google.com/books?id=P1kCtNr-pJsC&pg=PA117|date=2005|publisher=University Science Books|isbn=978-1-891389-22-1|page=117}}</ref> इसका अर्थ यह भी है कि F रूढ़िवादी सदिश क्षेत्र होना चाहिए। संभावित 'यू' अंतरिक्ष में प्रत्येक बिंदु x पर बल एफ को परिभाषित करता है, इसलिए बलों के सेट को [[ बल क्षेत्र (भौतिकी) |बल क्षेत्र (भौतिकी)]] कहा जाता है। | ||
=== संभावित ऊर्जा की गणना === | === संभावित ऊर्जा की गणना === | ||
एक बल क्षेत्र एफ ( | एक बल क्षेत्र एफ (xो देखते हुए, संभावित ऊर्जा से जुड़े स्केलर फ़ंक्शन को खोजने के लिए कवच प्रमेय का उपयोग करके कार्य अभिन्न का मूल्यांकन किया जा सकता है। यह पैरामिट्रीकृत वक्र की प्रारंभिक करके किया जाता है {{math|1=''γ''(''t'') = '''r'''(''t'')}} से {{math|1=''γ''(''a'') = ''A''}} को {{math|1=''γ''(''b'') = ''B''}}, और कंप्यूटिंग, | ||
<math display="block">\begin{align} | <math display="block">\begin{align} | ||
\int_{\gamma} \nabla\Phi(\mathbf{r}) \cdot d\mathbf{r} | \int_{\gamma} \nabla\Phi(\mathbf{r}) \cdot d\mathbf{r} | ||
| Line 81: | Line 66: | ||
काम के उदाहरण जिन्हें संभावित कार्यों से गणना की जा सकती है वे गुरुत्वाकर्षण और वसंत बल हैं।<ref>{{cite book|author=Burton Paul| title=प्लेनर मशीनरी की कीनेमेटीक्स और गतिशीलता|url=https://books.google.com/books?id=3UdSAAAAMAAJ| date=1979| publisher=Prentice-Hall| isbn=978-0-13-516062-6}}</ref> | काम के उदाहरण जिन्हें संभावित कार्यों से गणना की जा सकती है वे गुरुत्वाकर्षण और वसंत बल हैं।<ref>{{cite book|author=Burton Paul| title=प्लेनर मशीनरी की कीनेमेटीक्स और गतिशीलता|url=https://books.google.com/books?id=3UdSAAAAMAAJ| date=1979| publisher=Prentice-Hall| isbn=978-0-13-516062-6}}</ref> | ||
निकट पृथ्वी गुरुत्वाकर्षण के लिए संभावित ऊर्जा | |||
[[File:Trebuchet.jpg|thumb|एक [[ पत्थर फैकने का ईंजन |पत्थर फैकने का ईंजन]] दो सौ मीटर से अधिक प्रक्षेप्य फेंकने के लिए [[ प्रतिभार |प्रतिभार]] की गुरुत्वाकर्षण संभावित ऊर्जा का उपयोग करता है]]छोटी ऊँचाई में परिवर्तन के लिए, गुरुत्वीय स्थिति ऊर्जा का उपयोग करके गणना की जा सकती है | |||
[[File:Trebuchet.jpg|thumb|एक [[ पत्थर फैकने का ईंजन ]] दो सौ मीटर से अधिक प्रक्षेप्य फेंकने के लिए [[ प्रतिभार ]] की गुरुत्वाकर्षण संभावित ऊर्जा का उपयोग करता है]]छोटी ऊँचाई में परिवर्तन के लिए, गुरुत्वीय स्थिति ऊर्जा का उपयोग करके गणना की जा सकती है | |||
<math display="block">U_g = mgh,</math> | <math display="block">U_g = mgh,</math> | ||
जहां m किलोग्राम में द्रव्यमान है, g स्थानीय गुरुत्वाकर्षण क्षेत्र है (पृथ्वी पर 9.8 मीटर प्रति सेकंड वर्ग), h मीटर में | जहां m किलोग्राम में द्रव्यमान है, g स्थानीय गुरुत्वाकर्षण क्षेत्र है (पृथ्वी पर 9.8 मीटर प्रति सेकंड वर्ग), h मीटर में संदर्भ स्तर से ऊपर की ऊंचाई है, और U जूल में ऊर्जा है। | ||
मौलिक भौतिकी में, गुरुत्वाकर्षण | मौलिक भौतिकी में, गुरुत्वाकर्षण निरंतर नीचे की ओर बल लगाता है {{math|1='''''F''''' = (0, 0, ''F<sub>z</sub>'')}} पृथ्वी की सतह के पास गतिमान पिंड के द्रव्यमान के केंद्र पर। प्रक्षेपवक्र के साथ गतिमान पिंड पर गुरुत्वाकर्षण का कार्य {{math|1='''''r'''''(''t'') = (''x''(''t''), ''y''(''t''), ''z''(''t''))}}, जैसे रोलर कोस्टर के ट्रैक की गणना उसके वेग का उपयोग करके की जाती है, {{math|1='''''v''''' = (''v''<sub>x</sub>, ''v''<sub>y</sub>, ''v''<sub>z</sub>)}}, प्राप्त करने के लिए | ||
<math display="block">W = \int_{t_1}^{t_2} \boldsymbol{F} \cdot \boldsymbol{v} \, dt = \int_{t_1}^{t_2} F_z v_z \, dt = F_z\Delta z. </math> | <math display="block">W = \int_{t_1}^{t_2} \boldsymbol{F} \cdot \boldsymbol{v} \, dt = \int_{t_1}^{t_2} F_z v_z \, dt = F_z\Delta z. </math> | ||
जहां वेग के लंबवत घटक का अभिन्न अंग लंबवत दूरी है। गुरुत्वाकर्षण का कार्य केवल वक्र की ऊर्ध्वाधर गति पर निर्भर करता है {{math|'''''r'''''(''t'')}}. | जहां वेग के लंबवत घटक का अभिन्न अंग लंबवत दूरी है। गुरुत्वाकर्षण का कार्य केवल वक्र की ऊर्ध्वाधर गति पर निर्भर करता है {{math|'''''r'''''(''t'')}}. | ||
== रैखिक वसंत के लिए संभावित ऊर्जा == | == रैखिक वसंत के लिए संभावित ऊर्जा == | ||
{{Main article| | {{Main article|लोचदार ऊर्जा क्षमता}} | ||
[[File:Springs 009.jpg|thumb|right|वसंत (उपकरण) का उपयोग लोचदार संभावित ऊर्जा को संग्रहित करने के लिए किया जाता है]] | [[File:Springs 009.jpg|thumb|right|वसंत (उपकरण) का उपयोग लोचदार संभावित ऊर्जा को संग्रहित करने के लिए किया जाता है]] | ||
[[File:Longbowmen.jpg|thumb|right|[[ तीरंदाजी ]] लोचदार संभावित ऊर्जा के मानव जाति के सबसे पुराने अनुप्रयोगों में से | [[File:Longbowmen.jpg|thumb|right|[[ तीरंदाजी | तीरंदाजी]] लोचदार संभावित ऊर्जा के मानव जाति के सबसे पुराने अनुप्रयोगों में से है]]एक क्षैतिज वसंत बल लगाता है {{math|1='''F''' = (−''kx'', 0, 0)}} जो अक्षीय या x दिशा में इसके विरूपण के समानुपाती होता है। अंतरिक्ष वक्र के साथ चलने वाले पिंड पर इस स्प्रिंग का कार्य {{math|1='''s'''(''t'') = (''x''(''t''), ''y''(''t''), ''z''(''t''))}}, इसकी वेग का उपयोग करके गणना की जाती है, {{math|1='''v''' = (''v''<sub>x</sub>, ''v''<sub>y</sub>, ''v''<sub>z</sub>)}}, प्राप्त करने के लिए | ||
<math display="block">W = \int_0^t\mathbf{F}\cdot\mathbf{v}\,dt | <math display="block">W = \int_0^t\mathbf{F}\cdot\mathbf{v}\,dt | ||
= -\int_0^t kx v_x \, dt | = -\int_0^t kx v_x \, dt | ||
| Line 101: | Line 86: | ||
= \int_{x(t_0)}^{x(t)} k x \, dx | = \int_{x(t_0)}^{x(t)} k x \, dx | ||
= \frac{1}{2} kx^2 </math> | = \frac{1}{2} kx^2 </math> | ||
सुविधा के लिए, वसंत के साथ संपर्क पर विचार करें {{math|1=''t'' = 0}}, तो दूरी x और x-वेग, xv | सुविधा के लिए, वसंत के साथ संपर्क पर विचार करें {{math|1=''t'' = 0}}, तो दूरी x और x-वेग, xv<sub>x</sub>, के गुणनफल का समाकल है x<sup>2</sup>/2. है | ||
कार्यक्रम | कार्यक्रम | ||
| Line 107: | Line 92: | ||
रैखिक स्प्रिंग की स्थितिज ऊर्जा कहलाती है। | रैखिक स्प्रिंग की स्थितिज ऊर्जा कहलाती है। | ||
लोचदार संभावित ऊर्जा | लोचदार संभावित ऊर्जा लोच (भौतिकी) वस्तु (उदाहरण के लिए [[ धनुष (हथियार) |धनुष (हथियार)]] या गुलेल) की संभावित ऊर्जा है जो तनाव या संपीड़न (या औपचारिक शब्दावली में [[ तनाव (भौतिकी) |तनाव (भौतिकी)]] ) के अनुसार विकृत होती है। यह बल के परिणाम के रूप में उत्पन्न होता है जो वस्तु को उसके मूल आकार में मरम्मत करने का प्रयास करता है, जो कि वस्तु का गठन करने वाले परमाणुओं और अणुओं के बीच अधिकांशतः [[ विद्युत चुम्बकीय बल |बिजली चुम्बकीय बल]] होता है। यदि खिंचाव जारी किया जाता है, तो ऊर्जा [[ गतिज ऊर्जा |गतिज ऊर्जा]] में बदला जाती है। | ||
== दो निकायों के बीच गुरुत्वाकर्षण बलों के लिए संभावित ऊर्जा == | == दो निकायों के बीच गुरुत्वाकर्षण बलों के लिए संभावित ऊर्जा == | ||
| Line 113: | Line 98: | ||
गुरुत्वाकर्षण संभावित कार्य, जिसे गुरुत्वाकर्षण क्षमता ऊर्जा भी कहा जाता है, है: | गुरुत्वाकर्षण संभावित कार्य, जिसे गुरुत्वाकर्षण क्षमता ऊर्जा भी कहा जाता है, है: | ||
<math display="block"> U=-\frac{GMm}{r}, </math> | <math display="block"> U=-\frac{GMm}{r}, </math> | ||
ऋणात्मक चिन्ह इस रूटीन का अनुसरण करता है कि संभावित ऊर्जा के | ऋणात्मक चिन्ह इस रूटीन का अनुसरण करता है कि संभावित ऊर्जा के हानी से कार्य प्राप्त होता है। | ||
=== व्युत्पत्ति === | === व्युत्पत्ति === | ||
| Line 119: | Line 104: | ||
दूरी r द्वारा अलग किए गए द्रव्यमान M और m के दो पिंडों के बीच गुरुत्वाकर्षण बल न्यूटन के सार्वभौमिक गुरुत्वाकर्षण के नियम द्वारा दिया जाता है। न्यूटन का नियम | दूरी r द्वारा अलग किए गए द्रव्यमान M और m के दो पिंडों के बीच गुरुत्वाकर्षण बल न्यूटन के सार्वभौमिक गुरुत्वाकर्षण के नियम द्वारा दिया जाता है। न्यूटन का नियम | ||
<math display="block">\mathbf{F}=-\frac{GMm}{r^2}\mathbf{\hat{r}},</math> | <math display="block">\mathbf{F}=-\frac{GMm}{r^2}\mathbf{\hat{r}},</math> | ||
कहां <math>\mathbf{\hat{r}}</math> [[ इकाई वेक्टर ]] है जो M से m की ओर संकेत देना करता है और G [[ गुरुत्वाकर्षण स्थिरांक ]] है। | कहां <math>\mathbf{\hat{r}}</math> [[ इकाई वेक्टर |इकाई वेक्टर]] है जो M से m की ओर संकेत देना करता है और G [[ गुरुत्वाकर्षण स्थिरांक |गुरुत्वाकर्षण स्थिरांक]] है। | ||
द्रव्यमान m को वेग से चलने दें {{math|'''v'''}} फिर इस द्रव्यमान पर गुरुत्वाकर्षण का कार्य स्थिति से चलता है {{math|'''r'''(''t''<sub>1</sub>)}} को | द्रव्यमान m को वेग से चलने दें {{math|'''v'''}} फिर इस द्रव्यमान पर गुरुत्वाकर्षण का कार्य स्थिति से चलता है {{math|'''r'''(''t''<sub>1</sub>)}} को {{math|'''r'''(''t''<sub>2</sub>)}} द्वारा दिया गया है | ||
<math display="block"> W = -\int^{\mathbf{r}(t_2)}_{\mathbf{r}(t_1)} \frac{GMm}{r^3} \mathbf{r}\cdot d\mathbf{r} = -\int^{t_2}_{t_1} \frac{GMm}{r^3} \mathbf{r}\cdot\mathbf{v} \, dt.</math> | <math display="block"> W = -\int^{\mathbf{r}(t_2)}_{\mathbf{r}(t_1)} \frac{GMm}{r^3} \mathbf{r}\cdot d\mathbf{r} = -\int^{t_2}_{t_1} \frac{GMm}{r^3} \mathbf{r}\cdot\mathbf{v} \, dt.</math> | ||
द्रव्यमान m की स्थिति और वेग द्वारा दिया जाता है | द्रव्यमान m की स्थिति और वेग द्वारा दिया जाता है | ||
<math display="block">\mathbf{r} = r\mathbf{e}_r, \qquad\mathbf{v}=\dot{r}\mathbf{e}_r + r\dot{\theta}\mathbf{e}_t,</math> | <math display="block">\mathbf{r} = r\mathbf{e}_r, \qquad\mathbf{v}=\dot{r}\mathbf{e}_r + r\dot{\theta}\mathbf{e}_t,</math> | ||
जहां | जहां e<sub>''r''</sub> और e<sub>''t''</sub> M से m तक वेक्टर के सापेक्ष निर्देशित रेडियल और स्पर्शरेखा इकाई वैक्टर हैं। गुरुत्वाकर्षण के कार्य के सूत्र को सरल बनाने के लिए इसका उपयोग करें, | ||
<math display="block"> W = -\int^{t_2}_{t_1} \frac{GmM}{r^3} (r\mathbf{e}_r)\cdot(\dot{r}\mathbf{e}_r + r\dot{\theta}\mathbf{e}_t)\,dt = -\int^{t_2}_{t_1}\frac{GmM}{r^3}r\dot{r}dt = \frac{GMm}{r(t_2)}-\frac{GMm}{r(t_1)}.</math> | <math display="block"> W = -\int^{t_2}_{t_1} \frac{GmM}{r^3} (r\mathbf{e}_r)\cdot(\dot{r}\mathbf{e}_r + r\dot{\theta}\mathbf{e}_t)\,dt = -\int^{t_2}_{t_1}\frac{GmM}{r^3}r\dot{r}dt = \frac{GMm}{r(t_2)}-\frac{GMm}{r(t_1)}.</math> | ||
यह हिसाब इस तथ्य का उपयोग करती है कि | यह हिसाब इस तथ्य का उपयोग करती है कि | ||
<math display="block"> \frac{d}{dt}r^{-1} = -r^{-2}\dot{r} = -\frac{\dot{r}}{r^2}.</math> | <math display="block"> \frac{d}{dt}r^{-1} = -r^{-2}\dot{r} = -\frac{\dot{r}}{r^2}.</math> | ||
== दो निकायों के बीच इलेक्ट्रोस्टैटिक बलों के लिए संभावित ऊर्जा == | == दो निकायों के बीच इलेक्ट्रोस्टैटिक बलों के लिए संभावित ऊर्जा == | ||
एक आवेश Q द्वारा | एक आवेश Q द्वारा अन्य आवेश q पर लगाया गया इलेक्ट्रोस्टैटिक बल दूरी r द्वारा अलग किया जाता है, जिसे कूलम्ब के नियम द्वारा दिया जाता है | ||
<math display="block"> \mathbf{F}=\frac{1}{4\pi\varepsilon_0}\frac{Qq}{r^2}\mathbf{\hat{r}},</math> | <math display="block"> \mathbf{F}=\frac{1}{4\pi\varepsilon_0}\frac{Qq}{r^2}\mathbf{\hat{r}},</math> | ||
कहां <math>\mathbf{\hat{r}}</math> Q से q और ε की ओर संकेत देना करते हुए लंबाई 1 का | कहां <math>\mathbf{\hat{r}}</math> Q से q और ε<sub>0</sub> की ओर संकेत देना करते हुए लंबाई 1 का वेक्टर है [[ वैक्यूम परमिटिटिविटी |वैक्यूम परमिटिटिविटी]] है। इसे [[ कूलम्ब स्थिरांक |कूलम्ब स्थिरांक]] का उपयोग करके भी लिखा जा सकता है {{math|1=''k''<sub>e</sub> = 1 ⁄ 4''πε''<sub>0</sub>}}. | ||
इलेक्ट्रोस्टैटिक बल क्षेत्र में Q को ए से किसी बिंदु बी तक ले जाने के लिए आवश्यक कार्य डब्ल्यू को संभावित कार्य द्वारा दिया जाता है | इलेक्ट्रोस्टैटिक बल क्षेत्र में Q को ए से किसी बिंदु बी तक ले जाने के लिए आवश्यक कार्य डब्ल्यू को संभावित कार्य द्वारा दिया जाता है | ||
<math display="block">U(r) = \frac{1}{4\pi\varepsilon_0}\frac{Qq}{r}.</math> | <math display="block">U(r) = \frac{1}{4\pi\varepsilon_0}\frac{Qq}{r}.</math> | ||
== संदर्भ स्तर == | == संदर्भ स्तर == | ||
संभावित ऊर्जा | संभावित ऊर्जा अवस्था का एक कार्य है जिसमें एक प्रणाली है, और किसी विशेष अवस्था के लिए इसके सापेक्ष परिभाषित किया गया है। यह संदर्भ स्थिति हमेशा वास्तविक स्थिति नहीं होती है; यह सीमा भी हो सकती है, जैसे कि अनंत की ओर जाने वाले सभी शरीर के बीच की दूरी, बशर्ते कि उस सीमा तक जाने में सम्मिलित ऊर्जा हो, जैसे कि व्युत्क्रम-वर्ग कानून बलों के स्थिति में। किसी भी मनमानी संदर्भ स्थिति का उपयोग किया जा सकता है; इसलिए इसे सुविधा के आधार पर चुना जा सकता है। | ||
सामान्यतः किसी प्रणाली की संभावित ऊर्जा केवल उसके अवयव की सापेक्ष स्थिति पर निर्भर करती है, इसलिए संदर्भ स्थिति को सापेक्ष स्थिति के रूप में भी व्यक्त किया जा सकता है। | सामान्यतः किसी प्रणाली की संभावित ऊर्जा केवल उसके अवयव की सापेक्ष स्थिति पर निर्भर करती है, इसलिए संदर्भ स्थिति को सापेक्ष स्थिति के रूप में भी व्यक्त किया जा सकता है। | ||
== गुरुत्वीय स्थितिज ऊर्जा == | == गुरुत्वीय स्थितिज ऊर्जा == | ||
{{Main article| | {{Main article|गुरुत्वाकर्षण क्षमता|गुरुत्वाकर्षण ऊर्जा|गुरुत्वाकर्षण क्षेत्र}} | ||
गुरुत्वाकर्षण ऊर्जा [[ गुरुत्वाकर्षण बल ]] से जुड़ी संभावित ऊर्जा है, क्योंकि पृथ्वी के गुरुत्वाकर्षण के विरुद्ध वस्तुओं को ऊपर उठाने के लिए काम की आवश्यकता होती है। ऊंचे पदों के कारण संभावित ऊर्जा को गुरुत्वाकर्षण संभावित ऊर्जा कहा जाता है, और | गुरुत्वाकर्षण ऊर्जा [[ गुरुत्वाकर्षण बल |गुरुत्वाकर्षण बल]] से जुड़ी संभावित ऊर्जा है, क्योंकि पृथ्वी के गुरुत्वाकर्षण के विरुद्ध वस्तुओं को ऊपर उठाने के लिए काम की आवश्यकता होती है। ऊंचे पदों के कारण संभावित ऊर्जा को गुरुत्वाकर्षण संभावित ऊर्जा कहा जाता है, और ऊंचे जलाशय में पानी से इसका सबूत मिलता है या बांध के पीछे रखा जाता है। यदि कोई वस्तु गुरुत्वाकर्षण क्षेत्र के अंदर बिंदु से दूसरे बिंदु पर गिरती है, तो गुरुत्वाकर्षण बल वस्तु पर सकारात्मक कार्य करेगा, और गुरुत्वाकर्षण की स्थितिज ऊर्जा उतनी ही मात्रा में घट जाएगी। | ||
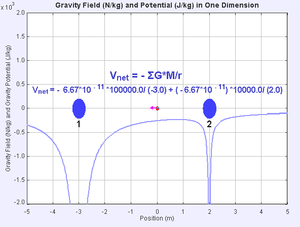
[[File:Solar sys.jpg|right|thumb|गुरुत्वाकर्षण बल ग्रहों को सूर्य के चारों ओर कक्षा में रखता है]]एक टेबल के ऊपर रखी | [[File:Solar sys.jpg|right|thumb|गुरुत्वाकर्षण बल ग्रहों को सूर्य के चारों ओर कक्षा में रखता है]]एक टेबल के ऊपर रखी किताब पर विचार करें। जैसे ही पुस्तक को फर्श से टेबल पर उठाया जाता है, कुछ बाहरी बल गुरुत्वाकर्षण बल के विरुद्ध काम करता है। यदि पुस्तक वापस फर्श पर गिरती है, तो पुस्तक को प्राप्त होने वाली गिरने वाली ऊर्जा गुरुत्वाकर्षण बल द्वारा प्रदान की जाती है। इस प्रकार, यदि पुस्तक मेज से गिर जाती है, तो यह संभावित ऊर्जा पुस्तक के द्रव्यमान को गति देने के लिए जाती है और गतिज ऊर्जा में परिवर्तित हो जाती है। जब किताब फर्श से टकराती है तो यह गतिज ऊर्जा प्रभाव से गर्मी, विरूपण और ध्वनि में परिवर्तित हो जाती है। | ||
किसी वस्तु की गुरुत्वीय स्थितिज ऊर्जा को प्रभावित करने वाले कारक हैं किसी संदर्भ बिंदु के सापेक्ष उसकी ऊंचाई, उसका द्रव्यमान और उसमें वर्तमान गुरुत्वाकर्षण क्षेत्र की ताकत। | किसी वस्तु की गुरुत्वीय स्थितिज ऊर्जा को प्रभावित करने वाले कारक हैं किसी संदर्भ बिंदु के सापेक्ष उसकी ऊंचाई, उसका द्रव्यमान और उसमें वर्तमान गुरुत्वाकर्षण क्षेत्र की ताकत। ही टेबल पर पड़ी भारी किताब की तुलना में लम्बे अलमारी के ऊपर और कम गुरुत्वाकर्षण संभावित ऊर्जा। चंद्रमा की सतह के ऊपर निश्चित ऊंचाई पर वस्तु में गुरुत्वाकर्षण संभावित ऊर्जा पृथ्वी की सतह के ऊपर समान ऊंचाई की तुलना में कम होती है क्योंकि चंद्रमा का गुरुत्वाकर्षण कमजोर होता है। शब्द के सामान्य अर्थ में ऊँचाई का उपयोग गुरुत्वाकर्षण संभावित ऊर्जा गणनाओं के लिए नहीं किया जा सकता है जब गुरुत्वाकर्षण को स्थिर नहीं माना जाता है। निम्नलिखित खंड अधिक विवरण प्रदान करते हैं। | ||
=== स्थानीय सन्निकटन === | === स्थानीय सन्निकटन === | ||
एक गुरुत्वाकर्षण क्षेत्र की ताकत स्थान के साथ बदलती रहती है। चूंकि, जब गुरुत्वाकर्षण क्षेत्र के स्रोत के केंद्र से दूरियों के संबंध में दूरी का परिवर्तन छोटा होता है, तो क्षेत्र की ताकत में यह उतार-चढ़ाव नगण्य होती है और हम मान सकते हैं कि किसी विशेष वस्तु पर गुरुत्वाकर्षण बल स्थिर है। उदाहरण के लिए, पृथ्वी की सतह के निकट, हम मानते हैं कि गुरुत्वाकर्षण के कारण त्वरण | एक गुरुत्वाकर्षण क्षेत्र की ताकत स्थान के साथ बदलती रहती है। चूंकि, जब गुरुत्वाकर्षण क्षेत्र के स्रोत के केंद्र से दूरियों के संबंध में दूरी का परिवर्तन छोटा होता है, तो क्षेत्र की ताकत में यह उतार-चढ़ाव नगण्य होती है और हम मान सकते हैं कि किसी विशेष वस्तु पर गुरुत्वाकर्षण बल स्थिर है। उदाहरण के लिए, पृथ्वी की सतह के निकट, हम मानते हैं कि गुरुत्वाकर्षण के कारण त्वरण स्थिर है {{math|1=''g'' = 9.8 m/s<sup>2</sup>}} ([[ मानक गुरुत्वाकर्षण ]])। इस स्थिति में, गुरुत्वीय स्थितिज ऊर्जा के लिए सरल व्यंजक का उपयोग करके प्राप्त किया जा सकता है {{math|1=''W'' = ''Fd''}} [[ यांत्रिक कार्य |यांत्रिक कार्य]] के लिए समीकरण, और समीकरण | ||
<math display="block">W_F = -\Delta U_F.</math> | <math display="block">W_F = -\Delta U_F.</math> | ||
किसी ऊँची वस्तु द्वारा धारण की गई गुरुत्वीय स्थितिज ऊर्जा की मात्रा उसे उठाने में गुरुत्वाकर्षण के विरुद्ध किए गए कार्य के बराबर होती है। किया गया कार्य इसे ऊपर की ओर ले जाने के लिए आवश्यक बल के बराबर होता है, जो ऊर्ध्वाधर दूरी से इसे स्थानांतरित किया जाता है (याद रखें {{math|1=''W'' = ''Fd''}}). | किसी ऊँची वस्तु द्वारा धारण की गई गुरुत्वीय स्थितिज ऊर्जा की मात्रा उसे उठाने में गुरुत्वाकर्षण के विरुद्ध किए गए कार्य के बराबर होती है। किया गया कार्य इसे ऊपर की ओर ले जाने के लिए आवश्यक बल के बराबर होता है, जो ऊर्ध्वाधर दूरी से इसे स्थानांतरित किया जाता है (याद रखें {{math|1=''W'' = ''Fd''}}). स्थिर वेग से चलते समय ऊपर की ओर लगने वाला बल भार के बराबर होता है, {{math|''mg''}}, किसी वस्तु का, इसलिए उसे ऊँचाई से उठाने में किया गया कार्य {{mvar|h}} उत्पाद है {{math|''mgh''}}. इस प्रकार, केवल [[ द्रव्यमान |द्रव्यमान]] , गुरुत्वाकर्षण और [[ ऊंचाई |ऊंचाई]] के लिए लेखांकन करते समय, समीकरण है:<ref>[https://feynmanlectures.caltech.edu/I_13.html The Feynman Lectures on Physics Vol. I Ch. 13: Work and Potential Energy (A)]</ref> | ||
<math display="block">U = mgh</math> | <math display="block">U = mgh</math> | ||
कहां {{math|''U''}} पृथ्वी की सतह पर होने के सापेक्ष वस्तु की संभावित ऊर्जा है, {{math|''m''}} वस्तु का द्रव्यमान है, {{math|''g''}} गुरुत्वाकर्षण के कारण त्वरण है, और h वस्तु की ऊँचाई है।<ref>{{cite web| url=http://hyperphysics.phy-astr.gsu.edu/Hbase/gpot.html| title=हाइपरफिजिक्स - गुरुत्वीय स्थितिज ऊर्जा}}</ref> यदि {{math|''m''}} [[ किलोग्राम ]] में व्यक्त किया जाता है, {{math|''g''}} मीटर प्रति सेकंड वर्ग में|मी/से<sup>2</sup> और {{math|''h''}} [[ मीटर ]] में तो {{math|''U''}} जूल में गणना की जाएगी। | कहां {{math|''U''}} पृथ्वी की सतह पर होने के सापेक्ष वस्तु की संभावित ऊर्जा है, {{math|''m''}} वस्तु का द्रव्यमान है, {{math|''g''}} गुरुत्वाकर्षण के कारण त्वरण है, और h वस्तु की ऊँचाई है।<ref>{{cite web| url=http://hyperphysics.phy-astr.gsu.edu/Hbase/gpot.html| title=हाइपरफिजिक्स - गुरुत्वीय स्थितिज ऊर्जा}}</ref> यदि {{math|''m''}} [[ किलोग्राम |किलोग्राम]] में व्यक्त किया जाता है, {{math|''g''}} मीटर प्रति सेकंड वर्ग में|मी/से<sup>2</sup> और {{math|''h''}} [[ मीटर |मीटर]] में तो {{math|''U''}} जूल में गणना की जाएगी। | ||
इसलिए, संभावित अंतर है | इसलिए, संभावित अंतर है | ||
| Line 167: | Line 149: | ||
=== सामान्य सूत्र === | === सामान्य सूत्र === | ||
चूंकि, दूरी में बड़े बदलाव पर, सन्निकटन कि {{math|''g''}} स्थिर है अब मान्य नहीं है, और हमें गुरुत्वाकर्षण संभावित ऊर्जा को निर्धारित करने के लिए कलन और कार्य की सामान्य गणितीय परिभाषा का उपयोग करना होगा। स्थितिज ऊर्जा की [[ गणना ]] के लिए, हम गुरुत्वाकर्षण बल का समाकलन कर सकते हैं, जिसका परिमाण सार्वभौमिक गुरुत्वाकर्षण के नियम द्वारा दिया गया है|न्यूटन के गुरुत्वाकर्षण के नियम, दूरी के संबंध में {{math|''r''}} दो शरीरों के बीच। उस परिभाषा का उपयोग करते हुए, जनता की | चूंकि, दूरी में बड़े बदलाव पर, सन्निकटन कि {{math|''g''}} स्थिर है अब मान्य नहीं है, और हमें गुरुत्वाकर्षण संभावित ऊर्जा को निर्धारित करने के लिए कलन और कार्य की सामान्य गणितीय परिभाषा का उपयोग करना होगा। स्थितिज ऊर्जा की [[ गणना |गणना]] के लिए, हम गुरुत्वाकर्षण बल का समाकलन कर सकते हैं, जिसका परिमाण सार्वभौमिक गुरुत्वाकर्षण के नियम द्वारा दिया गया है|न्यूटन के गुरुत्वाकर्षण के नियम, दूरी के संबंध में {{math|''r''}} दो शरीरों के बीच। उस परिभाषा का उपयोग करते हुए, जनता की प्रणाली की गुरुत्वाकर्षण संभावित ऊर्जा {{math|''m''<sub>1</sub>}} और {{math|''M''<sub>2</sub>}} दूरी पर {{math|''r''}} गुरुत्वाकर्षण स्थिरांक का उपयोग करना {{math|''G''}} है | ||
<math display="block">U = -G \frac{m_1 M_2}{r} + K,</math> | <math display="block">U = -G \frac{m_1 M_2}{r} + K,</math> | ||
जहाँ K एक ऐच्छिक स्थिरांक जो उस आधार के चुनाव पर निर्भर करता है जिससे क्षमता मापी जाती है। सम्मेलन का चयन कि {{math|1=''K'' = 0}} (अर्थात अनंत पर बिंदु के संबंध में) गणना को सरल बनाता है, ? बनाने की कीमत पर {{math|''U''}} नकारात्मक; यह शारीरिक रूप से उचित क्यों है, नीचे देखें। | |||
के लिए यह सूत्र दिया है {{math|''U''}}, की | के लिए यह सूत्र दिया है {{math|''U''}}, की प्रणाली की कुल संभावित ऊर्जा {{mvar|n}} शरीर सभी के लिए योग द्वारा पाया जाता है <math display="inline">\frac{n ( n - 1 )}{2}</math> दो निकायों के जोड़े, उन दो शव की प्रणाली की संभावित ऊर्जा। | ||
[[File:Gravitational potential summation 2.png|thumb|गुरुत्वाकर्षण संभावित योग <math>U = - m \left(G \frac{ M_1}{r_1} + G \frac{ M_2}{r_2}\right) </math>]]निकायों की प्रणाली को छोटे कणों के संयुक्त सेट के रूप में माना जाता है, और पिछले को कण स्तर पर लागू करने से हमें नकारात्मक [[ गुरुत्वाकर्षण बाध्यकारी ऊर्जा ]] मिलती है। यह क्षमता ऊर्जा निकायों की प्रणाली की कुल संभावित ऊर्जा की तुलना में अधिक अटलता से नकारात्मक है क्योंकि इसमें प्रत्येक शरीर की नकारात्मक गुरुत्वाकर्षण अनिवार्य ऊर्जा भी सम्मिलित | [[File:Gravitational potential summation 2.png|thumb|गुरुत्वाकर्षण संभावित योग <math>U = - m \left(G \frac{ M_1}{r_1} + G \frac{ M_2}{r_2}\right) </math>]]निकायों की प्रणाली को छोटे कणों के संयुक्त सेट के रूप में माना जाता है, और पिछले को कण स्तर पर लागू करने से हमें नकारात्मक [[ गुरुत्वाकर्षण बाध्यकारी ऊर्जा |गुरुत्वाकर्षण बाध्यकारी ऊर्जा]] मिलती है। यह क्षमता ऊर्जा निकायों की प्रणाली की कुल संभावित ऊर्जा की तुलना में अधिक अटलता से नकारात्मक है क्योंकि इसमें प्रत्येक शरीर की नकारात्मक गुरुत्वाकर्षण अनिवार्य ऊर्जा भी सम्मिलित है। पिंडों की प्रणाली की संभावित ऊर्जा, शरीर को दूसरे से अनंत तक अलग करने के लिए आवश्यक ऊर्जा का नकारात्मक है, जबकि गुरुत्वाकर्षण अनिवार्य ऊर्जा दूसरे से अनंत तक सभी कणों को अलग करने के लिए आवश्यक ऊर्जा है। | ||
<math display="block">U = - m \left(G \frac{ M_1}{r_1}+ G \frac{ M_2}{r_2}\right) </math> | <math display="block">U = - m \left(G \frac{ M_1}{r_1}+ G \frac{ M_2}{r_2}\right) </math> | ||
इसलिए, | इसलिए, | ||
| Line 181: | Line 163: | ||
===नकारात्मक गुरुत्वीय ऊर्जा=== | ===नकारात्मक गुरुत्वीय ऊर्जा=== | ||
जैसा कि सभी संभावित ऊर्जाओं के साथ होता है, अधिकांश भौतिक उद्देश्यों के लिए गुरुत्वाकर्षण संभावित ऊर्जा में केवल अंतर होता है, और शून्य बिंदु का चुनाव | जैसा कि सभी संभावित ऊर्जाओं के साथ होता है, अधिकांश भौतिक उद्देश्यों के लिए गुरुत्वाकर्षण संभावित ऊर्जा में केवल अंतर होता है, और शून्य बिंदु का चुनाव ऐच्छिक होता है। यह देखते हुए कि विशेष परिमित r को दूसरे पर वरीयता देने के लिए कोई उचित मानदंड नहीं है, दूरी के लिए केवल दो उचित विकल्प प्रतीत होते हैं जिस पर {{math|''U''}} शून्य हो जाता है: <math>r = 0</math> और <math>r = \infty</math>. का चुनाव <math>U = 0</math> अनंत पर अजीब लग सकता है, और इसका परिणाम यह हो सकता है कि गुरुत्वाकर्षण ऊर्जा हमेशा नकारात्मक होती है, यह उल्टा लग सकता है, किन्तु यह विकल्प गुरुत्वाकर्षण संभावित ऊर्जा मूल्यों को परिमित होने की अनुमति देता है, यद्यपि नकारात्मक। | ||
[[ गणितीय विलक्षणता ]] पर <math>r = 0</math> गुरुत्वाकर्षण संभावित ऊर्जा के सूत्र में इसका मतलब है कि सम्मेलन का एकमात्र अन्य स्पष्ट रूप से उचित वैकल्पिक विकल्प, के साथ <math>U = 0</math> के लिए <math>r = 0</math>, संभावित ऊर्जा सकारात्मक होने का परिणाम होगा, | [[ गणितीय विलक्षणता | गणितीय विलक्षणता]] पर <math>r = 0</math> गुरुत्वाकर्षण संभावित ऊर्जा के सूत्र में इसका मतलब है कि सम्मेलन का एकमात्र अन्य स्पष्ट रूप से उचित वैकल्पिक विकल्प, के साथ <math>U = 0</math> के लिए <math>r = 0</math>, संभावित ऊर्जा सकारात्मक होने का परिणाम होगा, किन्तु सभी गैर-शून्य मूल्यों के लिए अनंत रूप से बड़ा होगा {{math|''r''}}, और [[ वास्तविक संख्या |वास्तविक संख्या]] प्रणाली के साथ जो संभव है, उससे परे संभावित ऊर्जाओं के योग या अंतर को सम्मिलित करते हुए गणना करेगा।तब से भौतिक विज्ञानी अपनी गणनाओं में अनंत काल से घृणा करते हैं, और {{math|''r''}} अभ्यास में हमेशा गैर शून्य है, का चुनाव <math>U = 0</math> अनंत पर कहीं अधिक बेहतर विकल्प है, ? गुरुत्वाकर्षण के कुएं में नकारात्मक ऊर्जा का विचार पहले अनोखा लगता हो। | ||
गुरुत्वाकर्षण ऊर्जा के लिए नकारात्मक मान के भी गहरे आशय हैं जो इसे ब्रह्माण्ड सम्बंधित गणनाओं में अधिक उचित लगते हैं जहाँ ब्रह्मांड की कुल ऊर्जा को सार्थक रूप से माना जा सकता है; इस पर अधिक जानकारी के लिए [[ मुद्रास्फीति सिद्धांत ]] देखें।<ref>{{cite book|author=Guth, Alan|chapter=Appendix A, Gravitational Energy|title=मुद्रास्फीति ब्रह्मांड|publisher=Perseus Books|date=1997|isbn=0-201-14942-7|pages=289–293}}</ref> | गुरुत्वाकर्षण ऊर्जा के लिए नकारात्मक मान के भी गहरे आशय हैं जो इसे ब्रह्माण्ड सम्बंधित गणनाओं में अधिक उचित लगते हैं जहाँ ब्रह्मांड की कुल ऊर्जा को सार्थक रूप से माना जा सकता है; इस पर अधिक जानकारी के लिए [[ मुद्रास्फीति सिद्धांत |मुद्रास्फीति सिद्धांत]] देखें।<ref>{{cite book|author=Guth, Alan|chapter=Appendix A, Gravitational Energy|title=मुद्रास्फीति ब्रह्मांड|publisher=Perseus Books|date=1997|isbn=0-201-14942-7|pages=289–293}}</ref> | ||
=== उपयोग === | === उपयोग === | ||
{{Further| | {{Further|गुरुत्वाकर्षण संभावित ऊर्जा भंडारण}} | ||
गुरुत्वीय संभावित ऊर्जा के कई व्यावहारिक उपयोग हैं, विशेष रूप से [[ पंप-भंडारण पनबिजली |पंप-भंडारण पनबिजली]] का उत्पादन। उदाहरण के लिए, [[ डिनोरविग पावर स्टेशन |डिनोरविग पावर स्टेशन]] , वेल्स में, दो झीलें हैं, दूसरे की तुलना में अधिक ऊंचाई पर है। ऐसे समय में जब अधिशेष बिजली की आवश्यकता नहीं होती है (और तुलनात्मक रूप से सस्ता भी होता है), पानी को ऊंची झील तक पंप किया जाता है, इस प्रकार बिजली ऊर्जा (पंप को चलाना) को गुरुत्वाकर्षण संभावित ऊर्जा में परिवर्तित किया जाता है। बिजली की चरम मांग के समय, बिजली जनरेटर टर्बाइनों के माध्यम से पानी वापस नीचे बहता है, संभावित ऊर्जा को गतिज ऊर्जा में परिवर्तित करता है और फिर वापस बिजली में बदल जाता है। प्रक्रिया पूरी तरह से कुशल नहीं है और अधिशेष बिजली से कुछ मूल ऊर्जा वास्तव में घर्षण के कारण खो जाती है।<ref name="EconomistPSH">{{cite news|url=http://www.economist.com/node/21548495?frsc=dg%7Ca|title=ऊर्जा भंडारण - कुछ शक्ति पैक करना|newspaper=[[The Economist]]|date=3 March 2011}}</ref><ref name="thier">Jacob, Thierry.[http://www.stucky.ch/en/contenu/pdf/Pumped_storage_in_Switzerland_Dr_Jacob.pdf Pumped storage in Switzerland – an outlook beyond 2000] {{Webarchive|url=https://web.archive.org/web/20120317091142/http://www.stucky.ch/en/contenu/pdf/Pumped_storage_in_Switzerland_Dr_Jacob.pdf |date=17 March 2012 }} ''Stucky''. Accessed: 13 February 2012.</ref><ref name="Levine">Levine, Jonah G. [http://www.colorado.edu/engineering/energystorage/files/MSThesis_JGLevine_final.pdf Pumped Hydroelectric Energy Storage and Spatial Diversity of Wind Resources as Methods of Improving Utilization of Renewable Energy Sources] {{Webarchive|url=https://web.archive.org/web/20140801113053/http://www.colorado.edu/engineering/energystorage/files/MSThesis_JGLevine_final.pdf |date=1 August 2014 }} page 6, ''[[University of Colorado]]'', December 2007. Accessed: 12 February 2012.</ref><ref name="yang">Yang, Chi-Jen. [http://www.duke.edu/~cy42/PHS.pdf Pumped Hydroelectric Storage] {{webarchive| url=https://web.archive.org/web/20120905193845/http://www.duke.edu/~cy42/PHS.pdf |date=5 September 2012 }} ''[[Duke University]]''. Accessed: 12 February 2012.</ref><ref name="heco">[http://www.heco.com/portal/site/heco/menuitem.508576f78baa14340b4c0610c510b1ca/?vgnextoid=94600420af0db110VgnVCM1000005c011bacRCRD&vgnextchannel=ab020420af0db110VgnVCM1000005c011bacRCRD&vgnextfmt=default&vgnextrefresh=1&level=0&ct=article Energy Storage] {{webarchive|url=https://web.archive.org/web/20140407064054/http://www.heco.com/portal/site/heco/menuitem.508576f78baa14340b4c0610c510b1ca/?vgnextoid=94600420af0db110VgnVCM1000005c011bacRCRD&vgnextchannel=ab020420af0db110VgnVCM1000005c011bacRCRD&vgnextfmt=default&vgnextrefresh=1&level=0&ct=article |date=7 April 2014 }} ''[[Hawaiian Electric Company]]''. Accessed: 13 February 2012.</ref> | |||
गुरुत्वीय संभावित ऊर्जा के कई व्यावहारिक उपयोग हैं, विशेष रूप से [[ पंप-भंडारण पनबिजली ]] का उत्पादन। उदाहरण के लिए, [[ डिनोरविग पावर स्टेशन ]], वेल्स में, दो झीलें हैं, | गुरुत्वीय संभावित ऊर्जा का उपयोग उन घड़ियों को चलाने के लिए भी किया जाता है जिनमें गिरने वाले भार तंत्र को संचालित करते हैं। | ||
गुरुत्वीय संभावित ऊर्जा का उपयोग उन घड़ियों को चलाने के लिए भी किया जाता है जिनमें गिरने वाले भार तंत्र को संचालित करते हैं। | |||
[[ रोलर कोस्टर ]] संभावित ऊर्जा का उपयोग करने का | इसका उपयोग काउंटरवेट द्वारा लिफ्ट, क्रेन या [[ उठाने योग्य खिड़की |उठाने योग्य खिड़की]] को उठाने के लिए भी किया जाता है। | ||
[[ रोलर कोस्टर | रोलर कोस्टर]] संभावित ऊर्जा का उपयोग करने का मनोरंजक विधि / है - चेन का उपयोग कार को झुकाव (गुरुत्वाकर्षण संभावित ऊर्जा का निर्माण) करने के लिए किया जाता है, फिर उस ऊर्जा को गतिज ऊर्जा में परिवर्तित कर दिया जाता है। | |||
एक अन्य व्यावहारिक उपयोग | एक अन्य व्यावहारिक उपयोग ऑटोमोबाइल, ट्रक, रेलरोड ट्रेन, साइकिल, हवाई जहाज, या पाइपलाइन में तरल पदार्थ जैसे परिवहन में डाउनहिल (संभवतः तट) के नीचे उतरने के लिए गुरुत्वाकर्षण संभावित ऊर्जा का उपयोग कर रहा है। कुछ स्थितियों में उतरना की संभावित ऊर्जा से प्राप्त गतिज ऊर्जा का उपयोग अगली कक्षा में चढ़ने के लिए किया जा सकता है जैसे कि क्या होता है जब सड़क लहरदार होती है और बार-बार गिरती है।संग्रहीत ऊर्जा का व्यावसायीकरण (उच्च ऊंचाई तक उठाए गए रेल कारों के रूप में) जिसे विद्युत ग्रिड द्वारा आवश्यक होने पर विद्युत ऊर्जा में परिवर्तित किया जाता है, संयुक्त अवस्था अमेरिका में उन्नत रेल ऊर्जा भंडारण (एआरईएस) नामक प्रणाली में किया जा रहा है।<ref name="Economist-2012.03.03">[http://www.economist.com/node/21548495 Packing Some Power: Energy Technology: Better ways of storing energy are needed if electricity systems are to become cleaner and more efficient], ''[[The Economist]]'', 3 March 2012</ref><ref name="Bloomberg-2012.09.06">Downing, Louise. [https://www.bloomberg.com/news/print/2012-08-27/ski-lifts-help-open-25-billion-market-for-storing-power-energy.html Ski Lifts Help Open $25 Billion Market for Storing Power], [[Bloomberg News]] online, 6 September 2012</ref><ref>Kernan, Aedan. [http://www.leonardo-energy.org/storing-energy-rail-tracks Storing Energy on Rail Tracks] {{webarchive|url=https://web.archive.org/web/20140412182442/http://www.leonardo-energy.org/storing-energy-rail-tracks |date=12 April 2014 }}, Leonardo-Energy.org website, 30 October 2013</ref> | ||
== रासायनिक संभावित ऊर्जा == | == रासायनिक संभावित ऊर्जा == | ||
{{Main article| | {{Main article|रसायन ऊर्जा}} | ||
रासायनिक संभावित ऊर्जा परमाणुओं या अणुओं की संरचनात्मक व्यवस्था से संबंधित संभावित ऊर्जा का | |||
रासायनिक संभावित ऊर्जा परमाणुओं या अणुओं की संरचनात्मक व्यवस्था से संबंधित संभावित ऊर्जा का रूप है। यह व्यवस्था अणु के भीतर या अन्यथा [[ रासायनिक बंध |रासायनिक बंध]] ों का परिणाम हो सकती है। किसी रासायनिक पदार्थ की रासायनिक ऊर्जा को [[ रासायनिक प्रतिक्रिया |रासायनिक प्रतिक्रिया]] द्वारा ऊर्जा के अन्य रूपों में परिवर्तित किया जा सकता है। उदाहरण के रूप में, जब किसी ईंधन को जलाया जाता है तो रासायनिक ऊर्जा ऊष्मा में परिवर्तित हो जाती है, यही स्थिति जैविक जीव में उपापचयित भोजन के पाचन के स्थिति में भी है। हरे पौधे [[ प्रकाश संश्लेषण |प्रकाश संश्लेषण]] नामक प्रक्रिया के माध्यम से [[ सौर ऊर्जा |सौर ऊर्जा]] को रासायनिक ऊर्जा में बदलते हैं, और [[ विद्युत |बिजली]] ऊर्जा को बिजली रासायनिक प्रतिक्रियाओं के माध्यम से रासायनिक ऊर्जा में परिवर्तित किया जा सकता है। | |||
समान शब्द [[ रासायनिक क्षमता ]] का उपयोग किसी पदार्थ की क्षमता को विन्यास के परिवर्तन से गुजरने के लिए संकेत करने के लिए किया जाता है, चाहे वह रासायनिक प्रतिक्रिया, स्थानिक परिवहन, जलाशय के साथ कण विनिमय आदि के रूप में हो। | समान शब्द [[ रासायनिक क्षमता |रासायनिक क्षमता]] का उपयोग किसी पदार्थ की क्षमता को विन्यास के परिवर्तन से गुजरने के लिए संकेत करने के लिए किया जाता है, चाहे वह रासायनिक प्रतिक्रिया, स्थानिक परिवहन, जलाशय के साथ कण विनिमय आदि के रूप में हो। | ||
== बिजली संभावित ऊर्जा == | == बिजली संभावित ऊर्जा == | ||
{{Main article| | {{Main article|विद्युत संभावित ऊर्जा}} | ||
किसी वस्तु में उसके बिजली आवेश और उनकी उपस्थिति से संबंधित कई बलों के कारण स्थितिज ऊर्जा हो सकती है। इस तरह की संभावित ऊर्जा के दो मुख्य प्रकार हैं: इलेक्ट्रोस्टैटिक संभावित ऊर्जा, इलेक्ट्रोडायनामिक संभावित ऊर्जा (जिसे कभी-कभी चुंबकीय संभावित ऊर्जा भी कहा जाता है)। | किसी वस्तु में उसके बिजली आवेश और उनकी उपस्थिति से संबंधित कई बलों के कारण स्थितिज ऊर्जा हो सकती है। इस तरह की संभावित ऊर्जा के दो मुख्य प्रकार हैं: इलेक्ट्रोस्टैटिक संभावित ऊर्जा, इलेक्ट्रोडायनामिक संभावित ऊर्जा (जिसे कभी-कभी चुंबकीय संभावित ऊर्जा भी कहा जाता है)। | ||
[[File:Plasma-lamp 2.jpg|right|thumb|गैस भरे गोले के अंदर [[ प्लाज्मा (भौतिकी) ]] बनता है]] | [[File:Plasma-lamp 2.jpg|right|thumb|गैस भरे गोले के अंदर [[ प्लाज्मा (भौतिकी) |प्लाज्मा (भौतिकी)]] बनता है]] | ||
=== इलेक्ट्रोस्टैटिक संभावित ऊर्जा === | === इलेक्ट्रोस्टैटिक संभावित ऊर्जा === | ||
अंतरिक्ष में दो पिंडों के बीच इलेक्ट्रोस्टैटिक संभावित ऊर्जा | अंतरिक्ष में दो पिंडों के बीच इलेक्ट्रोस्टैटिक संभावित ऊर्जा चार्ज Q द्वारा दूसरे चार्ज q पर लगाए गए बल से प्राप्त होती है जो कि | ||
<math display="block"> \mathbf{F}_{e} = -\frac{1}{4\pi\varepsilon_0} \frac{Qq}{r^2} \mathbf{\hat{r}},</math> | <math display="block"> \mathbf{F}_{e} = -\frac{1}{4\pi\varepsilon_0} \frac{Qq}{r^2} \mathbf{\hat{r}},</math> | ||
कहां <math>\mathbf{\hat{r}}</math> Q से q और ε की ओर इशारा करते हुए लंबाई 1 का | कहां <math>\mathbf{\hat{r}}</math> Q से q और ε<sub>0</sub> की ओर इशारा करते हुए लंबाई 1 का सदिश है वैक्यूम परावैद्युतांक है। इसे कूलम्ब स्थिरांक का उपयोग करके भी लिखा जा सकता है {{math|1=''k''<sub>e</sub> = 1 ⁄ 4''πε''<sub>0</sub>}}. | ||
यदि किसी वस्तु के बिजली आवेश को स्थिर माना जा सकता है, तो अन्य आवेशित वस्तुओं के सापेक्ष इसकी स्थिति के कारण इसकी संभावित ऊर्जा होती है। बिजली संभावित ऊर्जा | यदि किसी वस्तु के बिजली आवेश को स्थिर माना जा सकता है, तो अन्य आवेशित वस्तुओं के सापेक्ष इसकी स्थिति के कारण इसकी संभावित ऊर्जा होती है। बिजली संभावित ऊर्जा बिजली क्षेत्र में बिजली आवेशित कण (आराम पर) की ऊर्जा है। इसे उस कार्य (भौतिकी) के रूप में परिभाषित किया गया है जिसे वस्तु पर गैर-बिजली बलों के लिए समायोजित, अनंत दूरी से अपने वर्तमान स्थान पर ले जाने के लिए किया जाना चाहिए। यदि कोई अन्य बिजली आवेशित वस्तु पास में है तो यह ऊर्जा सामान्यतः गैर-शून्य होगी। | ||
इलेक्ट्रोस्टैटिक बल क्षेत्र में q को A से किसी बिंदु B तक ले जाने के लिए आवश्यक कार्य W द्वारा दिया गया है | इलेक्ट्रोस्टैटिक बल क्षेत्र में q को A से किसी बिंदु B तक ले जाने के लिए आवश्यक कार्य W द्वारा दिया गया है | ||
<math display="block">\Delta U_{AB}({\mathbf{r}})=-\int_{A}^{B} \mathbf{F_e} \cdot d\mathbf{r} </math> | <math display="block">\Delta U_{AB}({\mathbf{r}})=-\int_{A}^{B} \mathbf{F_e} \cdot d\mathbf{r} </math> | ||
सामान्यतः जूल के लिए जे में दिया जाता है। बिजली क्षमता नामक | सामान्यतः जूल के लिए जे में दिया जाता है। बिजली क्षमता नामक संबंधित मात्रा (सामान्यतः वोल्टेज के लिए वी के साथ चिह्नित) प्रति यूनिट चार्ज बिजली संभावित ऊर्जा के बराबर होती है। | ||
===चुंबकीय स्थितिज ऊर्जा=== | ===चुंबकीय स्थितिज ऊर्जा=== | ||
एक चुंबकीय क्षण की ऊर्जा <math>\boldsymbol{\mu}</math> बाहरी रूप से उत्पादित [[ चुंबकीय क्षेत्र ]] में|चुंबकीय बी-क्षेत्र {{math|'''B'''}} संभावित ऊर्जा है<ref>{{cite book|last=Aharoni|first=Amikam|title=फेरोमैग्नेटिज्म के सिद्धांत का परिचय| date=1996|publisher=Clarendon Pr.|location=Oxford|isbn=0-19-851791-2|edition=Repr.| url=https://archive.org/details/introductiontoth00ahar}}</ref> | एक चुंबकीय क्षण की ऊर्जा <math>\boldsymbol{\mu}</math> बाहरी रूप से उत्पादित [[ चुंबकीय क्षेत्र |चुंबकीय क्षेत्र]] में|चुंबकीय बी-क्षेत्र {{math|'''B'''}} संभावित ऊर्जा है<ref>{{cite book|last=Aharoni|first=Amikam|title=फेरोमैग्नेटिज्म के सिद्धांत का परिचय| date=1996|publisher=Clarendon Pr.|location=Oxford|isbn=0-19-851791-2|edition=Repr.| url=https://archive.org/details/introductiontoth00ahar}}</ref> | ||
<math display="block">U=-\boldsymbol{\mu}\cdot\mathbf{B}. </math> | <math display="block">U=-\boldsymbol{\mu}\cdot\mathbf{B}. </math> | ||
चुंबकीयकरण {{math|'''M'''}} | चुंबकीयकरण {{math|'''M'''}} मैदान में है | ||
<math display="block"> U = -\frac{1}{2}\int \mathbf{M}\cdot\mathbf{B} \, dV, </math> | <math display="block"> U = -\frac{1}{2}\int \mathbf{M}\cdot\mathbf{B} \, dV, </math> | ||
जहां अभिन्न सभी स्थान पर हो सकता है या, समकक्ष, जहां {{math|'''M'''}} अशून्य है।<ref>{{cite book| last=Jackson| first=John David| author-link=John David Jackson (physicist)|title=शास्त्रीय इलेक्ट्रोडायनामिक्स| date=1975| publisher=Wiley| location=New York| isbn=0-471-43132-X| edition=2d|url=https://archive.org/details/classicalelectro00jack_0}}</ref> | जहां अभिन्न सभी स्थान पर हो सकता है या, समकक्ष, जहां {{math|'''M'''}} अशून्य है।<ref>{{cite book| last=Jackson| first=John David| author-link=John David Jackson (physicist)|title=शास्त्रीय इलेक्ट्रोडायनामिक्स| date=1975| publisher=Wiley| location=New York| isbn=0-471-43132-X| edition=2d|url=https://archive.org/details/classicalelectro00jack_0}}</ref> | ||
चुंबकीय संभावित ऊर्जा न केवल चुंबकीय सामग्री के बीच की दूरी से संबंधित ऊर्जा का रूप है, बल्कि क्षेत्र के भीतर उन सामग्रियों के अभिविन्यास, या संरेखण से भी संबंधित है। उदाहरण के लिए, कम्पास की सुई में सबसे कम चुंबकीय संभावित ऊर्जा होती है, जब इसे पृथ्वी के चुंबकीय क्षेत्र के उत्तरी और दक्षिणी ध्रुवों के साथ संरेखित किया जाता है। यदि सुई को किसी बाहरी बल द्वारा स्थानांतरित किया जाता है, तो पृथ्वी के चुंबकीय क्षेत्र द्वारा सुई के चुंबकीय द्विध्रुव पर टोक़ लगाया जाता है, जिससे यह संरेखण में वापस आ जाता है। सुई की चुंबकीय संभावित ऊर्जा उच्चतम होती है जब इसका क्षेत्र पृथ्वी के चुंबकीय क्षेत्र के समान दिशा में होता है। दो चुम्बकों में दूसरे के संबंध में और उनके बीच की दूरी के संबंध में संभावित ऊर्जा होगी, किन्तु यह उनके अभिविन्यास पर भी निर्भर करता है। यदि विपरीत ध्रुवों को दूर रखा जाता है, तो संभावित ऊर्जा जितनी दूर होगी उतनी ही अधिक होगी और वे जितने करीब होंगे उतनी ही कम होगी। इसके विपरीत, ध्रुवों की तरह साथ मजबूर होने पर उच्चतम संभावित ऊर्जा होगी, और सबसे कम जब वे अलग हो जाएंगे।<ref>{{cite book|first=James D.|last=Livingston|title=राइजिंग फोर्स: द मैजिक ऑफ मैग्नेटिक लेविटेशन| publisher=[[President and Fellows of Harvard College]]|date=2011|page=152}}</ref><ref>{{cite book| first=Narinder| last=Kumar| title=व्यापक भौतिकी बारहवीं| publisher=Laxmi Publications|date=2004|page=713}}</ref> | |||
प्रोटॉन और न्यूट्रॉन जैसे परमाणु कण विखंडन और संलयन प्रक्रियाओं में नष्ट नहीं होते हैं, | |||
== परमाणु संभावित ऊर्जा == | |||
परमाणु संभावित ऊर्जा [[ परमाणु नाभिक |परमाणु नाभिक]] के अंदर उपपरमाण्विक कण की संभावित ऊर्जा है। परमाणु कण साथ मजबूत परमाणु बल से बंधे होते हैं। कमजोर परमाणु बल [[ बीटा क्षय |बीटा क्षय]] जैसे कुछ प्रकार के रेडियोधर्मी क्षय के लिए संभावित ऊर्जा प्रदान करते हैं। | |||
प्रोटॉन और न्यूट्रॉन जैसे परमाणु कण विखंडन और संलयन प्रक्रियाओं में नष्ट नहीं होते हैं, किन्तु उनके संग्रह में कम द्रव्यमान हो सकता है यदि वे व्यक्तिगत रूप से स्वतंत्र थे, जिस स्थिति में इस द्रव्यमान अंतर को परमाणु प्रतिक्रियाओं (गर्मी और विकिरण) में गर्मी और विकिरण के रूप में मुक्त किया जा सकता है। विकिरण में लापता द्रव्यमान होता है, किन्तु यह अधिकांशतः सिस्टम से निकल जाता है, जहां इसे मापा नहीं जाता है)। सूर्य से ऊर्जा ऊर्जा रूपांतरण के इस रूप का उदाहरण है। सूर्य में, हाइड्रोजन संलयन की प्रक्रिया प्रति सेकंड लगभग 4 मिलियन टन सौर पदार्थ को [[ विद्युत चुम्बकीय ऊर्जा |बिजली चुम्बकीय ऊर्जा]] में परिवर्तित करती है, जो अंतरिक्ष में विकिरित होती है। | |||
== बल और संभावित ऊर्जा == | == बल और संभावित ऊर्जा == | ||
संभावित ऊर्जा बल (भौतिकी) से निकटता से जुड़ी हुई है। यदि किसी पिंड पर बल द्वारा किया गया कार्य जो A से B तक जाता है, इन बिंदुओं के बीच के पथ पर निर्भर नहीं करता है, तो A से मापे गए इस बल का कार्य अंतरिक्ष में हर दूसरे बिंदु को | संभावित ऊर्जा बल (भौतिकी) से निकटता से जुड़ी हुई है। यदि किसी पिंड पर बल द्वारा किया गया कार्य जो A से B तक जाता है, इन बिंदुओं के बीच के पथ पर निर्भर नहीं करता है, तो A से मापे गए इस बल का कार्य अंतरिक्ष में हर दूसरे बिंदु को स्केलर मान प्रदान करता है और स्केलर क्षमता को परिभाषित करता है। खेत। इस स्थिति में, बल को संभावित क्षेत्र के कवच के ऋणात्मक के रूप में परिभाषित किया जा सकता है। | ||
उदाहरण के लिए, गुरुत्वाकर्षण | उदाहरण के लिए, गुरुत्वाकर्षण संरक्षी बल है। संबंधित क्षमता [[ गुरुत्वाकर्षण क्षमता |गुरुत्वाकर्षण क्षमता]] है, जिसे अधिकांशतः निरूपित किया जाता है <math>\phi</math> या <math>V</math>, स्थिति के समारोह के रूप में ऊर्जा प्रति यूनिट द्रव्यमान के अनुरूप। द्रव्यमान M और m के दो कणों की गुरुत्वाकर्षण संभावित ऊर्जा दूरी r से अलग होती है | ||
<math display="block">U = -\frac{G M m}{r},</math> | <math display="block">U = -\frac{G M m}{r},</math> | ||
दो निकायों की गुरुत्वाकर्षण क्षमता ([[ विशिष्ट कक्षीय ऊर्जा ]]) है | दो निकायों की गुरुत्वाकर्षण क्षमता ([[ विशिष्ट कक्षीय ऊर्जा ]]) है | ||
| Line 244: | Line 231: | ||
कहां <math>\mu</math> घटा हुआ द्रव्यमान है। | कहां <math>\mu</math> घटा हुआ द्रव्यमान है। | ||
बिंदु A से | बिंदु A से [[ परीक्षण कण |परीक्षण कण]] को स्थानांतरित करके गुरुत्वाकर्षण के विरुद्ध किया गया कार्य <math>U = a</math> बी को इंगित करने के लिए <math>U = b</math> है <math>(b - a)</math> और किया गया काम दूसरे रास्ते से वापस जा रहा है <math>(a - b)</math> जिससे A से B तक जाने और A पर लौटने में किया गया कुल कार्य है | ||
<math display="block">U_{A \to B \to A} = (b - a) + (a - b) = 0. </math> | <math display="block">U_{A \to B \to A} = (b - a) + (a - b) = 0. </math> | ||
यदि संभावित को ए पर पुनर्परिभाषित किया जाता है <math>a + c</math> और B पर होने की क्षमता <math>b + c</math>, कहां <math>c</math> | यदि संभावित को ए पर पुनर्परिभाषित किया जाता है <math>a + c</math> और B पर होने की क्षमता <math>b + c</math>, कहां <math>c</math> स्थिरांक है (अर्थात् <math>c</math> धनात्मक या ऋणात्मक कोई भी संख्या हो सकती है, किन्तु यह A पर वही होनी चाहिए जो B पर है) तो A से B तक जाने में किया गया कार्य है | ||
<math display="block">U_{A \to B} = (b + c) - (a + c) = b - a </math> | <math display="block">U_{A \to B} = (b + c) - (a + c) = b - a </math> | ||
पहले जैसा। | पहले जैसा। | ||
व्यावहारिक रूप में, इसका मतलब है कि कोई शून्य सेट कर सकता है <math>U</math> और <math>\phi</math> कहीं भी कोई पसंद करता है। कोई इसे पृथ्वी की सतह पर शून्य पर सेट कर सकता है, या शून्य को अनंत पर सेट करना अधिक सुविधाजनक पा सकता है (जैसा कि इस खंड में पहले दिए गए भावों में है)। | व्यावहारिक रूप में, इसका मतलब है कि कोई शून्य सेट कर सकता है <math>U</math> और <math>\phi</math> कहीं भी कोई पसंद करता है। कोई इसे पृथ्वी की सतह पर शून्य पर सेट कर सकता है, या शून्य को अनंत पर सेट करना अधिक सुविधाजनक पा सकता है (जैसा कि इस खंड में पहले दिए गए भावों में है)। | ||
एक संरक्षी बल को अवकल ज्यामिति की भाषा में बंद अवकल रूप में अभिव्यक्त किया जा सकता है। जैसा कि [[ यूक्लिडियन अंतरिक्ष |यूक्लिडियन अंतरिक्ष]] सिकुड़ा हुआ स्थान है, इसकी [[ डॉ कहलमज गर्भाशय |डॉ कहलमज गर्भाशय]] गायब हो जाती है, इसलिए प्रत्येक बंद रूप भी [[ सटीक अंतर रूप |त्रुटिहीन अंतर रूप]] है, और इसे स्केलर क्षेत्र के कवच के रूप में व्यक्त किया जा सकता है। यह इस तथ्य का गणितीय औचित्य देता है कि सभी रूढ़िवादी बल संभावित क्षेत्र के कवच हैं। | |||
एक संरक्षी बल को अवकल ज्यामिति की भाषा में बंद अवकल रूप में अभिव्यक्त किया जा सकता है। जैसा कि [[ यूक्लिडियन अंतरिक्ष ]] सिकुड़ा हुआ स्थान है, इसकी [[ डॉ कहलमज गर्भाशय ]] गायब हो जाती है, इसलिए प्रत्येक बंद रूप भी | |||
==टिप्पणियाँ== | ==टिप्पणियाँ== | ||
| Line 271: | Line 254: | ||
{{Footer energy}} | {{Footer energy}} | ||
{{DEFAULTSORT:Potential Energy}} | |||
{{DEFAULTSORT:Potential Energy}} | |||
[[Category: | [[Category:Articles with hatnote templates targeting a nonexistent page|Potential Energy]] | ||
[[Category:Created On 26/12/2022]] | [[Category:Collapse templates|Potential Energy]] | ||
[[Category:Created On 26/12/2022|Potential Energy]] | |||
[[Category:Energy navigational boxes| ]] | |||
[[Category:Infobox templates|physical quantity]] | |||
[[Category:Lua-based templates|Potential Energy]] | |||
[[Category:Machine Translated Page|Potential Energy]] | |||
[[Category:Mechanics templates|Potential Energy]] | |||
[[Category:Navigational boxes| ]] | |||
[[Category:Navigational boxes without horizontal lists|Potential Energy]] | |||
[[Category:Pages with empty portal template|Potential Energy]] | |||
[[Category:Pages with script errors|Potential Energy]] | |||
[[Category:Physics sidebar templates|Potential Energy]] | |||
[[Category:Portal-inline template with redlinked portals|Potential Energy]] | |||
[[Category:Short description with empty Wikidata description|Potential Energy]] | |||
[[Category:Sidebars with styles needing conversion|Potential Energy]] | |||
[[Category:Template documentation pages|Documentation/doc]] | |||
[[Category:Templates Translated in Hindi|Potential Energy]] | |||
[[Category:Templates Vigyan Ready|Potential Energy]] | |||
[[Category:Templates generating microformats|Potential Energy]] | |||
[[Category:Templates that add a tracking category|Potential Energy]] | |||
[[Category:Templates that are not mobile friendly|Potential Energy]] | |||
[[Category:Templates that generate short descriptions|Potential Energy]] | |||
[[Category:Templates using TemplateData|Potential Energy]] | |||
[[Category:Webarchive template wayback links]] | |||
[[Category:Wikipedia metatemplates|Potential Energy]] | |||
Latest revision as of 16:09, 2 November 2023
| Part of a series on |
| चिरसम्मत यांत्रिकी |
|---|
भौतिक विज्ञान में, स्थितिज ऊर्जा वह ऊर्जा है जो किसी वस्तु द्वारा अन्य वस्तुओं के सापेक्ष उसकी स्थिति, स्वयं के भीतर तनाव, उसके बिजली आवेश या अन्य कारकों के कारण धारण की जाती है।[1][2]
सामान्य प्रकार की संभावित ऊर्जा में किसी वस्तु की गुरुत्वाकर्षण संभावित ऊर्जा, विस्तारित वसंत की लोचदार संभावित ऊर्जा, और बिजली क्षेत्र में बिजली आवेश की बिजली संभावित ऊर्जा सम्मिलित होती है। इकाइयों की अंतर्राष्ट्रीय प्रणाली (SI) में ऊर्जा की इकाई जूल है, जिसका प्रतीक J है।
संभावित ऊर्जा शब्द की प्रारंभिक 19वीं सदी के स्कॉटिश इंजीनियर और भौतिक विज्ञानी विलियम रैंकिन ने की थी।[3][4] चूंकि इसका संबंध यूनानी दार्शनिक अरस्तू की सामर्थ्य और वास्तविकता की अवधारणा से है। संभावित ऊर्जा उन बलों से जुड़ी होती है जो किसी पिंड पर इस तरह कार्य करते हैं कि इन बलों द्वारा पिंड पर किया गया कुल कार्य केवल अंतरिक्ष में पिंड की प्रारंभिक और अंतिम स्थिति पर निर्भर करता है। इन बलों, जिन्हें कंजर्वेटिव बल कहा जाता है, को अंतरिक्ष में हर बिंदु पर निश्चित स्केलर फ़ंक्शन के ग्रेडियेंट के रूप में व्यक्त वैक्टर द्वारादिखाया गया है किया जा सकता है जिसे संभावित कहा जाता है।
चूँकि किसी पिंड पर कार्य करने वाली संभावित शक्तियों का कार्य जो प्रारंभ से अंत की स्थिति तक जाता है, केवल इन दो स्थितियों से निर्धारित होता है, और यह शरीर के प्रक्षेपवक्र पर निर्भर नहीं करता है, जिसे क्षमता के रूप में जाना जाता है जिसका मूल्यांकन किया जा सकता है इस कार्य को निर्धारित करने के लिए दो पद है ।
अवलोकन
विभिन्न प्रकार की संभावित ऊर्जा होती है, प्रत्येक विशेष प्रकार के बल से जुड़ी होती है। उदाहरण के लिए, लोच (भौतिकी) बल के कार्य को लोचदार संभावित ऊर्जा कहा जाता है; गुरुत्वाकर्षण बल के कार्य को गुरुत्वाकर्षण स्थितिज ऊर्जा कहा जाता है; कूलम्ब बल के कार्य को बिजली स्थितिज ऊर्जा कहा जाता है; बेरिऑन आवेश (भौतिकी) पर कार्यरत प्रबल नाभिकीय बल या दुर्बल नाभिकीय बल के कार्य को नाभिकीय स्थितिज ऊर्जा कहते हैं; अन्तराअणुक बलों के कार्य को अन्तराअणुक स्थितिज ऊर्जा कहते हैं। रासायनिक संभावित ऊर्जा, जैसे कि जीवाश्म ईंधन में संग्रहीत ऊर्जा, परमाणुओं और अणुओं में इलेक्ट्रॉनों और नाभिकों के विन्यास की पुनर्व्यवस्था के समयकूलम्ब बल का कार्य है। ऊष्मीय ऊर्जा में सामान्यतः दो घटक होते हैं: कणों की यादृच्छिक गति की गतिज ऊर्जा और उनके विन्यास की संभावित ऊर्जा।
एक क्षमता से व्युत्पन्न बलों को संरक्षी बल भी कहा जाता है। रूढ़िवादी बल द्वारा किया गया कार्य है
संभावित ऊर्जा अन्य वस्तुओं के सापेक्ष किसी वस्तु की स्थिति के आधार पर ऊर्जा है।[5] संभावित ऊर्जा अधिकांशतः वसंत (उपकरण) या गुरुत्वाकर्षण बल जैसे बहाल करने वाली शक्तियों से जुड़ी होत है। किसी स्प्रिंग को खींचने या किसी द्रव्यमान को उठाने की क्रिया बाहरी बल द्वारा की जाती है जो क्षमता के बल क्षेत्र के विरुद्ध कार्य करता है। यह कार्य बल क्षेत्र में संग्रहित होता है, जिसे स्थितिज ऊर्जा के रूप में संग्रहित कहा जाता है। यदि बाहरी बल को हटा दिया जाता है तो बल क्षेत्र कार्य करने के लिए शरीर पर कार्य करता है क्योंकि यह शरीर को प्रारंभिक स्थिति में वापस ले जाता है, वसंत के खिंचाव को कम करता है या शरीर को गिरने का कारण बनता है।
एक गेंद पर विचार करें जिसका द्रव्यमान है m और किसकी ऊंचाई है h. त्वरण g फ्री फॉल लगभग स्थिर है, इसलिए गेंद का वजन बल mg स्थिर है। बल और विस्थापन के गुणनफल से किया गया कार्य प्राप्त होता है, जो इस प्रकार गुरुत्वीय स्थितिज ऊर्जा के बराबर होता है
काम और संभावित ऊर्जा
संभावित ऊर्जा बल (भौतिकी) से निकटता से जुड़ी हुई है। यदि किसी पिंड पर बल द्वारा किया गया कार्य जो A से B तक जाता है, इन बिंदुओं के बीच के पथ पर निर्भर नहीं करता है (यदि कार्य रूढ़िवादी बल द्वारा किया जाता है), तो A से मापे गए इस बल का कार्य अदिश मान प्रदान करता है अंतरिक्ष में हर दूसरे बिंदु पर और स्केलर संभावित क्षेत्र को परिभाषित करता है। इस स्थिति में, बल को संभावित क्षेत्र के कवच के ऋणात्मक के रूप में परिभाषित किया जा सकता है।
यदि लागू बल के लिए कार्य पथ से स्वतंत्र है, तो बल द्वारा किए गए कार्य का मूल्यांकन अनुप्रयोग बिंदु के प्रक्षेपवक्र के प्रारंभ से अंत तक किया जाता है। इसका मतलब यह है कि फ़ंक्शन U('x') है, जिसे संभावित कहा जाता है, जिसका मूल्यांकन दो बिंदुओं 'x'A पर किया जा सकता है और xB इन दो बिंदुओं के बीच किसी भी प्रक्षेपवक्र पर कार्य प्राप्त करने के लिए। इस कार्य को नकारात्मक संकेत के साथ परिभाषित करने का क्रम है जिससे सकारात्मक कार्य क्षमता में कमी हो, अर्थात
फलन U('x') आरोपित बल से संबद्ध स्थितिज ऊर्जा कहलाती है। संभावित ऊर्जा वाले बलों के उदाहरण गुरुत्वाकर्षण और वसंत बल हैं।
संभावित से व्युत्पन्न
इस खंड में कार्य और स्थितिज ऊर्जा के बीच संबंध को अधिक विस्तार से प्रस्तुत किया गया है। रेखा समाकल जो वक्र C के साथ कार्य को परिभाषित करता है, विशेष रूप लेता है यदि बल 'F' अदिश क्षेत्र U'('x') से संबंधित है जिससे
संभावित ऊर्जा U = - U'(x) पारंपरिक रूप से इस अदिश क्षेत्र के ऋणात्मक के रूप में परिभाषित किया जाता है जिससे बल क्षेत्र द्वारा कार्य संभावित ऊर्जा को कम कर दे, अर्थात
संभावित ऊर्जा की गणना
एक बल क्षेत्र एफ (xो देखते हुए, संभावित ऊर्जा से जुड़े स्केलर फ़ंक्शन को खोजने के लिए कवच प्रमेय का उपयोग करके कार्य अभिन्न का मूल्यांकन किया जा सकता है। यह पैरामिट्रीकृत वक्र की प्रारंभिक करके किया जाता है γ(t) = r(t) से γ(a) = A को γ(b) = B, और कंप्यूटिंग,
निकट पृथ्वी गुरुत्वाकर्षण के लिए संभावित ऊर्जा

छोटी ऊँचाई में परिवर्तन के लिए, गुरुत्वीय स्थिति ऊर्जा का उपयोग करके गणना की जा सकती है
मौलिक भौतिकी में, गुरुत्वाकर्षण निरंतर नीचे की ओर बल लगाता है F = (0, 0, Fz) पृथ्वी की सतह के पास गतिमान पिंड के द्रव्यमान के केंद्र पर। प्रक्षेपवक्र के साथ गतिमान पिंड पर गुरुत्वाकर्षण का कार्य r(t) = (x(t), y(t), z(t)), जैसे रोलर कोस्टर के ट्रैक की गणना उसके वेग का उपयोग करके की जाती है, v = (vx, vy, vz), प्राप्त करने के लिए
रैखिक वसंत के लिए संभावित ऊर्जा

एक क्षैतिज वसंत बल लगाता है F = (−kx, 0, 0) जो अक्षीय या x दिशा में इसके विरूपण के समानुपाती होता है। अंतरिक्ष वक्र के साथ चलने वाले पिंड पर इस स्प्रिंग का कार्य s(t) = (x(t), y(t), z(t)), इसकी वेग का उपयोग करके गणना की जाती है, v = (vx, vy, vz), प्राप्त करने के लिए
कार्यक्रम
रैखिक स्प्रिंग की स्थितिज ऊर्जा कहलाती है।
लोचदार संभावित ऊर्जा लोच (भौतिकी) वस्तु (उदाहरण के लिए धनुष (हथियार) या गुलेल) की संभावित ऊर्जा है जो तनाव या संपीड़न (या औपचारिक शब्दावली में तनाव (भौतिकी) ) के अनुसार विकृत होती है। यह बल के परिणाम के रूप में उत्पन्न होता है जो वस्तु को उसके मूल आकार में मरम्मत करने का प्रयास करता है, जो कि वस्तु का गठन करने वाले परमाणुओं और अणुओं के बीच अधिकांशतः बिजली चुम्बकीय बल होता है। यदि खिंचाव जारी किया जाता है, तो ऊर्जा गतिज ऊर्जा में बदला जाती है।
दो निकायों के बीच गुरुत्वाकर्षण बलों के लिए संभावित ऊर्जा
गुरुत्वाकर्षण संभावित कार्य, जिसे गुरुत्वाकर्षण क्षमता ऊर्जा भी कहा जाता है, है:
व्युत्पत्ति
दूरी r द्वारा अलग किए गए द्रव्यमान M और m के दो पिंडों के बीच गुरुत्वाकर्षण बल न्यूटन के सार्वभौमिक गुरुत्वाकर्षण के नियम द्वारा दिया जाता है। न्यूटन का नियम
द्रव्यमान m को वेग से चलने दें v फिर इस द्रव्यमान पर गुरुत्वाकर्षण का कार्य स्थिति से चलता है r(t1) को r(t2) द्वारा दिया गया है
दो निकायों के बीच इलेक्ट्रोस्टैटिक बलों के लिए संभावित ऊर्जा
एक आवेश Q द्वारा अन्य आवेश q पर लगाया गया इलेक्ट्रोस्टैटिक बल दूरी r द्वारा अलग किया जाता है, जिसे कूलम्ब के नियम द्वारा दिया जाता है
इलेक्ट्रोस्टैटिक बल क्षेत्र में Q को ए से किसी बिंदु बी तक ले जाने के लिए आवश्यक कार्य डब्ल्यू को संभावित कार्य द्वारा दिया जाता है
संदर्भ स्तर
संभावित ऊर्जा अवस्था का एक कार्य है जिसमें एक प्रणाली है, और किसी विशेष अवस्था के लिए इसके सापेक्ष परिभाषित किया गया है। यह संदर्भ स्थिति हमेशा वास्तविक स्थिति नहीं होती है; यह सीमा भी हो सकती है, जैसे कि अनंत की ओर जाने वाले सभी शरीर के बीच की दूरी, बशर्ते कि उस सीमा तक जाने में सम्मिलित ऊर्जा हो, जैसे कि व्युत्क्रम-वर्ग कानून बलों के स्थिति में। किसी भी मनमानी संदर्भ स्थिति का उपयोग किया जा सकता है; इसलिए इसे सुविधा के आधार पर चुना जा सकता है।
सामान्यतः किसी प्रणाली की संभावित ऊर्जा केवल उसके अवयव की सापेक्ष स्थिति पर निर्भर करती है, इसलिए संदर्भ स्थिति को सापेक्ष स्थिति के रूप में भी व्यक्त किया जा सकता है।
गुरुत्वीय स्थितिज ऊर्जा
गुरुत्वाकर्षण ऊर्जा गुरुत्वाकर्षण बल से जुड़ी संभावित ऊर्जा है, क्योंकि पृथ्वी के गुरुत्वाकर्षण के विरुद्ध वस्तुओं को ऊपर उठाने के लिए काम की आवश्यकता होती है। ऊंचे पदों के कारण संभावित ऊर्जा को गुरुत्वाकर्षण संभावित ऊर्जा कहा जाता है, और ऊंचे जलाशय में पानी से इसका सबूत मिलता है या बांध के पीछे रखा जाता है। यदि कोई वस्तु गुरुत्वाकर्षण क्षेत्र के अंदर बिंदु से दूसरे बिंदु पर गिरती है, तो गुरुत्वाकर्षण बल वस्तु पर सकारात्मक कार्य करेगा, और गुरुत्वाकर्षण की स्थितिज ऊर्जा उतनी ही मात्रा में घट जाएगी।
एक टेबल के ऊपर रखी किताब पर विचार करें। जैसे ही पुस्तक को फर्श से टेबल पर उठाया जाता है, कुछ बाहरी बल गुरुत्वाकर्षण बल के विरुद्ध काम करता है। यदि पुस्तक वापस फर्श पर गिरती है, तो पुस्तक को प्राप्त होने वाली गिरने वाली ऊर्जा गुरुत्वाकर्षण बल द्वारा प्रदान की जाती है। इस प्रकार, यदि पुस्तक मेज से गिर जाती है, तो यह संभावित ऊर्जा पुस्तक के द्रव्यमान को गति देने के लिए जाती है और गतिज ऊर्जा में परिवर्तित हो जाती है। जब किताब फर्श से टकराती है तो यह गतिज ऊर्जा प्रभाव से गर्मी, विरूपण और ध्वनि में परिवर्तित हो जाती है।
किसी वस्तु की गुरुत्वीय स्थितिज ऊर्जा को प्रभावित करने वाले कारक हैं किसी संदर्भ बिंदु के सापेक्ष उसकी ऊंचाई, उसका द्रव्यमान और उसमें वर्तमान गुरुत्वाकर्षण क्षेत्र की ताकत। ही टेबल पर पड़ी भारी किताब की तुलना में लम्बे अलमारी के ऊपर और कम गुरुत्वाकर्षण संभावित ऊर्जा। चंद्रमा की सतह के ऊपर निश्चित ऊंचाई पर वस्तु में गुरुत्वाकर्षण संभावित ऊर्जा पृथ्वी की सतह के ऊपर समान ऊंचाई की तुलना में कम होती है क्योंकि चंद्रमा का गुरुत्वाकर्षण कमजोर होता है। शब्द के सामान्य अर्थ में ऊँचाई का उपयोग गुरुत्वाकर्षण संभावित ऊर्जा गणनाओं के लिए नहीं किया जा सकता है जब गुरुत्वाकर्षण को स्थिर नहीं माना जाता है। निम्नलिखित खंड अधिक विवरण प्रदान करते हैं।
स्थानीय सन्निकटन
एक गुरुत्वाकर्षण क्षेत्र की ताकत स्थान के साथ बदलती रहती है। चूंकि, जब गुरुत्वाकर्षण क्षेत्र के स्रोत के केंद्र से दूरियों के संबंध में दूरी का परिवर्तन छोटा होता है, तो क्षेत्र की ताकत में यह उतार-चढ़ाव नगण्य होती है और हम मान सकते हैं कि किसी विशेष वस्तु पर गुरुत्वाकर्षण बल स्थिर है। उदाहरण के लिए, पृथ्वी की सतह के निकट, हम मानते हैं कि गुरुत्वाकर्षण के कारण त्वरण स्थिर है g = 9.8 m/s2 (मानक गुरुत्वाकर्षण )। इस स्थिति में, गुरुत्वीय स्थितिज ऊर्जा के लिए सरल व्यंजक का उपयोग करके प्राप्त किया जा सकता है W = Fd यांत्रिक कार्य के लिए समीकरण, और समीकरण
इसलिए, संभावित अंतर है
सामान्य सूत्र
चूंकि, दूरी में बड़े बदलाव पर, सन्निकटन कि g स्थिर है अब मान्य नहीं है, और हमें गुरुत्वाकर्षण संभावित ऊर्जा को निर्धारित करने के लिए कलन और कार्य की सामान्य गणितीय परिभाषा का उपयोग करना होगा। स्थितिज ऊर्जा की गणना के लिए, हम गुरुत्वाकर्षण बल का समाकलन कर सकते हैं, जिसका परिमाण सार्वभौमिक गुरुत्वाकर्षण के नियम द्वारा दिया गया है|न्यूटन के गुरुत्वाकर्षण के नियम, दूरी के संबंध में r दो शरीरों के बीच। उस परिभाषा का उपयोग करते हुए, जनता की प्रणाली की गुरुत्वाकर्षण संभावित ऊर्जा m1 और M2 दूरी पर r गुरुत्वाकर्षण स्थिरांक का उपयोग करना G है
के लिए यह सूत्र दिया है U, की प्रणाली की कुल संभावित ऊर्जा n शरीर सभी के लिए योग द्वारा पाया जाता है दो निकायों के जोड़े, उन दो शव की प्रणाली की संभावित ऊर्जा।
निकायों की प्रणाली को छोटे कणों के संयुक्त सेट के रूप में माना जाता है, और पिछले को कण स्तर पर लागू करने से हमें नकारात्मक गुरुत्वाकर्षण बाध्यकारी ऊर्जा मिलती है। यह क्षमता ऊर्जा निकायों की प्रणाली की कुल संभावित ऊर्जा की तुलना में अधिक अटलता से नकारात्मक है क्योंकि इसमें प्रत्येक शरीर की नकारात्मक गुरुत्वाकर्षण अनिवार्य ऊर्जा भी सम्मिलित है। पिंडों की प्रणाली की संभावित ऊर्जा, शरीर को दूसरे से अनंत तक अलग करने के लिए आवश्यक ऊर्जा का नकारात्मक है, जबकि गुरुत्वाकर्षण अनिवार्य ऊर्जा दूसरे से अनंत तक सभी कणों को अलग करने के लिए आवश्यक ऊर्जा है।
नकारात्मक गुरुत्वीय ऊर्जा
जैसा कि सभी संभावित ऊर्जाओं के साथ होता है, अधिकांश भौतिक उद्देश्यों के लिए गुरुत्वाकर्षण संभावित ऊर्जा में केवल अंतर होता है, और शून्य बिंदु का चुनाव ऐच्छिक होता है। यह देखते हुए कि विशेष परिमित r को दूसरे पर वरीयता देने के लिए कोई उचित मानदंड नहीं है, दूरी के लिए केवल दो उचित विकल्प प्रतीत होते हैं जिस पर U शून्य हो जाता है: और . का चुनाव अनंत पर अजीब लग सकता है, और इसका परिणाम यह हो सकता है कि गुरुत्वाकर्षण ऊर्जा हमेशा नकारात्मक होती है, यह उल्टा लग सकता है, किन्तु यह विकल्प गुरुत्वाकर्षण संभावित ऊर्जा मूल्यों को परिमित होने की अनुमति देता है, यद्यपि नकारात्मक।
गणितीय विलक्षणता पर गुरुत्वाकर्षण संभावित ऊर्जा के सूत्र में इसका मतलब है कि सम्मेलन का एकमात्र अन्य स्पष्ट रूप से उचित वैकल्पिक विकल्प, के साथ के लिए , संभावित ऊर्जा सकारात्मक होने का परिणाम होगा, किन्तु सभी गैर-शून्य मूल्यों के लिए अनंत रूप से बड़ा होगा r, और वास्तविक संख्या प्रणाली के साथ जो संभव है, उससे परे संभावित ऊर्जाओं के योग या अंतर को सम्मिलित करते हुए गणना करेगा।तब से भौतिक विज्ञानी अपनी गणनाओं में अनंत काल से घृणा करते हैं, और r अभ्यास में हमेशा गैर शून्य है, का चुनाव अनंत पर कहीं अधिक बेहतर विकल्प है, ? गुरुत्वाकर्षण के कुएं में नकारात्मक ऊर्जा का विचार पहले अनोखा लगता हो।
गुरुत्वाकर्षण ऊर्जा के लिए नकारात्मक मान के भी गहरे आशय हैं जो इसे ब्रह्माण्ड सम्बंधित गणनाओं में अधिक उचित लगते हैं जहाँ ब्रह्मांड की कुल ऊर्जा को सार्थक रूप से माना जा सकता है; इस पर अधिक जानकारी के लिए मुद्रास्फीति सिद्धांत देखें।[10]
उपयोग
गुरुत्वीय संभावित ऊर्जा के कई व्यावहारिक उपयोग हैं, विशेष रूप से पंप-भंडारण पनबिजली का उत्पादन। उदाहरण के लिए, डिनोरविग पावर स्टेशन , वेल्स में, दो झीलें हैं, दूसरे की तुलना में अधिक ऊंचाई पर है। ऐसे समय में जब अधिशेष बिजली की आवश्यकता नहीं होती है (और तुलनात्मक रूप से सस्ता भी होता है), पानी को ऊंची झील तक पंप किया जाता है, इस प्रकार बिजली ऊर्जा (पंप को चलाना) को गुरुत्वाकर्षण संभावित ऊर्जा में परिवर्तित किया जाता है। बिजली की चरम मांग के समय, बिजली जनरेटर टर्बाइनों के माध्यम से पानी वापस नीचे बहता है, संभावित ऊर्जा को गतिज ऊर्जा में परिवर्तित करता है और फिर वापस बिजली में बदल जाता है। प्रक्रिया पूरी तरह से कुशल नहीं है और अधिशेष बिजली से कुछ मूल ऊर्जा वास्तव में घर्षण के कारण खो जाती है।[11][12][13][14][15] गुरुत्वीय संभावित ऊर्जा का उपयोग उन घड़ियों को चलाने के लिए भी किया जाता है जिनमें गिरने वाले भार तंत्र को संचालित करते हैं।
इसका उपयोग काउंटरवेट द्वारा लिफ्ट, क्रेन या उठाने योग्य खिड़की को उठाने के लिए भी किया जाता है।
रोलर कोस्टर संभावित ऊर्जा का उपयोग करने का मनोरंजक विधि / है - चेन का उपयोग कार को झुकाव (गुरुत्वाकर्षण संभावित ऊर्जा का निर्माण) करने के लिए किया जाता है, फिर उस ऊर्जा को गतिज ऊर्जा में परिवर्तित कर दिया जाता है।
एक अन्य व्यावहारिक उपयोग ऑटोमोबाइल, ट्रक, रेलरोड ट्रेन, साइकिल, हवाई जहाज, या पाइपलाइन में तरल पदार्थ जैसे परिवहन में डाउनहिल (संभवतः तट) के नीचे उतरने के लिए गुरुत्वाकर्षण संभावित ऊर्जा का उपयोग कर रहा है। कुछ स्थितियों में उतरना की संभावित ऊर्जा से प्राप्त गतिज ऊर्जा का उपयोग अगली कक्षा में चढ़ने के लिए किया जा सकता है जैसे कि क्या होता है जब सड़क लहरदार होती है और बार-बार गिरती है।संग्रहीत ऊर्जा का व्यावसायीकरण (उच्च ऊंचाई तक उठाए गए रेल कारों के रूप में) जिसे विद्युत ग्रिड द्वारा आवश्यक होने पर विद्युत ऊर्जा में परिवर्तित किया जाता है, संयुक्त अवस्था अमेरिका में उन्नत रेल ऊर्जा भंडारण (एआरईएस) नामक प्रणाली में किया जा रहा है।[16][17][18]
रासायनिक संभावित ऊर्जा
रासायनिक संभावित ऊर्जा परमाणुओं या अणुओं की संरचनात्मक व्यवस्था से संबंधित संभावित ऊर्जा का रूप है। यह व्यवस्था अणु के भीतर या अन्यथा रासायनिक बंध ों का परिणाम हो सकती है। किसी रासायनिक पदार्थ की रासायनिक ऊर्जा को रासायनिक प्रतिक्रिया द्वारा ऊर्जा के अन्य रूपों में परिवर्तित किया जा सकता है। उदाहरण के रूप में, जब किसी ईंधन को जलाया जाता है तो रासायनिक ऊर्जा ऊष्मा में परिवर्तित हो जाती है, यही स्थिति जैविक जीव में उपापचयित भोजन के पाचन के स्थिति में भी है। हरे पौधे प्रकाश संश्लेषण नामक प्रक्रिया के माध्यम से सौर ऊर्जा को रासायनिक ऊर्जा में बदलते हैं, और बिजली ऊर्जा को बिजली रासायनिक प्रतिक्रियाओं के माध्यम से रासायनिक ऊर्जा में परिवर्तित किया जा सकता है।
समान शब्द रासायनिक क्षमता का उपयोग किसी पदार्थ की क्षमता को विन्यास के परिवर्तन से गुजरने के लिए संकेत करने के लिए किया जाता है, चाहे वह रासायनिक प्रतिक्रिया, स्थानिक परिवहन, जलाशय के साथ कण विनिमय आदि के रूप में हो।
बिजली संभावित ऊर्जा
किसी वस्तु में उसके बिजली आवेश और उनकी उपस्थिति से संबंधित कई बलों के कारण स्थितिज ऊर्जा हो सकती है। इस तरह की संभावित ऊर्जा के दो मुख्य प्रकार हैं: इलेक्ट्रोस्टैटिक संभावित ऊर्जा, इलेक्ट्रोडायनामिक संभावित ऊर्जा (जिसे कभी-कभी चुंबकीय संभावित ऊर्जा भी कहा जाता है)।

इलेक्ट्रोस्टैटिक संभावित ऊर्जा
अंतरिक्ष में दो पिंडों के बीच इलेक्ट्रोस्टैटिक संभावित ऊर्जा चार्ज Q द्वारा दूसरे चार्ज q पर लगाए गए बल से प्राप्त होती है जो कि
यदि किसी वस्तु के बिजली आवेश को स्थिर माना जा सकता है, तो अन्य आवेशित वस्तुओं के सापेक्ष इसकी स्थिति के कारण इसकी संभावित ऊर्जा होती है। बिजली संभावित ऊर्जा बिजली क्षेत्र में बिजली आवेशित कण (आराम पर) की ऊर्जा है। इसे उस कार्य (भौतिकी) के रूप में परिभाषित किया गया है जिसे वस्तु पर गैर-बिजली बलों के लिए समायोजित, अनंत दूरी से अपने वर्तमान स्थान पर ले जाने के लिए किया जाना चाहिए। यदि कोई अन्य बिजली आवेशित वस्तु पास में है तो यह ऊर्जा सामान्यतः गैर-शून्य होगी।
इलेक्ट्रोस्टैटिक बल क्षेत्र में q को A से किसी बिंदु B तक ले जाने के लिए आवश्यक कार्य W द्वारा दिया गया है
चुंबकीय स्थितिज ऊर्जा
एक चुंबकीय क्षण की ऊर्जा बाहरी रूप से उत्पादित चुंबकीय क्षेत्र में|चुंबकीय बी-क्षेत्र B संभावित ऊर्जा है[19]
चुंबकीय संभावित ऊर्जा न केवल चुंबकीय सामग्री के बीच की दूरी से संबंधित ऊर्जा का रूप है, बल्कि क्षेत्र के भीतर उन सामग्रियों के अभिविन्यास, या संरेखण से भी संबंधित है। उदाहरण के लिए, कम्पास की सुई में सबसे कम चुंबकीय संभावित ऊर्जा होती है, जब इसे पृथ्वी के चुंबकीय क्षेत्र के उत्तरी और दक्षिणी ध्रुवों के साथ संरेखित किया जाता है। यदि सुई को किसी बाहरी बल द्वारा स्थानांतरित किया जाता है, तो पृथ्वी के चुंबकीय क्षेत्र द्वारा सुई के चुंबकीय द्विध्रुव पर टोक़ लगाया जाता है, जिससे यह संरेखण में वापस आ जाता है। सुई की चुंबकीय संभावित ऊर्जा उच्चतम होती है जब इसका क्षेत्र पृथ्वी के चुंबकीय क्षेत्र के समान दिशा में होता है। दो चुम्बकों में दूसरे के संबंध में और उनके बीच की दूरी के संबंध में संभावित ऊर्जा होगी, किन्तु यह उनके अभिविन्यास पर भी निर्भर करता है। यदि विपरीत ध्रुवों को दूर रखा जाता है, तो संभावित ऊर्जा जितनी दूर होगी उतनी ही अधिक होगी और वे जितने करीब होंगे उतनी ही कम होगी। इसके विपरीत, ध्रुवों की तरह साथ मजबूर होने पर उच्चतम संभावित ऊर्जा होगी, और सबसे कम जब वे अलग हो जाएंगे।[21][22]
परमाणु संभावित ऊर्जा
परमाणु संभावित ऊर्जा परमाणु नाभिक के अंदर उपपरमाण्विक कण की संभावित ऊर्जा है। परमाणु कण साथ मजबूत परमाणु बल से बंधे होते हैं। कमजोर परमाणु बल बीटा क्षय जैसे कुछ प्रकार के रेडियोधर्मी क्षय के लिए संभावित ऊर्जा प्रदान करते हैं।
प्रोटॉन और न्यूट्रॉन जैसे परमाणु कण विखंडन और संलयन प्रक्रियाओं में नष्ट नहीं होते हैं, किन्तु उनके संग्रह में कम द्रव्यमान हो सकता है यदि वे व्यक्तिगत रूप से स्वतंत्र थे, जिस स्थिति में इस द्रव्यमान अंतर को परमाणु प्रतिक्रियाओं (गर्मी और विकिरण) में गर्मी और विकिरण के रूप में मुक्त किया जा सकता है। विकिरण में लापता द्रव्यमान होता है, किन्तु यह अधिकांशतः सिस्टम से निकल जाता है, जहां इसे मापा नहीं जाता है)। सूर्य से ऊर्जा ऊर्जा रूपांतरण के इस रूप का उदाहरण है। सूर्य में, हाइड्रोजन संलयन की प्रक्रिया प्रति सेकंड लगभग 4 मिलियन टन सौर पदार्थ को बिजली चुम्बकीय ऊर्जा में परिवर्तित करती है, जो अंतरिक्ष में विकिरित होती है।
बल और संभावित ऊर्जा
संभावित ऊर्जा बल (भौतिकी) से निकटता से जुड़ी हुई है। यदि किसी पिंड पर बल द्वारा किया गया कार्य जो A से B तक जाता है, इन बिंदुओं के बीच के पथ पर निर्भर नहीं करता है, तो A से मापे गए इस बल का कार्य अंतरिक्ष में हर दूसरे बिंदु को स्केलर मान प्रदान करता है और स्केलर क्षमता को परिभाषित करता है। खेत। इस स्थिति में, बल को संभावित क्षेत्र के कवच के ऋणात्मक के रूप में परिभाषित किया जा सकता है।
उदाहरण के लिए, गुरुत्वाकर्षण संरक्षी बल है। संबंधित क्षमता गुरुत्वाकर्षण क्षमता है, जिसे अधिकांशतः निरूपित किया जाता है या , स्थिति के समारोह के रूप में ऊर्जा प्रति यूनिट द्रव्यमान के अनुरूप। द्रव्यमान M और m के दो कणों की गुरुत्वाकर्षण संभावित ऊर्जा दूरी r से अलग होती है
बिंदु A से परीक्षण कण को स्थानांतरित करके गुरुत्वाकर्षण के विरुद्ध किया गया कार्य बी को इंगित करने के लिए है और किया गया काम दूसरे रास्ते से वापस जा रहा है जिससे A से B तक जाने और A पर लौटने में किया गया कुल कार्य है
व्यावहारिक रूप में, इसका मतलब है कि कोई शून्य सेट कर सकता है और कहीं भी कोई पसंद करता है। कोई इसे पृथ्वी की सतह पर शून्य पर सेट कर सकता है, या शून्य को अनंत पर सेट करना अधिक सुविधाजनक पा सकता है (जैसा कि इस खंड में पहले दिए गए भावों में है)।
एक संरक्षी बल को अवकल ज्यामिति की भाषा में बंद अवकल रूप में अभिव्यक्त किया जा सकता है। जैसा कि यूक्लिडियन अंतरिक्ष सिकुड़ा हुआ स्थान है, इसकी डॉ कहलमज गर्भाशय गायब हो जाती है, इसलिए प्रत्येक बंद रूप भी त्रुटिहीन अंतर रूप है, और इसे स्केलर क्षेत्र के कवच के रूप में व्यक्त किया जा सकता है। यह इस तथ्य का गणितीय औचित्य देता है कि सभी रूढ़िवादी बल संभावित क्षेत्र के कवच हैं।
टिप्पणियाँ
- ↑ Jain, Mahesh C. (2009). "Fundamental forces and laws: a brief review". इंजीनियरिंग भौतिकी की पाठ्यपुस्तक, भाग 1. PHI Learning Pvt. Ltd. p. 10. ISBN 978-81-203-3862-3.
- ↑ McCall, Robert P. (2010). "Energy, Work and Metabolism". मानव शरीर का भौतिकी. JHU Press. p. 74. ISBN 978-0-8018-9455-8.
- ↑ William John Macquorn Rankine (1853) "On the general law of the transformation of energy," Proceedings of the Philosophical Society of Glasgow, vol. 3, no. 5, pages 276–280; reprinted in: (1) Philosophical Magazine, series 4, vol. 5, no. 30, pp. 106–117 (February 1853); and (2) W. J. Millar, ed., Miscellaneous Scientific Papers: by W. J. Macquorn Rankine, ... (London, England: Charles Griffin and Co., 1881), part II, pp. 203–208.
- ↑ Smith, Crosbie (1998). ऊर्जा का विज्ञान - विक्टोरियन ब्रिटेन में ऊर्जा भौतिकी का एक सांस्कृतिक इतिहास. The University of Chicago Press. ISBN 0-226-76420-6.
- ↑ Brown, Theodore L. (2006). रसायन विज्ञान केंद्रीय विज्ञान. Upper Saddle River, New Jersey: Pearson Education, Inc. pp. 168. ISBN 0-13-109686-9.
- ↑ John Robert Taylor (2005). शास्त्रीय यांत्रिकी. University Science Books. p. 117. ISBN 978-1-891389-22-1.
- ↑ Burton Paul (1979). प्लेनर मशीनरी की कीनेमेटीक्स और गतिशीलता. Prentice-Hall. ISBN 978-0-13-516062-6.
- ↑ The Feynman Lectures on Physics Vol. I Ch. 13: Work and Potential Energy (A)
- ↑ "हाइपरफिजिक्स - गुरुत्वीय स्थितिज ऊर्जा".
- ↑ Guth, Alan (1997). "Appendix A, Gravitational Energy". मुद्रास्फीति ब्रह्मांड. Perseus Books. pp. 289–293. ISBN 0-201-14942-7.
- ↑ "ऊर्जा भंडारण - कुछ शक्ति पैक करना". The Economist. 3 March 2011.
- ↑ Jacob, Thierry.Pumped storage in Switzerland – an outlook beyond 2000 Archived 17 March 2012 at the Wayback Machine Stucky. Accessed: 13 February 2012.
- ↑ Levine, Jonah G. Pumped Hydroelectric Energy Storage and Spatial Diversity of Wind Resources as Methods of Improving Utilization of Renewable Energy Sources Archived 1 August 2014 at the Wayback Machine page 6, University of Colorado, December 2007. Accessed: 12 February 2012.
- ↑ Yang, Chi-Jen. Pumped Hydroelectric Storage Archived 5 September 2012 at the Wayback Machine Duke University. Accessed: 12 February 2012.
- ↑ Energy Storage Archived 7 April 2014 at the Wayback Machine Hawaiian Electric Company. Accessed: 13 February 2012.
- ↑ Packing Some Power: Energy Technology: Better ways of storing energy are needed if electricity systems are to become cleaner and more efficient, The Economist, 3 March 2012
- ↑ Downing, Louise. Ski Lifts Help Open $25 Billion Market for Storing Power, Bloomberg News online, 6 September 2012
- ↑ Kernan, Aedan. Storing Energy on Rail Tracks Archived 12 April 2014 at the Wayback Machine, Leonardo-Energy.org website, 30 October 2013
- ↑ Aharoni, Amikam (1996). फेरोमैग्नेटिज्म के सिद्धांत का परिचय (Repr. ed.). Oxford: Clarendon Pr. ISBN 0-19-851791-2.
- ↑ Jackson, John David (1975). शास्त्रीय इलेक्ट्रोडायनामिक्स (2d ed.). New York: Wiley. ISBN 0-471-43132-X.
- ↑ Livingston, James D. (2011). राइजिंग फोर्स: द मैजिक ऑफ मैग्नेटिक लेविटेशन. President and Fellows of Harvard College. p. 152.
- ↑ Kumar, Narinder (2004). व्यापक भौतिकी बारहवीं. Laxmi Publications. p. 713.
संदर्भ
- Serway, Raymond A.; Jewett, John W. (2010). Physics for Scientists and Engineers (8th ed.). Brooks/Cole cengage. ISBN 978-1-4390-4844-3.
- Tipler, Paul (2004). Physics for Scientists and Engineers: Mechanics, Oscillations and Waves, Thermodynamics (5th ed.). W. H. Freeman. ISBN 0-7167-0809-4.