हिल्बर्ट प्रणाली: Difference between revisions
No edit summary |
|||
| Line 1: | Line 1: | ||
{{Short description|System of formal deduction in logic}}[[गणितीय भौतिकी]] में, हिल्बर्ट प्रणाली ''C*-'' बीजगणित द्वारा वर्णित भौतिक प्रणाली के लिए कम उपयोग किया जाने वाला शब्द है। | {{Short description|System of formal deduction in logic}}[[गणितीय भौतिकी]] में, हिल्बर्ट प्रणाली ''C*-'' बीजगणित द्वारा वर्णित भौतिक प्रणाली के लिए कम उपयोग किया जाने वाला शब्द है। | ||
विशेष रूप से [[गणितीय तर्क]] में, हिल्बर्ट प्रणाली, जिसे कभी-कभी हिल्बर्ट कलन, हिल्बर्ट-शैली निगमनात्मक प्रणाली या हिल्बर्ट-एकरमैन प्रणाली कहा जाता है,[[भगवान फ्रीज का शुक्र है|गॉटलॉब फ्रेज]]<ref name="Máté & Ruzsa 1997">मेट एंड रूज़सा 1997:129</ref> और [[डेविड हिल्बर्ट]] के लिए निगमनात्मक तर्क की एक प्रकार की प्रणाली है। इन निगमनात्मक प्रणाली का अध्ययन अधिकांशतः पहले क्रम के तर्क के लिए किया जाता है, लेकिन अन्य तर्कों के लिए भी रुचि रखते हैं। | विशेष रूप से [[गणितीय तर्क]] में, हिल्बर्ट प्रणाली, जिसे कभी-कभी हिल्बर्ट कलन, हिल्बर्ट-शैली निगमनात्मक प्रणाली या हिल्बर्ट-एकरमैन प्रणाली कहा जाता है, [[भगवान फ्रीज का शुक्र है|गॉटलॉब फ्रेज]]<ref name="Máté & Ruzsa 1997">मेट एंड रूज़सा 1997:129</ref> और [[डेविड हिल्बर्ट]] के लिए निगमनात्मक तर्क की एक प्रकार की प्रणाली है। इन निगमनात्मक प्रणाली का अध्ययन अधिकांशतः पहले क्रम के तर्क के लिए किया जाता है, लेकिन अन्य तर्कों के लिए भी रुचि रखते हैं। | ||
हिल्बर्ट प्रणाली के अधिकांश संस्करण [[तार्किक स्वयंसिद्ध]] और अनुमान के नियमों के बीच दुविधा को संतुलित करने के तरीके में विशिष्ट व्यवहार करते हैं।<ref name="Máté & Ruzsa 1997" />हिल्बर्ट प्रणाली को तार्किक | हिल्बर्ट प्रणाली के अधिकांश संस्करण [[तार्किक स्वयंसिद्ध|तार्किक अभिगृहीत]] और अनुमान के नियमों के बीच दुविधा को संतुलित करने के तरीके में विशिष्ट व्यवहार करते हैं।<ref name="Máté & Ruzsa 1997" />हिल्बर्ट प्रणाली को तार्किक अभिगृहीतों की बड़ी संख्या में योजनाओं और अनुमान के नियमों के छोटे समूह की पसंद से चित्रित किया जा सकता है। [[प्राकृतिक कटौती|प्राकृतिक निगमन]] की प्रणालियाँ विपरीत कदम उठाती हैं, जिसमें कई निगमन नियम सम्मिलित हैं लेकिन बहुत कम या कोई [[स्वयंसिद्ध योजना|अभिगृहीत योजना]]एँ नहीं हैं। सबसे अधिक अध्ययन किए गए हिल्बर्ट प्रणाली में या तो अनुमान का सिर्फ एक नियम है{{snd}}प्रतिज्ञप्तिक कलन के लिए विधानात्मक हेतुफलानुमान{{snd}}या दो{{snd}}[[सार्वभौमिक सामान्यीकरण|सार्वव्यापकीकरण]] के साथ, निर्धारक तर्क को संभालने के लिए भी{{snd}} और कई अनंत अभिगृहीत योजनाएं है। साध्यात्मक [[मॉडल तर्क]] के लिए हिल्बर्ट प्रणाली, जिसे कभी-कभी [[हिल्बर्ट-लुईस प्रणाली]] कहा जाता है, सामान्यतः दो अतिरिक्त नियमों, [[आवश्यकता नियम]] और समान प्रतिस्थापन नियम के साथ अभिगृहीत होते हैं। | ||
हिल्बर्ट प्रणाली के कई रूपों की विशेषता यह है कि उनके अनुमान के किसी भी नियम में संदर्भ नहीं बदला जाता है, जबकि प्राकृतिक निगमन और अनुक्रमिक कलन दोनों में कुछ संदर्भ-बदलते नियम होते हैं। इस प्रकार, यदि कोई केवल पुनरुत्पादन (तर्क) की व्युत्पत्ति में रुचि रखता है, कोई काल्पनिक निर्णय नहीं है, तो कोई हिल्बर्ट प्रणाली को इस तरह से औपचारिक रूप दे सकता है कि इसके अनुमान के नियमों में केवल सरल रूप का [[निर्णय (गणितीय तर्क)]] होता है। अन्य दो निगमन प्रणालियों के साथ भी ऐसा नहीं किया जा सकता है: जैसा कि संदर्भ के उनके कुछ नियमों में संदर्भ बदल गया है, उन्हें औपचारिक रूप नहीं दिया जा सकता है जिससे कि काल्पनिक निर्णयों से बचा जा सके{{snd}} भले ही हम उनका उपयोग केवल पुनरुत्पादन की व्युत्पत्ति सिद्ध करने के लिए नहीं करना चाहते हैं। | हिल्बर्ट प्रणाली के कई रूपों की विशेषता यह है कि उनके अनुमान के किसी भी नियम में संदर्भ नहीं बदला जाता है, जबकि प्राकृतिक निगमन और अनुक्रमिक कलन दोनों में कुछ संदर्भ-बदलते नियम होते हैं। इस प्रकार, यदि कोई केवल पुनरुत्पादन (तर्क) की व्युत्पत्ति में रुचि रखता है, कोई काल्पनिक निर्णय नहीं है, तो कोई हिल्बर्ट प्रणाली को इस तरह से औपचारिक रूप दे सकता है कि इसके अनुमान के नियमों में केवल सरल रूप का [[निर्णय (गणितीय तर्क)]] होता है। अन्य दो निगमन प्रणालियों के साथ भी ऐसा नहीं किया जा सकता है: जैसा कि संदर्भ के उनके कुछ नियमों में संदर्भ बदल गया है, उन्हें औपचारिक रूप नहीं दिया जा सकता है जिससे कि काल्पनिक निर्णयों से बचा जा सके{{snd}}भले ही हम उनका उपयोग केवल पुनरुत्पादन की व्युत्पत्ति सिद्ध करने के लिए नहीं करना चाहते हैं। | ||
== निगमनात्मक तर्क == | == निगमनात्मक तर्क == | ||
[[File:Deduction architecture.png|right|300px|निगमन प्रणाली का एक ग्राफिक प्रतिनिधित्व]]हिल्बर्ट-शैली की निगमन प्रणाली में, निगमनात्मक तर्क सूत्रों का परिमित अनुक्रम है जिसमें प्रत्येक सूत्र या तो | [[File:Deduction architecture.png|right|300px|निगमन प्रणाली का एक ग्राफिक प्रतिनिधित्व]]हिल्बर्ट-शैली की निगमन प्रणाली में, निगमनात्मक तर्क सूत्रों का परिमित अनुक्रम है जिसमें प्रत्येक सूत्र या तो अभिगृहीत है या अनुमान के नियम द्वारा पिछले सूत्रों से प्राप्त किया जाता है। ये निगमनात्मक तर्क प्राकृतिक-भाषा के प्रमाणों को प्रतिबिंबित करने के लिए हैं, चूंकि वे कहीं अधिक विस्तृत हैं। | ||
मान लीजिए <math>\Gamma</math> सूत्रों का समूह है, जिसे परिकल्पना माना जाता है। उदाहरण के लिए, <math>\Gamma</math> [[समूह सिद्धांत]] या समुच्चय सिद्धांत के लिए | मान लीजिए <math>\Gamma</math> सूत्रों का समूह है, जिसे परिकल्पना माना जाता है। उदाहरण के लिए, <math>\Gamma</math> [[समूह सिद्धांत]] या समुच्चय सिद्धांत के लिए अभिगृहीतों का समुच्चय हो सकता है। अंकन <math>\Gamma \vdash \phi</math> इसका मतलब है कि एक निगमन है जो समाप्त होती है <math>\phi</math> अभिगृहीतों के रूप में केवल तार्किक अभिगृहीतों और तत्वों <math>\Gamma</math> का उपयोग करना है। इस प्रकार, अनौपचारिक रूप से, <math>\Gamma \vdash \phi</math> मतलब कि <math>\phi</math> में सभी सूत्रों <math>\Gamma</math> को मानकर सिद्ध होता है। | ||
हिल्बर्ट-शैली की निगमन प्रणालियों को तार्किक | हिल्बर्ट-शैली की निगमन प्रणालियों को तार्किक अभिगृहीतों की कई योजनाओं के उपयोग की विशेषता है। अभिगृहीत योजना विशिष्ट स्वरूप में किसी रूप के सभी सूत्रों को प्रतिस्थापित करके प्राप्त अभिगृहीतों का अनंत समुच्चय है। तार्किक अभिगृहीतों के समुच्चय में न केवल वे अभिगृहीत सम्मिलित होते हैं जो इस पैटर्न से उत्पन्न होते हैं, बल्कि उनमें से किसी एक अभिगृहीत का सामान्यीकरण भी सम्मिलित होता है। सूत्र पर शून्य या अधिक सार्वभौम परिमाणक लगाकर सूत्र का सामान्यीकरण प्राप्त किया जाता है; उदाहरण के लिए <math>\forall y ( \forall x Pxy \to Pty)</math> का सामान्यीकरण <math>\forall x Pxy \to Pty</math> है। | ||
=== तार्किक सिद्धांत === | === तार्किक सिद्धांत === | ||
विधेय तर्क के कई प्रकार के | विधेय तर्क के कई प्रकार के अभिगृहीत हैं, क्योंकि किसी भी तर्क के लिए अभिगृहीतों और नियमों को चुनने की स्वतंत्रता है जो उस तर्क को चित्रित करते हैं। हम यहां हिल्बर्ट प्रणाली का वर्णन करते हैं जिसमें नौ अभिगृहीत और सिर्फ नियम विधानात्मक हेतुफलानुमान हैं, जिसे हम एक-नियम अभिगृहीत कहते हैं और जो चिरसम्मत समीकरण तर्क का वर्णन करता है। हम इस तर्क के लिए न्यूनतम भाषा से संबोधित हैं, जहाँ सूत्र केवल संयोजकों का उपयोग करते हैं <math>\lnot</math> और <math>\to</math> और केवल परिमाणक <math>\forall</math> हैं, बाद में हम दिखाते हैं कि अतिरिक्त तार्किक संयोजकों को सम्मिलित करने के लिए प्रणाली को कैसे बढ़ाया जा सकता है, जैसे <math>\land</math> और <math>\lor</math> निगमन योग्य सूत्रों के वर्ग को बढ़ाए बिना बढ़ाया जा सकता है। | ||
तार्किक संयोजकों के हेरफेर के लिए पहली चार तार्किक | तार्किक संयोजकों के हेरफेर के लिए पहली चार तार्किक अभिगृहीत योजनाएँ (विधानात्मक हेतुफलानुमान के साथ) अनुमति देती हैं। | ||
:P1. <math>\phi \to \phi </math> | :P1. <math>\phi \to \phi </math> | ||
| Line 24: | Line 24: | ||
P4. <math>\left ( \lnot \phi \to \lnot \psi \right) \to \left( \psi \to \phi \right) </math> | P4. <math>\left ( \lnot \phi \to \lnot \psi \right) \to \left( \psi \to \phi \right) </math> | ||
अभिगृहीत P1 अनावश्यक है, क्योंकि यह P3, P2 और विधानात्मक हेतुफलानुमान से आता है (देखें) ये | अभिगृहीत P1 अनावश्यक है, क्योंकि यह P3, P2 और विधानात्मक हेतुफलानुमान से आता है (देखें) ये अभिगृहीत शास्त्रीय प्रस्तावात्मक तर्क का वर्णन करते हैं; अभिगृहीत P4 के बिना हमें [[इम्प्लीकेशनल प्रोपोज़िशनल कैलकुलस|प्रतिज्ञप्तिक कलन]] मिलता है। [[न्यूनतम तर्क]] या तो अभिगृहीत P4m जोड़कर या परिभाषित करके प्राप्त किया जाता है <math>\lnot \phi</math> जैसा <math>\phi \to \bot</math> है। | ||
:P4m. <math>\left( \phi \to \psi \right) \to \left(\left(\phi \to \lnot \psi \right) \to \lnot \phi \right)</math> | :P4m. <math>\left( \phi \to \psi \right) \to \left(\left(\phi \to \lnot \psi \right) \to \lnot \phi \right)</math> | ||
सकारात्मक निहितार्थ तर्क में अभिगृहीत P4i और P5i को जोड़कर, या न्यूनतम तर्क में | सकारात्मक निहितार्थ तर्क में अभिगृहीत P4i और P5i को जोड़कर, या न्यूनतम तर्क में अभिगृहीत P5i को जोड़कर [[अंतर्ज्ञानवादी तर्क]] प्राप्त किया जाता है। P4i और P5i दोनों चिरसम्मत प्रतिज्ञप्तिक कलन के प्रमेय हैं। | ||
:P4i. <math>\left(\phi \to \lnot \phi\right) \to \lnot \phi </math> | :P4i. <math>\left(\phi \to \lnot \phi\right) \to \lnot \phi </math> | ||
: P5i. <math>\lnot\phi \to \left( \phi \to \psi \right) </math> | : P5i. <math>\lnot\phi \to \left( \phi \to \psi \right) </math> | ||
ध्यान दें कि ये अभिगृहीत योजनाएँ हैं, जो अभिगृहीतों के असीम रूप से कई विशिष्ट उदाहरणों का प्रतिनिधित्व करती हैं। उदाहरण के लिए, P1 विशेष | ध्यान दें कि ये अभिगृहीत योजनाएँ हैं, जो अभिगृहीतों के असीम रूप से कई विशिष्ट उदाहरणों का प्रतिनिधित्व करती हैं। उदाहरण के लिए, P1 विशेष अभिगृहीत उदाहरण का प्रतिनिधित्व कर सकता है <math>p \to p </math>, या यह प्रतिनिधित्व कर सकता है <math>\left( p \to q \right) \to \left( p \to q \right) </math>: <math>\phi</math> वह स्थान है जहाँ कोई भी सूत्र रखा जा सकता है। इस तरह के चर जो सूत्रों से अधिक होते हैं उन्हें 'योजनाबद्ध चर' कहा जाता है। | ||
समान प्रतिस्थापन (यूएस) के दूसरे नियम के साथ, हम इनमें से प्रत्येक | समान प्रतिस्थापन (यूएस) के दूसरे नियम के साथ, हम इनमें से प्रत्येक अभिगृहीत योजनाओं को एकल अभिगृहीत में बदल सकते हैं, प्रत्येक योजनाबद्ध चर को कुछ प्रस्तावात्मक चर द्वारा प्रतिस्थापित कर सकते हैं जो किसी भी अभिगृहीत में उल्लिखित नहीं है जिसे हम संस्थागत अभिगृहीत कहते हैं। दोनों औपचारिकताओं में चर होते हैं, लेकिन जहां एक-नियम अभिगृहीतता में योजनाबद्ध चर होते हैं जो तर्क की भाषा के बाहर होते हैं, प्रतिस्थापन संबंधी अभिगृहीतता प्रस्तावक चर का उपयोग करती है जो प्रतिस्थापन का उपयोग करने वाले नियम के साथ सूत्रों पर चर के विचार को व्यक्त करके समान कार्य करते हैं। | ||
:यूएस. चलो <math>\phi(p)</math> प्रस्तावात्मक चर के एक या अधिक उदाहरणों के साथ सूत्र बनें <math>p</math>, और जाने <math>\psi</math> दूसरा सूत्र हो। फिर से <math>\phi(p)</math>, अनुमान <math>\phi(\psi)</math>हैं।{{dubious|Problems with Universal generalisation and Uniform substution|date=December 2018}} | :यूएस. चलो <math>\phi(p)</math> प्रस्तावात्मक चर के एक या अधिक उदाहरणों के साथ सूत्र बनें <math>p</math>, और जाने <math>\psi</math> दूसरा सूत्र हो। फिर से <math>\phi(p)</math>, अनुमान <math>\phi(\psi)</math>हैं।{{dubious|Problems with Universal generalisation and Uniform substution|date=December 2018}} | ||
अगली तीन तार्किक अभिगृहीत योजनाएं सार्वभौम परिमाणकों को जोड़ने, हेरफेर करने और हटाने के तरीके प्रदान करती हैं। | अगली तीन तार्किक अभिगृहीत योजनाएं सार्वभौम परिमाणकों को जोड़ने, हेरफेर करने और हटाने के तरीके प्रदान करती हैं। | ||
: Q5. <math> \forall x \left( \phi \right) \to \phi[x:=t]</math> जहां ''t'' | : Q5. <math> \forall x \left( \phi \right) \to \phi[x:=t]</math> जहां ''t'' को ''x'' के लिए <math>\,\!\phi</math> प्रतिस्थापित किया जा सकता है | ||
Q6. | Q6. <math>\forall x \left( \phi \to \psi \right) \to \left( \forall x \left( \phi \right) \to \forall x \left( \psi \right) \right)</math> | ||
Q7. <math> \phi \to \forall x \left( \phi \right) </math> जहाँ x मुक्त नहीं है <math>\phi</math>. | Q7. <math> \phi \to \forall x \left( \phi \right) </math> जहाँ x मुक्त नहीं है <math>\phi</math>. | ||
ये तीन अतिरिक्त नियम [[शास्त्रीय विधेय तर्क|चिरसम्मत विधेय तर्क]] को | ये तीन अतिरिक्त नियम [[शास्त्रीय विधेय तर्क|चिरसम्मत विधेय तर्क]] को अभिगृहीत करने के लिए प्रस्ताव प्रणाली का विस्तार करते हैं। इसी तरह, ये तीन नियम अंतर्ज्ञानवादी साध्यात्मक तर्क (P1-3 और P4i और P5i के साथ) के लिए [[अंतर्ज्ञानवादी विधेय तर्क]] के लिए प्रणाली का विस्तार करते हैं। | ||
सामान्यीकरण के अतिरिक्त नियम (मेटाथोरेम्स पर अनुभाग देखें) का उपयोग करते हुए सार्वभौमिक परिमाणीकरण को अधिकांशतः एक वैकल्पिक अभिगृहीतकरण दिया जाता है, इस मामले में नियम Q6 और Q7 अनावश्यक हैं।{{dubious|Problems with Universal generalisation and Uniform substution|date=December 2018}} | सामान्यीकरण के अतिरिक्त नियम (मेटाथोरेम्स पर अनुभाग देखें) का उपयोग करते हुए सार्वभौमिक परिमाणीकरण को अधिकांशतः एक वैकल्पिक अभिगृहीतकरण दिया जाता है, इस मामले में नियम Q6 और Q7 अनावश्यक हैं।{{dubious|Problems with Universal generalisation and Uniform substution|date=December 2018}} | ||
मानता प्रतीक वाले सूत्रों के साथ काम करने के लिए अंतिम | मानता प्रतीक वाले सूत्रों के साथ काम करने के लिए अंतिम अभिगृहीत योजनाओं की आवश्यकता होती है। | ||
:I8. <math>x = x</math> प्रत्येक चर x के लिए। | :I8. <math>x = x</math> प्रत्येक चर x के लिए। | ||
:I9. <math>\left( x = y \right) \to \left( \phi[z:=x] \to \phi[z:=y] \right)</math> | :I9. <math>\left( x = y \right) \to \left( \phi[z:=x] \to \phi[z:=y] \right)</math> | ||
== रूढ़िवादी विस्तार == | == रूढ़िवादी विस्तार == | ||
हिल्बर्ट-शैली की निगमन प्रणाली में निहितार्थ और निषेध के लिए केवल | हिल्बर्ट-शैली की निगमन प्रणाली में निहितार्थ और निषेध के लिए केवल अभिगृहीतों को सम्मिलित करना आम है। इन अभिगृहीतों को देखते हुए, [[कटौती प्रमेय|निगमन प्रमेय]] के [[रूढ़िवादी विस्तार]] करना संभव है जो अतिरिक्त संयोजकों के उपयोग की अनुमति देता है। इन विस्तारो को रूढ़िवादी कहा जाता है क्योंकि यदि सूत्र φ जिसमें नए संयोजक सम्मिलित हैं, को तार्किक तुल्यता सूत्र θ के रूप में फिर से लिखा जाता है जिसमें केवल निषेध, निहितार्थ और सार्वभौमिक मात्रा का ठहराव निष्कासनशामिल है, तो φ विस्तारित प्रणाली में व्युत्पन्न है यदि और केवल यदि θ मूल प्रणाली में व्युत्पन्न है। पूरी तरह से विस्तारित होने पर, हिल्बर्ट-शैली प्रणाली प्राकृतिक निगमन की प्रणाली के अधिक निकट होती है। | ||
=== अस्तित्वगत परिमाणीकरण === | === अस्तित्वगत परिमाणीकरण === | ||
| Line 58: | Line 58: | ||
:<math> \forall x(\phi \to \exists y(\phi[x:=y])) </math> | :<math> \forall x(\phi \to \exists y(\phi[x:=y])) </math> | ||
* उन्मूलन | * उन्मूलन | ||
:<math> \forall x(\phi \to \psi) \to \exists x(\phi) \to \psi </math> जहाँ <math>\psi</math>, | :<math> \forall x(\phi \to \psi) \to \exists x(\phi) \to \psi </math> जहाँ <math>\psi</math>, <math>x</math> का [[मुक्त चर]] नहीं है | ||
=== संयोजन और वियोजन === | === संयोजन और वियोजन === | ||
| Line 107: | Line 107: | ||
::(9) <math> (p \to (q \to r)) \to (q \to (p \to r)) </math> ((8) और (5) से विधानात्मक हेतुफलानुमान का उपयोग करके) | ::(9) <math> (p \to (q \to r)) \to (q \to (p \to r)) </math> ((8) और (5) से विधानात्मक हेतुफलानुमान का उपयोग करके) | ||
:(HS2) | :(HS2) <math>(p \to q) \to ((q \to r) \to (p \to r))</math> - काल्पनिक न्यायवाक्य का वैकल्पिक रूप। प्रमाण: | ||
::(1) <math>(q \to r) \to ((p \to q) \to (p \to r))</math> ((HS1) का उदाहरण) | ::(1) <math>(q \to r) \to ((p \to q) \to (p \to r))</math> ((HS1) का उदाहरण) | ||
::(2) <math>((q \to r) \to ((p \to q) \to (p \to r))) \to ((p \to q) \to ((q \to r) \to (p \to r)))</math> ((L2) का उदाहरण) | ::(2) <math>((q \to r) \to ((p \to q) \to (p \to r))) \to ((p \to q) \to ((q \to r) \to (p \to r)))</math> ((L2) का उदाहरण) | ||
::(3) <math>(p \to q) \to ((q \to r) \to (p \to r))</math> ((1) और (2) से विधानात्मक हेतुफलानुमान द्वारा) | ::(3) <math>(p \to q) \to ((q \to r) \to (p \to r))</math> ((1) और (2) से विधानात्मक हेतुफलानुमान द्वारा) | ||
:(TR1) <math> (p \to q) \to (\neg q \to \neg p) </math> - | :(TR1) <math> (p \to q) \to (\neg q \to \neg p) </math> - व्युत्क्रमण, प्रमाण देखें (व्युत्क्रमण की दूसरी दिशा (P4) है)। | ||
:(TR2) <math> (\neg p \to q) \to (\neg q \to p) </math> - व्युत्क्रमण का दूसरा रूप; प्रमाण: | :(TR2) <math> (\neg p \to q) \to (\neg q \to p) </math> - व्युत्क्रमण का दूसरा रूप; प्रमाण: | ||
| Line 134: | Line 134: | ||
::(11) <math> (\neg p \to p) \to p </math> ((7) और (10) काल्पनिक न्यायवाक्य मेटाथोरम का प्रयोग करके) | ::(11) <math> (\neg p \to p) \to p </math> ((7) और (10) काल्पनिक न्यायवाक्य मेटाथोरम का प्रयोग करके) | ||
== वैकल्पिक | == वैकल्पिक अभिगृहीतीकरण == | ||
{{Further|तर्क प्रणालियों की सूची}} | {{Further|तर्क प्रणालियों की सूची}} | ||
उपरोक्त | उपरोक्त अभिगृहीत 3 इसका श्रेय जन लुकासिविक्ज़ को दिया जाता है।<ref name="Tarski">A. Tarski, Logic, semantics, metamathematics, Oxford, 1956</ref> गॉटलॉब फ्रेगे की मूल प्रणाली में अभिगृहीत P2 और P3 थे लेकिन अभिगृहीत P4 के अतिरिक्त चार अन्य अभिगृहीत थे (देखें फ्रेगे का प्रस्तावपरक कलन)।, [[बर्ट्रेंड रसेल]] और [[अल्फ्रेड नॉर्थ व्हाइटहेड]] ने भी पांच प्रस्तावित सिद्धांतों के साथ एक प्रणाली का सुझाव दिया। | ||
== आगे के कनेक्शन == | == आगे के कनेक्शन == | ||
अभिगृहीत P1, P2 और P3, निगमनात्मक नियम विधानात्मक हेतुफलानुमान (औपचारिक रूप से [[अंतर्ज्ञानवादी प्रस्ताव तर्क]]) के साथ, अनुप्रयोग ऑपरेटर के साथ [[संयोजन तर्क]] बेस कॉम्बिनेटर I, K और S के अनुरूप हैं। हिल्बर्ट प्रणाली में प्रमाण तब संयोजी तर्क में संयोजी शब्दों के अनुरूप होते हैं। करी-हावर्ड पत्राचार भी देखें। | |||
== यह भी देखें == | == यह भी देखें == | ||
* [[हिल्बर्ट सिस्टम की सूची|हिल्बर्ट प्रणाली की सूची]] | * [[हिल्बर्ट सिस्टम की सूची|हिल्बर्ट प्रणाली की सूची]] | ||
| Line 163: | Line 163: | ||
* {{cite book |last1=Ruzsa |first1=Imre |last2=Máté |first2=András |year=1997 |title=Bevezetés a modern logikába |language=Hungarian |publisher=Osiris Kiadó |location=Budapest}} | * {{cite book |last1=Ruzsa |first1=Imre |last2=Máté |first2=András |year=1997 |title=Bevezetés a modern logikába |language=Hungarian |publisher=Osiris Kiadó |location=Budapest}} | ||
* {{cite book |last=Tarski |first=Alfred |year=1990 |title=Bizonyítás és igazság |language=Hungarian |publisher=Gondolat |location=Budapest}} It is a Hungarian translation of [[Alfred Tarski]]'s selected papers on [[semantic theory of truth]]. | * {{cite book |last=Tarski |first=Alfred |year=1990 |title=Bizonyítás és igazság |language=Hungarian |publisher=Gondolat |location=Budapest}} It is a Hungarian translation of [[Alfred Tarski]]'s selected papers on [[semantic theory of truth]]. | ||
* David Hilbert (1927) "The foundations of mathematics", translated by Stephan Bauer-Menglerberg and Dagfinn Føllesdal (pp. 464–479). | * David Hilbert (1927) "The foundations of mathematics", translated by Stephan Bauer-Menglerberg and Dagfinn Føllesdal (pp. 464–479). in: | ||
** {{cite book | ** {{cite book | ||
| last = van Heijenoort | | last = van Heijenoort | ||
| Line 176: | Line 176: | ||
| url-access = registration | | url-access = registration | ||
}} | }} | ||
** Hilbert's 1927, Based on an earlier 1925 "foundations" lecture (pp. 367–392), presents his 17 axioms -- axioms of implication #1-4, axioms about & and V #5-10, axioms of negation #11-12, his logical ε-axiom #13, axioms of equality #14-15, and axioms of number #16-17 -- along with the other necessary elements of his Formalist "proof theory" -- e.g. induction axioms, recursion axioms, etc; he also offers up a spirited defense against L.E.J. Brouwer's Intuitionism. Also see | ** Hilbert's 1927, Based on an earlier 1925 "foundations" lecture (pp. 367–392), presents his 17 axioms -- axioms of implication #1-4, axioms about & and V #5-10, axioms of negation #11-12, his logical ε-axiom #13, axioms of equality #14-15, and axioms of number #16-17 -- along with the other necessary elements of his Formalist "proof theory" -- e.g. induction axioms, recursion axioms, etc; he also offers up a spirited defense against L.E.J. Brouwer's Intuitionism. Also see Hermann Weyl's (1927) comments and rebuttal (pp. 480–484), Paul Bernay's (1927) appendix to Hilbert's lecture (pp. 485–489) and Luitzen Egbertus Jan Brouwer's (1927) response (pp. 490–495) | ||
* {{cite book | * {{cite book | ||
| last = Kleene | | last = Kleene | ||
| Line 200: | Line 200: | ||
{{Mathematical logic}} | {{Mathematical logic}} | ||
{{DEFAULTSORT:Hilbert System}} | {{DEFAULTSORT:Hilbert System}} | ||
[[Category: सबूत सिद्धांत]] | [[Category: सबूत सिद्धांत]] | ||
Revision as of 16:23, 22 February 2023
गणितीय भौतिकी में, हिल्बर्ट प्रणाली C*- बीजगणित द्वारा वर्णित भौतिक प्रणाली के लिए कम उपयोग किया जाने वाला शब्द है।
विशेष रूप से गणितीय तर्क में, हिल्बर्ट प्रणाली, जिसे कभी-कभी हिल्बर्ट कलन, हिल्बर्ट-शैली निगमनात्मक प्रणाली या हिल्बर्ट-एकरमैन प्रणाली कहा जाता है, गॉटलॉब फ्रेज[1] और डेविड हिल्बर्ट के लिए निगमनात्मक तर्क की एक प्रकार की प्रणाली है। इन निगमनात्मक प्रणाली का अध्ययन अधिकांशतः पहले क्रम के तर्क के लिए किया जाता है, लेकिन अन्य तर्कों के लिए भी रुचि रखते हैं।
हिल्बर्ट प्रणाली के अधिकांश संस्करण तार्किक अभिगृहीत और अनुमान के नियमों के बीच दुविधा को संतुलित करने के तरीके में विशिष्ट व्यवहार करते हैं।[1]हिल्बर्ट प्रणाली को तार्किक अभिगृहीतों की बड़ी संख्या में योजनाओं और अनुमान के नियमों के छोटे समूह की पसंद से चित्रित किया जा सकता है। प्राकृतिक निगमन की प्रणालियाँ विपरीत कदम उठाती हैं, जिसमें कई निगमन नियम सम्मिलित हैं लेकिन बहुत कम या कोई अभिगृहीत योजनाएँ नहीं हैं। सबसे अधिक अध्ययन किए गए हिल्बर्ट प्रणाली में या तो अनुमान का सिर्फ एक नियम है – प्रतिज्ञप्तिक कलन के लिए विधानात्मक हेतुफलानुमान – या दो – सार्वव्यापकीकरण के साथ, निर्धारक तर्क को संभालने के लिए भी – और कई अनंत अभिगृहीत योजनाएं है। साध्यात्मक मॉडल तर्क के लिए हिल्बर्ट प्रणाली, जिसे कभी-कभी हिल्बर्ट-लुईस प्रणाली कहा जाता है, सामान्यतः दो अतिरिक्त नियमों, आवश्यकता नियम और समान प्रतिस्थापन नियम के साथ अभिगृहीत होते हैं।
हिल्बर्ट प्रणाली के कई रूपों की विशेषता यह है कि उनके अनुमान के किसी भी नियम में संदर्भ नहीं बदला जाता है, जबकि प्राकृतिक निगमन और अनुक्रमिक कलन दोनों में कुछ संदर्भ-बदलते नियम होते हैं। इस प्रकार, यदि कोई केवल पुनरुत्पादन (तर्क) की व्युत्पत्ति में रुचि रखता है, कोई काल्पनिक निर्णय नहीं है, तो कोई हिल्बर्ट प्रणाली को इस तरह से औपचारिक रूप दे सकता है कि इसके अनुमान के नियमों में केवल सरल रूप का निर्णय (गणितीय तर्क) होता है। अन्य दो निगमन प्रणालियों के साथ भी ऐसा नहीं किया जा सकता है: जैसा कि संदर्भ के उनके कुछ नियमों में संदर्भ बदल गया है, उन्हें औपचारिक रूप नहीं दिया जा सकता है जिससे कि काल्पनिक निर्णयों से बचा जा सके – भले ही हम उनका उपयोग केवल पुनरुत्पादन की व्युत्पत्ति सिद्ध करने के लिए नहीं करना चाहते हैं।
निगमनात्मक तर्क
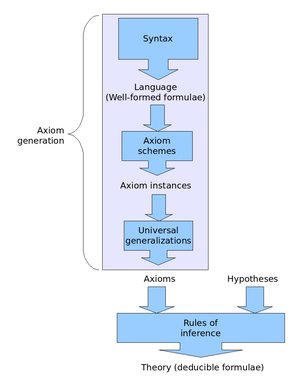
हिल्बर्ट-शैली की निगमन प्रणाली में, निगमनात्मक तर्क सूत्रों का परिमित अनुक्रम है जिसमें प्रत्येक सूत्र या तो अभिगृहीत है या अनुमान के नियम द्वारा पिछले सूत्रों से प्राप्त किया जाता है। ये निगमनात्मक तर्क प्राकृतिक-भाषा के प्रमाणों को प्रतिबिंबित करने के लिए हैं, चूंकि वे कहीं अधिक विस्तृत हैं।
मान लीजिए सूत्रों का समूह है, जिसे परिकल्पना माना जाता है। उदाहरण के लिए, समूह सिद्धांत या समुच्चय सिद्धांत के लिए अभिगृहीतों का समुच्चय हो सकता है। अंकन इसका मतलब है कि एक निगमन है जो समाप्त होती है अभिगृहीतों के रूप में केवल तार्किक अभिगृहीतों और तत्वों का उपयोग करना है। इस प्रकार, अनौपचारिक रूप से, मतलब कि में सभी सूत्रों को मानकर सिद्ध होता है।
हिल्बर्ट-शैली की निगमन प्रणालियों को तार्किक अभिगृहीतों की कई योजनाओं के उपयोग की विशेषता है। अभिगृहीत योजना विशिष्ट स्वरूप में किसी रूप के सभी सूत्रों को प्रतिस्थापित करके प्राप्त अभिगृहीतों का अनंत समुच्चय है। तार्किक अभिगृहीतों के समुच्चय में न केवल वे अभिगृहीत सम्मिलित होते हैं जो इस पैटर्न से उत्पन्न होते हैं, बल्कि उनमें से किसी एक अभिगृहीत का सामान्यीकरण भी सम्मिलित होता है। सूत्र पर शून्य या अधिक सार्वभौम परिमाणक लगाकर सूत्र का सामान्यीकरण प्राप्त किया जाता है; उदाहरण के लिए का सामान्यीकरण है।
तार्किक सिद्धांत
विधेय तर्क के कई प्रकार के अभिगृहीत हैं, क्योंकि किसी भी तर्क के लिए अभिगृहीतों और नियमों को चुनने की स्वतंत्रता है जो उस तर्क को चित्रित करते हैं। हम यहां हिल्बर्ट प्रणाली का वर्णन करते हैं जिसमें नौ अभिगृहीत और सिर्फ नियम विधानात्मक हेतुफलानुमान हैं, जिसे हम एक-नियम अभिगृहीत कहते हैं और जो चिरसम्मत समीकरण तर्क का वर्णन करता है। हम इस तर्क के लिए न्यूनतम भाषा से संबोधित हैं, जहाँ सूत्र केवल संयोजकों का उपयोग करते हैं और और केवल परिमाणक हैं, बाद में हम दिखाते हैं कि अतिरिक्त तार्किक संयोजकों को सम्मिलित करने के लिए प्रणाली को कैसे बढ़ाया जा सकता है, जैसे और निगमन योग्य सूत्रों के वर्ग को बढ़ाए बिना बढ़ाया जा सकता है।
तार्किक संयोजकों के हेरफेर के लिए पहली चार तार्किक अभिगृहीत योजनाएँ (विधानात्मक हेतुफलानुमान के साथ) अनुमति देती हैं।
- P1.
- P2.
- P3.
P4.
अभिगृहीत P1 अनावश्यक है, क्योंकि यह P3, P2 और विधानात्मक हेतुफलानुमान से आता है (देखें) ये अभिगृहीत शास्त्रीय प्रस्तावात्मक तर्क का वर्णन करते हैं; अभिगृहीत P4 के बिना हमें प्रतिज्ञप्तिक कलन मिलता है। न्यूनतम तर्क या तो अभिगृहीत P4m जोड़कर या परिभाषित करके प्राप्त किया जाता है जैसा है।
- P4m.
सकारात्मक निहितार्थ तर्क में अभिगृहीत P4i और P5i को जोड़कर, या न्यूनतम तर्क में अभिगृहीत P5i को जोड़कर अंतर्ज्ञानवादी तर्क प्राप्त किया जाता है। P4i और P5i दोनों चिरसम्मत प्रतिज्ञप्तिक कलन के प्रमेय हैं।
- P4i.
- P5i.
ध्यान दें कि ये अभिगृहीत योजनाएँ हैं, जो अभिगृहीतों के असीम रूप से कई विशिष्ट उदाहरणों का प्रतिनिधित्व करती हैं। उदाहरण के लिए, P1 विशेष अभिगृहीत उदाहरण का प्रतिनिधित्व कर सकता है , या यह प्रतिनिधित्व कर सकता है : वह स्थान है जहाँ कोई भी सूत्र रखा जा सकता है। इस तरह के चर जो सूत्रों से अधिक होते हैं उन्हें 'योजनाबद्ध चर' कहा जाता है।
समान प्रतिस्थापन (यूएस) के दूसरे नियम के साथ, हम इनमें से प्रत्येक अभिगृहीत योजनाओं को एकल अभिगृहीत में बदल सकते हैं, प्रत्येक योजनाबद्ध चर को कुछ प्रस्तावात्मक चर द्वारा प्रतिस्थापित कर सकते हैं जो किसी भी अभिगृहीत में उल्लिखित नहीं है जिसे हम संस्थागत अभिगृहीत कहते हैं। दोनों औपचारिकताओं में चर होते हैं, लेकिन जहां एक-नियम अभिगृहीतता में योजनाबद्ध चर होते हैं जो तर्क की भाषा के बाहर होते हैं, प्रतिस्थापन संबंधी अभिगृहीतता प्रस्तावक चर का उपयोग करती है जो प्रतिस्थापन का उपयोग करने वाले नियम के साथ सूत्रों पर चर के विचार को व्यक्त करके समान कार्य करते हैं।
- यूएस. चलो प्रस्तावात्मक चर के एक या अधिक उदाहरणों के साथ सूत्र बनें , और जाने दूसरा सूत्र हो। फिर से , अनुमान हैं।[dubious ]
अगली तीन तार्किक अभिगृहीत योजनाएं सार्वभौम परिमाणकों को जोड़ने, हेरफेर करने और हटाने के तरीके प्रदान करती हैं।
- Q5. जहां t को x के लिए प्रतिस्थापित किया जा सकता है
Q6.
Q7. जहाँ x मुक्त नहीं है .
ये तीन अतिरिक्त नियम चिरसम्मत विधेय तर्क को अभिगृहीत करने के लिए प्रस्ताव प्रणाली का विस्तार करते हैं। इसी तरह, ये तीन नियम अंतर्ज्ञानवादी साध्यात्मक तर्क (P1-3 और P4i और P5i के साथ) के लिए अंतर्ज्ञानवादी विधेय तर्क के लिए प्रणाली का विस्तार करते हैं।
सामान्यीकरण के अतिरिक्त नियम (मेटाथोरेम्स पर अनुभाग देखें) का उपयोग करते हुए सार्वभौमिक परिमाणीकरण को अधिकांशतः एक वैकल्पिक अभिगृहीतकरण दिया जाता है, इस मामले में नियम Q6 और Q7 अनावश्यक हैं।[dubious ]
मानता प्रतीक वाले सूत्रों के साथ काम करने के लिए अंतिम अभिगृहीत योजनाओं की आवश्यकता होती है।
- I8. प्रत्येक चर x के लिए।
- I9.
रूढ़िवादी विस्तार
हिल्बर्ट-शैली की निगमन प्रणाली में निहितार्थ और निषेध के लिए केवल अभिगृहीतों को सम्मिलित करना आम है। इन अभिगृहीतों को देखते हुए, निगमन प्रमेय के रूढ़िवादी विस्तार करना संभव है जो अतिरिक्त संयोजकों के उपयोग की अनुमति देता है। इन विस्तारो को रूढ़िवादी कहा जाता है क्योंकि यदि सूत्र φ जिसमें नए संयोजक सम्मिलित हैं, को तार्किक तुल्यता सूत्र θ के रूप में फिर से लिखा जाता है जिसमें केवल निषेध, निहितार्थ और सार्वभौमिक मात्रा का ठहराव निष्कासनशामिल है, तो φ विस्तारित प्रणाली में व्युत्पन्न है यदि और केवल यदि θ मूल प्रणाली में व्युत्पन्न है। पूरी तरह से विस्तारित होने पर, हिल्बर्ट-शैली प्रणाली प्राकृतिक निगमन की प्रणाली के अधिक निकट होती है।
अस्तित्वगत परिमाणीकरण
- परिचय
- उन्मूलन
- जहाँ , का मुक्त चर नहीं है
संयोजन और वियोजन
- संयोजन परिचय और उन्मूलन
- परिचय:
- उन्मूलन बाकी:
- उन्मूलन अधिकार:
- वियोजन परिचय और उन्मूलन
- परिचय:
- परिचय सही:
- उन्मूलन:
मेटाथोरेम्स
क्योंकि हिल्बर्ट-शैली प्रणालियों में बहुत कम निगमन नियम हैं, मेटाथोरम सिद्ध करना आम है जो दिखाता है कि अतिरिक्त निगमन नियम कोई निगमनात्मक शक्ति नहीं जोड़ते हैं, इस अर्थ में कि नए निगमन नियमों का उपयोग कर निगमन को केवल मूल निगमन का उपयोग करके निगमन नियम में परिवर्तित किया जा सकता है।
इस रूप के कुछ सामान्य रूपक हैं:
- निगमन प्रमेय: यदि और केवल यदि .
- यदि और केवल यदि और .
- विपर्यय : यदि तब .
- सार्वव्यापकीकरण: यदि और x के किसी भी सूत्र में मुक्त नहीं होता है तब .
कुछ उपयोगी प्रमेय और उनकी उपपत्तियाँ
प्रतिज्ञप्तिक कलन में निम्नलिखित कई प्रमेय उनके प्रमाणों के साथ (या अन्य लेखों में इन प्रमाणों के लिंक) हैं। ध्यान दें कि चूँकि (P1) स्वयं अन्य अभिगृहीतों का प्रयोग करके सिद्ध किया जा सकता है, वास्तव में (P2), (P3) और (P4) इन सभी प्रमेयों को सिद्ध करने के लिए पर्याप्त हैं।
- (HS1) - काल्पनिक न्यायवाक्य, प्रमाण देखें।
- (L1) - प्रमाण:
- (1) (का उदाहरण (P3))
- (2) ((P1) का उदाहरण)
- (3) (से (2) और (1)विधानात्मक हेतुफलानुमान द्वारा)
- (4) ((HS1) का उदाहरण)
- (5) (से (3) और (4) विधानात्मक हेतुफलानुमान द्वारा)
- (6) ((P2) का उदाहरण)
- (7) ((6) और (5) से विधानात्मक हेतुफलानुमान द्वारा)
निम्नलिखित दो प्रमेयों को एक साथ दोहरे निषेध के रूप में जाना जाता है:
- (DN1)
- (DN2)
- प्रमाण देखें।
- (L2) - इस प्रमाण के लिए हम काल्पनिक न्यायवाक्य मेटाथोरम की विधि का उपयोग कई प्रमाण चरणों के लिए आशुलिपि के रूप में करते हैं:
- (1) (का उदाहरण (P3))
- (2) ((HS1) का उदाहरण)
- (3) ((1) और (2) काल्पनिक न्यायवाक्य मेटाथोरम का प्रयोग करके)
- (4) (का उदाहरण (P3))
- (5) ((3) और (4) विधानात्मक हेतुफलानुमान का उपयोग करके)
- (6) ((P2) का उदाहरण)
- (7) ((P2) का उदाहरण)
- (8) ((6) और (7) से विधानात्मक हेतुफलानुमान का प्रयोग करके)
- (9) ((8) और (5) से विधानात्मक हेतुफलानुमान का उपयोग करके)
- (HS2) - काल्पनिक न्यायवाक्य का वैकल्पिक रूप। प्रमाण:
- (1) ((HS1) का उदाहरण)
- (2) ((L2) का उदाहरण)
- (3) ((1) और (2) से विधानात्मक हेतुफलानुमान द्वारा)
- (TR1) - व्युत्क्रमण, प्रमाण देखें (व्युत्क्रमण की दूसरी दिशा (P4) है)।
- (TR2) - व्युत्क्रमण का दूसरा रूप; प्रमाण:
- (1) ((TR1) का उदाहरण)
- (2) ((DN1) का उदाहरण)
- (3) ((HS1) का उदाहरण)
- (4) ((2) और (3) विधानात्मक हेतुफलानुमान से)
- (5) ((1) और (4) काल्पनिक न्यायवाक्य मेटाथोरम का प्रयोग करके)
- (L3) - प्रमाण:
- (1) ((P2) का उदाहरण)
- (2) ((P4) का उदाहरण)
- (3) ((1) और (2) काल्पनिक न्यायवाक्य मेटाथोरम का प्रयोग करके)
- (4) (का उदाहरण (P3))
- (5) (फॉर्म (3) और (4) विधानात्मक हेतुफलानुमान का उपयोग करके)
- (6) ((P4) का उदाहरण)
- (7) ((5) और (6) काल्पनिक न्यायवाक्य मेटाथोरम का प्रयोग करके)
- (8) ((P1) का उदाहरण)
- (9) ((L1) का उदाहरण)
- (10) ((8) और (9) विधानात्मक हेतुफलानुमान का उपयोग करके)
- (11) ((7) और (10) काल्पनिक न्यायवाक्य मेटाथोरम का प्रयोग करके)
वैकल्पिक अभिगृहीतीकरण
उपरोक्त अभिगृहीत 3 इसका श्रेय जन लुकासिविक्ज़ को दिया जाता है।[2] गॉटलॉब फ्रेगे की मूल प्रणाली में अभिगृहीत P2 और P3 थे लेकिन अभिगृहीत P4 के अतिरिक्त चार अन्य अभिगृहीत थे (देखें फ्रेगे का प्रस्तावपरक कलन)।, बर्ट्रेंड रसेल और अल्फ्रेड नॉर्थ व्हाइटहेड ने भी पांच प्रस्तावित सिद्धांतों के साथ एक प्रणाली का सुझाव दिया।
आगे के कनेक्शन
अभिगृहीत P1, P2 और P3, निगमनात्मक नियम विधानात्मक हेतुफलानुमान (औपचारिक रूप से अंतर्ज्ञानवादी प्रस्ताव तर्क) के साथ, अनुप्रयोग ऑपरेटर के साथ संयोजन तर्क बेस कॉम्बिनेटर I, K और S के अनुरूप हैं। हिल्बर्ट प्रणाली में प्रमाण तब संयोजी तर्क में संयोजी शब्दों के अनुरूप होते हैं। करी-हावर्ड पत्राचार भी देखें।
यह भी देखें
- हिल्बर्ट प्रणाली की सूची
- प्राकृतिक निगमन
टिप्पणियाँ
संदर्भ
- Curry, Haskell B.; Robert Feys (1958). Combinatory Logic Vol. I. Vol. 1. Amsterdam: North Holland.
- Monk, J. Donald (1976). Mathematical Logic. Graduate Texts in Mathematics. Berlin, New York: Springer-Verlag. ISBN 978-0-387-90170-1.
- Ruzsa, Imre; Máté, András (1997). Bevezetés a modern logikába (in Hungarian). Budapest: Osiris Kiadó.
{{cite book}}: CS1 maint: unrecognized language (link) - Tarski, Alfred (1990). Bizonyítás és igazság (in Hungarian). Budapest: Gondolat.
{{cite book}}: CS1 maint: unrecognized language (link) It is a Hungarian translation of Alfred Tarski's selected papers on semantic theory of truth. - David Hilbert (1927) "The foundations of mathematics", translated by Stephan Bauer-Menglerberg and Dagfinn Føllesdal (pp. 464–479). in:
- van Heijenoort, Jean (1967). From Frege to Gödel: A Source Book in Mathematical Logic, 1879–1931 (3rd printing 1976 ed.). Cambridge MA: Harvard University Press. ISBN 0-674-32449-8.
- Hilbert's 1927, Based on an earlier 1925 "foundations" lecture (pp. 367–392), presents his 17 axioms -- axioms of implication #1-4, axioms about & and V #5-10, axioms of negation #11-12, his logical ε-axiom #13, axioms of equality #14-15, and axioms of number #16-17 -- along with the other necessary elements of his Formalist "proof theory" -- e.g. induction axioms, recursion axioms, etc; he also offers up a spirited defense against L.E.J. Brouwer's Intuitionism. Also see Hermann Weyl's (1927) comments and rebuttal (pp. 480–484), Paul Bernay's (1927) appendix to Hilbert's lecture (pp. 485–489) and Luitzen Egbertus Jan Brouwer's (1927) response (pp. 490–495)
- Kleene, Stephen Cole (1952). Introduction to Metamathematics (10th impression with 1971 corrections ed.). Amsterdam NY: North Holland Publishing Company. ISBN 0-7204-2103-9.
- See in particular Chapter IV Formal System (pp. 69–85) wherein Kleene presents subchapters §16 Formal symbols, §17 Formation rules, §18 Free and bound variables (including substitution), §19 Transformation rules (e.g. modus ponens) -- and from these he presents 21 "postulates" -- 18 axioms and 3 "immediate-consequence" relations divided as follows: Postulates for the propostional calculus #1-8, Additional postulates for the predicate calculus #9-12, and Additional postulates for number theory #13-21.
बाहरी संबंध
- Gaifman, Haim. "A Hilbert Type Deductive System for Sentential Logic, Completeness and Compactness" (PDF).
- Farmer, W. M. "Propositional logic" (PDF). It describes (among others) a part of the Hilbert-style deduction system (restricted to propositional calculus).