केशिका क्रिया: Difference between revisions
| Line 109: | Line 109: | ||
सोरप्टिविटी निर्माण सामग्री की एक प्रासंगिक संपत्ति है, क्योंकि यह नम (संरचनात्मक) # बढ़ती नमी की मात्रा को प्रभावित करती है। निर्माण सामग्री की सार्वभौमता के लिए कुछ मान नीचे दी गई तालिका में हैं। | सोरप्टिविटी निर्माण सामग्री की एक प्रासंगिक संपत्ति है, क्योंकि यह नम (संरचनात्मक) # बढ़ती नमी की मात्रा को प्रभावित करती है। निर्माण सामग्री की सार्वभौमता के लिए कुछ मान नीचे दी गई तालिका में हैं। | ||
{| class="wikitable" | {| class="wikitable" | ||
|+ | |+चयनित सामग्रियों की सोरप्टिविटी (स्रोत:<ref name="hall-hoff-p122">हॉल और हॉफ, पृष्ठ 122</ref>) | ||
|- | |- | ||
! | ! सामग्री || सोरप्टिविटी <br> (मिमी·मिनट<sup>−1/2</sup>) | ||
|- | |- | ||
| | | वातित कंक्रीट || 0.50 | ||
|- | |- | ||
| | | जिप्सम प्लास्टर || 3.50 | ||
|- | |- | ||
| | | मिट्टी की ईंट || 1.16 | ||
|- | |- | ||
| | | मोर्टार || 0.70 | ||
|- | |- | ||
| | | कंक्रीट की ईंट || 0.20 | ||
|} | |} | ||
[[Category:All articles with unsourced statements]] | |||
[[Category:Articles with hatnote templates targeting a nonexistent page]] | |||
[[Category:Articles with invalid date parameter in template]] | |||
[[Category:Articles with unsourced statements from August 2022]] | |||
[[Category:Articles with unsourced statements from July 2022]] | |||
[[Category:Collapse templates]] | |||
[[Category:Commons category link is the pagename]] | |||
[[Category:Created On 03/04/2023]] | |||
[[Category:Machine Translated Page]] | |||
[[Category:Navigational boxes| ]] | |||
== यह भी देखें == | == यह भी देखें == | ||
Revision as of 16:19, 23 June 2023
This article needs additional citations for verification. (November 2022) (Learn how and when to remove this template message) |
| Part of a series on |
| सातत्यक यांत्रिकी |
|---|

केशिका क्रिया (जिसे कभी-कभी केशिकात्व, केशिका गति, केशिका वृद्धि, केशिका प्रभाव, या विकिंग कहा जाता है) गुरुत्वाकर्षण की तरह किसी भी बाहरी बल की सहायता के बिना, या यहां तक कि विरोध में एक संकीर्ण स्थान में बहने वाली तरल की प्रक्रिया है। पेंट-ब्रश के बालों के बीच, एक पतली ट्यूब में, झरझरा सामग्री जैसे कागज और प्लास्टर में, कुछ गैर-छिद्रपूर्ण सामग्री जैसे रेत और तरलीकृत कार्बन फाइबर में, या में तरल पदार्थ के आरेखण में प्रभाव देखा जा सकता है। एक जैविक कोशिका। यह तरल और आसपास की ठोस सतहों के बीच अंतर-आणविक बलों के कारण होता है। यदि ट्यूब का व्यास पर्याप्त रूप से छोटा है, तो सतह तनाव का संयोजन (जो तरल के भीतर सामंजस्य (रसायन विज्ञान) के कारण होता है) और तरल और कंटेनर दीवार के बीच आसंजन तरल को आगे बढ़ाने के लिए कार्य करता है।[citation needed]
व्युत्पत्ति
केशिका लैटिन शब्द कैपिलारिस से आती है, जिसका अर्थ है या बाल जैसा दिखता है। अर्थ एक केशिका के छोटे, बालों के समान व्यास से उपजा है। जबकि केशिका आमतौर पर एक संज्ञा के रूप में प्रयोग किया जाता है, शब्द भी एक विशेषण के रूप में प्रयोग किया जाता है, जैसा कि केशिका क्रिया में होता है, जिसमें एक तरल साथ-साथ ऊपर की ओर, गुरुत्वाकर्षण के विरुद्ध होता है- क्योंकि तरल केशिकाओं की आंतरिक सतह पर आकर्षित होता है।
इतिहास
केशिका क्रिया का पहला रिकॉर्ड किया गया अवलोकन लियोनार्डो दा विंची द्वारा किया गया था।[1][2] कहा जाता है कि गैलीलियो गैलीली के एक पूर्व छात्र, निकोलो एगियुन्टी ने केशिका क्रिया की जांच की थी।[3] 1660 में, केशिका क्रिया अभी भी आयरिश रसायनज्ञ रॉबर्ट बॉयल के लिए एक नवीनता थी, जब उन्होंने बताया कि कुछ जिज्ञासु फ्रांसीसी पुरुषों ने देखा था कि जब एक केशिका ट्यूब को पानी में डुबोया जाता था, तो पानी पाइप में कुछ ऊंचाई तक चढ़ जाता था। बॉयल ने तब एक प्रयोग की सूचना दी जिसमें उन्होंने एक केशिका ट्यूब को रेड वाइन में डुबोया और फिर ट्यूब को आंशिक वैक्यूम के अधीन किया। उन्होंने पाया कि केशिका में तरल की ऊंचाई पर निर्वात का कोई प्रत्यक्ष प्रभाव नहीं था, इसलिए केशिका नलियों में तरल पदार्थ का व्यवहार पारा बैरोमीटर को नियंत्रित करने वाली घटना से अलग कुछ घटना के कारण था।[4] अन्य लोगों ने जल्द ही बॉयल की अगुवाई की।[5] कुछ (जैसे, होनोरे फैब्री,[6] जैकब बर्नौली[7]) ने सोचा कि तरल पदार्थ केशिकाओं में ऊपर उठते हैं क्योंकि हवा केशिकाओं में तरल पदार्थों की तरह आसानी से प्रवेश नहीं कर सकती है, इसलिए केशिकाओं के अंदर हवा का दबाव कम था। अन्य (जैसे, आइजैक वोसियस,[8] जियोवन्नी अल्फोंसो बोरेली,[9] लुइस कैरे (गणितज्ञ) | लुइस कैरे,[10] फ्रांसिस हॉक्सबी,[11] जोसियस वीटब्रेच[12]) ने सोचा कि द्रव के कण एक-दूसरे की ओर और केशिका की दीवारों की ओर आकर्षित होते हैं।
यद्यपि प्रयोगात्मक अध्ययन 18वीं शताब्दी के दौरान जारी रहे,[13] केशिका क्रिया का एक सफल मात्रात्मक उपचार[14] 1805 तक दो जांचकर्ताओं द्वारा प्राप्त नहीं किया गया था: यूनाइटेड किंगडम के थॉमस यंग (वैज्ञानिक)।[15] और फ्रांस के पियरे-साइमन लाप्लास।[16] उन्होंने केशिका क्रिया के यंग-लाप्लास समीकरण को व्युत्पन्न किया। 1830 तक, जर्मन गणितज्ञ कार्ल फ्रेडरिक गॉस ने केशिका क्रिया (यानी, तरल-ठोस इंटरफ़ेस पर स्थितियां) को नियंत्रित करने वाली सीमा शर्तों को निर्धारित किया था।[17] 1871 में, ब्रिटिश भौतिक विज्ञानी विलियम थॉमसन, प्रथम बैरन केल्विन (बाद में लॉर्ड केल्विन) ने तरल के वाष्प दबाव पर मेनिस्कस (तरल) के प्रभाव को निर्धारित किया - एक संबंध जिसे केल्विन समीकरण के रूप में जाना जाता है।[18] जर्मन भौतिक विज्ञानी फ्रांज अर्न्स्ट न्यूमैन (1798-1895) ने बाद में दो अमिश्रणीय तरल पदार्थों के बीच बातचीत को निर्धारित किया।[19] अल्बर्ट आइंस्टीन का पहला पेपर, जो 1900 में एनल्स ऑफ फिजिक्स को प्रस्तुत किया गया था, केशिकात्व पर था।[20][21]
घटना और भौतिकी

झरझरा मीडिया में केशिका प्रवेश अपने गतिशील तंत्र को खोखले ट्यूबों में प्रवाह के साथ साझा करता है, क्योंकि दोनों प्रक्रियाओं को चिपचिपा बलों द्वारा विरोध किया जाता है।[22] नतीजतन, घटना को प्रदर्शित करने के लिए इस्तेमाल किया जाने वाला एक सामान्य उपकरण केशिका ट्यूब है। जब एक कांच की नली के निचले सिरे को एक तरल जैसे पानी में रखा जाता है, तो एक अवतल मेनिस्कस (तरल) बनता है। आसंजन तरल पदार्थ और ठोस आंतरिक दीवार के बीच तरल स्तंभ को तब तक खींचता है जब तक कि इन अंतर-आणविक बलों को दूर करने के लिए गुरुत्वाकर्षण बलों के लिए तरल का पर्याप्त द्रव्यमान न हो। तरल स्तंभ के शीर्ष और ट्यूब के बीच की संपर्क लंबाई (किनारे के आसपास) ट्यूब की त्रिज्या के समानुपाती होती है, जबकि तरल स्तंभ का वजन ट्यूब के त्रिज्या के वर्ग के समानुपाती होता है। इसलिए, एक संकीर्ण ट्यूब एक व्यापक ट्यूब विल की तुलना में एक तरल स्तंभ खींचती है, यह देखते हुए कि आंतरिक पानी के अणु बाहरी लोगों के साथ पर्याप्त रूप से जुड़ते हैं।
उदाहरण
निर्मित वातावरण में, वाष्पीकरण सीमित केशिका पैठ ठोस और चिनाई में नम (संरचनात्मक) की घटना के लिए जिम्मेदार है, जबकि उद्योग और नैदानिक चिकित्सा में इस घटना का कागज-आधारित माइक्रोफ्लुइडिक्स के क्षेत्र में तेजी से दोहन किया जा रहा है।[22]
फिजियोलॉजी में, केशिका क्रिया आंख से लगातार उत्पादित आंसू द्रव के जल निकासी के लिए आवश्यक है। पलक के अंदरूनी कोने में छोटे व्यास की दो नलिकाएँ मौजूद होती हैं, जिन्हें नासोलैक्रिमल वाहिनी भी कहा जाता है; जब पलकें उलटी होती हैं तो अश्रु थैली के भीतर उनके खुलेपन को नंगी आंखों से देखा जा सकता है।
विकिंग एक मोमबत्ती की बत्ती के तरीके से एक सामग्री द्वारा तरल का अवशोषण है। कागज़ के तौलिये केशिका क्रिया के माध्यम से तरल को अवशोषित करते हैं, जिससे द्रव स्टैटिक्स को सतह से तौलिया में स्थानांतरित किया जा सकता है। स्पंज (उपकरण) के छोटे छिद्र छोटी केशिकाओं के रूप में कार्य करते हैं, जिससे यह बड़ी मात्रा में द्रव को अवशोषित कर लेता है। कहा जाता है कि कुछ कपड़ा कपड़े पसीने को त्वचा से दूर करने के लिए केशिका क्रिया का उपयोग करते हैं। मोमबत्ती और दीपक मोमबत्ती बत्ती के केशिका गुणों के बाद, इन्हें अक्सर स्तरित कपड़ों # विकिंग-सामग्री के रूप में जाना जाता है।
पतली परत क्रोमैटोग्राफी में केशिका क्रिया देखी जाती है, जिसमें एक विलायक केशिका क्रिया के माध्यम से एक प्लेट को ऊपर की ओर ले जाता है। इस मामले में छिद्र बहुत छोटे कणों के बीच अंतराल होते हैं।
कैपिलरी एक्शन पेन के अंदर जलाशय या कार्ट्रिज से फ़ाउंटेन पेन निब (कलम) की युक्तियों पर स्याही खींचता है।
पारा (तत्व) और कांच जैसे कुछ पदार्थों के जोड़े के साथ, तरल के भीतर अंतर-आणविक बल ठोस और तरल के बीच से अधिक होते हैं, इसलिए एक विक्ट: उत्तल मेनिस्कस रूपों और केशिका क्रिया रिवर्स में काम करती है।
जल विज्ञान में, केशिका क्रिया मिट्टी के कणों के लिए पानी के अणुओं के आकर्षण का वर्णन करती है। केशिका क्रिया भूजल को मिट्टी के गीले क्षेत्रों से शुष्क क्षेत्रों में ले जाने के लिए जिम्मेदार है। मृदा जल क्षमता में अंतर () मिट्टी में केशिका क्रिया को चलाएं।
केशिका क्रिया का एक व्यावहारिक अनुप्रयोग केशिका क्रिया साइफन है। एक खोखले ट्यूब (अधिकांश साइफन के रूप में) का उपयोग करने के बजाय, इस डिवाइस में एक रेशेदार सामग्री (कपास की रस्सी या स्ट्रिंग अच्छी तरह से काम करती है) से बने कॉर्ड की लंबाई होती है। कॉर्ड को पानी से संतृप्त करने के बाद, एक (भारित) छोर को पानी से भरे जलाशय में रखा जाता है, और दूसरे सिरे को एक रिसीविंग बर्तन में रखा जाता है। जलाशय प्राप्त पोत से अधिक होना चाहिए।[citation needed] एक संबंधित लेकिन सरलीकृत केशिका साइफन में केवल दो हुक-आकार की स्टेनलेस स्टील की छड़ें होती हैं, जिनकी सतह हाइड्रोफिलिक होती है, जिससे पानी उनके बीच संकीर्ण खांचे को गीला कर देता है। [23] केशिका क्रिया और गुरुत्वाकर्षण के कारण, जलाशय से पानी धीरे-धीरे प्राप्त करने वाले बर्तन में स्थानांतरित हो जाएगा। इस सरल उपकरण का उपयोग घर के पौधों को पानी देने के लिए किया जा सकता है जब कोई भी घर पर न हो। इस संपत्ति का उपयोग स्वचालित स्नेहक # विक फ़ीड स्नेहक में भी किया जाता है: असर (यांत्रिक) के लिए अग्रणी वितरण पाइपों में जलाशयों से तेल निकालने के लिए खराब होने वाली बत्तियों का उपयोग किया जाता है।[24]
पौधों और जानवरों में
केशिका क्रिया कई पौधों में देखी जाती है, और वाष्पोत्सर्जन में एक भूमिका निभाती है। वृक्षों में शाखाओं द्वारा पानी को ऊपर लाया जाता है; पत्तियों पर वाष्पीकरण से अवसाद पैदा होता है; शायद जड़ों में जोड़े गए आसमाटिक दबाव से; और संभवतः पौधे के अंदर अन्य स्थानों पर, विशेष रूप से जब हवा की जड़ों से नमी एकत्रित कर रहे हों।[25][26][27] विदेशी लीग जैसे कुछ छोटे जंतुओं में पानी ग्रहण करने की केशिका क्रिया का वर्णन किया गया है[28] और भयानक मोलोच[29]
मेनिस्कस की ऊंचाई
एक केशिका में तरल का केशिका उदय
एक तरल स्तंभ की ऊँचाई ज ज्यूरिन के नियम द्वारा दी गई है[30]
कहाँ तरल-वायु सतह तनाव (बल/इकाई लंबाई) है, θ संपर्क कोण है, ρ तरल (द्रव्यमान/आयतन) का घनत्व है, जी स्थानीय गुरुत्वाकर्षण त्वरण (लंबाई/समय का वर्ग) है[31]), और आर ट्यूब की त्रिज्या है।
चूँकि r हर में होता है, द्रव जितना पतला स्थान ले सकता है, वह उतना ही ऊपर की ओर जाता है। इसी तरह, हल्का तरल और कम गुरुत्वाकर्षण स्तंभ की ऊंचाई बढ़ाता है।
मानक प्रयोगशाला स्थितियों में हवा में पानी से भरे ग्लास ट्यूब के लिए, γ = 0.0728 N/m 20 बजे डिग्री सेल्सियस, ρ = 1000 kg/m3, और g = 9.81 m/s2. क्योंकि साफ कांच पर पानी गीला होने के कारण प्रभावी संतुलन संपर्क कोण लगभग शून्य होता है।[32] इन मानों के लिए, जल स्तंभ की ऊँचाई है
इस प्रकार ए के लिए 2 m (6.6 ft) ऊपर दी गई लैब स्थितियों में त्रिज्या ग्लास ट्यूब, पानी एक ध्यान देने योग्य नहीं होगा 0.007 mm (0.00028 in). हालाँकि, ए के लिए 2 cm (0.79 in) त्रिज्या ट्यूब, पानी ऊपर उठेगा 0.7 mm (0.028 in), और ए के लिए 0.2 mm (0.0079 in) त्रिज्या ट्यूब, पानी ऊपर उठेगा 70 mm (2.8 in).
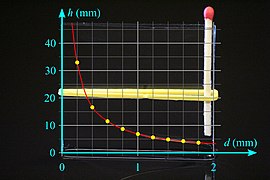
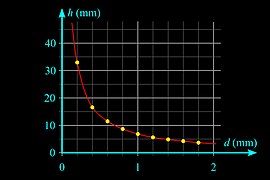
दो कांच की प्लेटों के बीच द्रव का केशिका उत्थान
परत की मोटाई (d) और ऊंचाई की ऊंचाई (h) का गुणनफल स्थिर (d·h = स्थिर) है, दो मात्राएं हैं Proportionality_(mathematics)#Inverse_proportionality. तलों के बीच द्रव की सतह अतिपरवलय है।
- Water between two glass plates
झरझरा मीडिया में तरल परिवहन
जब किसी शुष्क सरंध्र माध्यम को किसी द्रव के संपर्क में लाया जाता है, तो वह उस दर पर द्रव को अवशोषित करेगा जो समय के साथ घटती जाती है। वाष्पीकरण पर विचार करते समय, तरल प्रवेश तापमान, आर्द्रता और पारगम्यता के पैरामीटर पर निर्भर सीमा तक पहुंच जाएगा। इस प्रक्रिया को वाष्पीकरण सीमित केशिका प्रवेश के रूप में जाना जाता है [22]और कागज में द्रव अवशोषण और कंक्रीट या चिनाई की दीवारों में बढ़ती नमी सहित सामान्य स्थितियों में व्यापक रूप से देखा जाता है। क्रॉस-सेक्शनल एरिया ए के साथ सामग्री के एक बार के आकार वाले खंड के लिए जो एक छोर पर गीला होता है, एक समय टी के बाद अवशोषित तरल की संचयी मात्रा वी है
जहां S, m·s की इकाइयों में, माध्यम की लघुता है−1/2 या मिमी·मिनट−1/2. यह समय निर्भरता संबंध केशिकाओं और झरझरा मीडिया में वाशिंग के लिए वाशबर्न के समीकरण के समान है।[33] मात्रा
लंबाई के आयाम के साथ संचयी तरल सेवन कहा जाता है। बार की गीली लंबाई, यानी बार के गीले सिरे और तथाकथित गीले मोर्चे के बीच की दूरी, आवाजों द्वारा कब्जा कर ली गई मात्रा के अंश एफ पर निर्भर है। यह संख्या f माध्यम की सरंध्रता है; गीली लंबाई तब है
कुछ लेखक मात्रा S/f का उपयोग सोरप्टिविटी के रूप में करते हैं।[34] उपरोक्त विवरण उस मामले के लिए है जहां गुरुत्वाकर्षण और वाष्पीकरण कोई भूमिका नहीं निभाते हैं।
सोरप्टिविटी निर्माण सामग्री की एक प्रासंगिक संपत्ति है, क्योंकि यह नम (संरचनात्मक) # बढ़ती नमी की मात्रा को प्रभावित करती है। निर्माण सामग्री की सार्वभौमता के लिए कुछ मान नीचे दी गई तालिका में हैं।
| सामग्री | सोरप्टिविटी (मिमी·मिनट−1/2) |
|---|---|
| वातित कंक्रीट | 0.50 |
| जिप्सम प्लास्टर | 3.50 |
| मिट्टी की ईंट | 1.16 |
| मोर्टार | 0.70 |
| कंक्रीट की ईंट | 0.20 |
यह भी देखें
- बॉन्ड नंबर
- बाउंड वॉटर
- केशिका फ्रिंज
- केशिका दबाव – Pressure between two fluids from forces between the fluids and tube walls
- केशिका तरंग – Wave on the surface of a fluid, dominated by surface tension
- केशिका पुल
- डैम्प प्रूफिंग
- डार्सी का नियम
- फ्रॉस्ट फ्लावर
- फ्रॉस्ट हीविंग
- हिन्दू दूध चमत्कार
- क्रोघ मॉडल
- पोरोसिमेट्री – Measurement and characterization of the porosity of a material
- नीडल आइस
- सतह तनाव – Tendency of a liquid surface to shrink to reduce surface area
- वॉशबर्न का समीकरण
- यंग-लाप्लास समीकरण – Describing pressure difference over an interface in fluid mechanics
संदर्भ
- ↑ See:
- Manuscripts of Léonardo de Vinci (Paris), vol. N, folios 11, 67, and 74.
- Guillaume Libri, Histoire des sciences mathématiques en Italie, depuis la Renaissance des lettres jusqu'a la fin du dix-septième siecle [History of the mathematical sciences in Italy, from the Renaissance until the end of the seventeenth century] (Paris, France: Jules Renouard et cie., 1840), vol. 3, page 54 Archived 2016-12-24 at the Wayback Machine. From page 54: "Enfin, deux observations capitales, celle de l'action capillaire (7) et celle de la diffraction (8), dont jusqu'à présent on avait méconnu le véritable auteur, sont dues également à ce brillant génie." (Finally, two major observations, that of capillary action (7) and that of diffraction (8), the true author of which until now had not been recognized, are also due to this brilliant genius.)
- C. Wolf (1857) "Vom Einfluss der Temperatur auf die Erscheinungen in Haarröhrchen" (On the influence of temperature on phenomena in capillary tubes) Annalen der Physik und Chemie, 101 (177) : 550–576 ; see footnote on page 551 Archived 2014-06-29 at the Wayback Machine by editor Johann C. Poggendorff. From page 551: " ... nach Libri (Hist. des sciences math. en Italie, T. III, p. 54) in den zu Paris aufbewahrten Handschriften des grossen Künstlers Leonardo da Vinci (gestorben 1519) schon Beobachtungen dieser Art vorfinden; ... " ( ... according to Libri (History of the mathematical sciences in Italy, vol. 3, p. 54) observations of this kind [i.e., of capillary action] are already to be found in the manuscripts of the great artist Leonardo da Vinci (died 1519), which are preserved in Paris; ... )
- ↑ More detailed histories of research on capillary action can be found in:
- David Brewster, ed., Edinburgh Encyclopaedia (Philadelphia, Pennsylvania: Joseph and Edward Parker, 1832), volume 10, pp. 805–823 Archived 2016-12-24 at the Wayback Machine.
- Maxwell, James Clerk; Strutt, John William (1911). . In Chisholm, Hugh (ed.). Encyclopædia Britannica (in English). Vol. 5 (11th ed.). Cambridge University Press. pp. 256–275.
- John Uri Lloyd (1902) "References to capillarity to the end of the year 1900," Archived 2014-12-14 at the Wayback Machine Bulletin of the Lloyd Library and Museum of Botany, Pharmacy and Materia Medica, 1 (4) : 99–204.
- ↑ In his book of 1759, Giovani Batista Clemente Nelli (1725–1793) stated (p. 87) that he had "un libro di problem vari geometrici ec. e di speculazioni, ed esperienze fisiche ec." (a book of various geometric problems and of speculation and physical experiments, etc.) by Aggiunti. On pages 91–92, he quotes from this book: Aggiunti attributed capillary action to "moto occulto" (hidden/secret motion). He proposed that mosquitoes, butterflies, and bees feed via capillary action, and that sap ascends in plants via capillary action. See: Giovambatista Clemente Nelli, Saggio di Storia Letteraria Fiorentina del Secolo XVII ... [Essay on Florence's literary history in the 17th century, ... ] (Lucca, (Italy): Vincenzo Giuntini, 1759), pp. 91–92. Archived 2014-07-27 at the Wayback Machine
- ↑ Robert Boyle, New Experiments Physico-Mechanical touching the Spring of the Air, ... (Oxford, England: H. Hall, 1660), pp. 265–270. Available on-line at: Echo (Max Planck Institute for the History of Science; Berlin, Germany) Archived 2014-03-05 at the Wayback Machine.
- ↑ See, for example:
- Robert Hooke (1661) An attempt for the explication of the Phenomena observable in an experiment published by the Right Hon. Robert Boyle, in the 35th experiment of his Epistolical Discourse touching the Air, in confirmation of a former conjecture made by R. Hooke. [pamphlet].
- Hooke's An attempt for the explication ... was reprinted (with some changes) in: Robert Hooke, Micrographia ... (London, England: James Allestry, 1667), pp. 12–22, "Observ. IV. Of small Glass Canes." Archived 2016-12-24 at the Wayback Machine
- Geminiano Montanari, Pensieri fisico-matematici sopra alcune esperienze fatte in Bologna ... Archived 2016-12-29 at the Wayback Machine [Physical-mathematical ideas about some experiments done in Bologna ... ] (Bologna, (Italy): 1667).
- George Sinclair, Ars Nova et Magna Gravitatis et Levitatis Archived 2017-11-03 at the Wayback Machine [New and great powers of weight and levity] (Rotterdam, Netherlands: Arnold Leers, Jr., 1669).
- Johannes Christoph Sturm, Collegium Experimentale sive Curiosum [Catalog of experiments, or Curiosity] (Nüremberg (Norimbergæ), (Germany): Wolfgang Moritz Endter & the heirs of Johann Andreas Endter, 1676). See: "Tentamen VIII. Canaliculorum angustiorum recens-notata Phænomena, ... " Archived 2014-06-29 at the Wayback Machine (Essay 8. Recently noted phenomena of narrow capillaries, ... ), pp. 44–48.
- ↑ See:
- Honorato Fabri, Dialogi physici ... ((Lyon (Lugdunum), France: 1665), pages 157 ff Archived 2016-12-24 at the Wayback Machine "Dialogus Quartus. In quo, de libratis suspensisque liquoribus & Mercurio disputatur. (Dialogue four. In which the balance and suspension of liquids and mercury is discussed).
- Honorato Fabri, Dialogi physici ... ((Lyon (Lugdunum), France: Antoine Molin, 1669), pages 267 ff Archived 2017-04-07 at the Wayback Machine "Alithophilus, Dialogus quartus, in quo nonnulla discutiuntur à D. Montanario opposita circa elevationem Humoris in canaliculis, etc." (Alithophilus, Fourth dialogue, in which Dr. Montanari's opposition regarding the elevation of liquids in capillaries is utterly refuted).
- ↑ Jacob Bernoulli, Dissertatio de Gravitate Ætheris Archived 2017-04-07 at the Wayback Machine (Amsterdam, Netherlands: Hendrik Wetsten, 1683).
- ↑ Isaac Vossius, De Nili et Aliorum Fluminum Origine [On the sources of the Nile and other rivers] (Hague (Hagæ Comitis), Netherlands: Adrian Vlacq, 1666), pages 3–7 Archived 2017-04-07 at the Wayback Machine (chapter 2).
- ↑ Borelli, Giovanni Alfonso De motionibus naturalibus a gravitate pendentibus (Lyon, France: 1670), page 385, Cap. 8 Prop. CLXXXV (Chapter 8, Proposition 185.). Available on-line at: Echo (Max Planck Institute for the History of Science; Berlin, Germany) Archived 2016-12-23 at the Wayback Machine.
- ↑ Carré (1705) "Experiences sur les tuyaux Capillaires" Archived 2017-04-07 at the Wayback Machine (Experiments on capillary tubes), Mémoires de l'Académie Royale des Sciences, pp. 241–254.
- ↑ See:
- Francis Hauksbee (1708) "Several Experiments Touching the Seeming Spontaneous Ascent of Water," Archived 2014-06-29 at the Wayback Machine Philosophical Transactions of the Royal Society of London, 26 : 258–266.
- Francis Hauksbee, Physico-mechanical Experiments on Various Subjects ... (London, England: (Self-published), 1709), pages 139–169.
- Francis Hauksbee (1711) "An account of an experiment touching the direction of a drop of oil of oranges, between two glass planes, towards any side of them that is nearest press'd together," Philosophical Transactions of the Royal Society of London, 27 : 374–375.
- Francis Hauksbee (1712) "An account of an experiment touching the ascent of water between two glass planes, in an hyperbolick figure," Philosophical Transactions of the Royal Society of London, 27 : 539–540.
- ↑ See:
- Josia Weitbrecht (1736) "Tentamen theoriae qua ascensus aquae in tubis capillaribus explicatur" Archived 2014-06-29 at the Wayback Machine (Theoretical essay in which the ascent of water in capillary tubes is explained), Commentarii academiae scientiarum imperialis Petropolitanae (Memoirs of the imperial academy of sciences in St. Petersburg), 8 : 261–309.
- Josias Weitbrecht (1737) "Explicatio difficilium experimentorum circa ascensum aquae in tubis capillaribus" Archived 2014-11-05 at the Wayback Machine (Explanation of difficult experiments concerning the ascent of water in capillary tubes), Commentarii academiae scientiarum imperialis Petropolitanae (Memoirs of the imperial academy of sciences in St. Petersburg), 9 : 275–309.
- ↑ For example:
- In 1740, Christlieb Ehregott Gellert (1713–1795) observed that like mercury, molten lead would not adhere to glass and therefore the level of molten lead was depressed in a capillary tube. See: C. E. Gellert (1740) "De phenomenis plumbi fusi in tubis capillaribus" (On phenomena of molten lead in capillary tubes) Commentarii academiae scientiarum imperialis Petropolitanae (Memoirs of the imperial academy of sciences in St. Petersburg), 12 : 243–251. Available on-line at: Archive.org Archived 2016-03-17 at the Wayback Machine.
- Gaspard Monge (1746–1818) investigated the force between panes of glass that were separated by a film of liquid. See: Gaspard Monge (1787) "Mémoire sur quelques effets d'attraction ou de répulsion apparente entre les molécules de matière" Archived 2016-03-16 at the Wayback Machine (Memoir on some effects of the apparent attraction or repulsion between molecules of matter), Histoire de l'Académie royale des sciences, avec les Mémoires de l'Académie Royale des Sciences de Paris (History of the Royal Academy of Sciences, with the Memoirs of the Royal Academy of Sciences of Paris), pp. 506–529. Monge proposed that particles of a liquid exert, on each other, a short-range force of attraction, and that this force produces the surface tension of the liquid. From p. 529: "En supposant ainsi que l'adhérence des molécules d'un liquide n'ait d'effet sensible qu'à la surface même, & dans le sens de la surface, il seroit facile de déterminer la courbure des surfaces des liquides dans le voisinage des parois qui les conteinnent ; ces surfaces seroient des lintéaires dont la tension, constante dans tous les sens, seroit par-tout égale à l'adhérence de deux molécules ; & les phénomènes des tubes capillaires n'auroient plus rein qui ne pût être déterminé par l'analyse." (Thus by assuming that the adhesion of a liquid's molecules has a significant effect only at the surface itself, and in the direction of the surface, it would be easy to determine the curvature of the surfaces of liquids in the vicinity of the walls that contain them ; these surfaces would be menisci whose tension, [being] constant in every direction, would be everywhere equal to the adhesion of two molecules ; and the phenomena of capillary tubes would have nothing that could not be determined by analysis [i.e., calculus].)
- ↑ In the 18th century, some investigators did attempt a quantitative treatment of capillary action. See, for example, Alexis Claude Clairaut (1713–1765) Theorie de la Figure de la Terre tirée des Principes de l'Hydrostatique [Theory of the figure of the Earth based on principles of hydrostatics] (Paris, France: David fils, 1743), Chapitre X. De l'élevation ou de l'abaissement des Liqueurs dans les Tuyaux capillaires (Chapter 10. On the elevation or depression of liquids in capillary tubes), pages 105–128. Archived 2016-04-09 at the Wayback Machine
- ↑ Thomas Young (January 1, 1805) "An essay on the cohesion of fluids," Archived 2014-06-30 at the Wayback Machine Philosophical Transactions of the Royal Society of London, 95 : 65–87.
- ↑ Pierre Simon marquis de Laplace, Traité de Mécanique Céleste, volume 4, (Paris, France: Courcier, 1805), Supplément au dixième livre du Traité de Mécanique Céleste, pages 1–79 Archived 2016-12-24 at the Wayback Machine.
- ↑ Carl Friedrich Gauss, Principia generalia Theoriae Figurae Fluidorum in statu Aequilibrii [General principles of the theory of fluid shapes in a state of equilibrium] (Göttingen, (Germany): Dieterichs, 1830). Available on-line at: Hathi Trust.
- ↑ William Thomson (1871) "On the equilibrium of vapour at a curved surface of liquid," Archived 2014-10-26 at the Wayback Machine Philosophical Magazine, series 4, 42 (282) : 448–452.
- ↑ Franz Neumann with A. Wangerin, ed., Vorlesungen über die Theorie der Capillarität [Lectures on the theory of capillarity] (Leipzig, Germany: B. G. Teubner, 1894).
- ↑ Albert Einstein (1901) "Folgerungen aus den Capillaritätserscheinungen" Archived 2017-10-25 at the Wayback Machine (Conclusions [drawn] from capillary phenomena), Annalen der Physik, 309 (3) : 513–523.
- ↑ Hans-Josef Kuepper. "अल्बर्ट आइंस्टीन के वैज्ञानिक प्रकाशनों की सूची". Einstein-website.de. Archived from the original on 2013-05-08. Retrieved 2013-06-18.
- ↑ 22.0 22.1 22.2 Liu, Mingchao; Wu, Jian; Gan, Yixiang; Hanaor, Dorian A.H.; Chen, C.Q. (2018). "Tuning capillary penetration in porous media: Combining geometrical and evaporation effects" (PDF). International Journal of Heat and Mass Transfer. 123: 239–250. doi:10.1016/j.ijheatmasstransfer.2018.02.101. S2CID 51914846.
- ↑ Wang, K.; et al. (2022). "केशिका साइफन खोलें". Journal of Fluid Mechanics. Cambridge University Press. 932. Bibcode:2022JFM...932R...1W. doi:10.1017/jfm.2021.1056. S2CID 244957617.
- ↑ Ahrons, Ernest Leopold (1922). लोकोमोटिव का स्नेहन. London: Locomotive Publishing Company. p. 26. OCLC 795781750.
- ↑ Tree physics Archived 2013-11-28 at the Wayback Machine at "Neat, Plausible And" scientific discussion website.
- ↑ Water in Redwood and other trees, mostly by evaporation Archived 2012-01-29 at the Wayback Machine article at wonderquest website.
- ↑ Poudel, Sajag; Zou, An; Maroo, Shalabh C. (2022-06-15). "नकली पेड़ में असम्बद्ध दाब प्रेरित जल वाष्पोत्सर्जन". Journal of Colloid and Interface Science (in English). 616: 895–902. doi:10.1016/j.jcis.2022.02.108. ISSN 0021-9797. PMID 35259719. S2CID 244478643.
- ↑ Ishii D, Horiguchi H, Hirai Y, Yabu H, Matsuo Y, Ijiro K, Tsujii K, Shimozawa T, Hariyama T, Shimomura M (October 23, 2013). "जैविक सतहों पर प्रत्यक्ष सतह संशोधनों द्वारा विश्लेषित खुली केशिकाओं के माध्यम से जल परिवहन तंत्र". Scientific Reports. 3: 3024. Bibcode:2013NatSR...3E3024I. doi:10.1038/srep03024. PMC 3805968. PMID 24149467.
- ↑ Bentley PJ, Blumer WF (1962). "छिपकली द्वारा पानी का ग्रहण, मोलोच हॉरिडस". Nature. 194 (4829): 699–670 (1962). Bibcode:1962Natur.194..699B. doi:10.1038/194699a0. PMID 13867381. S2CID 4289732.
- ↑ G.K. Batchelor, 'An Introduction To Fluid Dynamics', Cambridge University Press (1967) ISBN 0-521-66396-2,
- ↑ Hsai-Yang Fang, john L. Daniels, Introductory Geotechnical Engineering: An Environmental Perspective
- ↑ "Capillary Tubes - an overview | ScienceDirect Topics". www.sciencedirect.com. Retrieved 2021-10-29.
- ↑ Liu, M.; et al. (2016). "झरझरा मीडिया में वाष्पीकरण सीमित रेडियल केशिका पैठ" (PDF). Langmuir. 32 (38): 9899–9904. doi:10.1021/acs.langmuir.6b02404. PMID 27583455.
- ↑ C. Hall, W.D. Hoff, Water transport in brick, stone, and concrete. (2002) page 131 on Google books Archived 2014-02-20 at the Wayback Machine
- ↑ हॉल और हॉफ, पृष्ठ 122
अग्रिम पठन
- de Gennes, Pierre-Gilles; Brochard-Wyart, Françoise; Quéré, David (2004). Capillarity and Wetting Phenomena. Springer New York. doi:10.1007/978-0-387-21656-0. ISBN 978-1-4419-1833-8.