अनुकूलता (यांत्रिकी)

सातत्य यांत्रिकी में, निकाय में अनुकूल परिमित विरूपण टेंसर (या तनाव टेंसर ) क्षेत्र वह अद्वितीय टेंसर क्षेत्र होता है जो तब प्राप्त होता है जब निकाय निरंतर कार्य, एकल-मूल्यवान, विस्थापन क्षेत्र (यांत्रिकी) के अधीन होता है। अनुकूलता उन परिस्थितियों का अध्ययन है जिनके अनुसार ऐसे विस्थापन क्षेत्र की गारंटी दी जा सकती है। इस प्रकार अनुकूलता स्थितियाँ अभिन्नता स्थितियों के विशेष स्थिति हैं और इन्हें पहली बार 1864 में बैरे डी सेंट-वेनेंट द्वारा रैखिक लोच के लिए प्राप्त किया गया था और 1886 में यूजेनियो बेल्ट्रामी द्वारा कठोरता से सिद्ध किया गया था।

ठोस पिंड के सातत्य विवरण में हम कल्पना करते हैं कि यह पिंड अनंत छोटे आयतनों या भौतिक बिंदुओं के समूह से बना है। प्रत्येक वॉल्यूम को बिना किसी अंतराल या ओवरलैप के अपने निकट से जुड़ा हुआ माना जाता है। इस प्रकार यह सुनिश्चित करने के लिए कुछ गणितीय नियमो को पूरा करना होगा कि सातत्य निकाय के विकृत होने पर अंतराल/ओवरलैप विकसित नही होते है। ऐसा निकाय जो बिना किसी अंतराल/ओवरलैप के विकृत हो जाता है, उसे अनुकूल निकाय कहा जाता है। इस प्रकार अनुकूलता स्थितियाँ गणितीय स्थितियाँ हैं जो यह निर्धारित करती हैं कि कोई विशेष विकृति किसी निकाय को अनुकूल स्थिति में छोड़ देगी या नहीं छोडती है।

अपरिमित तनाव सिद्धांत के संदर्भ में, ये स्थितियाँ यह बताने के समान हैं कि किसी पिंड में विस्थापन अपरिमित तनाव सिद्धांतों को एकीकृत करके प्राप्त किया जा सकता है। ऐसा एकीकरण संभव है यदि सेंट-वेनैंट का टेंसर (या असंगति टेंसर) ${\boldsymbol {R}}({\boldsymbol {\varepsilon }})$ सरलता से जुड़े हुए निकाय में लुप्त हो जाता है जहाँ ${\boldsymbol {\varepsilon }}$ इनफिनिटसिमल तनाव सिद्धांत है और

${\boldsymbol {R}}:={\boldsymbol {\nabla }}\times ({\boldsymbol {\nabla }}\times {\boldsymbol {\varepsilon }})^{T}={\boldsymbol {0}}~.$

परिमित विकृतियों सिद्धांत के लिए अनुकूलता स्थितियाँ रूप लेती हैं

${\boldsymbol {R}}:={\boldsymbol {\nabla }}\times {\boldsymbol {F}}={\boldsymbol {0}}$

जहाँ ${\boldsymbol {F}}$ विरूपण प्रवणता है.

अत्यंत सूक्ष्म तनाव के लिए अनुकूलता की स्थितियाँ

रैखिक लोच में अनुकूलता स्थितियाँ यह देखकर प्राप्त की जाती हैं कि छह तनाव-विस्थापन संबंध हैं जो केवल तीन अज्ञात विस्थापनों के कार्य हैं। इससे पता चलता है कि तीन विस्थापनों को सूचना की हानि के बिना समीकरणों की प्रणाली से हटाया जा सकता है। इस प्रकार केवल तनाव के संदर्भ में परिणामी अभिव्यक्तियाँ तनाव क्षेत्र के संभावित रूपों पर बाधाएं प्रदान करती हैं।

2-आयाम

द्वि-आयामी, समतल तनाव समस्याओं के लिए तनाव-विस्थापन संबंध हैं

$\varepsilon _{11}={\cfrac {\partial u_{1}}{\partial x_{1}}}~;~~\varepsilon _{12}={\cfrac {1}{2}}\left[{\cfrac {\partial u_{1}}{\partial x_{2}}}+{\cfrac {\partial u_{2}}{\partial x_{1}}}\right]~;~~\varepsilon _{22}={\cfrac {\partial u_{2}}{\partial x_{2}}}$

विस्थापन $u_{1}$ और $u_{2}$ को दूर करने के लिए इन संबंधों का बार-बार विभेदन होता है, इस प्रकार हमें तनाव के लिए द्वि-आयामी अनुकूलता स्थिति प्रदान करता है

${\cfrac {\partial ^{2}\varepsilon _{11}}{\partial x_{2}^{2}}}-2{\cfrac {\partial ^{2}\varepsilon _{12}}{\partial x_{1}\partial x_{2}}}+{\cfrac {\partial ^{2}\varepsilon _{22}}{\partial x_{1}^{2}}}=0$

एकमात्र विस्थापन क्षेत्र जिसे अनुकूल समतल तनाव क्षेत्र द्वारा अनुमति दी जाती है, वह समतल विस्थापन क्षेत्र है, अर्थात, $\mathbf {u} =\mathbf {u} (x_{1},x_{2})$.

3-आयाम

तीन आयामों में, दो आयामों के लिए देखे गए स्वरूप के दो और समीकरणों के अतिरिक्त स्वरूप के तीन और समीकरण हैं

${\cfrac {\partial ^{2}\varepsilon _{33}}{\partial x_{1}\partial x_{2}}}={\cfrac {\partial }{\partial x_{3}}}\left[{\cfrac {\partial \varepsilon _{23}}{\partial x_{1}}}+{\cfrac {\partial \varepsilon _{31}}{\partial x_{2}}}-{\cfrac {\partial \varepsilon _{12}}{\partial x_{3}}}\right]$

इसलिए 3⁴=81 आंशिक अंतर समीकरण हैं, चूंकि समरूपता स्थितियों के कारण यह संख्या छह भिन्न-भिन्न अनुकूलता स्थितियों तक कम हो जाती है। इस प्रकार हम इन नियमो को सूचकांक नोटेशन में इस प्रकार लिख सकते हैं

$e_{ikr}~e_{jls}~\varepsilon _{ij,kl}=0$

जहाँ $e_{ijk}$ क्रमपरिवर्तन प्रतीक है. प्रत्यक्ष टेंसर नोटेशन में

${\boldsymbol {\nabla }}\times ({\boldsymbol {\nabla }}\times {\boldsymbol {\varepsilon }})^{T}={\boldsymbol {0}}$

जहां कर्ल ऑपरेटर को ऑर्थोनॉर्मल समन्वय प्रणाली ${\boldsymbol {\nabla }}\times {\boldsymbol {\varepsilon }}=e_{ijk}\varepsilon _{rj,i}\mathbf {e} _{k}\otimes \mathbf {e} _{r}$ के रूप में व्यक्त किया जा सकता है .

दूसरे क्रम का टेंसर

${\boldsymbol {R}}:={\boldsymbol {\nabla }}\times ({\boldsymbol {\nabla }}\times {\boldsymbol {\varepsilon }})^{T}~;~~R_{rs}:=e_{ikr}~e_{jls}~\varepsilon _{ij,kl}$

असंगति टेंसर के रूप में जाना जाता है, और यह सेंट-वेनैंट की अनुकूलता स्थिति या क्रम 2 टेंसर क्षेत्र्स या सेंट-वेनैंट अनुकूलता टेंसर के समान है

परिमित तनाव के लिए अनुकूलता की स्थिति

उन ठोस पदार्थों के लिए जिनमें विकृतियों का छोटा होना आवश्यक नहीं है, अनुकूलता की स्थितियाँ रूप ले लेती हैं

${\boldsymbol {\nabla }}\times {\boldsymbol {F}}={\boldsymbol {0}}$

जहाँ ${\boldsymbol {F}}$ विरूपण प्रवणता है. इस प्रकार कार्टेशियन समन्वय प्रणाली के संबंध में अवयवो के संदर्भ में हम इन अनुकूलता संबंधों को इस प्रकार लिख सकते हैं

$e_{ABC}~{\cfrac {\partial F_{iB}}{\partial X_{A}}}=0$

यदि विरूपण निरंतर होना है और मानचित्रण $\mathbf {x} ={\boldsymbol {\chi }}(\mathbf {X} ,t)$ से प्राप्त होना है तो यह नियम आवश्यक है (परिमित तनाव सिद्धांत देखें)। यही स्थिति सरल रूप से जुड़े निकाय में अनुकूलता सुनिश्चित करने के लिए भी पर्याप्त है।

सही कॉची-ग्रीन विरूपण टेंसर के लिए अनुकूलता स्थिति

परिमित तनाव सिद्धांत के लिए अनुकूलता की स्थिति या सही कॉची-ग्रीन विरूपण टेंसर को इस प्रकार व्यक्त किया जा सकता है

$R_{\alpha \beta \rho }^{\gamma }:={\frac {\partial }{\partial X^{\rho }}}[\Gamma _{\alpha \beta }^{\gamma }]-{\frac {\partial }{\partial X^{\beta }}}[\Gamma _{\alpha \rho }^{\gamma }]+\Gamma _{\mu \rho }^{\gamma }~\Gamma _{\alpha \beta }^{\mu }-\Gamma _{\mu \beta }^{\gamma }~\Gamma _{\alpha \rho }^{\mu }=0$

जहाँ $\Gamma _{ij}^{k}$ वक्ररेखीय निर्देशांक है. इस प्रकार मात्रा $R_{ijk}^{m}$ रीमैन-क्रिस्टोफ़ेल वक्रता टेंसर के मिश्रित अवयवो का प्रतिनिधित्व करता है।

सामान्य अनुकूलता समस्या

सातत्य यांत्रिकी में अनुकूलता की समस्या में सरल रूप से जुड़े निकायों पर स्वीकार्य एकल-मूल्य वाले निरंतर क्षेत्रों का निर्धारण सम्मिलित है। अधिक स्पष्ट रूप से, समस्या को निम्नलिखित विधि से बताया जा सकता है।

चित्र 1. सातत्य पिंड की गति।

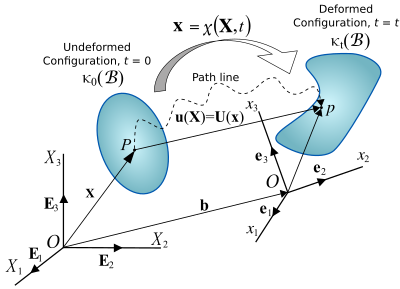
चित्र 1 में दिखाए गए किसी पिंड के विरूपण पर विचार करें। यदि हम सभी सदिश को संदर्भ समन्वय प्रणाली के संदर्भ में व्यक्त करते हैं इस प्रकार $\{(\mathbf {E} _{1},\mathbf {E} _{2},\mathbf {E} _{3}),O\}$, निकाय में बिंदु का विस्थापन द्वारा दिया जाता है

$\mathbf {u} =\mathbf {x} -\mathbf {X} ~;~~u_{i}=x_{i}-X_{i}$

भी

${\boldsymbol {\nabla }}\mathbf {u} ={\frac {\partial \mathbf {u} }{\partial \mathbf {X} }}~;~~{\boldsymbol {\nabla }}\mathbf {x} ={\frac {\partial \mathbf {x} }{\partial \mathbf {X} }}$

किसी निकाय पर दिए गए दूसरे क्रम के टेंसर क्षेत्र ${\boldsymbol {A}}(\mathbf {X} )$ पर कौन सी स्थितियाँ आवश्यक और पर्याप्त हैं जिससे एक अद्वितीय सदिश क्षेत्र $\mathbf {v} (\mathbf {X} )$ उपस्थितहो जो संतुष्ट हो

${\boldsymbol {\nabla }}\mathbf {v} ={\boldsymbol {A}}\quad \equiv \quad v_{i,j}=A_{ij}$

आवश्यक नियम

आवश्यक नियमो के लिए हम मानते हैं कि क्षेत्र $\mathbf {v}$ उपस्थितहै और $v_{i,j}=A_{ij}$ को संतुष्ट करता है, तब

$v_{i,jk}=A_{ij,k}~;~~v_{i,kj}=A_{ik,j}$

चूँकि विभेदन का क्रम परिवर्तन से हमारे प्राप्त परिणाम पर कोई प्रभाव नहीं पड़ता है

$v_{i,jk}=v_{i,kj}$

इस तरह

$A_{ij,k}=A_{ik,j}$

टेंसर व्युत्पन्न (सातत्य यांत्रिकी) के लिए प्रसिद्ध पहचान से हमें आवश्यक नियम मिलती है

${\boldsymbol {\nabla }}\times {\boldsymbol {A}}={\boldsymbol {0}}$

पर्याप्त स्थितियाँ

चित्र 2. अनुकूलता के लिए पर्याप्तता नियमो को सिद्ध करने में उपयोग किए जाने वाले एकीकरण पथ।

यह सिद्ध करने के लिए कि यह स्थिति अनुकूल दूसरे क्रम के टेंसर क्षेत्र के अस्तित्व की गारंटी देने के लिए पर्याप्त है, हम इस धारणा से नियम करते हैं कि क्षेत्र ${\boldsymbol {A}}$ ऐसा उपस्थित है

${\boldsymbol {\nabla }}\times {\boldsymbol {A}}={\boldsymbol {0}}$

हम सदिश क्षेत्र खोजने के लिए इस क्षेत्र को एकीकृत करेंगे $\mathbf {v}$ बिंदुओं के मध्य रेखा के साथ $A$ और $B$ (चित्र 2 देखें), अर्थात,

$\mathbf {v} (\mathbf {X} _{B})-\mathbf {v} (\mathbf {X} _{A})=\int _{\mathbf {X} _{A}}^{\mathbf {X} _{B}}{\boldsymbol {\nabla }}\mathbf {v} \cdot ~d\mathbf {X} =\int _{\mathbf {X} _{A}}^{\mathbf {X} _{B}}{\boldsymbol {A}}(\mathbf {X} )\cdot d\mathbf {X}$

यदि सदिश क्षेत्र $\mathbf {v}$ एकल-मूल्यवान होना है तो अभिन्न का मूल्य आगे बढ़ने के लिए अपनाए गए पथ से स्वतंत्र होना चाहिए इस प्रकार $A$ को $B$.

स्टोक्स के प्रमेय से, संवृत पथ के साथ दूसरे क्रम के टेंसर का अभिन्न अंग दिया जाता है

$\oint _{\partial \Omega }{\boldsymbol {A}}\cdot d\mathbf {s} =\int _{\Omega }\mathbf {n} \cdot ({\boldsymbol {\nabla }}\times {\boldsymbol {A}})~da$

इस धारणा का उपयोग करते हुए कि कर्ल ${\boldsymbol {A}}$ शून्य है, हमें मिलता है

$\oint _{\partial \Omega }{\boldsymbol {A}}\cdot d\mathbf {s} =0\quad \implies \quad \int _{AB}{\boldsymbol {A}}\cdot d\mathbf {X} +\int _{BA}{\boldsymbol {A}}\cdot d\mathbf {X} =0$

इसलिए इंटीग्रल पथ स्वतंत्र है और अद्वितीयता सुनिश्चित करने के लिए अनुकूलता स्थिति $\mathbf {v}$ क्षेत्र पर्याप्त है, परंतु निकाय केवल जुड़ा हुआ होता है।

विरूपण प्रवणता की अनुकूलता

विरूपण प्रवणता के लिए अनुकूलता की स्थिति उपरोक्त प्रमाण से सीधे अवलोकन करके प्राप्त की जाती है

${\boldsymbol {F}}={\cfrac {\partial \mathbf {x} }{\partial \mathbf {X} }}={\boldsymbol {\nabla }}\mathbf {x}$

फिर अनुकूल के अस्तित्व के लिए आवश्यक और पर्याप्त नियम ${\boldsymbol {F}}$ साधारण रूप से जुड़े हुए निकाय पर क्षेत्र हैं

${\boldsymbol {\nabla }}\times {\boldsymbol {F}}={\boldsymbol {0}}$

अतिसूक्ष्म तनाव की अनुकूलता

छोटे तनाव के लिए अनुकूलता समस्या को निम्नानुसार बताया जा सकता है।

एक सममित दूसरे क्रम के टेंसर क्षेत्र ${\boldsymbol {\epsilon }}$ को देखते हुए एक सदिश क्षेत्र $\mathbf {u}$ का निर्माण करना कब संभव है जैसे कि

${\boldsymbol {\epsilon }}={\frac {1}{2}}[{\boldsymbol {\nabla }}\mathbf {u} +({\boldsymbol {\nabla }}\mathbf {u} )^{T}]$

आवश्यक नियम

मान लीजिए कि $\mathbf {u}$ का अस्तित्व इस प्रकार है कि ${\boldsymbol {\epsilon }}$ के लिए अभिव्यक्ति धारण है। अब

${\boldsymbol {\nabla }}\mathbf {u} ={\boldsymbol {\epsilon }}+{\boldsymbol {\omega }}$

जहाँ

${\boldsymbol {\omega }}:={\frac {1}{2}}[{\boldsymbol {\nabla }}\mathbf {u} -({\boldsymbol {\nabla }}\mathbf {u} )^{T}]$

इसलिए, सूचकांक संकेतन में,

${\boldsymbol {\nabla }}{\boldsymbol {\omega }}\equiv \omega _{ij,k}={\frac {1}{2}}(u_{i,jk}-u_{j,ik})={\frac {1}{2}}(u_{i,jk}+u_{k,ji}-u_{j,ik}-u_{k,ji})=\varepsilon _{ik,j}-\varepsilon _{jk,i}$

यदि ${\boldsymbol {\omega }}$ निरंतर अवकलनीय है तो हमारे निकट $\omega _{ij,kl}=\omega _{ij,lk}$ इसलिए है

$\varepsilon _{ik,jl}-\varepsilon _{jk,il}-\varepsilon _{il,jk}+\varepsilon _{jl,ik}=0$

प्रत्यक्ष टेंसर नोटेशन में

${\boldsymbol {\nabla }}\times ({\boldsymbol {\nabla }}\times {\boldsymbol {\epsilon }})^{T}={\boldsymbol {0}}$

उपरोक्त आवश्यक नियम हैं. यदि $\mathbf {w}$ तो यह अनन्तसूक्ष्म तनाव ${\boldsymbol {\nabla }}\times {\boldsymbol {\epsilon }}={\boldsymbol {\nabla }}\mathbf {w} +{\boldsymbol {\nabla }}\mathbf {w} ^{T}$ सिद्धांत है अतः आवश्यक नियम को इस प्रकार भी लिखा जा सकता है ${\boldsymbol {\nabla }}\times ({\boldsymbol {\nabla }}\mathbf {w} +{\boldsymbol {\nabla }}\mathbf {w} ^{T})^{T}={\boldsymbol {0}}$.

पर्याप्त स्थितियाँ

आइए अब मान लें कि स्थिति ${\boldsymbol {\nabla }}\times ({\boldsymbol {\nabla }}\times {\boldsymbol {\epsilon }})^{T}={\boldsymbol {0}}$ निकाय के भाग में संतुष्ट है. क्या यह स्थिति निरंतर, एकल-मूल्य वाले विस्थापन क्षेत्र $\mathbf {u}$ के अस्तित्व की गारंटी देने के लिए पर्याप्त है ?

इस प्रक्रिया में पहला चरण यह दिखाना है कि इस स्थिति का तात्पर्य यह है कि अपरिमित घूर्णन टेंसर ${\boldsymbol {\omega }}$ विशिष्ट रूप से परिभाषित है। ऐसा करने के लिए हम ${\boldsymbol {\nabla }}\mathbf {w}$ को $\mathbf {X} _{A}$ को $\mathbf {X} _{B}$ पथ के साथ एकीकृत करते हैं, अर्थात,

$\mathbf {w} (\mathbf {X} _{B})-\mathbf {w} (\mathbf {X} _{A})=\int _{\mathbf {X} _{A}}^{\mathbf {X} _{B}}{\boldsymbol {\nabla }}\mathbf {w} \cdot d\mathbf {X} =\int _{\mathbf {X} _{A}}^{\mathbf {X} _{B}}({\boldsymbol {\nabla }}\times {\boldsymbol {\epsilon }})\cdot d\mathbf {X}$

ध्यान दें कि कठोर निकाय के घूर्णन को ठीक करने के लिए हमें एक संदर्भ $\mathbf {w} (\mathbf {X} _{A})$ जानने की आवश्यकता है। फील्ड $\mathbf {w} (\mathbf {X} )$ विशिष्ट रूप से केवल तभी निर्धारित होता है जब रूपरेखा संवृत रूपरेखा के साथ अभिन्न होता है इस प्रकार $\mathbf {X} _{A}$ और $\mathbf {X} _{b}$ शून्य है, अर्थात,

$\oint _{\mathbf {X} _{A}}^{\mathbf {X} _{B}}({\boldsymbol {\nabla }}\times {\boldsymbol {\epsilon }})\cdot d\mathbf {X} ={\boldsymbol {0}}$

किन्तु स्टोक्स के प्रमेय से सरल रूप से जुड़े निकाय और अनुकूलता के लिए आवश्यक नियम के लिए

$\oint _{\mathbf {X} _{A}}^{\mathbf {X} _{B}}({\boldsymbol {\nabla }}\times {\boldsymbol {\epsilon }})\cdot d\mathbf {X} =\int _{\Omega _{AB}}\mathbf {n} \cdot ({\boldsymbol {\nabla }}\times {\boldsymbol {\nabla }}\times {\boldsymbol {\epsilon }})~da={\boldsymbol {0}}$

इसलिए, क्षेत्र $\mathbf {w}$ विशिष्ट रूप से परिभाषित किया गया है जिसका अर्थ है कि अनंत लघु घूर्णन टेंसर ${\boldsymbol {\omega }}$ इसे भी विशिष्ट रूप से परिभाषित किया गया है, परंतु निकाय सामान्यतः जुड़ा हुआ होन चाहिए।

प्रक्रिया के अगले चरण में हम विस्थापन क्षेत्र $\mathbf {u}$ की विशिष्टता पर विचार करेंगे, पहले की तरह हम विस्थापन प्रवणता को एकीकृत करते हैं

$\mathbf {u} (\mathbf {X} _{B})-\mathbf {u} (\mathbf {X} _{A})=\int _{\mathbf {X} _{A}}^{\mathbf {X} _{B}}{\boldsymbol {\nabla }}\mathbf {u} \cdot d\mathbf {X} =\int _{\mathbf {X} _{A}}^{\mathbf {X} _{B}}({\boldsymbol {\epsilon }}+{\boldsymbol {\omega }})\cdot d\mathbf {X}$

स्टोक्स के प्रमेय से और हमारे निकट उपस्थित संबंध ${\boldsymbol {\nabla }}\times {\boldsymbol {\epsilon }}={\boldsymbol {\nabla }}\mathbf {w} =-{\boldsymbol {\nabla }}\times \omega$ का उपयोग करके

$\oint _{\mathbf {X} _{A}}^{\mathbf {X} _{B}}({\boldsymbol {\epsilon }}+{\boldsymbol {\omega }})\cdot d\mathbf {X} =\int _{\Omega _{AB}}\mathbf {n} \cdot ({\boldsymbol {\nabla }}\times {\boldsymbol {\epsilon }}+{\boldsymbol {\nabla }}\times {\boldsymbol {\omega }})~da={\boldsymbol {0}}$

इसलिए विस्थापन क्षेत्र $\mathbf {u}$ भी विशिष्ट रूप से निर्धारित किया जाता है। इसलिए अनुकूलता स्थितियाँ सरलता से जुड़े निकाय में अद्वितीय विस्थापन क्षेत्र $\mathbf {u}$ के अस्तित्व की गारंटी के लिए पर्याप्त हैं .

राइट कॉची-ग्रीन विरूपण क्षेत्र के लिए अनुकूलता

राइट कॉची-ग्रीन विरूपण क्षेत्र के लिए अनुकूलता समस्या को निम्नानुसार प्रस्तुत किया जा सकता है।

समस्या: मान लीजिए ${\boldsymbol {C}}(\mathbf {X} )$ संदर्भ विन्यास पर परिभाषित एक धनात्मक निश्चित सममित टेंसर क्षेत्र है। इस प्रकार ${\boldsymbol {C}}$ पर किन परिस्थितियों में स्थिति क्षेत्र $\mathbf {x} (\mathbf {X} )$ द्वारा चिह्नित विकृत विन्यास उपस्थित है जैसे कि

$(1)\quad \left({\frac {\partial \mathbf {x} }{\partial \mathbf {X} }}\right)^{T}\left({\frac {\partial \mathbf {x} }{\partial \mathbf {X} }}\right)={\boldsymbol {C}}$

आवश्यक नियम

मान लीजिए कि क्षेत्र $\mathbf {x} (\mathbf {X} )$ उपस्थित है जो नियम (1) को संतुष्ट करता है। इस प्रकार आयताकार कार्टेशियन आधार के संबंध में अवयवो के संदर्भ में

${\frac {\partial x^{i}}{\partial X^{\alpha }}}{\frac {\partial x^{i}}{\partial X^{\beta }}}=C_{\alpha \beta }$

परिमित तनाव सिद्धांत से हम यह जानते हैं कि $C_{\alpha \beta }=g_{\alpha \beta }$. इसलिए हम लिख सकते हैं

$\delta _{ij}~{\frac {\partial x^{i}}{\partial X^{\alpha }}}~{\frac {\partial x^{j}}{\partial X^{\beta }}}=g_{\alpha \beta }$

दो सममित द्वितीय-क्रम टेंसर क्षेत्र के लिए जिन्हें एक-से-एक मैप किया जाता है, हमारे निकट परिमित तनाव सिद्धांत भी है इस प्रकार विरूपण उपायों और क्रिस्टोफ़ेल प्रतीकों के मध्य कुछ संबंध

$G_{ij}={\frac {\partial X^{\alpha }}{\partial x^{i}}}~{\frac {\partial X^{\beta }}{\partial x^{j}}}~g_{\alpha \beta }$

$G_{ij}$ और $g_{\alpha \beta }$ के मध्य के संबंध से जो $\delta _{ij}=G_{ij}$ हमारे पास है

$_{(x)}\Gamma _{ij}^{k}=0$

फिर, सम्बन्ध से

${\frac {\partial ^{2}x^{m}}{\partial X^{\alpha }\partial X^{\beta }}}={\frac {\partial x^{m}}{\partial X^{\mu }}}\,_{(X)}\Gamma _{\alpha \beta }^{\mu }-{\frac {\partial x^{i}}{\partial X^{\alpha }}}~{\frac {\partial x^{j}}{\partial X^{\beta }}}\,_{(x)}\Gamma _{ij}^{m}$

हमारे निकट है

${\frac {\partial F_{~\alpha }^{m}}{\partial X^{\beta }}}=F_{~\mu }^{m}\,_{(X)}\Gamma _{\alpha \beta }^{\mu }\qquad ;~~F_{~\alpha }^{i}:={\frac {\partial x^{i}}{\partial X^{\alpha }}}$

परिमित तनाव सिद्धांत से विरूपण उपायों और क्रिस्टोफ़ेल प्रतीकों के मध्य कुछ संबंध भी हमारे निकट हैं

$_{(X)}\Gamma _{\alpha \beta \gamma }={\frac {1}{2}}\left({\frac {\partial g_{\alpha \gamma }}{\partial X^{\beta }}}+{\frac {\partial g_{\beta \gamma }}{\partial X^{\alpha }}}-{\frac {\partial g_{\alpha \beta }}{\partial X^{\gamma }}}\right)~;~~_{(X)}\Gamma _{\alpha \beta }^{\nu }=g^{\nu \gamma }\,_{(X)}\Gamma _{\alpha \beta \gamma }~;~~g_{\alpha \beta }=C_{\alpha \beta }~;~~g^{\alpha \beta }=C^{\alpha \beta }$

इसलिए,

$\,_{(X)}\Gamma _{\alpha \beta }^{\mu }={\cfrac {C^{\mu \gamma }}{2}}\left({\frac {\partial C_{\alpha \gamma }}{\partial X^{\beta }}}+{\frac {\partial C_{\beta \gamma }}{\partial X^{\alpha }}}-{\frac {\partial C_{\alpha \beta }}{\partial X^{\gamma }}}\right)$

और हमारे निकट है

${\frac {\partial F_{~\alpha }^{m}}{\partial X^{\beta }}}=F_{~\mu }^{m}~{\cfrac {C^{\mu \gamma }}{2}}\left({\frac {\partial C_{\alpha \gamma }}{\partial X^{\beta }}}+{\frac {\partial C_{\beta \gamma }}{\partial X^{\alpha }}}-{\frac {\partial C_{\alpha \beta }}{\partial X^{\gamma }}}\right)$

फिर से, विभेदन के क्रम की क्रमविनिमेय प्रकृति का उपयोग करते हुए, हमारे निकट है

${\frac {\partial ^{2}F_{~\alpha }^{m}}{\partial X^{\beta }\partial X^{\rho }}}={\frac {\partial ^{2}F_{~\alpha }^{m}}{\partial X^{\rho }\partial X^{\beta }}}\implies {\frac {\partial F_{~\mu }^{m}}{\partial X^{\rho }}}\,_{(X)}\Gamma _{\alpha \beta }^{\mu }+F_{~\mu }^{m}~{\frac {\partial }{\partial X^{\rho }}}[\,_{(X)}\Gamma _{\alpha \beta }^{\mu }]={\frac {\partial F_{~\mu }^{m}}{\partial X^{\beta }}}\,_{(X)}\Gamma _{\alpha \rho }^{\mu }+F_{~\mu }^{m}~{\frac {\partial }{\partial X^{\beta }}}[\,_{(X)}\Gamma _{\alpha \rho }^{\mu }]$

या

$F_{~\gamma }^{m}\,_{(X)}\Gamma _{\mu \rho }^{\gamma }\,_{(X)}\Gamma _{\alpha \beta }^{\mu }+F_{~\mu }^{m}~{\frac {\partial }{\partial X^{\rho }}}[\,_{(X)}\Gamma _{\alpha \beta }^{\mu }]=F_{~\gamma }^{m}\,_{(X)}\Gamma _{\mu \beta }^{\gamma }\,_{(X)}\Gamma _{\alpha \rho }^{\mu }+F_{~\mu }^{m}~{\frac {\partial }{\partial X^{\beta }}}[\,_{(X)}\Gamma _{\alpha \rho }^{\mu }]$

नियमो को एकत्रित करने के पश्चात् हमें मिलता है

$F_{~\gamma }^{m}\left(\,_{(X)}\Gamma _{\mu \rho }^{\gamma }\,_{(X)}\Gamma _{\alpha \beta }^{\mu }+{\frac {\partial }{\partial X^{\rho }}}[\,_{(X)}\Gamma _{\alpha \beta }^{\gamma }]-\,_{(X)}\Gamma _{\mu \beta }^{\gamma }\,_{(X)}\Gamma _{\alpha \rho }^{\mu }-{\frac {\partial }{\partial X^{\beta }}}[\,_{(X)}\Gamma _{\alpha \rho }^{\gamma }]\right)=0$

$F_{\gamma }^{m}$ की परिभाषा से हम पाते हैं कि यह विपरीत है और इसलिए शून्य नहीं हो सकता है। इसलिए,

$R_{\alpha \beta \rho }^{\gamma }:={\frac {\partial }{\partial X^{\rho }}}[\,_{(X)}\Gamma _{\alpha \beta }^{\gamma }]-{\frac {\partial }{\partial X^{\beta }}}[\,_{(X)}\Gamma _{\alpha \rho }^{\gamma }]+\,_{(X)}\Gamma _{\mu \rho }^{\gamma }\,_{(X)}\Gamma _{\alpha \beta }^{\mu }-\,_{(X)}\Gamma _{\mu \beta }^{\gamma }\,_{(X)}\Gamma _{\alpha \rho }^{\mu }=0$

हम दिखा सकते हैं कि यह रीमैन-क्रिस्टोफ़ेल वक्रता टेंसर के मिश्रित अवयव हैं। इसलिए, के लिए आवश्यक नियम ${\boldsymbol {C}}$-अनुकूलता यह है कि विरूपण की रीमैन-क्रिस्टोफ़ेल वक्रता शून्य है।

पर्याप्त स्थितियाँ

पर्याप्तता का प्रमाण थोड़ा अधिक सम्मिलित है। हम इस धारणा से नियम करते हैं कि

$R_{\alpha \beta \rho }^{\gamma }=0~;~~g_{\alpha \beta }=C_{\alpha \beta }$

हमें यह दिखाना होगा कि $\mathbf {x}$ और $\mathbf {X}$ ऐसे उपस्थित हैं

${\frac {\partial x^{i}}{\partial X^{\alpha }}}{\frac {\partial x^{i}}{\partial X^{\beta }}}=C_{\alpha \beta }$

टी.वाई.थॉमस के प्रमेय से हम जानते हैं कि समीकरणों की प्रणाली

${\frac {\partial F_{~\alpha }^{i}}{\partial X^{\beta }}}=F_{~\gamma }^{i}~\,_{(X)}\Gamma _{\alpha \beta }^{\gamma }$

सरल रूप से जुड़े डोमेन पर अद्वितीय समाधान $F_{~\alpha }^{i}$ है

$_{(X)}\Gamma _{\alpha \beta }^{\gamma }=_{(X)}\Gamma _{\beta \alpha }^{\gamma }~;~~R_{\alpha \beta \rho }^{\gamma }=0$

इनमें से पहला $\Gamma _{jk}^{i}$ की परिभाषा से सत्य है और दूसरा मान लिया गया है। इसलिए स्वीकृत स्थिति हमें एक अद्वितीय $F_{~\alpha }^{i}$ देती है जो कि $C^{2}$ निरंतर है।

आगे समीकरणों की प्रणाली पर विचार करें

${\frac {\partial x^{i}}{\partial X^{\alpha }}}=F_{~\alpha }^{i}$

चूँकि $F_{~\alpha }^{i}$ $C^{2}$ है और निकाय सामान्यतः जुड़ा हुआ है, इसलिए उपरोक्त समीकरणों के लिए कुछ समाधान $x^{i}(X^{\alpha })$ मौजूद है। इस प्रकार हम दिखा सकते हैं कि $x^{i}$ उस गुण को भी संतुष्ट करता है

$\det \left|{\frac {\partial x^{i}}{\partial X^{\alpha }}}\right|\neq 0$

हम वह सम्बन्ध भी दिखा सकते हैं

${\frac {\partial x^{i}}{\partial X^{\alpha }}}~g^{\alpha \beta }~{\frac {\partial x^{j}}{\partial X^{\beta }}}=\delta ^{ij}$

तात्पर्य यह है

$g_{\alpha \beta }=C_{\alpha \beta }={\frac {\partial x^{k}}{\partial X^{\alpha }}}~{\frac {\partial x^{k}}{\partial X^{\beta }}}$

यदि हम इन मात्राओं को टेंसर क्षेत्र के साथ जोड़ते हैं तो हम यह दिखा सकते हैं कि ${\frac {\partial \mathbf {x} }{\partial \mathbf {X} }}$ विपरीत है और निर्मित टेंसर क्षेत्र ${\boldsymbol {C}}$ के लिए अभिव्यक्ति को संतुष्ट करता है

यह भी देखें

• सेंट-वेनैंट की अनुकूलता स्थिति
• रेखीय लोच
• विरूपण (यांत्रिकी)
• अनंतिम तनाव सिद्धांत
• परिमित तनाव सिद्धांत
• टेंसर व्युत्पन्न (सातत्य यांत्रिकी)
• वक्ररेखीय निर्देशांक

बाहरी संबंध

• Amit Acharya's notes on compatibility on iMechanica
• Plasticity by J. Lubliner, sec. 1.2.4 p. 35