अनंत आवेग प्रतिक्रिया

अनंत आवेग प्रतिक्रिया (IIR) कई रैखिक समय-अपरिवर्तनीय प्रणालियों पर लागू होने वाली एक संपत्ति है जो एक आवेग प्रतिक्रिया होने से प्रतिष्ठित होती है $h(t)$ जो एक निश्चित बिंदु के ठीक बाद शून्य नहीं हो जाता है, लेकिन अनिश्चित काल तक जारी रहता है। यह एक परिमित आवेग प्रतिक्रिया (एफआईआर) प्रणाली के विपरीत है जिसमें आवेग प्रतिक्रिया कई बार बिल्कुल शून्य हो जाती है $t>T$ कुछ परिमित के लिए $T$, इस प्रकार सीमित अवधि के होने के नाते। रैखिक समय-अपरिवर्तनीय प्रणालियों के सामान्य उदाहरण अधिकांश इलेक्ट्रॉनिक फिल्टर और डिजिटल फिल्टर हैं। इस गुण वाले सिस्टम को IIR सिस्टम या IIR फ़िल्टर के रूप में जाना जाता है।

व्यवहार में, आवेग प्रतिक्रिया, यहां तक ​​​​कि आईआईआर सिस्टम की भी, आमतौर पर शून्य तक पहुंच जाती है और एक निश्चित बिंदु से पहले उपेक्षित किया जा सकता है। हालाँकि भौतिक प्रणालियाँ जो IIR या एफआईआर प्रतिक्रियाओं को जन्म देती हैं, वे भिन्न हैं, और इसमें अंतर का महत्व है। उदाहरण के लिए, प्रतिरोधों, कैपेसिटर, और/या इंडक्टर्स (और शायद रैखिक एम्पलीफायरों) से बना एनालॉग इलेक्ट्रॉनिक फ़िल्टर आम तौर पर आईआईआर फ़िल्टर होते हैं। दूसरी ओर, असतत-समय फ़िल्टर (आमतौर पर डिजिटल फ़िल्टर) बिना किसी प्रतिक्रिया के टैप की गई विलंब रेखा पर आधारित प्राथमिकी फ़िल्टर होते हैं। एनालॉग फिल्टर में कैपेसिटर (या इंडक्टर्स) में एक मेमोरी होती है और उनकी आंतरिक स्थिति कभी भी आवेग के बाद पूरी तरह से आराम नहीं करती है (कैपेसिटर और इंडक्टर्स के शास्त्रीय मॉडल को मानते हुए जहां क्वांटम प्रभाव को नजरअंदाज कर दिया जाता है)। लेकिन बाद के मामले में, एक आवेग टैप की गई देरी रेखा के अंत तक पहुंचने के बाद, सिस्टम को उस आवेग की कोई और स्मृति नहीं है और वह अपनी प्रारंभिक स्थिति में वापस आ गया है; उस बिंदु से परे इसकी आवेग प्रतिक्रिया बिल्कुल शून्य है।

कार्यान्वयन और डिजाइन

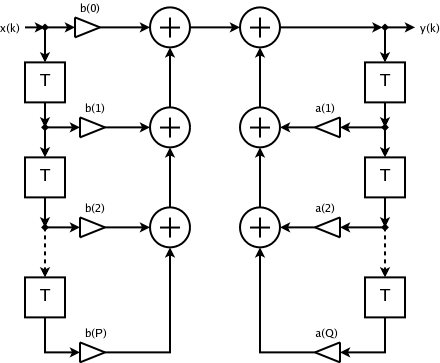
हालांकि लगभग सभी एनालॉग फिल्टर इलेक्ट्रॉनिक फिल्टर आईआईआर हैं, डिजिटल फिल्टर या तो आईआईआर या एफआईआर हो सकते हैं। असतत-समय फ़िल्टर (जैसे नीचे दिखाया गया ब्लॉक आरेख) की टोपोलॉजी में प्रतिक्रिया की उपस्थिति आम तौर पर एक आईआईआर प्रतिक्रिया बनाती है। आईआईआर फिल्टर के जेड को बदलने स्थानांतरण प्रकार्य में एक गैर-तुच्छ हर होता है, जो उन फीडबैक शर्तों का वर्णन करता है। दूसरी ओर, एक एफआईआर फिल्टर के स्थानांतरण कार्य में केवल एक अंश होता है, जैसा कि नीचे दिए गए सामान्य रूप में व्यक्त किया गया है। के सभी $a_{i}$ के साथ गुणांक $i>0$ (प्रतिक्रिया शर्तें) शून्य हैं और फ़िल्टर का कोई परिमित ध्रुव-शून्य प्लॉट नहीं है।

आईआईआर एनालॉग इलेक्ट्रॉनिक फिल्टर से संबंधित स्थानांतरण कार्यों का व्यापक अध्ययन किया गया है और उनके आयाम और चरण विशेषताओं के लिए अनुकूलित किया गया है। ये निरंतर-समय फ़िल्टर फ़ंक्शन लाप्लास डोमेन में वर्णित हैं। वांछित समाधान असतत-समय फिल्टर के मामले में स्थानांतरित किए जा सकते हैं, जिनके स्थानांतरण कार्य z डोमेन में व्यक्त किए जाते हैं, कुछ गणितीय तकनीकों जैसे कि द्विरेखीय परिवर्तन , आवेग invariance या पोल-ज़ीरो मिलान विधि के उपयोग के माध्यम से। इस प्रकार डिजिटल आईआईआर फिल्टर एनालॉग फिल्टर के लिए जाने-माने समाधानों पर आधारित हो सकते हैं जैसे कि चेबीशेव फ़िल्टर , बटरवर्थ फ़िल्टर और अण्डाकार फिल्टर , जो उन समाधानों की विशेषताओं को विरासत में मिला है।

ट्रांसफर फंक्शन व्युत्पत्ति

डिजिटल फिल्टर को अक्सर अंतर समीकरण के संदर्भ में वर्णित और कार्यान्वित किया जाता है जो परिभाषित करता है कि आउटपुट सिग्नल इनपुट सिग्नल से कैसे संबंधित है:

${\begin{aligned}y[n]{}=&{\frac {1}{a_{0}}}(b_{0}x[n]+b_{1}x[n-1]+\cdots +b_{P}x[n-P]\\&{}-a_{1}y[n-1]-a_{2}y[n-2]-\cdots -a_{Q}y[n-Q])\end{aligned}}$

कहाँ पे:

• $\ P$ फीडफॉरवर्ड फिल्टर ऑर्डर है
• $\ b_{i}$ फीडफॉरवर्ड फिल्टर गुणांक हैं
• $\ Q$ फीडबैक फ़िल्टर ऑर्डर है
• $\ a_{i}$ प्रतिक्रिया फ़िल्टर गुणांक हैं
• $\ x[n]$ इनपुट सिग्नल है
• $\ y[n]$ आउटपुट सिग्नल है।

अंतर समीकरण का एक अधिक संघनित रूप है:

$\ y[n]={\frac {1}{a_{0}}}\left(\sum _{i=0}^{P}b_{i}x[n-i]-\sum _{j=1}^{Q}a_{j}y[n-j]\right)$

जो, पुनर्व्यवस्थित होने पर बन जाता है:

$\ \sum _{j=0}^{Q}a_{j}y[n-j]=\sum _{i=0}^{P}b_{i}x[n-i]$

फ़िल्टर के स्थानांतरण फ़ंक्शन को खोजने के लिए, हम पहले उपरोक्त समीकरण के प्रत्येक पक्ष का Z- परिवर्तन लेते हैं, जहाँ हम प्राप्त करने के लिए Z-transform#Properties|time-shift गुण का उपयोग करते हैं:

$\ \sum _{j=0}^{Q}a_{j}z^{-j}Y(z)=\sum _{i=0}^{P}b_{i}z^{-i}X(z)$

हम स्थानांतरण फ़ंक्शन को परिभाषित करते हैं:

${\begin{aligned}H(z)&={\frac {Y(z)}{X(z)}}\\&={\frac {\sum _{i=0}^{P}b_{i}z^{-i}}{\sum _{j=0}^{Q}a_{j}z^{-j}}}\end{aligned}}$

यह देखते हुए कि अधिकांश IIR फ़िल्टर में गुणांक डिज़ाइन किया गया है$\ a_{0}$ 1 है, IIR फ़िल्टर स्थानांतरण फ़ंक्शन अधिक पारंपरिक रूप लेता है:

$H(z)={\frac {\sum _{i=0}^{P}b_{i}z^{-i}}{1+\sum _{j=1}^{Q}a_{j}z^{-j}}}$

IIR फ़िल्टर के ब्लॉक आरेख का एक उदाहरण। $z^{-1}$ h> ब्लॉक एक इकाई विलंब है।

स्थिरता

ट्रांसफर फ़ंक्शन किसी को यह निर्धारित करने की अनुमति देता है कि कोई सिस्टम बाउंडेड-इनपुट, बाउंडेड-आउटपुट स्टेबिलिटी | बाउंडेड-इनपुट, बाउंडेड-आउटपुट (BIBO) स्थिर है या नहीं। विशिष्ट होने के लिए, BIBO स्थिरता मानदंड के लिए आवश्यक है कि सिस्टम के अभिसरण की त्रिज्या में यूनिट सर्कल शामिल हो। उदाहरण के लिए, एक कारण प्रणाली के लिए, स्थानांतरण फ़ंक्शन के सभी Pole_(complex_analysis) का निरपेक्ष मान एक से छोटा होना चाहिए। दूसरे शब्दों में, सभी ध्रुवों को एक इकाई वृत्त के भीतर स्थित होना चाहिए $z$-विमान।

ध्रुवों को के मूल्यों के रूप में परिभाषित किया गया है $z$ जो का हर बनाते हैं $H(z)$ 0 के बराबर:

$\ 0=\sum _{j=0}^{Q}a_{j}z^{-j}$

स्पष्ट है, यदि $a_{j}\neq 0$ तो ध्रुवों के मूल में स्थित नहीं होते हैं $z$-विमान। यह परिमित आवेग प्रतिक्रिया फिल्टर के विपरीत है जहां सभी ध्रुव मूल स्थान पर स्थित होते हैं, और इसलिए हमेशा स्थिर होते हैं।

आईआईआर फिल्टर को कभी-कभी एफआईआर फिल्टर पर पसंद किया जाता है क्योंकि एक आईआईआर फिल्टर उसी क्रम के एफआईआर फिल्टर की तुलना में बहुत तेज संक्रमण क्षेत्र धड़ल्ले से बोलना प्राप्त कर सकता है।

उदाहरण

स्थानांतरण कार्य करने दें $H(z)$ असतत-समय फ़िल्टर द्वारा दिया जाना चाहिए:

$H(z)={\frac {B(z)}{A(z)}}={\frac {1}{1-az^{-1}}}$

पैरामीटर द्वारा शासित $a$, एक वास्तविक संख्या के साथ $0<|a|<1$. $H(z)$ एक ध्रुव के साथ स्थिर और कारण है $a$. टाइम-डोमेन आवेग प्रतिक्रिया द्वारा दिया जा सकता है:

$h(n)=a^{n}u(n)$

कहाँ पे $u(n)$ हेविसाइड स्टेप फंक्शन#असतत रूप है। यह देखा जा सकता है $h(n)$ सभी के लिए शून्य नहीं है $n\geq 0$, इस प्रकार एक आवेग प्रतिक्रिया जो असीम रूप से जारी रहती है।

फायदे और नुकसान

पासबैंड, स्टॉपबैंड, रिपल, और/या रोल-ऑफ के संदर्भ में एक विनिर्देश को पूरा करने के लिए डिजिटल आईआईआर फिल्टर का प्राथमिक लाभ प्राथमिकी फिल्टर से अधिक है, कार्यान्वयन में उनकी दक्षता है। विनिर्देशों के इस तरह के एक सेट को कम ऑर्डर (उपरोक्त सूत्रों में क्यू) आईआईआर फ़िल्टर के साथ पूरा किया जा सकता है, जो समान आवश्यकताओं को पूरा करने वाले एफआईआर फ़िल्टर के लिए आवश्यक होगा। यदि एक सिग्नल प्रोसेसर में लागू किया जाता है, तो इसका मतलब है कि प्रति समय कदम की गणना की संख्या कम है; कम्प्यूटेशनल बचत अक्सर एक बड़े कारक की होती है।

दूसरी ओर, एफआईआर फिल्टर डिजाइन करना आसान हो सकता है, उदाहरण के लिए, एक विशेष आवृत्ति प्रतिक्रिया आवश्यकता से मेल खाने के लिए। यह विशेष रूप से सच है जब आवश्यकता सामान्य मामलों (हाई-पास, लो-पास, नॉच, आदि) में से एक नहीं है, जिसका अध्ययन और एनालॉग फिल्टर के लिए अनुकूलित किया गया है। इसके अलावा एफआईआर फिल्टर को आसानी से रैखिक चरण (निरंतर समूह विलंब बनाम आवृत्ति) बनाया जा सकता है - एक संपत्ति जिसे आसानी से आईआईआर फिल्टर का उपयोग करके पूरा नहीं किया जाता है और फिर केवल एक अनुमान के रूप में (उदाहरण के लिए बेसेल फिल्टर के साथ)। डिजिटल आईआईआर फिल्टर के संबंध में एक और मुद्दा निष्क्रिय होने पर सीमा चक्र व्यवहार की संभावना है, परिमाणीकरण के साथ प्रतिक्रिया प्रणाली के कारण।

डिजाइन के तरीके

आवेग आक्रमण

इंपल्स इनवेरिएंस निरंतर-समय के फिल्टर से असतत-समय अनंत-आवेग-प्रतिक्रिया (IIR) फिल्टर को डिजाइन करने की एक तकनीक है जिसमें असतत-समय प्रणाली की आवेग प्रतिक्रिया का उत्पादन करने के लिए निरंतर-समय प्रणाली की आवेग प्रतिक्रिया का नमूना लिया जाता है। एस-प्लेन से जेड-प्लेन तक मैपिंग की दो बुनियादी आवश्यकताओं को पूरा करने के लिए इंपल्स इनवेरिएंस आमतौर पर इस्तेमाल की जाने वाली विधियों में से एक है। यह T(z) को हल करके प्राप्त किया जाता है जिसका एनालॉग फ़िल्टर के समान नमूना समय पर समान आउटपुट मान होता है, और यह केवल तभी लागू होता है जब इनपुट पल्स में हों।
ध्यान दें कि इस विधि द्वारा उत्पन्न डिजिटल फ़िल्टर के सभी इनपुट अनुमानित मान हैं, पल्स इनपुट को छोड़कर जो बहुत सटीक हैं। यह सबसे सरल IIR फ़िल्टर डिज़ाइन विधि है। यह कम आवृत्तियों पर सबसे सटीक है, इसलिए इसे आमतौर पर कम-पास फ़िल्टर में उपयोग किया जाता है।

लैपलेस ट्रांसफॉर्म या जेड-ट्रांसफॉर्म के लिए, ट्रांसफॉर्मेशन के बाद का आउटपुट सिर्फ इनपुट को संबंधित ट्रांसफॉर्मेशन फंक्शन, टी (एस) या टी (जेड) से गुणा किया जाता है। Y(s) और Y(z) क्रमशः इनपुट X(s) और इनपुट X(z) के परिवर्तित आउटपुट हैं।

$Y(s)=T(s)X(s)$

$Y(z)=T(z)X(z)$

यूनिट आवेग पर लैपलेस ट्रांसफॉर्म या जेड-ट्रांसफॉर्म को लागू करते समय, परिणाम 1 होता है। इसलिए, रूपांतरण के बाद आउटपुट परिणाम
हैं

$Y(s)=T(s)$

$Y(z)=T(z)$

अब एनालॉग फिल्टर का आउटपुट टाइम डोमेन में उलटा लाप्लास ट्रांसफॉर्म है।

$y(t)=L^{-1}[Y(s)]=L^{-1}[T(s)]$

यदि हम t के बजाय nT का उपयोग करते हैं, तो हम नमूना समय पर पल्स से प्राप्त आउटपुट y(nT) प्राप्त कर सकते हैं। इसे y(n)
. के रूप में भी व्यक्त किया जा सकता है

$y(n)=y(nT)=y(t)|_{t=sT}$

इस असतत समय संकेत को T(z) प्राप्त करने के लिए z-transform लागू किया जा सकता है

$T(z)=Y(z)=Z[y(n)]$

$T(z)=Z[y(n)]=Z[y(nT)]$

$T(z)=Z\left\{L^{-1}[T(s)]_{t=nT}\right\}$

अंतिम समीकरण गणितीय रूप से वर्णन करता है कि एक डिजिटल आईआईआर फिल्टर एनालॉग सिग्नल पर जेड-ट्रांसफॉर्म करना है जिसे लैपलेस द्वारा नमूना और टी (एस) में परिवर्तित किया गया है, जिसे आमतौर पर सरल किया जाता है

$T(z)=Z[T(s)]*T$

इस तथ्य पर ध्यान दें कि सूत्र में एक गुणक T दिखाई दे रहा है। ऐसा इसलिए है क्योंकि यूनिट पल्स के लिए लैपलेस ट्रांसफॉर्म और जेड-ट्रांसफॉर्म 1 होने पर भी पल्स ही जरूरी नहीं है। एनालॉग संकेतों के लिए, पल्स का एक अनंत मान होता है, लेकिन क्षेत्र t=0 पर 1 होता है, लेकिन यह असतत-समय पल्स t=0 पर 1 होता है, इसलिए गुणक T के अस्तित्व की आवश्यकता होती है।

स्टेप इनवेरिएंस

स्टेप इनवेरिएंस इंपल्स इनवेरिएंट की तुलना में एक बेहतर डिजाइन विधि है। नमूना लेते समय डिजिटल फ़िल्टर में विभिन्न स्थिरांक के साथ इनपुट के कई खंड होते हैं, जो असतत चरणों से बना होता है। चरण अपरिवर्तनीय IIR फ़िल्टर ADC के समान इनपुट चरण संकेत की तुलना में कम सटीक है। हालांकि, यह आवेग अपरिवर्तनीय की तुलना में किसी भी इनपुट के लिए बेहतर सन्निकटन है।
जब टी (जेड) और टी (एस) दोनों चरण इनपुट होते हैं तो चरण अपरिवर्तनीय समान नमूना मानों की समस्या को हल करता है। डिजिटल फ़िल्टर का इनपुट u(n) है, और एनालॉग फ़िल्टर का इनपुट u(t) है। कनवर्ट किए गए आउटपुट सिग्नल को प्राप्त करने के लिए इन दो इनपुट पर z-ट्रांसफॉर्म और लैपलेस ट्रांसफॉर्म लागू करें।
चरण इनपुट पर z- परिवर्तन निष्पादित करें $Z[u(n)]={\dfrac {z}{z-1}}$
जेड-ट्रांसफॉर्म के बाद परिवर्तित आउटपुट $Y(z)=T(z)U(z)=T(z){\dfrac {z}{z-1}}$
स्टेप इनपुट पर लाप्लास ट्रांसफॉर्म करें $L[u(t)]={\dfrac {1}{s}}$
लाप्लास परिवर्तन के बाद परिवर्तित आउटपुट $Y(s)=T(s)U(s)={\dfrac {T(s)}{s}}$
एनालॉग फिल्टर का आउटपुट y(t) है, जो Y(s) का उलटा लाप्लास ट्रांसफॉर्म है। यदि प्रत्येक टी सेकंड में नमूना लिया जाता है, तो यह वाई (एन) है, जो वाई (जेड) का उलटा रूपांतरण है। इन संकेतों का उपयोग डिजिटल फ़िल्टर और एनालॉग फ़िल्टर के लिए हल करने के लिए किया जाता है और नमूना समय पर समान आउटपुट होता है।
निम्नलिखित समीकरण टी (जेड) के समाधान को इंगित करता है, जो एनालॉग फ़िल्टर के लिए अनुमानित सूत्र है।

$T(z)={\dfrac {z-1}{z}}Y(z)$

$T(z)={\dfrac {z-1}{z}}Z[y(n)]$

$T(z)={\dfrac {z-1}{z}}Z[Y(s)]$

$T(z)={\dfrac {z-1}{z}}Z[{\dfrac {T(s)}{s}}]$

बिलिनियर ट्रांसफॉर्म

बिलिनियर ट्रांसफॉर्म एक कंफर्मल मैपिंग का एक विशेष मामला है, जिसका इस्तेमाल अक्सर ट्रांसफर फंक्शन को बदलने के लिए किया जाता है $H_{a}(s)$ ट्रांसफर फ़ंक्शन के लिए निरंतर-समय डोमेन (जिसे अक्सर एनालॉग फ़िल्टर कहा जाता है) में एक रैखिक, समय-अपरिवर्तनीय (एलटीआई) फ़िल्टर का $H_{d}(z)$ असतत-समय डोमेन में एक रैखिक, शिफ्ट-अपरिवर्तनीय फ़िल्टर का। बिलिनियर ट्रांसफॉर्म प्राकृतिक लॉगरिदम फ़ंक्शन का प्रथम-क्रम अनुमान है जो एस-प्लेन के लिए जेड-प्लेन का सटीक मानचित्रण है। जब लाप्लास परिवर्तन एक असतत-समय संकेत पर किया जाता है (एक संगत विलंबित इकाई आवेग से जुड़े असतत-समय अनुक्रम के प्रत्येक तत्व के साथ), तो परिणाम असतत-समय अनुक्रम का Z परिवर्तन होता है जिसमें प्रतिस्थापन होता है

${\begin{aligned}z&=e^{sT}\\&={\frac {e^{sT/2}}{e^{-sT/2}}}\\&\approx {\frac {1+sT/2}{1-sT/2}}\end{aligned}}$

कहाँ पे $T$ द्विरेखीय रूपांतरण व्युत्पत्ति में प्रयुक्त समलम्बाकार नियम का संख्यात्मक एकीकरण चरण आकार है; या, दूसरे शब्दों में, नमूना अवधि। उपरोक्त द्विरेखीय सन्निकटन को के लिए हल किया जा सकता है $s$ या इसी तरह के सन्निकटन के लिए $s=(1/T)\ln(z)$ किया जासकताहे।

इस मानचित्रण का व्युत्क्रम (और इसका प्रथम-क्रम द्विरेखीय सन्निकटन) है

${\begin{aligned}s&={\frac {1}{T}}\ln(z)\\&={\frac {2}{T}}\left[{\frac {z-1}{z+1}}+{\frac {1}{3}}\left({\frac {z-1}{z+1}}\right)^{3}+{\frac {1}{5}}\left({\frac {z-1}{z+1}}\right)^{5}+{\frac {1}{7}}\left({\frac {z-1}{z+1}}\right)^{7}+\cdots \right]\\&\approx {\frac {2}{T}}{\frac {z-1}{z+1}}\\&={\frac {2}{T}}{\frac {1-z^{-1}}{1+z^{-1}}}\end{aligned}}$

इस संबंध का उपयोग किसी भी एनालॉग फिल्टर के लैपलेस ट्रांसफर फ़ंक्शन या एनालॉग फिल्टर के डिजिटल अनंत आवेग प्रतिक्रिया (IIR) फ़िल्टर T(z) में किया जाता है।
बिलिनियर ट्रांसफॉर्म अनिवार्य रूप से इस पहले ऑर्डर सन्निकटन का उपयोग करता है और निरंतर-समय हस्तांतरण फ़ंक्शन में स्थानापन्न करता है, $H_{a}(s)$

$s\leftarrow {\frac {2}{T}}{\frac {z-1}{z+1}}.$

वह है

$H_{d}(z)=H_{a}(s){\bigg |}_{s={\frac {2}{T}}{\frac {z-1}{z+1}}}=H_{a}\left({\frac {2}{T}}{\frac {z-1}{z+1}}\right).\$

जिसका उपयोग आईआईआर डिजिटल फिल्टर की गणना के लिए किया जाता है, जो एनालॉग फिल्टर के लैपलेस ट्रांसफर फ़ंक्शन से शुरू होता है।

यह भी देखें

• स्वतः प्रतिगामी मॉडल
• इलेक्ट्रॉनिक फिल्टर
• परिमित आवेग प्रतिक्रिया
• पुनरावृत्ति संबंध , गणितीय औपचारिकता
• प्रणाली विश्लेषण

बाहरी संबंध

• The fifth module of the BORES Signal Processing DSP course - Introduction to DSP] at the Wayback Machine (archived July 2, 2016)
• IIR Digital Filter Design Applet at the Wayback Machine (archived February 13, 2010)
• IIR Digital Filter design tool - produces coefficients, graphs, poles, zeros, and C code
• EngineerJS Online IIR Design Tool - does not require Java