अनादर्श संपीड़ित द्रव गतिकी

डी डी लवल नोजल अपसारी खंड में मैक संख्या एम का गैर-मोनोटोनिक फ़ंक्शन विकास। द्रव सिलोक्सेन एमएम (हेक्सामेथिलडिसिलोक्सेन

{\ce {C6H18OSi2}}

है ) गैर-आदर्श गैसडायनामिक व्यवस्था में विकसित हो रहा है।

अनादर्श संपीड़ित द्रव गतिकी (एनआईसीएफडी), या अनादर्श संपीड़ित प्रवाह, द्रव यांत्रिकी की शाखा है जो आदर्श गैस या आदर्श-गैस थर्मोडायनामिक्स का पालन नहीं करने वाले द्रव पदार्थों के गतिशील व्यवहार का अध्ययन करती है। यह उदाहरण के लिए घने वाष्प, अत्यंत सूक्ष्म प्रवाह और संपीड़ित दो-चरण प्रवाह या दो-चरण प्रवाह की स्थिति है। इस प्रकार घने वाष्प शब्द के साथ, हम संतृप्ति और महत्वपूर्ण बिंदु (थर्मोडायनामिक्स) के निकट थर्मोडायनामिक स्थितियों की विशेषता वाले गैस में सभी द्रव पदार्थों को निरुपित करते हैं।^[1] अत्यंत सूक्ष्म द्रव पदार्थों में दाब और तापमान के मान उनके महत्वपूर्ण मानों से अधिक होते हैं,^[2] जबकि दो-चरण प्रवाह को द्रव और गैस दोनों चरणों की साथ उपस्थिति की विशेषता होती है।^[3] इन सभी स्थितियों में, द्रव पदार्थ को वास्तविक गैस के रूप में मॉडल करने की आवश्यकता होती है, क्योंकि इसका थर्मोडायनामिक व्यवहार आदर्श गैस से अधिक भिन्न होता है, जो इसके विपरीत पतला थर्मोडायनामिक स्थितियों के लिए प्रकट होता है। आदर्श-गैस नियम को सामान्य रूप से कम दाब और उच्च तापमान के लिए द्रव थर्मोडायनामिक्स के उचित अनुमान के रूप में नियोजित किया जा सकता है। अन्यथा, अंतर-आणविक बल और द्रव कणों का आयाम, जो आदर्श-गैस सन्निकटन में उपेक्षित हैं, प्रासंगिक हो जाते हैं और द्रव व्यवहार को महत्वपूर्ण रूप से प्रभावित कर सकते हैं।^[4] यह सम्मिश्र और भारी अणुओं से बनी गैसों के लिए अत्यधिक मान्य है, इस प्रकार जो आदर्श मॉडल से अधिक विचलित होती हैं।^[5] जबकि आदर्श परिस्थितियों में संपीड़ित प्रवाह की द्रव गतिकी अच्छी तरह से स्थापित है और विभिन्न विश्लेषणात्मक परिणामों की विशेषता है,^[6] जब गैर-आदर्श थर्मोडायनामिक स्थितियों पर विचार किया जाता है, जिससे संभवतः अद्वितीय घटनाएं घटित होती हैं। यह विशेष रूप से सुपरसोनिक गति स्थितियों में मान्य है, अर्थात् विचारित द्रव पदार्थ में ध्वनि की गति से अधिक प्रवाह वेग के लिए। सुपरसोनिक प्रवाह की सभी विशिष्ट विशेषताएं गैर-आदर्श थर्मोडायनामिक्स से प्रभावित होती हैं, जिसके परिणामस्वरूप आदर्श गैस गतिकी के संबंध में मानत्मक और गुणात्मक दोनों अंतर होते हैं।^[7]

गैर-आदर्श थर्मोडायनामिक्स

कम दाब और तापमान के विभिन्न मानो के लिए संपीड़न कारक Z।

पतले थर्मोडायनामिक स्थितियों के लिए, अवस्था का आदर्श-गैस समीकरण (ईओएस) द्रव थर्मोडायनामिक्स के मॉडलिंग में पर्याप्त स्पष्ट परिणाम प्रदान करता है। यह सामान्यतः कम दाब के कम मानो और कम तापमान के उच्च मानो के लिए होता है, जहां कम गुण शब्द निश्चित थर्मोडायनामिक मान और उसके महत्वपूर्ण मान के अनुपात को संदर्भित करता है। इस प्रकार वायु जैसे कुछ द्रव पदार्थों के लिए, आदर्श स्थितियों पर विचार करने की धारणा पूरी तरह से उचित है और इसका व्यापक रूप से उपयोग किया जाता है।^[6]

दूसरी ओर, जब थर्मोडायनामिक स्थितियां संक्षेपण और महत्वपूर्ण बिंदु तक पहुंचती हैं या जब उच्च दाब सम्मिलित होता है, तो वास्तविक द्रव व्यवहार को पकड़ने के लिए वास्तविक-गैस मॉडल की आवश्यकता होती है। इन स्थितियों में, वास्तव में, अंतर-आणविक बल और संपीड़न प्रभाव कार्य में आते हैं।^[4]

द्रव पदार्थ की गैर-आदर्शता का माप संपीड़न कारक $Z$ द्वारा दिया जाता है ^[8] जिसे इस प्रकार परिभाषित किया गया है

Z={\frac {Pv}{RT}}

जहाँ

$P$ दाब [Pa] है;
$v$ विशिष्ट आयतन [m³/kg] है;
$R$ विशिष्ट गैस स्थिरांक [J/(kg K)] है, अर्थात गैस स्थिरांक को द्रव के आणविक द्रव्यमान से विभाजित किया जाता है;
$T$ पूर्ण तापमान [K] है।

संपीड्यता कारक आयामहीन मान है जो आदर्श गैसों के लिए 1 के समान है और गैर-आदर्शता के बढ़ते स्तर के लिए एकता से विचलित हो जाती है।^[9] अवस्था के सबसे सरल घन समीकरणों (जैसे वैन डेर वाल्स समीकरण) से विभिन्न गैर-आदर्श मॉडल उपस्थित हैं ^[4]^[10] और पेंग-रॉबिन्सन समीकरण या पेंग-रॉबिन्सन ^[11] मॉडल) अवस्था के स्पैन-वैग्नर समीकरण सहित सम्मिश्र बहु-मापदंड वाले तक ^[12]^[13] अवस्था के अत्याधुनिक समीकरण थर्मोडायनामिक लाइब्रेरीज़, जैसे फ्लुइडप्रॉप या ओपन-सोर्स सॉफ़्टवेयर कूलप्रॉप के माध्यम से सरलता से पहुंच योग्य हैं।^[14]

गैर-आदर्श गैसगतिक व्यवस्थाएँ

संपीड़ित प्रवाह का गतिशील व्यवहार आयामहीन थर्मोडायनामिक मान $\Gamma$ द्वारा नियंत्रित होता है जिसे गैसडायनामिक्स के मौलिक व्युत्पन्न के रूप में जाना जाता है ^[15] और इसे इस प्रकार परिभाषित किया गया है

\Gamma ={\frac {v^{3}}{2c^{2}}}\left({\frac {\partial ^{2}P}{\partial v^{2}}}\right)_{s}=1+{\frac {c}{v}}\left({\frac {\partial c}{\partial P}}\right)_{s}

जहाँ

$c$ ध्वनि की गति [m/s] है ;
$s$ प्रति इकाई द्रव्यमान विशिष्ट एन्ट्रापी [J/(kg K)] है ।

गणितीय दृष्टिकोण से, मौलिक व्युत्पन्न दाब-आयतन आरेख या दाब-मान थर्मोडायनामिक विमान में इसेंट्रोपिक प्रक्रिया की वक्रता का गैर-आयामी माप है। इस प्रकार भौतिक दृष्टिकोण से, जिसकी परिभाषा $\Gamma$ बताता है कि ध्वनि की गति मानों के लिए आइसेंट्रोपिक परिवर्तनों में दाब $\Gamma >1$ के साथ बढ़ती है , जबकि, इसके विपरीत, यह दाब $\Gamma <1$ के साथ घटता जाता है .

$\Gamma$ के मान के आधार पर , तीन गैसडायनामिक व्यवस्थाों को परिभाषित किया जा सकता है:^[15]

$\Gamma >1$ के लिए आदर्श गैसडायनामिक व्यवस्था ;
$0<\Gamma <1$ के लिए गैर-आदर्श मौलिक गैसडायनामिक व्यवस्था ;
$\Gamma <0$ गैर-मौलिक गैसडायनामिक व्यवस्था .

आदर्श गैसडायनामिक व्यवस्था

आदर्श व्यवस्था में, सामान्य आदर्श-गैस व्यवहार गुणात्मक रूप से सही हो जाता है। एक आदर्श गैस के लिए, वास्तव में, मौलिक व्युत्पन्न का मान स्थिर मान $\Gamma ={\frac {\gamma +1}{2}}$ तक कम हो जाता है, जहां $\gamma$ ताप क्षमता अनुपात है। परिभाषा के अनुसार, $\gamma$ स्थिर दबाव और स्थिर आयतन विशिष्ट ऊष्मा के मध्य का अनुपात है, इसलिए यह 1 से बड़ा है, जिससे $\Gamma$ का मान भी 1 से बड़ा हो जाता है।^[6]

इस व्यवस्था में, आदर्श मॉडल के संबंध में केवल मानत्मक अंतर सामने आते हैं। वास्तव में प्रवाह विकास कुल, या मच नंबर, थर्मोडायनामिक स्थितियों पर निर्भर करता है। उदाहरण के लिए, डी लावल नोजल में आदर्श गैस का मैक संख्या विकास केवल ताप क्षमता अनुपात (अर्थात् द्रव पदार्थ पर) और निकास-से-स्थिर दाब अनुपात पर निर्भर करता है।^[6] इस प्रकार वास्तविक-गैस प्रभावों को ध्यान में रखते हुए, इसके अतिरिक्त, द्रव और दाब अनुपात को सही करने पर भी, भिन्न-भिन्न कुल अवस्थाएं भिन्न-भिन्न मैक प्रोफाइल उत्पन्न करती हैं।^[16] सामान्यतः, सरल अणुओं से बने एकल-चरण द्रव पदार्थों के लिए, केवल आदर्श गैसडायनामिक व्यवस्था तक पहुंचा जा सकता है, यहां तक कि संतृप्ति के बहुत निकट थर्मोडायनामिक स्थितियों के लिए भी उपयोग किया जाता है। उदाहरण के लिए, यह नाइट्रोजन या कार्बन डाईऑक्साइड जैसे डायटोमिक अणु या ट्रायटोमिक अणु अणुओं का स्थिति है, जो आदर्श व्यवहार से केवल छोटे विचलन का अनुभव कर सकते हैं।^[5]

गैर-आदर्श मौलिक गैसडायनामिक व्यवस्था

सिलोक्सेन द्रव के लिए कम दबाव-मात्रा थर्मोडायनामिक आरेखएमएम (हेक्सामेथिलडिसिलोक्सेन

{\ce {C6H18OSi2}}

) जिसमें द्रव-वाष्प संतृप्ति वक्र, कुछ आइसेंट्रोप्स और गैस गतिकी

\Gamma

गैर

0<\Gamma <1

के मौलिक व्युत्पन्न के कुछ आइसोलाइन सम्मिलित हैं) को संतृप्ति वक्र के निकट दिखाया गया है।

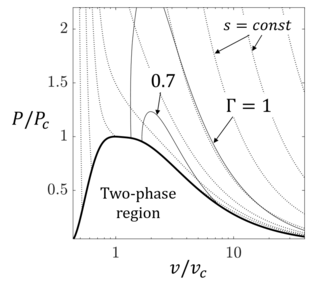
उच्च आणविक सम्मिश्रता वाले द्रव पदार्थों के लिए, अत्याधुनिक थर्मोडायनामिक मॉडल के मानो $0<\Gamma <1$ की पूर्वानुमान करते हैं संतृप्ति वक्र के निकट एकल-चरण क्षेत्र में, जहां ध्वनि की गति अधिक सीमा तक आइसेंट्रोप के साथ घनत्व भिन्नता के प्रति संवेदनशील होती है।^[17] ऐसे द्रव पदार्थ रासायनिक यौगिक के विभिन्न वर्गों से संबंधित होते हैं, जिनमें हाइड्रोकार्बन, सिलोक्सेन और शीतल सम्मिलित हैं।^[5]^[17] गैर-आदर्श व्यवस्था में, आदर्श गैसगतिकी के संबंध में भी गुणात्मक अंतर पाया जा सकता है, जिसका अर्थ है कि भिन्न-भिन्न कुल स्थितियों के लिए प्रवाह विकास दृढ़ता से भिन्न हो सकता है। इस प्रकार गैर-आदर्श व्यवस्था की सबसे अद्वितीय घटना सुपरसोनिक व्यवस्था में होने वाली आइसेंट्रोपिक विस्तृत में मैक संख्या में कमी है, अर्थात् ऐसी प्रक्रियाएं जिनमें द्रव घनत्व कम हो जाता है।^[18] वास्तव में, आदर्श गैस के लिए अभिसरण-अपसारी नोजल में आइसोट्रोपिक रूप से विस्तार होता है, घनत्व कम होने के साथ मैक संख्या एकरस रूप से बढ़ जाती है।^[6] इसके विपरीत, गैर-आदर्श व्यवस्था में विकसित होने वाले प्रवाह के लिए, अपसारी अनुभाग में गैर-मोनोटोन मैक संख्या विकास संभव है, जबकि घनत्व में कमी मोनोटोनिक बनी हुई है (लीड अनुभाग में चित्र देखें)। यह विशेष घटना मान $J$ द्वारा नियंत्रित होती है , जो आइसेंट्रोपिक प्रक्रियाओं में घनत्व के संबंध में मच संख्या व्युत्पन्न का गैर-आयामी माप है:^[18]

J={\frac {\rho }{M}}{\frac {dM}{d\rho }}=1-\Gamma -{\frac {1}{M^{2}}}

जहाँ

$M$ मच संख्या है;
$\rho$ घनत्व [kg/M³] है .

$J$ की परिभाषा से मानों की विशेषता वाली प्रवाह स्थितियों के लिए घनत्व $J>0$ के साथ मच संख्या बढ़ती है वास्तव में, यह केवल मानो $\Gamma <1$ के लिए ही संभव है , वह गैर-आदर्श व्यवस्था में है। चूंकि, गैर-मोनोटोन मच संख्या के प्रकट होने के लिए यह पर्याप्त स्थिति नहीं है, क्योंकि इसका मान पर्याप्त रूप से बड़ा है जहाँ $M$ भी आवश्यक है. विशेष रूप से, सुपरसोनिक स्थितियाँ ( $M>1$ ) आवश्यक हैं।^[18]

प्रांटल-मेयर विस्तार पंखे के चारों ओर विस्तार में समान प्रभाव का सामना करना पड़ता है: उपयुक्त थर्मोडायनामिक स्थितियों के लिए, रैंप के डाउनस्ट्रीम की मच संख्या अपस्ट्रीम से कम हो सकती है।^[19] इसके विपरीत, तिरछी शॉक तरंगें के पश्चात् की मच संख्या प्री-शॉक से बड़ी हो सकती है।^[20]

गैर-मौलिक गैस-गतिशील व्यवस्था

अंत में, उच्चतर आणविक सम्मिश्रता वाले द्रव पदार्थ संतृप्ति के निकट एकल-चरण वाष्प क्षेत्र में गैर-मौलिक व्यवहार प्रदर्शित कर सकते हैं। उन्हें भौतिक विज्ञानी हंस बेथे के नाम पर बेथे-ज़ेल्डोविच-थॉम्पसन (बीजेडटी) द्रव पदार्थ कहा जाता है।^[21] याकोव ज़ेल्डोविच या याकोव ज़ेल्डोविच,^[22] और फिलिप थॉम्पसन,^[23]^[24] जिन्होंने सबसे पहले इस प्रकार के द्रव पदार्थों पर कार्य किया था।

गैर-मौलिक व्यवस्था में पड़ी थर्मोडायनामिक स्थितियों के लिए, आइसेंट्रोपिक विस्तार में मच संख्या का गैर-मोनोटोन विकास सबसोनिक स्थितियों में भी पाया जा सकता है। वास्तव में, के मानो के लिए $\Gamma <0$ , के सकारात्मक मान $J$ सबसोनिक प्रवाह $M<1$ में भी पहुंचा जा सकता है दूसरे शब्दों में, आइसेंट्रोपिक नोजल के अभिसरण अनुभाग में गैर-मोनोटोन मैक संख्या विकास भी संभव है।^[24] इसके अतिरिक्त, गैर-मौलिक व्यवस्था की अद्वितीय घटना तथाकथित विपरीत गैस-गतिकी है। इस प्रकार मौलिक व्यवस्था में, विस्तार सुचारू आइसेंट्रोपिक प्रक्रियाएं हैं, जबकि संपीड़न शॉक तरंगें के माध्यम से होता है, जो प्रवाह में असंतुलन है। यदि गैस-गतिकी को विपरीत कर दिया जाता है, तो विपरीत होता है, अर्थात् रेयरफैक्शन शॉक तरंगें शारीरिक रूप से स्वीकार्य होती हैं और चिकनी आइसेंट्रोपिक प्रक्रियाओं के माध्यम से संपीड़न होता है।^[23]

$\Gamma$ के ऋणात्मक मान के परिणामस्वरूप , बीजेडटी द्रव पदार्थों के लिए दो अन्य अद्वितीय घटनाएं घटित हो सकती हैं: इस प्रकार शॉक स्प्लिटिंग और मिश्रित तरंगें है। शॉक स्प्लिटिंग तब होती है जब अस्वीकार्य दाब असंतोष दो सशक्त शॉक तरंगों को उत्पन्न करके समय के साथ विकसित होता है।^[25]^[26] इसके अतिरिक्त, समग्र तरंगों को उस घटना के रूप में संदर्भित किया जाता है जिसमें दो प्राथमिक तरंगें इकाई के रूप में विस्तृत होती हैं।^[7]^[27] इस प्रकार गैर-मौलिक गैस-गतिशील व्यवस्था का प्रायोगिक साक्ष्य अभी तक उपलब्ध नहीं है। मुख्य कारण ऐसी चुनौतीपूर्ण थर्मोडायनामिक स्थितियों में प्रयोग करने की सम्मिश्रता और इन बहुत सम्मिश्र अणुओं का तापीय अपघटन है।^[28]

अनुप्रयोग

गैर-आदर्श परिस्थितियों में संपीड़ित प्रवाह विभिन्न औद्योगिक और एयरोस्पेस अनुप्रयोगों में सामने आते हैं। उदाहरण के लिए इन्हें जैविक रैंकिन चक्र (ओआरसी) में नियोजित किया जाता है।^[29] और अत्यंत सूक्ष्म कार्बन डाइऑक्साइड (sCO₂) प्रणाली ^[30] विद्युत उत्पादन के लिए. एयरोस्पेस क्षेत्र में, संतृप्ति के निकट की स्थितियों में द्रव पदार्थ का उपयोग हाइब्रिड-प्रणोदक रॉकेट में ऑक्साइड के रूप में या रॉकेट इंजन नोजल की सतह को ठंडा करने के लिए किया जा सकता है।^[31] उच्च रेनॉल्ड्स संख्या प्राप्त करने के लिए वायु के अतिरिक्त उच्च आणविक द्रव्यमान के अणुओं से बनी गैसों का उपयोग सुपरसोनिक वायु सुरंग में किया जा सकता है।^[32] अंत में, गैर-आदर्श प्रवाह का उपयोग उच्च गति पर ईंधन परिवहन और CO₂ के अत्यंत सूक्ष्म समाधान (आरईएसएस) के तीव्र विस्तार में कणों के निर्माण या रसायनों के निष्कर्षण के लिए किया जाता है।^[33]

कार्बनिक रैंकिन चक्र

फिनलैंड के लप्पीनरन्ता में एलयूटी विश्वविद्यालय में ओआरसी टर्बो जनरेटर^[34]

सामान्य रैंकिन चक्र थर्मोडायनामिक चक्र हैं जो तापीय स्रोतों से विद्युत ऊर्जा का उत्पादन करने के लिए पानी को कार्यशील द्रव पदार्थ के रूप में नियोजित करते हैं।^[35] इस प्रकार इसके विपरीत, कार्बनिक रैंकिन चक्रों में, पानी को आणविक रूप से सम्मिश्र कार्बनिक यौगिक द्वारा प्रतिस्थापित किया जाता है। चूँकि इस प्रकार के द्रव पदार्थों का वाष्पीकरण तापमान वायुमंडलीय दाब पर पानी के वाष्पीकरण तापमान से कम होता है, इसलिए निम्न-से-मध्यम तापमान स्रोतों का उपयोग उष्म पुनर्प्राप्ति भाप जनरेटर के लिए किया जा सकता है, उदाहरण के लिए, बायोमास (ऊर्जा) दहन, औद्योगिक अपशिष्ट ताप से, या भूतापीय ऊर्जा.^[36] इन कारणों से, ओआरसी तकनीक नवीकरणीय ऊर्जा की श्रेणी से संबंधित है।

ओआरसी संयंत्रों में कार्य करने वाले टर्बाइन जैसे यांत्रिक घटकों के डिजाइन के लिए, विशिष्ट गैर-आदर्श गैस-गतिशील घटनाओं को ध्यान में रखना मौलिक है। वास्तव में, ओआरसी टरबाइन स्टेटर के इनलेट पर एकल-चरण वाष्प सामान्यतः द्रव-वाष्प संतृप्ति वक्र और महत्वपूर्ण बिंदु के निकट गैर-आदर्श थर्मोडायनामिक क्षेत्र में विकसित होता है। इस प्रकार इसके अतिरिक्त, नियोजित सम्मिश्र कार्बनिक यौगिकों के उच्च आणविक द्रव्यमान के कारण, इन द्रव पदार्थों में ध्वनि की गति वायु और अन्य सरल गैसों की तुलना में कम है। इसलिए, टरबाइन स्टेटर में सुपरसोनिक प्रवाह सम्मिलित होने की बहुत संभावना है, तथापि प्रवाह वेग कम हो जाता है ।^[37] उच्च सुपरसोनिक प्रवाह शॉक तरंगों की घटना के कारण टरबाइन ब्लेड में बड़े हानि और यांत्रिक तनाव (यांत्रिकी) उत्पन्न कर सकता है, जो सशक्त दाब बढ़ने का कारण बनता है।^[38] चूंकि, जब बीजेडटी वर्ग के कार्यशील द्रव पदार्थों को नियोजित किया जाता है, तो कुछ गैर-मौलिक घटनाओं का लाभ उठाकर विस्तारक प्रदर्शन में सुधार किया जा सकता है।^[39]^[40]

अत्यंत सूक्ष्म कार्बन डाइऑक्साइड चक्र

जब कार्बन डाइऑक्साइड को उसके क्रांतिक दाब (73.773 बार) से ऊपर रखा जाता है ^[41] और तापमान (30.9780 डिग्री सेल्सियस),^[41] यह गैस और द्रव दोनों के रूप में व्यवहार कर सकता है, अर्थात यह गैस की तरह अपने कंटेनर को पूर्ण रूप से भरने के लिए फैलता है किन्तु इसका घनत्व द्रव के समान होता है।

अत्यंत सूक्ष्म CO₂ रासायनिक स्थिरता है, बहुत सस्ता है, और ज्वलनशीलता और ज्वलनशीलता या गैर-ज्वलनशील है, जो इसे ट्रांसक्रिटिकल चक्र के लिए कार्यशील द्रव पदार्थ के रूप में उपयुक्त बनाता है।^[42] उदाहरण के लिए, इसका उपयोग घरेलू जल ताप पंप में किया जाता है, जो उच्च दक्षता तक पहुँच सकता है।^[42]

इसके अतिरिक्त, जब ब्रेटन चक्र और रैंकिन चक्रों को नियोजित करने वाले विद्युत उत्पादन संयंत्रों में उपयोग किया जाता है, जिससे यह दक्षता और विद्युत उत्पादन में सुधार कर सकता है। इस प्रकार इसका उच्च घनत्व टर्बोमशीन आयामों में सशक्त कमी को सक्षम बनाता है, फिर भी इन घटकों की उच्च दक्षता सुनिश्चित करता है। इसलिए सरल डिज़ाइन अपनाए जा सकते हैं, जबकि वाष्प टरबाइन को विभिन्न टरबाइन चरणों की आवश्यकता होती है, जो आवश्यक रूप से बड़े आयाम और निवेश उत्पन्न करते हैं।^[43] इसके विपरीत, sCO₂ के अन्दर यांत्रिक घटक ब्रेटन चक्र, विशेष रूप से टर्बोमशीनरी और उष्म रूपान्तरण, जंग से ग्रस्त हैं।^[44]

यह भी देखें

संपीड़ित प्रवाह
स्थिति के समीकरण
मच संख्या
जैविक रैंकिन चक्र
प्रांटल-मेयर विस्तार प्रशंसक
वास्तविक गैस
शॉक प्रवाह
अत्यंत सूक्ष्म कार्बन डाइऑक्साइड
सुपरसोनिक नोजल प्रवाह

संदर्भ

↑ Callen, Herbert B. (1985). थर्मोडायनामिक्स और थर्मोस्टैटिस्टिक्स का परिचय (2nd ed.). New York: J. Wiley & Sons. pp. 255–261. ISBN 978-0-471-86256-7.
↑ Schlosky, Kevin M. (1989). "बहुत उच्च दबाव पर सुपरक्रिटिकल चरण संक्रमण". Journal of Chemical Education (in English). 66 (12): 989. Bibcode:1989JChEd..66..989S. doi:10.1021/ed066p989. ISSN 0021-9584.
↑ Faghri, Amir; Zhang, Yuwen (2006-01-01), Faghri, Amir; Zhang, Yuwen (eds.), "Two-Phase Flow and Heat Transfer", Transport Phenomena in Multiphase Systems (in English), Boston: Academic Press, pp. 853–949, doi:10.1016/b978-0-12-370610-2.50016-7, ISBN 978-0-12-370610-2, S2CID 98384899, retrieved 2023-07-06
↑ ^{Jump up to: 4.0} ^4.1 ^4.2 Waals, J. D. van der; Rowlinson, John Shipley (1988). गैसीय और तरल अवस्थाओं की निरंतरता पर. Studies in statistical mechanics. Amsterdam: North-Holland. ISBN 978-0-444-87077-3.
↑ ^{Jump up to: 5.0} ^5.1 ^5.2 Colonna, P.; Guardone, A. (2006). "वैन डेर वाल्स मॉडल के तहत घने वाष्प की गैर-शास्त्रीय गैस गतिशीलता की आणविक व्याख्या". Physics of Fluids. 18 (5): 056101–056101–14. Bibcode:2006PhFl...18e6101C. doi:10.1063/1.2196095. ISSN 1070-6631.
↑ ^{Jump up to: 6.0} ^6.1 ^6.2 ^6.3 ^6.4 Thompson, Philip A. (1972). संपीड़ित-द्रव गतिशीलता. Advanced engineering series. New York: McGraw-Hill. pp. 76–99. ISBN 978-0-07-064405-2.
↑ ^{Jump up to: 7.0} ^7.1 Menikoff, Ralph; Plohr, Bradley J. (1989-01-01). "वास्तविक सामग्रियों के द्रव प्रवाह के लिए रीमैन समस्या". Reviews of Modern Physics. 61 (1): 75–130. Bibcode:1989RvMP...61...75M. doi:10.1103/revmodphys.61.75. ISSN 0034-6861.
↑ Zucker, Robert D.; Biblarz, Oscar (2002). गैस गतिकी के मूल सिद्धांत (2nd ed.). Hoboken, NJ: Wiley. p. 327. ISBN 978-0-471-05967-7.
↑ Thompson, Philip A. (1972). संपीड़ित-द्रव गतिशीलता. Advanced engineering series. New York: McGraw-Hill. pp. 99–101. ISBN 978-0-07-064405-2.
↑ Parsegian, V. Adrian (2005). Van der Waals Forces: A Handbook for Biologists, Chemists, Engineers, and Physicists. Cambridge: Cambridge University Press. doi:10.1017/cbo9780511614606. ISBN 978-0-521-83906-8.
↑ Peng, Ding-Yu; Robinson, Donald B. (February 1976). "राज्य का एक नया दो-स्थिर समीकरण". Industrial & Engineering Chemistry Fundamentals (in English). 15 (1): 59–64. doi:10.1021/i160057a011. ISSN 0196-4313. S2CID 98225845.
↑ Span, R.; Wagner, W. (2003-01-01). "तकनीकी अनुप्रयोगों के लिए राज्य के समीकरण. I. गैर-ध्रुवीय और ध्रुवीय तरल पदार्थों के लिए एक साथ अनुकूलित कार्यात्मक रूप". International Journal of Thermophysics (in English). 24 (1): 1–39. doi:10.1023/A:1022390430888. ISSN 1572-9567. S2CID 116961558.
↑ Span, Roland (2000), "Describing Mixtures with Multiparameter Equations of State", Multiparameter Equations of State, Berlin, Heidelberg: Springer Berlin Heidelberg, pp. 319–340, doi:10.1007/978-3-662-04092-8_8, ISBN 978-3-642-08671-7, retrieved 2023-07-05
↑ Bell, Ian H.; Wronski, Jorrit; Quoilin, Sylvain; Lemort, Vincent (2014-01-27). "शुद्ध और छद्म-शुद्ध द्रव थर्मोफिजिकल संपत्ति मूल्यांकन और ओपन-सोर्स थर्मोफिजिकल संपत्ति लाइब्रेरी कूलप्रॉप". Industrial & Engineering Chemistry Research. 53 (6): 2498–2508. doi:10.1021/ie4033999. ISSN 0888-5885. PMC 3944605. PMID 24623957.
↑ ^{Jump up to: 15.0} ^15.1 Thompson, Philip A. (1971). "गैसडायनामिक्स में एक मौलिक व्युत्पन्न". Physics of Fluids. 14 (9): 1843–1849. Bibcode:1971PhFl...14.1843T. doi:10.1063/1.1693693. ISSN 0031-9171.
↑ Tsien, Hsue-Shen (1946). "वेंडर वाल के राज्य समीकरण द्वारा विशेषता गैस का एक-आयामी प्रवाह". Journal of Mathematics and Physics. 25 (1–4): 301–324. doi:10.1002/sapm1946251301. ISSN 0097-1421.
↑ ^{Jump up to: 17.0} ^17.1 Kluwick, Alfred (2004-05-01). "सघन गैसों का आंतरिक प्रवाह". Acta Mechanica. 169 (1–4): 123–143. doi:10.1007/s00707-004-0096-z. ISSN 0001-5970. S2CID 121634296.
↑ ^{Jump up to: 18.0} ^18.1 ^18.2 Cramer, M. S.; Best, L. M. (1991). "सघन गैसों का स्थिर, आइसेंट्रोपिक प्रवाह". Physics of Fluids A: Fluid Dynamics. 3 (1): 219–226. Bibcode:1991PhFlA...3..219C. doi:10.1063/1.857855. ISSN 0899-8213.
↑ Cramer, M. S.; Crickenberger, A. B. (1992). "सघन गैसों के लिए प्रांटल-मेयर फ़ंक्शन". AIAA Journal. 30 (2): 561–564. Bibcode:1992AIAAJ..30..561C. doi:10.2514/3.10956. ISSN 0001-1452.
↑ Vimercati, Davide; Gori, Giulio; Guardone, Alberto (2018-05-21). "गैर-आदर्श तिरछी शॉक तरंगें". Journal of Fluid Mechanics. 847: 266–285. Bibcode:2018JFM...847..266V. doi:10.1017/jfm.2018.328. hdl:11311/1063005. ISSN 0022-1120. S2CID 125447693.
↑ Bethe, H. A. (1998), "On the Theory of Shock Waves for an Arbitrary Equation of State", Classic Papers in Shock Compression Science, New York, NY: Springer New York, pp. 421–495, doi:10.1007/978-1-4612-2218-7_11, ISBN 978-1-4612-7461-2, retrieved 2023-07-05
↑ "14. On the Possibility of Rarefaction Shock Waves", Selected Works of Yakov Borisovich Zeldovich, Volume I, Princeton University Press, pp. 152–154, 1992-12-31, doi:10.1515/9781400862979.152, ISBN 9781400862979, retrieved 2023-07-05
↑ ^{Jump up to: 23.0} ^23.1 Thompson, P. A.; Lambrakis, K. C. (1973-08-21). "नकारात्मक आघात तरंगें". Journal of Fluid Mechanics. 60 (1): 187–208. Bibcode:1973JFM....60..187T. doi:10.1017/s002211207300011x. ISSN 0022-1120. S2CID 123608377.
↑ ^{Jump up to: 24.0} ^24.1 Lambrakis, Konstantine C. (1972). "Existence of Real Fluids with a Negative Fundamental Derivative Γ". Physics of Fluids. 15 (5): 933–935. Bibcode:1972PhFl...15..933L. doi:10.1063/1.1694004. ISSN 0031-9171.
↑ Cramer, M. S. (February 1989). "एकल-चरण गैसों में शॉक विभाजन". Journal of Fluid Mechanics. 199: 281–296. Bibcode:1989JFM...199..281C. doi:10.1017/s0022112089000388. ISSN 0022-1120. S2CID 124690578.
↑ Cramer, M. S. (1991), "Nonclassical Dynamics of Classical Gases", Nonlinear Waves in Real Fluids, Vienna: Springer Vienna, pp. 91–145, doi:10.1007/978-3-7091-2608-0_5, ISBN 978-3-211-82277-7, retrieved 2023-07-05
↑ KLUWICK, ALFRED (2001), "Rarefaction Shocks", Handbook of Shock Waves, Elsevier, pp. 339–411, doi:10.1016/b978-012086430-0/50008-7, ISBN 9780120864300
↑ Borisov, A. A.; Borisov, Al. A.; Kutateladze, S. S.; Nakoryakov, V. E. (January 1983). "Rarefaction shock wave near the critical liquid–vapour point". Journal of Fluid Mechanics. 126: 59–73. Bibcode:1983JFM...126...59B. doi:10.1017/s002211208300004x. ISSN 0022-1120. S2CID 123399921.
↑ Angelino, G.; Invernizzi, C.; Macchi, E. (1991), "Organic Working Fluid Optimization for Space Power Cycles", Modern Research Topics in Aerospace Propulsion, New York, NY: Springer New York, pp. 297–326, doi:10.1007/978-1-4612-0945-4_16, ISBN 978-1-4612-6956-4, retrieved 2023-07-05
↑ Feher, E.G. (1968). "सुपरक्रिटिकल थर्मोडायनामिक पावर चक्र". Energy Conversion. 8 (2): 85–90. doi:10.1016/0013-7480(68)90105-8. ISSN 0013-7480.
↑ "Rocket Propulsion Elements. 2nd edition. George P. Sutton. J. Wiley and Sons Inc., New York, 1956. 483 pp. Illustrated. 82s". The Journal of the Royal Aeronautical Society. 61 (559): 503. 1957. doi:10.1017/s0368393100128512. ISSN 0368-3931.
↑ Sagnier, P.; Vérant, J.-L. (1998). "उच्च एन्थैल्पी पवन सुरंग सिमुलेशन के सत्यापन पर". Aerospace Science and Technology. 2 (7): 425–437. doi:10.1016/s1270-9638(99)80002-9. ISSN 1270-9638.
↑ Helfgen, B.; Türk, M.; Schaber, K. (2003). "सुपरक्रिटिकल समाधानों के तीव्र विस्तार की हाइड्रोडायनामिक और एयरोसोल मॉडलिंग (आरईएसएस-प्रक्रिया)". The Journal of Supercritical Fluids. 26 (3): 225–242. doi:10.1016/s0896-8446(02)00159-6. ISSN 0896-8446.
↑ Turunen-Saaresti, Teemu; Uusitalo, Antti; Honkatukia, Juha (2017). "कार्यशील तरल पदार्थ के रूप में सिलोक्सेन का उपयोग करके उच्च तापमान माइक्रो-ओआरसी परीक्षण स्टैंड का डिजाइन और परीक्षण". Journal of Physics: Conference Series. 821 (1): 012024. Bibcode:2017JPhCS.821a2024T. doi:10.1088/1742-6596/821/1/012024. ISSN 1742-6588. S2CID 114806415.
↑ Saitoh, T.S.; Hoshi, A. (2004). "Proposed solar Rankine cycle system with phase change steam accumulator and CPC solar collector". IECEC '02. 2002 37th Intersociety Energy Conversion Engineering Conference, 2002. IEEE. pp. 725–730. doi:10.1109/iecec.2002.1392137. ISBN 0-7803-7296-4. S2CID 110987716.{{cite book}}: CS1 maint: date and year (link)
↑ Quoilin, Sylvain; Broek, Martijn Van Den; Declaye, Sébastien; Dewallef, Pierre; Lemort, Vincent (2013). "ऑर्गेनिक रैंकिन साइकिल (ओआरसी) प्रणालियों का तकनीकी-आर्थिक सर्वेक्षण". Renewable and Sustainable Energy Reviews. 22: 168–186. doi:10.1016/j.rser.2013.01.028. ISSN 1364-0321.
↑ Brown, Brady; Argrow, Brian (1999-01-11). "कार्बनिक रैंकिन चक्र इंजनों में बेथे-ज़ेल्डोविच-थॉम्पसन तरल पदार्थ का अनुप्रयोग". 37th Aerospace Sciences Meeting and Exhibit. Reston, Virigina: American Institute of Aeronautics and Astronautics. doi:10.2514/6.1999-462.
↑ Denton, J. D.; Xu, L. (1989-06-04). "ट्रांसोनिक टर्बाइन ब्लेड्स का ट्रेलिंग एज लॉस". Volume 1: Turbomachinery. American Society of Mechanical Engineers. doi:10.1115/89-gt-278. ISBN 978-0-7918-7913-9. S2CID 111017969.
↑ Kluwick, A. (1994), "Interacting laminar boundary layers of dense gases", Fluid- and Gasdynamics, Vienna: Springer Vienna, pp. 335–349, doi:10.1007/978-3-7091-9310-5_37, ISBN 978-3-211-82495-5, retrieved 2023-07-06
↑ CRAMER, M. S.; PARK, S. (1999). "On the suppression of shock-induced separation in Bethe–Zel'dovich–Thompson fluids". Journal of Fluid Mechanics. 393 (1): 1–21. Bibcode:1999JFM...393....1C. doi:10.1017/s0022112099005479. ISSN 0022-1120. S2CID 122254018.
↑ ^{Jump up to: 41.0} ^41.1 Span, Roland; Wagner, Wolfgang (1996-11-01). "A New Equation of State for Carbon Dioxide Covering the Fluid Region from the Triple-Point Temperature to 1100 K at Pressures up to 800 MPa". Journal of Physical and Chemical Reference Data. 25 (6): 1509–1596. doi:10.1063/1.555991. ISSN 0047-2689.
↑ ^{Jump up to: 42.0} ^42.1 Ma, Yitai; Liu, Zhongyan; Tian, Hua (2013). "ट्रांसक्रिटिकल कार्बन डाइऑक्साइड ताप पंप और प्रशीतन चक्र की समीक्षा". Energy. 55: 156–172. doi:10.1016/j.energy.2013.03.030. ISSN 0360-5442.
↑ Fleming, Darryn; Pasch, Jim; Conboy, Thomas; Carlson, Matt (2013-06-03). "Testing Platform and Commercialization Plan for Heat Exchanging Systems for SCO2 Power Cycles". Volume 8: Supercritical CO2 Power Cycles; Wind Energy; Honors and Awards. American Society of Mechanical Engineers. doi:10.1115/gt2013-95125. ISBN 978-0-7918-5529-4. OSTI 1115493.
↑ Fleming, Darryn; Kruizenga, Alan; Pasch, James; Conboy, Tom; Carlson, Matt (2014-06-16). "Corrosion and Erosion Behavior in Supercritical CO2 Power Cycles". Volume 3B: Oil and Gas Applications; Organic Rankine Cycle Power Systems; Supercritical CO2 Power Cycles; Wind Energy. American Society of Mechanical Engineers. doi:10.1115/gt2014-25136. ISBN 978-0-7918-4566-0. OSTI 1221554.

अग्रिम पठन

Anderson, John David (2003). Modern Compressible Flow: With Historical Perspective (in English). McGraw-Hill.
di Mare, Francesca; Spinelli, Andrea; Pini, Matteo (2018). Non-Ideal Compressible Fluid Dynamics for Propulsion and Power (in English). Springer Link.
Feher, E.G. (1968). "The supercritical thermodynamic power cycle". Energy Conversion. 8 (2): 85–90. doi:10.1016/0013-7480(68)90105-8.
Kluwick, Alfred (2017). "Non-Ideal Compressible Fluid Dynamics: A Challenge for Theory". Journal of Physics. 821 (1): 012001. Bibcode:2017JPhCS.821a2001K. doi:10.1088/1742-6596/821/1/012001. S2CID 125325704.
Macchi, Ennio; Astolfi, Marco (2016). Organic Rankine Cycle (ORC) Power Systems (in English) (1st ed.). Elsevier. ISBN 9780081005101.

बाहरी संबंध

[1] Callen, Herbert B. (1985). थर्मोडायनामिक्स और थर्मोस्टैटिस्टिक्स का परिचय (2nd ed.). New York: J. Wiley & Sons. pp. 255–261. ISBN 978-0-471-86256-7.

[2] Schlosky, Kevin M. (1989). "बहुत उच्च दबाव पर सुपरक्रिटिकल चरण संक्रमण". Journal of Chemical Education (in English). 66 (12): 989. Bibcode:1989JChEd..66..989S. doi:10.1021/ed066p989. ISSN 0021-9584.

[3] Faghri, Amir; Zhang, Yuwen (2006-01-01), Faghri, Amir; Zhang, Yuwen (eds.), "Two-Phase Flow and Heat Transfer", Transport Phenomena in Multiphase Systems (in English), Boston: Academic Press, pp. 853–949, doi:10.1016/b978-0-12-370610-2.50016-7, ISBN 978-0-12-370610-2, S2CID 98384899, retrieved 2023-07-06

[:0-4] {Jump up to: 4.0} ^4.1 ^4.2 Waals, J. D. van der; Rowlinson, John Shipley (1988). गैसीय और तरल अवस्थाओं की निरंतरता पर. Studies in statistical mechanics. Amsterdam: North-Holland. ISBN 978-0-444-87077-3.

[:3-5] {Jump up to: 5.0} ^5.1 ^5.2 Colonna, P.; Guardone, A. (2006). "वैन डेर वाल्स मॉडल के तहत घने वाष्प की गैर-शास्त्रीय गैस गतिशीलता की आणविक व्याख्या". Physics of Fluids. 18 (5): 056101–056101–14. Bibcode:2006PhFl...18e6101C. doi:10.1063/1.2196095. ISSN 1070-6631.

[:4-6] {Jump up to: 6.0} ^6.1 ^6.2 ^6.3 ^6.4 Thompson, Philip A. (1972). संपीड़ित-द्रव गतिशीलता. Advanced engineering series. New York: McGraw-Hill. pp. 76–99. ISBN 978-0-07-064405-2.

[:1-7] {Jump up to: 7.0} ^7.1 Menikoff, Ralph; Plohr, Bradley J. (1989-01-01). "वास्तविक सामग्रियों के द्रव प्रवाह के लिए रीमैन समस्या". Reviews of Modern Physics. 61 (1): 75–130. Bibcode:1989RvMP...61...75M. doi:10.1103/revmodphys.61.75. ISSN 0034-6861.

[8] Zucker, Robert D.; Biblarz, Oscar (2002). गैस गतिकी के मूल सिद्धांत (2nd ed.). Hoboken, NJ: Wiley. p. 327. ISBN 978-0-471-05967-7.

[9] Thompson, Philip A. (1972). संपीड़ित-द्रव गतिशीलता. Advanced engineering series. New York: McGraw-Hill. pp. 99–101. ISBN 978-0-07-064405-2.

[10] Parsegian, V. Adrian (2005). Van der Waals Forces: A Handbook for Biologists, Chemists, Engineers, and Physicists. Cambridge: Cambridge University Press. doi:10.1017/cbo9780511614606. ISBN 978-0-521-83906-8.

[11] Peng, Ding-Yu; Robinson, Donald B. (February 1976). "राज्य का एक नया दो-स्थिर समीकरण". Industrial & Engineering Chemistry Fundamentals (in English). 15 (1): 59–64. doi:10.1021/i160057a011. ISSN 0196-4313. S2CID 98225845.

[12] Span, R.; Wagner, W. (2003-01-01). "तकनीकी अनुप्रयोगों के लिए राज्य के समीकरण. I. गैर-ध्रुवीय और ध्रुवीय तरल पदार्थों के लिए एक साथ अनुकूलित कार्यात्मक रूप". International Journal of Thermophysics (in English). 24 (1): 1–39. doi:10.1023/A:1022390430888. ISSN 1572-9567. S2CID 116961558.

[13] Span, Roland (2000), "Describing Mixtures with Multiparameter Equations of State", Multiparameter Equations of State, Berlin, Heidelberg: Springer Berlin Heidelberg, pp. 319–340, doi:10.1007/978-3-662-04092-8_8, ISBN 978-3-642-08671-7, retrieved 2023-07-05

[:5-14] Bell, Ian H.; Wronski, Jorrit; Quoilin, Sylvain; Lemort, Vincent (2014-01-27). "शुद्ध और छद्म-शुद्ध द्रव थर्मोफिजिकल संपत्ति मूल्यांकन और ओपन-सोर्स थर्मोफिजिकल संपत्ति लाइब्रेरी कूलप्रॉप". Industrial & Engineering Chemistry Research. 53 (6): 2498–2508. doi:10.1021/ie4033999. ISSN 0888-5885. PMC 3944605. PMID 24623957.

[:6-15] {Jump up to: 15.0} ^15.1 Thompson, Philip A. (1971). "गैसडायनामिक्स में एक मौलिक व्युत्पन्न". Physics of Fluids. 14 (9): 1843–1849. Bibcode:1971PhFl...14.1843T. doi:10.1063/1.1693693. ISSN 0031-9171.

[16] Tsien, Hsue-Shen (1946). "वेंडर वाल के राज्य समीकरण द्वारा विशेषता गैस का एक-आयामी प्रवाह". Journal of Mathematics and Physics. 25 (1–4): 301–324. doi:10.1002/sapm1946251301. ISSN 0097-1421.

[:7-17] {Jump up to: 17.0} ^17.1 Kluwick, Alfred (2004-05-01). "सघन गैसों का आंतरिक प्रवाह". Acta Mechanica. 169 (1–4): 123–143. doi:10.1007/s00707-004-0096-z. ISSN 0001-5970. S2CID 121634296.

[:8-18] {Jump up to: 18.0} ^18.1 ^18.2 Cramer, M. S.; Best, L. M. (1991). "सघन गैसों का स्थिर, आइसेंट्रोपिक प्रवाह". Physics of Fluids A: Fluid Dynamics. 3 (1): 219–226. Bibcode:1991PhFlA...3..219C. doi:10.1063/1.857855. ISSN 0899-8213.

[19] Cramer, M. S.; Crickenberger, A. B. (1992). "सघन गैसों के लिए प्रांटल-मेयर फ़ंक्शन". AIAA Journal. 30 (2): 561–564. Bibcode:1992AIAAJ..30..561C. doi:10.2514/3.10956. ISSN 0001-1452.

[20] Vimercati, Davide; Gori, Giulio; Guardone, Alberto (2018-05-21). "गैर-आदर्श तिरछी शॉक तरंगें". Journal of Fluid Mechanics. 847: 266–285. Bibcode:2018JFM...847..266V. doi:10.1017/jfm.2018.328. hdl:11311/1063005. ISSN 0022-1120. S2CID 125447693.

[21] Bethe, H. A. (1998), "On the Theory of Shock Waves for an Arbitrary Equation of State", Classic Papers in Shock Compression Science, New York, NY: Springer New York, pp. 421–495, doi:10.1007/978-1-4612-2218-7_11, ISBN 978-1-4612-7461-2, retrieved 2023-07-05

[22] "14. On the Possibility of Rarefaction Shock Waves", Selected Works of Yakov Borisovich Zeldovich, Volume I, Princeton University Press, pp. 152–154, 1992-12-31, doi:10.1515/9781400862979.152, ISBN 9781400862979, retrieved 2023-07-05

[:2-23] {Jump up to: 23.0} ^23.1 Thompson, P. A.; Lambrakis, K. C. (1973-08-21). "नकारात्मक आघात तरंगें". Journal of Fluid Mechanics. 60 (1): 187–208. Bibcode:1973JFM....60..187T. doi:10.1017/s002211207300011x. ISSN 0022-1120. S2CID 123608377.

[:9-24] {Jump up to: 24.0} ^24.1 Lambrakis, Konstantine C. (1972). "Existence of Real Fluids with a Negative Fundamental Derivative Γ". Physics of Fluids. 15 (5): 933–935. Bibcode:1972PhFl...15..933L. doi:10.1063/1.1694004. ISSN 0031-9171.

[25] Cramer, M. S. (February 1989). "एकल-चरण गैसों में शॉक विभाजन". Journal of Fluid Mechanics. 199: 281–296. Bibcode:1989JFM...199..281C. doi:10.1017/s0022112089000388. ISSN 0022-1120. S2CID 124690578.

[26] Cramer, M. S. (1991), "Nonclassical Dynamics of Classical Gases", Nonlinear Waves in Real Fluids, Vienna: Springer Vienna, pp. 91–145, doi:10.1007/978-3-7091-2608-0_5, ISBN 978-3-211-82277-7, retrieved 2023-07-05

[27] KLUWICK, ALFRED (2001), "Rarefaction Shocks", Handbook of Shock Waves, Elsevier, pp. 339–411, doi:10.1016/b978-012086430-0/50008-7, ISBN 9780120864300

[28] Borisov, A. A.; Borisov, Al. A.; Kutateladze, S. S.; Nakoryakov, V. E. (January 1983). "Rarefaction shock wave near the critical liquid–vapour point". Journal of Fluid Mechanics. 126: 59–73. Bibcode:1983JFM...126...59B. doi:10.1017/s002211208300004x. ISSN 0022-1120. S2CID 123399921.

[29] Angelino, G.; Invernizzi, C.; Macchi, E. (1991), "Organic Working Fluid Optimization for Space Power Cycles", Modern Research Topics in Aerospace Propulsion, New York, NY: Springer New York, pp. 297–326, doi:10.1007/978-1-4612-0945-4_16, ISBN 978-1-4612-6956-4, retrieved 2023-07-05

[30] Feher, E.G. (1968). "सुपरक्रिटिकल थर्मोडायनामिक पावर चक्र". Energy Conversion. 8 (2): 85–90. doi:10.1016/0013-7480(68)90105-8. ISSN 0013-7480.

[31] "Rocket Propulsion Elements. 2nd edition. George P. Sutton. J. Wiley and Sons Inc., New York, 1956. 483 pp. Illustrated. 82s". The Journal of the Royal Aeronautical Society. 61 (559): 503. 1957. doi:10.1017/s0368393100128512. ISSN 0368-3931.

[32] Sagnier, P.; Vérant, J.-L. (1998). "उच्च एन्थैल्पी पवन सुरंग सिमुलेशन के सत्यापन पर". Aerospace Science and Technology. 2 (7): 425–437. doi:10.1016/s1270-9638(99)80002-9. ISSN 1270-9638.

[33] Helfgen, B.; Türk, M.; Schaber, K. (2003). "सुपरक्रिटिकल समाधानों के तीव्र विस्तार की हाइड्रोडायनामिक और एयरोसोल मॉडलिंग (आरईएसएस-प्रक्रिया)". The Journal of Supercritical Fluids. 26 (3): 225–242. doi:10.1016/s0896-8446(02)00159-6. ISSN 0896-8446.

[34] Turunen-Saaresti, Teemu; Uusitalo, Antti; Honkatukia, Juha (2017). "कार्यशील तरल पदार्थ के रूप में सिलोक्सेन का उपयोग करके उच्च तापमान माइक्रो-ओआरसी परीक्षण स्टैंड का डिजाइन और परीक्षण". Journal of Physics: Conference Series. 821 (1): 012024. Bibcode:2017JPhCS.821a2024T. doi:10.1088/1742-6596/821/1/012024. ISSN 1742-6588. S2CID 114806415.

[35] Saitoh, T.S.; Hoshi, A. (2004). "Proposed solar Rankine cycle system with phase change steam accumulator and CPC solar collector". IECEC '02. 2002 37th Intersociety Energy Conversion Engineering Conference, 2002. IEEE. pp. 725–730. doi:10.1109/iecec.2002.1392137. ISBN 0-7803-7296-4. S2CID 110987716.{{cite book}}: CS1 maint: date and year (link)

[36] Quoilin, Sylvain; Broek, Martijn Van Den; Declaye, Sébastien; Dewallef, Pierre; Lemort, Vincent (2013). "ऑर्गेनिक रैंकिन साइकिल (ओआरसी) प्रणालियों का तकनीकी-आर्थिक सर्वेक्षण". Renewable and Sustainable Energy Reviews. 22: 168–186. doi:10.1016/j.rser.2013.01.028. ISSN 1364-0321.

[37] Brown, Brady; Argrow, Brian (1999-01-11). "कार्बनिक रैंकिन चक्र इंजनों में बेथे-ज़ेल्डोविच-थॉम्पसन तरल पदार्थ का अनुप्रयोग". 37th Aerospace Sciences Meeting and Exhibit. Reston, Virigina: American Institute of Aeronautics and Astronautics. doi:10.2514/6.1999-462.

[38] Denton, J. D.; Xu, L. (1989-06-04). "ट्रांसोनिक टर्बाइन ब्लेड्स का ट्रेलिंग एज लॉस". Volume 1: Turbomachinery. American Society of Mechanical Engineers. doi:10.1115/89-gt-278. ISBN 978-0-7918-7913-9. S2CID 111017969.

[39] Kluwick, A. (1994), "Interacting laminar boundary layers of dense gases", Fluid- and Gasdynamics, Vienna: Springer Vienna, pp. 335–349, doi:10.1007/978-3-7091-9310-5_37, ISBN 978-3-211-82495-5, retrieved 2023-07-06

[40] CRAMER, M. S.; PARK, S. (1999). "On the suppression of shock-induced separation in Bethe–Zel'dovich–Thompson fluids". Journal of Fluid Mechanics. 393 (1): 1–21. Bibcode:1999JFM...393....1C. doi:10.1017/s0022112099005479. ISSN 0022-1120. S2CID 122254018.

[:10-41] {Jump up to: 41.0} ^41.1 Span, Roland; Wagner, Wolfgang (1996-11-01). "A New Equation of State for Carbon Dioxide Covering the Fluid Region from the Triple-Point Temperature to 1100 K at Pressures up to 800 MPa". Journal of Physical and Chemical Reference Data. 25 (6): 1509–1596. doi:10.1063/1.555991. ISSN 0047-2689.

[:11-42] {Jump up to: 42.0} ^42.1 Ma, Yitai; Liu, Zhongyan; Tian, Hua (2013). "ट्रांसक्रिटिकल कार्बन डाइऑक्साइड ताप पंप और प्रशीतन चक्र की समीक्षा". Energy. 55: 156–172. doi:10.1016/j.energy.2013.03.030. ISSN 0360-5442.

[43] Fleming, Darryn; Pasch, Jim; Conboy, Thomas; Carlson, Matt (2013-06-03). "Testing Platform and Commercialization Plan for Heat Exchanging Systems for SCO2 Power Cycles". Volume 8: Supercritical CO2 Power Cycles; Wind Energy; Honors and Awards. American Society of Mechanical Engineers. doi:10.1115/gt2013-95125. ISBN 978-0-7918-5529-4. OSTI 1115493.

[44] Fleming, Darryn; Kruizenga, Alan; Pasch, James; Conboy, Tom; Carlson, Matt (2014-06-16). "Corrosion and Erosion Behavior in Supercritical CO2 Power Cycles". Volume 3B: Oil and Gas Applications; Organic Rankine Cycle Power Systems; Supercritical CO2 Power Cycles; Wind Energy. American Society of Mechanical Engineers. doi:10.1115/gt2014-25136. ISBN 978-0-7918-4566-0. OSTI 1221554.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[20]

[21]

[22]

[23]

[24]

[25]

[26]

[27]

[28]

[29]

[30]

[31]

[32]

[33]

[34]

[35]

[36]

[37]

[38]

[39]

[40]

[41]

[42]

[43]

[44]

Anonymous

Search

अनादर्श संपीड़ित द्रव गतिकी

Namespaces

More

Page actions

Contents

गैर-आदर्श थर्मोडायनामिक्स