कार्य (भौतिकी)
| Part of a series on |
| चिरसम्मत यांत्रिकी |
|---|
भौतिकी में, कार्य विस्थापन (सदिश) के साथ बल के प्रयोग के माध्यम से किसी वस्तु से या किसी वस्तु में स्थानांतरित ऊर्जा है। अपने सरलतम रूप में, गति की दिशा के साथ संरेखित निरंतर बल के लिए, कार्य बल की शक्ति और तय की गई दूरी के उत्पाद के बराबर होता है। बल को 'धनात्मक कार्य' करने के लिए कहा जाता है यदि लागू होने पर आवेदन के बिंदु के विस्थापन की दिशा में इसका घटक होता है। इस प्रकार बल के आवेदन के बिंदु पर विस्थापन की दिशा के विपरीत घटक होने पर बल 'ऋणात्मक कार्य' करता है।[1] उदाहरण के लिए, जब गेंद को जमीन के ऊपर रखा जाता है और फिर गिरा दिया जाता है, तो गेंद पर गुरुत्वाकर्षण बल द्वारा किया गया कार्य धनात्मक होता है, और यह गेंद के भार के बराबर होता है, इस प्रकार जो गेंद की दूरी से गुणा करके प्राप्त होता है। यदि गेंद को ऊपर की ओर फेंका जाता है, तो उसके भार द्वारा किया गया कार्य ऋणात्मक होता है, और इस प्रकार ऊपर की दिशा में विस्थापन द्वारा भार के गुणनफल के बराबर होता है।
जब बल F स्थिर है और बल और विस्थापन s के बीच का कोण θ है, तो इस प्रकार किया गया कार्य इस प्रकार दिया जाता है:
कार्य अदिश राशि (भौतिकी) है,[2] इसलिए इसका केवल परिमाण है और इस प्रकार कोई दिशा नहीं होती है। कार्य ऊर्जा को स्थान से दूसरे स्थान पर या रूप से दूसरे रूप में स्थानांतरित करता है। इस प्रकार कार्य की SI इकाई जूल (J) है, वही इकाई ऊर्जा की है।इतिहास
प्राचीन यूनानी प्रौद्योगिकी सरल मशीनों (बलों का संतुलन) के स्थैतिकी तक सीमित थी, और इसमें गतिकी (यांत्रिकी) या कार्य की अवधारणा सम्मिलित नहीं थी। पुनर्जागरण के समय यांत्रिक शक्तियों की गतिकी, जैसा कि सरल मशीनों को कहा जाता था, इस प्रकार इसका अध्ययन इस दृष्टिकोण से किया जाने लगा कि वे कितनी दूर तक भार उठा सकती हैं, इस बल के अतिरिक्त जो वे लागू कर सकते थे, इस प्रकार अंततः यांत्रिक की नई अवधारणा के लिए अग्रणी कार्य के रूप में इनका उपयोग किये जाने लगा। सरल मशीनों के पूर्ण गतिशील सिद्धांत को इतालवी वैज्ञानिक गैलीलियो गैलीली ने 1600 में ले मेकैनिके (ऑन मैकेनिक्स) में कार्य किया था, जिसमें उन्होंने मशीनों की अंतर्निहित गणितीय समानता को बल प्रवर्धक के रूप में दिखाया था।[3][4] इस प्रकार वह सबसे पहले व्यक्ति थे जिन्होंने समझाया कि सरल मशीनें ऊर्जा का निर्माण नहीं करतीं, केवल इसे रूपांतरित करती हैं।[3]
व्युत्पत्ति
मैक्स जैमर द्वारा 1957 की भौतिकी की पाठ्यपुस्तक के अनुसार,[5] कार्य शब्द के प्रारंभ 1826 में फ्रांसीसी गणितज्ञ गैसपार्ड-गुस्ताव कोरिओलिस ने की थी।[6] ऊंचाई के माध्यम से भार उठाने के रूप में, जो बाढ़ वाली अयस्क खदानों से पानी की बाल्टियों को उठाने के लिए प्रारंभिक भाप इंजनों के उपयोग पर आधारित है। रेने दुगास, फ्रांसीसी इंजीनियर और इतिहासकार के अनुसार, यह सॉलोमन डी कॉस के लिए है कि हम शब्द कार्य को इस अर्थ में देते हैं कि यह अब यांत्रिकी में उपयोग किया जाता है।[7] चूंकि इस प्रकार 1826 तक कार्य का औपचारिक रूप से उपयोग नहीं किया गया था, किन्तु इस प्रकार इससे पहले समान अवधारणाएं सम्मिलित थीं। 1759 में, जॉन स्मीटन ने मात्रा का वर्णन किया जिसे उन्होंने गति उत्पन्न करने के लिए शक्ति, गुरुत्वाकर्षण, आवेग, या दबाव के परिश्रम को इंगित करने के लिए शक्ति कहा हैं। स्मेटन की प्रस्तुति है कि इस मात्रा की गणना की जा सकती है यदि उठाए गए भार को ऊंचाई से गुणा किया जाता है जिससे इसे निश्चित समय में उठाया जा सकता है, इस परिभाषा को उल्लेखनीय रूप से कोरिओलिस के समान बना देता है।[8]
इकाइयां
कार्य की इकाइयों की अंतर्राष्ट्रीय प्रणाली जूल (J) है, इस प्रकार जिसका नाम 19वीं सदी के अंग्रेजी भौतिक विज्ञानी जेम्स प्रेस्कॉट जूल के नाम पर रखा गया है, जिसे मीटर के विस्थापन के माध्यम से न्यूटन (यूनिट) के बल को लागू करने के लिए आवश्यक कार्य के रूप में परिभाषित किया गया है। .
विमीय रूप से समतुल्य न्यूटन-मीटर (न्यूटन मीटर) का उपयोग कभी-कभी कार्य के लिए मापन इकाई के रूप में किया जाता है, किन्तु इसे बलाघूर्ण की माप इकाई के साथ भ्रमित किया जा सकता है। इस प्रकार भार और माप पर सामान्य सम्मेलन द्वारा न्यूटन मीटर के उपयोग को हतोत्साहित किया जाता है, क्योंकि इससे भ्रम उत्पन्न हो सकता है कि क्या न्यूटन-मीटर में व्यक्त की गई मात्रा टोक़ माप है, या कार्य की माप है।[9] इस प्रकार कार्य की गैर-एसआई इकाइयों में न्यूटन-मीटर, एर्ग, फुट-पाउंड (ऊर्जा) या फुट-पाउंड, फुट-पाउंडल, किलोवाट घंटा, लीटर-वातावरण, और अश्वशक्ति या हॉर्सपावर-घंटे सम्मिलित हैं। इस प्रकार गर्मी के समान आयामी विश्लेषण वाले कार्य के कारण, कभी-कभी माप इकाइयां सामान्यतः गर्मी या ऊर्जा सामग्री, जैसे थर्म, बीटीयू और कैलोरी के लिए आरक्षित होती हैं, को मापने वाली इकाई के रूप में उपयोग किया जाता है।
कार्य और ऊर्जा
कार्य W परिमाण के निरंतर बल द्वारा किया गया F बिंदु पर जो विस्थापन s को स्थानांतरित करता है इस प्रकार बल की दिशा में सीधी रेखा में उत्पाद है
उदाहरण के लिए, यदि 10 न्यूटन का बल (F = 10 N) बिंदु के साथ कार्य करता है जो 2 मीटर की यात्रा करता है। इस प्रकार विस्थापन s = 2 m होने पर W = Fs = (10 N) (2 m) = 20 J का मान प्राप्त होता हैं। यह गुरुत्वाकर्षण के बल के विरुद्ध किसी व्यक्ति के सिर के ऊपर से 1 किग्रा की वस्तु को जमीनी स्तर से उठाने में किया गया कार्य है।
कार्य को दुगुना किया जाता है या तो समान दूरी का दुगना भार उठाने से अथवा दुगनी दूरी से समान भार उठाने से कार्य दुगुना हो जाता है।
कार्य का ऊर्जा से गहरा संबंध है। कार्य-ऊर्जा सिद्धांत बताता है कि द्रढ़ पदार्थ की गतिज ऊर्जा में वृद्धि उस पदार्थ पर परिणामी बल द्वारा पदार्थ पर किए गए धनात्मक कार्य की समान मात्रा के कारण होती है। इस प्रकार इसके विपरीत, गतिज ऊर्जा में कमी परिणामी बल द्वारा किए गए ऋणात्मक कार्य की समान मात्रा के कारण होती है। इस प्रकार, यदि शुद्ध कार्य धनात्मक है, तो कण की गतिज ऊर्जा कार्य की मात्रा से बढ़ जाती है। इस प्रकार यदि किया गया शुद्ध कार्य ऋणात्मक है, तो कण की गतिज ऊर्जा कार्य की मात्रा से घट जाती है।[10]
न्यूटन के गति के नियमों से|न्यूटन के दूसरे नियम से, इस प्रकार यह दिखाया जा सकता है कि मुक्त (कोई क्षेत्र नहीं), कठोर (स्वतंत्रता की कोई आंतरिक डिग्री नहीं) शरीर पर कार्य, गतिज ऊर्जा Ek में परिवर्तन के बराबर है, उस शरीर के रैखिक वेग और कोणीय वेग के अनुरूप,
बाधा बल
बाधा बल प्रणाली में वस्तु के विस्थापन को निर्धारित करते हैं, इसे सीमा के भीतर सीमित करते हैं। उदाहरण के लिए, ढलान और गुरुत्व के स्थिति में, वस्तु ढलान से चिपकी रहती है और, जब तने हुए तार से जुड़ी होती है, तो यह स्ट्रिंग को किसी भी 'तना हुआ' बनाने के लिए बाहर की दिशा में नहीं जा सकती हैं। इस प्रकार यह उस दिशा में सभी विस्थापनों को समाप्त करता है, अर्थात, बाधा की दिशा में वेग 0 तक सीमित होता है, जिससे कि बाधा बल प्रणाली पर कार्य नहीं कर सकता हैं।
एक यांत्रिक प्रणाली के लिए[11] बाधा बल उस दिशा में गति को समाप्त कर देते हैं जो बाधा की विशेषता है। इस प्रकार बाधा के बलों द्वारा किया गया आभासी कार्य शून्य है, परिणाम जो केवल तभी सत्य होता है जब घर्षण बल को हटा दिया जाए।[12] स्थिर घर्षण रहित बाधा बल सिस्टम पर कार्य नहीं करते हैं,[13] क्योंकि इस प्रकार गति और बाधा बलों के बीच का कोण सदैव समकोण होता है|90°।[13]कार्यहीन बाधाओं के उदाहरण हैं: कणों के बीच कठोर अंतर्संबंध, घर्षण रहित सतह पर फिसलने वाली गति, और बिना खिसके रोलिंग संपर्क करता हैं।[14] इस प्रकार उदाहरण के लिए, एटवुड मशीन जैसी चरखी प्रणाली में, रस्सी पर और सहायक चरखी पर आंतरिक बल प्रणाली पर कोई कार्य नहीं करते हैं। इसलिए, कार्य की गणना केवल पिंडों पर कार्यरत गुरुत्वाकर्षण बलों के लिए की जानी चाहिए। अन्य उदाहरण समान गोलाकार गति में गेंद पर स्ट्रिंग द्वारा अंदर की ओर लगाया जाने वाला अभिकेन्द्रीय बल है, जो गेंद को वृत्ताकार गति के लिए बाध्य करता है, जिससे वृत्त के केंद्र से दूर इसकी गति सीमित हो जाती है। इस प्रकार यह बल शून्य कार्य करता है क्योंकि यह गेंद के वेग के लंबवत होता है।
आवेशित कण पर चुंबकीय बल होता है F = qv × B, जहाँ q आरोप है, v कण का वेग है, और B चुंबकीय क्षेत्र है। क्रॉस उत्पाद का परिणाम सदैव दोनों मूल सदिशों के लिए लंबवत होता है, इसलिए F ⊥ v. दो लंब सदिशों का बिंदु गुणनफल सदैव शून्य होता है, इसलिए कार्य W = F ⋅ v = 0, और चुंबकीय बल कार्य नहीं करता है। यह गति की दिशा परिवर्तित कर सकता है किन्तु गति कभी नहीं बदल सकता है।
गणितीय गणना
गतिमान वस्तुओं के लिए, कार्य/समय (शक्ति) की मात्रा बल के अनुप्रयोग के बिंदु के प्रक्षेपवक्र के साथ एकीकृत होती है। इस प्रकार, किसी भी क्षण, बल द्वारा किए गए कार्य की दर (जूल/सेकेंड, या वाट में मापा जाता है) बल (एक सदिश) का स्केलर उत्पाद है, और आवेदन के बिंदु का वेग सदिश है। बल और वेग के इस अदिश गुणनफल को तात्कालिक शक्ति (भौतिकी) के रूप में जाना जाता है। जिस प्रकार कैलकुलस के मौलिक प्रमेय द्वारा कुल दूरी प्राप्त करने के लिए समय के साथ वेगों को एकीकृत किया जा सकता है, उसी प्रकार पथ के साथ कुल कार्य उसी तरह से अनुप्रयोग के बिंदु के प्रक्षेपवक्र के साथ लागू तात्कालिक शक्ति का समय-अभिन्न होता है।[15] कार्य बिंदु पर बल का परिणाम है जो वक्र X का अनुसरण करता है, इस प्रकार वेग से v, हर पल। कार्य की छोटी राशि δW यह पल में होता है dt के रूप में गणना की जाती है
जहां F ⋅ v पल भर की शक्ति है dt. बिंदु के प्रक्षेपवक्र पर कार्य की इन छोटी मात्राओं का योग कार्य देता है,
यदि बल सदैव इस रेखा के साथ निर्देशित होता है, और बल का परिमाण F होता है , इस प्रकार यह समाकलन सरल हो जाता है
इस गणना को स्थिर बल के लिए सामान्यीकृत किया जा सकता है जो कण के बाद रेखा के साथ निर्देशित नहीं होता है। इस प्रकार इस स्थिति में डॉट उत्पाद F ⋅ ds = F cos θ ds, जहाँ θ बल सदिश और गति की दिशा के बीच का कोण है,[15] इस प्रकार किया गया कार्य कुछ इस प्रकार होगा-
जब कोई बल घटक वस्तु के विस्थापन के लम्बवत् होता है (जैसे कि जब कोई पिंड किसी केंद्रीय बल के अधीन वृत्ताकार पथ में गति करता है), तो कोई कार्य नहीं होता है, क्योंकि 90° का कोसाइन शून्य होता है।[10] इस प्रकार, गोलाकार कक्षा वाले ग्रह पर गुरुत्वाकर्षण द्वारा कोई कार्य नहीं किया जा सकता है, यह आदर्श अवस्था है, क्योंकि इस प्रकार सभी कक्षाएँ थोड़ी अंडाकार रहती हैं। इसके अतिरिक्त, यांत्रिक बल द्वारा विवश होने पर स्थिर गति से गोलाकार गति करने वाले शरीर पर कोई कार्य नहीं किया जाता है, जैसे घर्षण रहित आदर्श अपकेंद्रित्र में स्थिर गति से चलता हैं।
परिवर्ती बल द्वारा किया गया कार्य
कार्य की बल समय के रूप में गणना करना सीधा पथ खंड केवल सबसे सरल परिस्थितियों में लागू होगा, जैसा कि ऊपर बताया गया है। यदि बल बदल रहा है, या यदि शरीर घुमावदार पथ के साथ आगे बढ़ रहा है, संभवतः घूर्णन कर रहा है और जरूरी नहीं कि कठोर हो, तो बल के आवेदन बिंदु का मार्ग केवल किए गए कार्य के लिए प्रासंगिक है, और इस प्रकार केवल समानांतर बल का घटक अनुप्रयोग बिंदु वेग कार्य कर रहा है (धनात्मक कार्य जब ही दिशा में होता है, और ऋणात्मक जब वेग की विपरीत दिशा में होता है)। इस प्रकार बल के इस घटक को स्केलर मात्रा द्वारा वर्णित किया जा सकता है जिसे स्केलर स्पर्शरेखा घटक F cos(θ) कहा जाता है (जहाँ θ बल और वेग के बीच का कोण है)। और फिर कार्य की सबसे सामान्य परिभाषा निम्नानुसार तैयार की जा सकती है:
यदि बल बदलता है (उदाहरण के लिए एक वसंत को संपीड़ित करना) तो हमें किए गए कार्य को खोजने के लिए कलन का उपयोग करने की आवश्यकता है। यदि बल द्वारा दिया गया है F(x) (a function of x) फिर एक्स-अक्ष के साथ बल द्वारा किया गया कार्य a to b:
आघूर्ण और घूर्णन
एक युगल (यांत्रिकी) द्रढ़ पदार्थ के दो अलग-अलग बिंदुओं पर कार्य करने वाली समान और विपरीत शक्तियों से उत्पन्न होता है। इस प्रकार इन बलों का योग (परिणामस्वरूप) रद्द हो सकता है, किन्तु शरीर पर उनका प्रभाव युगल या बलाघूर्ण T है। बलाघूर्ण के कार्य की गणना इस प्रकार की जाती है
इस अभिन्न की गणना द्रढ़ पदार्थ के प्रक्षेपवक्र के साथ कोणीय वेग ω के साथ की जाती है, जो समय के साथ परिवर्तित होता रहता है, और इसलिए इसे पथ पर निर्भर कहा जाता है।
यदि कोणीय वेग सदिश स्थिर दिशा बनाए रखता है, तो इस प्रकार यह उक्त रूप ले लेता है,
अगर आघूर्ण कोणीय वेग सदिश के साथ संरेखित किया जाता है जिससे कि,
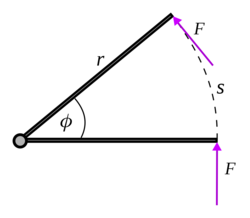
और दोनों टोक़ और कोणीय वेग स्थिर हैं, तो कार्य रूप लेता है,[2]निरंतर परिमाण के बल से उत्पन्न होने वाले टोक़ पर विचार करके इस परिणाम को और अधिक सरलता से समझा जा सकता है F, कुछ दूरी पर लीवर आर्म पर लंबवत रूप से लगाया जा रहा है , जैसा कि चित्र में दिखाया गया है। इस प्रकार यह बल वृत्ताकार चाप के साथ दूरी के माध्यम , से कार्य करेगा, इस प्रकार किया गया कार्य है
कार्य और संभावित ऊर्जा
बल का अदिश गुणनफल F और वेग v इसके अनुप्रयोग का बिंदु पल में प्रणाली में शक्ति (भौतिकी) इनपुट को परिभाषित करता है। इस प्रकार आवेदन के बिंदु के प्रक्षेपवक्र पर इस शक्ति का एकीकरण, C = x(t), बल द्वारा सिस्टम में कार्य इनपुट को परिभाषित करता है।
पथ निर्भरता
इसलिए, बल द्वारा किया गया यांत्रिक कार्य F वस्तु पर जो वक्र के साथ यात्रा करती है, इस प्रकार C लाइन इंटीग्रल द्वारा दिया गया है:
कार्य के लिए अभिन्न का समय व्युत्पन्न तात्कालिक शक्ति उत्पन्न करता है,
पथ स्वतंत्रता
यदि लागू बल के लिए कार्य पथ से स्वतंत्र है, तो बल द्वारा किया गया कार्य, ढाल प्रमेय द्वारा, संभावित कार्य को परिभाषित करता है जिसका मूल्यांकन अनुप्रयोग बिंदु के प्रक्षेपवक्र के प्रारंभ और अंत में किया जाता है। इसका मतलब है कि संभावित कार्य U(x) है, जिसका मूल्यांकन दो बिंदुओं पर किया जा सकता है, इस प्रकार x(t1) और x(t2) इन दो बिंदुओं के बीच किसी भी प्रक्षेपवक्र पर कार्य प्राप्त करने के लिए। इस कार्य को ऋणात्मक संकेत के साथ परिभाषित करने की परंपरा है जिससे कि धनात्मक कार्य क्षमता में कमी हो, अर्थात
इस स्थिति में, इस प्रकार किये गए कार्य के कारण उत्पन्न हुए ढाल का मान इस प्रकार होगा-
और बल F को विभव से व्युत्पन्न कहा जाता है।[16] क्योंकि क्षमता U बल F परिभाषित करता है जो हर बिंदु x पर अंतरिक्ष में, बलों के समूह को बल क्षेत्र (भौतिकी) कहा जाता है। इस प्रकार बल क्षेत्र द्वारा किसी पिंड पर लागू की गई शक्ति को गति की दिशा में कार्य, या क्षमता के ढाल से प्राप्त किया जाता है V शरीर का, अर्थात्गुरुत्वाकर्षण द्वारा कार्य
अन्य बलों की अनुपस्थिति में, गुरुत्वाकर्षण के परिणामस्वरूप प्रत्येक स्वतंत्र रूप से गतिमान वस्तु का निरंतर नीचे की ओर त्वरण होता है। पृथ्वी की सतह के निकट गुरुत्वाकर्षण के कारण त्वरण g = 9.8 m⋅s−2 है, और द्रव्यमान m की वस्तु पर गुरुत्वाकर्षण बल Fg = mg है, इस प्रकार वस्तु के द्रव्यमान के केंद्र पर केंद्रित इस गुरुत्वाकर्षण बल की कल्पना करना सुविधाजनक है।
यदि किसी वस्तु का भार है mg ऊर्ध्वाधर दूरी पर ऊपर या नीचे की ओर विस्थापित y2 − y1 होता है, कार्य W वस्तु पर किया जाता है:
अंतरिक्ष में गुरुत्व द्वारा कार्य
द्रव्यमान द्वारा लगाया गया गुरुत्वाकर्षण बल M दूसरे द्रव्यमान पर m द्वारा दिया गया है
द्रव्यमान दें m वेग से चलते हैं v; फिर इस द्रव्यमान पर गुरुत्वाकर्षण का कार्य स्थिति से चलता है। r(t1) को r(t2) द्वारा दिया गया है
एक स्वतंत्र द्वारा कार्य
एक स्वतंत्र पर विचार करें जो क्षैतिज बल लगाता है F = (−kx, 0, 0) यह एक्स दिशा में इसके विक्षेपण के समानुपाती होता है, इस बात से स्वतंत्र कि कोई पिंड कैसे चलता है। इस प्रकार उक्त वक्र के साथ अंतरिक्ष में गतिमान पिंड पर इस स्प्रिंग का कार्य X(t) = (x(t), y(t), z(t)), इसकी वेग का उपयोग करके गणना की जाती है, v = (vx, vy, vz), प्राप्त करने के लिए
गैस द्वारा कार्य
कार्य अपने परिवेश पर गैस के पिंड द्वारा किया जाता है:
कार्य-ऊर्जा सिद्धांत
कार्य और गतिज ऊर्जा का सिद्धांत (जिसे कार्य-ऊर्जा सिद्धांत के रूप में भी जाना जाता है) दर्शाता है कि कण पर कार्यरत सभी बलों द्वारा किया गया कार्य (परिणामी बल का कार्य) कण की गतिज ऊर्जा में परिवर्तन के बराबर होता है। [17] अर्थात्, इस प्रकार किसी कण पर परिणामी बल द्वारा किया गया कार्य W कण की गतिज ऊर्जा में परिवर्तन के बराबर होता है,[2]
कार्य-ऊर्जा सिद्धांत की व्युत्पत्ति न्यूटन के गति के दूसरे नियम और कण पर परिणामी बल से प्रारंभ होती है। कण के वेग के साथ बलों के स्केलर उत्पाद की गणना प्रणाली में जोड़े गए तात्क्षणिक शक्ति का मूल्यांकन करती है।[18] बाधाएँ यह सुनिश्चित करके कण की गति की दिशा को परिभाषित करती हैं कि बाधा बल की दिशा में वेग का कोई घटक नहीं है। इसका यह भी अर्थ है कि बाधा बल तात्कालिक शक्ति में नहीं जुड़ते हैं। इस स्केलर समीकरण का समय अभिन्न तात्कालिक शक्ति से कार्य करता है, और वेग और त्वरण के स्केलर उत्पाद से गतिज ऊर्जा के द्वारा प्रदर्शित होता है। इस प्रकार तथ्य यह है कि कार्य-ऊर्जा सिद्धांत बाधा बलों को समाप्त करता है लैग्रैंगियन यांत्रिकी के अंतर्गत आता है।[19]
यह खंड कार्य-ऊर्जा सिद्धांत पर केंद्रित है क्योंकि यह कण गतिकी पर लागू होता है। अधिक सामान्य प्रणालियों में कार्य यांत्रिक उपकरण की संभावित ऊर्जा, तापीय प्रणाली में तापीय ऊर्जा, या विद्युत उपकरण में विद्युत ऊर्जा को बदल सकता है। कार्य ऊर्जा को स्थान से दूसरे स्थान या रूप से दूसरे रूप में स्थानांतरित करता है।
सीधी रेखा में गतिमान कण की व्युत्पत्ति
परिणामी बल के स्थिति में F परिमाण और दिशा दोनों में स्थिर है, और कण के वेग के समानांतर, कण सीधी रेखा के साथ निरंतर त्वरण a के साथ घूम रहा है।[20] नेट बल और त्वरण के बीच संबंध समीकरण द्वारा दिया गया है, इसे F = ma (न्यूटन का दूसरा नियम), और कण विस्थापन (सदिश) s समीकरण द्वारा व्यक्त किया जा सकता है
(गति के समीकरण देखें)।
शुद्ध बल के कार्य की गणना उसके परिमाण और कण विस्थापन के गुणनफल के रूप में की जाती है। उपरोक्त समीकरणों को प्रतिस्थापित करने पर, प्राप्त होता है:
एक कण के लिए कार्य-ऊर्जा सिद्धांत की सामान्य व्युत्पत्ति
किसी भी घुमावदार पथ के साथ चलने वाले कण पर अभिनय करने वाले किसी भी शुद्ध बल के लिए, यह प्रदर्शित किया जा सकता है कि इसका कार्य उपरोक्त समीकरण के समान सरल व्युत्पन्न द्वारा कण की गतिज ऊर्जा में परिवर्तन के बराबर है। इसे कार्य-ऊर्जा सिद्धांत के रूप में जाना जाता है:
विवश गति में कण के लिए व्युत्पत्ति
कण गतिकी में, गतिज ऊर्जा में इसके परिवर्तन के लिए प्रणाली पर लागू कार्य को समान करने वाला सूत्र न्यूटन के गति के नियमों के पहले अभिन्न अंग के रूप में प्राप्त किया जाता है|न्यूटन की गति का दूसरा नियम। यह नोटिस करना उपयोगी है कि न्यूटन के नियमों में प्रयुक्त परिणामी बल को उन बलों में विभाजित किया जा सकता है जो कण पर लागू होते हैं और कण की गति पर बाधाओं द्वारा लगाए गए बल के समान होता हैं। उल्लेखनीय रूप से, बाधा बल का कार्य शून्य है, इसलिए इस प्रकार कार्य-ऊर्जा सिद्धांत में केवल लागू बलों के कार्य पर विचार किया जाना चाहिए।
इसे देखने के लिए, कण P पर विचार करें जो प्रक्षेपवक्र का अनुसरण करता है X(t) बल के साथ F का मान निकाला जाता हैं। इस प्रकार बाधा बलों को निस्तारित करने के लिए कण को उसके वातावरण से अलग करें R, तब न्यूटन का नियम रूप लेता है
सदिश सूत्रीकरण
ध्यान दें कि सदिश के ऊपर स्थित n बिंदु इसके nवें समय के अवकलज को इंगित करते हैं। वेग सदिश के साथ न्यूटन के नियम के प्रत्येक पक्ष का अदिश गुणनफल प्राप्त होता है
निम्नलिखित पहचान का उपयोग करके न्यूटन के समीकरणों के पहले अभिन्न के दाहिने पक्ष को सरल बनाया जा सकता है
स्पर्शरेखा और सामान्य घटक
प्रक्षेपवक्र के साथ स्पर्शरेखा और सामान्य घटकों में वेग और त्वरण वैक्टर X(t) को हल करना उपयोगी है , ऐसा है कि
एक सीधी रेखा में चलना (एक स्टॉप पर स्किड करना)
एक ड्राइविंग बल और गुरुत्वाकर्षण की कार्रवाई के तहत सीधे क्षैतिज प्रक्षेपवक्र के साथ चलने वाले वाहन के स्थिति पर विचार करें F. वाहन और सड़क के बीच बाधा बल R परिभाषित करते हैं, इस प्रकार हमारे पास यह समीकरण प्राप्त होता है
झुकी हुई सतह (गुरुत्वाकर्षण रेसिंग) को नीचे करना
एक वाहन के स्थिति पर विचार करें जो आराम से प्रारंभ होता है और झुकी हुई सतह (जैसे पहाड़ की सड़क) से नीचे की ओर बढ़ता है, कार्य-ऊर्जा सिद्धांत उस न्यूनतम दूरी की गणना करने में सहायक होता है जो वाहन वेग तक पहुँचने के लिए यात्रा करता है। इस प्रकार V के अनुसार मान लीजिए 60 मील प्रति घंटे (88 एफपीएस) है। तो इस प्रकार रोलिंग प्रतिरोध और एयर ड्रैग वाहन को धीमा कर देगा इसलिए वास्तविक दूरी अधिक होगी यदि इन बलों की उपेक्षा की जाती है।
सड़क का अनुसरण करने वाले वाहन का प्रक्षेपवक्र होने दें X(t) जो त्रि-आयामी अंतरिक्ष में वक्र है। इस प्रकार वाहन पर कार्य करने वाला बल जो इसे सड़क से नीचे धकेलता है, गुरुत्वाकर्षण का निरंतर बल F = (0, 0, W) है , जबकि वाहन पर सड़क का बल बाधा बल R है। इस प्रकार न्यूटन का दूसरा नियम उत्पन्न करता है,
सड़क के साथ दूरी निर्धारित करने के लिए मान लें कि डाउनग्रेड 6% है, जो खड़ी सड़क है। इसका आशय है कि हर 100 फीट की यात्रा के लिए ऊंचाई 6 फीट कम हो जाती है—ऐसे छोटे कोणों के लिए sin और tan के कार्य लगभग बराबर होते हैं। इसलिए दूरी s वेग तक पहुँचने के लिए 6% ग्रेड नीचे फुट में V कम से कम है
दृढ़ पिंड पर कार्य करने वाली शक्तियों का कार्य
एक दृढ़ पिंड पर विभिन्न बिंदुओं पर कार्य करने वाले बलों के कार्य की गणना परिणामी बल के कार्य से की जा सकती है। इसे देखने के लिए, मान लीजिए कि बल F1, F2, ..., Fn बिंदु X पर कार्य करें1, X2, ..., Xn द्रढ़ पदार्थ में।
Xi के प्रक्षेपवक्र, i = 1, ..., n को दृढ़ पिंड की गति द्वारा परिभाषित किया जाता है। यह विवाद भौतिकी में संदर्भ बिंदु के घूर्णन [A (t)] और प्रक्षेपवक्र 'd' (t) के समूह द्वारा दिया जाता है। इस प्रकार माना निर्देशांक 'x'i i = 1, ..., n इन बिंदुओं को गतिमान कठोर पिंड के कार्टेशियन कोऑर्डिनेट सिस्टम M में परिभाषित करता है, जिससे कि निश्चित फ्रेम F में ट्रैजेक्टोरियों का पता लगाया जा सके
छोटे विस्थापनों पर बलों द्वारा कार्य की छोटी मात्रा δri द्वारा विस्थापन δr = vδt का अनुमान लगाकर निर्धारित किया जा सकता है। इसलिए
संदर्भ
- ↑ NCERT (2020). "भौतिकी पुस्तक" (PDF). ncert.nic.in. Retrieved 24 November 2021.
- ↑ Jump up to: 2.0 2.1 2.2 Hugh D. Young & Roger A. Freedman (2008). विश्वविद्यालय भौतिकी (12th ed.). Addison-Wesley. p. 329. ISBN 978-0-321-50130-1.
- ↑ Jump up to: 3.0 3.1 Krebs, Robert E. (2004). ग्राउंडब्रेकिंग प्रयोग, आविष्कार और मध्य युग की खोज. Greenwood Publishing Group. p. 163. ISBN 978-0-313-32433-8. Retrieved 2008-05-21.
- ↑ Stephen, Donald; Lowell Cardwell (2001). पहिए, घड़ियां और रॉकेट: प्रौद्योगिकी का इतिहास. US: W.W. Norton & Company. pp. 85–87. ISBN 978-0-393-32175-3.
- ↑ Jammer, Max (1957). बल की अवधारणाएँ. Dover Publications, Inc. p. 167; footnote 14. ISBN 0-486-40689-X.
- ↑ Coriolis, Gustave (1829). मशीनों के प्रभाव की गणना, या इंजनों के उपयोग पर विचार और उनका मूल्यांकन. Carilian-Goeury, Libraire (Paris).
- ↑ Dugas, R. (1955). यांत्रिकी का इतिहास. Switzerland: Éditions du Griffon.
- ↑ Smeaton, John (1759). "सर्कुलर मोशन के आधार पर मिलों और अन्य मशीनों को चालू करने के लिए पानी और हवा की प्राकृतिक शक्तियों के संबंध में प्रायोगिक पूछताछ". Philosophical Transactions of the Royal Society. 51: 105. doi:10.1098/rstl.1759.0019. S2CID 186213498.
- ↑ "Units with special names and symbols; units that incorporate special names and symbols". इकाइयों की अंतर्राष्ट्रीय प्रणाली (एसआई) (8th ed.). International Bureau of Weights and Measures. 2006. Archived from the original on 2013-04-20. Retrieved 2012-10-27.
- ↑ Jump up to: 10.0 10.1 Walker, Jearl; Halliday, David; Resnick, Robert (2011). भौतिकी के मूल तत्व (9th ed.). Hoboken, NJ: Wiley. p. 154. ISBN 9780470469118.
- ↑ Goldstein, Herbert (2002). शास्त्रीय यांत्रिकी (3rd ed.). San Francisco: Addison Wesley. ISBN 978-0-201-65702-9. OCLC 47056311.
- ↑ Rogalski, Mircea S. (2018). उन्नत विश्वविद्यालय भौतिकी (2nd ed.). Boca Raton: Chapman and Hall/CRC. ISBN 9781351991988.
- ↑ Jump up to: 13.0 13.1 "फिजिक्स वॉल्यूम पर फेनमैन व्याख्यान। मैं चौ। 14: कार्य और स्थितिज ऊर्जा (निष्कर्ष)". feynmanlectures.caltech.edu.
- ↑ Greenwood, Donald T. (1997). शास्त्रीय गतिकी. Mineola, N.Y.: Dover Publications. ISBN 9780486138794.
- ↑ Jump up to: 15.0 15.1 Resnick, Robert, Halliday, David (1966), Physics, Section 1–3 (Vol I and II, Combined edition), Wiley International Edition, Library of Congress Catalog Card No. 66-11527
- ↑ J. R. Taylor, Classical Mechanics, University Science Books, 2005.
- ↑ Andrew Pytel; Jaan Kiusalaas (2010). इंजीनियरिंग यांत्रिकी: गतिशीलता - एसआई संस्करण, खंड 2 (3rd ed.). Cengage Learning. p. 654. ISBN 9780495295631.
- ↑ Paul, Burton (1979). प्लेनर मशीनरी की कीनेमेटीक्स और गतिशीलता (in English). Prentice-Hall. ISBN 978-0-13-516062-6.
- ↑ Whittaker, E. T. (1904). कणों और कठोर निकायों की विश्लेषणात्मक गतिशीलता पर एक ग्रंथ (in English). Cambridge University Press.
- ↑ "कार्य-ऊर्जा सिद्धांत". www.wwu.edu. Archived from the original on 2012-05-30. Retrieved 2012-08-06.
ग्रन्थसूची
- Serway, Raymond A.; Jewett, John W. (2004). Physics for Scientists and Engineers (6th ed.). Brooks/Cole. ISBN 0-534-40842-7.
- Tipler, Paul (1991). Physics for Scientists and Engineers: Mechanics (3rd ed., extended version ed.). W. H. Freeman. ISBN 0-87901-432-6.