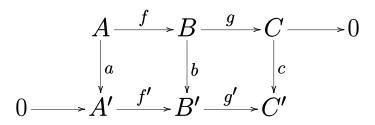सजातीय बीजगणित

साँप लेम्मा में प्रयुक्त एक आरेख, सजातीय बीजगणित में एक मूल परिणाम।

सजातीय बीजगणित गणित की वह शाखा है जो सामान्य बीजीय सेटिंग में समरूपता का अध्ययन करती है। यह अपेक्षाकृत युवा अनुशासन है, जिसकी उत्पत्ति 19वीं सदी के अंत में मुख्य रूप से हेनरी पोनकारे और डेविड हिल्बर्ट द्वारा सांयोगिक टोपोलॉजी (बीजगणितीय टोपोलॉजी का पूर्ववर्ती) और अमूर्त बीजगणित (मॉड्यूल और सिज़ीजी का सिद्धांत) में परीक्षण से पता लगाया जा सकता है।

सजातीय बीजगणित, सजातीय फ़नकारकों और उनसे जुड़ी सम्मिश्र बीजीय संरचनाओं का अध्ययन है; इसके विकास का श्रेणी सिद्धांत के उद्भव के साथ घनिष्ठ संबंध था। केंद्रीय अवधारणा श्रृंखला परिसरों की है, जिनका अध्ययन उनकी समरूपता और सहसंबद्धता दोनों के माध्यम से किया जा सकता है।

सजातीय बीजगणित इन परिसरों में निहित जानकारी को निकालने और इसे वलयों, मॉड्यूल, टोपोलॉजिकल रिक्त स्थान और अन्य 'मूर्त' गणितीय वस्तुओं के सजातीय अपरिवर्तनीय के रूप में प्रस्तुत करने का साधन प्रदान करता है। ऐसा करने के लिए एक प्रभावशाली उपकरण वर्णक्रमीय अनुक्रम द्वारा प्रदान किया गया है।

इसने बीजीय टोपोलॉजी में बहुत बड़ी भूमिका निभाई है। इसके प्रभाव का धीरे-धीरे विस्तार हुआ है और वर्तमान में इसमें क्रमविनिमेय बीजगणित, बीजगणितीय ज्यामिति, बीजगणितीय संख्या सिद्धांत, प्रतिनिधित्व सिद्धांत, गणितीय भौतिकी, संचालिका बीजगणित, सम्मिश्र विश्लेषण और आंशिक अंतर समीकरणों का सिद्धांत सम्मिलित है। K-सिद्धांत स्वतंत्र अनुशासन है जो सजातीय बीजगणित के विधियों पर आधारित है, जैसा कि एलेन कोन्स की गैर-अनुवांशिक ज्यामिति पर होता है।

इतिहास

सजातीय बीजगणित का अध्ययन 1800 के दशक में टोपोलॉजी की शाखा के रूप में अपने सबसे बुनियादी रूप में किया जाने लगा, लेकिन ऐसा तब तक नहीं हुआ था जब तक 1940 के दशक में यह एक्सट फंक्टर और टोर फंक्टर जैसी अन्य वस्तुओं के अध्ययन के साथ एक स्वतंत्र विषय बन गया था।

श्रृंखला परिसर और समरूपता

Main article: श्रृंखला जटिल

श्रृंखला सम्मिश्रता की धारणा सजातीय बीजगणित में केंद्रीय है। अमूर्त श्रृंखला परिसर एबेलियन समूहों और समूह समरूपताओं का अनुक्रम $(C_{\bullet },d_{\bullet })$ है, इस संपत्ति के साथ कि किन्हीं दो लगातार मानचित्रों की संरचना शून्य है:

$C_{\bullet }:\cdots \longrightarrow C_{n+1}{\stackrel {d_{n+1}}{\longrightarrow }}C_{n}{\stackrel {d_{n}}{\longrightarrow }}C_{n-1}{\stackrel {d_{n-1}}{\longrightarrow }}\cdots ,\quad d_{n}\circ d_{n+1}=0.$

C_n के तत्वों को n-श्रृंखला कहा जाता है और समरूपताओं d_n को सीमा मानचित्र या अंतर कहा जाता है। श्रृंखला समूह C_n को अतिरिक्त संरचना से संपन्न किया जा सकता है; उदाहरण के लिए, वे एक निश्चित वलय r पर सदिश स्पेस या मॉड्यूल हो सकते हैं। यदि उपस्थित है तो अंतर को अतिरिक्त संरचना को संरक्षित करना होगा; उदाहरण के लिए, वे R-मॉड्यूल के रैखिक मानचित्र या समरूपताएँ होनी चाहिए। उल्लेखनीय सुविधा के लिए, एबेलियन समूहों पर ध्यान केंद्रित करें (अधिक सही ढंग से, एबेलियन समूहों की श्रेणी Ab तक); बैरी मिशेल द्वारा प्रसिद्ध प्रमेय का अर्थ है कि परिणाम किसी भी एबेलियन श्रेणी के लिए सामान्यीकृत होंगे। प्रत्येक श्रृंखला परिसर एबेलियन समूहों के दो और अनुक्रमों को परिभाषित करता है, चक्र Z_n = Ker d_n और सीमाएँ B_n = Im d_n+1, जहाँ Ker d औरIm d कर्नेल और d की छवि को दर्शाते हैं। चूँकि दो लगातार सीमा मानचित्रों की संरचना शून्य है, ये समूह दूसरे में अंतर्निहित हैं।

$B_{n}\subseteq Z_{n}\subseteq C_{n}.$

एबेलियन समूहों के उपसमूह स्वतः सामान्य हैं; इसलिए हम n-सीमाओं द्वारा n-चक्रों के कारक समूह के रूप में nवें समरूपता समूह H_n(C) को परिभाषित कर सकते हैं,

$H_{n}(C)=Z_{n}/B_{n}=\operatorname {Ker} \,d_{n}/\operatorname {Im} \,d_{n+1}.$

श्रृंखला परिसर को एसाइक्लिक या यथार्थ अनुक्रम कहा जाता है यदि इसके सभी समरूप समूह शून्य हैं।

अमूर्त बीजगणित और बीजगणितीय टोपोलॉजी में श्रृंखला कॉम्प्लेक्स बहुतायत में उत्पन्न होते हैं। उदाहरण के लिए, यदि X टोपोलॉजिकल स्पेस है तो एकवचन श्रृंखला C_n(X) मानक n-सिंप्लेक्स से X तक निरंतर मानचित्रों के औपचारिक रैखिक संयोजन हैं; यदि K सरल सम्मिश्र है तो श्रृंखला (बीजगणितीय टोपोलॉजी) C_n(K) K के n-सरलताओं के औपचारिक रैखिक संयोजन हैं; यदि A = F/R समूह की प्रस्तुति द्वारा एबेलियन समूह A की प्रस्तुति है, जहां F जनरेटर द्वारा फैलाया गया मुक्त एबेलियन समूह है और R संबंधों का उपसमूह है, तो C₁(A) = R, C₀(A) = F, और C_n(A) = 0 सभी n के लिए 0 एबेलियन समूहों के अनुक्रम को परिभाषित करता है। इन सभी मामलों में, प्राकृतिक अंतर हैं C_n बनाना श्रृंखला परिसर में, जिसकी समरूपता टोपोलॉजिकल स्पेस X, सरल कॉम्प्लेक्स के, या एबेलियन समूह A की संरचना को दर्शाती है। टोपोलॉजिकल स्पेस के मामले में, हम एकवचन समरूपता की धारणा पर पहुंचते हैं, जो परीक्षण में मौलिक भूमिका निभाता है ऐसे स्थानों के गुण, उदाहरण के लिए, कई गुना।

दार्शनिक स्तर पर, सजातीय बीजगणित हमें सिखाता है कि बीजगणितीय या ज्यामितीय वस्तुओं (टोपोलॉजिकल स्पेस, सरल कॉम्प्लेक्स, r-मॉड्यूल) से जुड़े कुछ श्रृंखला परिसरों में उनके बारे में बहुत सारी मूल्यवान बीजगणितीय जानकारी होती है, समरूपता केवल सबसे आसानी से उपलब्ध हिस्सा है . तकनीकी स्तर पर, सजातीय बीजगणित परिसरों में हेरफेर करने और इस जानकारी को निकालने के लिए उपकरण प्रदान करता है। यहां दो सामान्य उदाहरण दिए गए हैं.

• दो वस्तुएँ X और Y उनके बीच मानचित्र f द्वारा जुड़ी हुई हैं। सजातीय बीजगणित, X और Y से जुड़े श्रृंखला परिसरों और उनकी समरूपता के बीच, मानचित्र एफ द्वारा प्रेरित संबंध का अध्ययन करता है। इसे कई वस्तुओं और उन्हें जोड़ने वाले मानचित्रों के मामले में सामान्यीकृत किया जाता है। श्रेणी सिद्धांत की भाषा में वाक्यांशबद्ध, सजातीय बीजगणित श्रृंखला परिसरों के विभिन्न निर्माणों और इन परिसरों की समरूपता के कारक का अध्ययन करता है।
• ऑब्जेक्ट X कई विवरणों को स्वीकार करता है (उदाहरण के लिए, टोपोलॉजिकल स्पेस के रूप में और सरल कॉम्प्लेक्स के रूप में) या कॉम्प्लेक्स $C_{\bullet }(X)$ X की कुछ 'प्रस्तुति' का उपयोग करके बनाया गया है, जिसमें गैर-विहित विकल्प सम्मिलित हैं। X से जुड़े श्रृंखला परिसरों पर X के विवरण में परिवर्तन के प्रभाव को जानना महत्वपूर्ण है। सामान्यतः, परिसर और इसकी समरूपता $H_{\bullet }(C)$ प्रस्तुतिकरण के संबंध में कार्यात्मक हैं; और समरूपता (हालाँकि स्वयं सम्मिश्र नहीं) वास्तव में चुनी गई प्रस्तुति से स्वतंत्र है, इस प्रकार यह X का अपरिवर्तनीय (गणित) है।

मानक उपकरण

यथार्थ अनुक्रम

Main article: सटीक क्रम

समूह सिद्धांत के संदर्भ में, एक अनुक्रम

$G_{0}\;\xrightarrow {f_{1}} \;G_{1}\;\xrightarrow {f_{2}} \;G_{2}\;\xrightarrow {f_{3}} \;\cdots \;\xrightarrow {f_{n}} \;G_{n}$

समूह (गणित) और समूह समरूपता को यथार्थ कहा जाता है यदि प्रत्येक समरूपता की छवि (गणित) अगले के कर्नेल (बीजगणित) के बराबर है:

$\mathrm {im} (f_{k})=\mathrm {ker} (f_{k+1}).\!$

ध्यान दें कि समूहों और समरूपताओं का क्रम या तो परिमित या अनंत हो सकता है।

कुछ अन्य बीजीय संरचनाओं के लिए भी ऐसी ही परिभाषा बनाई जा सकती है। उदाहरण के लिए, किसी के पास सदिश रिक्त स्थान और रैखिक मानचित्र, या मॉड्यूल (गणित) और मॉड्यूल समरूपता का यथार्थ अनुक्रम हो सकता है। अधिक सामान्यतः यथार्थ अनुक्रम की धारणा कर्नेल (श्रेणी सिद्धांत) और कोकर्नेल के साथ किसी भी श्रेणी (गणित) में समझ में आती है।

संक्षिप्त यथार्थ क्रम

यथार्थ अनुक्रम का सबसे सामान्य प्रकार संक्षिप्त यथार्थ अनुक्रम है। यह फॉर्म का यथार्थ क्रम है

$A\;{\overset {f}{\hookrightarrow }}\;B\;{\overset {g}{\twoheadrightarrow }}\;C$

जहां˒ समाकृतिकता है और जी अभिरूपी है। इस मामले में, A, B का उप-वस्तु है, और संबंधित भागफल C के लिए एकरूपता है:

$C\cong B/f(A).$ (जहाँ f(A) = im(f)).

एबेलियन समूहों का संक्षिप्त यथार्थ अनुक्रम पांच शब्दों के साथ यथार्थ अनुक्रम के रूप में भी लिखा जा सकता है:

$0\;\xrightarrow {} \;A\;\xrightarrow {f} \;B\;\xrightarrow {g} \;C\;\xrightarrow {} \;0$

जहां 0 प्रारंभिक और टर्मिनल वस्तुओं का प्रतिनिधित्व करता है, जैसे कि तुच्छ समूह या शून्य-आयामी सदिश स्थान। 0 की शक्तियों का स्थान एकरूपता है और g अभिरूपी है (नीचे देखें)।

लंबा यथार्थ क्रम

एक लंबा यथार्थ अनुक्रम प्राकृतिक संख्याओं द्वारा अनुक्रमित यथार्थ अनुक्रम है।

पांच लेम्मा

Main article: पांच लेम्मा

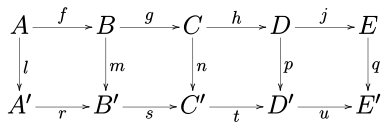
किसी भी एबेलियन श्रेणी (जैसे एबेलियन समूहों की श्रेणी या किसी दिए गए क्षेत्र (बीजगणित) पर सदिश रिक्त स्थान की श्रेणी) या समूह (गणित) की श्रेणी में निम्नलिखित क्रमविनिमेय आरेख पर विचार करें।

पांच लेम्मा में कहा गया है कि, यदि पंक्तियाँ यथार्थ अनुक्रम हैं, m और p समरूपता हैं, l एक अभिरूपी है, और q एक एकरूपता है, तो n भी एक समाकृतिकता है।

सर्प लेम्मा

Main article: सर्प लेम्मा

एबेलियन श्रेणी में (जैसे कि एबेलियन समूहों की श्रेणी या किसी दिए गए क्षेत्र (बीजगणित) पर सदिश रिक्त स्थान की श्रेणी), एक क्रमविनिमेय आरेख पर विचार करें:

जहाँ पंक्तियाँ यथार्थ अनुक्रम हैं और 0 शून्य वस्तु है।

फिर A, B, और C के कर्नेल (श्रेणी सिद्धांत) और कोकर्नेल से संबंधित एक यथार्थ अनुक्रम है:

$\ker a\to \ker b\to \ker c{\overset {d}{\to }}\operatorname {coker} a\to \operatorname {coker} b\to \operatorname {coker} c$

इसके अलावा, यदि रूपवाद एफ एक एकरूपता है, तो रूपवाद केर A → केर B भी है, और यदि जी' एक अभिरूपी है, तो कोकर B → कोकर C भी है।

एबेलियन श्रेणियाँ

Main article: एबेलियन श्रेणी

गणित में, एबेलियन श्रेणी एक श्रेणी (श्रेणी सिद्धांत) है जिसमें रूपवाद और वस्तुओं को जोड़ा जा सकता है और जिसमें कर्नेल (श्रेणी सिद्धांत) और कोकर्नेल उपस्थित हैं और वांछनीय गुण हैं। एबेलियन श्रेणी का प्रेरक प्रोटोटाइप उदाहरण एबेलियन समूहों की श्रेणी, एब है। इस सिद्धांत की उत्पत्ति अलेक्जेंडर ग्रोथेंडिक द्वारा कई कोहोमोलॉजी सिद्धांतों को एकजुट करने के एक अस्थायी प्रयास में हुई थी। एबेलियन श्रेणियां बहुत स्थिर श्रेणियां हैं, उदाहरण के लिए वे नियमित श्रेणी हैं और वे साँप लेम्मा को संतुष्ट करती हैं। एबेलियन श्रेणियों का वर्ग कई श्रेणीबद्ध निर्माणों के अंतर्गत बंद है, उदाहरण के लिए, एबेलियन श्रेणी के श्रृंखला परिसरों की श्रेणी, या छोटी श्रेणी से एबेलियन श्रेणी तक फ़ैक्टर्स की श्रेणी भी एबेलियन हैं। ये स्थिरता गुण उन्हें सजातीय बीजगणित और उससे आगे अपरिहार्य बनाते हैं; इस सिद्धांत का बीजगणितीय ज्यामिति, सह-समरूपता और शुद्ध श्रेणी सिद्धांत में प्रमुख अनुप्रयोग है। एबेलियन श्रेणियों का नाम नील्स हेनरिक एबेल के नाम पर रखा गया है।

अधिक ठोस रूप से, एक श्रेणी एबेलियन है यदि

• इसमें शून्य वस्तु है,
• इसमें सभी बाइनरी उत्पाद (श्रेणी सिद्धांत) और बाइनरी सह-उत्पाद हैं, और
• इसमें सभी कर्नेल (श्रेणी सिद्धांत) और कोकर्नेल हैं।
• सभी एकरूपता और आकारिता सामान्य रूपवाद हैं।

एक्सट कारक

Main article: एक्सट फ़ैनक्टर

R को एक वलय होने दें और Mod_R को R के ऊपर मॉड्यूल की श्रेणी होने दें। मान लें कि B Mod_R में है और Mod_R में निश्चित A के लिए T(B) = Hom_R(A,B), समूह करें। यह एक बायां यथार्थ फ़ैनक्टर है और इस प्रकार इसमें दाएं व्युत्पन्न फ़ैनक्टर RⁿT है। एक्सट फ़ैक्टर को परिभाषित किया गया है

$\operatorname {Ext} _{R}^{n}(A,B)=(R^{n}T)(B).$

इसकी गणना किसी भी विशेषण संकल्प को लेकर की जा सकती है

$0\rightarrow B\rightarrow I^{0}\rightarrow I^{1}\rightarrow \cdots ,$

और कंप्यूटिंग

$0\rightarrow \operatorname {Hom} _{R}(A,I^{0})\rightarrow \operatorname {Hom} _{R}(A,I^{1})\rightarrow \cdots .$

फिर (RⁿT)(B) इस परिसर की समरूपता (गणित) है। ध्यान दें कि Hom_R(A,B) को कॉम्प्लेक्स से बाहर रखा गया है।

कारक G(A)=Hom_R(A,B).का उपयोग करके एक वैकल्पिक परिभाषा दी गई है। एक निश्चित मॉड्यूल B के लिए, यह एक सहप्रसरण है और फ़ैक्टरों का विपरीत यथार्थ कारक छोड़ दिया गया है, और इस प्रकार हमारे पास दाएं व्युत्पन्न फ़ैक्टर्स RⁿG भी हैं, और परिभाषित कर सकते हैं

$\operatorname {Ext} _{R}^{n}(A,B)=(R^{n}G)(A).$

इसकी गणना किसी भी प्रक्षेप्य स्थिरता को चुनकर की जा सकती है

$\dots \rightarrow P^{1}\rightarrow P^{0}\rightarrow A\rightarrow 0,$

और गणना द्वारा दोहरी रूप से आगे बढ़ना

$0\rightarrow \operatorname {Hom} _{R}(P^{0},B)\rightarrow \operatorname {Hom} _{R}(P^{1},B)\rightarrow \cdots .$

फिर (RⁿG)(A) इस परिसर की समरूपता है। पुनः ध्यान दें कि Hom_R(A,B) को बाहर रखा गया है।

ये दो निर्माण समरूपी परिणाम उत्पन्न करते हैं, और इसलिए दोनों का उपयोग एक्सट कारक की गणना के लिए किया जा सकता है।

टोर ऑपरेटर

Main article: टोर फ़ैक्टर

मान लीजिए कि r एक वलय (गणित) है, और R-Mod द्वारा मॉड्यूल (गणित) के श्रेणी सिद्धांत को दर्शाया गया है। बाएं r-मॉड्यूल और Mod-R द्वारा दाएं r-मॉड्यूल की श्रेणी को दर्शाया गया है (यदि r क्रमविनिमेय वलय है) , दोनों श्रेणियां मेल खाती हैं)। R-Mod में एक मॉड्यूल B को ठीक करें। Mod-R में A के लिए, T(A) = A⊗_RB तब T Mod-R से एबेलियन समूहों की श्रेणी 'Ab' तक एक सही यथार्थ फ़नकार है (उस स्थिति में जब r क्रमविनिमेय है, यह Mod-R से Mod-R तक एक सही यथार्थ फ़नकार है- R) और इसके व्युत्पन्न फ़ंक्शनल L_nT परिभाषित हैं। हमलोग तैयार हैं

$\mathrm {Tor} _{n}^{R}(A,B)=(L_{n}T)(A)$

यानि हम एक प्रक्षेपी स्थिरिता लेते हैं

$\cdots \rightarrow P_{2}\rightarrow P_{1}\rightarrow P_{0}\rightarrow A\rightarrow 0$

फिर A शब्द को हटा दें और कॉम्प्लेक्स प्राप्त करने के लिए B के साथ प्रक्षेप्य स्थिरिता को टेंसर करें

$\cdots \rightarrow P_{2}\otimes _{R}B\rightarrow P_{1}\otimes _{R}B\rightarrow P_{0}\otimes _{R}B\rightarrow 0$

(ध्यान दें कि A⊗_RB प्रकट नहीं होता है और अंतिम तीर केवल शून्य मानचित्र है) और इस परिसर की समरूपता (गणित) लें।

वर्णक्रम अनुक्रम

Main article: वर्णक्रमीय अनुक्रम

एक एबेलियन श्रेणी को ठीक करें, जैसे कि वलय के ऊपर मॉड्यूल की एक श्रेणी। वर्णक्रमीय अनुक्रम एक गैर-ऋणात्मक पूर्णांक r₀ का एक विकल्प और तीन अनुक्रमों का संग्रह है:

1. सभी पूर्णांकों r ≥ r₀ के लिए, एक ऑब्जेक्ट E_r, जिसे एक शीट कहा जाता है (जैसा कि कागज की एक शीट में), या कभी-कभी एक पृष्ठ या एक शब्द।
2. एंडोमोर्फिज्म d_r : E_r → E_r संतोषजनक d_r o d_r = 0, जिसे सीमा मानचित्र या अंतर कहा जाता है।
3. H(E_r) के साथ E_r+1 की समरूपता, d_r के संबंध में E_r की समरूपता।

E₂ कोहॉमोलॉजिकल वर्णक्रमीय अनुक्रम की शीट

दोहरे श्रेणीबद्ध वर्णक्रमीय अनुक्रम में ट्रैक रखने के लिए भारी मात्रा में डेटा होता है, लेकिन एक सामान्य विज़ुअलाइज़ेशन तकनीक है जो वर्णक्रमीय अनुक्रम की संरचना को स्पष्ट करती है। हमारे पास तीन सूचकांक हैं, r, p, और q। प्रत्येक r के लिए, कल्पना करें कि हमारे पास ग्राफ़ पेपर की एक शीट है। इस शीट पर, हम क्षैतिज दिशा के रूप में p और ऊर्ध्वाधर दिशा के रूप में q लेंगे। प्रत्येक जालक बिंदु $E_{r}^{p,q}$ पर हमारे पास वस्तु होती है।

वर्णक्रमीय अनुक्रम में n = p + q का एक अन्य प्राकृतिक सूचकांक होना बहुत आम है। n प्रत्येक शीट पर तिरछे, उत्तर-पश्चिम से दक्षिण-पूर्व तक चलता है। सजातीय मामले में, अंतरों में द्विघात (-r, r − 1) होता है, इसलिए वे n को एक से कम करते हैं। कोहोमोलॉजिकल मामले में, n एक से बढ़ जाता है। जब r शून्य होता है, तो अंतर वस्तुओं को एक स्थान नीचे या ऊपर ले जाता है। यह एक श्रृंखला परिसर पर अंतर के समान है। जब r एक होता है, तो अंतर वस्तुओं को एक स्थान बाएँ या दाएँ ले जाता है। जब r दो होता है, तो अंतर शतरंज में एक शूरवीर (शतरंज) की चाल की तरह ही वस्तुओं को स्थानांतरित करता है। उच्च r के लिए, अंतर एक सामान्यीकृत शूरवीर चाल की तरह कार्य करता है।

व्युत्पन्न कारक

Main article: व्युत्पन्न फ़ंक्टर

मान लीजिए कि हमें दो एबेलियन श्रेणी 'A' और 'B' के बीच एक सहसंयोजक बाएं यथार्थ फ़ंक्शनर F : A → B दिया गया है। यदि 0 → A → B → C → 0 में एक संक्षिप्त यथार्थ अनुक्रम है, तो F लगाने से यथार्थ अनुक्रम 0 → F(A) → F(B) → F(C) प्राप्त होता है और कोई पूछ सकता है कि इसे कैसे जारी रखा जाए एक लंबा यथार्थ क्रम बनाने के लिए इस क्रम को दाईं ओर रखें। कड़ाई से कहें तो, यह प्रश्न गलत है, क्योंकि किसी दिए गए यथार्थ अनुक्रम को दाईं ओर जारी रखने के लिए हमेशा कई अलग-अलग विधियों होते हैं। लेकिन यह पता चला है कि (यदि 'A' काफी अच्छा है) ऐसा करने का एक विहित रूप विधि है, जो एफ के सही व्युत्पन्न कारक द्वारा दिया गया है। प्रत्येक i≥1 के लिए, एक कारक r है RⁱF: A → B और उपरोक्त अनुक्रम इस प्रकार जारी रहता है: 0 → F(A) → F(B) → F(C) → R¹F(A) → R¹F(B) → R¹F(C) → R²F(A) → R²F(B) → ... . इससे हम देखते हैं कि F एक यथार्थ फ़नकार है यदि और केवल यदि R¹F = 0; तो एक अर्थ में F के सही व्युत्पन्न कारक मापते हैं कि F यथार्थ होने से कितनी दूर है।

कार्यात्मकता

टोपोलॉजिकल रिक्त स्थान का एक सतत मानचित्र सभी n के लिए उनके nवें समरूपता समूहों के बीच एक समरूपता को जन्म देता है। बीजगणितीय टोपोलॉजी का यह मूल तथ्य श्रृंखला परिसरों के कुछ गुणों के माध्यम से एक प्राकृतिक व्याख्या पाता है। चूंकि पढ़ाई करना बहुत आम बात है एक साथ कई टोपोलॉजिकल रिक्त स्थान, सजातीय बीजगणित में एक को कई श्रृंखला परिसरों पर एक साथ विचार करने के लिए प्रेरित किया जाता है।

दो श्रृंखला परिसरों के बीच एक 'रूपवाद', $F:C_{\bullet }\to D_{\bullet },$ एबेलियन समूहों की समरूपताओं का एक परिवार है $F_{n}:C_{n}\to D_{n}$ जो अंतर के साथ परिवर्तित होता है, इस अर्थ में $F_{n-1}\circ d_{n}^{C}=d_{n}^{D}\circ F_{n}$ सभी के लिए n. श्रृंखला परिसरों का एक रूपवाद एक रूपवाद को प्रेरित करता है $H_{\bullet }(F)$ उनके समरूपता समूहों में समरूपताएं सम्मिलित हैं $H_{n}(F):H_{n}(C)\to H_{n}(D)$ सभी के लिए n. एक रूपवाद F को 'अर्ध-समरूपतावाद' कहा जाता है यदि यह सभी n के लिए nवें समरूपता पर एक समरूपता उत्पन्न करता है।

बीजगणित और ज्यामिति में उत्पन्न होने वाले श्रृंखला परिसरों के कई निर्माण, जिनमें एकवचन समरूपता भी सम्मिलित है, में निम्नलिखित कार्यात्मकता गुण हैं: यदि दो वस्तुएं X और Y एक मानचित्र एफ द्वारा जुड़े हुए हैं, तो संबंधित श्रृंखला परिसर एक रूपवाद द्वारा जुड़े हुए हैं $F=C(f):C_{\bullet }(X)\to C_{\bullet }(Y),$ और इसके अलावा, रचना $g\circ f$ मानचित्रों का f: X → Y और g: Y → Z रूपवाद को प्रेरित करता है $C(g\circ f):C_{\bullet }(X)\to C_{\bullet }(Z)$ जो रचना से मेल खाता है $C(g)\circ C(f).$ यह इस प्रकार है कि समरूपता समूह $H_{\bullet }(C)$ कार्यात्मक भी हैं, ताकि बीजगणितीय या टोपोलॉजिकल वस्तुओं के बीच आकारिकी उनके समरूपता के बीच संगत मानचित्रों को जन्म दे सके।

निम्नलिखित परिभाषा बीजगणित और टोपोलॉजी में एक विशिष्ट स्थिति से उत्पन्न होती है। एक ट्रिपल जिसमें तीन श्रृंखला परिसर होते हैं $L_{\bullet },M_{\bullet },N_{\bullet }$ और उनके बीच दो आकारिकी, $f:L_{\bullet }\to M_{\bullet },g:M_{\bullet }\to N_{\bullet },$ इसे यथार्थ ट्रिपल, या कॉम्प्लेक्स का संक्षिप्त यथार्थ अनुक्रम कहा जाता है, और इसे इस प्रकार लिखा जाता है

$0\longrightarrow L_{\bullet }{\overset {f}{\longrightarrow }}M_{\bullet }{\overset {g}{\longrightarrow }}N_{\bullet }\longrightarrow 0,$

यदि किसी n के लिए, अनुक्रम

$0\longrightarrow L_{n}{\overset {f_{n}}{\longrightarrow }}M_{n}{\overset {g_{n}}{\longrightarrow }}N_{n}\longrightarrow 0$

एबेलियन समूहों का एक संक्षिप्त यथार्थ क्रम है। परिभाषा के अनुसार, इसका मतलब यह है कि f_n एक इंजेक्शन (गणित) है, g_n एक अनुमान है, और मैं δ_n क्योंकि सजातीय बीजगणित के सबसे बुनियादी प्रमेयों में से एक, जिसे कभी-कभी ज़िगज़ैग लेम्मा के रूप में जाना जाता है, बताता है कि, इस मामले में, समरूपता में एक लंबा यथार्थ अनुक्रम है

$\cdots \longrightarrow H_{n}(L){\overset {H_{n}(f)}{\longrightarrow }}H_{n}(M){\overset {H_{n}(g)}{\longrightarrow }}H_{n}(N){\overset {\delta _{n}}{\longrightarrow }}H_{n-1}(L){\overset {H_{n-1}(f)}{\longrightarrow }}H_{n-1}(M)\longrightarrow \cdots ,$

जहां l, m और n के समरूपता समूह चक्रीय रूप से एक दूसरे का अनुसरण करते हैं, और δ_n एफ और जी द्वारा निर्धारित कुछ समरूपताएँ हैं, जिन्हें 'कनेक्टिंग समरूपताएँ' कहा जाता है। इस प्रमेय की टोपोलॉजिकल अभिव्यक्तियों में मेयर-विएटोरिस अनुक्रम और सापेक्ष समरूपता के लिए लंबा यथार्थ अनुक्रम सम्मिलित है।

मूलभूत पहलू

कोहोलॉजी सिद्धांतों को कई अलग-अलग वस्तुओं के लिए परिभाषित किया गया है जैसे कि टोपोलॉजिकल स्पेस, शीफ (गणित), समूह (गणित), वलय (गणित), ली बीजगणित, और C*-बीजगणित। आधुनिक बीजगणितीय ज्यामिति का अध्ययन शीफ़ कोहोमोलोजी के बिना लगभग अकल्पनीय होगा।

सजातीय बीजगणित के केंद्र में यथार्थ अनुक्रम की धारणा है; इनका उपयोग वास्तविक गणना करने के लिए किया जा सकता है। सजातीय बीजगणित का एक शास्त्रीय उपकरण व्युत्पन्न फ़ंक्टर का है; सबसे बुनियादी उदाहरण कारक, विस्तारक और टोर कारक हैं।

अनुप्रयोगों के विविध समूह को ध्यान में रखते हुए, पूरे विषय को एक समान आधार पर रखने का प्रयास करना स्वाभाविक था। मामला शांत होने से पहले कई प्रयास हुए। एक अनुमानित इतिहास इस प्रकार बताया जा सकता है:

• हेनरी कर्तन -सैमुअल इलेनबर्ग: अपनी 1956 की पुस्तक सजातीय अलजेब्रा में, इन लेखकों ने प्रोजेक्टिव रेजोल्यूशन और इंजेक्टिव रेजोल्यूशन का उपयोग किया।
• 'तोहोकू': अलेक्जेंडर ग्रोथेंडिक द्वारा ग्रोथेंडिक के तोहोकू पेपर में दृष्टिकोण जो 1957 में तोहोकू गणितीय जर्नल की दूसरी श्रृंखला में एबेलियन श्रेणी अवधारणा (एबेलियन समूहों के शीफ (गणित) को सम्मिलित करने के लिए) का उपयोग करते हुए दिखाई दिया।
• ग्रोथेंडिक और जीन-लुई वर्डियर की व्युत्पन्न श्रेणी। व्युत्पन्न श्रेणियाँ वर्डियर की 1967 की थीसिस से मिलती जुलती हैं। वे कई आधुनिक सिद्धांतों में प्रयुक्त त्रिकोणीय श्रेणी के उदाहरण हैं।

ये संगणनीयता से व्यापकता की ओर बढ़ते हैं।

कम्प्यूटेशनल स्लेजहैमर सर्वोत्कृष्टता वर्णक्रमीय अनुक्रम है; ये कार्टन-एलेनबर्ग और तोहोकू दृष्टिकोणों में आवश्यक हैं जहां इनकी आवश्यकता होती है, उदाहरण के लिए, दो फ़ैक्टर्स की संरचना के व्युत्पन्न फ़ैक्टर्स की गणना करने के लिए। व्युत्पन्न श्रेणी दृष्टिकोण में वर्णक्रमीय अनुक्रम कम आवश्यक हैं, लेकिन जब भी ठोस गणना आवश्यक होती है तब भी एक भूमिका निभाते हैं।

'नॉन-कम्यूटेटिव' सिद्धांतों पर प्रयास किए गए हैं जो पहले कोहॉमोलॉजी को टॉर्सर्स के रूप में विस्तारित करते हैं (गैलोइस कोहोमोलॉजी में महत्वपूर्ण)।

यह भी देखें

• सार निरर्थक, समरूप बीजगणित और श्रेणी सिद्धांत के लिए एक शब्द
• व्युत्पन्न
• समस्थानिक बीजगणित
• सजातीय बीजगणित विषयों की सूची

संदर्भ

• Henri Cartan, Samuel Eilenberg, Homological algebra. With an appendix by David A. Buchsbaum. Reprint of the 1956 original. Princeton Landmarks in Mathematics. Princeton University Press, Princeton, NJ, 1999. xvi+390 pp. ISBN 0-691-04991-2
• Grothendieck, Alexander (1957). "Sur quelques points d'algèbre homologique, I". Tohoku Mathematical Journal. 9 (2): 119–221. doi:10.2748/tmj/1178244839.
• Saunders Mac Lane, Homology. Reprint of the 1975 edition. Classics in Mathematics. Springer-Verlag, Berlin, 1995. x+422 pp. ISBN 3-540-58662-8
• Peter Hilton; Stammbach, U. A course in homological algebra. Second edition. Graduate Texts in Mathematics, 4. Springer-Verlag, New York, 1997. xii+364 pp. ISBN 0-387-94823-6
• Gelfand, Sergei I.; Yuri Manin, Methods of homological algebra. Translated from Russian 1988 edition. Second edition. Springer Monographs in Mathematics. Springer-Verlag, Berlin, 2003. xx+372 pp. ISBN 3-540-43583-2
• Gelfand, Sergei I.; Yuri Manin, Homological algebra. Translated from the 1989 Russian original by the authors. Reprint of the original English edition from the series Encyclopaedia of Mathematical Sciences (Algebra, V, Encyclopaedia Math. Sci., 38, Springer, Berlin, 1994). Springer-Verlag, Berlin, 1999. iv+222 pp. ISBN 3-540-65378-3
• Weibel, Charles A. (1994). An introduction to homological algebra. Cambridge Studies in Advanced Mathematics. Vol. 38. Cambridge University Press. ISBN 978-0-521-55987-4. MR 1269324. OCLC 36131259.