जटिल संख्या: Difference between revisions
(Created page with "{{Short description|Number with a real and an imaginary part}} {{More citations needed|date=July 2022}} {{Use dmy dates|date=June 2020}} File:A plus bi.svg|thumb|upright=1....") |
No edit summary |
||
| Line 1: | Line 1: | ||
{{Short description|Number with a real and an imaginary part}} | {{Short description|Number with a real and an imaginary part}} | ||
{{More citations needed|date=July 2022}} | {{More citations needed|date=July 2022}} | ||
{{Use dmy dates|date=June 2020}} | {{Use dmy dates|date=June 2020|cs1-dates = l}} | ||
[[File:A plus bi.svg|thumb|upright=1.15|right|एक | [[File:A plus bi.svg|thumb|upright=1.15|right|एक जटिल संख्या को संख्याओं की एक जोड़ी के रूप में नेत्रहीन रूप से दर्शाया जा सकता है {{math|(''a'', ''b'')}} आरेख पर एक सदिश का निर्माण करना, जिसे Argand आरेख कहा जाता है, जो जटिल तल का प्रतिनिधित्व करता है। Re वास्तविक अक्ष है, Im काल्पनिक अक्ष है, और {{mvar|i}} [[काल्पनिक इकाई]] है, जो संतुष्ट करती है {{math|1=''i''{{sup|2}} = −1}}.]]गणित में, एक जटिल संख्या एक [[संख्या प्रणाली]] का एक तत्व है जो [[वास्तविक संख्या]] को एक विशिष्ट तत्व के साथ विस्तारित करता है {{mvar|i}}, काल्पनिक इकाई कहलाती है और [[समीकरण]] को संतुष्ट करती है <math>i^{2}= -1</math>; प्रत्येक सम्मिश्र संख्या को रूप में व्यक्त किया जा सकता है <math>a + bi</math>, कहाँ पे {{mvar|a}} तथा {{mvar|b}} वास्तविक संख्याएँ हैं। क्योंकि कोई भी वास्तविक संख्या उपरोक्त समीकरण को संतुष्ट नहीं करती है, {{mvar|i}} रेने डेसकार्टेस द्वारा एक [[काल्पनिक संख्या]] कहा गया था। जटिल संख्या के लिए <math>a+bi</math>, {{mvar|a}} कहा जाता है{{visible anchor|real part}}, तथा {{mvar|b}} कहा जाता है{{visible anchor|imaginary part}}. सम्मिश्र संख्याओं के समुच्चय को किसी भी प्रतीक द्वारा निरूपित किया जाता है <math>\mathbb C</math> या {{math|'''C'''}}. ऐतिहासिक नामकरण काल्पनिक होने के बावजूद, [[गणितीय विज्ञान]] में जटिल संख्याओं को वास्तविक संख्याओं के समान ही वास्तविक माना जाता है और प्राकृतिक दुनिया के वैज्ञानिक विवरण के कई पहलुओं में मौलिक हैं।<ref>For an extensive account of the history of "imaginary" numbers, from initial skepticism to ultimate acceptance, see {{cite book |last=Bourbaki |first=Nicolas |author-link=Nicolas Bourbaki |year=1998 |title=Elements of the History of Mathematics |chapter=Foundations of Mathematics § Logic: Set theory |pages=18–24 |publisher=Springer}} | ||
गणित में, एक जटिल संख्या एक [[ संख्या प्रणाली ]] का एक तत्व है जो [[ वास्तविक संख्या ]] | |||
</ref>{{efn| "Complex numbers, as much as reals, and perhaps even more, find a unity with nature that is truly remarkable. It is as though Nature herself is as impressed by the scope and consistency of the complex-number system as we are ourselves, and has entrusted to these numbers the precise operations of her world at its minutest scales." — R. Penrose (2016, <!-- [https://books.google.com/books?id=VWTNCwAAQBAJ&pg=PA73 ] --> p. 73)<ref>{{cite book |first=Roger |last=Penrose |year=2016 |title=The Road to Reality: A complete guide to the laws of the universe |edition=reprint |publisher=Random House |isbn=978-1-4464-1820-8 |pages=72–73 |url=https://books.google.com/books?id=VWTNCwAAQBAJ&pg=PA73}}</ref> }} | </ref>{{efn| "Complex numbers, as much as reals, and perhaps even more, find a unity with nature that is truly remarkable. It is as though Nature herself is as impressed by the scope and consistency of the complex-number system as we are ourselves, and has entrusted to these numbers the precise operations of her world at its minutest scales." — R. Penrose (2016, <!-- [https://books.google.com/books?id=VWTNCwAAQBAJ&pg=PA73 ] --> p. 73)<ref>{{cite book |first=Roger |last=Penrose |year=2016 |title=The Road to Reality: A complete guide to the laws of the universe |edition=reprint |publisher=Random House |isbn=978-1-4464-1820-8 |pages=72–73 |url=https://books.google.com/books?id=VWTNCwAAQBAJ&pg=PA73}}</ref> }} | ||
जटिल संख्याएं सभी [[बहुपद समीकरण]]ों के समाधान की अनुमति देती हैं, यहां तक कि उनका भी जिनका वास्तविक संख्या में कोई समाधान नहीं है। अधिक सटीक रूप से, बीजगणित के मौलिक प्रमेय का दावा है कि वास्तविक या जटिल गुणांक वाले प्रत्येक गैर-निरंतर बहुपद समीकरण का एक समाधान होता है जो एक जटिल संख्या है। उदाहरण के लिए, समीकरण | |||
<math>(x+1)^2 = -9</math> | <math>(x+1)^2 = -9</math> | ||
इसका कोई वास्तविक समाधान नहीं है, क्योंकि वास्तविक संख्या का वर्ग ऋणात्मक नहीं हो सकता है, लेकिन इसके दो अवास्तविक जटिल समाधान हैं | इसका कोई वास्तविक समाधान नहीं है, क्योंकि वास्तविक संख्या का वर्ग ऋणात्मक नहीं हो सकता है, लेकिन इसके दो अवास्तविक जटिल समाधान हैं <math>-1+3i</math> तथा <math>-1-3i</math>. | ||
जटिल संख्याओं के जोड़, घटाव और गुणा को | नियम का उपयोग करके जटिल संख्याओं के जोड़, घटाव और गुणा को स्वाभाविक रूप से परिभाषित किया जा सकता है <math>i^{2}=-1</math> साहचर्य कानून, [[विनिमेय कानून]] और [[वितरण कानून]]ों के साथ संयुक्त। प्रत्येक अशून्य सम्मिश्र संख्या का गुणनात्मक व्युत्क्रम होता है। यह सम्मिश्र संख्याओं को एक ऐसा [[क्षेत्र (गणित)]] बनाता है जिसमें उपक्षेत्र के रूप में वास्तविक संख्याएँ होती हैं। सम्मिश्र संख्याएँ भी आयाम दो का एक वास्तविक सदिश स्थान बनाती हैं, साथ में {{math|{{mset|1, ''i''}}}} [[मानक आधार]] के रूप में। | ||
यह मानक आधार सम्मिश्र संख्याओं को कार्तीय तल बनाता है, जिसे सम्मिश्र तल | यह मानक आधार सम्मिश्र संख्याओं को कार्तीय तल बनाता है, जिसे सम्मिश्र तल कहा जाता है। यह जटिल संख्याओं और उनके संचालन की एक ज्यामितीय व्याख्या की अनुमति देता है, और इसके विपरीत कुछ ज्यामितीय गुणों और निर्माणों को जटिल संख्याओं के रूप में व्यक्त करता है। उदाहरण के लिए, वास्तविक संख्याएँ [[वास्तविक रेखा]] बनाती हैं जिसे जटिल तल के क्षैतिज अक्ष से पहचाना जाता है। निरपेक्ष मान की सम्मिश्र संख्याएँ इकाई वृत्त बनाती हैं। जटिल संख्या का जोड़ जटिल विमान में एक [[अनुवाद (ज्यामिति)]] है, और जटिल संख्या से गुणा एक [[समानता (ज्यामिति)]] है जो मूल पर केंद्रित है। वास्तविक अक्ष के संबंध में [[जटिल संयुग्मन]] [[प्रतिबिंब समरूपता]] है। जटिल निरपेक्ष मान एक [[यूक्लिडियन मानदंड]] है। | ||
संक्षेप में, जटिल संख्याएं एक समृद्ध संरचना बनाती हैं जो एक साथ एक | संक्षेप में, जटिल संख्याएं एक समृद्ध संरचना बनाती हैं जो एक साथ एक बीजगणितीय रूप से बंद क्षेत्र, वास्तविकताओं पर एक कम्यूटेटिव बीजगणित (संरचना) और आयाम दो का एक [[यूक्लिडियन वेक्टर अंतरिक्ष]] है। | ||
{{TOC limit|3}} | {{TOC limit|3}} | ||
| Line 20: | Line 19: | ||
== परिभाषा == | == परिभाषा == | ||
[[File:Illustration of a complex number.svg|right|thumb|upright=1.05| | [[File:Illustration of a complex number.svg|right|thumb|upright=1.05|जटिल संख्या का एक उदाहरण {{math|1=''z'' = ''x'' + ''iy''}} जटिल तल पर। असली हिस्सा है {{mvar|x}}, और इसका काल्पनिक हिस्सा है {{mvar|y}}.]]एक सम्मिश्र संख्या रूप की एक संख्या है {{math|1=''a'' + ''bi''}}, कहाँ पे {{mvar|a}} तथा {{mvar|b}} [[वास्तविक संख्या]]एँ हैं, और {{math|''i''}} एक अनिश्चित संतोषजनक है {{math|1=''i''<sup>2</sup> = −1}}. उदाहरण के लिए, {{math|2 + 3''i''}} एक जटिल संख्या है।<ref>{{cite book|title=कॉलेज अल्जेबरा|url=https://archive.org/details/collegealgebrawi00axle |url-access=limited |last=Axler |first=Sheldon |page=[https://archive.org/details/collegealgebrawi00axle/page/n285 262]|publisher=Wiley|year=2010|isbn=9780470470770 }}</ref> | ||
एक सम्मिश्र संख्या | इस तरह, एक सम्मिश्र संख्या को एकल अनिश्चित में वास्तविक गुणांक वाले [[बहुपद]] के रूप में परिभाषित किया जाता है {{math|''i''}}, जिसके लिए संबंध {{math|''i''<sup>2</sup> + 1 {{=}} 0}} लगाया जाता है। इस परिभाषा के आधार पर, बहुपदों के योग और गुणन का उपयोग करके जटिल संख्याओं को जोड़ा और गुणा किया जा सकता है। सम्बन्ध {{math|''i''<sup>2</sup> + 1 {{=}} 0}} समानता को प्रेरित करता है {{math|''i''<sup>4''k''</sup> {{=}} 1, ''i''<sup>4''k''+1</sup> {{=}} ''i'', ''i''<sup>4''k''+2</sup> {{=}} −1,}} तथा {{math|''i''<sup>4''k''+3</sup> {{=}} −''i'',}} जो सभी पूर्णांकों के लिए है {{mvar|k}}; ये किसी भी बहुपद को कम करने की अनुमति देते हैं जो सम्मिश्र संख्याओं के जोड़ और गुणा से एक रेखीय बहुपद में परिणामित होता है {{mvar|i}}, फिर से फॉर्म का {{math|1=''a'' + ''bi''}} वास्तविक गुणांक के साथ {{mvar|a, b.}} | ||
इस तरह, एक | वास्तविक संख्या {{mvar|a}} सम्मिश्र संख्या का वास्तविक भाग कहलाता है {{math|''a'' + ''bi''}}; वास्तविक संख्या {{mvar|b}} उसका काल्पनिक भाग कहलाता है। जोर देने के लिए, काल्पनिक भाग में एक कारक शामिल नहीं होता है {{mvar|i}}; वह है, काल्पनिक हिस्सा है {{mvar|b}}, नहीं {{math|''bi''}}.<ref>{{cite book |last1=Spiegel |first1= M.R. |last2=Lipschutz |first2= S. |last3= Schiller |first3= J.J. |last4=Spellman |first4=D. |title= जटिल चर|edition=2nd |series=Schaum's Outline Series |publisher= McGraw Hill |isbn= 978-0-07-161569-3|date= 14 April 2009 }}</ref><ref>{{cite book |title=कॉलेज बीजगणित और त्रिकोणमिति|edition=6 |first1=Richard N. |last1=Aufmann |first2=Vernon C. |last2=Barker |first3=Richard D. |last3=Nation |publisher=Cengage Learning |year=2007 |isbn=978-0-618-82515-8 |page=66 |chapter-url=https://books.google.com/books?id=g5j-cT-vg_wC&pg=PA66 |chapter=Chapter P}}</ref> | ||
वास्तविक संख्या {{mvar|a}} सम्मिश्र संख्या का वास्तविक भाग कहलाता है {{math|''a'' + ''bi''}}; वास्तविक संख्या {{mvar|b}} उसका काल्पनिक भाग कहलाता है। जोर देने के लिए, काल्पनिक भाग में एक कारक शामिल नहीं है {{mvar|i}}; | औपचारिक रूप से, जटिल संख्याओं को अनिश्चित काल में बहुपद वलय के भागफल वलय के रूप में परिभाषित किया जाता है {{math|''i''}}, बहुपद द्वारा उत्पन्न आदर्श (रिंग थ्योरी) द्वारा {{math|''i''<sup>2</sup> + 1}} (#Construction को भागफल क्षेत्र के रूप में देखें)।<ref name= Bourbaki 1998 loc=§VIII.1>{{harvnb|Bourbaki|1998|loc=§VIII.1}}</रेफरी> | ||
औपचारिक रूप से, जटिल संख्याओं को अनिश्चित में | |||
== | == नोटेशन == | ||
एक वास्तविक संख्या {{mvar|a}} एक जटिल संख्या के रूप में माना जा सकता है {{math|''a'' + 0''i''}}, जिसका काल्पनिक भाग 0 | एक वास्तविक संख्या {{mvar|a}} एक जटिल संख्या के रूप में माना जा सकता है {{math|''a'' + 0''i''}}, जिसका काल्पनिक भाग 0. एक विशुद्ध रूप से काल्पनिक संख्या है {{math|''bi''}} एक जटिल संख्या है {{math|0 + ''bi''}}, जिसका वास्तविक भाग शून्य है। जैसा कि बहुपदों के साथ होता है, लिखना सामान्य है {{mvar|a}} के लिये {{math|''a'' + 0''i''}} तथा {{math|''bi''}} के लिये {{math|0 + ''bi''}}. इसके अलावा, जब काल्पनिक भाग नकारात्मक होता है, अर्थात, {{math|1=''b'' = −''{{!}}b{{!}}'' < 0}}, लिखना आम बात है {{math|''a'' − ''{{!}}b{{!}}i''}} के बजाय {{math|''a'' + (−''{{!}}b{{!}}'')''i''}}; उदाहरण के लिए, के लिए {{math|1=''b'' = −4}}, {{math|3 − 4''i''}} की जगह लिखा जा सकता है {{math|3 + (−4)''i''}}. | ||
अनिश्चित के गुणन के बाद से {{math|''i''}} और एक वास्तविक वास्तविक गुणांक | अनिश्चित के गुणन के बाद से {{math|''i''}} और एक वास्तविक बहुपद में वास्तविक गुणांक, बहुपद के साथ क्रमविनिमेय है {{math|''a'' + ''bi''}} रूप में लिखा जा सकता है {{math|''a'' + ''ib''.}} यह अक्सर भावों द्वारा निरूपित काल्पनिक भागों के लिए समीचीन होता है, उदाहरण के लिए, जब {{mvar|b}} एक कट्टरपंथी है।{{sfn|Ahlfors|1979}} | ||
एक सम्मिश्र संख्या का वास्तविक भाग {{mvar|z}} द्वारा | एक सम्मिश्र संख्या का वास्तविक भाग {{mvar|z}} द्वारा निरूपित किया जाता है {{math|Re(''z'')}}, <math>\mathcal{Re}(z)</math>, या <math>\mathfrak{R}(z)</math>; एक जटिल संख्या का काल्पनिक हिस्सा {{mvar|z}} द्वारा निरूपित किया जाता है {{math|Im(''z'')}}, <math>\mathcal{Im}(z)</math>, या <math>\mathfrak{I}(z).</math> उदाहरण के लिए, | ||
<math display=block> \operatorname{Re}(2 + 3i) = 2 \quad \text{ and } \quad \operatorname{Im}(2 + 3i) = 3~.</math> | <math display=block> \operatorname{Re}(2 + 3i) = 2 \quad \text{ and } \quad \operatorname{Im}(2 + 3i) = 3~.</math> | ||
सभी सम्मिश्र संख्याओं के समुच्चय (गणित) को द्वारा निरूपित किया जाता है <math>\Complex</math> ([[ ब्लैकबोर्ड बोल्ड ]]) या {{math|'''C'''}} ( | सभी सम्मिश्र संख्याओं के समुच्चय (गणित) को किसके द्वारा निरूपित किया जाता है <math>\Complex</math> ([[ब्लैकबोर्ड बोल्ड]]) या {{math|'''C'''}} (सीधा बोल्ड)। | ||
कुछ विषयों में, विशेष रूप से [[ विद्युत ]] चुंबकत्व और [[ विद्युत अभियन्त्रण ]] में, {{mvar|j}} | कुछ विषयों में, विशेष रूप से [[विद्युत]] चुंबकत्व और [[विद्युत अभियन्त्रण]] में, {{mvar|j}} की जगह प्रयोग किया जाता है {{mvar|i}} जैसा {{mvar|i}} अक्सर [[विद्युत प्रवाह]] का प्रतिनिधित्व करने के लिए प्रयोग किया जाता है।<ref>{{cite book |last1=Brown |first1=James Ward |last2=Churchill |first2=Ruel V. |title=जटिल चर और अनुप्रयोग|year=1996 |publisher=McGraw-Hill |location=New York |isbn=978-0-07-912147-9 |edition=6th |page=2 |quote=विद्युत अभियांत्रिकी में, ''i'' के स्थान पर ''j'' अक्षर का प्रयोग किया जाता है।}}</ref> इन मामलों में, सम्मिश्र संख्याएँ इस प्रकार लिखी जाती हैं {{math|''a'' + ''bj''}}, या {{math|''a'' + ''jb''}}. | ||
==विज़ुअलाइज़ेशन== | == विज़ुअलाइज़ेशन == | ||
{{Main|Complex plane}} | {{Main|Complex plane}} | ||
[[File:Complex number illustration.svg|thumb|right|एक जटिल संख्या {{mvar|z}}, एक बिंदु | [[File:Complex number illustration.svg|thumb|right|एक जटिल संख्या {{mvar|z}}, एक बिंदु (काला) और इसकी स्थिति वेक्टर (नीला) के रूप में]]एक जटिल संख्या {{mvar|z}} इस प्रकार एक आदेशित जोड़ी के साथ पहचाना जा सकता है <math>(\Re (z),\Im (z))</math> वास्तविक संख्याएँ, जिन्हें बदले में द्वि-आयामी अंतरिक्ष में एक बिंदु के निर्देशांक के रूप में व्याख्या किया जा सकता है। सबसे तात्कालिक स्थान यूक्लिडियन विमान उपयुक्त निर्देशांक के साथ है, जिसे तब जटिल विमान या अरगंड आरेख कहा जाता है,<ref>{{cite book |last=Pedoe |first=Dan |author-link=Daniel Pedoe |title=ज्यामिति: एक व्यापक पाठ्यक्रम|publisher=Dover |year=1988 |isbn=978-0-486-65812-4}}</ref>{{efn| {{harvnb|Solomentsev|2001}}: "The plane <math>\R^2</math> whose points are identified with the elements of <math>\Complex</math> is called the complex plane ... The complete geometric interpretation of complex numbers and operations on them appeared first in the work of C. Wessel (1799). The geometric representation of complex numbers, sometimes called the 'Argand diagram', came into use after the publication in 1806 and 1814 of papers by J.R. Argand, who rediscovered, largely independently, the findings of Wessel".}}<ref name=":2">{{Cite web |last=Weisstein |first=Eric W. |title=जटिल संख्या|url=https://mathworld.wolfram.com/ComplexNumber.html |access-date=2020-08-12 |website=mathworld.wolfram.com}}</ref> [[जीन-रॉबर्ट अरगंड]] के नाम पर। एक अन्य प्रमुख स्थान जिस पर निर्देशांक प्रक्षेपित किए जा सकते हैं, वह एक गोले की द्वि-आयामी सतह है, जिसे तब [[रीमैन क्षेत्र]] कहा जाता है। | ||
एक जटिल संख्या {{mvar|z}} इस प्रकार एक आदेशित जोड़ी के साथ पहचाना जा सकता है <math>(\Re (z),\Im (z))</math> वास्तविक | |||
=== कार्तीय जटिल | === कार्तीय जटिल तल === | ||
जटिल संख्याओं की परिभाषा जिसमें दो मनमाने वास्तविक मूल्य शामिल हैं, तुरंत जटिल विमान में कार्टेशियन निर्देशांक के उपयोग का सुझाव देते हैं। क्षैतिज (वास्तविक) अक्ष का उपयोग आम तौर पर वास्तविक भाग को प्रदर्शित करने के लिए किया जाता है, बढ़ते मूल्यों के साथ दाईं ओर, और काल्पनिक भाग ऊर्ध्वाधर (काल्पनिक) अक्ष को चिह्नित करता है, बढ़ते मूल्यों के साथ ऊपर की ओर। | |||
एक चार्टेड संख्या | एक चार्टेड संख्या या तो विक्ट के रूप में देखी जा सकती है: समन्वय बिंदु या मूल से इस बिंदु तक एक [[वेक्टर (ज्यामितीय)]] के रूप में। एक सम्मिश्र संख्या के निर्देशांक मान {{mvar|z}} इसलिए इसके कार्टेशियन, आयताकार, या बीजगणितीय रूप में व्यक्त किया जा सकता है। | ||
विशेष रूप से, जोड़ और | विशेष रूप से, जोड़ और गुणन के संचालन एक बहुत ही प्राकृतिक ज्यामितीय चरित्र पर ले जाते हैं, जब जटिल संख्याओं को स्थिति वैक्टर के रूप में देखा जाता है: जोड़ यूक्लिडियन वेक्टर #जोड़ और घटाव से मेल खाता है, जबकि गुणन (ध्रुवीय रूप में #गुणा और विभाजन देखें) गुणन से मेल खाता है उनके परिमाण और उनके द्वारा वास्तविक अक्ष के साथ बनाए गए कोणों को जोड़ना। इस तरह से देखने पर, एक सम्मिश्र संख्या का गुणा द्वारा {{math|''i''}} मूल के बारे में एक चौथाई [[मोड़ (ज्यामिति)]] (समकोण | 90 °) द्वारा स्थिति सदिश [[अभिविन्यास (ज्यामिति)]] को घुमाने के अनुरूप है - एक तथ्य जिसे बीजगणितीय रूप से निम्नानुसार व्यक्त किया जा सकता है: | ||
<math display=block>(a + bi)\cdot i = ai + b(i)^2 = -b + ai .</math> | <math display=block>(a + bi)\cdot i = ai + b(i)^2 = -b + ai .</math> | ||
=== ध्रुवीय जटिल विमान {{anchor|Polar form}}=== <!-- [[Nth root]] links to this section --> | ===ध्रुवीय जटिल विमान {{anchor|Polar form}}=== <!-- [[Nth root]] links to this section --> | ||
{{Main|Polar coordinate system}} | {{Main|Polar coordinate system}} | ||
{{Redirect|Polar form|the higher-dimensional analogue|Polar decomposition}} | {{Redirect|Polar form|the higher-dimensional analogue|Polar decomposition}} | ||
[[File:Complex number illustration modarg.svg|right|thumb|बहस {{mvar|φ}} और मापांक {{mvar|r}} जटिल विमान में एक बिंदु का पता लगाएं।]] | [[File:Complex number illustration modarg.svg|right|thumb|बहस {{mvar|φ}} और मापांक {{mvar|r}} जटिल विमान में एक बिंदु का पता लगाएं।]] | ||
==== मापांक और तर्क ==== | |||
====मापांक और तर्क ==== | जटिल तल में निर्देशांक के लिए एक वैकल्पिक विकल्प [[ध्रुवीय समन्वय प्रणाली]] है जो बिंदु की दूरी का उपयोग करती है {{mvar|z}} उत्पत्ति से (गणित) ({{mvar|O}}), और धनात्मक वास्तविक अक्ष और रेखा खंड के बीच अंतरित कोण {{mvar|Oz}} वामावर्त अर्थ में। यह ध्रुवीय रूप की ओर जाता है | ||
जटिल तल में निर्देशांक के लिए एक वैकल्पिक विकल्प [[ ध्रुवीय समन्वय प्रणाली ]] है जो बिंदु की दूरी का उपयोग | |||
:<math>z=re^{i\varphi}=r(\cos\varphi +i\sin\varphi) </math> | :<math>z=re^{i\varphi}=r(\cos\varphi +i\sin\varphi) </math> | ||
एक सम्मिश्र संख्या का, जहाँ {{mvar|r}} का | एक सम्मिश्र संख्या का, जहाँ {{mvar|r}} का परम मूल्य है {{mvar|z}}, तथा <math>\varphi</math> का [[तर्क (जटिल विश्लेषण)]] है {{mvar|z}}. | ||
किसी सम्मिश्र संख्या का निरपेक्ष मान (या मापांक या परिमाण) {{math|1=''z'' = ''x'' + ''yi''}} है{{sfn|Apostol|1981|p=18}} | किसी सम्मिश्र संख्या का निरपेक्ष मान (या मापांक या परिमाण)। {{math|1=''z'' = ''x'' + ''yi''}} है{{sfn|Apostol|1981|p=18}} | ||
<math display=block>r=|z|=\sqrt{x^2+y^2}.</math> | <math display=block>r=|z|=\sqrt{x^2+y^2}.</math> | ||
यदि {{mvar|z}} एक वास्तविक संख्या है (अर्थात, यदि {{math|1=''y'' = 0}}), फिर {{math|1=''r'' = {{!}}''x''{{!}}}}. अर्थात्, एक वास्तविक संख्या का निरपेक्ष मान एक सम्मिश्र संख्या के रूप में उसके निरपेक्ष मान के बराबर होता है। | यदि {{mvar|z}} एक वास्तविक संख्या है (अर्थात, यदि {{math|1=''y'' = 0}}), फिर {{math|1=''r'' = {{!}}''x''{{!}}}}. अर्थात्, एक वास्तविक संख्या का निरपेक्ष मान एक सम्मिश्र संख्या के रूप में उसके निरपेक्ष मान के बराबर होता है। | ||
पाइथागोरस प्रमेय के अनुसार, एक सम्मिश्र संख्या का निरपेक्ष मान सम्मिश्र तल में सम्मिश्र संख्या | पाइथागोरस प्रमेय के अनुसार, एक सम्मिश्र संख्या का निरपेक्ष मान सम्मिश्र तल में सम्मिश्र संख्या का प्रतिनिधित्व करने वाले बिंदु की उत्पत्ति की दूरी है। | ||
का तर्क {{mvar|z}} (कई अनुप्रयोगों में | का तर्क {{mvar|z}} (कई अनुप्रयोगों में चरण के रूप में जाना जाता है {{mvar|φ}})<ref name=":2" />त्रिज्या का कोण है {{mvar|Oz}} सकारात्मक वास्तविक अक्ष के साथ, और के रूप में लिखा है {{math|arg ''z''}}. मापांक की तरह, तर्क को आयताकार रूप से पाया जा सकता है {{mvar|x + yi}}<ref>{{cite book | ||
|title= | |title=जटिल चर: सिद्धांत और अनुप्रयोग|edition=2nd | ||
|edition=2nd | |||
|chapter=Chapter 1 | |chapter=Chapter 1 | ||
|first1=H.S. | |first1=H.S. | ||
| Line 78: | Line 73: | ||
|isbn=978-81-203-2641-5 | |isbn=978-81-203-2641-5 | ||
|page=14 | |page=14 | ||
|chapter-url=https://books.google.com/books?id=rFhiJqkrALIC&pg=PA14}}</ref> | |chapter-url=https://books.google.com/books?id=rFhiJqkrALIC&pg=PA14}}</ref>- काल्पनिक-दर-वास्तविक भागों के भागफल के व्युत्क्रम स्पर्शरेखा को लागू करके। अर्ध-कोण पहचान का उपयोग करके, आर्कटान की एक शाखा सीमा को कवर करने के लिए पर्याप्त होती है {{open-closed|−''π'', ''π''}} की {{math|arg}}-फ़ंक्शन, और अधिक सूक्ष्म केस-बाय-केस विश्लेषण से बचा जाता है | ||
<math display=block>\varphi = \arg (x+yi) = \begin{cases} | <math display=block>\varphi = \arg (x+yi) = \begin{cases} | ||
| Line 85: | Line 80: | ||
\text{undefined} &\text{if } x = 0 \text{ and } y = 0. | \text{undefined} &\text{if } x = 0 \text{ and } y = 0. | ||
\end{cases}</math> | \end{cases}</math> | ||
आम तौर पर, जैसा कि ऊपर दिया गया है, अंतराल में | आम तौर पर, जैसा कि ऊपर दिया गया है, अंतराल में मुख्य मूल्य {{open-closed|−{{mvar|π}}, {{mvar|π}}}} चुना जाता है। यदि तर्क मान ऋणात्मक है, तो श्रेणी में मान {{open-closed|−{{mvar|π}}, {{mvar|π}}}} या {{closed-open|0, 2{{mvar|π}}}} जोड़कर प्राप्त किया जा सकता है {{math|2''π''}}.<!--don't change this into π. Doing so produces *another* complex number.--> का मूल्य {{mvar|φ}} इस आलेख में [[कांति]] में व्यक्त किया गया है। यह किसी भी पूर्णांक गुणक से बढ़ सकता है {{math|2''π''}} और अभी भी वही कोण देते हैं, जिसे सकारात्मक वास्तविक अक्ष की किरणों द्वारा और मूल से के माध्यम से अंतरित के रूप में देखा जाता है {{mvar|z}}. इसलिए, आर्ग फ़ंक्शन को कभी-कभी बहुविकल्पीय फ़ंक्शन माना जाता है। सम्मिश्र संख्या 0 के लिए ध्रुवीय कोण अनिश्चित है, लेकिन ध्रुवीय कोण 0 का मनमाना चयन आम है। | ||
का मूल्य {{mvar|φ}} [[ atan2 ]] के परिणाम के बराबर है: | का मूल्य {{mvar|φ}} [[atan2]] के परिणाम के बराबर है: | ||
<math display=block>\varphi = \operatorname{atan2}\left(\operatorname{Im}(z),\operatorname{Re}(z) \right).</math> | <math display=block>\varphi = \operatorname{atan2}\left(\operatorname{Im}(z),\operatorname{Re}(z) \right).</math> | ||
साथ साथ, {{mvar|r}} तथा {{mvar|φ}} | साथ साथ, {{mvar|r}} तथा {{mvar|φ}} जटिल संख्याओं का प्रतिनिधित्व करने का एक और तरीका, ध्रुवीय रूप दें, क्योंकि मॉड्यूलस और तर्क का संयोजन पूरी तरह से विमान पर एक बिंदु की स्थिति निर्दिष्ट करता है। मूल आयताकार निर्देशांक को ध्रुवीय रूप से पुनर्प्राप्त करना त्रिकोणमितीय रूप नामक सूत्र द्वारा किया जाता है | ||
<math display=block> z = r(\cos \varphi + i\sin \varphi ).</math> | <math display=block> z = r(\cos \varphi + i\sin \varphi ).</math> | ||
यूलर के सूत्र का | यूलर के सूत्र का उपयोग करके इसे इस रूप में लिखा जा सकता है | ||
<math display=block>z = r e^{i \varphi} \text{ or } z = r \exp i \varphi.</math> | <math display=block>z = r e^{i \varphi} \text{ or } z = r \exp i \varphi.</math> | ||
का उपयोग करते हुए {{math|[[Cis (mathematics)|cis]]}} | का उपयोग करते हुए {{math|[[Cis (mathematics)|cis]]}} कार्य, इसे कभी-कभी संक्षिप्त किया जाता है | ||
<math display=block> z = r \operatorname\mathrm{cis} \varphi. </math> | <math display=block> z = r \operatorname\mathrm{cis} \varphi. </math> | ||
कोण संकेतन में, आयाम के साथ फेजर (साइन तरंगों) का प्रतिनिधित्व करने के लिए अक्सर [[इलेक्ट्रानिक्स]] में उपयोग किया जाता है {{mvar|r}} और चरण {{mvar|φ}}, के रूप में लिखा जाता है<ref> | |||
{{cite book | {{cite book | ||
|first1=James William |last1=Nilsson | |first1=James William |last1=Nilsson | ||
| Line 110: | Line 105: | ||
===जटिल | === जटिल रेखांकन === | ||
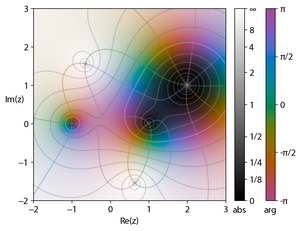
{{main|Domain coloring}} | {{main|Domain coloring}} | ||
[[File:Complex-plot.png|right|thumb| | [[File:Complex-plot.png|right|thumb|अभिव्यक्ति का एक रंग पहिया ग्राफ | ||
{{math|{{sfrac|(''z''<sup>2</sup> − 1)(''z'' − 2 − ''i'')<sup>2</sup>|''z''<sup>2</sup> + 2 + 2''i''}}}}]] | {{math|{{sfrac|(''z''<sup>2</sup> − 1)(''z'' − 2 − ''i'')<sup>2</sup>|''z''<sup>2</sup> + 2 + 2''i''}}}}]][[जटिल विश्लेषण]] की कल्पना करते समय, एक जटिल इनपुट और आउटपुट दोनों की आवश्यकता होती है। क्योंकि प्रत्येक सम्मिश्र संख्या को दो आयामों में दर्शाया जाता है, एक जटिल कार्य को नेत्रहीन रेखांकन करने के लिए [[चार आयामी स्थान]] की धारणा की आवश्यकता होती है, जो केवल अनुमानों में संभव है। इस वजह से, जटिल कार्यों को देखने के अन्य तरीके डिजाइन किए गए हैं। | ||
[[ जटिल विश्लेषण ]] की कल्पना करते समय, एक जटिल इनपुट और आउटपुट दोनों की आवश्यकता होती है। | |||
[[ डोमेन रंग ]] में आउटपुट | [[डोमेन रंग]] में आउटपुट आयाम क्रमशः रंग और चमक द्वारा दर्शाए जाते हैं। डोमेन के रूप में जटिल विमान में प्रत्येक बिंदु अलंकृत है, आमतौर पर जटिल संख्या के तर्क का प्रतिनिधित्व करने वाले रंग के साथ, और परिमाण का प्रतिनिधित्व करने वाली चमक। डार्क स्पॉट मोडुली को शून्य के करीब चिह्नित करते हैं, चमकीले धब्बे मूल से दूर होते हैं, ग्रेडेशन बंद हो सकता है, लेकिन इसे नीरस माना जाता है। रंग अक्सर चरणों में भिन्न होते हैं {{sfrac|{{pi}}|3}} के लिये {{math|0}} प्रति {{math|2{{pi}}}} लाल, पीला, हरा, सियान, नीला, मैजेंटा से। इन भूखंडों को डोमेन कलरिंग कहा जाता है। यह जानकारी खोए बिना कार्यों की कल्पना करने का एक आसान तरीका प्रदान करता है। चित्र के लिए शून्य दिखाता है {{math|±1, (2 + ''i'')}} और डंडे पर <math>\pm \sqrt{{-2-2i}}.</math> | ||
==इतिहास== | == इतिहास == | ||
{{See also|Negative number#History}} | {{See also|Negative number#History}} | ||
एक सामान्य [[ घन समीकरण ]] के nवें मूल (त्रिकोणमितीय कार्यों के बिना) में समाधान, जब इसकी तीनों जड़ें वास्तविक | एक सामान्य [[घन समीकरण]] के nवें मूल (त्रिकोणमितीय कार्यों के बिना) में समाधान, जब इसकी तीनों जड़ें वास्तविक संख्याएँ होती हैं, तो ऋणात्मक संख्याओं के वर्गमूल होते हैं, ऐसी स्थिति जिसे परिमेय मूल परीक्षण द्वारा सहायता प्राप्त गुणनखण्ड द्वारा ठीक नहीं किया जा सकता है, यदि घन [[अलघुकरणीय बहुपद]] है; यह तथाकथित [[एक अपरिवर्तनीय मौका]] (इर्रेड्यूसिबिल केस) है। इस पहेली ने इतालवी गणितज्ञ [[जेरोम कार्डानो]] को 1545 के आसपास अपनी एर्स मैग्ना में जटिल संख्याओं की कल्पना करने के लिए प्रेरित किया।<ref>{{cite book|first=Morris |last= Kline|title=गणितीय विचार का इतिहास, खंड 1|page=253}}</ref> हालाँकि उनकी समझ अल्पविकसित थी; इसके अलावा उन्होंने बाद में सम्मिश्र संख्याओं को सूक्ष्म कहकर खारिज कर दिया क्योंकि वे अनुपयोगी हैं।<ref>{{Cite book|last=Jurij.|first=Kovič|url=http://worldcat.org/oclc/1080410598|title=ट्रिस्टन नीधम, विज़ुअल कॉम्प्लेक्स एनालिसिस, ऑक्सफोर्ड यूनिवर्सिटी प्रेस इंक।, न्यूयॉर्क, 1998, 592 स्ट्रानी|oclc=1080410598}}</ref> कार्डानो ने काल्पनिक संख्याओं का उपयोग किया, लेकिन उन्हें "मानसिक यातना" के रूप में वर्णित किया। <ref>O’Connor and Robertson (2016), “Girolamo Cardano.”</ref> यह ग्राफिकल कॉम्प्लेक्स प्लेन के उपयोग से पहले था। 1500 के दशक में कार्डानो और अन्य इतालवी गणितज्ञों, विशेष रूप से [[स्किपियो डेल फेरो]] ने घन समीकरणों को हल करने के लिए एक एल्गोरिथ्म बनाया, जिसमें आम तौर पर एक वास्तविक समाधान और एक काल्पनिक संख्या वाले दो समाधान होते थे। चूँकि उन्होंने काल्पनिक संख्याओं वाले उत्तरों को नज़रअंदाज़ कर दिया, इसलिए कार्डानो ने उन्हें बेकार पाया।<ref>Nahin, Paul J. An Imaginary Tale: The Story of √-1. Princeton: Princeton University Press, 1998.</ref> | ||
सामान्य बहुपदों की समस्या पर काम | सामान्य बहुपदों की समस्या पर काम अंततः बीजगणित के मौलिक प्रमेय का नेतृत्व करता है, जो दर्शाता है कि जटिल संख्याओं के साथ, एक या उच्चतर डिग्री के प्रत्येक बहुपद समीकरण के लिए एक समाधान मौजूद है। सम्मिश्र संख्याएँ इस प्रकार एक बीजगणितीय रूप से बंद क्षेत्र बनाती हैं, जहाँ किसी भी बहुपद समीकरण में एक फलन का मूल होता है। | ||
कई गणितज्ञों ने जटिल संख्याओं के विकास में योगदान दिया। जटिल संख्याओं के जोड़, घटाव, गुणा और मूल निकालने के नियम इतालवी गणितज्ञ [[राफेल बॉम्बेली]] द्वारा विकसित किए गए थे।<ref>{{cite book |last1=Katz |first1=Victor J. |title=गणित का इतिहास, संक्षिप्त संस्करण|section= 9.1.4 |publisher=[[Addison-Wesley]] |isbn=978-0-321-16193-2 |year=2004}}</ref> आयरिश गणितज्ञ [[विलियम रोवन हैमिल्टन]] द्वारा जटिल संख्याओं के लिए एक अधिक अमूर्त औपचारिकता को और विकसित किया गया, जिन्होंने इस अमूर्तता को चतुष्कोणों के सिद्धांत तक बढ़ाया।<ref>{{cite journal |last1=Hamilton |first1=Wm. |title=चतुष्कोणों के सिद्धांत से जुड़ी काल्पनिक मात्राओं की एक नई प्रजाति पर|journal=Proceedings of the Royal Irish Academy |date=1844 |volume=2 |pages=424–434 |url=https://babel.hathitrust.org/cgi/pt?id=njp.32101040410779&view=1up&seq=454}}</ref> | |||
[[ ऋणात्मक संख्या ]]ओं के [[ वर्गमूल ]]ों | [[ऋणात्मक संख्या]]ओं के [[वर्गमूल]]ों का सबसे पहला क्षणभंगुर संदर्भ शायद पहली शताब्दी ईस्वी में [[हेलेनिस्टिक गणित]] [[अलेक्जेंड्रिया के हीरो]] के काम में पाया जा सकता है, जहाँ उन्होंने अपने हीरो ऑफ़ अलेक्जेंड्रिया#ग्रंथ सूची में, स्पष्ट रूप से गलती से, मात्रा पर विचार किया शब्द पर पहुंचने के लिए [[पिरामिड]] का एक असंभव छिन्नक <math>\sqrt{81 - 144}</math> उनकी गणना में, जो आज सरल होगा <math>\sqrt{-63} = 3i\sqrt{7}</math>. हेलेनिस्टिक गणित में नकारात्मक मात्रा की कल्पना नहीं की गई थी और हीरो ने इसे केवल इसके सकारात्मक द्वारा बदल दिया था <math>\sqrt{144 - 81} = 3\sqrt{7}.</math><ref>{{cite book |title=एक काल्पनिक कहानी: √-1 की कहानी|last=Nahin |first=Paul J. |year=2007 |publisher=[[Princeton University Press]] |isbn=978-0-691-12798-9 |url=http://mathforum.org/kb/thread.jspa?forumID=149&threadID=383188&messageID=1181284 |access-date=20 April 2011 |archive-url=https://web.archive.org/web/20121012090553/http://mathforum.org/kb/thread.jspa?forumID=149&threadID=383188&messageID=1181284 |archive-date=12 October 2012 |url-status=live }}</ref> | ||
अपने आप में एक विषय के रूप में जटिल संख्याओं का अध्ययन करने की प्रेरणा पहली बार 16 वीं शताब्दी में उठी जब क्यूबिक समीकरण और क्वार्टिक समीकरण | अपने आप में एक विषय के रूप में जटिल संख्याओं का अध्ययन करने की प्रेरणा पहली बार 16 वीं शताब्दी में उठी जब क्यूबिक समीकरण और क्वार्टिक समीकरण बहुपदों की जड़ों के लिए [[बीजगणितीय समाधान]] इतालवी गणितज्ञों द्वारा खोजे गए (देखें निकोलो फोंटाना टारटाग्लिया, गेरोलामो कार्डानो)। यह जल्द ही महसूस किया गया (लेकिन बहुत बाद में साबित हुआ)<ref name=Casus/>कि ये सूत्र, भले ही कोई केवल वास्तविक समाधानों में रुचि रखता हो, कभी-कभी ऋणात्मक संख्याओं के वर्गमूलों में हेरफेर की आवश्यकता होती है। एक उदाहरण के रूप में, फार्म के घन समीकरण के लिए टार्टाग्लिया का सूत्र {{math|''x''{{sup|3}} {{=}} ''px'' + ''q''}}{{efn|In modern notation, Tartaglia's solution is based on expanding the cube of the sum of two cube roots: <math>\left(\sqrt[3]{u} + \sqrt[3]{v}\right)^3 = 3 \sqrt[3]{uv} \left(\sqrt[3]{u} + \sqrt[3]{v}\right) + u + v</math> With <math>x = \sqrt[3]{u} + \sqrt[3]{v}</math>, <math>p = 3 \sqrt[3]{uv}</math>, <math>q = u + v</math>, {{mvar|u}} and {{mvar|v}} can be expressed in terms of {{mvar|p}} and {{mvar|q}} as <math>u = q/2 + \sqrt{(q/2)^2-(p/3)^3}</math> and <math>v = q/2 - \sqrt{(q/2)^2-(p/3)^3}</math>, respectively. Therefore, <math>x = \sqrt[3]{q/2 + \sqrt{(q/2)^2-(p/3)^3}} + \sqrt[3]{q/2 - \sqrt{(q/2)^2-(p/3)^3}}</math>. कब <math>(q/2)^2-(p/3)^3</math> नकारात्मक है (कैसस इरेड्यूसिबिलिस), दूसरे घनमूल को पहले वाले के जटिल संयुग्म के रूप में माना जाना चाहिए।}} समीकरण का समाधान देता है {{math|1=''x''<sup>3</sup> = ''x''}} जैसा | ||
<math display=block>\tfrac{1}{\sqrt{3}}\left(\left(\sqrt{-1}\right)^{1/3}+\left(\sqrt{-1}\right)^{-1/3}\right).</math> | <math display=block>\tfrac{1}{\sqrt{3}}\left(\left(\sqrt{-1}\right)^{1/3}+\left(\sqrt{-1}\right)^{-1/3}\right).</math> | ||
पहली नज़र में यह बकवास लग रहा है। हालाँकि, जटिल संख्याओं के साथ औपचारिक गणना दर्शाती है कि समीकरण {{math|1=''z''<sup>3</sup> = ''i''}} तीन समाधान हैं: <math>-i, \frac{\sqrt{3} + i}{2}, \frac{-\sqrt{3}+i}{2}.</math> बदले में इन्हें प्रतिस्थापित करना <math>\sqrt{-1}^{1/3}</math> टारटाग्लिया के घन सूत्र और सरलीकरण में, 0, 1 और -1 के समाधान के रूप में प्राप्त होता है {{math|1=''x''<sup>3</sup> − ''x'' = 0}}. बेशक इस विशेष समीकरण को देखते ही हल किया जा सकता है, लेकिन यह स्पष्ट करता है कि जब वास्तविक जड़ों वाले घन समीकरणों को हल करने के लिए सामान्य सूत्रों का उपयोग किया जाता है, जैसा कि बाद के गणितज्ञों ने सख्ती से दिखाया,{{efn|It has been proved that imaginary numbers have necessarily to appear in the cubic formula when the equation has three real, different roots by Pierre Laurent Wantzel in 1843, Vincenzo Mollame in 1890, Otto Hölder in 1891 and Adolf Kneser in 1892. Paolo Ruffini also provided an incomplete proof in 1799. — S. Confalonieri (2015)<ref name=Casus>{{cite book |title=The Unattainable Attempt to Avoid the Casus Irreducibilis for Cubic Equations: Gerolamo Cardano's De Regula Aliza |first=Sara |last=Confalonieri |publisher=Springer |year=2015 |pages=15–16 (note 26) |isbn=978-3658092757 }}</ref>}} जटिल संख्याओं का उपयोग कैसस इरेड्यूसीबिलिस। राफेल बॉम्बेली क्यूबिक समीकरणों के इन प्रतीत होने वाले विरोधाभासी समाधानों को स्पष्ट रूप से संबोधित करने वाले पहले व्यक्ति थे और इन मुद्दों को हल करने की कोशिश कर रहे जटिल अंकगणितीय के लिए नियम विकसित किए। | |||
इन | इन राशियों के लिए काल्पनिक शब्द 1637 में रेने डेसकार्टेस द्वारा गढ़ा गया था, जो अपनी अवास्तविक प्रकृति पर जोर देने के लिए दर्द में थे।<ref>{{cite book |title=ला ज्योमेट्री {{पाइप}} पहले संस्करण की प्रतिकृति के साथ रेने डेसकार्टेस की ज्यामिति|last=Descartes |first=René |author-link=René Descartes |year=1954 |orig-year=1637 |publisher=[[Dover Publications]] |isbn=978-0-486-60068-0 |url=https://archive.org/details/geometryofrenede00rend |access-date=20 April 2011 }}</ref> | ||
{{blockquote|... sometimes only imaginary, that is one can imagine as many as I said in each equation, but sometimes there exists no quantity that matches that which we imagine.<br/> | {{blockquote|... sometimes only imaginary, that is one can imagine as many as I said in each equation, but sometimes there exists no quantity that matches that which we imagine.<br/> | ||
[''... quelquefois seulement imaginaires c'est-à-dire que l'on peut toujours en imaginer autant que j'ai dit en chaque équation, mais qu'il n'y a quelquefois aucune quantité qui corresponde à celle qu'on imagine.'']}} | [''... quelquefois seulement imaginaires c'est-à-dire que l'on peut toujours en imaginer autant que j'ai dit en chaque équation, mais qu'il n'y a quelquefois aucune quantité qui corresponde à celle qu'on imagine.'']}} | ||
भ्रम का एक और स्रोत | भ्रम का एक और स्रोत समीकरण था <math>\sqrt{-1}^2 = \sqrt{-1}\sqrt{-1} = -1</math> बीजगणितीय पहचान के साथ विचित्र रूप से असंगत लग रहा था <math>\sqrt{a}\sqrt{b} = \sqrt{ab}</math>, जो गैर-ऋणात्मक वास्तविक संख्याओं के लिए मान्य है {{mvar|a}} तथा {{mvar|b}}, और जिसका उपयोग जटिल संख्या गणनाओं में से एक के साथ भी किया गया था {{mvar|a}}, {{mvar|b}} सकारात्मक और दूसरा नकारात्मक। इस पहचान का गलत उपयोग (और संबंधित पहचान <math display=inline>\frac{1}{\sqrt{a}} = \sqrt{\frac{1}{a}}</math>) मामले में जब दोनों {{mvar|a}} तथा {{mvar|b}} शैतानी शैतान [[लियोनहार्ड यूलर]] तक नकारात्मक हैं। इस कठिनाई ने अंततः विशेष प्रतीक का उपयोग करने के सम्मेलन को जन्म दिया {{math|''i''}} की जगह में <math>\sqrt{-1}</math> इस गलती से बचाव के लिए।{{Citation needed|date=April 2011}} फिर भी, यूलर ने छात्रों को आज की तुलना में बहुत पहले जटिल संख्याओं से परिचित कराना स्वाभाविक समझा। अपनी प्रारंभिक बीजगणित पाठ्य पुस्तक, [[बीजगणित के तत्व]] में, वह इन नंबरों को लगभग एक बार में पेश करता है और फिर उन्हें प्राकृतिक तरीके से उपयोग करता है। | ||
18वीं शताब्दी में जटिल संख्याओं का व्यापक उपयोग हुआ, क्योंकि यह देखा गया कि त्रिकोणमितीय कार्यों से जुड़ी गणनाओं को सरल बनाने के लिए जटिल अभिव्यक्तियों के औपचारिक हेरफेर का उपयोग किया जा सकता है। उदाहरण के लिए, 1730 में [[ अब्राहम डी मोइवरे ]] ने | 18वीं शताब्दी में जटिल संख्याओं का व्यापक उपयोग हुआ, क्योंकि यह देखा गया कि त्रिकोणमितीय कार्यों से जुड़ी गणनाओं को सरल बनाने के लिए जटिल अभिव्यक्तियों के औपचारिक हेरफेर का उपयोग किया जा सकता है। उदाहरण के लिए, 1730 में [[अब्राहम डी मोइवरे]] ने नोट किया कि कोण के एक पूर्णांक बहु के त्रिकोणमितीय कार्यों से संबंधित पहचान उस कोण के त्रिकोणमितीय कार्यों की शक्तियों को निम्नलिखित डी मोइवर के सूत्र द्वारा फिर से व्यक्त की जा सकती है: | ||
<math display=block>(\cos \theta + i\sin \theta)^{n} = \cos n \theta + i\sin n \theta. </math> | <math display=block>(\cos \theta + i\sin \theta)^{n} = \cos n \theta + i\sin n \theta. </math> | ||
1748 में, यूलर ने आगे | 1748 में, यूलर ने और आगे जाकर जटिल विश्लेषण के लिए यूलर का सूत्र प्राप्त किया:<ref>{{cite book |last1=Euler |first1=Leonard |title=इनफिनिटिमल्स के विश्लेषण का एक परिचय|trans-title=Introduction to the Analysis of the Infinite |date=1748 |publisher=Marc Michel Bosquet & Co. |location=Lucerne, Switzerland |volume=1 |page=104 |url=https://books.google.com/books?id=jQ1bAAAAQAAJ&pg=PA104 |language=la}}</ref> | ||
<math display=block>\cos \theta + i\sin \theta = e ^{i\theta } </math> | <math display=block>\cos \theta + i\sin \theta = e ^{i\theta } </math> | ||
औपचारिक रूप से जटिल शक्ति श्रृंखला में हेरफेर करके और देखा कि इस सूत्र का उपयोग किसी भी त्रिकोणमितीय पहचान को बहुत सरल घातीय पहचान | औपचारिक रूप से जटिल शक्ति श्रृंखला में हेरफेर करके और देखा कि इस सूत्र का उपयोग किसी भी त्रिकोणमितीय पहचान को बहुत सरल घातीय पहचान में कम करने के लिए किया जा सकता है। | ||
जटिल | जटिल तल (#जटिल समतल) में एक बिंदु के रूप में एक सम्मिश्र संख्या का विचार पहली बार 1799 में [[डेनमार्क]]-[[नॉर्वे]] [[गणितज्ञ]] [[कैस्पर वेसल]] द्वारा वर्णित किया गया था,<ref>{{cite journal |last1=Wessel |first1=Caspar |title=दिशा के विश्लेषणात्मक संकेतन पर, एक प्रयोग, समतल और गोलाकार बहुभुजों के समाधान के लिए स्पष्ट रूप से लागू किया गया|journal=Nye Samling af det Kongelige Danske Videnskabernes Selskabs Skrifter [New Collection of the Writings of the Royal Danish Science Society] |date=1799 |volume=5 |pages=469–518 |url=https://babel.hathitrust.org/cgi/pt?id=ien.35556000979690&view=1up&seq=527 |trans-title=On the analytic representation of direction, an effort applied in particular to the determination of plane and spherical polygons |language=da}}</ref> हालांकि जॉन वालिस|वालिस के बीजगणित के ग्रंथ में 1685 में ही इसका अनुमान लगा लिया गया था।<ref>{{cite book |last=Wallis |first=John |date=1685 |title=बीजगणित का एक ग्रंथ, दोनों ऐतिहासिक और व्यावहारिक ...|url=https://echo.mpiwg-berlin.mpg.de/ECHOdocuView?url=/permanent/library/H3GRV5AU/pageimg&start=291&mode=imagepath&pn=291|location=London, England |publisher=printed by John Playford, for Richard Davis |pages=264–273 }}</ref> | ||
वेसेल का संस्मरण [[कोपेनहेगन अकादमी]] की कार्यवाही में दिखाई दिया, लेकिन काफी हद तक किसी का ध्यान नहीं गया। 1806 में जीन-रॉबर्ट अरगंड ने स्वतंत्र रूप से जटिल संख्याओं पर एक पैम्फलेट जारी किया और बीजगणित # इतिहास के मौलिक प्रमेय का एक कठोर प्रमाण प्रदान किया।<ref>{{cite book |last1=Argand |title=ज्यामितीय निर्माणों में काल्पनिक मात्राओं का प्रतिनिधित्व करने के तरीके पर निबंध|trans-title=Essay on a way to represent complex quantities by geometric constructions |date=1806 |publisher=Madame Veuve Blanc |location=Paris, France |url=http://www.bibnum.education.fr/mathematiques/geometrie/essai-sur-une-maniere-de-representer-des-quantites-imaginaires-dans-les-cons |language=fr}}</ref> [[कार्ल फ्रेडरिक गॉस]] ने पहले 1797 में प्रमेय का एक अनिवार्य रूप से [[टोपोलॉजी]] प्रमाण प्रकाशित किया था, लेकिन उस समय -1 के वर्गमूल के वास्तविक तत्वमीमांसा के बारे में अपने संदेह व्यक्त किए थे।<ref>Gauss, Carl Friedrich (1799) [https://books.google.com/books?id=g3VaAAAAcAAJ&pg=PP1#v=onepage&q&f=fals ''"Demonstratio nova theorematis omnem functionem algebraicam rationalem integram unius variabilis in factores reales primi vel secundi gradus resolvi posse."''] [New proof of the theorem that any rational integral algebraic function of a single variable can be resolved into real factors of the first or second degree.] Ph.D. thesis, University of Helmstedt, (Germany). (in Latin)</ref> यह 1831 तक नहीं था कि उन्होंने इन संदेहों पर काबू पाया और विमान में बिंदुओं के रूप में जटिल संख्याओं पर अपना ग्रंथ प्रकाशित किया।<ref name=Ewald>{{cite book |last=Ewald |first=William B. |date=1996 |title=कांट से हिल्बर्ट: गणित की नींव में एक स्रोत पुस्तक|volume=1 |page=313 |publisher=Oxford University Press |isbn=9780198505358|url=https://books.google.com/books?id=rykSDAAAQBAJ&pg=PA313 |access-date=18 March 2020}}</ref> बड़े पैमाने पर आधुनिक संकेतन और शब्दावली की स्थापना:{{sfn|Gauss|1831|p=638}} | |||
<blockquote>यदि किसी ने | <blockquote>यदि किसी ने पूर्व में इस विषय पर झूठे दृष्टिकोण से विचार किया था और इसलिए एक रहस्यमय अंधकार पाया, तो यह बड़े पैमाने पर अनाड़ी शब्दावली के लिए जिम्मेदार है। अगर किसी ने +1, -1 नहीं कहा होता, <math>\sqrt{-1}</math> सकारात्मक, नकारात्मक, या काल्पनिक (या असंभव भी) इकाइयाँ, लेकिन इसके बजाय, प्रत्यक्ष, उलटा, या पार्श्व इकाइयाँ कहें, तो ऐसे अंधेरे की बात शायद ही हो सकती थी।</blockquote> | ||
19वीं शताब्दी की शुरुआत में, अन्य गणितज्ञों ने स्वतंत्र रूप से जटिल संख्याओं के ज्यामितीय | 19वीं शताब्दी की शुरुआत में, अन्य गणितज्ञों ने स्वतंत्र रूप से जटिल संख्याओं के ज्यामितीय प्रतिनिधित्व की खोज की: बुई,<ref>{{cite web| url = https://mathshistory.st-andrews.ac.uk/Biographies/Buee/| title = एड्रियन क्वेंटिन ब्यू (1745-1845): मैकट्यूटर}}</ref><ref>{{cite journal |last1=Buée |title=काल्पनिक मात्रा पर मेमोरी|journal=Philosophical Transactions of the Royal Society of London |date=1806 |volume=96 |pages=23–88 |doi=10.1098/rstl.1806.0003 |s2cid=110394048 |url=https://royalsocietypublishing.org/doi/pdf/10.1098/rstl.1806.0003 |trans-title=Memoir on imaginary quantities |language=fr}}</ref> सीवी मौरे,<ref>{{cite book |last1=Mourey |first1=C.V. |title=ऋणात्मक मात्राओं का सच्चा सिद्धांत और कथित रूप से काल्पनिक मात्राएँ|trans-title=The true theory of negative quantities and of alleged imaginary quantities |date=1861 |publisher=Mallet-Bachelier |location=Paris, France |url=https://archive.org/details/bub_gb_8YxKAAAAYAAJ |language=fr}} 1861 reprint of 1828 original.</ref> [[जॉन वॉरेन (गणितज्ञ)]],<ref>{{cite book |last1=Warren |first1=John |title=नकारात्मक मात्राओं के वर्गमूलों के ज्यामितीय प्रतिनिधित्व पर एक ग्रंथ|date=1828 |publisher=Cambridge University Press |location=Cambridge, England |url=https://archive.org/details/treatiseongeomet00warrrich}}</ref><ref>{{cite journal |last1=Warren |first1=John |title=ऋणात्मक राशियों के वर्गमूलों के ज्यामितीय निरूपण के विरुद्ध उठाई गई आपत्तियों पर विचार|journal=Philosophical Transactions of the Royal Society of London |date=1829 |volume=119 |pages=241–254 |s2cid=186211638 |doi=10.1098/rstl.1829.0022 |doi-access=free }}</ref><ref>{{cite journal |last1=Warren |first1=John |title=मात्राओं की शक्तियों के ज्यामितीय प्रतिनिधित्व पर, जिनके सूचकांकों में ऋणात्मक संख्याओं के वर्गमूल शामिल होते हैं|journal=Philosophical Transactions of the Royal Society of London |date=1829 |volume=119 |pages=339–359 |s2cid=125699726 |doi=10.1098/rstl.1829.0031 |doi-access=free }}</ref> जैक्स फ़्रेडरिक फ़्रैंकैस | फ़्रैंकैस और उनके भाई, [[दायां बेलावाइटिस]]<ref>{{cite journal |last1=Français |first1=J.F. |title=स्थितीय ज्यामिति के नए सिद्धांत, और काल्पनिक प्रतीकों की ज्यामितीय व्याख्या|journal=Annales des mathématiques pures et appliquées |date=1813 |volume=4 |pages=61–71 |url=https://babel.hathitrust.org/cgi/pt?id=uc1.$c126478&view=1up&seq=69 |trans-title=New principles of the geometry of position, and geometric interpretation of complex [number] symbols |language=fr}}</ref><ref>{{cite book |title=दो संस्कृतियाँ|editor= Kim Williams |last1=Caparrini |first1=Sandro |chapter=On the Common Origin of Some of the Works on the Geometrical Interpretation of Complex Numbers |year=2000 |publisher=Birkhäuser |isbn=978-3-7643-7186-9 |page=139 |url=https://books.google.com/books?id=voFsJ1EhCnYC |chapter-url=https://books.google.com/books?id=voFsJ1EhCnYC&pg=PA139}}</ref> | ||
अंग्रेजी गणितज्ञ जी.एच. हार्डी ने टिप्पणी की कि गॉस | अंग्रेजी गणितज्ञ जी.एच. हार्डी ने टिप्पणी की कि गॉस 'वास्तव में आत्मविश्वास और वैज्ञानिक तरीके' से जटिल संख्याओं का उपयोग करने वाले पहले गणितज्ञ थे, हालांकि नॉर्वे [[नील्स हेनरिक एबेल]] और [[कार्ल गुस्ताव जैकब जैकोबी]] जैसे गणितज्ञ आवश्यक रूप से गॉस के 1831 के ग्रंथ को प्रकाशित करने से पहले नियमित रूप से उनका उपयोग कर रहे थे।<ref>{{cite book |title=संख्या के सिद्धांत का परिचय|last1=Hardy |first1=G.H. |last2=Wright |first2=E.M. |year=2000 |orig-year=1938 |publisher=[[Oxford University Press|OUP Oxford]] |isbn= 978-0-19-921986-5 |page=189 (fourth edition)}}</ref> | ||
[[ ऑगस्टिन-लुई कॉची ]] और [[ बर्नहार्ड | [[ऑगस्टिन-लुई कॉची]] और [[बर्नहार्ड रीमैन]] ने मिलकर कॉची के मामले में 1825 के आसपास शुरू करते हुए #जटिल विश्लेषण के मौलिक विचारों को पूर्णता की उच्च स्थिति में ला दिया। | ||
सिद्धांत में प्रयुक्त सामान्य शब्द | सिद्धांत में प्रयुक्त सामान्य शब्द मुख्य रूप से संस्थापकों के कारण हैं। अरगंड ने फोन किया {{math|cos ''φ'' + ''i'' sin ''φ''}} दिशा कारक, और <math>r = \sqrt{a^2 + b^2}</math> मापांक;{{efn| {{harvnb|Argand|1814|p=204}} defines the modulus of a complex number but he doesn't name it:<br/>''"Dans ce qui suit, les accens, indifféremment placés, seront employés pour indiquer la grandeur absolue des quantités qu'ils affectent; ainsi, si <math>a = m + n\sqrt{-1}</math>, <math>m</math> et <math>n</math> étant réels, on devra entendre que <math>a_'</math> ou <math>a' = \sqrt{m^2 + n^2}</math>."''<br/>[In what follows, accent marks, wherever they're placed, will be used to indicate the absolute size of the quantities to which they're assigned; thus if <math>a = m + n\sqrt{-1}</math>, <math>m</math> and <math>n</math> being real, one should understand that <math>a_'</math> or <math>a' = \sqrt{m^2 + n^2}</math>.]<br/> | ||
{{harvnb|Argand|1814|p=208}} defines and names the ''module'' and the ''direction factor'' of a complex number: ''"... <math>a = \sqrt{m^2 + n^2}</math> pourrait être appelé le ''module'' de <math>a + b \sqrt{-1}</math>, et représenterait la ''grandeur absolue'' de la ligne <math>a + b \sqrt{-1}</math>, tandis que l'autre facteur, dont le module est l'unité, en représenterait la direction."''<br/>[... <math>a = \sqrt{m^2 + n^2}</math> could be called the ''module'' of <math>a + b \sqrt{-1}</math> and would represent the ''absolute size'' of the line <math>a + b \sqrt{-1}\,,</math> (Note that Argand represented complex numbers as vectors.) whereas the other factor [namely, <math>\tfrac{a}{\sqrt{a^2 + b^2}} + \tfrac{b}{\sqrt{a^2 + b^2}} \sqrt{-1} </math>], जिसका मॉड्यूल | {{harvnb|Argand|1814|p=208}} defines and names the ''module'' and the ''direction factor'' of a complex number: ''"... <math>a = \sqrt{m^2 + n^2}</math> pourrait être appelé le ''module'' de <math>a + b \sqrt{-1}</math>, et représenterait la ''grandeur absolue'' de la ligne <math>a + b \sqrt{-1}</math>, tandis que l'autre facteur, dont le module est l'unité, en représenterait la direction."''<br/>[... <math>a = \sqrt{m^2 + n^2}</math> could be called the ''module'' of <math>a + b \sqrt{-1}</math> and would represent the ''absolute size'' of the line <math>a + b \sqrt{-1}\,,</math> (Note that Argand represented complex numbers as vectors.) whereas the other factor [namely, <math>\tfrac{a}{\sqrt{a^2 + b^2}} + \tfrac{b}{\sqrt{a^2 + b^2}} \sqrt{-1} </math>], जिसका मॉड्यूल यूनिटी [1] है, इसकी दिशा को दर्शाएगा।]}}<ref>{{cite web |author=Jeff Miller |date=Sep 21, 1999 |title=मापांक|url=http://members.aol.com/jeff570/m.html|archive-url=https://web.archive.org/web/19991003034827/http://members.aol.com/jeff570/m.html |work=Earliest Known Uses of Some of the Words of Mathematics (M) |archive-date=1999-10-03 |url-status=usurped}}</ref> कॉची (1821) ने बुलाया {{math|cos ''φ'' + ''i'' sin ''φ''}} घटा हुआ रूप<ref>{{cite book |last=Cauchy |first=Augustin-Louis |date=1821 |title=रॉयल पॉलिटेक्निक स्कूल में विश्लेषण पाठ्यक्रम|url=https://archive.org/details/coursdanalysede00caucgoog/page/n209/mode/2up |location=Paris, France |publisher=L'Imprimerie Royale |volume=1 |page=183 |language=fr }}</ref> और स्पष्ट रूप से तर्क शब्द का परिचय दिया; गॉस ने प्रयोग किया {{math|''i''}} के लिये <math>\sqrt{-1}</math>,{{efn| Gauss writes:<ref>{{harvnb|Gauss|1831|p=96}}</ref>''"Quemadmodum scilicet arithmetica sublimior in quaestionibus hactenus pertractatis inter solos numeros integros reales versatur, ita theoremata circa residua biquadratica tunc tantum in summa simplicitate ac genuina venustate resplendent, quando campus arithmeticae ad quantitates ''imaginarias'' extenditur, ita ut absque restrictione ipsius obiectum constituant numeri formae ''a + bi'', denotantibus ''i'', pro more quantitatem imaginariam <math>\sqrt{-1}</math>, atque ''a, b'' indefinite omnes numeros reales integros inter -<math>\infty</math> et +<math>\infty</math>."'' [Of course just as the higher arithmetic has been investigated so far in problems only among real integer numbers, so theorems regarding biquadratic residues then shine in greatest simplicity and genuine beauty, when the field of arithmetic is extended to ''imaginary'' quantities, so that, without restrictions on it, numbers of the form ''a + bi'' — ''i'' denoting by convention the imaginary quantity <math>\sqrt{-1}</math>, and the variables ''a, b'' [denoting] all real integer numbers between <math>-\infty</math> and <math>+\infty</math> — constitute an object.]}} के लिए जटिल संख्या शब्द की शुरुआत की {{math|''a'' + ''bi''}},{{efn|Gauss:<ref>{{harvnb|Gauss|1831|p=96}}</ref>''"Tales numeros vocabimus numeros integros complexos, ita quidem, ut reales complexis non opponantur, sed tamquam species sub his contineri censeantur."'' [We will call such numbers [namely, numbers of the form ''a + bi'' ] "complex integer numbers", so that real [numbers] are regarded not as the opposite of complex [numbers] but [as] a type [of number that] is, so to speak, contained within them.]}} और बुलाया {{math|''a''<sup>2</sup> + ''b''<sup>2</sup>}} नियम।{{efn|Gauss:<ref>{{harvnb|Gauss|1831|p=98}}</ref> ''"Productum numeri complexi per numerum ipsi conjunctum utriusque ''normam'' vocamus. Pro norma itaque numeri realis, ipsius quadratum habendum est."'' [We call a "norm" the product of a complex number [e.g,. ''a + ib'' ] with its conjugate [''a - ib'' ]. Therefore the square of a real number should be regarded as its norm.]}} अभिव्यक्ति दिशा गुणांक, अक्सर के लिए प्रयोग किया जाता है {{math|cos ''φ'' + ''i'' sin ''φ''}}हैंकेल (1867) के कारण है,<ref>{{cite book |last=Hankel |first=Hermann |date=1867 |title=जटिल संख्याओं और उनके कार्यों पर व्याख्यान|trans-title=Lectures About the Complex Numbers and Their Functions |url=https://books.google.com/books?id=754KAAAAYAAJ&pg=PA71 |location=Leipzig, [Germany] |publisher=Leopold Voss |volume=1 |page=71 |language=de }} From p. 71: ''"Wir werden den Factor (''cos'' φ + i ''sin'' φ) haüfig den ''Richtungscoefficienten'' nennen."'' (We will often call the factor (cos φ + i sin φ) the "coefficient of direction".)</ref> और मापांक के लिए निरपेक्ष मान, वीयरस्ट्रैस के कारण होता है। | ||
सामान्य सिद्धांत पर बाद के शास्त्रीय लेखकों में [[ रिचर्ड डेडेकिंड ]], ओटो होल्डर, [[ फेलिक्स क्लेन ]], हेनरी | सामान्य सिद्धांत पर बाद के शास्त्रीय लेखकों में [[रिचर्ड डेडेकिंड]], ओटो होल्डर, [[फेलिक्स क्लेन]], हेनरी पॉइनकेयर, [[हरमन ब्लैक]], [[कार्ल वीयरस्ट्रास]] और कई अन्य शामिल हैं। 20वीं सदी की शुरुआत में जटिल बहुभिन्नरूपी कलन में महत्वपूर्ण कार्य (व्यवस्थितीकरण सहित) शुरू किया गया है। 1927 में [[विलियम विर्टिंगर]] द्वारा महत्वपूर्ण परिणाम प्राप्त किए गए हैं। | ||
==संबंध और संचालन == | == संबंध और संचालन == | ||
===समानता=== | === समानता === | ||
सम्मिश्र संख्याओं | सम्मिश्र संख्याओं की समानता की परिभाषा वास्तविक संख्याओं के समान होती है; दो जटिल संख्याएँ {{math|''a''<sub>1</sub> + ''b''<sub>1</sub>''i''}} तथा {{math|''a''<sub>2</sub> + ''b''<sub>2</sub>''i''}} समान हैं यदि और केवल यदि उनके वास्तविक और काल्पनिक दोनों भाग समान हैं, अर्थात यदि {{math|1=''a''<sub>1</sub> = ''a''<sub>2</sub>}} तथा {{math|1=''b''<sub>1</sub> = ''b''<sub>2</sub>}}. [[ध्रुवीय रूप]] में लिखी गई अशून्य जटिल संख्याएँ समान होती हैं यदि और केवल यदि उनका परिमाण समान होता है और उनके तर्क एक पूर्णांक गुणक से भिन्न होते हैं {{math|2''π''}}. | ||
=== आदेश देना === | === आदेश देना === | ||
वास्तविक संख्याओं के विपरीत, सम्मिश्र संख्याओं का कोई प्राकृतिक क्रम नहीं होता है। विशेष रूप से, जटिल संख्याओं पर कोई | वास्तविक संख्याओं के विपरीत, सम्मिश्र संख्याओं का कोई प्राकृतिक क्रम नहीं होता है। विशेष रूप से, जटिल संख्याओं पर कोई रेखीय क्रम नहीं है जो जोड़ और गुणा के साथ संगत हो। इसलिए, सम्मिश्र संख्याओं में एक आदेशित फ़ील्ड की संरचना नहीं होती है। इसके लिए एक स्पष्टीकरण यह है कि एक आदेशित क्षेत्र में वर्गों का प्रत्येक गैर-तुच्छ योग#nontrivialSquareSum अशून्य है, और {{math|1=''i''<sup>2</sup> + 1<sup>2</sup> = 0}} वर्गों का एक गैर-तुच्छ योग है। इस प्रकार, जटिल संख्याओं को स्वाभाविक रूप से द्वि-आयामी विमान पर मौजूद माना जाता है। | ||
=== संयुग्म === | === संयुग्म === | ||
{{See also|Complex conjugate}} | {{See also|Complex conjugate}} | ||
[[File:Complex conjugate picture.svg|right|thumb|upright=0.8|का ज्यामितीय प्रतिनिधित्व {{mvar|z}} और इसके | [[File:Complex conjugate picture.svg|right|thumb|upright=0.8|का ज्यामितीय प्रतिनिधित्व {{mvar|z}} और इसके संयुग्मी {{mvar|{{overline|z}}}} जटिल विमान में]]सम्मिश्र संख्या का सम्मिश्र संयुग्म {{math|1=''z'' = ''x'' + ''yi''}} द्वारा दिया गया है {{math|''x'' − ''yi''}}. यह या तो द्वारा दर्शाया गया है {{mvar|{{overline|z}}}} या {{math|''z''*}}.<ref>For the former notation, see {{harvnb|Apostol|1981|pp=15–16}}</ref> सम्मिश्र संख्याओं पर यह एकात्मक संक्रिया केवल उनकी मूल संक्रियाओं जोड़, घटाव, गुणा और भाग को लागू करके व्यक्त नहीं की जा सकती। | ||
सम्मिश्र संख्या का सम्मिश्र संयुग्म {{math|1=''z'' = ''x'' + ''yi''}} द्वारा दिया गया है {{math|''x'' − ''yi''}}. | |||
ज्यामितीय रूप से, {{mvar|{{overline|z}}}} प्रतिबिंब समरूपता है| का प्रतिबिंब {{mvar|z}} वास्तविक | ज्यामितीय रूप से, {{mvar|{{overline|z}}}} प्रतिबिंब समरूपता है | का प्रतिबिंब {{mvar|z}} वास्तविक अक्ष के बारे में दो बार संयुग्मन करने से मूल सम्मिश्र संख्या प्राप्त होती है | ||
<math display=block>\overline{\overline{z}}=z,</math> | <math display=block>\overline{\overline{z}}=z,</math> | ||
जो इस | जो इस संक्रिया को एक अंतर्वलन (गणित) बनाता है। प्रतिबिंब वास्तविक भाग और परिमाण दोनों को छोड़ देता है {{mvar|z}} अपरिवर्तित, अर्थात् | ||
<math display=block>\operatorname{Re}(\overline{z}) = \operatorname{Re}(z)\quad</math> तथा <math>\quad |\overline{z}| = |z|.</math> | <math display=block>\operatorname{Re}(\overline{z}) = \operatorname{Re}(z)\quad</math> तथा <math>\quad |\overline{z}| = |z|.</math> | ||
एक सम्मिश्र संख्या का | काल्पनिक भाग और एक सम्मिश्र संख्या का तर्क {{mvar|z}} संयुग्मन के तहत अपना चिन्ह बदलें | ||
<math display=block>\operatorname{Im}(\overline{z}) = -\operatorname{Im}(z)\quad \text{ and } \quad \operatorname{arg} \overline{z} \equiv -\operatorname{arg} z \pmod {2\pi}.</math> | <math display=block>\operatorname{Im}(\overline{z}) = -\operatorname{Im}(z)\quad \text{ and } \quad \operatorname{arg} \overline{z} \equiv -\operatorname{arg} z \pmod {2\pi}.</math> | ||
तर्क और परिमाण | तर्क और परिमाण पर विवरण के लिए, #ध्रुवीय रूप पर अनुभाग देखें। | ||
एक | एक जटिल संख्या का उत्पाद {{math|''z'' {{=}} ''x'' + ''yi''}} और इसके संयुग्म को [[पूर्ण वर्ग]] के रूप में जाना जाता है। यह हमेशा एक गैर-ऋणात्मक वास्तविक संख्या होती है और प्रत्येक के परिमाण के वर्ग के बराबर होती है: | ||
<math display=block>z\cdot \overline{z} = x^2 + y^2 = |z|^2 = |\overline{z}|^2.</math> | <math display=block>z\cdot \overline{z} = x^2 + y^2 = |z|^2 = |\overline{z}|^2.</math> | ||
दिए गए भाजक के संयुग्म द्वारा भिन्न के अंश और हर दोनों का विस्तार करके इस गुण का उपयोग जटिल भाजक वाले भिन्न को वास्तविक भाजक वाले समतुल्य भिन्न में बदलने के लिए किया जा सकता है। इस प्रक्रिया को कभी-कभी भाजक का [[युक्तिकरण (गणित)]] कहा जाता है (हालांकि अंतिम अभिव्यक्ति में भाजक एक अपरिमेय वास्तविक संख्या हो सकती है), क्योंकि यह एक भाजक में सरल भावों से जड़ों को हटाने की विधि जैसा दिखता है। | |||
सम्मिश्र संख्या के वास्तविक और काल्पनिक भाग {{mvar|z}} संयुग्मन का उपयोग करके निकाला जा सकता है: | एक सम्मिश्र संख्या के वास्तविक और काल्पनिक भाग {{mvar|z}} संयुग्मन का उपयोग करके निकाला जा सकता है: | ||
<math display=block>\operatorname{Re}(z) = \dfrac{z+\overline{z}}{2},\quad \text{ and } \quad \operatorname{Im}(z) = \dfrac{z-\overline{z}}{2i}.</math> | <math display=block>\operatorname{Re}(z) = \dfrac{z+\overline{z}}{2},\quad \text{ and } \quad \operatorname{Im}(z) = \dfrac{z-\overline{z}}{2i}.</math> | ||
इसके अलावा, एक सम्मिश्र संख्या वास्तविक होती है यदि और केवल यदि | इसके अलावा, एक सम्मिश्र संख्या वास्तविक होती है यदि और केवल यदि यह अपने स्वयं के संयुग्म के बराबर होती है। | ||
संयुग्मन बुनियादी जटिल अंकगणितीय | संयुग्मन बुनियादी जटिल अंकगणितीय कार्यों पर वितरित करता है: | ||
<math display=block>\begin{align} | <math display=block>\begin{align} | ||
\overline{z\pm w} &= \overline{z} \pm \overline{w}, \\ | \overline{z\pm w} &= \overline{z} \pm \overline{w}, \\ | ||
| Line 192: | Line 185: | ||
\overline{z/w} &= \overline{z}/\overline{w}. | \overline{z/w} &= \overline{z}/\overline{w}. | ||
\end{align}</math> | \end{align}</math> | ||
संयुग्मन | संयुग्मन को [[उलटा ज्यामिति]] में भी नियोजित किया जाता है, ज्यामिति की एक शाखा एक रेखा के बारे में एक से अधिक सामान्य प्रतिबिंबों का अध्ययन करती है। [[नेटवर्क विश्लेषण (विद्युत सर्किट)]] में, जटिल संयुग्म का उपयोग समतुल्य प्रतिबाधा खोजने में किया जाता है जब [[अधिकतम शक्ति हस्तांतरण प्रमेय]] की तलाश की जाती है। | ||
=== जोड़ और | === जोड़ और घटाव === | ||
[[File:Vector Addition.svg|right|thumb| | [[File:Vector Addition.svg|right|thumb|समांतर चतुर्भुज की रचना करके दो सम्मिश्र संख्याओं का योग ज्यामितीय रूप से किया जा सकता है।]]दो सम्मिश्र संख्याएँ <math>a =x+yi</math> तथा <math>b =u+vi</math> उनके वास्तविक और काल्पनिक भागों को अलग-अलग जोड़कर सबसे आसानी से जोड़ा जाता है। यानी: | ||
दो सम्मिश्र | |||
<math display=block>a + b =(x+yi) + (u+vi) = (x+u) + (y+v)i.</math> | <math display=block>a + b =(x+yi) + (u+vi) = (x+u) + (y+v)i.</math> | ||
इसी | इसी प्रकार, [[घटाव]] के रूप में किया जा सकता है | ||
<math display=block>a - b =(x+yi) - (u+vi) = (x-u) + (y-v)i.</math> | <math display=block>a - b =(x+yi) - (u+vi) = (x-u) + (y-v)i.</math> | ||
एक | एक जटिल संख्या का गुणन <math>a =x+yi</math> और एक वास्तविक संख्या {{mvar|r}} अलग-अलग गुणा करके इसी प्रकार किया जा सकता है {{mvar|r}} और के वास्तविक और काल्पनिक भाग {{mvar|a}}: | ||
<math display=block>ra=r(x+yi) = rx + ryi.</math> | <math display=block>ra=r(x+yi) = rx + ryi.</math> | ||
विशेष रूप से, | विशेष रूप से, [[वापस लेने]] को नकार कर घटाव किया जा सकता है (जो इसे गुणा कर रहा है {{math|–1}}) और परिणाम को [[minuend]] में जोड़ना: | ||
<math display=block>a - b =a + (-1)\,b.</math> | <math display=block>a - b =a + (-1)\,b.</math> | ||
जटिल विमान में जटिल संख्याओं के विज़ुअलाइज़ेशन का उपयोग करते हुए, जोड़ की निम्नलिखित ज्यामितीय व्याख्या है: दो जटिल संख्याओं का योग {{mvar|a}} तथा {{mvar|b}}, जटिल तल में बिंदुओं के रूप में व्याख्या की गई, वह बिंदु है जो तीन शीर्षों से समांतर चतुर्भुज बनाकर प्राप्त किया जाता है {{mvar|O}}, और लेबल किए गए तीरों के बिंदु {{mvar|a}} तथा {{mvar|b}} (बशर्ते कि वे एक लाइन पर न हों)। समान रूप से, इन बिंदुओं को कॉल करना {{mvar|A}}, {{mvar|B}}, क्रमशः और समांतर चतुर्भुज का चौथा बिंदु {{mvar|X}} [[त्रिकोण]] {{mvar|OAB}} तथा {{mvar|XBA}} [[सर्वांगसमता (ज्यामिति)]] हैं। | |||
=== | === गुणन और वर्ग{{anchor|Multiplication|Square}}=== | ||
वितरण संपत्ति के नियम, | वितरण संपत्ति के नियम, क्रमविनिमेय संपत्ति (जोड़ और गुणा की), और परिभाषित संपत्ति {{math|1=''i''{{sup|2}} = −1}} जटिल संख्याओं पर लागू करें। यह इस प्रकार है कि | ||
<math display=block>(x+yi)\, (u+vi)= (xu - yv) + (xv + yu)i.</math> | <math display=block>(x+yi)\, (u+vi)= (xu - yv) + (xv + yu)i.</math> | ||
विशेष रूप से, | विशेष रूप से, | ||
| Line 214: | Line 206: | ||
=== | === व्युत्क्रम और विभाजन === | ||
संयुग्मन का उपयोग | संयुग्मन का उपयोग करना, एक अशून्य सम्मिश्र संख्या का गुणक व्युत्क्रम {{math|1=''z'' = ''x'' + ''yi''}} कभी भी तोड़ा जा सकता है | ||
<math display=block>\frac{1}{z}=\frac{\overline{z}}{z \overline{z}} = \frac{\overline{z}}{|z|^2}=\frac{\overline{z}}{x^2+y^2}=\frac{x}{x^2+y^2} -\frac{y}{x^2+y^2}i,</math> | <math display=block>\frac{1}{z}=\frac{\overline{z}}{z \overline{z}} = \frac{\overline{z}}{|z|^2}=\frac{\overline{z}}{x^2+y^2}=\frac{x}{x^2+y^2} -\frac{y}{x^2+y^2}i,</math> | ||
चूंकि गैर-शून्य का तात्पर्य है {{math|''x''{{sup|2}} + ''y''{{sup|2}}}} शून्य से बड़ा है। | |||
इसका उपयोग | इसका उपयोग मनमाना जटिल संख्या के विभाजन को व्यक्त करने के लिए किया जा सकता है {{math|''w'' {{=}} ''u'' + ''vi''}} एक गैर-शून्य जटिल संख्या द्वारा {{mvar|z}} जैसा | ||
<math display=block>\frac {w}{z}= w\cdot \frac {1}{z}= (u+vi)\cdot \left(\frac{x}{x^2+y^2} -\frac{y}{x^2+y^2}i\right)= \frac{(ux+vy)+(vx-uy)i} {x^2+y^2}.</math> | <math display=block>\frac {w}{z}= w\cdot \frac {1}{z}= (u+vi)\cdot \left(\frac{x}{x^2+y^2} -\frac{y}{x^2+y^2}i\right)= \frac{(ux+vy)+(vx-uy)i} {x^2+y^2}.</math> | ||
=== ध्रुवीय रूप में गुणा और भाग === | === ध्रुवीय रूप में गुणा और भाग === | ||
[[File:Complex multi.svg|right|thumb|का गुणन {{math|2 + ''i''}} (नीला त्रिकोण) और {{math|3 + ''i''}} (लाल त्रिकोण)। लाल | [[File:Complex multi.svg|right|thumb|का गुणन {{math|2 + ''i''}} (नीला त्रिकोण) और {{math|3 + ''i''}} (लाल त्रिकोण)। लाल त्रिकोण को नीले त्रिकोण के शीर्ष से मिलाने के लिए घुमाया जाता है (दोनों कोणों को φ के संदर्भ में जोड़कर)<sub>1</sub>+ च<sub>2</sub> समीकरण में) और नीले त्रिकोण के [[कर्ण]] की लंबाई (दोनों त्रिज्याओं का गुणन, शब्द r के अनुसार) द्वारा बढ़ाया गया<sub>1</sub>r<sub>2</sub> समीकरण में)।]]गुणन, विभाजन और घातांक के सूत्र कार्तीय निर्देशांकों में संबंधित सूत्रों की तुलना में ध्रुवीय रूप में सरल होते हैं। दो सम्मिश्र संख्याएँ दी हैं {{math|1=''z''<sub>1</sub> = ''r''<sub>1</sub>(cos ''φ''<sub>1</sub> + ''i'' sin ''φ''<sub>1</sub>)}} तथा {{math|1=''z''<sub>2</sub> = ''r''<sub>2</sub>(cos ''φ''<sub>2</sub> + ''i'' sin ''φ''<sub>2</sub>)}}, त्रिकोणमितीय सर्वसमिकाओं के कारण | ||
<math display=block>\begin{alignat}{4} | <math display=block>\begin{alignat}{4} | ||
\cos a \cos b & - \sin a \sin b & {}={} & \cos(a + b) \\ | \cos a \cos b & - \sin a \sin b & {}={} & \cos(a + b) \\ | ||
| Line 233: | Line 224: | ||
<math display=block>z_1 z_2 = r_1 r_2 (\cos(\varphi_1 + \varphi_2) + i \sin(\varphi_1 + \varphi_2)).</math> | <math display=block>z_1 z_2 = r_1 r_2 (\cos(\varphi_1 + \varphi_2) + i \sin(\varphi_1 + \varphi_2)).</math> | ||
दूसरे शब्दों में, निरपेक्ष मूल्यों को गुणा किया जाता है और उत्पाद के ध्रुवीय रूप को प्राप्त करने के लिए तर्क जोड़े जाते हैं। उदाहरण के लिए, से गुणा करना {{math|''i''}} एक चौथाई | दूसरे शब्दों में, निरपेक्ष मूल्यों को गुणा किया जाता है और उत्पाद के ध्रुवीय रूप को प्राप्त करने के लिए तर्क जोड़े जाते हैं। उदाहरण के लिए, से गुणा करना {{math|''i''}} एक चौथाई मोड़ (ज्यामिति) वामावर्त से मेल खाता है, जो वापस देता है {{math|1=''i''<sup>2</sup> = −1}}. दाईं ओर की तस्वीर के गुणन को दर्शाती है | ||
<math display=block>(2+i)(3+i)=5+5i. </math> | <math display=block>(2+i)(3+i)=5+5i. </math> | ||
के वास्तविक और काल्पनिक भाग के बाद से {{math|5 + 5''i''}} बराबर हैं, उस संख्या का तर्क 45 डिग्री है, या {{math|''π''/4}} (रेडियन में)। दूसरी ओर, यह लाल और नीले त्रिभुजों के मूल में कोणों का योग भी है जो क्रमशः [[ | के वास्तविक और काल्पनिक भाग के बाद से {{math|5 + 5''i''}} बराबर हैं, उस संख्या का तर्क 45 डिग्री है, या {{math|''π''/4}} (रेडियन में)। दूसरी ओर, यह लाल और नीले त्रिभुजों के मूल में कोणों का योग भी है जो क्रमशः [[artan]] (1/3) और आर्कटान (1/2) हैं। इस प्रकार, सूत्र | ||
<math display=block>\frac{\pi}{4} = \arctan\left(\frac{1}{2}\right) + \arctan\left(\frac{1}{3}\right) </math> | <math display=block>\frac{\pi}{4} = \arctan\left(\frac{1}{2}\right) + \arctan\left(\frac{1}{3}\right) </math> | ||
रखती है। चूंकि आर्कटान फ़ंक्शन को अत्यधिक कुशलता से अनुमानित किया जा सकता है, इस तरह के सूत्र - मशीन-जैसे सूत्रों के रूप में जाने जाते हैं - पीआई के उच्च-परिशुद्धता सन्निकटन के लिए उपयोग किए जाते हैं।{{pi}}. | |||
इसी प्रकार, विभाजन द्वारा दिया जाता है | इसी प्रकार, विभाजन द्वारा दिया जाता है | ||
| Line 243: | Line 234: | ||
=== वर्गमूल === | ===वर्गमूल=== | ||
{{see also|Square root#Square roots of negative and complex numbers|l1=Square roots of negative and complex numbers}} | {{see also|Square root#Square roots of negative and complex numbers|l1=Square roots of negative and complex numbers}} | ||
वर्गमूल {{math|''a'' + ''bi''}} (साथ {{math|''b'' ≠ 0}}) हैं <math> \pm (\gamma + \delta i)</math>, कहाँ पे | का वर्गमूल {{math|''a'' + ''bi''}} (साथ {{math|''b'' ≠ 0}}) हैं <math> \pm (\gamma + \delta i)</math>, कहाँ पे | ||
<math display=block>\gamma = \sqrt{\frac{a + \sqrt{a^2 + b^2}}{2}}</math> | <math display=block>\gamma = \sqrt{\frac{a + \sqrt{a^2 + b^2}}{2}}</math> | ||
| Line 251: | Line 242: | ||
<math display=block>\delta = (\sgn b)\sqrt{\frac{-a + \sqrt{a^2 + b^2}}{2}},</math> | <math display=block>\delta = (\sgn b)\sqrt{\frac{-a + \sqrt{a^2 + b^2}}{2}},</math> | ||
कहाँ पे {{math|sgn}} [[ साइन | कहाँ पे {{math|sgn}} [[साइन समारोह]] फंक्शन है। इसे वर्ग करके देखा जा सकता है <math> \pm (\gamma + \delta i)</math> प्राप्त करने के लिए {{math|''a'' + ''bi''}}.<ref>{{cite book | ||
|title= | |title=सूत्र, रेखांकन और गणितीय तालिकाओं के साथ गणितीय कार्यों की पुस्तिका|first1=Milton | ||
|first1=Milton | |||
|last1=Abramowitz | |last1=Abramowitz | ||
|first2=Irene A. | |first2=Irene A. | ||
| Line 267: | Line 257: | ||
|url-status=live | |url-status=live | ||
}}, [http://www.math.sfu.ca/~cbm/aands/page_17.htm Section 3.7.26, p. 17] {{Webarchive|url=https://web.archive.org/web/20090910094533/http://www.math.sfu.ca/~cbm/aands/page_17.htm |date=10 September 2009 }}</ref><ref>{{cite book | }}, [http://www.math.sfu.ca/~cbm/aands/page_17.htm Section 3.7.26, p. 17] {{Webarchive|url=https://web.archive.org/web/20090910094533/http://www.math.sfu.ca/~cbm/aands/page_17.htm |date=10 September 2009 }}</ref><ref>{{cite book | ||
|title= | |title=शास्त्रीय बीजगणित: इसकी प्रकृति, उत्पत्ति और उपयोग|first1=Roger | ||
|first1=Roger | |||
|last1=Cooke | |last1=Cooke | ||
|publisher=John Wiley and Sons | |publisher=John Wiley and Sons | ||
| Line 279: | Line 268: | ||
|archive-date=24 April 2016 | |archive-date=24 April 2016 | ||
|url-status=live | |url-status=live | ||
}}, [https://books.google.com/books?id=lUcTsYopfhkC&pg=PA59 Extract: page 59] {{Webarchive|url=https://web.archive.org/web/20160423183239/https://books.google.com/books?id=lUcTsYopfhkC&pg=PA59 |date=23 April 2016 }}</ref> यहां <math>\sqrt{a^2 + b^2}</math> का निरपेक्ष मान कहलाता है {{math|''a'' + ''bi''}}, और वर्गमूल चिह्न गैर-ऋणात्मक वास्तविक भाग वाले वर्गमूल को इंगित करता है, जिसे | }}, [https://books.google.com/books?id=lUcTsYopfhkC&pg=PA59 Extract: page 59] {{Webarchive|url=https://web.archive.org/web/20160423183239/https://books.google.com/books?id=lUcTsYopfhkC&pg=PA59 |date=23 April 2016 }}</ref> यहां <math>\sqrt{a^2 + b^2}</math> का निरपेक्ष मान कहलाता है {{math|''a'' + ''bi''}}, और वर्गमूल चिह्न गैर-ऋणात्मक वास्तविक भाग वाले वर्गमूल को इंगित करता है, जिसे मुख्य वर्गमूल कहा जाता है; भी <math>\sqrt{a^2 + b^2}= \sqrt{z\overline{z}},</math> कहाँ पे {{math|''z'' {{=}} ''a'' + ''bi''}}.{{sfn|Ahlfors|1979|p=3}} | ||
=== घातीय | === घातीय समारोह === | ||
घातीय कार्य <math>\exp \colon \Complex \to \Complex ; z \mapsto \exp z </math> प्रत्येक | घातीय कार्य <math>\exp \colon \Complex \to \Complex ; z \mapsto \exp z </math> प्रत्येक जटिल संख्या के लिए परिभाषित किया जा सकता है {{mvar|z}} शक्ति श्रृंखला द्वारा | ||
<math display=block>\exp z= \sum_{n=0}^\infty \frac {z^n}{n!},</math> | <math display=block>\exp z= \sum_{n=0}^\infty \frac {z^n}{n!},</math> | ||
जिसमें अभिसरण की अनंत त्रिज्या है। | जिसमें अभिसरण की अनंत त्रिज्या है। | ||
पर मूल्य {{math|1}} चरघातांकी फलन का यूलर संख्या है | |||
<math display=block>e = \exp 1 = \sum_{n=0}^\infty \frac1{n!}\approx 2.71828.</math> | <math display=block>e = \exp 1 = \sum_{n=0}^\infty \frac1{n!}\approx 2.71828.</math> | ||
यदि {{mvar|z}} | यदि {{mvar|z}} वास्तविक है, एक के पास है | ||
<math>\exp z=e^z.</math> | <math>\exp z=e^z.</math> | ||
[[ विश्लेषणात्मक निरंतरता ]] इस समानता को | [[विश्लेषणात्मक निरंतरता]] इस समानता को प्रत्येक जटिल मूल्य के लिए विस्तारित करने की अनुमति देती है {{mvar|z}}, और इस प्रकार आधार के साथ जटिल घातांक को परिभाषित करना {{mvar|e}} जैसा | ||
<math display=block>e^z=\exp z.</math> | <math display=block>e^z=\exp z.</math> | ||
==== [[ कार्यात्मक समीकरण ]] ==== | ==== [[कार्यात्मक समीकरण]] ==== | ||
चरघातांकी फलन फलन समीकरण को संतुष्ट करता है <math>e^{z+t}=e^ze^t.</math> | |||
यह या तो दोनों सदस्यों के शक्ति श्रृंखला विस्तार की तुलना करके या समीकरण के प्रतिबंध से वास्तविक तर्कों तक विश्लेषणात्मक निरंतरता को लागू करके साबित किया जा सकता है। | यह या तो दोनों सदस्यों के शक्ति श्रृंखला विस्तार की तुलना करके या समीकरण के प्रतिबंध से लेकर वास्तविक तर्कों तक विश्लेषणात्मक निरंतरता को लागू करके साबित किया जा सकता है। | ||
==== यूलर का सूत्र ==== | ==== यूलर का सूत्र ==== | ||
यूलर का सूत्र बताता है कि, किसी भी वास्तविक संख्या के लिए {{mvar|y}}, | यूलर का सूत्र बताता है कि, किसी भी वास्तविक संख्या के लिए {{mvar|y}}, | ||
<math display=block>e^{iy} = \cos y + i\sin y .</math> | <math display=block>e^{iy} = \cos y + i\sin y .</math> | ||
कार्यात्मक समीकरण का तात्पर्य इस प्रकार है कि, यदि {{mvar|x}} तथा {{mvar|y}} असली हैं, एक के पास है | |||
<math display=block>e^{x+iy} = e^x(\cos y + i\sin y) = e^x \cos y + i e^x \sin y ,</math> | <math display=block>e^{x+iy} = e^x(\cos y + i\sin y) = e^x \cos y + i e^x \sin y ,</math> | ||
जो | जो घातीय फलन का उसके वास्तविक और काल्पनिक भागों में अपघटन है। | ||
===जटिल लघुगणक === | === जटिल लघुगणक === | ||
वास्तविक स्थिति में, [[ प्राकृतिक ]] लघुगणक को व्युत्क्रम फलन के रूप में परिभाषित किया जा सकता है | वास्तविक स्थिति में, [[प्राकृतिक]] लघुगणक को व्युत्क्रम फलन के रूप में परिभाषित किया जा सकता है | ||
<math>\ln \colon \R^+ \to \R ; x \mapsto \ln x </math> घातीय | <math>\ln \colon \R^+ \to \R ; x \mapsto \ln x </math> घातीय समारोह का। इसे जटिल डोमेन तक विस्तारित करने के लिए, यूलर के सूत्र से शुरू किया जा सकता है। इसका तात्पर्य है कि, यदि एक सम्मिश्र संख्या <math>z\in \Complex^\times</math> ध्रुवीय रूप में लिखा गया है | ||
<math display=block> z = r(\cos \varphi + i\sin \varphi )</math> | <math display=block> z = r(\cos \varphi + i\sin \varphi )</math> | ||
साथ <math>r, \varphi \in \R ,</math> फिर साथ | साथ <math>r, \varphi \in \R ,</math> फिर साथ | ||
<math display=block> \ln z = \ln r + i \varphi </math> | <math display=block> \ln z = \ln r + i \varphi </math> | ||
[[ जटिल लघुगणक ]] के रूप में एक उचित व्युत्क्रम होता है: | [[जटिल लघुगणक]] के रूप में एक उचित व्युत्क्रम होता है: | ||
<math display=block> \exp \ln z = \exp(\ln r + i \varphi ) = r \exp i \varphi = r(\cos \varphi + i\sin \varphi ) = z .</math> | <math display=block> \exp \ln z = \exp(\ln r + i \varphi ) = r \exp i \varphi = r(\cos \varphi + i\sin \varphi ) = z .</math> | ||
हालाँकि, क्योंकि कोसाइन और साइन आवधिक कार्य हैं, एक पूर्णांक | हालाँकि, क्योंकि कोसाइन और साइन आवधिक कार्य हैं, एक पूर्णांक गुणक का जोड़ {{math|2''π''}} प्रति {{mvar|φ}} नहीं बदलता {{mvar|z}}. उदाहरण के लिए, {{math|1=''e''{{sup|''iπ''}} = ''e''{{sup|3''iπ''}} = −1}} , तो दोनों {{mvar|iπ}} तथा {{math|3''iπ''}} के प्राकृतिक लघुगणक के संभावित मान हैं {{math|−1}}. | ||
इसलिए, यदि जटिल लघुगणक को | इसलिए, यदि जटिल लघुगणक को बहु-मूल्यवान फ़ंक्शन के रूप में परिभाषित नहीं किया जाना है | ||
<math display=block> \ln z = \left\{ \ln r + i (\varphi + 2\pi k) \mid k \in \Z \right\},</math> | <math display=block> \ln z = \left\{ \ln r + i (\varphi + 2\pi k) \mid k \in \Z \right\},</math> | ||
किसी को [[ शाखा | किसी को [[शाखा काटी]] का उपयोग करना पड़ता है और [[कोडोमेन]] को प्रतिबंधित करना पड़ता है, जिसके परिणामस्वरूप विशेषण कार्य होता है | ||
<math display=block>\ln \colon \; \Complex^\times \; \to \; \; \; \R^+ + \; i \, \left(-\pi, \pi\right] .</math> | <math display=block>\ln \colon \; \Complex^\times \; \to \; \; \; \R^+ + \; i \, \left(-\pi, \pi\right] .</math> | ||
यदि <math>z \in \Complex \setminus \left( -\R_{\ge 0} \right)</math> एक गैर-सकारात्मक वास्तविक संख्या | यदि <math>z \in \Complex \setminus \left( -\R_{\ge 0} \right)</math> एक गैर-सकारात्मक वास्तविक संख्या (एक सकारात्मक या एक गैर-वास्तविक संख्या) नहीं है, जिसके परिणामस्वरूप जटिल लघुगणक का मुख्य मूल्य प्राप्त होता है {{math|−''π'' < ''φ'' < ''π''}}. यह ऋणात्मक वास्तविक संख्याओं के बाहर एक विश्लेषणात्मक फलन है, लेकिन इसे किसी ऐसे फलन में विस्तारित नहीं किया जा सकता है जो किसी भी ऋणात्मक वास्तविक संख्या पर निरंतर हो <math>z \in -\R^+ </math>, जहां मुख्य मूल्य है {{math|1=ln ''z'' = ln(−''z'') + ''iπ''}}.{{efn|However for another inverse function of the complex exponential function (and not the above defined principal value), the branch cut could be taken at any other [[Line (geometry)#Ray|ray]] thru the origin.}} | ||
=== घातांक === | === घातांक === | ||
यदि {{math|''x'' > 0}} | यदि {{math|''x'' > 0}} वास्तविक है और {{mvar|z}} जटिल, घातांक के रूप में परिभाषित किया गया है | ||
<math display=block>x^z=e^{z\ln x},</math> | <math display=block>x^z=e^{z\ln x},</math> | ||
कहाँ पे {{math|ln}} प्राकृतिक लघुगणक को दर्शाता है। | कहाँ पे {{math|ln}} प्राकृतिक लघुगणक को दर्शाता है। | ||
इस सूत्र | के जटिल मानों के लिए इस सूत्र का विस्तार करना स्वाभाविक प्रतीत होता है {{mvar|x}}, लेकिन इस तथ्य से उत्पन्न कुछ कठिनाइयाँ हैं कि जटिल लघुगणक वास्तव में एक फ़ंक्शन नहीं है, बल्कि एक बहुविकल्पीय फ़ंक्शन है। | ||
इससे पता चलता है कि अगर {{mvar|z}} ऊपर के रूप में है, और यदि {{mvar|t}} एक और सम्मिश्र संख्या है, तो घातांक बहु-मूल्यवान फलन है | |||
<math display=block>z^t=\left\{e^{t\ln r}\,(\cos(\varphi t+ 2 \pi kt)+i\sin(\varphi t+ 2 \pi kt))\}\mid k\in \mathbb Z\right\}</math> | <math display=block>z^t=\left\{e^{t\ln r}\,(\cos(\varphi t+ 2 \pi kt)+i\sin(\varphi t+ 2 \pi kt))\}\mid k\in \mathbb Z\right\}</math> | ||
====पूर्णांक और भिन्नात्मक घातांक ==== | ==== पूर्णांक और भिन्नात्मक घातांक ==== | ||
{{Visualisation complex number roots|1=upright=1.35}} | {{Visualisation complex number roots|1=upright=1.35}} | ||
यदि, पूर्ववर्ती सूत्र में, {{mvar|t}} एक पूर्णांक है, तो ज्या और कोज्या स्वतंत्र हैं {{mvar|k}}. इस प्रकार, यदि | यदि, पूर्ववर्ती सूत्र में, {{mvar|t}} एक पूर्णांक है, तो ज्या और कोज्या से स्वतंत्र हैं {{mvar|k}}. इस प्रकार, यदि प्रतिपादक {{mvar|n}} एक पूर्णांक है, तो {{math|''z''{{sup|''n''}}}} अच्छी तरह से परिभाषित है, और घातांक सूत्र डी मोइवर के सूत्र को सरल करता है: | ||
<math display=block> z^{n}=(r(\cos \varphi + i\sin \varphi ))^n = r^n \, (\cos n\varphi + i \sin n \varphi).</math> | <math display=block> z^{n}=(r(\cos \varphi + i\sin \varphi ))^n = r^n \, (\cos n\varphi + i \sin n \varphi).</math> | ||
{{mvar|n}} }} | {{mvar|n}} }} nवीं जड़|{{mvar|n}}एक सम्मिश्र संख्या की वें जड़ें {{mvar|z}} द्वारा दिए गए हैं | ||
<math display=block>z^{1/n} = \sqrt[n]r \left( \cos \left(\frac{\varphi+2k\pi}{n}\right) + i \sin \left(\frac{\varphi+2k\pi}{n}\right)\right)</math> | <math display=block>z^{1/n} = \sqrt[n]r \left( \cos \left(\frac{\varphi+2k\pi}{n}\right) + i \sin \left(\frac{\varphi+2k\pi}{n}\right)\right)</math> | ||
के लिये {{math|0 ≤ ''k'' ≤ ''n'' − 1}}. (यहां <math>\sqrt[n]r</math> सामान्य है (सकारात्मक) {{mvar|n}}धनात्मक वास्तविक संख्या का वां मूल {{mvar|r}}।) क्योंकि साइन और कोसाइन आवधिक हैं, अन्य पूर्णांक मान {{mvar|k}} अन्य मूल्य न दें। | के लिये {{math|0 ≤ ''k'' ≤ ''n'' − 1}}. (यहां <math>\sqrt[n]r</math> सामान्य है (सकारात्मक) {{mvar|n}}धनात्मक वास्तविक संख्या का वां मूल {{mvar|r}}।) क्योंकि साइन और कोसाइन आवधिक हैं, के अन्य पूर्णांक मान {{mvar|k}} अन्य मूल्य न दें। | ||
जब {{mvar|n}}एक सकारात्मक वास्तविक संख्या की जड़ {{mvar|r}} | जब {{mvar|n}}एक सकारात्मक वास्तविक संख्या की जड़ {{mvar|r}} धनात्मक वास्तविक संख्या के रूप में चुना जाता है {{mvar|c}} संतुष्टि देने वाला {{math|1=''c''<sup>''n''</sup> = ''r''}}, एक विशेष परिसर को अलग करने का कोई स्वाभाविक तरीका नहीं है {{mvar|n}}एक सम्मिश्र संख्या का वें मूल। इसलिए {{mvar|n}}रूट एक मल्टीवैल्यूड फंक्शन है |{{mvar|n}}- का मूल्यवान कार्य {{mvar|z}}. इसका तात्पर्य यह है कि, सकारात्मक वास्तविक संख्याओं के मामले के विपरीत, किसी के पास है | ||
<math display=block>(z^n)^{1/n} \ne z,</math> | <math display=block>(z^n)^{1/n} \ne z,</math> | ||
चूंकि बाएं हाथ के | चूंकि बाएं हाथ के हिस्से में शामिल हैं {{mvar|n}} मान, और दाईं ओर एक एकल मान है। | ||
== गुण == | == गुण == | ||
=== क्षेत्र संरचना === | === क्षेत्र संरचना === | ||
सेट <math>\Complex</math> | सेट <math>\Complex</math> जटिल संख्याओं का एक क्षेत्र (गणित) है।{{sfn|Apostol|1981|pp=15–16}} संक्षेप में, इसका मतलब यह है कि निम्नलिखित तथ्य मान्य हैं: सबसे पहले, किन्हीं भी दो सम्मिश्र संख्याओं को जोड़ा और गुणा किया जा सकता है ताकि एक और सम्मिश्र संख्या प्राप्त हो सके। दूसरा, किसी सम्मिश्र संख्या के लिए {{mvar|z}}, इसका योगात्मक व्युत्क्रम {{math|–''z''}} एक सम्मिश्र संख्या भी है; और तीसरा, प्रत्येक अशून्य सम्मिश्र संख्या में एक गुणक व्युत्क्रम सम्मिश्र संख्या होती है। इसके अलावा, ये ऑपरेशन कई कानूनों को संतुष्ट करते हैं, उदाहरण के लिए किन्हीं दो सम्मिश्र संख्याओं के लिए योग और गुणन की [[क्रमविनिमेयता]] का नियम {{math|''z''<sub>1</sub>}} तथा {{math|''z''<sub>2</sub>}}: | ||
<math display=block>\begin{align} | <math display=block>\begin{align} | ||
z_1 + z_2 & = z_2 + z_1 ,\\ | z_1 + z_2 & = z_2 + z_1 ,\\ | ||
z_1 z_2 & = z_2 z_1 . | z_1 z_2 & = z_2 z_1 . | ||
\end{align}</math> | \end{align}</math> | ||
इन दो कानूनों और एक क्षेत्र पर अन्य आवश्यकताओं को ऊपर दिए गए सूत्रों द्वारा सिद्ध किया जा सकता है, इस तथ्य का उपयोग करते हुए कि वास्तविक संख्याएं स्वयं एक क्षेत्र बनाती हैं। | |||
असली के विपरीत, <math>\Complex</math> एक [[आदेशित क्षेत्र]] नहीं है, अर्थात किसी संबंध को परिभाषित करना संभव नहीं है {{math|''z''<sub>1</sub> < ''z''<sub>2</sub>}} जो जोड़ और गुणा के साथ संगत है। वास्तव में, किसी भी आदेशित क्षेत्र में, किसी भी तत्व का वर्ग आवश्यक रूप से सकारात्मक होता है, इसलिए {{math|1=''i''<sup>2</sup> = −1}} [[कुल आदेश]] के अस्तित्व को रोकता है <math>\Complex.</math>{{sfn|Apostol|1981|p=25}} | |||
जब | जब गणितीय विषय या निर्माण के लिए अंतर्निहित क्षेत्र जटिल संख्याओं का क्षेत्र होता है, तो उस तथ्य को दर्शाने के लिए विषय का नाम आमतौर पर संशोधित किया जाता है। उदाहरण के लिए: जटिल विश्लेषण, जटिल [[मैट्रिक्स (गणित)]], जटिल बहुपद, और जटिल [[झूठ बीजगणित]]। | ||
===बहुपद समीकरणों के समाधान === | === बहुपद समीकरणों के समाधान === | ||
किसी भी जटिल संख्या को देखते हुए (गुणांक कहा जाता है) {{math|''a''<sub>0</sub>, ..., ''a''<sub>''n''</sub>}}, समीकरण | किसी भी जटिल संख्या को देखते हुए (गुणांक कहा जाता है) {{math|''a''<sub>0</sub>, ..., ''a''<sub>''n''</sub>}}, समीकरण | ||
<math display=block>a_n z^n + \dotsb + a_1 z + a_0 = 0</math> | <math display=block>a_n z^n + \dotsb + a_1 z + a_0 = 0</math> | ||
कम से कम एक जटिल समाधान z है, बशर्ते कि | कम से कम एक जटिल समाधान z है, बशर्ते कि कम से कम एक उच्च गुणांक हो {{math|''a''<sub>1</sub>, ..., ''a''<sub>''n''</sub>}} शून्येतर है।<ref name= Bourbaki 1998 loc=§VIII.1 /> यह कार्ल फ्रेडरिक गॉस और जीन ले रोंड डी'अलेम्बर्ट के बीजगणित के मौलिक प्रमेय का कथन है। इस तथ्य के कारण, <math>\Complex</math> बीजगणितीय रूप से बंद क्षेत्र कहा जाता है। यह गुण [[परिमेय संख्या]] पर लागू नहीं होता <math>\Q</math> (बहुपद {{math|''x''<sup>2</sup> − 2}} परिमेय मूल नहीं है, क्योंकि 2|√2 का वर्गमूल परिमेय संख्या नहीं है) और न ही वास्तविक संख्याएँ <math>\R</math> (बहुपद {{math|''x''<sup>2</sup> + ''a''}} के लिए कोई वास्तविक जड़ नहीं है {{math|''a'' > 0}}, के वर्ग के बाद से {{mvar|x}} किसी भी वास्तविक संख्या के लिए सकारात्मक है {{mvar|x}}). | ||
इस प्रमेय के विभिन्न प्रमाण हैं, या तो विश्लेषणात्मक तरीकों | इस प्रमेय के विभिन्न प्रमाण हैं, या तो विश्लेषणात्मक तरीकों जैसे कि लिउविल के प्रमेय (जटिल विश्लेषण) | लिउविल के प्रमेय, या टोपोलॉजी वाले जैसे कि [[घुमावदार संख्या]], या गैलोइस सिद्धांत के संयोजन के प्रमाण और तथ्य यह है कि विषम डिग्री के किसी भी वास्तविक बहुपद में कम से कम एक वास्तविक जड़। | ||
इस तथ्य के कारण, | इस तथ्य के कारण, बीजगणितीय रूप से बंद क्षेत्र के लिए धारण करने वाले प्रमेय लागू होते हैं <math>\Complex.</math> उदाहरण के लिए, किसी भी गैर-खाली जटिल [[स्क्वायर मैट्रिक्स]] में कम से कम एक (जटिल) [[eigenvalue]] होता है। | ||
=== | === बीजगणितीय लक्षण वर्णन === | ||
फील्ड <math>\Complex</math> निम्नलिखित तीन गुण हैं: | फील्ड <math>\Complex</math> निम्नलिखित तीन गुण हैं: | ||
* सबसे पहले, इसकी [[ विशेषता (बीजगणित) ]] 0 है। इसका मतलब है कि {{math|1=1 + 1 + ⋯ + 1 ≠ 0}} किसी भी संख्या | * सबसे पहले, इसकी [[विशेषता (बीजगणित)]] 0 है। इसका मतलब यह है कि {{math|1=1 + 1 + ⋯ + 1 ≠ 0}} योग की किसी भी संख्या के लिए (जिनमें से सभी एक के बराबर हैं)। | ||
* दूसरा, इसकी [[ | * दूसरा, इसकी [[श्रेष्ठता की डिग्री]] खत्म <math>\Q</math>, का प्रमुख क्षेत्र <math>\Complex,</math> [[सातत्य की प्रमुखता]] है। | ||
* तीसरा, यह | * तीसरा, यह [[बीजगणितीय रूप से बंद]] है (ऊपर देखें)। | ||
यह दिखाया जा सकता है कि इन गुणों वाला कोई भी क्षेत्र [[ | यह दिखाया जा सकता है कि इन गुणों वाला कोई भी क्षेत्र [[समरूप]] (एक क्षेत्र के रूप में) है <math>\Complex.</math> उदाहरण के लिए, क्षेत्र का [[बीजगणितीय समापन]] <math>\Q_p</math> पी-एडिक नंबर का|{{mvar|p}}-आदिक संख्या भी इन तीन गुणों को संतुष्ट करती है, इसलिए ये दो फ़ील्ड आइसोमॉर्फिक हैं (फ़ील्ड के रूप में, लेकिन टोपोलॉजिकल फ़ील्ड के रूप में नहीं)।<ref>{{cite book | ||
| last = Marker | first = David | | last = Marker | first = David | ||
| editor1-last = Marker | editor1-first = D. | | editor1-last = Marker | editor1-first = D. | ||
| Line 386: | Line 375: | ||
| publisher = Springer-Verlag | location = Berlin | | publisher = Springer-Verlag | location = Berlin | ||
| series = Lecture Notes in Logic | | series = Lecture Notes in Logic | ||
| title = | | title = खेतों का मॉडल सिद्धांत| volume = 5 | ||
| year = 1996}}</ref> भी, <math>\Complex</math> जटिल [[प्यूसेक्स श्रृंखला]] के क्षेत्र के लिए आइसोमोर्फिक है। हालांकि, एक समरूपता को निर्दिष्ट करने के लिए पसंद के स्वयंसिद्ध की आवश्यकता होती है। इस बीजगणितीय लक्षण वर्णन का एक और परिणाम यह है कि <math>\Complex</math> कई उचित उप-क्षेत्र शामिल हैं जो आइसोमोर्फिक हैं <math>\Complex</math>. | |||
| year = 1996}}</ref> भी, <math>\Complex</math> जटिल | |||
=== एक | === एक सामयिक क्षेत्र के रूप में लक्षण वर्णन === | ||
के पूर्ववर्ती लक्षण वर्णन <math>\Complex</math> के केवल बीजगणितीय पहलुओं का वर्णन करता है <math>\Complex.</math> कहने का मतलब यह है कि [[पड़ोस (टोपोलॉजी)]] और [[निरंतरता (टोपोलॉजी)]] के गुण, जो [[गणितीय विश्लेषण]] और टोपोलॉजी जैसे क्षेत्रों में मायने रखते हैं, से निपटा नहीं जाता है। निम्नलिखित विवरण <math>\Complex</math> [[टोपोलॉजिकल रिंग]] के रूप में (अर्थात, एक ऐसा क्षेत्र जो एक [[टोपोलॉजिकल स्पेस]] से लैस है, जो अभिसरण की धारणा की अनुमति देता है) टोपोलॉजिकल गुणों को ध्यान में रखता है। <math>\Complex</math> एक उपसमुच्चय शामिल है {{math|''P''}} (अर्थात् धनात्मक वास्तविक संख्याओं का समुच्चय) अशून्य तत्वों का निम्नलिखित तीन स्थितियों को संतुष्ट करता है: | |||
* {{math|''P''}} जोड़, गुणा और | * {{math|''P''}} जोड़, गुणा और व्युत्क्रम लेने के तहत बंद है। | ||
* यदि {{mvar|x}} तथा {{mvar|y}} के विशिष्ट तत्व हैं {{math|''P''}}, तो कोई {{math|''x'' − ''y''}} या {{math|''y'' − ''x''}} में है {{math|''P''}}. | * यदि {{mvar|x}} तथा {{mvar|y}} के विशिष्ट तत्व हैं {{math|''P''}}, तो कोई {{math|''x'' − ''y''}} या {{math|''y'' − ''x''}} में है {{math|''P''}}. | ||
* यदि {{mvar|S}} का कोई | * यदि {{mvar|S}} का कोई गैररिक्त उपसमुच्चय है {{math|''P''}}, फिर {{math|1=''S'' + ''P'' = ''x'' + ''P''}} कुछ के लिए {{mvar|x}} में <math>\Complex.</math> | ||
इसके अतिरिक्त, <math>\Complex</math> एक गैर-तुच्छ समावेशन (गणित) [[ | इसके अतिरिक्त, <math>\Complex</math> एक गैर-तुच्छ समावेशन (गणित) [[automorphism]] है {{math|''x'' ↦ ''x''*}} (अर्थात् जटिल संयुग्मन), जैसे कि {{math|''x x''*}} में है {{math|''P''}} किसी भी शून्य के लिए {{mvar|x}} में <math>\Complex.</math> | ||
किसी भी क्षेत्र {{mvar|F}} इन गुणों के साथ सेट लेकर एक टोपोलॉजी | किसी भी क्षेत्र {{mvar|F}} इन गुणों के साथ सेट लेकर एक टोपोलॉजी से संपन्न किया जा सकता है {{math|1= ''B''(''x'', ''p'') = { ''y'' {{!}} ''p'' − (''y'' − ''x'')(''y'' − ''x'')* ∈ ''P'' } }} [[आधार (टोपोलॉजी)]] के रूप में, जहाँ {{mvar|x}} क्षेत्र भर में पर्वतमाला और {{mvar|p}} से अधिक है {{math|''P''}}. इस टोपोलॉजी के साथ {{mvar|F}} एक सामयिक क्षेत्र के रूप में आइसोमोर्फिक है <math>\Complex.</math> | ||
[[स्थानीय रूप से कॉम्पैक्ट]] टोपोलॉजिकल रिंग से जुड़ा एकमात्र स्थान है <math>\R</math> तथा <math>\Complex.</math> यह का एक और लक्षण वर्णन देता है <math>\Complex</math> एक सामयिक क्षेत्र के रूप में, चूंकि <math>\Complex</math> से अलग किया जा सकता है <math>\R</math> क्योंकि अशून्य जटिल संख्याएँ जुड़ी हुई जगह हैं, जबकि अशून्य वास्तविक संख्याएँ नहीं हैं।{{sfn|Bourbaki|1998|loc=§VIII.4}} | |||
==औपचारिक निर्माण== | == औपचारिक निर्माण == | ||
=== | === ऑर्डर किए गए जोड़े के रूप में निर्माण === | ||
विलियम रोवन हैमिल्टन ने सेट को परिभाषित करने के लिए दृष्टिकोण पेश किया <math>\Complex</math> जटिल संख्याओं का<ref>{{cite book|title= | विलियम रोवन हैमिल्टन ने सेट को परिभाषित करने के लिए दृष्टिकोण पेश किया <math>\Complex</math> जटिल संख्याओं का<ref>{{cite book|title=संख्याओं का संक्षिप्त इतिहास|first=Leo |last=Corry|publisher=Oxford University Press|year=2015|pages=215–16}}</ref> सेट के रूप में <math>\mathbb{R}^2</math> का {{nowrap|[[ordered pair]]s {{math|(''a'', ''b'')}}}} वास्तविक संख्याओं का, जिसमें योग और गुणन के निम्नलिखित नियम लागू होते हैं:{{sfn|Apostol|1981|pp=15–16}} | ||
<math display=block>\begin{align} | <math display=block>\begin{align} | ||
| Line 409: | Line 397: | ||
(a, b) \cdot (c, d) &= (ac - bd, bc + ad). | (a, b) \cdot (c, d) &= (ac - bd, bc + ad). | ||
\end{align}</math> | \end{align}</math> | ||
यह | यह तब व्यक्त करने के लिए केवल संकेतन की बात है {{math|(''a'', ''b'')}} जैसा {{math|''a'' + ''bi''}}. | ||
=== भागफल क्षेत्र के रूप में निर्माण === | === भागफल क्षेत्र के रूप में निर्माण === | ||
हालांकि यह निम्न-स्तरीय निर्माण जटिल संख्याओं की संरचना का | हालांकि यह निम्न-स्तरीय निर्माण जटिल संख्याओं की संरचना का सही-सही वर्णन करता है, निम्नलिखित समतुल्य परिभाषा से बीजगणितीय प्रकृति का पता चलता है <math>\Complex</math> अधिक तुरंत। यह लक्षण वर्णन क्षेत्रों और बहुपदों की धारणा पर निर्भर करता है। एक फ़ील्ड जोड़, घटाव, गुणा और भाग संक्रियाओं से संपन्न एक ऐसा समुच्चय है जो परिमेय संख्याओं से परिचित व्यवहार करता है। उदाहरण के लिए, वितरण कानून | ||
<math display=block>(x+y) z = xz + yz</math> | <math display=block>(x+y) z = xz + yz</math> | ||
किसी भी तीन तत्वों के लिए धारण करना चाहिए {{mvar|x}}, {{mvar|y}} तथा {{mvar|z}} एक मैदान का। सेट <math>\R</math> वास्तविक संख्याओं का एक क्षेत्र बनता है। एक बहुपद {{math|''p''(''X'')}} वास्तविक गुणांक के साथ रूप की अभिव्यक्ति है | |||
<math display=block>a_nX^n+\dotsb+a_1X+a_0,</math> | <math display=block>a_nX^n+\dotsb+a_1X+a_0,</math> | ||
जहां {{math|''a''<sub>0</sub>, ..., ''a''<sub>''n''</sub>}} वास्तविक संख्याएँ हैं। बहुपदों का सामान्य जोड़ और | जहां {{math|''a''<sub>0</sub>, ..., ''a''<sub>''n''</sub>}} वास्तविक संख्याएँ हैं। बहुपदों का सामान्य जोड़ और गुणा सेट को संपन्न करता है <math>\R[X]</math> एक वलय (गणित) संरचना वाले ऐसे सभी बहुपदों का। इस वलय को वास्तविक संख्याओं पर बहुपद वलय कहा जाता है। | ||
सम्मिश्र संख्याओं के समुच्चय को भागफल वलय के रूप में परिभाषित किया जाता है <math>\R[X]/(X^2+1).</math><ref name= Bourbaki 1998 loc=§VIII.1 /> इस | सम्मिश्र संख्याओं के समुच्चय को भागफल वलय के रूप में परिभाषित किया जाता है <math>\R[X]/(X^2+1).</math><ref name= Bourbaki 1998 loc=§VIII.1 /> इस विस्तार क्षेत्र में दो वर्गमूल हैं {{math|−1}}, अर्थात् ([[सह समुच्चय]]) {{math|''X''}} तथा {{math|−''X''}}, क्रमश। (कोसेट) {{math|1}} तथा {{math|''X''}} का आधार बनता है <math>\mathbb{R}[X]/(X^2 + 1)</math> एक वास्तविक सदिश स्थान के रूप में, जिसका अर्थ है कि विस्तार क्षेत्र के प्रत्येक तत्व को इन दो तत्वों में एक [[रैखिक संयोजन]] के रूप में विशिष्ट रूप से लिखा जा सकता है। समतुल्य रूप से, विस्तार क्षेत्र के तत्वों को क्रमबद्ध जोड़े के रूप में लिखा जा सकता है {{math|(''a'', ''b'')}} वास्तविक संख्याओं का। भागफल वलय एक क्षेत्र है, क्योंकि {{math|''X''<sup>2</sup> + 1}} इरेड्यूसिबल बहुपद खत्म है <math>\R,</math> इसलिए यह जो आदर्श उत्पन्न करता है वह [[अधिकतम आदर्श]] है। | ||
रिंग में | रिंग में जोड़ने और गुणा करने के सूत्र <math>\R[X],</math> सापेक्ष संबंध {{math|''X''<sup>2</sup> {{=}} −1}}, क्रमित जोड़े के रूप में परिभाषित जटिल संख्याओं के योग और गुणन के सूत्रों के अनुरूप हैं। तो क्षेत्र की दो परिभाषाएँ <math>\Complex</math> समरूपता (फ़ील्ड के रूप में) हैं। | ||
इसे स्वीकार करना <math>\Complex</math> बीजगणितीय रूप से बंद है, क्योंकि यह का [[ | इसे स्वीकार करना <math>\Complex</math> बीजगणितीय रूप से बंद है, क्योंकि यह का [[बीजगणितीय विस्तार]] है <math>\mathbb{R}</math> इस दृष्टिकोण में, <math>\Complex</math> इसलिए का बीजगणितीय समापन है <math>\R.</math> | ||
=== जटिल संख्याओं का मैट्रिक्स प्रतिनिधित्व ===<!-- .This section is linked from [[Cauchy-Riemann equations]] --> | === जटिल संख्याओं का मैट्रिक्स प्रतिनिधित्व ===<!-- .This section is linked from [[Cauchy-Riemann equations]] --> | ||
जटिल आंकड़े {{math|''a'' + ''bi''}} द्वारा भी | जटिल आंकड़े {{math|''a'' + ''bi''}} द्वारा भी दर्शाया जा सकता है {{math|2 × 2}} मैट्रिक्स (गणित) जिसका रूप है: | ||
<!-- | <!-- | ||
This definition with the minus sign in the upper right corner matches the article [[Rotation matrix]]. Please do not change it. | This definition with the minus sign in the upper right corner matches the article [[Rotation matrix]]. Please do not change it. | ||
| Line 436: | Line 424: | ||
\end{pmatrix} | \end{pmatrix} | ||
</math> | </math> | ||
यहाँ प्रविष्टियाँ {{mvar|a}} तथा {{mvar|b}} वास्तविक संख्याएँ हैं। चूँकि दो ऐसे आव्यूहों का योग और गुणनफल फिर से इस रूप का होता है, ये आव्यूह वलय का उपवलय बनाते हैं {{math|2 × 2}} मैट्रिक्स। | |||
एक साधारण गणना से पता चलता है कि नक्शा: | एक साधारण गणना से पता चलता है कि नक्शा: | ||
| Line 443: | Line 431: | ||
b & \;\; a | b & \;\; a | ||
\end{pmatrix}</math> | \end{pmatrix}</math> | ||
जटिल संख्याओं के क्षेत्र से इन | जटिल संख्याओं के क्षेत्र से इन मेट्रिसेस के वलय तक एक वलय समरूपता है। यह समरूपता एक जटिल संख्या के पूर्ण मूल्य के वर्ग को संबंधित मैट्रिक्स के निर्धारक के साथ जोड़ती है, और एक जटिल संख्या के संयुग्म को मैट्रिक्स के स्थानान्तरण के साथ जोड़ती है। | ||
जटिल संख्याओं के गुणन का ज्यामितीय विवरण [[रोटेशन मैट्रिक्स]] के संदर्भ में जटिल संख्याओं और ऐसे मैट्रिक्स के बीच इस पत्राचार का उपयोग करके भी व्यक्त किया जा सकता है। वेक्टर पर मैट्रिक्स की क्रिया {{math|(''x'', ''y'')}} के गुणन से मेल खाता है {{math|''x'' + ''iy''}} द्वारा {{math|''a'' + ''ib''}}. विशेष रूप से, यदि निर्धारक है {{math|1}}, एक वास्तविक संख्या है {{mvar|t}} ऐसा है कि मैट्रिक्स का रूप है: | |||
<math display=block>\begin{pmatrix} | <math display=block>\begin{pmatrix} | ||
\cos t & - \sin t \\ | \cos t & - \sin t \\ | ||
\sin t & \;\; \cos t | \sin t & \;\; \cos t | ||
\end{pmatrix}</math> | \end{pmatrix}</math> | ||
इस मामले में, वैक्टर पर मैट्रिक्स की कार्रवाई और जटिल संख्या से गुणा <math>\cos t+i\sin t</math> | इस मामले में, वैक्टर पर मैट्रिक्स की कार्रवाई और जटिल संख्या से गुणा <math>\cos t+i\sin t</math> कोण के घूर्णन (गणित) दोनों हैं {{mvar|t}}. | ||
==जटिल विश्लेषण == | == जटिल विश्लेषण == | ||
[[File:Sin1z-cplot.svg|thumb|डोमेन रंग {{math|sin(1/''z'')}}. अंदर के काले भाग | [[File:Sin1z-cplot.svg|thumb|डोमेन का रंग {{math|sin(1/''z'')}}. अंदर के काले भाग बड़े निरपेक्ष मान वाले नंबरों को संदर्भित करते हैं।]] | ||
{{main|Complex analysis}} | {{main|Complex analysis}} | ||
<!-- | <!-- | ||
| Line 473: | Line 461: | ||
--> | --> | ||
एक जटिल चर के कार्यों के अध्ययन को जटिल विश्लेषण के रूप में जाना जाता है और | एक जटिल चर के कार्यों के अध्ययन को जटिल विश्लेषण के रूप में जाना जाता है और [[व्यावहारिक गणित]] के साथ-साथ गणित की अन्य शाखाओं में इसका बहुत व्यावहारिक उपयोग होता है। अक्सर, [[वास्तविक विश्लेषण]] या सम [[संख्या सिद्धांत]] में बयानों के लिए सबसे प्राकृतिक सबूत जटिल विश्लेषण से तकनीकों को नियोजित करते हैं (उदाहरण के लिए अभाज्य संख्या प्रमेय देखें)। वास्तविक कार्यों के विपरीत, जिन्हें आमतौर पर द्वि-आयामी ग्राफ के रूप में दर्शाया जाता है, जटिल कार्यों में चार-आयामी ग्राफ होते हैं और उपयोगी रूप से दो चर के फ़ंक्शन के ग्राफ को रंग-कोडिंग द्वारा चित्रित किया जा सकता है। चार आयामों का सुझाव देने के लिए त्रि-आयामी ग्राफ, या द्वारा जटिल विमान के जटिल कार्य के गतिशील परिवर्तन को एनिमेट करना। | ||
===जटिल | === जटिल चरघातांकी और संबंधित फलन === | ||
[[ अभिसरण श्रृंखला ]] और (वास्तविक) विश्लेषण में [[ निरंतर कार्य ]]ों की | [[अभिसरण श्रृंखला]] और (वास्तविक) विश्लेषण में [[निरंतर कार्य]]ों की धारणा जटिल विश्लेषण में प्राकृतिक अनुरूप हैं। एक क्रम <!--(''a''<sub>''n''</sub>)<sub>''n'' ≥ 0</sub>--> सम्मिश्र संख्याओं की संख्या को [[अभिसरण अनुक्रम]] कहा जाता है यदि और केवल यदि इसके वास्तविक और काल्पनिक भाग करते हैं। यह (ε, δ)-सीमा की परिभाषा के समतुल्य है, जहां वास्तविक संख्याओं के निरपेक्ष मान को सम्मिश्र संख्याओं में से एक से बदल दिया जाता है। अधिक अमूर्त दृष्टिकोण से, <math>\mathbb{C}</math>, [[मीट्रिक (गणित)]] के साथ संपन्न | ||
<math display=block>\operatorname{d}(z_1, z_2) = |z_1 - z_2|</math> | <math display=block>\operatorname{d}(z_1, z_2) = |z_1 - z_2|</math> | ||
एक पूर्ण [[ मीट्रिक स्थान ]] है, जिसमें विशेष रूप से त्रिभुज असमानता शामिल है | एक पूर्ण [[मीट्रिक स्थान]] है, जिसमें विशेष रूप से त्रिभुज असमानता शामिल है | ||
<math display=block>|z_1 + z_2| \le |z_1| + |z_2|</math> | <math display=block>|z_1 + z_2| \le |z_1| + |z_2|</math> | ||
किन्हीं दो | किन्हीं दो जटिल संख्याओं के लिए {{math|''z''<sub>1</sub>}} तथा {{math|''z''<sub>2</sub>}}. | ||
वास्तविक विश्लेषण की तरह, अभिसरण की इस धारणा का उपयोग कई | वास्तविक विश्लेषण की तरह, अभिसरण की इस धारणा का उपयोग कई प्राथमिक कार्यों के निर्माण के लिए किया जाता है: घातीय कार्य {{math|exp ''z''}}, लिखा भी है {{math|''e''<sup>''z''</sup>}}, को [[अनंत श्रृंखला]] के रूप में परिभाषित किया गया है | ||
<math display=block>\exp z:= 1+z+\frac{z^2}{2\cdot 1}+\frac{z^3}{3\cdot 2\cdot 1}+\cdots = \sum_{n=0}^{\infty} \frac{z^n}{n!}. </math> | <math display=block>\exp z:= 1+z+\frac{z^2}{2\cdot 1}+\frac{z^3}{3\cdot 2\cdot 1}+\cdots = \sum_{n=0}^{\infty} \frac{z^n}{n!}. </math> | ||
वास्तविक त्रिकोणमितीय कार्यों | वास्तविक त्रिकोणमितीय कार्यों साइन और [[कोज्या]] को परिभाषित करने वाली श्रृंखला, साथ ही साथ [[अतिशयोक्तिपूर्ण कार्य]]ों sinh और cosh को भी बिना किसी बदलाव के जटिल तर्कों पर ले जाया जाता है। अन्य त्रिकोणमितीय और अतिशयोक्तिपूर्ण कार्यों के लिए, जैसे [[स्पर्शरेखा (फ़ंक्शन)]], चीजें थोड़ी अधिक जटिल होती हैं, क्योंकि परिभाषित श्रृंखला सभी जटिल मूल्यों के लिए अभिसरण नहीं करती है। इसलिए, उन्हें या तो साइन, कोसाइन और एक्सपोनेंशियल के रूप में परिभाषित करना चाहिए, या, समकक्ष रूप से, विश्लेषणात्मक निरंतरता की विधि का उपयोग करके। | ||
यूलर का सूत्र कहता है: | यूलर का सूत्र कहता है: | ||
| Line 490: | Line 478: | ||
किसी भी वास्तविक संख्या के लिए {{mvar|φ}}, विशेष रूप से | किसी भी वास्तविक संख्या के लिए {{mvar|φ}}, विशेष रूप से | ||
<math display=block>\exp(i \pi) = -1 </math>, जो यूलर की पहचान है। | <math display=block>\exp(i \pi) = -1 </math>, जो यूलर की पहचान है। | ||
वास्तविक संख्याओं की स्थिति के विपरीत, जटिल समाधानों का एक अनंत सेट होता है {{mvar|z}} समीकरण का | वास्तविक संख्याओं की स्थिति के विपरीत, जटिल समाधानों का एक [[अनंत सेट]] होता है {{mvar|z}} समीकरण का | ||
<math display=block>\exp z = w </math> | <math display=block>\exp z = w </math> | ||
किसी भी | किसी भी जटिल संख्या के लिए {{math|''w'' ≠ 0}}. यह दिखाया जा सकता है कि ऐसा कोई समाधान {{mvar|z}} - का जटिल लघुगणक कहा जाता है {{mvar|w}} - संतुष्ट करता है | ||
<math display=block>\log w = \ln|w| + i\arg w, </math> | <math display=block>\log w = \ln|w| + i\arg w, </math> | ||
जहाँ arg [[आर्ग (गणित)]] परिभाषित #ध्रुवीय रूप है, और ln (वास्तविक) प्राकृतिक लघुगणक है। जैसा कि तर्क एक बहुविकल्पीय कार्य है, केवल एक से अधिक तक अद्वितीय है {{math|2''π''}}, लॉग भी बहुविकल्पीय है। लॉग का मुख्य मूल्य अक्सर काल्पनिक भाग को [[अंतराल (गणित)]] तक सीमित करके लिया जाता है {{open-closed|−''π'', ''π''}}. | |||
जटिल [[ घातांक ]] {{math|''z''<sup>''ω''</sup>}} की तरह परिभाषित किया गया है | जटिल [[घातांक]] {{math|''z''<sup>''ω''</sup>}} की तरह परिभाषित किया गया है | ||
<math display=block>z^\omega = \exp(\omega \log z), </math> | <math display=block>z^\omega = \exp(\omega \log z), </math> | ||
और बहु-मूल्यवान है, सिवाय इसके कि कब {{mvar|ω}} एक पूर्णांक है। के लिये {{math|1=''ω'' = 1 / ''n''}}, कुछ प्राकृतिक संख्या के लिए {{mvar|n}}, यह गैर-विशिष्टता को पुनः प्राप्त करता है {{mvar|n}}ऊपर | और बहु-मूल्यवान है, सिवाय इसके कि कब {{mvar|ω}} एक पूर्णांक है। के लिये {{math|1=''ω'' = 1 / ''n''}}, कुछ प्राकृतिक संख्या के लिए {{mvar|n}}, यह की गैर-विशिष्टता को पुनः प्राप्त करता है {{mvar|n}}ऊपर वर्णित वें जड़ें। | ||
जटिल संख्याएं, वास्तविक संख्याओं के विपरीत, | जटिल संख्याएं, वास्तविक संख्याओं के विपरीत, आम तौर पर असंशोधित शक्ति और लघुगणक पहचान को संतुष्ट नहीं करती हैं, खासकर जब भोलेपन से एकल-मूल्यवान कार्यों के रूप में व्यवहार किया जाता है; घातांक#शक्ति की विफलता और लघुगणक सर्वसमिका देखें। उदाहरण के लिए, वे संतुष्ट नहीं हैं | ||
<math display=block>a^{bc} = \left(a^b\right)^c.</math> | <math display=block>a^{bc} = \left(a^b\right)^c.</math> | ||
समीकरण के दोनों | समीकरण के दोनों पक्षों को यहां दी गई जटिल घातांक की परिभाषा द्वारा बहु-मूल्यवान किया गया है, और बाईं ओर के मान दाईं ओर के सबसेट हैं। | ||
=== होलोमोर्फिक | === होलोमोर्फिक फ़ंक्शन === | ||
एक समारोह | एक समारोह च: <math>\mathbb{C}</math> → <math>\mathbb{C}</math> [[होलोमॉर्फिक फ़ंक्शन]] कहा जाता है यदि यह कॉची-रीमैन समीकरणों को संतुष्ट करता है। उदाहरण के लिए, कोई रैखिक रूपांतरण#परिभाषा और प्रथम परिणाम|<math>\mathbb{R}</math>-रैखिक नक्शा <math>\mathbb{C}</math> → <math>\mathbb{C}</math> रूप में लिखा जा सकता है | ||
<math display=block>f(z)=az+b\overline{z}</math> | <math display=block>f(z)=az+b\overline{z}</math> | ||
जटिल गुणांक के साथ {{mvar|a}} तथा {{mvar|b}}. यह नक्शा होलोमोर्फिक है अगर और केवल अगर {{math|1=''b'' = 0}}. दूसरा | जटिल गुणांक के साथ {{mvar|a}} तथा {{mvar|b}}. यह नक्शा होलोमोर्फिक है अगर और केवल अगर {{math|1=''b'' = 0}}. दूसरा योग <math>b \overline z</math> वास्तविक-विभेदक है, लेकिन कॉची-रीमैन समीकरणों को संतुष्ट नहीं करता है। | ||
जटिल विश्लेषण | जटिल विश्लेषण कुछ विशेषताओं को वास्तविक विश्लेषण में स्पष्ट नहीं दिखाता है। उदाहरण के लिए, कोई भी दो होलोमॉर्फिक कार्य {{mvar|f}} तथा {{mvar|g}} के एक मनमाने ढंग से छोटे खुले उपसमुच्चय पर सहमत हैं <math>\mathbb{C}</math> अनिवार्य रूप से हर जगह सहमत हैं। [[मेरोमॉर्फिक फ़ंक्शन]], फ़ंक्शंस जिन्हें स्थानीय रूप से लिखा जा सकता है {{math|''f''(''z'')/(''z'' − ''z''<sub>0</sub>)<sup>''n''</sup>}} एक होलोमोर्फिक फ़ंक्शन के साथ {{mvar|f}}, अभी भी होलोमोर्फिक कार्यों की कुछ विशेषताओं को साझा करते हैं। अन्य कार्यों में [[आवश्यक विलक्षणता]] होती है, जैसे {{math|sin(1/''z'')}} पर {{math|1=''z'' = 0}}. | ||
== | == अनुप्रयोग == | ||
[[ संकेत का प्रक्रमण ]], [[ नियंत्रण सिद्धांत ]], | [[संकेत का प्रक्रमण]], [[नियंत्रण सिद्धांत]], इलेक्ट्रोमैग्नेटिज्म, [[द्रव गतिविज्ञान]], [[क्वांटम यांत्रिकी]], [[नक्शानवीसी]] और वाइब्रेशन # वाइब्रेशन एनालिसिस सहित कई वैज्ञानिक क्षेत्रों में जटिल संख्याओं के अनुप्रयोग हैं। इनमें से कुछ अनुप्रयोगों का वर्णन नीचे किया गया है। | ||
===ज्यामिति === | === ज्यामिति === | ||
==== आकार ==== | ==== आकार ==== | ||
तीन | तीन संरेखता | असंरेख बिंदु <math>u, v, w</math> समतल में त्रिभुज की आकृति#समानता वर्ग निर्धारित करें <math>\{u, v, w\}</math>. जटिल तल में बिंदुओं का पता लगाने के लिए, त्रिकोण के इस आकार को जटिल अंकगणित द्वारा व्यक्त किया जा सकता है | ||
<math display=block>S(u, v, w) = \frac {u - w}{u - v}. </math> | <math display=block>S(u, v, w) = \frac {u - w}{u - v}. </math> | ||
आकार <math>S</math> एक | आकार <math>S</math> एक त्रिकोण का समान रहेगा, जब जटिल विमान अनुवाद या फैलाव (एक [[affine परिवर्तन]] द्वारा) द्वारा रूपांतरित होता है, जो आकार की सहज धारणा के अनुरूप होता है, और समानता (ज्यामिति) का वर्णन करता है। इस प्रकार प्रत्येक त्रिकोण <math>\{u, v, w\}</math> एक आकार में है# समान आकार वाले त्रिभुजों की समरूपता वर्ग।<ref>{{cite journal |last=Lester |first=J.A. |title=त्रिभुज I: आकृतियाँ|journal=[[Aequationes Mathematicae]] |volume=52 |pages=30–54 |year=1994 |doi=10.1007/BF01818325 |s2cid=121095307}}</ref> | ||
==== | ==== भग्न ज्यामिति ==== | ||
[[File:Mandelset hires.png|right|thumb| | [[File:Mandelset hires.png|right|thumb|मंडेलब्रॉट लेबल वाले वास्तविक और काल्पनिक अक्षों के साथ सेट।]][[मैंडेलब्रॉट सेट]] जटिल तल पर बनने वाले फ्रैक्टल का एक लोकप्रिय उदाहरण है। यह हर स्थान की साजिश करके परिभाषित किया गया है <math>c</math> जहां क्रम की पुनरावृत्ति हो रही है <math>f_c(z)=z^2+c</math> अपसरण (स्थिरता सिद्धांत) नहीं करता है जब पुनरावृत्ति असीम रूप से होती है। इसी तरह, [[जूलिया सेट]] के समान नियम हैं, सिवाय इसके कि कहाँ <math>c</math> स्थिर रहता है। | ||
[[ | |||
==== त्रिकोण ==== | ==== त्रिकोण ==== | ||
प्रत्येक त्रिभुज में एक अद्वितीय [[ | प्रत्येक त्रिभुज में एक अद्वितीय [[स्टाइनर [[अंडाकार]]]] होता है - त्रिभुज के अंदर एक दीर्घवृत्त और त्रिभुज की तीनों भुजाओं के मध्यबिंदुओं पर स्पर्शरेखा। मार्डन के प्रमेय के अनुसार त्रिभुज के स्टेनर इनलिप्स का [[फोकस (ज्यामिति)]] निम्नानुसार पाया जा सकता है:<ref>{{cite journal |last1=Kalman|first1=Dan|title=मार्डन की प्रमेय का एक प्राथमिक प्रमाण|url=http://mathdl.maa.org/mathDL/22/?pa=content&sa=viewDocument&nodeId=3338&pf=1 |journal=[[American Mathematical Monthly]] |volume=115 |issue=4 |pages=330–38 |year=2008a |doi=10.1080/00029890.2008.11920532 |s2cid=13222698 |issn=0002-9890 |access-date=1 January 2012 |archive-url=https://web.archive.org/web/20120308104622/http://mathdl.maa.org/mathDL/22/?pa=content&sa=viewDocument&nodeId=3338&pf=1 |archive-date=8 March 2012|url-status=live}}</ref><ref>{{cite journal |last1=Kalman |first1=Dan |title=गणित में सबसे अद्भुत प्रमेय|url=http://mathdl.maa.org/mathDL/4/?pa=content&sa=viewDocument&nodeId=1663 |journal=[[Journal of Online Mathematics and Its Applications]] |year=2008b |access-date=1 January 2012|archive-url=https://web.archive.org/web/20120208014954/http://mathdl.maa.org/mathDL/4/?pa=content&sa=viewDocument&nodeId=1663 |archive-date=8 February 2012 |url-status=live}}</ref> जटिल तल में त्रिभुज के शीर्षों को निरूपित करें {{math|1=''a'' = ''x''<sub>''A''</sub> + ''y''<sub>''A''</sub>''i''}}, {{math|1=''b'' = ''x''<sub>''B''</sub> + ''y''<sub>''B''</sub>''i''}}, तथा {{math|1=''c'' = ''x''<sub>''C''</sub> + ''y''<sub>''C''</sub>''i''}}. घन समीकरण लिखिए <math>(x-a)(x-b)(x-c)=0</math>, इसका व्युत्पन्न लें, और (द्विघात) व्युत्पन्न को शून्य के बराबर करें। मार्डेन के प्रमेय का कहना है कि इस समीकरण के समाधान स्टीनर इनलिप्स के दो फॉसी के स्थानों को दर्शाते हुए जटिल संख्याएं हैं। | ||
=== | ===बीजगणितीय संख्या सिद्धांत=== | ||
[[File:Pentagon construct.gif|right|thumb|एक नियमित पेंटागन | [[File:Pentagon construct.gif|right|thumb|एक नियमित पेंटागन [[कम्पास और सीधा निर्माण]] का निर्माण।]]जैसा कि ऊपर उल्लेख किया गया है, किसी भी गैर-स्थिर बहुपद समीकरण (जटिल गुणांकों में) में एक समाधान है <math>\mathbb{C}</math>. हालाँकि, यदि समीकरण में परिमेय गुणांक हैं, तो वही सत्य है। ऐसे समीकरणों के मूल [[बीजगणितीय संख्या]] कहलाते हैं - वे [[बीजगणितीय संख्या सिद्धांत]] में अध्ययन की एक प्रमुख वस्तु हैं। की तुलना में <math>\overline{\mathbb{Q}}</math>, का बीजगणितीय समापन <math>\mathbb{Q}</math>, जिसमें सभी बीजगणितीय संख्याएँ भी शामिल हैं, <math>\mathbb{C}</math> ज्यामितीय शर्तों में आसानी से समझने योग्य होने का लाभ है। इस तरह, बीजगणितीय विधियों का उपयोग ज्यामितीय प्रश्नों के अध्ययन के लिए किया जा सकता है और इसके विपरीत। बीजगणितीय विधियों के साथ, अधिक विशेष रूप से [[क्षेत्र सिद्धांत (गणित)]] की मशीनरी को [[एकता की जड़]] वाले [[संख्या क्षेत्र]] में लागू करते हुए, यह दिखाया जा सकता है कि एक नियमित [[नॉनगोन]] कम्पास और सीधा निर्माण - एक विशुद्ध ज्यामितीय समस्या का निर्माण करना संभव नहीं है। | ||
जैसा कि ऊपर उल्लेख किया गया है, किसी भी गैर-स्थिर बहुपद समीकरण (जटिल गुणांकों में) | |||
एक अन्य उदाहरण [[ | एक अन्य उदाहरण [[गॉसियन पूर्णांक]] है; वह है, रूप की संख्या {{math|''x'' + ''iy''}}, कहाँ पे {{mvar|x}} तथा {{mvar|y}} पूर्णांक हैं, जिनका उपयोग फ़र्मेट के प्रमेय को दो वर्गों के योग पर वर्गीकृत करने के लिए किया जा सकता है। | ||
=== विश्लेषणात्मक संख्या सिद्धांत === | === विश्लेषणात्मक संख्या सिद्धांत === | ||
{{main|Analytic number theory}} | {{main|Analytic number theory}} | ||
विश्लेषणात्मक संख्या सिद्धांत | विश्लेषणात्मक संख्या सिद्धांत अध्ययन संख्या, अक्सर पूर्णांक या परिमेय, इस तथ्य का लाभ उठाते हुए कि उन्हें जटिल संख्या के रूप में माना जा सकता है, जिसमें विश्लेषणात्मक विधियों का उपयोग किया जा सकता है। यह जटिल-मूल्यवान कार्यों में संख्या-सैद्धांतिक जानकारी को एन्कोडिंग द्वारा किया जाता है। उदाहरण के लिए, [[रीमैन जीटा फ़ंक्शन]] {{math|ζ(''s'')}} [[अभाज्य संख्या]]ओं के वितरण से संबंधित है। | ||
=== अनुचित | === अनुचित इंटीग्रल === | ||
लागू क्षेत्रों में, जटिल-मूल्यवान कार्यों के माध्यम से जटिल संख्याओं का उपयोग अक्सर कुछ वास्तविक-मूल्यवान अनुचित इंटीग्रल की गणना करने के लिए किया जाता है। ऐसा करने के लिए कई तरीके मौजूद हैं; [[ समोच्च एकीकरण के तरीके ]] देखें। | लागू क्षेत्रों में, जटिल-मूल्यवान कार्यों के माध्यम से, जटिल संख्याओं का उपयोग अक्सर कुछ वास्तविक-मूल्यवान अनुचित इंटीग्रल की गणना करने के लिए किया जाता है। ऐसा करने के लिए कई तरीके मौजूद हैं; [[समोच्च एकीकरण के तरीके]] देखें। | ||
===गतिशील समीकरण === | === गतिशील समीकरण === | ||
अवकल समीकरणों में, पहले सभी सम्मिश्र | अवकल समीकरणों में, पहले सभी सम्मिश्र मूलों को ज्ञात करना सामान्य है {{mvar|r}} रेखीय अवकल समीकरण#सजातीय समीकरण एक रेखीय अवकल समीकरण या समीकरण प्रणाली के निरंतर गुणांक के साथ और फिर फॉर्म के आधार कार्यों के संदर्भ में प्रणाली को हल करने का प्रयास करते हैं {{math|1=''f''(''t'') = ''e''<sup>''rt''</sup>}}. इसी तरह, [[अंतर समीकरण]]ों में, जटिल जड़ें {{mvar|r}} फार्म के आधार कार्यों के संदर्भ में प्रणाली को हल करने का प्रयास करने के लिए अंतर समीकरण प्रणाली के चारित्रिक समीकरण का उपयोग किया जाता है {{math|1=''f''(''t'') = ''r''<sup>''t''</sup>}}. | ||
=== | === रेखीय बीजगणित === | ||
मैट्रिक्स का | मैट्रिक्स का Eigedecomposition मैट्रिक्स शक्तियों और मैट्रिक्स घातांकों की गणना के लिए एक उपयोगी उपकरण है। हालाँकि, इसे अक्सर जटिल संख्याओं के उपयोग की आवश्यकता होती है, भले ही मैट्रिक्स वास्तविक हो (उदाहरण के लिए, एक रोटेशन मैट्रिक्स)। | ||
सम्मिश्र संख्याएँ अक्सर उन अवधारणाओं को सामान्यीकृत करती हैं जो मूल रूप से वास्तविक संख्याओं में कल्पना की गई थीं। उदाहरण के लिए, संयुग्म स्थानान्तरण, स्थानांतरण को सामान्य करता है, [[हर्मिटियन मैट्रिक्स]] [[सममित मैट्रिक्स]] को सामान्य करता है, और [[एकात्मक मैट्रिक्स]] [[ऑर्थोगोनल मैट्रिक्स]] को सामान्य करता है। | |||
=== लागू गणित में === | === लागू गणित में === | ||
| Line 554: | Line 540: | ||
==== नियंत्रण सिद्धांत ==== | ==== नियंत्रण सिद्धांत ==== | ||
{{see also|Complex plane#Use in control theory}} | {{see also|Complex plane#Use in control theory}} | ||
नियंत्रण सिद्धांत में, सिस्टम अक्सर समय डोमेन से जटिल [[ आवृत्ति डोमेन ]] में | नियंत्रण सिद्धांत में, सिस्टम अक्सर [[लाप्लास रूपांतरण]] का उपयोग करके समय डोमेन से जटिल [[आवृत्ति डोमेन]] में परिवर्तित हो जाते हैं। सिस्टम के [[शून्य और ध्रुव]]ों का जटिल विमान में विश्लेषण किया जाता है। [[रूट लोकस]], [[न्यक्विस्ट प्लॉट]], और [[निकोलस प्लॉट]] तकनीक सभी जटिल विमान का उपयोग करते हैं। | ||
रूट लोकस विधि में, यह महत्वपूर्ण है कि क्या शून्य और ध्रुव | रूट लोकस विधि में, यह महत्वपूर्ण है कि क्या शून्य और ध्रुव बाएँ या दाएँ आधे विमानों में हैं, अर्थात वास्तविक भाग शून्य से अधिक या उससे कम है। यदि एक रेखीय, समय-अपरिवर्तनीय (LTI) प्रणाली में ध्रुव हैं जो हैं | ||
* दाहिने आधे तल में [[ अस्थिर ]] | * दाहिने आधे तल में, यह [[अस्थिर]] होगा, | ||
* सभी | * सभी बाएँ आधे तल में, यह BIBO स्थिरता होगी, | ||
*काल्पनिक अक्ष पर इसमें [[ सीमांत स्थिरता ]] होगी। | * काल्पनिक अक्ष पर, इसमें [[सीमांत स्थिरता]] होगी। | ||
यदि | यदि सिस्टम के दाहिने आधे विमान में शून्य है, तो यह एक गैर-न्यूनतम चरण प्रणाली है। | ||
==== सिग्नल विश्लेषण ==== | ==== सिग्नल विश्लेषण ==== | ||
समय-समय पर अलग-अलग संकेतों के | समय-समय पर अलग-अलग संकेतों के सुविधाजनक विवरण के लिए सिग्नल विश्लेषण और अन्य क्षेत्रों में जटिल संख्याओं का उपयोग किया जाता है। वास्तविक भौतिक मात्राओं का प्रतिनिधित्व करने वाले दिए गए वास्तविक कार्यों के लिए, अक्सर ज्या और कोसाइन के संदर्भ में, संबंधित जटिल कार्यों पर विचार किया जाता है, जिनमें से वास्तविक भाग मूल मात्राएं हैं। किसी दी गई [[आवृत्ति]] की साइन लहर के लिए, निरपेक्ष मान {{math|{{!}}''z''{{!}}}} तदनुरूपी {{mvar|z}} [[आयाम]] और तर्क है (जटिल विश्लेषण) {{math|arg ''z''}} चरण (तरंगें) है। | ||
यदि [[ फूरियर विश्लेषण ]] को किसी दिए गए वास्तविक-मूल्यवान | यदि [[फूरियर विश्लेषण]] को किसी दिए गए वास्तविक-मूल्यवान संकेत को आवधिक कार्यों के योग के रूप में लिखने के लिए नियोजित किया जाता है, तो इन आवधिक कार्यों को अक्सर प्रपत्र के जटिल-मूल्यवान कार्यों के रूप में लिखा जाता है। | ||
<math display=block>x(t) = \operatorname{Re} \{X( t ) \} </math> | <math display=block>x(t) = \operatorname{Re} \{X( t ) \} </math> | ||
| Line 573: | Line 559: | ||
<math display=block>X( t ) = A e^{i\omega t} = a e^{ i \phi } e^{i\omega t} = a e^{i (\omega t + \phi) } </math> | <math display=block>X( t ) = A e^{i\omega t} = a e^{ i \phi } e^{i\omega t} = a e^{i (\omega t + \phi) } </math> | ||
जहां ω [[कोणीय आवृत्ति]] का प्रतिनिधित्व करता है और जटिल संख्या A चरण और आयाम को एन्कोड करता है जैसा कि ऊपर बताया गया है। | |||
यह उपयोग [[अंकीय संकेत प्रक्रिया]] और [[डिजिटल इमेज प्रोसेसिंग]] में भी विस्तारित है, जो फूरियर विश्लेषण (और तरंगिका विश्लेषण) के डिजिटल संस्करणों का उपयोग संचारित करने, डेटा संपीड़न, पुनर्स्थापित करने और अन्यथा डिजिटल डेटा [[ध्वनि]] संकेतों, स्थिर छवियों और [[वीडियो]] संकेतों को संसाधित करने के लिए करता है। | |||
एएम रेडियो के आयाम मॉडुलन के दो पार्श्व बैंडों के लिए प्रासंगिक एक और उदाहरण है: | |||
<math display=block>\begin{align} | <math display=block>\begin{align} | ||
| Line 591: | Line 577: | ||
=== भौतिकी में === | === भौतिकी में === | ||
====विद्युत चुंबकत्व और | ==== विद्युत चुंबकत्व और इलेक्ट्रिकल इंजीनियरिंग ==== | ||
{{Main|Alternating current}} | {{Main|Alternating current}} | ||
इलेक्ट्रिकल इंजीनियरिंग में, [[ फुरियर रूपांतरण ]] का उपयोग अलग-अलग [[ वोल्टेज ]] और | इलेक्ट्रिकल इंजीनियरिंग में, [[फुरियर रूपांतरण]] का उपयोग अलग-अलग [[वोल्टेज]] और इलेक्ट्रिक करंट का विश्लेषण करने के लिए किया जाता है। बाद के दो के लिए काल्पनिक, आवृत्ति-निर्भर प्रतिरोधों को पेश करके और [[विद्युत प्रतिबाधा]] नामक एक जटिल संख्या में तीनों को जोड़कर प्रतिरोधों, [[संधारित्र]] और [[प्रारंभ करनेवाला]]्स के उपचार को एकीकृत किया जा सकता है। इस दृष्टिकोण को फेजर कैलकुलस कहा जाता है। | ||
इलेक्ट्रिकल इंजीनियरिंग में, काल्पनिक इकाई | इलेक्ट्रिकल इंजीनियरिंग में, काल्पनिक इकाई द्वारा निरूपित किया जाता है {{mvar|j}}, भ्रम से बचने के लिए {{mvar|I}}, जो आम तौर पर विद्युत प्रवाह को निरूपित करने के लिए उपयोग किया जाता है, या अधिक विशेष रूप से, {{mvar|i}}, जो आम तौर पर तात्कालिक विद्युत प्रवाह को दर्शाने के लिए उपयोग में होता है। | ||
चूंकि एक एसी [[ विद्युत परिपथ ]] में वोल्टेज दोलन कर रहा है, इसे इस | चूंकि एक एसी [[विद्युत परिपथ]] में वोल्टेज दोलन कर रहा है, इसे इस रूप में दर्शाया जा सकता है | ||
<math display=block> V(t) = V_0 e^{j \omega t} = V_0 \left (\cos\omega t + j \sin\omega t \right ),</math> | <math display=block> V(t) = V_0 e^{j \omega t} = V_0 \left (\cos\omega t + j \sin\omega t \right ),</math> | ||
| Line 603: | Line 589: | ||
<math display=block> v(t) = \operatorname{Re}(V) = \operatorname{Re}\left [ V_0 e^{j \omega t} \right ] = V_0 \cos \omega t.</math> | <math display=block> v(t) = \operatorname{Re}(V) = \operatorname{Re}\left [ V_0 e^{j \omega t} \right ] = V_0 \cos \omega t.</math> | ||
जटिल-मूल्यवान संकेत {{math|''V''(''t'')}} वास्तविक-मूल्यवान, मापने योग्य | जटिल-मूल्यवान संकेत {{math|''V''(''t'')}} वास्तविक-मूल्यवान, मापने योग्य संकेत का [[विश्लेषणात्मक संकेत]] प्रतिनिधित्व कहा जाता है {{math|''v''(''t'')}}. | ||
<ref>{{cite book |last1=Grant |first1=I.S. |title= | <ref>{{cite book |last1=Grant |first1=I.S. |title=विद्युत चुंबकत्व|year=2008|edition=2 |publisher=Manchester Physics Series |isbn=978-0-471-92712-9 |last2=Phillips |first2=W.R.}}</ref> | ||
==== द्रव गतिकी ==== | ==== द्रव गतिकी ==== | ||
द्रव गतिकी में, [[ दो आयामों में संभावित प्रवाह ]] का वर्णन करने के लिए जटिल कार्यों का उपयोग किया जाता है। | द्रव गतिकी में, [[दो आयामों में संभावित प्रवाह]] का वर्णन करने के लिए जटिल कार्यों का उपयोग किया जाता है। | ||
==== क्वांटम यांत्रिकी ==== | ==== क्वांटम यांत्रिकी ==== | ||
जटिल संख्या क्षेत्र क्वांटम यांत्रिकी के गणितीय | जटिल संख्या क्षेत्र [[क्वांटम यांत्रिकी के गणितीय योग]]ों के लिए आंतरिक है, जहां जटिल हिल्बर्ट रिक्त स्थान ऐसे एक सूत्रीकरण के लिए संदर्भ प्रदान करते हैं जो सुविधाजनक और शायद सबसे मानक है। क्वांटम यांत्रिकी के मूल आधार सूत्र - श्रोडिंगर समीकरण और हाइजेनबर्ग के [[मैट्रिक्स यांत्रिकी]] - जटिल संख्याओं का उपयोग करते हैं। | ||
==== सापेक्षता ==== | ==== सापेक्षता ==== | ||
[[ विशेष सापेक्षता ]] और [[ सामान्य सापेक्षता ]] में, [[ अंतरिक्ष समय ]] पर मीट्रिक के लिए कुछ सूत्र सरल हो जाते हैं यदि कोई स्पेसटाइम सातत्य के समय घटक को काल्पनिक मानता है। (यह दृष्टिकोण | [[विशेष सापेक्षता]] और [[सामान्य सापेक्षता]] में, [[अंतरिक्ष समय]] पर मीट्रिक के लिए कुछ सूत्र सरल हो जाते हैं यदि कोई स्पेसटाइम सातत्य के समय घटक को काल्पनिक मानता है। (यह दृष्टिकोण शास्त्रीय सापेक्षता में अब मानक नहीं है, लेकिन [[क्वांटम क्षेत्र सिद्धांत]] में [[बाती का घूमना]] है।) स्पिनरों के लिए जटिल संख्याएं आवश्यक हैं, जो सापेक्षता में उपयोग किए जाने वाले [[टेन्सर]]ों का एक सामान्यीकरण है। | ||
== सामान्यीकरण और संबंधित धारणाएं == | == सामान्यीकरण और संबंधित धारणाएं == | ||
[[File:Cayley_Q8_quaternion_multiplication_graph.svg|thumb|upright=1.05|लिंक ={{filepath:Cayley_Q8_quaternion_multiplication_graph.svg}}|केली Q8 | [[File:Cayley_Q8_quaternion_multiplication_graph.svg|thumb|upright=1.05|लिंक ={{filepath:Cayley_Q8_quaternion_multiplication_graph.svg}}|केली Q8 चतुष्कोणीय ग्राफ गुणन के चक्रों को दिखा रहा है {{red|'''i'''}}, {{green|'''j'''}} तथा {{blue|'''k'''}}]]क्षेत्र के विस्तार की प्रक्रिया <math>\mathbb R</math> वास्तविक के लिए <math>\mathbb C</math> केली-डिक्सन निर्माण के रूप में जाना जाता है। इसे चतुष्कोणों की उपज, उच्च आयामों तक ले जाया जा सकता है <math>\mathbb H</math> और [[ऑक्टोनियन]] <math>\mathbb{O}</math> जो (वास्तविक सदिश स्थान के रूप में) क्रमशः आयाम 4 और 8 के हैं। | ||
क्षेत्र के विस्तार की प्रक्रिया <math>\mathbb R</math> वास्तविक के <math>\mathbb C</math> केली- | इस संदर्भ में सम्मिश्र संख्याओं को बायनेरियंस कहा गया है।<ref>{{cite book |first=Kevin |last=McCrimmon |year=2004 |title=जॉर्डन अल्जेब्रस का स्वाद|page=64 |series=Universitext |publisher=Springer |isbn=0-387-95447-3}} {{mr|id=2014924}}</ref> | ||
इस संदर्भ में सम्मिश्र संख्याओं को | जिस तरह वास्तविक पर निर्माण लागू करने से आदेशित क्षेत्र की संपत्ति खो जाती है, वास्तविक और जटिल संख्याओं से परिचित गुण प्रत्येक विस्तार के साथ गायब हो जाते हैं। चतुष्कोण कम्यूटेटिविटी खो देते हैं, अर्थात, {{math|''x''·''y'' ≠ ''y''·''x''}} कुछ चतुष्कोणों के लिए {{math|''x'', ''y''}}, और अष्टक का गुणन, इसके अतिरिक्त क्रमविनिमेय नहीं होने के कारण, साहचर्य होने में विफल रहता है: {{math|(''x''·''y'')·''z'' ≠ ''x''·(''y''·''z'')}} कुछ ऑक्टोनियंस के लिए {{math|''x'', ''y'', ''z''}}. | ||
जिस तरह | |||
वास्तविक, सम्मिश्र | वास्तविक, सम्मिश्र संख्याएँ, चतुर्धातुक और अष्टक सभी मानक विभाजन बीजगणित हैं <math>\mathbb R</math>. हर्विट्ज़ के प्रमेय (सामान्य विभाजन बीजगणित) द्वारा | हर्विट्ज़ के प्रमेय वे ही हैं; [[sedenion]]्स, केली-डिक्सन निर्माण में अगला चरण, इस संरचना को बनाने में विफल रहा। | ||
केली- | केली-डिक्सन निर्माण के [[नियमित प्रतिनिधित्व]] से निकटता से संबंधित है <math>\mathbb C,</math> एक के रूप में सोचा <math>\mathbb R</math>-अलजेब्रा (रिंग थ्योरी) (ए <math>\mathbb{R}</math>-वेक्टर स्पेस गुणा के साथ), आधार के संबंध में {{math|(1, ''i'')}}. इसका मतलब निम्नलिखित है: <math>\mathbb R</math>-रैखिक नक्शा | ||
<math display=block>\begin{align} | <math display=block>\begin{align} | ||
\mathbb{C} &\rightarrow \mathbb{C} \\ | \mathbb{C} &\rightarrow \mathbb{C} \\ | ||
z &\mapsto wz | z &\mapsto wz | ||
\end{align}</math> | \end{align}</math> | ||
कुछ निश्चित | कुछ निश्चित जटिल संख्या के लिए {{mvar|w}} ए द्वारा प्रतिनिधित्व किया जा सकता है {{math|2 × 2}} मैट्रिक्स (एक बार एक आधार चुना गया है)। आधार के संबंध में {{math|(1, ''i'')}}, यह मैट्रिक्स है | ||
<math display=block>\begin{pmatrix} | <math display=block>\begin{pmatrix} | ||
\operatorname{Re}(w) & -\operatorname{Im}(w) \\ | \operatorname{Re}(w) & -\operatorname{Im}(w) \\ | ||
\operatorname{Im}(w) & \operatorname{Re}(w) | \operatorname{Im}(w) & \operatorname{Re}(w) | ||
\end{pmatrix},</math> | \end{pmatrix},</math> | ||
यही है, ऊपर जटिल संख्याओं के मैट्रिक्स प्रतिनिधित्व पर अनुभाग में वर्णित एक है। जबकि यह एक [[रैखिक प्रतिनिधित्व]] है <math>\mathbb C</math> 2 × 2 वास्तविक मैट्रिक्स में, यह केवल एक ही नहीं है। कोई मैट्रिक्स | |||
<math display=block>J = \begin{pmatrix}p & q \\ r & -p \end{pmatrix}, \quad p^2 + qr + 1 = 0</math> | <math display=block>J = \begin{pmatrix}p & q \\ r & -p \end{pmatrix}, \quad p^2 + qr + 1 = 0</math> | ||
संपत्ति है कि इसका वर्ग पहचान मैट्रिक्स का ऋणात्मक है: {{math|1=''J''<sup>2</sup> = −''I''}}. फिर | |||
<math display=block>\{ z = a I + b J : a,b \in \mathbb{R} \}</math> | <math display=block>\{ z = a I + b J : a,b \in \mathbb{R} \}</math> | ||
क्षेत्र के लिए भी | क्षेत्र के लिए भी आइसोमोर्फिक है <math>\mathbb C,</math> और एक वैकल्पिक जटिल संरचना देता है <math>\mathbb R^2.</math> यह एक रेखीय जटिल संरचना की धारणा से सामान्यीकृत है। | ||
[[ हाइपरकॉम्प्लेक्स संख्या ]] | [[हाइपरकॉम्प्लेक्स संख्या]] भी सामान्यीकरण करते हैं <math>\mathbb R,</math> <math>\mathbb C,</math> <math>\mathbb H,</math> तथा <math>\mathbb{O}.</math> उदाहरण के लिए, इस धारणा में [[विभाजित-जटिल संख्या]]एँ हैं, जो वलय के तत्व हैं <math>\mathbb R[x]/(x^2-1)</math> (विरोध के रूप में <math>\mathbb R[x]/(x^2+1)</math> जटिल संख्या के लिए)। इस वलय में, समीकरण {{math|1=''a''<sup>2</sup> = 1}} चार उपाय हैं। | ||
फील्ड <math>\mathbb R</math> का समापन है <math>\mathbb Q,</math> सामान्य निरपेक्ष मान मीट्रिक (गणित) के संबंध में परिमेय संख्याओं का क्षेत्र। | फील्ड <math>\mathbb R</math> का समापन है <math>\mathbb Q,</math> सामान्य निरपेक्ष मान मीट्रिक (गणित) के संबंध में परिमेय संख्याओं का क्षेत्र। मीट्रिक (गणित) के अन्य विकल्पों पर <math>\mathbb Q</math> खेतों की ओर ले जाता है <math>\mathbb Q_p</math> पी-एडिक संख्या का|{{mvar|p}}-एडिक नंबर (किसी भी अभाज्य संख्या के लिए {{mvar|p}}), जो इसके अनुरूप हैं <math>\mathbb{R}</math>. पूरा करने का कोई अन्य गैर-तुच्छ तरीका नहीं है <math>\mathbb Q</math> बजाय <math>\mathbb R</math> तथा <math>\mathbb Q_p,</math> ओस्ट्रोव्स्की के प्रमेय द्वारा। बीजीय बंद हो जाता है <math>\overline {\mathbb{Q}_p}</math> का <math>\mathbb Q_p</math> अभी भी एक मानदंड है, लेकिन (विपरीत <math>\mathbb C</math>) इसके संबंध में पूर्ण नहीं हैं। पूर्ण <math>\mathbb{C}_p</math> का <math>\overline {\mathbb{Q}_p}</math> बीजगणितीय रूप से बंद हो जाता है। सादृश्य से, क्षेत्र कहा जाता है {{mvar|p}}-adic जटिल संख्या। | ||
मैदान <math>\mathbb R,</math> <math>\mathbb Q_p,</math> और उनके परिमित क्षेत्र विस्तार, | मैदान <math>\mathbb R,</math> <math>\mathbb Q_p,</math> और उनके परिमित क्षेत्र विस्तार, सहित <math>\mathbb C,</math> [[स्थानीय क्षेत्र]] कहलाते हैं। | ||
==यह भी देखें== | == यह भी देखें == | ||
{{Commons category|Complex numbers}} | {{Commons category|Complex numbers}} | ||
*[[ | * [[बीजगणितीय सतह]] | ||
* | * वर्तुल गति#जटिल संख्याओं का उपयोग करना | ||
*[[ जटिल-आधार प्रणाली ]] | * [[जटिल-आधार प्रणाली]] | ||
*[[ जटिल ज्यामिति ]] | * [[जटिल ज्यामिति]] | ||
*दोहरी जटिल संख्या | * [[दोहरी जटिल संख्या]] | ||
* [[ | * [[आइज़ेंस्टीन पूर्णांक]] | ||
*यूलर की पहचान | * यूलर की पहचान | ||
* ज्यामितीय बीजगणित#यूनिट | * ज्यामितीय बीजगणित#यूनिट स्यूडोस्केलर्स (जिसमें 2-आयामी स्पिनर के रूप में जटिल विमान शामिल है#दो आयाम उप-स्थान <math>\mathcal{G}_2^+</math>) | ||
*[[ इकाई | * [[इकाई जटिल संख्या]] | ||
{{Classification of numbers}} | {{Classification of numbers}} | ||
| Line 672: | Line 657: | ||
=== उद्धृत कार्य === | === उद्धृत कार्य === | ||
{{refbegin}} | {{refbegin}} | ||
* {{cite book |last=Ahlfors |first=Lars |author-link=Lars Ahlfors |year=1979 |title= | * {{cite book |last=Ahlfors |first=Lars |author-link=Lars Ahlfors |year=1979 |title=जटिल विश्लेषण|edition=3rd |publisher=McGraw-Hill |url=https://archive.org/details/lars-ahlfors-complex-analysis-third-edition-mcgraw-hill-science_engineering_math-1979/page/n1/mode/2up |url-access=registration |isbn=978-0-07-000657-7}} | ||
* {{cite book |last=Apostol |first=Tom |author-link=Tom Apostol |year=1981 |title= | * {{cite book |last=Apostol |first=Tom |author-link=Tom Apostol |year=1981 |title=गणितीय विश्लेषण|publisher=Addison-Wesley}} | ||
* {{cite journal |last=Argand |date=1814 |title= | * {{cite journal |last=Argand |date=1814 |title=कल्पनाओं के नए सिद्धांत पर विचार, विश्लेषण के प्रमेय के प्रमाण के लिए एक आवेदन के बाद|journal=Annales de mathématiques pures et appliquées |volume=5 |pages=197–209 |url=https://babel.hathitrust.org/cgi/pt?id=uc1.$c126479&view=1up&seq=209 |trans-title=Reflections on the new theory of complex numbers, followed by an application to the proof of a theorem of analysis |language=fr}} | ||
* {{cite journal |last=Gauss |first=C. F. |date= 1831 |title= | * {{cite journal |last=Gauss |first=C. F. |date= 1831 |title=द्विघात अवशेषों का सिद्धांत। एक दूसरी टिप्पणी।|trans-title=Theory of biquadratic residues. Second memoir. |url=https://babel.hathitrust.org/cgi/pt?id=mdp.39015073697180&view=1up&seq=292 |journal=Commentationes Societatis Regiae Scientiarum Gottingensis Recentiores |volume=7 |pages=89–148 |language=la |author-link= Carl Friedrich Gauss}} | ||
* {{springer |id=c/c024140 |title=Complex number |year=2001|first=E.D. |last=Solomentsev}} | * {{springer |id=c/c024140 |title=Complex number |year=2001|first=E.D. |last=Solomentsev}} | ||
{{refend}} | {{refend}} | ||
| Line 692: | Line 677: | ||
=== | === गणितीय === | ||
{{refbegin}} | {{refbegin}} | ||
* {{cite book |ref=none |last=Ahlfors |first=Lars |author-link=Lars Ahlfors |title= | * {{cite book |ref=none |last=Ahlfors |first=Lars |author-link=Lars Ahlfors |title=जटिल विश्लेषण|publisher=McGraw-Hill |year=1979 |edition=3rd |isbn=978-0-07-000657-7}} | ||
* {{cite book |ref=none |last=Conway |first=John B. |title= | * {{cite book |ref=none |last=Conway |first=John B. |title=एक जटिल चर I के कार्य|year=1986 |publisher=Springer |isbn=978-0-387-90328-6}} | ||
* {{cite book |ref=none |last1=Joshi |first1=Kapil D. |title= | * {{cite book |ref=none |last1=Joshi |first1=Kapil D. |title=असतत गणित की नींव|publisher=[[John Wiley & Sons]] |location=New York |isbn=978-0-470-21152-6 |year=1989}} | ||
* {{cite book |ref=none |last=Pedoe |first=Dan |author-link=Daniel Pedoe |title= | * {{cite book |ref=none |last=Pedoe |first=Dan |author-link=Daniel Pedoe |title=ज्यामिति: एक व्यापक पाठ्यक्रम|publisher=Dover |year=1988 |isbn=978-0-486-65812-4}} | ||
* {{cite book |ref=none |last1=Press |first1=W.H. |last2=Teukolsky |first2=S.A. |last3=Vetterling |first3=W.T. |last4=Flannery |first4=B.P. |year=2007 |title= | * {{cite book |ref=none |last1=Press |first1=W.H. |last2=Teukolsky |first2=S.A. |last3=Vetterling |first3=W.T. |last4=Flannery |first4=B.P. |year=2007 |title=संख्यात्मक व्यंजनों: वैज्ञानिक कंप्यूटिंग की कला|edition=3rd |publisher=Cambridge University Press |location=New York |isbn=978-0-521-88068-8 |chapter=Section 5.5 Complex Arithmetic |chapter-url=http://apps.nrbook.com/empanel/index.html?pg=225}} | ||
* {{springer|ref=none|id=c/c024140|title=Complex number|year=2001|first=E.D.|last=Solomentsev}} | * {{springer|ref=none|id=c/c024140|title=Complex number|year=2001|first=E.D.|last=Solomentsev}} | ||
{{refend}} | {{refend}} | ||
=== ऐतिहासिक === | ===ऐतिहासिक === | ||
{{refbegin}} | {{refbegin}} | ||
* {{cite book |ref=none |last=Bourbaki |first=Nicolas |author-link=Nicolas Bourbaki |title= | * {{cite book |ref=none |last=Bourbaki |first=Nicolas |author-link=Nicolas Bourbaki |title= गणित के इतिहास के तत्व|chapter= Foundations of mathematics § logic: set theory |publisher= Springer |year= 1998}} | ||
* {{cite book |ref=none |last1=Burton |first1=David M. |title= | * {{cite book |ref=none |last1=Burton |first1=David M. |title=गणित का इतिहास|publisher=[[McGraw-Hill]] |location=New York |edition= 3rd |isbn=978-0-07-009465-9 |year=1995}} | ||
* {{cite book |ref=none |last1=Katz |first1=Victor J. |title= | * {{cite book |ref=none |last1=Katz |first1=Victor J. |title=गणित का इतिहास, संक्षिप्त संस्करण|publisher=[[Addison-Wesley]] |isbn=978-0-321-16193-2 |year=2004}} | ||
* {{cite book |ref=none |title= | * {{cite book |ref=none |title=एक काल्पनिक कहानी: <गणित>\scriptstyle\sqrt{-1}</math> की कहानी|first=Paul J. |last=Nahin |publisher=Princeton University Press |isbn=978-0-691-02795-1 |year=1998}} - जटिल संख्याओं के इतिहास और जटिल विश्लेषण की शुरुआत का एक सौम्य परिचय। | ||
* {{cite book |ref=none |first1=H. D. |last1= Ebbinghaus |first2=H. |last2= Hermes |first3=F. |last3=Hirzebruch |first4=M. |last4=Koecher |first5=K. |last5= Mainzer |first6=J. |last6= Neukirch |first7=A. |last7=Prestel |first8=R. |last8=Remmert |title= | * {{cite book |ref=none |first1=H. D. |last1= Ebbinghaus |first2=H. |last2= Hermes |first3=F. |last3=Hirzebruch |first4=M. |last4=Koecher |first5=K. |last5= Mainzer |first6=J. |last6= Neukirch |first7=A. |last7=Prestel |first8=R. |last8=Remmert |title=नंबर|publisher=Springer |isbn=978-0-387-97497-2 |edition=hardcover |year=1991}} - संख्या की अवधारणा के ऐतिहासिक विकास पर एक उन्नत परिप्रेक्ष्य। | ||
{{refend}} | {{refend}} | ||
| Line 719: | Line 704: | ||
{{DEFAULTSORT:Complex Number}} | {{DEFAULTSORT:Complex Number}} | ||
श्रेणी:संरचना बीजगणित | श्रेणी:संरचना बीजगणित | ||
श्रेणी:जटिल | श्रेणी:जटिल संख्याएँ | ||
[[Category: Machine Translated Page]] | [[Category: Machine Translated Page]] | ||
[[Category:Created On | [[Category:Created On 15/12/2022]] | ||
Revision as of 15:32, 15 December 2022
This article needs additional citations for verification. (July 2022) (Learn how and when to remove this template message) |

गणित में, एक जटिल संख्या एक संख्या प्रणाली का एक तत्व है जो वास्तविक संख्या को एक विशिष्ट तत्व के साथ विस्तारित करता है i, काल्पनिक इकाई कहलाती है और समीकरण को संतुष्ट करती है ; प्रत्येक सम्मिश्र संख्या को रूप में व्यक्त किया जा सकता है , कहाँ पे a तथा b वास्तविक संख्याएँ हैं। क्योंकि कोई भी वास्तविक संख्या उपरोक्त समीकरण को संतुष्ट नहीं करती है, i रेने डेसकार्टेस द्वारा एक काल्पनिक संख्या कहा गया था। जटिल संख्या के लिए , a कहा जाता हैreal part, तथा b कहा जाता हैimaginary part. सम्मिश्र संख्याओं के समुच्चय को किसी भी प्रतीक द्वारा निरूपित किया जाता है या C. ऐतिहासिक नामकरण काल्पनिक होने के बावजूद, गणितीय विज्ञान में जटिल संख्याओं को वास्तविक संख्याओं के समान ही वास्तविक माना जाता है और प्राकृतिक दुनिया के वैज्ञानिक विवरण के कई पहलुओं में मौलिक हैं।[1][lower-alpha 1]
जटिल संख्याएं सभी बहुपद समीकरणों के समाधान की अनुमति देती हैं, यहां तक कि उनका भी जिनका वास्तविक संख्या में कोई समाधान नहीं है। अधिक सटीक रूप से, बीजगणित के मौलिक प्रमेय का दावा है कि वास्तविक या जटिल गुणांक वाले प्रत्येक गैर-निरंतर बहुपद समीकरण का एक समाधान होता है जो एक जटिल संख्या है। उदाहरण के लिए, समीकरण इसका कोई वास्तविक समाधान नहीं है, क्योंकि वास्तविक संख्या का वर्ग ऋणात्मक नहीं हो सकता है, लेकिन इसके दो अवास्तविक जटिल समाधान हैं तथा .
नियम का उपयोग करके जटिल संख्याओं के जोड़, घटाव और गुणा को स्वाभाविक रूप से परिभाषित किया जा सकता है साहचर्य कानून, विनिमेय कानून और वितरण कानूनों के साथ संयुक्त। प्रत्येक अशून्य सम्मिश्र संख्या का गुणनात्मक व्युत्क्रम होता है। यह सम्मिश्र संख्याओं को एक ऐसा क्षेत्र (गणित) बनाता है जिसमें उपक्षेत्र के रूप में वास्तविक संख्याएँ होती हैं। सम्मिश्र संख्याएँ भी आयाम दो का एक वास्तविक सदिश स्थान बनाती हैं, साथ में {1, i} मानक आधार के रूप में।
यह मानक आधार सम्मिश्र संख्याओं को कार्तीय तल बनाता है, जिसे सम्मिश्र तल कहा जाता है। यह जटिल संख्याओं और उनके संचालन की एक ज्यामितीय व्याख्या की अनुमति देता है, और इसके विपरीत कुछ ज्यामितीय गुणों और निर्माणों को जटिल संख्याओं के रूप में व्यक्त करता है। उदाहरण के लिए, वास्तविक संख्याएँ वास्तविक रेखा बनाती हैं जिसे जटिल तल के क्षैतिज अक्ष से पहचाना जाता है। निरपेक्ष मान की सम्मिश्र संख्याएँ इकाई वृत्त बनाती हैं। जटिल संख्या का जोड़ जटिल विमान में एक अनुवाद (ज्यामिति) है, और जटिल संख्या से गुणा एक समानता (ज्यामिति) है जो मूल पर केंद्रित है। वास्तविक अक्ष के संबंध में जटिल संयुग्मन प्रतिबिंब समरूपता है। जटिल निरपेक्ष मान एक यूक्लिडियन मानदंड है।
संक्षेप में, जटिल संख्याएं एक समृद्ध संरचना बनाती हैं जो एक साथ एक बीजगणितीय रूप से बंद क्षेत्र, वास्तविकताओं पर एक कम्यूटेटिव बीजगणित (संरचना) और आयाम दो का एक यूक्लिडियन वेक्टर अंतरिक्ष है।
परिभाषा
एक सम्मिश्र संख्या रूप की एक संख्या है a + bi, कहाँ पे a तथा b वास्तविक संख्याएँ हैं, और i एक अनिश्चित संतोषजनक है i2 = −1. उदाहरण के लिए, 2 + 3i एक जटिल संख्या है।[3]
इस तरह, एक सम्मिश्र संख्या को एकल अनिश्चित में वास्तविक गुणांक वाले बहुपद के रूप में परिभाषित किया जाता है i, जिसके लिए संबंध i2 + 1 = 0 लगाया जाता है। इस परिभाषा के आधार पर, बहुपदों के योग और गुणन का उपयोग करके जटिल संख्याओं को जोड़ा और गुणा किया जा सकता है। सम्बन्ध i2 + 1 = 0 समानता को प्रेरित करता है i4k = 1, i4k+1 = i, i4k+2 = −1, तथा i4k+3 = −i, जो सभी पूर्णांकों के लिए है k; ये किसी भी बहुपद को कम करने की अनुमति देते हैं जो सम्मिश्र संख्याओं के जोड़ और गुणा से एक रेखीय बहुपद में परिणामित होता है i, फिर से फॉर्म का a + bi वास्तविक गुणांक के साथ a, b.
वास्तविक संख्या a सम्मिश्र संख्या का वास्तविक भाग कहलाता है a + bi; वास्तविक संख्या b उसका काल्पनिक भाग कहलाता है। जोर देने के लिए, काल्पनिक भाग में एक कारक शामिल नहीं होता है i; वह है, काल्पनिक हिस्सा है b, नहीं bi.[4][5]
औपचारिक रूप से, जटिल संख्याओं को अनिश्चित काल में बहुपद वलय के भागफल वलय के रूप में परिभाषित किया जाता है i, बहुपद द्वारा उत्पन्न आदर्श (रिंग थ्योरी) द्वारा i2 + 1 (#Construction को भागफल क्षेत्र के रूप में देखें)।Cite error: Invalid <ref> tag; invalid names, e.g. too many इन मामलों में, सम्मिश्र संख्याएँ इस प्रकार लिखी जाती हैं a + bj, या a + jb.
विज़ुअलाइज़ेशन
एक जटिल संख्या z इस प्रकार एक आदेशित जोड़ी के साथ पहचाना जा सकता है वास्तविक संख्याएँ, जिन्हें बदले में द्वि-आयामी अंतरिक्ष में एक बिंदु के निर्देशांक के रूप में व्याख्या किया जा सकता है। सबसे तात्कालिक स्थान यूक्लिडियन विमान उपयुक्त निर्देशांक के साथ है, जिसे तब जटिल विमान या अरगंड आरेख कहा जाता है,[6][lower-alpha 2][7] जीन-रॉबर्ट अरगंड के नाम पर। एक अन्य प्रमुख स्थान जिस पर निर्देशांक प्रक्षेपित किए जा सकते हैं, वह एक गोले की द्वि-आयामी सतह है, जिसे तब रीमैन क्षेत्र कहा जाता है।
कार्तीय जटिल तल
जटिल संख्याओं की परिभाषा जिसमें दो मनमाने वास्तविक मूल्य शामिल हैं, तुरंत जटिल विमान में कार्टेशियन निर्देशांक के उपयोग का सुझाव देते हैं। क्षैतिज (वास्तविक) अक्ष का उपयोग आम तौर पर वास्तविक भाग को प्रदर्शित करने के लिए किया जाता है, बढ़ते मूल्यों के साथ दाईं ओर, और काल्पनिक भाग ऊर्ध्वाधर (काल्पनिक) अक्ष को चिह्नित करता है, बढ़ते मूल्यों के साथ ऊपर की ओर।
एक चार्टेड संख्या या तो विक्ट के रूप में देखी जा सकती है: समन्वय बिंदु या मूल से इस बिंदु तक एक वेक्टर (ज्यामितीय) के रूप में। एक सम्मिश्र संख्या के निर्देशांक मान z इसलिए इसके कार्टेशियन, आयताकार, या बीजगणितीय रूप में व्यक्त किया जा सकता है।
विशेष रूप से, जोड़ और गुणन के संचालन एक बहुत ही प्राकृतिक ज्यामितीय चरित्र पर ले जाते हैं, जब जटिल संख्याओं को स्थिति वैक्टर के रूप में देखा जाता है: जोड़ यूक्लिडियन वेक्टर #जोड़ और घटाव से मेल खाता है, जबकि गुणन (ध्रुवीय रूप में #गुणा और विभाजन देखें) गुणन से मेल खाता है उनके परिमाण और उनके द्वारा वास्तविक अक्ष के साथ बनाए गए कोणों को जोड़ना। इस तरह से देखने पर, एक सम्मिश्र संख्या का गुणा द्वारा i मूल के बारे में एक चौथाई मोड़ (ज्यामिति) (समकोण | 90 °) द्वारा स्थिति सदिश अभिविन्यास (ज्यामिति) को घुमाने के अनुरूप है - एक तथ्य जिसे बीजगणितीय रूप से निम्नानुसार व्यक्त किया जा सकता है:
ध्रुवीय जटिल विमान
मापांक और तर्क
जटिल तल में निर्देशांक के लिए एक वैकल्पिक विकल्प ध्रुवीय समन्वय प्रणाली है जो बिंदु की दूरी का उपयोग करती है z उत्पत्ति से (गणित) (O), और धनात्मक वास्तविक अक्ष और रेखा खंड के बीच अंतरित कोण Oz वामावर्त अर्थ में। यह ध्रुवीय रूप की ओर जाता है
एक सम्मिश्र संख्या का, जहाँ r का परम मूल्य है z, तथा का तर्क (जटिल विश्लेषण) है z.
किसी सम्मिश्र संख्या का निरपेक्ष मान (या मापांक या परिमाण)। z = x + yi है[8]
पाइथागोरस प्रमेय के अनुसार, एक सम्मिश्र संख्या का निरपेक्ष मान सम्मिश्र तल में सम्मिश्र संख्या का प्रतिनिधित्व करने वाले बिंदु की उत्पत्ति की दूरी है।
का तर्क z (कई अनुप्रयोगों में चरण के रूप में जाना जाता है φ)[7]त्रिज्या का कोण है Oz सकारात्मक वास्तविक अक्ष के साथ, और के रूप में लिखा है arg z. मापांक की तरह, तर्क को आयताकार रूप से पाया जा सकता है x + yi[9]- काल्पनिक-दर-वास्तविक भागों के भागफल के व्युत्क्रम स्पर्शरेखा को लागू करके। अर्ध-कोण पहचान का उपयोग करके, आर्कटान की एक शाखा सीमा को कवर करने के लिए पर्याप्त होती है (−π, π] की arg-फ़ंक्शन, और अधिक सूक्ष्म केस-बाय-केस विश्लेषण से बचा जाता है
का मूल्य φ atan2 के परिणाम के बराबर है:
जटिल रेखांकन
जटिल विश्लेषण की कल्पना करते समय, एक जटिल इनपुट और आउटपुट दोनों की आवश्यकता होती है। क्योंकि प्रत्येक सम्मिश्र संख्या को दो आयामों में दर्शाया जाता है, एक जटिल कार्य को नेत्रहीन रेखांकन करने के लिए चार आयामी स्थान की धारणा की आवश्यकता होती है, जो केवल अनुमानों में संभव है। इस वजह से, जटिल कार्यों को देखने के अन्य तरीके डिजाइन किए गए हैं।
डोमेन रंग में आउटपुट आयाम क्रमशः रंग और चमक द्वारा दर्शाए जाते हैं। डोमेन के रूप में जटिल विमान में प्रत्येक बिंदु अलंकृत है, आमतौर पर जटिल संख्या के तर्क का प्रतिनिधित्व करने वाले रंग के साथ, और परिमाण का प्रतिनिधित्व करने वाली चमक। डार्क स्पॉट मोडुली को शून्य के करीब चिह्नित करते हैं, चमकीले धब्बे मूल से दूर होते हैं, ग्रेडेशन बंद हो सकता है, लेकिन इसे नीरस माना जाता है। रंग अक्सर चरणों में भिन्न होते हैं π/3 के लिये 0 प्रति 2π लाल, पीला, हरा, सियान, नीला, मैजेंटा से। इन भूखंडों को डोमेन कलरिंग कहा जाता है। यह जानकारी खोए बिना कार्यों की कल्पना करने का एक आसान तरीका प्रदान करता है। चित्र के लिए शून्य दिखाता है ±1, (2 + i) और डंडे पर
इतिहास
एक सामान्य घन समीकरण के nवें मूल (त्रिकोणमितीय कार्यों के बिना) में समाधान, जब इसकी तीनों जड़ें वास्तविक संख्याएँ होती हैं, तो ऋणात्मक संख्याओं के वर्गमूल होते हैं, ऐसी स्थिति जिसे परिमेय मूल परीक्षण द्वारा सहायता प्राप्त गुणनखण्ड द्वारा ठीक नहीं किया जा सकता है, यदि घन अलघुकरणीय बहुपद है; यह तथाकथित एक अपरिवर्तनीय मौका (इर्रेड्यूसिबिल केस) है। इस पहेली ने इतालवी गणितज्ञ जेरोम कार्डानो को 1545 के आसपास अपनी एर्स मैग्ना में जटिल संख्याओं की कल्पना करने के लिए प्रेरित किया।[11] हालाँकि उनकी समझ अल्पविकसित थी; इसके अलावा उन्होंने बाद में सम्मिश्र संख्याओं को सूक्ष्म कहकर खारिज कर दिया क्योंकि वे अनुपयोगी हैं।[12] कार्डानो ने काल्पनिक संख्याओं का उपयोग किया, लेकिन उन्हें "मानसिक यातना" के रूप में वर्णित किया। [13] यह ग्राफिकल कॉम्प्लेक्स प्लेन के उपयोग से पहले था। 1500 के दशक में कार्डानो और अन्य इतालवी गणितज्ञों, विशेष रूप से स्किपियो डेल फेरो ने घन समीकरणों को हल करने के लिए एक एल्गोरिथ्म बनाया, जिसमें आम तौर पर एक वास्तविक समाधान और एक काल्पनिक संख्या वाले दो समाधान होते थे। चूँकि उन्होंने काल्पनिक संख्याओं वाले उत्तरों को नज़रअंदाज़ कर दिया, इसलिए कार्डानो ने उन्हें बेकार पाया।[14] सामान्य बहुपदों की समस्या पर काम अंततः बीजगणित के मौलिक प्रमेय का नेतृत्व करता है, जो दर्शाता है कि जटिल संख्याओं के साथ, एक या उच्चतर डिग्री के प्रत्येक बहुपद समीकरण के लिए एक समाधान मौजूद है। सम्मिश्र संख्याएँ इस प्रकार एक बीजगणितीय रूप से बंद क्षेत्र बनाती हैं, जहाँ किसी भी बहुपद समीकरण में एक फलन का मूल होता है।
कई गणितज्ञों ने जटिल संख्याओं के विकास में योगदान दिया। जटिल संख्याओं के जोड़, घटाव, गुणा और मूल निकालने के नियम इतालवी गणितज्ञ राफेल बॉम्बेली द्वारा विकसित किए गए थे।[15] आयरिश गणितज्ञ विलियम रोवन हैमिल्टन द्वारा जटिल संख्याओं के लिए एक अधिक अमूर्त औपचारिकता को और विकसित किया गया, जिन्होंने इस अमूर्तता को चतुष्कोणों के सिद्धांत तक बढ़ाया।[16] ऋणात्मक संख्याओं के वर्गमूलों का सबसे पहला क्षणभंगुर संदर्भ शायद पहली शताब्दी ईस्वी में हेलेनिस्टिक गणित अलेक्जेंड्रिया के हीरो के काम में पाया जा सकता है, जहाँ उन्होंने अपने हीरो ऑफ़ अलेक्जेंड्रिया#ग्रंथ सूची में, स्पष्ट रूप से गलती से, मात्रा पर विचार किया शब्द पर पहुंचने के लिए पिरामिड का एक असंभव छिन्नक उनकी गणना में, जो आज सरल होगा . हेलेनिस्टिक गणित में नकारात्मक मात्रा की कल्पना नहीं की गई थी और हीरो ने इसे केवल इसके सकारात्मक द्वारा बदल दिया था [17] अपने आप में एक विषय के रूप में जटिल संख्याओं का अध्ययन करने की प्रेरणा पहली बार 16 वीं शताब्दी में उठी जब क्यूबिक समीकरण और क्वार्टिक समीकरण बहुपदों की जड़ों के लिए बीजगणितीय समाधान इतालवी गणितज्ञों द्वारा खोजे गए (देखें निकोलो फोंटाना टारटाग्लिया, गेरोलामो कार्डानो)। यह जल्द ही महसूस किया गया (लेकिन बहुत बाद में साबित हुआ)[18]कि ये सूत्र, भले ही कोई केवल वास्तविक समाधानों में रुचि रखता हो, कभी-कभी ऋणात्मक संख्याओं के वर्गमूलों में हेरफेर की आवश्यकता होती है। एक उदाहरण के रूप में, फार्म के घन समीकरण के लिए टार्टाग्लिया का सूत्र x3 = px + q[lower-alpha 3] समीकरण का समाधान देता है x3 = x जैसा
इन राशियों के लिए काल्पनिक शब्द 1637 में रेने डेसकार्टेस द्वारा गढ़ा गया था, जो अपनी अवास्तविक प्रकृति पर जोर देने के लिए दर्द में थे।[19]
... sometimes only imaginary, that is one can imagine as many as I said in each equation, but sometimes there exists no quantity that matches that which we imagine.
[... quelquefois seulement imaginaires c'est-à-dire que l'on peut toujours en imaginer autant que j'ai dit en chaque équation, mais qu'il n'y a quelquefois aucune quantité qui corresponde à celle qu'on imagine.]
भ्रम का एक और स्रोत समीकरण था बीजगणितीय पहचान के साथ विचित्र रूप से असंगत लग रहा था , जो गैर-ऋणात्मक वास्तविक संख्याओं के लिए मान्य है a तथा b, और जिसका उपयोग जटिल संख्या गणनाओं में से एक के साथ भी किया गया था a, b सकारात्मक और दूसरा नकारात्मक। इस पहचान का गलत उपयोग (और संबंधित पहचान ) मामले में जब दोनों a तथा b शैतानी शैतान लियोनहार्ड यूलर तक नकारात्मक हैं। इस कठिनाई ने अंततः विशेष प्रतीक का उपयोग करने के सम्मेलन को जन्म दिया i की जगह में इस गलती से बचाव के लिए।[citation needed] फिर भी, यूलर ने छात्रों को आज की तुलना में बहुत पहले जटिल संख्याओं से परिचित कराना स्वाभाविक समझा। अपनी प्रारंभिक बीजगणित पाठ्य पुस्तक, बीजगणित के तत्व में, वह इन नंबरों को लगभग एक बार में पेश करता है और फिर उन्हें प्राकृतिक तरीके से उपयोग करता है।
18वीं शताब्दी में जटिल संख्याओं का व्यापक उपयोग हुआ, क्योंकि यह देखा गया कि त्रिकोणमितीय कार्यों से जुड़ी गणनाओं को सरल बनाने के लिए जटिल अभिव्यक्तियों के औपचारिक हेरफेर का उपयोग किया जा सकता है। उदाहरण के लिए, 1730 में अब्राहम डी मोइवरे ने नोट किया कि कोण के एक पूर्णांक बहु के त्रिकोणमितीय कार्यों से संबंधित पहचान उस कोण के त्रिकोणमितीय कार्यों की शक्तियों को निम्नलिखित डी मोइवर के सूत्र द्वारा फिर से व्यक्त की जा सकती है:
जटिल तल (#जटिल समतल) में एक बिंदु के रूप में एक सम्मिश्र संख्या का विचार पहली बार 1799 में डेनमार्क-नॉर्वे गणितज्ञ कैस्पर वेसल द्वारा वर्णित किया गया था,[21] हालांकि जॉन वालिस|वालिस के बीजगणित के ग्रंथ में 1685 में ही इसका अनुमान लगा लिया गया था।[22] वेसेल का संस्मरण कोपेनहेगन अकादमी की कार्यवाही में दिखाई दिया, लेकिन काफी हद तक किसी का ध्यान नहीं गया। 1806 में जीन-रॉबर्ट अरगंड ने स्वतंत्र रूप से जटिल संख्याओं पर एक पैम्फलेट जारी किया और बीजगणित # इतिहास के मौलिक प्रमेय का एक कठोर प्रमाण प्रदान किया।[23] कार्ल फ्रेडरिक गॉस ने पहले 1797 में प्रमेय का एक अनिवार्य रूप से टोपोलॉजी प्रमाण प्रकाशित किया था, लेकिन उस समय -1 के वर्गमूल के वास्तविक तत्वमीमांसा के बारे में अपने संदेह व्यक्त किए थे।[24] यह 1831 तक नहीं था कि उन्होंने इन संदेहों पर काबू पाया और विमान में बिंदुओं के रूप में जटिल संख्याओं पर अपना ग्रंथ प्रकाशित किया।[25] बड़े पैमाने पर आधुनिक संकेतन और शब्दावली की स्थापना:[26]
यदि किसी ने पूर्व में इस विषय पर झूठे दृष्टिकोण से विचार किया था और इसलिए एक रहस्यमय अंधकार पाया, तो यह बड़े पैमाने पर अनाड़ी शब्दावली के लिए जिम्मेदार है। अगर किसी ने +1, -1 नहीं कहा होता, सकारात्मक, नकारात्मक, या काल्पनिक (या असंभव भी) इकाइयाँ, लेकिन इसके बजाय, प्रत्यक्ष, उलटा, या पार्श्व इकाइयाँ कहें, तो ऐसे अंधेरे की बात शायद ही हो सकती थी।
19वीं शताब्दी की शुरुआत में, अन्य गणितज्ञों ने स्वतंत्र रूप से जटिल संख्याओं के ज्यामितीय प्रतिनिधित्व की खोज की: बुई,[27][28] सीवी मौरे,[29] जॉन वॉरेन (गणितज्ञ),[30][31][32] जैक्स फ़्रेडरिक फ़्रैंकैस | फ़्रैंकैस और उनके भाई, दायां बेलावाइटिस[33][34] अंग्रेजी गणितज्ञ जी.एच. हार्डी ने टिप्पणी की कि गॉस 'वास्तव में आत्मविश्वास और वैज्ञानिक तरीके' से जटिल संख्याओं का उपयोग करने वाले पहले गणितज्ञ थे, हालांकि नॉर्वे नील्स हेनरिक एबेल और कार्ल गुस्ताव जैकब जैकोबी जैसे गणितज्ञ आवश्यक रूप से गॉस के 1831 के ग्रंथ को प्रकाशित करने से पहले नियमित रूप से उनका उपयोग कर रहे थे।[35] ऑगस्टिन-लुई कॉची और बर्नहार्ड रीमैन ने मिलकर कॉची के मामले में 1825 के आसपास शुरू करते हुए #जटिल विश्लेषण के मौलिक विचारों को पूर्णता की उच्च स्थिति में ला दिया।
सिद्धांत में प्रयुक्त सामान्य शब्द मुख्य रूप से संस्थापकों के कारण हैं। अरगंड ने फोन किया cos φ + i sin φ दिशा कारक, और मापांक;[lower-alpha 5][36] कॉची (1821) ने बुलाया cos φ + i sin φ घटा हुआ रूप[37] और स्पष्ट रूप से तर्क शब्द का परिचय दिया; गॉस ने प्रयोग किया i के लिये ,[lower-alpha 6] के लिए जटिल संख्या शब्द की शुरुआत की a + bi,[lower-alpha 7] और बुलाया a2 + b2 नियम।[lower-alpha 8] अभिव्यक्ति दिशा गुणांक, अक्सर के लिए प्रयोग किया जाता है cos φ + i sin φहैंकेल (1867) के कारण है,[41] और मापांक के लिए निरपेक्ष मान, वीयरस्ट्रैस के कारण होता है।
सामान्य सिद्धांत पर बाद के शास्त्रीय लेखकों में रिचर्ड डेडेकिंड, ओटो होल्डर, फेलिक्स क्लेन, हेनरी पॉइनकेयर, हरमन ब्लैक, कार्ल वीयरस्ट्रास और कई अन्य शामिल हैं। 20वीं सदी की शुरुआत में जटिल बहुभिन्नरूपी कलन में महत्वपूर्ण कार्य (व्यवस्थितीकरण सहित) शुरू किया गया है। 1927 में विलियम विर्टिंगर द्वारा महत्वपूर्ण परिणाम प्राप्त किए गए हैं।
संबंध और संचालन
समानता
सम्मिश्र संख्याओं की समानता की परिभाषा वास्तविक संख्याओं के समान होती है; दो जटिल संख्याएँ a1 + b1i तथा a2 + b2i समान हैं यदि और केवल यदि उनके वास्तविक और काल्पनिक दोनों भाग समान हैं, अर्थात यदि a1 = a2 तथा b1 = b2. ध्रुवीय रूप में लिखी गई अशून्य जटिल संख्याएँ समान होती हैं यदि और केवल यदि उनका परिमाण समान होता है और उनके तर्क एक पूर्णांक गुणक से भिन्न होते हैं 2π.
आदेश देना
वास्तविक संख्याओं के विपरीत, सम्मिश्र संख्याओं का कोई प्राकृतिक क्रम नहीं होता है। विशेष रूप से, जटिल संख्याओं पर कोई रेखीय क्रम नहीं है जो जोड़ और गुणा के साथ संगत हो। इसलिए, सम्मिश्र संख्याओं में एक आदेशित फ़ील्ड की संरचना नहीं होती है। इसके लिए एक स्पष्टीकरण यह है कि एक आदेशित क्षेत्र में वर्गों का प्रत्येक गैर-तुच्छ योग#nontrivialSquareSum अशून्य है, और i2 + 12 = 0 वर्गों का एक गैर-तुच्छ योग है। इस प्रकार, जटिल संख्याओं को स्वाभाविक रूप से द्वि-आयामी विमान पर मौजूद माना जाता है।
संयुग्म
सम्मिश्र संख्या का सम्मिश्र संयुग्म z = x + yi द्वारा दिया गया है x − yi. यह या तो द्वारा दर्शाया गया है z या z*.[42] सम्मिश्र संख्याओं पर यह एकात्मक संक्रिया केवल उनकी मूल संक्रियाओं जोड़, घटाव, गुणा और भाग को लागू करके व्यक्त नहीं की जा सकती।
ज्यामितीय रूप से, z प्रतिबिंब समरूपता है | का प्रतिबिंब z वास्तविक अक्ष के बारे में दो बार संयुग्मन करने से मूल सम्मिश्र संख्या प्राप्त होती है
एक जटिल संख्या का उत्पाद z = x + yi और इसके संयुग्म को पूर्ण वर्ग के रूप में जाना जाता है। यह हमेशा एक गैर-ऋणात्मक वास्तविक संख्या होती है और प्रत्येक के परिमाण के वर्ग के बराबर होती है:
एक सम्मिश्र संख्या के वास्तविक और काल्पनिक भाग z संयुग्मन का उपयोग करके निकाला जा सकता है:
संयुग्मन बुनियादी जटिल अंकगणितीय कार्यों पर वितरित करता है:
जोड़ और घटाव
दो सम्मिश्र संख्याएँ तथा उनके वास्तविक और काल्पनिक भागों को अलग-अलग जोड़कर सबसे आसानी से जोड़ा जाता है। यानी:
गुणन और वर्ग
वितरण संपत्ति के नियम, क्रमविनिमेय संपत्ति (जोड़ और गुणा की), और परिभाषित संपत्ति i2 = −1 जटिल संख्याओं पर लागू करें। यह इस प्रकार है कि
विशेष रूप से,
व्युत्क्रम और विभाजन
संयुग्मन का उपयोग करना, एक अशून्य सम्मिश्र संख्या का गुणक व्युत्क्रम z = x + yi कभी भी तोड़ा जा सकता है
इसका उपयोग मनमाना जटिल संख्या के विभाजन को व्यक्त करने के लिए किया जा सकता है w = u + vi एक गैर-शून्य जटिल संख्या द्वारा z जैसा
ध्रुवीय रूप में गुणा और भाग

गुणन, विभाजन और घातांक के सूत्र कार्तीय निर्देशांकों में संबंधित सूत्रों की तुलना में ध्रुवीय रूप में सरल होते हैं। दो सम्मिश्र संख्याएँ दी हैं z1 = r1(cos φ1 + i sin φ1) तथा z2 = r2(cos φ2 + i sin φ2), त्रिकोणमितीय सर्वसमिकाओं के कारण
इसी प्रकार, विभाजन द्वारा दिया जाता है
वर्गमूल
का वर्गमूल a + bi (साथ b ≠ 0) हैं , कहाँ पे
घातीय समारोह
घातीय कार्य प्रत्येक जटिल संख्या के लिए परिभाषित किया जा सकता है z शक्ति श्रृंखला द्वारा
पर मूल्य 1 चरघातांकी फलन का यूलर संख्या है
विश्लेषणात्मक निरंतरता इस समानता को प्रत्येक जटिल मूल्य के लिए विस्तारित करने की अनुमति देती है z, और इस प्रकार आधार के साथ जटिल घातांक को परिभाषित करना e जैसा
कार्यात्मक समीकरण
चरघातांकी फलन फलन समीकरण को संतुष्ट करता है यह या तो दोनों सदस्यों के शक्ति श्रृंखला विस्तार की तुलना करके या समीकरण के प्रतिबंध से लेकर वास्तविक तर्कों तक विश्लेषणात्मक निरंतरता को लागू करके साबित किया जा सकता है।
यूलर का सूत्र
यूलर का सूत्र बताता है कि, किसी भी वास्तविक संख्या के लिए y,
जटिल लघुगणक
वास्तविक स्थिति में, प्राकृतिक लघुगणक को व्युत्क्रम फलन के रूप में परिभाषित किया जा सकता है
घातीय समारोह का। इसे जटिल डोमेन तक विस्तारित करने के लिए, यूलर के सूत्र से शुरू किया जा सकता है। इसका तात्पर्य है कि, यदि एक सम्मिश्र संख्या ध्रुवीय रूप में लिखा गया है
इसलिए, यदि जटिल लघुगणक को बहु-मूल्यवान फ़ंक्शन के रूप में परिभाषित नहीं किया जाना है
घातांक
यदि x > 0 वास्तविक है और z जटिल, घातांक के रूप में परिभाषित किया गया है
कहाँ पे ln प्राकृतिक लघुगणक को दर्शाता है।
के जटिल मानों के लिए इस सूत्र का विस्तार करना स्वाभाविक प्रतीत होता है x, लेकिन इस तथ्य से उत्पन्न कुछ कठिनाइयाँ हैं कि जटिल लघुगणक वास्तव में एक फ़ंक्शन नहीं है, बल्कि एक बहुविकल्पीय फ़ंक्शन है।
इससे पता चलता है कि अगर z ऊपर के रूप में है, और यदि t एक और सम्मिश्र संख्या है, तो घातांक बहु-मूल्यवान फलन है
पूर्णांक और भिन्नात्मक घातांक
यदि, पूर्ववर्ती सूत्र में, t एक पूर्णांक है, तो ज्या और कोज्या से स्वतंत्र हैं k. इस प्रकार, यदि प्रतिपादक n एक पूर्णांक है, तो zn अच्छी तरह से परिभाषित है, और घातांक सूत्र डी मोइवर के सूत्र को सरल करता है:
n }} nवीं जड़|nएक सम्मिश्र संख्या की वें जड़ें z द्वारा दिए गए हैं
जब nएक सकारात्मक वास्तविक संख्या की जड़ r धनात्मक वास्तविक संख्या के रूप में चुना जाता है c संतुष्टि देने वाला cn = r, एक विशेष परिसर को अलग करने का कोई स्वाभाविक तरीका नहीं है nएक सम्मिश्र संख्या का वें मूल। इसलिए nरूट एक मल्टीवैल्यूड फंक्शन है |n- का मूल्यवान कार्य z. इसका तात्पर्य यह है कि, सकारात्मक वास्तविक संख्याओं के मामले के विपरीत, किसी के पास है
चूंकि बाएं हाथ के हिस्से में शामिल हैं n मान, और दाईं ओर एक एकल मान है।
गुण
क्षेत्र संरचना
सेट जटिल संख्याओं का एक क्षेत्र (गणित) है।[46] संक्षेप में, इसका मतलब यह है कि निम्नलिखित तथ्य मान्य हैं: सबसे पहले, किन्हीं भी दो सम्मिश्र संख्याओं को जोड़ा और गुणा किया जा सकता है ताकि एक और सम्मिश्र संख्या प्राप्त हो सके। दूसरा, किसी सम्मिश्र संख्या के लिए z, इसका योगात्मक व्युत्क्रम –z एक सम्मिश्र संख्या भी है; और तीसरा, प्रत्येक अशून्य सम्मिश्र संख्या में एक गुणक व्युत्क्रम सम्मिश्र संख्या होती है। इसके अलावा, ये ऑपरेशन कई कानूनों को संतुष्ट करते हैं, उदाहरण के लिए किन्हीं दो सम्मिश्र संख्याओं के लिए योग और गुणन की क्रमविनिमेयता का नियम z1 तथा z2:
असली के विपरीत, एक आदेशित क्षेत्र नहीं है, अर्थात किसी संबंध को परिभाषित करना संभव नहीं है z1 < z2 जो जोड़ और गुणा के साथ संगत है। वास्तव में, किसी भी आदेशित क्षेत्र में, किसी भी तत्व का वर्ग आवश्यक रूप से सकारात्मक होता है, इसलिए i2 = −1 कुल आदेश के अस्तित्व को रोकता है [47] जब गणितीय विषय या निर्माण के लिए अंतर्निहित क्षेत्र जटिल संख्याओं का क्षेत्र होता है, तो उस तथ्य को दर्शाने के लिए विषय का नाम आमतौर पर संशोधित किया जाता है। उदाहरण के लिए: जटिल विश्लेषण, जटिल मैट्रिक्स (गणित), जटिल बहुपद, और जटिल झूठ बीजगणित।
बहुपद समीकरणों के समाधान
किसी भी जटिल संख्या को देखते हुए (गुणांक कहा जाता है) a0, ..., an, समीकरण
<ref> tag; invalid names, e.g. too many यह कार्ल फ्रेडरिक गॉस और जीन ले रोंड डी'अलेम्बर्ट के बीजगणित के मौलिक प्रमेय का कथन है। इस तथ्य के कारण, बीजगणितीय रूप से बंद क्षेत्र कहा जाता है। यह गुण परिमेय संख्या पर लागू नहीं होता (बहुपद x2 − 2 परिमेय मूल नहीं है, क्योंकि 2|√2 का वर्गमूल परिमेय संख्या नहीं है) और न ही वास्तविक संख्याएँ (बहुपद x2 + a के लिए कोई वास्तविक जड़ नहीं है a > 0, के वर्ग के बाद से x किसी भी वास्तविक संख्या के लिए सकारात्मक है x).
इस प्रमेय के विभिन्न प्रमाण हैं, या तो विश्लेषणात्मक तरीकों जैसे कि लिउविल के प्रमेय (जटिल विश्लेषण) | लिउविल के प्रमेय, या टोपोलॉजी वाले जैसे कि घुमावदार संख्या, या गैलोइस सिद्धांत के संयोजन के प्रमाण और तथ्य यह है कि विषम डिग्री के किसी भी वास्तविक बहुपद में कम से कम एक वास्तविक जड़।
इस तथ्य के कारण, बीजगणितीय रूप से बंद क्षेत्र के लिए धारण करने वाले प्रमेय लागू होते हैं उदाहरण के लिए, किसी भी गैर-खाली जटिल स्क्वायर मैट्रिक्स में कम से कम एक (जटिल) eigenvalue होता है।
बीजगणितीय लक्षण वर्णन
फील्ड निम्नलिखित तीन गुण हैं:
- सबसे पहले, इसकी विशेषता (बीजगणित) 0 है। इसका मतलब यह है कि 1 + 1 + ⋯ + 1 ≠ 0 योग की किसी भी संख्या के लिए (जिनमें से सभी एक के बराबर हैं)।
- दूसरा, इसकी श्रेष्ठता की डिग्री खत्म , का प्रमुख क्षेत्र सातत्य की प्रमुखता है।
- तीसरा, यह बीजगणितीय रूप से बंद है (ऊपर देखें)।
यह दिखाया जा सकता है कि इन गुणों वाला कोई भी क्षेत्र समरूप (एक क्षेत्र के रूप में) है उदाहरण के लिए, क्षेत्र का बीजगणितीय समापन पी-एडिक नंबर का|p-आदिक संख्या भी इन तीन गुणों को संतुष्ट करती है, इसलिए ये दो फ़ील्ड आइसोमॉर्फिक हैं (फ़ील्ड के रूप में, लेकिन टोपोलॉजिकल फ़ील्ड के रूप में नहीं)।[48] भी, जटिल प्यूसेक्स श्रृंखला के क्षेत्र के लिए आइसोमोर्फिक है। हालांकि, एक समरूपता को निर्दिष्ट करने के लिए पसंद के स्वयंसिद्ध की आवश्यकता होती है। इस बीजगणितीय लक्षण वर्णन का एक और परिणाम यह है कि कई उचित उप-क्षेत्र शामिल हैं जो आइसोमोर्फिक हैं .
एक सामयिक क्षेत्र के रूप में लक्षण वर्णन
के पूर्ववर्ती लक्षण वर्णन के केवल बीजगणितीय पहलुओं का वर्णन करता है कहने का मतलब यह है कि पड़ोस (टोपोलॉजी) और निरंतरता (टोपोलॉजी) के गुण, जो गणितीय विश्लेषण और टोपोलॉजी जैसे क्षेत्रों में मायने रखते हैं, से निपटा नहीं जाता है। निम्नलिखित विवरण टोपोलॉजिकल रिंग के रूप में (अर्थात, एक ऐसा क्षेत्र जो एक टोपोलॉजिकल स्पेस से लैस है, जो अभिसरण की धारणा की अनुमति देता है) टोपोलॉजिकल गुणों को ध्यान में रखता है। एक उपसमुच्चय शामिल है P (अर्थात् धनात्मक वास्तविक संख्याओं का समुच्चय) अशून्य तत्वों का निम्नलिखित तीन स्थितियों को संतुष्ट करता है:
- P जोड़, गुणा और व्युत्क्रम लेने के तहत बंद है।
- यदि x तथा y के विशिष्ट तत्व हैं P, तो कोई x − y या y − x में है P.
- यदि S का कोई गैररिक्त उपसमुच्चय है P, फिर S + P = x + P कुछ के लिए x में
इसके अतिरिक्त, एक गैर-तुच्छ समावेशन (गणित) automorphism है x ↦ x* (अर्थात् जटिल संयुग्मन), जैसे कि x x* में है P किसी भी शून्य के लिए x में किसी भी क्षेत्र F इन गुणों के साथ सेट लेकर एक टोपोलॉजी से संपन्न किया जा सकता है B(x, p) = { y | p − (y − x)(y − x)* ∈ P } आधार (टोपोलॉजी) के रूप में, जहाँ x क्षेत्र भर में पर्वतमाला और p से अधिक है P. इस टोपोलॉजी के साथ F एक सामयिक क्षेत्र के रूप में आइसोमोर्फिक है स्थानीय रूप से कॉम्पैक्ट टोपोलॉजिकल रिंग से जुड़ा एकमात्र स्थान है तथा यह का एक और लक्षण वर्णन देता है एक सामयिक क्षेत्र के रूप में, चूंकि से अलग किया जा सकता है क्योंकि अशून्य जटिल संख्याएँ जुड़ी हुई जगह हैं, जबकि अशून्य वास्तविक संख्याएँ नहीं हैं।[49]
औपचारिक निर्माण
ऑर्डर किए गए जोड़े के रूप में निर्माण
विलियम रोवन हैमिल्टन ने सेट को परिभाषित करने के लिए दृष्टिकोण पेश किया जटिल संख्याओं का[50] सेट के रूप में का ordered pairs (a, b) वास्तविक संख्याओं का, जिसमें योग और गुणन के निम्नलिखित नियम लागू होते हैं:[46]
भागफल क्षेत्र के रूप में निर्माण
हालांकि यह निम्न-स्तरीय निर्माण जटिल संख्याओं की संरचना का सही-सही वर्णन करता है, निम्नलिखित समतुल्य परिभाषा से बीजगणितीय प्रकृति का पता चलता है अधिक तुरंत। यह लक्षण वर्णन क्षेत्रों और बहुपदों की धारणा पर निर्भर करता है। एक फ़ील्ड जोड़, घटाव, गुणा और भाग संक्रियाओं से संपन्न एक ऐसा समुच्चय है जो परिमेय संख्याओं से परिचित व्यवहार करता है। उदाहरण के लिए, वितरण कानून
सम्मिश्र संख्याओं के समुच्चय को भागफल वलय के रूप में परिभाषित किया जाता है Cite error: Invalid <ref> tag; invalid names, e.g. too many इस विस्तार क्षेत्र में दो वर्गमूल हैं −1, अर्थात् (सह समुच्चय) X तथा −X, क्रमश। (कोसेट) 1 तथा X का आधार बनता है एक वास्तविक सदिश स्थान के रूप में, जिसका अर्थ है कि विस्तार क्षेत्र के प्रत्येक तत्व को इन दो तत्वों में एक रैखिक संयोजन के रूप में विशिष्ट रूप से लिखा जा सकता है। समतुल्य रूप से, विस्तार क्षेत्र के तत्वों को क्रमबद्ध जोड़े के रूप में लिखा जा सकता है (a, b) वास्तविक संख्याओं का। भागफल वलय एक क्षेत्र है, क्योंकि X2 + 1 इरेड्यूसिबल बहुपद खत्म है इसलिए यह जो आदर्श उत्पन्न करता है वह अधिकतम आदर्श है।
रिंग में जोड़ने और गुणा करने के सूत्र सापेक्ष संबंध X2 = −1, क्रमित जोड़े के रूप में परिभाषित जटिल संख्याओं के योग और गुणन के सूत्रों के अनुरूप हैं। तो क्षेत्र की दो परिभाषाएँ समरूपता (फ़ील्ड के रूप में) हैं।
इसे स्वीकार करना बीजगणितीय रूप से बंद है, क्योंकि यह का बीजगणितीय विस्तार है इस दृष्टिकोण में, इसलिए का बीजगणितीय समापन है
जटिल संख्याओं का मैट्रिक्स प्रतिनिधित्व
जटिल आंकड़े a + bi द्वारा भी दर्शाया जा सकता है 2 × 2 मैट्रिक्स (गणित) जिसका रूप है:
एक साधारण गणना से पता चलता है कि नक्शा:
जटिल संख्याओं के गुणन का ज्यामितीय विवरण रोटेशन मैट्रिक्स के संदर्भ में जटिल संख्याओं और ऐसे मैट्रिक्स के बीच इस पत्राचार का उपयोग करके भी व्यक्त किया जा सकता है। वेक्टर पर मैट्रिक्स की क्रिया (x, y) के गुणन से मेल खाता है x + iy द्वारा a + ib. विशेष रूप से, यदि निर्धारक है 1, एक वास्तविक संख्या है t ऐसा है कि मैट्रिक्स का रूप है:
जटिल विश्लेषण
एक जटिल चर के कार्यों के अध्ययन को जटिल विश्लेषण के रूप में जाना जाता है और व्यावहारिक गणित के साथ-साथ गणित की अन्य शाखाओं में इसका बहुत व्यावहारिक उपयोग होता है। अक्सर, वास्तविक विश्लेषण या सम संख्या सिद्धांत में बयानों के लिए सबसे प्राकृतिक सबूत जटिल विश्लेषण से तकनीकों को नियोजित करते हैं (उदाहरण के लिए अभाज्य संख्या प्रमेय देखें)। वास्तविक कार्यों के विपरीत, जिन्हें आमतौर पर द्वि-आयामी ग्राफ के रूप में दर्शाया जाता है, जटिल कार्यों में चार-आयामी ग्राफ होते हैं और उपयोगी रूप से दो चर के फ़ंक्शन के ग्राफ को रंग-कोडिंग द्वारा चित्रित किया जा सकता है। चार आयामों का सुझाव देने के लिए त्रि-आयामी ग्राफ, या द्वारा जटिल विमान के जटिल कार्य के गतिशील परिवर्तन को एनिमेट करना।
जटिल चरघातांकी और संबंधित फलन
अभिसरण श्रृंखला और (वास्तविक) विश्लेषण में निरंतर कार्यों की धारणा जटिल विश्लेषण में प्राकृतिक अनुरूप हैं। एक क्रम सम्मिश्र संख्याओं की संख्या को अभिसरण अनुक्रम कहा जाता है यदि और केवल यदि इसके वास्तविक और काल्पनिक भाग करते हैं। यह (ε, δ)-सीमा की परिभाषा के समतुल्य है, जहां वास्तविक संख्याओं के निरपेक्ष मान को सम्मिश्र संख्याओं में से एक से बदल दिया जाता है। अधिक अमूर्त दृष्टिकोण से, , मीट्रिक (गणित) के साथ संपन्न
वास्तविक विश्लेषण की तरह, अभिसरण की इस धारणा का उपयोग कई प्राथमिक कार्यों के निर्माण के लिए किया जाता है: घातीय कार्य exp z, लिखा भी है ez, को अनंत श्रृंखला के रूप में परिभाषित किया गया है
यूलर का सूत्र कहता है:
जटिल घातांक zω की तरह परिभाषित किया गया है
जटिल संख्याएं, वास्तविक संख्याओं के विपरीत, आम तौर पर असंशोधित शक्ति और लघुगणक पहचान को संतुष्ट नहीं करती हैं, खासकर जब भोलेपन से एकल-मूल्यवान कार्यों के रूप में व्यवहार किया जाता है; घातांक#शक्ति की विफलता और लघुगणक सर्वसमिका देखें। उदाहरण के लिए, वे संतुष्ट नहीं हैं
होलोमोर्फिक फ़ंक्शन
एक समारोह च: → होलोमॉर्फिक फ़ंक्शन कहा जाता है यदि यह कॉची-रीमैन समीकरणों को संतुष्ट करता है। उदाहरण के लिए, कोई रैखिक रूपांतरण#परिभाषा और प्रथम परिणाम|-रैखिक नक्शा → रूप में लिखा जा सकता है
जटिल विश्लेषण कुछ विशेषताओं को वास्तविक विश्लेषण में स्पष्ट नहीं दिखाता है। उदाहरण के लिए, कोई भी दो होलोमॉर्फिक कार्य f तथा g के एक मनमाने ढंग से छोटे खुले उपसमुच्चय पर सहमत हैं अनिवार्य रूप से हर जगह सहमत हैं। मेरोमॉर्फिक फ़ंक्शन, फ़ंक्शंस जिन्हें स्थानीय रूप से लिखा जा सकता है f(z)/(z − z0)n एक होलोमोर्फिक फ़ंक्शन के साथ f, अभी भी होलोमोर्फिक कार्यों की कुछ विशेषताओं को साझा करते हैं। अन्य कार्यों में आवश्यक विलक्षणता होती है, जैसे sin(1/z) पर z = 0.
अनुप्रयोग
संकेत का प्रक्रमण, नियंत्रण सिद्धांत, इलेक्ट्रोमैग्नेटिज्म, द्रव गतिविज्ञान, क्वांटम यांत्रिकी, नक्शानवीसी और वाइब्रेशन # वाइब्रेशन एनालिसिस सहित कई वैज्ञानिक क्षेत्रों में जटिल संख्याओं के अनुप्रयोग हैं। इनमें से कुछ अनुप्रयोगों का वर्णन नीचे किया गया है।
ज्यामिति
आकार
तीन संरेखता | असंरेख बिंदु समतल में त्रिभुज की आकृति#समानता वर्ग निर्धारित करें . जटिल तल में बिंदुओं का पता लगाने के लिए, त्रिकोण के इस आकार को जटिल अंकगणित द्वारा व्यक्त किया जा सकता है
भग्न ज्यामिति
मैंडेलब्रॉट सेट जटिल तल पर बनने वाले फ्रैक्टल का एक लोकप्रिय उदाहरण है। यह हर स्थान की साजिश करके परिभाषित किया गया है जहां क्रम की पुनरावृत्ति हो रही है अपसरण (स्थिरता सिद्धांत) नहीं करता है जब पुनरावृत्ति असीम रूप से होती है। इसी तरह, जूलिया सेट के समान नियम हैं, सिवाय इसके कि कहाँ स्थिर रहता है।
त्रिकोण
प्रत्येक त्रिभुज में एक अद्वितीय [[स्टाइनर अंडाकार]] होता है - त्रिभुज के अंदर एक दीर्घवृत्त और त्रिभुज की तीनों भुजाओं के मध्यबिंदुओं पर स्पर्शरेखा। मार्डन के प्रमेय के अनुसार त्रिभुज के स्टेनर इनलिप्स का फोकस (ज्यामिति) निम्नानुसार पाया जा सकता है:[52][53] जटिल तल में त्रिभुज के शीर्षों को निरूपित करें a = xA + yAi, b = xB + yBi, तथा c = xC + yCi. घन समीकरण लिखिए , इसका व्युत्पन्न लें, और (द्विघात) व्युत्पन्न को शून्य के बराबर करें। मार्डेन के प्रमेय का कहना है कि इस समीकरण के समाधान स्टीनर इनलिप्स के दो फॉसी के स्थानों को दर्शाते हुए जटिल संख्याएं हैं।
बीजगणितीय संख्या सिद्धांत

जैसा कि ऊपर उल्लेख किया गया है, किसी भी गैर-स्थिर बहुपद समीकरण (जटिल गुणांकों में) में एक समाधान है . हालाँकि, यदि समीकरण में परिमेय गुणांक हैं, तो वही सत्य है। ऐसे समीकरणों के मूल बीजगणितीय संख्या कहलाते हैं - वे बीजगणितीय संख्या सिद्धांत में अध्ययन की एक प्रमुख वस्तु हैं। की तुलना में , का बीजगणितीय समापन , जिसमें सभी बीजगणितीय संख्याएँ भी शामिल हैं, ज्यामितीय शर्तों में आसानी से समझने योग्य होने का लाभ है। इस तरह, बीजगणितीय विधियों का उपयोग ज्यामितीय प्रश्नों के अध्ययन के लिए किया जा सकता है और इसके विपरीत। बीजगणितीय विधियों के साथ, अधिक विशेष रूप से क्षेत्र सिद्धांत (गणित) की मशीनरी को एकता की जड़ वाले संख्या क्षेत्र में लागू करते हुए, यह दिखाया जा सकता है कि एक नियमित नॉनगोन कम्पास और सीधा निर्माण - एक विशुद्ध ज्यामितीय समस्या का निर्माण करना संभव नहीं है।
एक अन्य उदाहरण गॉसियन पूर्णांक है; वह है, रूप की संख्या x + iy, कहाँ पे x तथा y पूर्णांक हैं, जिनका उपयोग फ़र्मेट के प्रमेय को दो वर्गों के योग पर वर्गीकृत करने के लिए किया जा सकता है।
विश्लेषणात्मक संख्या सिद्धांत
विश्लेषणात्मक संख्या सिद्धांत अध्ययन संख्या, अक्सर पूर्णांक या परिमेय, इस तथ्य का लाभ उठाते हुए कि उन्हें जटिल संख्या के रूप में माना जा सकता है, जिसमें विश्लेषणात्मक विधियों का उपयोग किया जा सकता है। यह जटिल-मूल्यवान कार्यों में संख्या-सैद्धांतिक जानकारी को एन्कोडिंग द्वारा किया जाता है। उदाहरण के लिए, रीमैन जीटा फ़ंक्शन ζ(s) अभाज्य संख्याओं के वितरण से संबंधित है।
अनुचित इंटीग्रल
लागू क्षेत्रों में, जटिल-मूल्यवान कार्यों के माध्यम से, जटिल संख्याओं का उपयोग अक्सर कुछ वास्तविक-मूल्यवान अनुचित इंटीग्रल की गणना करने के लिए किया जाता है। ऐसा करने के लिए कई तरीके मौजूद हैं; समोच्च एकीकरण के तरीके देखें।
गतिशील समीकरण
अवकल समीकरणों में, पहले सभी सम्मिश्र मूलों को ज्ञात करना सामान्य है r रेखीय अवकल समीकरण#सजातीय समीकरण एक रेखीय अवकल समीकरण या समीकरण प्रणाली के निरंतर गुणांक के साथ और फिर फॉर्म के आधार कार्यों के संदर्भ में प्रणाली को हल करने का प्रयास करते हैं f(t) = ert. इसी तरह, अंतर समीकरणों में, जटिल जड़ें r फार्म के आधार कार्यों के संदर्भ में प्रणाली को हल करने का प्रयास करने के लिए अंतर समीकरण प्रणाली के चारित्रिक समीकरण का उपयोग किया जाता है f(t) = rt.
रेखीय बीजगणित
मैट्रिक्स का Eigedecomposition मैट्रिक्स शक्तियों और मैट्रिक्स घातांकों की गणना के लिए एक उपयोगी उपकरण है। हालाँकि, इसे अक्सर जटिल संख्याओं के उपयोग की आवश्यकता होती है, भले ही मैट्रिक्स वास्तविक हो (उदाहरण के लिए, एक रोटेशन मैट्रिक्स)।
सम्मिश्र संख्याएँ अक्सर उन अवधारणाओं को सामान्यीकृत करती हैं जो मूल रूप से वास्तविक संख्याओं में कल्पना की गई थीं। उदाहरण के लिए, संयुग्म स्थानान्तरण, स्थानांतरण को सामान्य करता है, हर्मिटियन मैट्रिक्स सममित मैट्रिक्स को सामान्य करता है, और एकात्मक मैट्रिक्स ऑर्थोगोनल मैट्रिक्स को सामान्य करता है।
लागू गणित में
नियंत्रण सिद्धांत
नियंत्रण सिद्धांत में, सिस्टम अक्सर लाप्लास रूपांतरण का उपयोग करके समय डोमेन से जटिल आवृत्ति डोमेन में परिवर्तित हो जाते हैं। सिस्टम के शून्य और ध्रुवों का जटिल विमान में विश्लेषण किया जाता है। रूट लोकस, न्यक्विस्ट प्लॉट, और निकोलस प्लॉट तकनीक सभी जटिल विमान का उपयोग करते हैं।
रूट लोकस विधि में, यह महत्वपूर्ण है कि क्या शून्य और ध्रुव बाएँ या दाएँ आधे विमानों में हैं, अर्थात वास्तविक भाग शून्य से अधिक या उससे कम है। यदि एक रेखीय, समय-अपरिवर्तनीय (LTI) प्रणाली में ध्रुव हैं जो हैं
- दाहिने आधे तल में, यह अस्थिर होगा,
- सभी बाएँ आधे तल में, यह BIBO स्थिरता होगी,
- काल्पनिक अक्ष पर, इसमें सीमांत स्थिरता होगी।
यदि सिस्टम के दाहिने आधे विमान में शून्य है, तो यह एक गैर-न्यूनतम चरण प्रणाली है।
सिग्नल विश्लेषण
समय-समय पर अलग-अलग संकेतों के सुविधाजनक विवरण के लिए सिग्नल विश्लेषण और अन्य क्षेत्रों में जटिल संख्याओं का उपयोग किया जाता है। वास्तविक भौतिक मात्राओं का प्रतिनिधित्व करने वाले दिए गए वास्तविक कार्यों के लिए, अक्सर ज्या और कोसाइन के संदर्भ में, संबंधित जटिल कार्यों पर विचार किया जाता है, जिनमें से वास्तविक भाग मूल मात्राएं हैं। किसी दी गई आवृत्ति की साइन लहर के लिए, निरपेक्ष मान |z| तदनुरूपी z आयाम और तर्क है (जटिल विश्लेषण) arg z चरण (तरंगें) है।
यदि फूरियर विश्लेषण को किसी दिए गए वास्तविक-मूल्यवान संकेत को आवधिक कार्यों के योग के रूप में लिखने के लिए नियोजित किया जाता है, तो इन आवधिक कार्यों को अक्सर प्रपत्र के जटिल-मूल्यवान कार्यों के रूप में लिखा जाता है।
यह उपयोग अंकीय संकेत प्रक्रिया और डिजिटल इमेज प्रोसेसिंग में भी विस्तारित है, जो फूरियर विश्लेषण (और तरंगिका विश्लेषण) के डिजिटल संस्करणों का उपयोग संचारित करने, डेटा संपीड़न, पुनर्स्थापित करने और अन्यथा डिजिटल डेटा ध्वनि संकेतों, स्थिर छवियों और वीडियो संकेतों को संसाधित करने के लिए करता है।
एएम रेडियो के आयाम मॉडुलन के दो पार्श्व बैंडों के लिए प्रासंगिक एक और उदाहरण है:
भौतिकी में
विद्युत चुंबकत्व और इलेक्ट्रिकल इंजीनियरिंग
इलेक्ट्रिकल इंजीनियरिंग में, फुरियर रूपांतरण का उपयोग अलग-अलग वोल्टेज और इलेक्ट्रिक करंट का विश्लेषण करने के लिए किया जाता है। बाद के दो के लिए काल्पनिक, आवृत्ति-निर्भर प्रतिरोधों को पेश करके और विद्युत प्रतिबाधा नामक एक जटिल संख्या में तीनों को जोड़कर प्रतिरोधों, संधारित्र और प्रारंभ करनेवाला्स के उपचार को एकीकृत किया जा सकता है। इस दृष्टिकोण को फेजर कैलकुलस कहा जाता है।
इलेक्ट्रिकल इंजीनियरिंग में, काल्पनिक इकाई द्वारा निरूपित किया जाता है j, भ्रम से बचने के लिए I, जो आम तौर पर विद्युत प्रवाह को निरूपित करने के लिए उपयोग किया जाता है, या अधिक विशेष रूप से, i, जो आम तौर पर तात्कालिक विद्युत प्रवाह को दर्शाने के लिए उपयोग में होता है।
चूंकि एक एसी विद्युत परिपथ में वोल्टेज दोलन कर रहा है, इसे इस रूप में दर्शाया जा सकता है
द्रव गतिकी
द्रव गतिकी में, दो आयामों में संभावित प्रवाह का वर्णन करने के लिए जटिल कार्यों का उपयोग किया जाता है।
क्वांटम यांत्रिकी
जटिल संख्या क्षेत्र क्वांटम यांत्रिकी के गणितीय योगों के लिए आंतरिक है, जहां जटिल हिल्बर्ट रिक्त स्थान ऐसे एक सूत्रीकरण के लिए संदर्भ प्रदान करते हैं जो सुविधाजनक और शायद सबसे मानक है। क्वांटम यांत्रिकी के मूल आधार सूत्र - श्रोडिंगर समीकरण और हाइजेनबर्ग के मैट्रिक्स यांत्रिकी - जटिल संख्याओं का उपयोग करते हैं।
सापेक्षता
विशेष सापेक्षता और सामान्य सापेक्षता में, अंतरिक्ष समय पर मीट्रिक के लिए कुछ सूत्र सरल हो जाते हैं यदि कोई स्पेसटाइम सातत्य के समय घटक को काल्पनिक मानता है। (यह दृष्टिकोण शास्त्रीय सापेक्षता में अब मानक नहीं है, लेकिन क्वांटम क्षेत्र सिद्धांत में बाती का घूमना है।) स्पिनरों के लिए जटिल संख्याएं आवश्यक हैं, जो सापेक्षता में उपयोग किए जाने वाले टेन्सरों का एक सामान्यीकरण है।
सामान्यीकरण और संबंधित धारणाएं
क्षेत्र के विस्तार की प्रक्रिया वास्तविक के लिए केली-डिक्सन निर्माण के रूप में जाना जाता है। इसे चतुष्कोणों की उपज, उच्च आयामों तक ले जाया जा सकता है और ऑक्टोनियन जो (वास्तविक सदिश स्थान के रूप में) क्रमशः आयाम 4 और 8 के हैं।
इस संदर्भ में सम्मिश्र संख्याओं को बायनेरियंस कहा गया है।[55] जिस तरह वास्तविक पर निर्माण लागू करने से आदेशित क्षेत्र की संपत्ति खो जाती है, वास्तविक और जटिल संख्याओं से परिचित गुण प्रत्येक विस्तार के साथ गायब हो जाते हैं। चतुष्कोण कम्यूटेटिविटी खो देते हैं, अर्थात, x·y ≠ y·x कुछ चतुष्कोणों के लिए x, y, और अष्टक का गुणन, इसके अतिरिक्त क्रमविनिमेय नहीं होने के कारण, साहचर्य होने में विफल रहता है: (x·y)·z ≠ x·(y·z) कुछ ऑक्टोनियंस के लिए x, y, z.
वास्तविक, सम्मिश्र संख्याएँ, चतुर्धातुक और अष्टक सभी मानक विभाजन बीजगणित हैं . हर्विट्ज़ के प्रमेय (सामान्य विभाजन बीजगणित) द्वारा | हर्विट्ज़ के प्रमेय वे ही हैं; sedenion्स, केली-डिक्सन निर्माण में अगला चरण, इस संरचना को बनाने में विफल रहा।
केली-डिक्सन निर्माण के नियमित प्रतिनिधित्व से निकटता से संबंधित है एक के रूप में सोचा -अलजेब्रा (रिंग थ्योरी) (ए -वेक्टर स्पेस गुणा के साथ), आधार के संबंध में (1, i). इसका मतलब निम्नलिखित है: -रैखिक नक्शा
हाइपरकॉम्प्लेक्स संख्या भी सामान्यीकरण करते हैं तथा उदाहरण के लिए, इस धारणा में विभाजित-जटिल संख्याएँ हैं, जो वलय के तत्व हैं (विरोध के रूप में जटिल संख्या के लिए)। इस वलय में, समीकरण a2 = 1 चार उपाय हैं।
फील्ड का समापन है सामान्य निरपेक्ष मान मीट्रिक (गणित) के संबंध में परिमेय संख्याओं का क्षेत्र। मीट्रिक (गणित) के अन्य विकल्पों पर खेतों की ओर ले जाता है पी-एडिक संख्या का|p-एडिक नंबर (किसी भी अभाज्य संख्या के लिए p), जो इसके अनुरूप हैं . पूरा करने का कोई अन्य गैर-तुच्छ तरीका नहीं है बजाय तथा ओस्ट्रोव्स्की के प्रमेय द्वारा। बीजीय बंद हो जाता है का अभी भी एक मानदंड है, लेकिन (विपरीत ) इसके संबंध में पूर्ण नहीं हैं। पूर्ण का बीजगणितीय रूप से बंद हो जाता है। सादृश्य से, क्षेत्र कहा जाता है p-adic जटिल संख्या।
मैदान और उनके परिमित क्षेत्र विस्तार, सहित स्थानीय क्षेत्र कहलाते हैं।
यह भी देखें
- बीजगणितीय सतह
- वर्तुल गति#जटिल संख्याओं का उपयोग करना
- जटिल-आधार प्रणाली
- जटिल ज्यामिति
- दोहरी जटिल संख्या
- आइज़ेंस्टीन पूर्णांक
- यूलर की पहचान
- ज्यामितीय बीजगणित#यूनिट स्यूडोस्केलर्स (जिसमें 2-आयामी स्पिनर के रूप में जटिल विमान शामिल है#दो आयाम उप-स्थान )
- इकाई जटिल संख्या
टिप्पणियाँ
- ↑ "Complex numbers, as much as reals, and perhaps even more, find a unity with nature that is truly remarkable. It is as though Nature herself is as impressed by the scope and consistency of the complex-number system as we are ourselves, and has entrusted to these numbers the precise operations of her world at its minutest scales." — R. Penrose (2016, p. 73)[2]
- ↑ Solomentsev 2001: "The plane whose points are identified with the elements of is called the complex plane ... The complete geometric interpretation of complex numbers and operations on them appeared first in the work of C. Wessel (1799). The geometric representation of complex numbers, sometimes called the 'Argand diagram', came into use after the publication in 1806 and 1814 of papers by J.R. Argand, who rediscovered, largely independently, the findings of Wessel".
- ↑ In modern notation, Tartaglia's solution is based on expanding the cube of the sum of two cube roots: With , , , u and v can be expressed in terms of p and q as and , respectively. Therefore, . कब नकारात्मक है (कैसस इरेड्यूसिबिलिस), दूसरे घनमूल को पहले वाले के जटिल संयुग्म के रूप में माना जाना चाहिए।
- ↑ It has been proved that imaginary numbers have necessarily to appear in the cubic formula when the equation has three real, different roots by Pierre Laurent Wantzel in 1843, Vincenzo Mollame in 1890, Otto Hölder in 1891 and Adolf Kneser in 1892. Paolo Ruffini also provided an incomplete proof in 1799. — S. Confalonieri (2015)[18]
- ↑ Argand 1814, p. 204 defines the modulus of a complex number but he doesn't name it:
"Dans ce qui suit, les accens, indifféremment placés, seront employés pour indiquer la grandeur absolue des quantités qu'ils affectent; ainsi, si , et étant réels, on devra entendre que ou ."
[In what follows, accent marks, wherever they're placed, will be used to indicate the absolute size of the quantities to which they're assigned; thus if , and being real, one should understand that or .]
Argand 1814, p. 208 defines and names the module and the direction factor of a complex number: "... pourrait être appelé le module de , et représenterait la grandeur absolue de la ligne , tandis que l'autre facteur, dont le module est l'unité, en représenterait la direction."
[... could be called the module of and would represent the absolute size of the line (Note that Argand represented complex numbers as vectors.) whereas the other factor [namely, ], जिसका मॉड्यूल यूनिटी [1] है, इसकी दिशा को दर्शाएगा।] - ↑ Gauss writes:[38]"Quemadmodum scilicet arithmetica sublimior in quaestionibus hactenus pertractatis inter solos numeros integros reales versatur, ita theoremata circa residua biquadratica tunc tantum in summa simplicitate ac genuina venustate resplendent, quando campus arithmeticae ad quantitates imaginarias extenditur, ita ut absque restrictione ipsius obiectum constituant numeri formae a + bi, denotantibus i, pro more quantitatem imaginariam , atque a, b indefinite omnes numeros reales integros inter - et +." [Of course just as the higher arithmetic has been investigated so far in problems only among real integer numbers, so theorems regarding biquadratic residues then shine in greatest simplicity and genuine beauty, when the field of arithmetic is extended to imaginary quantities, so that, without restrictions on it, numbers of the form a + bi — i denoting by convention the imaginary quantity , and the variables a, b [denoting] all real integer numbers between and — constitute an object.]
- ↑ Gauss:[39]"Tales numeros vocabimus numeros integros complexos, ita quidem, ut reales complexis non opponantur, sed tamquam species sub his contineri censeantur." [We will call such numbers [namely, numbers of the form a + bi ] "complex integer numbers", so that real [numbers] are regarded not as the opposite of complex [numbers] but [as] a type [of number that] is, so to speak, contained within them.]
- ↑ Gauss:[40] "Productum numeri complexi per numerum ipsi conjunctum utriusque normam vocamus. Pro norma itaque numeri realis, ipsius quadratum habendum est." [We call a "norm" the product of a complex number [e.g,. a + ib ] with its conjugate [a - ib ]. Therefore the square of a real number should be regarded as its norm.]
- ↑ However for another inverse function of the complex exponential function (and not the above defined principal value), the branch cut could be taken at any other ray thru the origin.
संदर्भ
- ↑ For an extensive account of the history of "imaginary" numbers, from initial skepticism to ultimate acceptance, see Bourbaki, Nicolas (1998). "Foundations of Mathematics § Logic: Set theory". Elements of the History of Mathematics. Springer. pp. 18–24.
- ↑ Penrose, Roger (2016). The Road to Reality: A complete guide to the laws of the universe (reprint ed.). Random House. pp. 72–73. ISBN 978-1-4464-1820-8.
- ↑ Axler, Sheldon (2010). कॉलेज अल्जेबरा. Wiley. p. 262. ISBN 9780470470770.
- ↑ Spiegel, M.R.; Lipschutz, S.; Schiller, J.J.; Spellman, D. (14 April 2009). जटिल चर. Schaum's Outline Series (2nd ed.). McGraw Hill. ISBN 978-0-07-161569-3.
- ↑ Aufmann, Richard N.; Barker, Vernon C.; Nation, Richard D. (2007). "Chapter P". कॉलेज बीजगणित और त्रिकोणमिति (6 ed.). Cengage Learning. p. 66. ISBN 978-0-618-82515-8.
- ↑ Pedoe, Dan (1988). ज्यामिति: एक व्यापक पाठ्यक्रम. Dover. ISBN 978-0-486-65812-4.
- ↑ 7.0 7.1 Weisstein, Eric W. "जटिल संख्या". mathworld.wolfram.com. Retrieved 12 August 2020.
- ↑ Apostol 1981, p. 18.
- ↑ Kasana, H.S. (2005). "Chapter 1". जटिल चर: सिद्धांत और अनुप्रयोग (2nd ed.). PHI Learning Pvt. Ltd. p. 14. ISBN 978-81-203-2641-5.
- ↑ Nilsson, James William; Riedel, Susan A. (2008). "Chapter 9". Electric circuits (8th ed.). Prentice Hall. p. 338. ISBN 978-0-13-198925-2.
- ↑ Kline, Morris. गणितीय विचार का इतिहास, खंड 1. p. 253.
- ↑ Jurij., Kovič. ट्रिस्टन नीधम, विज़ुअल कॉम्प्लेक्स एनालिसिस, ऑक्सफोर्ड यूनिवर्सिटी प्रेस इंक।, न्यूयॉर्क, 1998, 592 स्ट्रानी. OCLC 1080410598.
- ↑ O’Connor and Robertson (2016), “Girolamo Cardano.”
- ↑ Nahin, Paul J. An Imaginary Tale: The Story of √-1. Princeton: Princeton University Press, 1998.
- ↑ Katz, Victor J. (2004). "9.1.4". गणित का इतिहास, संक्षिप्त संस्करण. Addison-Wesley. ISBN 978-0-321-16193-2.
- ↑ Hamilton, Wm. (1844). "चतुष्कोणों के सिद्धांत से जुड़ी काल्पनिक मात्राओं की एक नई प्रजाति पर". Proceedings of the Royal Irish Academy. 2: 424–434.
- ↑ Nahin, Paul J. (2007). एक काल्पनिक कहानी: √-1 की कहानी. Princeton University Press. ISBN 978-0-691-12798-9. Archived from the original on 12 October 2012. Retrieved 20 April 2011.
- ↑ 18.0 18.1 Confalonieri, Sara (2015). The Unattainable Attempt to Avoid the Casus Irreducibilis for Cubic Equations: Gerolamo Cardano's De Regula Aliza. Springer. pp. 15–16 (note 26). ISBN 978-3658092757.
- ↑ Descartes, René (1954) [1637]. ला ज्योमेट्री [[:Template:पाइप]] पहले संस्करण की प्रतिकृति के साथ रेने डेसकार्टेस की ज्यामिति. Dover Publications. ISBN 978-0-486-60068-0. Retrieved 20 April 2011.
{{cite book}}: URL–wikilink conflict (help) - ↑ Euler, Leonard (1748). इनफिनिटिमल्स के विश्लेषण का एक परिचय [Introduction to the Analysis of the Infinite] (in Latina). Vol. 1. Lucerne, Switzerland: Marc Michel Bosquet & Co. p. 104.
- ↑ Wessel, Caspar (1799). "दिशा के विश्लेषणात्मक संकेतन पर, एक प्रयोग, समतल और गोलाकार बहुभुजों के समाधान के लिए स्पष्ट रूप से लागू किया गया" [On the analytic representation of direction, an effort applied in particular to the determination of plane and spherical polygons]. Nye Samling af det Kongelige Danske Videnskabernes Selskabs Skrifter [New Collection of the Writings of the Royal Danish Science Society] (in dansk). 5: 469–518.
- ↑ Wallis, John (1685). बीजगणित का एक ग्रंथ, दोनों ऐतिहासिक और व्यावहारिक ... London, England: printed by John Playford, for Richard Davis. pp. 264–273.
- ↑ Argand (1806). ज्यामितीय निर्माणों में काल्पनिक मात्राओं का प्रतिनिधित्व करने के तरीके पर निबंध [Essay on a way to represent complex quantities by geometric constructions] (in français). Paris, France: Madame Veuve Blanc.
- ↑ Gauss, Carl Friedrich (1799) "Demonstratio nova theorematis omnem functionem algebraicam rationalem integram unius variabilis in factores reales primi vel secundi gradus resolvi posse." [New proof of the theorem that any rational integral algebraic function of a single variable can be resolved into real factors of the first or second degree.] Ph.D. thesis, University of Helmstedt, (Germany). (in Latin)
- ↑ Ewald, William B. (1996). कांट से हिल्बर्ट: गणित की नींव में एक स्रोत पुस्तक. Vol. 1. Oxford University Press. p. 313. ISBN 9780198505358. Retrieved 18 March 2020.
- ↑ Gauss 1831, p. 638.
- ↑ "एड्रियन क्वेंटिन ब्यू (1745-1845): मैकट्यूटर".
- ↑ Buée (1806). "काल्पनिक मात्रा पर मेमोरी" [Memoir on imaginary quantities]. Philosophical Transactions of the Royal Society of London (in français). 96: 23–88. doi:10.1098/rstl.1806.0003. S2CID 110394048.
- ↑ Mourey, C.V. (1861). ऋणात्मक मात्राओं का सच्चा सिद्धांत और कथित रूप से काल्पनिक मात्राएँ [The true theory of negative quantities and of alleged imaginary quantities] (in français). Paris, France: Mallet-Bachelier. 1861 reprint of 1828 original.
- ↑ Warren, John (1828). नकारात्मक मात्राओं के वर्गमूलों के ज्यामितीय प्रतिनिधित्व पर एक ग्रंथ. Cambridge, England: Cambridge University Press.
- ↑ Warren, John (1829). "ऋणात्मक राशियों के वर्गमूलों के ज्यामितीय निरूपण के विरुद्ध उठाई गई आपत्तियों पर विचार". Philosophical Transactions of the Royal Society of London. 119: 241–254. doi:10.1098/rstl.1829.0022. S2CID 186211638.
- ↑ Warren, John (1829). "मात्राओं की शक्तियों के ज्यामितीय प्रतिनिधित्व पर, जिनके सूचकांकों में ऋणात्मक संख्याओं के वर्गमूल शामिल होते हैं". Philosophical Transactions of the Royal Society of London. 119: 339–359. doi:10.1098/rstl.1829.0031. S2CID 125699726.
- ↑ Français, J.F. (1813). "स्थितीय ज्यामिति के नए सिद्धांत, और काल्पनिक प्रतीकों की ज्यामितीय व्याख्या" [New principles of the geometry of position, and geometric interpretation of complex [number] symbols]. Annales des mathématiques pures et appliquées (in français). 4: 61–71.
- ↑ Caparrini, Sandro (2000). "On the Common Origin of Some of the Works on the Geometrical Interpretation of Complex Numbers". In Kim Williams (ed.). दो संस्कृतियाँ. Birkhäuser. p. 139. ISBN 978-3-7643-7186-9.
- ↑ Hardy, G.H.; Wright, E.M. (2000) [1938]. संख्या के सिद्धांत का परिचय. OUP Oxford. p. 189 (fourth edition). ISBN 978-0-19-921986-5.
- ↑ Jeff Miller (21 September 1999). "मापांक". Earliest Known Uses of Some of the Words of Mathematics (M). Archived from the original on 3 October 1999.
{{cite web}}: CS1 maint: unfit URL (link) - ↑ Cauchy, Augustin-Louis (1821). रॉयल पॉलिटेक्निक स्कूल में विश्लेषण पाठ्यक्रम (in français). Vol. 1. Paris, France: L'Imprimerie Royale. p. 183.
- ↑ Gauss 1831, p. 96
- ↑ Gauss 1831, p. 96
- ↑ Gauss 1831, p. 98
- ↑ Hankel, Hermann (1867). जटिल संख्याओं और उनके कार्यों पर व्याख्यान [Lectures About the Complex Numbers and Their Functions] (in Deutsch). Vol. 1. Leipzig, [Germany]: Leopold Voss. p. 71. From p. 71: "Wir werden den Factor (cos φ + i sin φ) haüfig den Richtungscoefficienten nennen." (We will often call the factor (cos φ + i sin φ) the "coefficient of direction".)
- ↑ For the former notation, see Apostol 1981, pp. 15–16
- ↑ Abramowitz, Milton; Stegun, Irene A. (1964). सूत्र, रेखांकन और गणितीय तालिकाओं के साथ गणितीय कार्यों की पुस्तिका. Courier Dover Publications. p. 17. ISBN 978-0-486-61272-0. Archived from the original on 23 April 2016. Retrieved 16 February 2016., Section 3.7.26, p. 17 Archived 10 September 2009 at the Wayback Machine
- ↑ Cooke, Roger (2008). शास्त्रीय बीजगणित: इसकी प्रकृति, उत्पत्ति और उपयोग. John Wiley and Sons. p. 59. ISBN 978-0-470-25952-8. Archived from the original on 24 April 2016. Retrieved 16 February 2016., Extract: page 59 Archived 23 April 2016 at the Wayback Machine
- ↑ Ahlfors 1979, p. 3.
- ↑ 46.0 46.1 Apostol 1981, pp. 15–16.
- ↑ Apostol 1981, p. 25.
- ↑ Marker, David (1996). "Introduction to the Model Theory of Fields". In Marker, D.; Messmer, M.; Pillay, A. (eds.). खेतों का मॉडल सिद्धांत. Lecture Notes in Logic. Vol. 5. Berlin: Springer-Verlag. pp. 1–37. ISBN 978-3-540-60741-0. MR 1477154.
- ↑ Bourbaki 1998, §VIII.4.
- ↑ Corry, Leo (2015). संख्याओं का संक्षिप्त इतिहास. Oxford University Press. pp. 215–16.
- ↑ Lester, J.A. (1994). "त्रिभुज I: आकृतियाँ". Aequationes Mathematicae. 52: 30–54. doi:10.1007/BF01818325. S2CID 121095307.
- ↑ Kalman, Dan (2008a). "मार्डन की प्रमेय का एक प्राथमिक प्रमाण". American Mathematical Monthly. 115 (4): 330–38. doi:10.1080/00029890.2008.11920532. ISSN 0002-9890. S2CID 13222698. Archived from the original on 8 March 2012. Retrieved 1 January 2012.
- ↑ Kalman, Dan (2008b). "गणित में सबसे अद्भुत प्रमेय". Journal of Online Mathematics and Its Applications. Archived from the original on 8 February 2012. Retrieved 1 January 2012.
- ↑ Grant, I.S.; Phillips, W.R. (2008). विद्युत चुंबकत्व (2 ed.). Manchester Physics Series. ISBN 978-0-471-92712-9.
- ↑ McCrimmon, Kevin (2004). जॉर्डन अल्जेब्रस का स्वाद. Universitext. Springer. p. 64. ISBN 0-387-95447-3. MR2014924
उद्धृत कार्य
- Ahlfors, Lars (1979). जटिल विश्लेषण (3rd ed.). McGraw-Hill. ISBN 978-0-07-000657-7.
- Apostol, Tom (1981). गणितीय विश्लेषण. Addison-Wesley.
- Argand (1814). "कल्पनाओं के नए सिद्धांत पर विचार, विश्लेषण के प्रमेय के प्रमाण के लिए एक आवेदन के बाद" [Reflections on the new theory of complex numbers, followed by an application to the proof of a theorem of analysis]. Annales de mathématiques pures et appliquées (in français). 5: 197–209.
- Gauss, C. F. (1831). "द्विघात अवशेषों का सिद्धांत। एक दूसरी टिप्पणी।" [Theory of biquadratic residues. Second memoir.]. Commentationes Societatis Regiae Scientiarum Gottingensis Recentiores (in Latina). 7: 89–148.
- Solomentsev, E.D. (2001) [1994], "Complex number", Encyclopedia of Mathematics, EMS Press
अग्रिम पठन
- Penrose, Roger (2005). The Road to Reality: A complete guide to the laws of the universe. Alfred A. Knopf. ISBN 978-0-679-45443-4.
- Derbyshire, John (2006). Unknown Quantity: A real and imaginary history of algebra. Joseph Henry Press. ISBN 978-0-309-09657-7.
- Needham, Tristan (1997). Visual Complex Analysis. Clarendon Press. ISBN 978-0-19-853447-1.
गणितीय
- Ahlfors, Lars (1979). जटिल विश्लेषण (3rd ed.). McGraw-Hill. ISBN 978-0-07-000657-7.
- Conway, John B. (1986). एक जटिल चर I के कार्य. Springer. ISBN 978-0-387-90328-6.
- Joshi, Kapil D. (1989). असतत गणित की नींव. New York: John Wiley & Sons. ISBN 978-0-470-21152-6.
- Pedoe, Dan (1988). ज्यामिति: एक व्यापक पाठ्यक्रम. Dover. ISBN 978-0-486-65812-4.
- Press, W.H.; Teukolsky, S.A.; Vetterling, W.T.; Flannery, B.P. (2007). "Section 5.5 Complex Arithmetic". संख्यात्मक व्यंजनों: वैज्ञानिक कंप्यूटिंग की कला (3rd ed.). New York: Cambridge University Press. ISBN 978-0-521-88068-8.
- Solomentsev, E.D. (2001) [1994], "Complex number", Encyclopedia of Mathematics, EMS Press
ऐतिहासिक
- Bourbaki, Nicolas (1998). "Foundations of mathematics § logic: set theory". गणित के इतिहास के तत्व. Springer.
- Burton, David M. (1995). गणित का इतिहास (3rd ed.). New York: McGraw-Hill. ISBN 978-0-07-009465-9.
- Katz, Victor J. (2004). गणित का इतिहास, संक्षिप्त संस्करण. Addison-Wesley. ISBN 978-0-321-16193-2.
- Nahin, Paul J. (1998). एक काल्पनिक कहानी: <गणित>\scriptstyle\sqrt{-1}</math> की कहानी. Princeton University Press. ISBN 978-0-691-02795-1. - जटिल संख्याओं के इतिहास और जटिल विश्लेषण की शुरुआत का एक सौम्य परिचय।
- Ebbinghaus, H. D.; Hermes, H.; Hirzebruch, F.; Koecher, M.; Mainzer, K.; Neukirch, J.; Prestel, A.; Remmert, R. (1991). नंबर (hardcover ed.). Springer. ISBN 978-0-387-97497-2. - संख्या की अवधारणा के ऐतिहासिक विकास पर एक उन्नत परिप्रेक्ष्य।
श्रेणी:संरचना बीजगणित
श्रेणी:जटिल संख्याएँ