प्रक्षेपी ज्यामिति: Difference between revisions
No edit summary |
No edit summary |
||
| Line 2: | Line 2: | ||
{{General geometry |branches}} | {{General geometry |branches}} | ||
गणित में, प्रक्षेपी ज्यामिति ज्यामितीय गुणों का अध्ययन है जो प्रक्षेपी परिवर्तनों के संबंध में अपरिवर्तनीय हैं। इसका मतलब यह है कि प्राथमिक [[ यूक्लिडियन ज्यामिति ]] की तुलना में, प्रक्षेपी ज्यामिति की अलग सेटिंग, [[ प्रक्षेपण स्थान ]] और बुनियादी ज्यामितीय अवधारणाओं का एक चयनात्मक सेट है। मूल अंतर्ज्ञान यह है कि किसी दिए गए आयाम के [[ जटिल प्रक्षेप्य स्थान ]] में [[ यूक्लिडियन अंतरिक्ष ]] की तुलना में अधिक अंक हैं, और [[ ज्यामितीय परिवर्तन ]] की अनुमति है जो अतिरिक्त बिंदुओं (कहा जाता है [[ अनंत पर बिंदु ]]) को यूक्लिडियन बिंदुओं में परिवर्तित करते हैं, और इसके विपरीत। | गणित में, '''प्रक्षेपी ज्यामिति''' ज्यामितीय गुणों का अध्ययन है जो प्रक्षेपी परिवर्तनों के संबंध में अपरिवर्तनीय हैं। इसका मतलब यह है कि प्राथमिक [[ यूक्लिडियन ज्यामिति ]] की तुलना में, प्रक्षेपी ज्यामिति की अलग सेटिंग, [[ प्रक्षेपण स्थान ]] और बुनियादी ज्यामितीय अवधारणाओं का एक चयनात्मक सेट है। मूल अंतर्ज्ञान यह है कि किसी दिए गए आयाम के [[ जटिल प्रक्षेप्य स्थान ]] में [[ यूक्लिडियन अंतरिक्ष ]] की तुलना में अधिक अंक हैं, और [[ ज्यामितीय परिवर्तन ]] की अनुमति है जो अतिरिक्त बिंदुओं (कहा जाता है [[ अनंत पर बिंदु ]]) को यूक्लिडियन बिंदुओं में परिवर्तित करते हैं, और इसके विपरीत। | ||
प्रक्षेपी ज्यामिति के लिए अर्थपूर्ण गुणों को परिवर्तन के इस नए विचार द्वारा सम्मानित किया जाता है, जो [[ परिवर्तन मैट्रिक्स ]] और [[ अनुवाद (ज्यामिति) ]] ([[ affine परिवर्तन | इफ़्फ़ानी परिवर्तन]] ) द्वारा व्यक्त किए जा सकने वाले प्रभावों की तुलना में अधिक कट्टरपंथी है। जियोमीटर के लिए पहला मुद्दा यह है कि किस तरह की ज्यामिति एक नई स्थिति के लिए पर्याप्त है। प्रक्षेपी ज्यामिति में [[ कोण ]] को संदर्भित करना संभव नहीं है क्योंकि यह यूक्लिडियन ज्यामिति में है, क्योंकि कोण एक अवधारणा का उदाहरण है जो प्रक्षेपी परिवर्तनों के संबंध में अपरिवर्तनीय नहीं है, जैसा कि परिप्रेक्ष्य ड्राइंग में देखा गया है। प्रक्षेपी ज्यामिति का एक स्रोत वास्तव में परिप्रेक्ष्य का सिद्धांत था। प्रारंभिक ज्यामिति से एक और अंतर यह है कि जिस तरह से [[ समानांतर (ज्यामिति) ]] को अनंत पर एक बिंदु पर मिलने के लिए कहा जा सकता है, अवधारणा को प्रोजेक्टिव ज्यामिति के शब्दों में अनुवादित किया जाता है। फिर से इस धारणा का सहज आधार है, जैसे कि रेलवे ट्रैक एक परिप्रेक्ष्य ड्राइंग में क्षितिज पर मिलते हैं। दो आयामों में प्रक्षेपी ज्यामिति की मूल बातों के लिए प्रक्षेपी तल देखें। | प्रक्षेपी ज्यामिति के लिए अर्थपूर्ण गुणों को परिवर्तन के इस नए विचार द्वारा सम्मानित किया जाता है, जो [[ परिवर्तन मैट्रिक्स ]] और [[ अनुवाद (ज्यामिति) ]] ([[ affine परिवर्तन | इफ़्फ़ानी परिवर्तन]] ) द्वारा व्यक्त किए जा सकने वाले प्रभावों की तुलना में अधिक कट्टरपंथी है। जियोमीटर के लिए पहला मुद्दा यह है कि किस तरह की ज्यामिति एक नई स्थिति के लिए पर्याप्त है। प्रक्षेपी ज्यामिति में [[ कोण ]] को संदर्भित करना संभव नहीं है क्योंकि यह यूक्लिडियन ज्यामिति में है, क्योंकि कोण एक अवधारणा का उदाहरण है जो प्रक्षेपी परिवर्तनों के संबंध में अपरिवर्तनीय नहीं है, जैसा कि परिप्रेक्ष्य ड्राइंग में देखा गया है। प्रक्षेपी ज्यामिति का एक स्रोत वास्तव में परिप्रेक्ष्य का सिद्धांत था। प्रारंभिक ज्यामिति से एक और अंतर यह है कि जिस तरह से [[ समानांतर (ज्यामिति) ]] को अनंत पर एक बिंदु पर मिलने के लिए कहा जा सकता है, अवधारणा को प्रोजेक्टिव ज्यामिति के शब्दों में अनुवादित किया जाता है। फिर से इस धारणा का सहज आधार है, जैसे कि रेलवे ट्रैक एक परिप्रेक्ष्य ड्राइंग में क्षितिज पर मिलते हैं। दो आयामों में प्रक्षेपी ज्यामिति की मूल बातों के लिए प्रक्षेपी तल देखें। | ||
Latest revision as of 12:24, 2 November 2023
| ज्यामिति |
|---|
 |
| जियोमेटर्स |
गणित में, प्रक्षेपी ज्यामिति ज्यामितीय गुणों का अध्ययन है जो प्रक्षेपी परिवर्तनों के संबंध में अपरिवर्तनीय हैं। इसका मतलब यह है कि प्राथमिक यूक्लिडियन ज्यामिति की तुलना में, प्रक्षेपी ज्यामिति की अलग सेटिंग, प्रक्षेपण स्थान और बुनियादी ज्यामितीय अवधारणाओं का एक चयनात्मक सेट है। मूल अंतर्ज्ञान यह है कि किसी दिए गए आयाम के जटिल प्रक्षेप्य स्थान में यूक्लिडियन अंतरिक्ष की तुलना में अधिक अंक हैं, और ज्यामितीय परिवर्तन की अनुमति है जो अतिरिक्त बिंदुओं (कहा जाता है अनंत पर बिंदु ) को यूक्लिडियन बिंदुओं में परिवर्तित करते हैं, और इसके विपरीत।
प्रक्षेपी ज्यामिति के लिए अर्थपूर्ण गुणों को परिवर्तन के इस नए विचार द्वारा सम्मानित किया जाता है, जो परिवर्तन मैट्रिक्स और अनुवाद (ज्यामिति) ( इफ़्फ़ानी परिवर्तन ) द्वारा व्यक्त किए जा सकने वाले प्रभावों की तुलना में अधिक कट्टरपंथी है। जियोमीटर के लिए पहला मुद्दा यह है कि किस तरह की ज्यामिति एक नई स्थिति के लिए पर्याप्त है। प्रक्षेपी ज्यामिति में कोण को संदर्भित करना संभव नहीं है क्योंकि यह यूक्लिडियन ज्यामिति में है, क्योंकि कोण एक अवधारणा का उदाहरण है जो प्रक्षेपी परिवर्तनों के संबंध में अपरिवर्तनीय नहीं है, जैसा कि परिप्रेक्ष्य ड्राइंग में देखा गया है। प्रक्षेपी ज्यामिति का एक स्रोत वास्तव में परिप्रेक्ष्य का सिद्धांत था। प्रारंभिक ज्यामिति से एक और अंतर यह है कि जिस तरह से समानांतर (ज्यामिति) को अनंत पर एक बिंदु पर मिलने के लिए कहा जा सकता है, अवधारणा को प्रोजेक्टिव ज्यामिति के शब्दों में अनुवादित किया जाता है। फिर से इस धारणा का सहज आधार है, जैसे कि रेलवे ट्रैक एक परिप्रेक्ष्य ड्राइंग में क्षितिज पर मिलते हैं। दो आयामों में प्रक्षेपी ज्यामिति की मूल बातों के लिए प्रक्षेपी तल देखें।
जबकि विचार पहले उपलब्ध थे, प्रक्षेपी ज्यामिति मुख्य रूप से 19वीं शताब्दी का विकास था। इसमें जटिल प्रक्षेपी विमान का सिद्धांत सम्मिलित था, किए गए निर्देशांक (सजातीय निर्देशांक ) जटिल संख्याएं हैं। कई प्रमुख प्रकार के अधिक अमूर्त गणित (अपरिवर्तनीय सिद्धांत , बीजगणितीय ज्यामिति के इतालवी स्कूल , और फेलिक्स क्लेन के एरलांगन कार्यक्रम के परिणामस्वरूप मौलिक समूह के अध्ययन में सम्मिलित हैं) प्रोजेक्टिव ज्यामिति से प्रेरित थे। सिंथेटिक ज्यामिति के रूप में, यह कई चिकित्सकों के लिए एक विषय भी था। प्रक्षेपी ज्यामिति के स्वयंसिद्ध अध्ययनों से विकसित एक अन्य विषय परिमित ज्यामिति है।
प्रक्षेपी ज्यामिति का विषय ही अब कई अनुसंधान उप-विषयों में विभाजित है , जिनमें से दो उदाहरण प्रक्षेपी बीजगणितीय ज्यामिति (बीजगणितीय किस्म, प्रक्षेपी किस्मों का अध्ययन) और प्रक्षेपी अंतर ज्यामिति (प्रक्षेपी परिवर्तनों के अंतर ज्यामिति का अध्ययन) हैं।
सिंहावलोकन
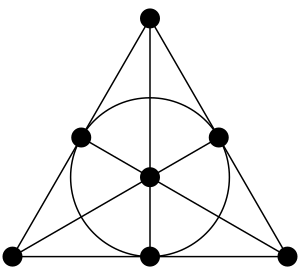
प्रोजेक्टिव ज्यामिति ज्यामिति का एक प्रारंभिक गैर-मीट्रिक (गणित) रूप है, जिसका अर्थ है कि यह दूरी की अवधारणा पर आधारित नहीं है। दो आयामों में यह बिंदु (ज्यामिति) और रेखा (ज्यामिति) के विन्यास (ज्यामिति) के अध्ययन से शुरू होता है। इस विरल सेटिंग में वास्तव में कुछ ज्यामितीय रुचि है, यह पहली बार जेरार्ड डेसार्गेस और अन्य लोगों द्वारा परिप्रेक्ष्य के सिद्धांतों (ग्राफिकल) की खोज में स्थापित किया गया था। [1] उच्च आयाम स्थानों में हाइपरप्लेन (जो हमेशा मिलते हैं), और अन्य रैखिक उप-स्थान माने जाते हैं, जो #द्वैतता प्रदर्शित करते हैं। द्वैत का सबसे सरल उदाहरण प्रोजेक्टिव प्लेन में है, जहां दो अलग-अलग बिंदु एक अनूठी रेखा (अर्थात उनके बीच की रेखा) का निर्धारण करते हैं और दो अलग - अलग रेखाएं एक अद्वितीय बिंदु (अर्थात उनके चौराहे का बिंदु) को निर्धारित करती हैं, वही संरचना को प्रस्ताव के रूप में दर्शाती हैं। प्रोजेक्टिव ज्योमेट्री को सीधे बढ़त | स्ट्रेट-एज अकेले के साथ निर्माण की ज्यामिति के रूप में भी देखा जा सकता है। [2] चूंकि प्रक्षेपी ज्यामिति कम्पास (ड्राफ्टिंग) निर्माणों को बाहर करती है, इसलिए कोई वृत्त नहीं हैं , कोई कोण नहीं है , कोई माप नहीं है , कोई समानता नहीं है , और विक्ट की कोई अवधारणा नहीं है: मध्यस्थ। [3] यह महसूस किया गया कि प्रक्षेपी ज्यामिति पर लागू होने वाले प्रमेय सरल कथन हैं। उदाहरण के लिए, विभिन्न शंकु खंड सभी (जटिल) प्रक्षेपी ज्यामिति में समतुल्य हैं, और मंडलियों के बारे में कुछ प्रमेयों को इन सामान्य प्रमेयों के विशेष स्थितियों के रूप में माना जा सकता है।
19वीं शताब्दी की शुरुआत के दौरान जीन-विक्टर पोंसेलेट , लाज़ारे कार्नोट और अन्य के काम ने गणित के एक स्वतंत्र क्षेत्र के रूप में प्रक्षेपी ज्यामिति की स्थापना की।
[3] इसकी कठोर नींव को कार्ल वॉन स्टॉड्ट द्वारा संबोधित किया गया था और 19 वीं शताब्दी के अंत में इटालियंस जोसेफ पीनो , मारियो पियरी , एलेसेंड्रो पडोआ और गीनो फानो द्वारा सिद्ध किया गया था। [4] एफाइन ज्यामिति और यूक्लिडियन ज्यामिति की तरह प्रोजेक्टिव ज्यामिति को भी फेलिक्स क्लेन के एर्लांगेन कार्यक्रम से विकसित किया जा सकता है; प्रक्षेपी ज्यामिति प्रक्षेपी समूह के परिवर्तन (ज्यामिति) के प्रारंभिक अपरिवर्तनीय (गणित) द्वारा विशेषता है।
इस विषय में बहुत बड़ी संख्या में प्रमेयों पर बहुत काम करने के बाद, प्रक्षेपी ज्यामिति की मूल बातें समझ में आ गईं। घटना संरचना और क्रॉस-अनुपात प्रक्षेपी परिवर्तनों के प्रारंभिक मौलिक अपरिवर्तनीय हैं। प्रोजेक्टिव ज्योमेट्री को इफ़्फ़ानी ज्यामिति (या एफ़िन स्पेस) प्लस एक लाइन (हाइपरप्लेन) द्वारा अनंत पर बनाया जा सकता है और फिर उस लाइन (या हाइपरप्लेन) को साधारण माना जा सकता है। [5] विश्लेषणात्मक ज्यामिति की शैली में प्रक्षेपी ज्यामिति करने के लिए एक बीजगणितीय मॉडल सजातीय निर्देशांक द्वारा दिया जाता है। [6] [7] दूसरी ओर, स्वयंसिद्ध अध्ययनों ने गैर-डिसर्गेसियन विमानों के अस्तित्व का खुलासा किया, यह दिखाने के लिए उदाहरण हैं कि घटना के सिद्धांतों को सजातीय समन्वय प्रणालियों के माध्यम से तर्क के लिए सुलभ संरचनाओं द्वारा (केवल दो आयामों में) प्रतिरूपित किया जा सकता है।
एक मूलभूत अर्थ में, प्रक्षेपी ज्यामिति और आदेशित ज्यामिति प्राथमिक हैं क्योंकि उनमें कम से कम स्वयंसिद्ध सम्मिलित हैं और या तो एफ़िन ज्यामिति और यूक्लिडियन ज्यामिति के लिए नींव के रूप में उपयोग किया जा सकता है। [8] [9] प्रोजेक्टिव ज्यामिति का आदेश नहीं दिया गया है [3] और इसलिए यह ज्यामिति के लिए एक विशिष्ट आधार है।गणित और कला
इतिहास
प्रक्षेपी प्रकृति के पहले ज्यामितीय गुणों की खोज तीसरी शताब्दी के दौरान अलेक्जेंड्रिया के पप्पस ने की थी। [3] फ़िलिपो ब्रुनेलेस्ची (1404 -1472) ने 1425 के दौरान परिप्रेक्ष्य की ज्यामिति की जांच शुरू की [10] (परिप्रेक्ष्य (ग्राफ़िकल) # इतिहास देखें ललित कलाओं में काम की अधिक गहन चर्चा के लिए जिसने प्रक्षेपी ज्यामिति के विकास को बहुत प्रेरित किया)। जोहान्स केप्लर (1571-1630) और जेरार्ड डेसार्गेस (1591-1661) ने स्वतंत्र रूप से अनंत पर बिंदु की अवधारणा विकसित की। [11] डिसारगस ने गायब होने वाले बिंदुओं के उपयोग को सामान्यीकृत करके परिप्रेक्ष्य चित्रों के निर्माण का एक वैकल्पिक तरीका विकसित किया है, जब ये असीम रूप से दूर हैं। उन्होंने यूक्लिडियन ज्यामिति को बनाया, जहाँ समानांतर रेखाएँ वास्तव में समानांतर होती हैं, एक सर्वव्यापी ज्यामितीय प्रणाली के एक विशेष स्थितियों में। शंकु वर्गों पर डिसारगस के अध्ययन ने 16 वर्षीय ब्लेस पास्कल का ध्यान आकर्षित किया और उसे पास्कल के प्रमेय को तैयार करने में मदद की। 18वीं के अंत और 19वीं सदी की शुरुआत में गैसपार्ड मोंगे के कार्य प्रक्षेपी ज्यामिति के बाद के विकास के लिए महत्वपूर्ण थे। 1845 के दौरान माइकल चेसल्स को एक हस्तलिखित प्रति मिलने तक डेसार्गेस के काम को नजरअंदाज कर दिया गया था। इस बीच , जीन-विक्टर पोंसलेट ने 1822 के दौरान प्रोजेक्टिव ज्योमेट्री पर मूलभूत ग्रंथ प्रकाशित किया था। पोंसलेट ने वस्तुओं के प्रोजेक्टिव गुणों (केंद्रीय प्रक्षेपण के प्रारंभिक अपरिवर्तनीय) की जांच की और, ठोस ध्रुव और एक वृत्त के संबंध में ध्रुवीय संबंध पर अपने सिद्धांत को आधार बनाकर मीट्रिक और प्रक्षेपी गुणों के बीच संबंध स्थापित किया। इसके तुरंत बाद खोजे गए गैर-यूक्लिडियन ज्यामिति | गैर-यूक्लिडियन ज्यामिति को अंततः प्रोजेक्टिव ज्यामिति से संबंधित अतिशयोक्तिपूर्ण स्थान के छोटा मॉडल जैसे मॉडल के रूप में प्रदर्शित किया गया।
1855 में ए.एफ. मोबियस ने जटिल विमान में सामान्यीकृत हलकों के क्रमपरिवर्तन के बारे में एक लेख लिखा, जिसे अब मोबियस ट्रांसफॉर्मेशन कहा जाता है। ये परिवर्तन जटिल प्रोजेक्टिव लाइन की प्रोजेक्टिविटी की प्रतिनिधित्व करते हैं। अंतरिक्ष में रेखाओं के अध्ययन में , जूलियस प्लकर ने अपने विवरण में सजातीय निर्देशांक का उपयोग किया, और लाइनों के सेट को क्लेन क्वाड्रिक पर देखा गया, बीजगणितीय ज्यामिति नामक एक नए क्षेत्र में प्रक्षेपी ज्यामिति के प्रारंभिक योगदानों में से एक, विश्लेषणात्मक ज्यामिति का एक शाखा अनुमानित विचारों के साथ।
हाइपरबोलिक विमान के लिए समन्वय प्रणालियों के लिए मॉडल (तर्क) प्रदान करके हाइपरबोलिक ज्यामिति के संबंध में लोबाचेव्स्की और बोल्याई की अटकलों के सत्यापन में प्रोजेक्टिव ज्यामिति सहायक थी: [12] उदाहरण के लिए, पॉइंकेयर डिस्क मॉडल जहां यूनिट सर्कल के लम्बवत सामान्यीकृत सर्कल हाइपरबॉलिक लाइनों ( गौंडा-सेचना ) के अनुरूप होते हैं, और इस मॉडल के अनुवादों को मोबियस ट्रांसफॉर्मेशन द्वारा वर्णित किया जाता है जो यूनिट डिस्क को खुद से मैप करता है। बिंदुओं के बीच की दूरी एक केली-क्लेन मीट्रिक द्वारा दी गई है, जिसे अनुवाद के प्रारंभिक अपरिवर्तनीय माना जाता है क्योंकि यह क्रॉस-अनुपात पर निर्भर करता है, जो एक प्रमुख प्रक्षेप्य अपरिवर्तनीय है। अनुवाद को मीट्रिक अंतरिक्ष सिद्धांत में सममितीय के रूप में विभिन्न रूप से वर्णित किया गया है, औपचारिक रूप से रैखिक भिन्नात्मक परिवर्तन के रूप में , और प्रक्षेपी रैखिक समूह के प्रक्षेपी रैखिक परिवर्तन के रूप में, इस स्थितियों में एस यू (1, 1)।
जीन-विक्टर पोंसेलेट, जैकब स्टेनर और अन्य का काम विश्लेषणात्मक ज्यामिति का विस्तार करने का इरादा नहीं था। तकनीकों को सिंथेटिक ज्यामिति माना जाता था: प्रभाव में प्रोजेक्टिव स्पेस जैसा कि अब समझा जाता है,स्वयंसिद्ध रूप से पेश किया जाना था। परिणाम स्वरुप, प्रोजेक्टिव ज्यामिति में प्रारंभिक काम को सुधारना जिससे यह कठोरता के जटिल मानकों को पूरा कर सके, कुछ हद तक हो सकता है। केवल प्रक्षेपी तल के स्थितियों में भी, स्वयंसिद्ध दृष्टिकोण का परिणाम मॉडल सिद्धांत में हो सकता है जो रैखिक बीजगणित के माध्यम से वर्णित नहीं किया जा सकता है।
ज्यामिति में इस अवधि को क्लीबस्च , बर्नहार्ड रीमैन , मैक्स नोथेर और अन्य द्वारा सामान्य बीजगणितीय वक्र पर शोध से आगे निकल गया, जिसने प्रारंभिक तकनीकों को बढ़ाया, और फिर अपरिवर्तनीय सिद्धांत द्वारा। सदी के अंत में, बीजगणितीय ज्यामिति के इतालवी स्कूल (फेडेरिको एनरिक्स , कॉनराड सेग्रे , फ्रांसिस सेवेरी ) ने पारंपरिक विषय वस्तु से गहन तकनीकों की मांग वाले क्षेत्र में तोड़ दिया।
19वीं शताब्दी के उत्तरार्ध के दौरान, प्रक्षेपी ज्यामिति का विस्तृत अध्ययन कम फैशनेबल हो गया, चूंकि साहित्य बड़ा है। शुबर्ट द्वारा विशेष रूप से गणनात्मक ज्यामिति में कुछ महत्वपूर्ण कार्य किया गया था, जिसे अब चेर्न वर्ग के सिद्धांत का अनुमान लगाने के रूप में माना जाता है, जिसे ग्रासमानियन के बीजगणितीय टोपोलॉजी का प्रतिनिधित्व करने के रूप में लिया जाता है।
प्रोजेक्टिव ज्यामिति बाद में क्वांटम यांत्रिकी के पॉल डिराक के आविष्कार के लिए महत्वपूर्ण सिद्ध हुई। एक मूलभूत स्तर पर, यह खोज कि क्वांटम उपायों को करने में विफल हो सकता है, ने वर्नर हाइजेनबर्ग को परेशान और निराश किया था, लेकिन गैर-संभावित रिंगों पर प्रक्षेपी विमानों के पिछले अध्ययन ने संभवतः डिराक को निराश कर दिया था। अधिक उन्नत कार्य में, विशेष रूप से बीजगणितीय औपचारिकता में अपने काम को लिखने से पहले, डिराक ने अपने समीकरणों के सहज अर्थ को समझने के लिए प्रक्षेपी ज्यामिति में व्यापक रेखाचित्रों का उपयोग किया। [13]
विवरण
यूक्लिडियन ज्यामिति या एफ़िन ज्यामिति की तुलना में प्रोजेक्टिव ज्यामिति कम प्रतिबंधात्मक है। यह आंतरिक रूप से गैर-मीट्रिक (गणित) ज्यामिति है, जिसका अर्थ है कि तथ्य किसी भी मीट्रिक संरचना से स्वतंत्र हैं। प्रक्षेपी परिवर्तनों के प्रारंभिक, घटना संरचना और प्रक्षेपी हार्मोनिक संयुग्म के संबंध संरक्षित हैं। एक प्रक्षेप्य सीमा एक आयामी नींव है। प्रोजेक्टिव ज्यामिति परिप्रेक्ष्य कला के केंद्रीय सिद्धांतों में से एक को औपचारिक रूप देती है: समानांतर (ज्यामिति) रेखाएं अनंत पर मिलती हैं, और इसलिए इस तरह खींची जाती हैं। संक्षेप में, एक प्रक्षेपी ज्यामिति को यूक्लिडियन ज्यामिति के विस्तार के रूप में माना जा सकता है जिसमें प्रत्येक रेखा की दिशा को एक अतिरिक्त बिंदु के रूप में रेखा के भीतर समाहित किया जाता है, और जिसमें समतलीय रेखाओं से संबंधित दिशाओं के क्षितिज को एक रेखा के रूप में माना जाता है। इस प्रकार, दो समानांतर रेखाएँ एक ही दिशा को समाविष्ट करने के कारण क्षितिज रेखा पर मिलती हैं।
आदर्शीकृत दिशाओं को अनंत बिंदुओं के रूप में संदर्भित किया जाता है, जबकि आदर्शित क्षितिजों को अनंत पर रेखाओं के रूप में संदर्भित किया जाता है। बदले में, ये सभी रेखाएँ अनंत पर समतल में स्थित होती हैं। यद्यपि, अनंत एक मीट्रिक अवधारणा है, इसलिए विशुद्ध रूप से प्रक्षेपी ज्यामिति इस संबंध में किसी भी बिंदु, रेखाओं या विमानों को अलग नहीं करती है - अनंत पर किसी भी अन्य की तरह ही व्यवहार किया जाता है।
क्योंकि एक यूक्लिडियन ज्यामिति एक प्रक्षेपी ज्यामिति के भीतर समाहित है - प्रक्षेपी ज्यामिति के साथ एक सरल नींव है - यूक्लिडियन ज्यामिति में सामान्य परिणाम अधिक पारदर्शी तरीके से प्राप्त किए जा सकते हैं, जहां यूक्लिडियन ज्यामिति के अलग-अलग लेकिन समान प्रमेयों को सामूहिक रूप से प्रक्षेपी के ढांचे के भीतर संभाला जा सकता है। ज्यामिति। उदाहरण के लिए, समानांतर और गैर-समानांतर रेखाओं को अलग-अलग स्थितियों के रूप में नहीं माना जाना चाहिए; बल्कि एक मन के अनुकूल सही से प्रक्षेपी विमान को आदर्श विमान के रूप में चुना जाता है और सजातीय निर्देशांक का उपयोग करके अनंत पर स्थित होता है।
मौलिक महत्व के अतिरिक्त गुणों में सम्मिलित हैं डिसारगस 'प्रमेय और पप्पस के षट्भुज प्रमेय। आयाम 3 या उससे अधिक के प्रोजेक्टिव रिक्त स्थान में एक निर्माण होता है जो किसी को डिसारगस 'प्रमेय सिद्ध करने की अनुमति देता है। लेकिन आयाम 2 के लिए, इसे अलग से पोस्ट किया जाना चाहिए।
डिसारगस' प्रमेय का उपयोग, अन्य स्वयंसिद्धों के साथ मिलकर, अंकगणित के बुनियादी संचालन को ज्यामितीय रूप से परिभाषित करना संभव है। परिणामी संक्रियाएँ एक क्षेत्र के स्वयंसिद्धों को संतुष्ट करती हैं - सिवाय इसके कि गुणन की क्रमविनिमेयता के लिए पप्पस के षट्भुज प्रमेय की आवश्यकता होती है। परिणाम स्वरुप, प्रत्येक पंक्ति के अंक एक दिए गए क्षेत्र के साथ एक-से-एक पत्राचार में हैं, F, एक अतिरिक्त तत्व द्वारा पूरक, ∞, जैसे कि r ⋅ ∞ = ∞, −∞ = ∞, r + ∞ = ∞, r / 0 = ∞, r / ∞ = 0, ∞ − r = r − ∞ = ∞, सिवाय इसके कि 0 / 0, ∞ / ∞, ∞ + ∞, ∞ − ∞, 0 ⋅ ∞ और ∞ ⋅ 0 अपरिभाषित रहना।
प्रक्षेपी ज्यामिति में शंकु वर्गों का एक पूर्ण सिद्धांत भी सम्मिलित है, एक विषय भी व्यापक रूप से यूक्लिडियन ज्यामिति में विकसित हुआ है। एक अतिपरवलय और एक दीर्घवृत्त के बारे में सोचने में सक्षम होने के फायदे हैं, जिस तरह से अतिपरवलय अनंत पर रेखा के पार स्थित है; और यह कि एक परवलय को केवल एक ही रेखा पर स्पर्शरेखा होने से पहचाना जाता है। मंडलियों के पूरे परिवार को अनंत पर रेखा पर दो दिए गए बिंदुओं से गुजरने वाले शंकुओं के रूप में माना जा सकता है - जटिल संख्या निर्देशांक की आवश्यकता की कीमत पर। चूँकि निर्देशांक संश्लिष्ट नहीं होते हैं, एक रेखा और उस पर दो बिंदुओं को फिक्स करके और उन बिंदुओं से गुजरने वाले सभी शांकवों की रैखिक प्रणाली को अध्ययन की मूल वस्तु के रूप में देखते हुए उन्हें प्रतिस्थापित किया जाता है। यह विधि प्रतिभावान ज्यामितिविदों के लिए बहुत आकर्षक सिद्ध हुई और इस विषय का गहन अध्ययन किया गया। इस पद्धति का एक उदाहरण एच एफ बेकर द्वारा बहु-मात्रा ग्रंथ है।
कई प्रक्षेपी ज्यामिति हैं, जिन्हें असतत और निरंतर में विभाजित किया जा सकता है: एक असतत ज्यामिति में बिंदुओं का एक समूह होता है, जो संख्या में परिमित हो सकता है या नहीं भी हो सकता है, जबकि एक निरंतर ज्यामिति में असीम रूप से कई बिंदु होते हैं जिनके बीच में कोई अंतराल नहीं होता है।
आयाम 0 का एकमात्र प्रक्षेपी ज्यामिति एक बिंदु है। आयाम 1 की प्रक्षेपी ज्यामिति में कम से कम 3 बिंदुओं वाली एक रेखा होती है। इनमें से किसी भी स्थिति में अंकगणितीय संक्रियाओं का ज्यामितीय निर्माण नहीं किया जा सकता है। आयाम 2 के लिए, डिसारगस' प्रमेय की अनुपस्थिति के आधार पर एक समृद्ध संरचना है।
सबसे छोटा 2-आयामी प्रक्षेपी ज्यामिति (जो कि सबसे कम बिंदुओं के साथ है) फ़ानो विमान है, जिसमें प्रत्येक पंक्ति पर 3 बिंदु हैं, जिसमें 7 अंक और 7 रेखाएँ हैं, जिनमें निम्नलिखित समरूपताएँ हैं:
- [ABC]
- [ADE]
- [AFG]
- [BDG]
- [BEF]
- [CDF]
- [CEG]
सजातीय निर्देशांक के साथ A = (0,0,1), B = (0,1,1), C = (0,1,0), D = (1,0,1), E = (1,0,0), F = (1,1,1), G = (1,1,0), या, एफ़िन निर्देशांक में, A = (0,0), B = (0,1), C = (∞), D = (1,0), E = (0), F = (1,1)और G = (1). एफ़िन एक डिसारगसian समतल में उन बिंदुओं के लिए निर्देशांक करता है जिन्हें अनंत पर बिंदुओं के रूप में नामित किया गया है (इस उदाहरण में: C, E और G) को कई अन्य तरीकों से परिभाषित किया जा सकता है।
मानक संकेतन में, एक परिमित प्रक्षेपी ज्यामिति लिखी जाती है PG(a, b) कहां:
- a प्रक्षेपी (या ज्यामितीय) आयाम है, और
- b एक रेखा पर बिंदुओं की संख्या से एक कम होता है (जिसे ज्यामिति का क्रम कहा जाता है)।
इस प्रकार, केवल 7 बिंदुओं वाला उदाहरण लिखा गया है PG(2, 2).
प्रक्षेपी ज्यामिति शब्द का प्रयोग कभी-कभी सामान्यीकृत अंतर्निहित अमूर्त ज्यामिति को इंगित करने के लिए किया जाता है, और कभी-कभी व्यापक रुचि के एक विशेष ज्यामिति को इंगित करने के लिए किया जाता है, जैसे कि समतल स्थान की मीट्रिक ज्यामिति जिसे हम सजातीय निर्देशांक के उपयोग के माध्यम से विश्लेषण करते हैं, और जिसमें यूक्लिडियन ज्यामिति हो सकती है एम्बेडेड होना चाहिए (इसलिए इसका नाम, प्रोजेक्टिव प्लेन कुछ उदाहरण)।
मौलिक संपत्ति जो सभी प्रोजेक्टिव ज्यामिति को अलग करती है वह अंडाकार घटना (गणित) संपत्ति है जो किसी भी दो अलग-अलग रेखाएं होती है L और M प्रक्षेपी तल में बिल्कुल एक बिंदु पर प्रतिच्छेद करता है P. समानांतर रेखाओं की विश्लेषणात्मक ज्यामिति में विशेष मामला अनंत पर एक रेखा के चिकने रूप में समाहित है, जिस पर P झूठ। अनंत पर रेखा इस प्रकार सिद्धांत में किसी भी अन्य रेखा की तरह है: यह किसी भी तरह से विशेष या विशिष्ट नहीं है। (एर्लांगेन कार्यक्रम की बाद की भावना में कोई इस बात की ओर इशारा कर सकता है कि परिवर्तनों का समूह (गणित) किसी भी रेखा को अनंत तक ले जा सकता है)।
अण्डाकार, यूक्लिडियन और अतिपरवलयिक ज्यामिति के समानांतर गुण निम्नानुसार हैं:
- एक पंक्ति दी l और एक बिंदु P लाइन पर नहीं,
- अण्डाकार ज्यामिति
- इसके माध्यम से कोई रेखा उपस्थित नहीं है P जो नहीं मिलता है l
- यूक्लिडियन ज्यामिति
- इसके माध्यम से ठीक एक रेखा उपस्थित है P जो नहीं मिलता है l
- अतिपरवलयिक ज्यामिति
- इसके माध्यम से एक से अधिक रेखाएँ उपस्थित हैं P जो नहीं मिलता है l
अण्डाकार ज्यामिति की समानांतर संपत्ति प्रमुख विचार है जो प्रक्षेपी द्वैत के सिद्धांत की ओर ले जाती है, संभवतः सबसे महत्वपूर्ण संपत्ति है जो सभी प्रक्षेपी ज्यामितीय समान हैं।
द्वैत
1825 में, जोसेफ गेरगोन ने प्रक्षेपी समतल ज्यामिति की विशेषता वाले द्वैत (प्रोजेक्टिव ज्यामिति) के सिद्धांत को नोट किया: उस ज्यामिति की किसी भी प्रमेय या परिभाषा को देखते हुए, लाइन के लिए बिंदु को प्रतिस्थापित करना, पास के माध्यम से लेटना, समवर्ती के लिए समरेख, जुड़ने के लिए चौराहा, या इसके विपरीत। प्रारंभिक, किसी अन्य प्रमेय या मान्य परिभाषा में परिणत होता है, पहले का द्वैत। इसी तरह 3 आयामों में, द्वैत संबंध बिंदुओं और विमानों के बीच होता है, जिससे किसी भी प्रमेय को अदला-बदली बिंदु और विमान द्वारा रूपांतरित किया जा सकता है, इसमें समाहित होता है और समाहित होता है। अधिक सामान्यतः, आयाम एन के प्रोजेक्टिव रिक्त स्थान के लिए, आयाम आर और आयाम एन-आर-1 के उप-स्थानों के बीच एक द्वंद्व है। एन = 2 के लिए, यह द्वैत के सबसे सामान्य रूप से ज्ञात रूप में माहिर है - जो कि बिंदुओं और रेखाओं के बीच है।
द्वैत सिद्धांत की खोज स्वतंत्र रूप से जीन-विक्टर पोंसेलेट ने की थी।
द्वैत को स्थापित करने के लिए केवल प्रमेयों को स्थापित करने की आवश्यकता होती है जो प्रश्न में आयाम के स्वयंसिद्धों के दोहरे संस्करण हैं। इस प्रकार, 3-आयामी रिक्त स्थान के लिए, यह दिखाने की आवश्यकता है कि (1*) प्रत्येक बिंदु 3 अलग-अलग विमानों में स्थित है, (2*) प्रत्येक दो विमान एक अद्वितीय रेखा में प्रतिच्छेद करते हैं और प्रभाव के लिए (3*) का दोहरा संस्करण: यदि समतल P और Q का प्रतिच्छेदन तल R और S के प्रतिच्छेदन के साथ समतलीय है, तो समतल P और R, Q और S के संबंधित प्रतिच्छेदन भी समान हैं (विमानों P और S को Q और R से भिन्न मानते हुए)।
व्यवहार में, द्वैत का सिद्धांत हमें दो ज्यामितीय निर्माणों के बीच एक द्वैत पत्राचार स्थापित करने की अनुमति देता है। इनमें से सबसे प्रसिद्ध एक शंक्वाकार वक्र (2 आयामों में) या एक चतुष्कोणीय सतह (3 आयामों में) में दो आकृतियों की ध्रुवीयता या पारस्परिकता है। दोहरे बहुतल प्राप्त करने के लिए एक संकेंद्रित क्षेत्र में एक सममित पॉलीहेड्रॉन के पारस्परिककरण में एक सामान्य उदाहरण पाया जाता है।
एक अन्य उदाहरण ब्रायनचोन की प्रमेय है, पहले से उल्लिखित पास्कल की प्रमेय की दोहरी, और जिसका एक प्रमाण केवल पास्कल के द्वैत के सिद्धांत को लागू करना है। यहाँ इन दो प्रमेयों के तुलनात्मक कथन हैं (दोनों ही स्थितियों में प्रक्षेपी तल के ढांचे के भीतर):
- 'पास्कल:' यदि एक षट्भुज के सभी छह कोने एक शंक्वाकार खंड पर स्थित हैं # वास्तविक प्रक्षेपी तल में, तो इसके विपरीत पक्षों के चौराहों (पूर्ण रेखाओं के रूप में माने जाते हैं, क्योंकि प्रक्षेपी तल में रेखा जैसी कोई चीज नहीं होती है) खंड ) तीन संरेख बिंदु हैं। उन्हें मिलाने वाली रेखा तब षट्भुज की 'पास्कल रेखा' कहलाती है।
- 'ब्रायनचॉन:' यदि एक षट्भुज की सभी छह भुजाएँ एक शंकु की स्पर्शरेखा हैं, तो इसके विकर्ण (अर्थात विपरीत शीर्षों को मिलाने वाली रेखाएँ) तीन समवर्ती रेखाएँ होती हैं। उनके प्रतिच्छेदन बिंदु को तब षट्भुज का 'ब्रायनचोन बिंदु' कहा जाता है।
- (यदि शंक्वाकार दो सीधी रेखाओं में विलीन हो जाता है, तो पास्कल पप्पस का षट्भुज प्रमेय बन जाता है। पप्पस का प्रमेय, जिसमें कोई दिलचस्प दोहरी नहीं है, क्योंकि ब्रायनचोन बिंदु तुच्छ रूप से दो रेखाओं का प्रतिच्छेदन बिंदु बन जाता है।)
प्रोजेक्टिव ज्यामिति के सिद्धांत
किसी भी दी गई ज्यामिति को स्वयंसिद्ध के उपयुक्त समुच्चय से निकाला जा सकता है। प्रक्षेपी ज्यामिति की विशेषता अण्डाकार समानांतर स्वयंसिद्ध है, कि कोई भी दो विमान हमेशा केवल एक पंक्ति में मिलते हैं, या विमान में, कोई भी दो रेखाएँ हमेशा केवल एक बिंदु पर मिलती हैं। दूसरे शब्दों में, प्रक्षेपी ज्यामिति में समानांतर रेखाएँ या समतल जैसी कोई चीज़ नहीं होती है।
प्रक्षेपी ज्यामिति के लिए स्वयंसिद्धों के कई वैकल्पिक सेट प्रस्तावित किए गए हैं (उदाहरण के लिए कॉक्सेटर 2003, हिल्बर्ट और कोह्न-वॉसन 1999, ग्रीनबर्ग 1980 देखें)।
व्हाइटहेड के स्वयंसिद्ध
ये स्वयंसिद्ध अल्फ्रेड नॉर्थ व्हाइटहेड , द एक्सिओम्स ऑफ़ प्रोजेक्टिव ज्योमेट्री पर आधारित हैं। दो प्रकार, बिंदु और रेखाएँ हैं, और बिंदुओं और रेखाओं के बीच एक घटना संबंध है। तीन स्वयंसिद्ध हैं:
- G1: प्रत्येक पंक्ति में कम से कम 3 बिंदु होते हैं
- G2: हर दो अलग-अलग बिंदु, A और B, एक अद्वितीय रेखा AB पर स्थित हैं।
- G3: यदि रेखाएँ AB और CD प्रतिच्छेद करती हैं, तो रेखाएँ AC और BD भी काटती हैं (जहाँ यह माना जाता है कि A और D, B और C से भिन्न हैं)।
प्रत्येक पंक्ति में कम से कम 3 बिंदुओं को सम्मिलित करने का कारण कुछ पतित स्थितियों को खत्म करना है। रिक्त स्थान इन्हें संतुष्ट करते हैं
तीन अभिगृहीतों में या तो अधिकतम एक रेखा होती है, या एक विभाजन वलय पर किसी आयाम के प्रक्षेपी स्थान होते हैं, या गैर-देसार्गेसियन तल होते हैं।
अतिरिक्त स्वयंसिद्ध
कोई आयाम या समन्वय रिंग को प्रतिबंधित करने वाले और सिद्धांत जोड़ सकता है। उदाहरण के लिए, कॉक्सेटर की प्रक्षेपी ज्यामिति, [14] वेब्लेन का संदर्भ [15] उपरोक्त तीन अभिगृहीतों में, साथ में अन्य 5 अभिगृहीत हैं जो आयाम 3 और निर्देशांक वलय को विशेषता 2 नहीं का क्रमविनिमेय क्षेत्र बनाते हैं।
त्रिअंगी संबंध का प्रयोग करने वाले अभिगृहीत
तीन बिंदुओं (सभी आवश्यक रूप से अलग नहीं) के संरेख होने पर निरूपित करने के लिए, एक टर्नरी संबंध, [एबीसी] को अभिगृहीत करके स्वयंसिद्धता का अनुसरण किया जा सकता है। इस संबंध के संदर्भ में एक स्वसिद्धता को भी लिखा जा सकता है:
- सी0: [एबीए]
- C1: यदि A और B दो बिंदु हैं जैसे कि [ABC] और [ABD] तो [BDC]
- C2: यदि A और B दो बिंदु हैं तो एक तीसरा बिंदु C ऐसा है कि [ABC]
- C3: यदि A और C दो बिंदु हैं, B और D भी, [BCE] के साथ, [ADE] लेकिन [ABE] नहीं तो एक बिंदु F है जैसे कि [ACF] और [BDF]।
दो अलग-अलग बिंदुओं, ए और बी के लिए, रेखा एबी को सभी बिंदुओं सी से मिलकर परिभाषित किया गया है, जिसके लिए [ABC]। अभिगृहीत C0 और C1 तब G2 की औपचारिकता प्रदान करते हैं; G1 के लिए C2 और G3 के लिए C3।
रेखा की अवधारणा विमानों और उच्च-आयामी उप-स्थानों के लिए सामान्यीकृत होती है। एक उप-समष्टि, AB...XY इस प्रकार पुनरावर्ती रूप से उप-समष्टि AB...X के संदर्भ में परिभाषित की जा सकती है, क्योंकि इसमें YZ की सभी रेखाओं के सभी बिंदु होते हैं, क्योंकि Z की सीमा AB...X से अधिक होती है। संपार्श्विकता तब स्वतंत्रता के संबंध का सामान्यीकरण करती है। बिंदुओं का एक सेट { A, B, ..., Z } स्वतंत्र है, [AB...Z] यदि {A, B, ..., Z} उप-स्थान AB...Z के लिए एक न्यूनतम जनरेटिंग उपसमुच्चय है .
प्रक्षेपी स्वयंसिद्धों को अंतरिक्ष के आयाम पर आगे की अभिधारणाओं की सीमाओं द्वारा पूरक किया जा सकता है। न्यूनतम आयाम आवश्यक आकार के एक स्वतंत्र सेट के अस्तित्व से निर्धारित होता है। निम्नतम आयामों के लिए, प्रासंगिक स्थितियों को समतुल्य में कहा जा सकता है
निम्नानुसार रूप। एक प्रक्षेप्य स्थान है:
- (L1) कम से कम आयाम 0 यदि इसमें कम से कम 1 बिंदु है,
- (L2) कम से कम आयाम 1 यदि इसमें कम से कम 2 अलग बिंदु हैं (और इसलिए एक रेखा),
- (L3) कम से कम आयाम 2यदि इसमें कम से कम 3 गैर-संरेख बिंदु हैं (या दो रेखाएँ, या एक रेखा और एक बिंदु जो रेखा पर नहीं है),
- (L4) कम से कम डायमेंशन 3 यदि इसमें कम से कम 4 नॉन-कोप्लानर पॉइंट हैं।
अधिकतम आयाम भी इसी तरह से निर्धारित किया जा सकता है। निम्नतम आयामों के लिए, वे निम्नलिखित रूप धारण करते हैं। एक प्रक्षेप्य स्थान है:
- (M1) अधिकतम आयाम 0 पर यदि इसमें 1 बिंदु से अधिक नहीं है,
- (M2) अधिक से अधिक आयाम 1 यदि इसमें 1 से अधिक रेखा नहीं है,
- (M3) अधिक से अधिक आयाम 2 यदि इसमें 1 से अधिक समतल नहीं है,
और इसी तरह। यह एक सामान्य प्रमेय (स्वयंसिद्ध (3) का एक परिणाम) है कि सभी समतलीय रेखाएँ प्रतिच्छेद करती हैं - बहुत ही सिद्धांत प्रक्षेपी ज्यामिति का मूल रूप से अवतार लेने का इरादा था। इसलिए, संपत्ति (M3) को समान रूप से कहा जा सकता है कि सभी रेखाएँ एक दूसरे को काटती हैं।
आमतौर पर यह माना जाता है कि प्रोजेक्टिव स्पेस कम से कम डायमेंशन 2 के होते हैं। कुछ स्थितियों में, यदि फोकस प्रोजेक्टिव प्लेन पर होता है, तो M3 के एक वेरिएंट को पोस्ट किया जा सकता है। उदाहरण के लिए (ईव्स 1997: 111) के स्वयंसिद्धों में (1), (2), (एल3) और (एम3) सम्मिलित हैं। अभिगृहीत (3) (M3) के प्रारंभिक रिक्त रूप से सत्य हो जाता है और इसलिए इस संदर्भ में इसकी आवश्यकता नहीं है।
प्रक्षेपी तलों के लिए अभिगृहीत
घटना ज्यामिति में, अधिकांश लेखक [16] एक उपचार दें जो फैनो विमान पीजी (2, 2) को सबसे छोटे परिमित प्रोजेक्टिव विमान के रूप में गले लगाता है। इसे प्राप्त करने वाली स्वयंसिद्ध प्रणाली इस प्रकार है:
- (P1) कोई भी दो भिन्न बिंदु एक अद्वितीय रेखा पर स्थित होते हैं।
- (P2) कोई भी दो भिन्न रेखाएँ एक अद्वितीय बिंदु पर मिलती हैं।
- (P3) कम से कम चार बिंदुओं का अस्तित्व है जिनमें से कोई भी तीन संरेख नहीं हैं।
कॉक्सेटर्स इंट्रोडक्शन टू ज्योमेट्री [17] बचमन को जिम्मेदार प्रक्षेपी विमान की अधिक प्रतिबंधात्मक अवधारणा के लिए पांच स्वयंसिद्धों की एक सूची देता है, पप्पस के षट्भुज प्रमेय को जोड़ता है। पप्पस के प्रमेय को उपरोक्त स्वयंसिद्धों की सूची में सम्मिलित करता है (जो गैर-डिसार्गेसियन विमानों को समाप्त करता है) और विशेषता 2 के क्षेत्रों में प्रक्षेपी विमानों को छोड़कर ( जो फ़ानो के स्वयंसिद्ध को संतुष्ट नहीं करते हैं)। इस तरह से दिए गए प्रतिबंधित विमान वास्तविक प्रक्षेपी विमान के अधिक निकट हैं।
परिप्रेक्ष्य और प्रोजेक्टिविटी
तीन गैर-समरेख बिंदुओं को देखते हुए, उन्हें जोड़ने वाली तीन रेखाएँ हैं, लेकिन चार बिंदुओं के साथ, तीन संरेख नहीं हैं, छह जोड़ने वाली रेखाएँ हैं और तीन अतिरिक्त विकर्ण बिंदु उनके चौराहों द्वारा निर्धारित किए गए हैं। प्रक्षेपी ज्यामिति का विज्ञान इस अधिशेष को एक चतुर्धातुक संबंध और प्रोजेक्टिविटी के माध्यम से चार बिंदुओं द्वारा निर्धारित करता है जो पूर्ण चतुर्भुज विन्यास को संरक्षित करता है।
एक रेखा पर बिंदुओं का एक हार्मोनिक चौगुना तब होता है जब एक पूर्ण चतुर्भुज होता है जिसके दो विकर्ण बिंदु चतुर्भुज की पहली और तीसरी स्थिति में होते हैं, और अन्य दो स्थान तीसरे विकर्ण बिंदु के माध्यम से दो चतुर्भुज बिंदुओं को मिलाने वाली रेखाओं पर बिंदु होते हैं। .[18]
एक तल में प्रक्षेपी विन्यास का स्थानिक परिप्रेक्ष्य दूसरे में ऐसा विन्यास उत्पन्न करता है, और यह पूर्ण चतुर्भुज के विन्यास पर लागू होता है। इस प्रकार हार्मोनिक चतुर्भुज परिप्रेक्ष्य से संरक्षित होते हैं। यदि एक परिप्रेक्ष्य दूसरे का अनुसरण करता है तो विन्यास साथ-साथ चलते हैं। दो दृष्टिकोण की रचना अब एक परिप्रेक्ष्य नहीं है, बल्कि एक प्रोजेक्टिविटी है।
जबकि एक परिप्रेक्ष्य के संबंधित बिंदु सभी एक बिंदु पर अभिसरण करते हैं, यह अभिसरण एक प्रोजेक्टिविटी के लिए नहीं सत्य है जो एक परिप्रेक्ष्य नहीं है। प्रोजेक्टिव ज्योमेट्री में एक प्लेन में प्रोजेक्टिविटी के संगत बिंदुओं द्वारा बनाई गई रेखाओं का प्रतिच्छेदन विशेष रुचि का होता है। इस तरह के चौराहों के सेट को प्रोजेक्टिव शांकव कहा जाता है, और जैकब स्टीनर के काम की स्वीकृति में, इसे स्टेनर शांकव कहा जाता है।
मान लीजिए कि एक मध्यस्थ पी द्वारा एक्स से एक्स के संबंध में बिंदु ए और बी पर केंद्रित दो दृष्टिकोणों से एक प्रोजेक्टिविटी बनती है:
प्रोजेक्टिविटी तब है फिर प्रोजेक्टिविटी दी प्रेरित शांकव है
एक शंक्वाकार C और एक बिंदु P दिया हुआ है जो उस पर नहीं है, P से होकर जाने वाली दो भिन्न छेदक रेखाएँ C को चार बिंदुओं पर प्रतिच्छेद करती हैं। ये चार बिंदु एक चतुर्भुज निर्धारित करते हैं जिसमें से पी एक विकर्ण बिंदु है। अन्य दो विकर्ण बिंदुओं से होकर जाने वाली रेखा को ध्रुव और ध्रुवीय कहा जाता है और P इस रेखा का 'ध्रुव' है। [19] वैकल्पिक रूप से, P की ध्रुवीय रेखा P और C से होकर गुजरने वाली एक चर छेदक रेखा पर P के प्रक्षेपी हार्मोनिक संयुग्मों का समुच्चय है।
यह भी देखें
- प्रक्षेपी रेखा
- प्रोजेक्टिव प्लेन
- घटना (गणित)
- प्रक्षेपी ज्यामिति का मौलिक प्रमेय
- Desargues 'प्रमेय
- पप्पस की षट्भुज प्रमेय
- पास्कल का प्रमेय
- रिंग के ऊपर प्रोजेक्टिव लाइन
- जोसेफ वेडरबर्न
- ग्रासमैन-केली बीजगणित
टिप्पणियाँ
- ↑ Ramanan 1997, p. 88.
- ↑ Coxeter 2003, p. v.
- ↑ 3.0 3.1 3.2 3.3 Coxeter 1969, p. 229.
- ↑ Coxeter 2003, p. 14.
- ↑ Coxeter 1969, p. 93, 261.
- ↑ Coxeter 1969, p. 234–238.
- ↑ Coxeter 2003, p. 111–132.
- ↑ Coxeter 1969, p. 175–262.
- ↑ Coxeter 2003, p. 102–110.
- ↑ Coxeter 2003, p. 2.
- ↑ Coxeter 2003, p. 3.
- ↑ John Milnor (1982) Hyperbolic geometry: The first 150 years, Bulletin of the American Mathematical Society via Project Euclid
- ↑ Farmelo, Graham (15 September 2005). "डिराक की छिपी हुई ज्यामिति" (PDF). Essay. Nature. Nature Publishing Group. 437 (7057): 323. doi:10.1038/437323a. PMID 16163331. S2CID 34940597.
- ↑ Coxeter 2003, p. 14–15.
- ↑ Veblen & Young 1938, p. 16, 18, 24, 45.
- ↑ Bennett 1995, p. 4, Beutelspacher & Rosenbaum 1998, p. 8, Casse 2006, p. 29, Cederberg 2001, p. 9, Garner 1981, p. 7, Hughes & Piper 1973, p. 77, Mihalek 1972, p. 29, Polster 1998, p. 5 and Samuel 1988, p. 21 among the references given.
- ↑ Coxeter 1969, p. 229–234.
- ↑ Halsted 1906, p. 15, 16.
- ↑ Halsted 1906, p. 25.
संदर्भ
- Bachmann, F. (2013) [1959]. Aufbau der Geometrie aus dem Spiegelungsbegriff (2nd ed.). Springer-Verlag. ISBN 978-3-642-65537-1.
- Baer, Reinhold (2005). Linear Algebra and Projective Geometry. Mineola NY: Dover. ISBN 0-486-44565-8.
- Bennett, M.K. (1995). Affine and Projective Geometry. New York: Wiley. ISBN 0-471-11315-8.
- Beutelspacher, Albrecht; Rosenbaum, Ute (1998). Projective Geometry: From Foundations to Applications. Cambridge: Cambridge University Press. ISBN 0-521-48277-1.
- Casse, Rey (2006). Projective Geometry: An Introduction. Oxford University Press. ISBN 0-19-929886-6.
- Cederberg, Judith N. (2001). A Course in Modern Geometries. Springer-Verlag. ISBN 0-387-98972-2.
- Coxeter, H.S.M. (2013) [1993]. The Real Projective Plane (3rd ed.). Springer Verlag. ISBN 9781461227342.
- Coxeter, H.S.M. (2003). Projective Geometry (2nd ed.). Springer Verlag. ISBN 978-0-387-40623-7.
- Coxeter, H.S.M. (1969). Introduction to Geometry. Wiley. ISBN 0-471-50458-0.
- Dembowski, Peter (1968). Finite Geometries. Ergebnisse der Mathematik und ihrer Grenzgebiete, Band 44. Berlin, New York: Springer-Verlag. ISBN 3-540-61786-8. MR 0233275.
- Eves, Howard (2012) [1997]. Foundations and Fundamental Concepts of Mathematics (3rd ed.). Courier Corporation. ISBN 978-0-486-13220-4.
- Garner, Lynn E. (1981). An Outline of Projective Geometry. North Holland. ISBN 0-444-00423-8.
- Greenberg, M.J. (2008). Euclidean and Non-Euclidean Geometries: Development and History (4th ed.). W. H. Freeman. ISBN 978-1-4292-8133-1.
- Halsted, G. B. (1906). Synthetic Projective Geometry. New York Wiley.
- Hartley, Richard; Zisserman, Andrew (2003). Multiple view geometry in computer vision (2nd ed.). Cambridge University Press. ISBN 0-521-54051-8.
- Hartshorne, Robin (2009). Foundations of Projective Geometry (2nd ed.). Ishi Press. ISBN 978-4-87187-837-1.
- Hartshorne, Robin (2013) [2000]. Geometry: Euclid and Beyond. Springer. ISBN 978-0-387-22676-7.
- Hilbert, D.; Cohn-Vossen, S. (1999). Geometry and the Imagination (2nd ed.). American Mathematical Society. ISBN 978-0-8218-1998-2.
- Hughes, D.R.; Piper, F.C. (1973). Projective Planes. Springer-Verlag. ISBN 978-3-540-90044-3.
- Mihalek, R.J. (1972). Projective Geometry and Algebraic Structures. New York: Academic Press. ISBN 0-12-495550-9.
- Polster, Burkard (1998). A Geometrical Picture Book. Springer-Verlag. ISBN 0-387-98437-2.
- Ramanan, S. (August 1997). "Projective geometry". Resonance. Springer India. 2 (8): 87–94. doi:10.1007/BF02835009. ISSN 0971-8044. S2CID 195303696.
- Samuel, Pierre (1988). Projective Geometry. Springer-Verlag. ISBN 0-387-96752-4.
- Santaló, Luis (1966) Geometría proyectiva, Editorial Universitaria de Buenos Aires
- Veblen, Oswald; Young, J. W. A. (1938). Projective Geometry. Boston: Ginn & Co. ISBN 978-1-4181-8285-4.
बाहरी कड़ियाँ
- Projective Geometry for Machine Vision — tutorial by Joe Mundy and Andrew Zisserman.
- Notes based on Coxeter's The Real Projective Plane.
- Projective Geometry for Image Analysis — free tutorial by Roger Mohr and Bill Triggs.
- Projective Geometry. — free tutorial by Tom Davis.
- The Grassmann method in projective geometry A compilation of three notes by Cesare Burali-Forti on the application of exterior algebra to projective geometry
- C. Burali-Forti, "Introduction to Differential Geometry, following the method of H. Grassmann" (English translation of book)
- E. Kummer, "General theory of rectilinear ray systems" (English translation)
- M. Pasch, "On the focal surfaces of ray systems and the singularity surfaces of complexes" (English translation)