सातत्यक यांत्रिकी: Difference between revisions
(→उद्धरण) |
mNo edit summary |
||
| Line 2: | Line 2: | ||
{{Use dmy dates|date=August 2020}} | {{Use dmy dates|date=August 2020}} | ||
{{Continuum mechanics}} | {{Continuum mechanics}} | ||
सातत्यक यांत्रिकी, [[ यांत्रिकी |यांत्रिकी]] की एक शाखा है जो [[ बिंदु कण |अनिरन्तर् कण]] के बजाय एक निरंतर [[ द्रव्यमान |द्रव्यमान]] के रूप में बनायी गई [[ सामग्री |सामग्री]] के यांत्रिक व्यवहार से संबंधित है। सातत्यक यांत्रिकी को निरंतर यांत्रिकी भी कहते है ।19वीं शताब्दी में इस तरह के | सातत्यक यांत्रिकी, [[ यांत्रिकी |यांत्रिकी]] की एक शाखा है जो [[ बिंदु कण |अनिरन्तर् कण]] के बजाय एक निरंतर [[ द्रव्यमान |द्रव्यमान]] के रूप में बनायी गई [[ सामग्री |सामग्री]] के यांत्रिक व्यवहार से संबंधित है। सातत्यक यांत्रिकी को निरंतर यांत्रिकी भी कहते है ।19वीं शताब्दी में इस तरह के प्रतिरूपण को तैयार करने वाले पहले फ्रांसीसी गणितज्ञ [[ ऑगस्टिन-लुइस कॉची |ऑगस्टिन-लुइस कॉची]] थे। | ||
== '''<u><big>स्पष्टीकरण</big></u>''' == | == '''<u><big>स्पष्टीकरण</big></u>''' == | ||
{{Classical mechanics|cTopic=Branches}} | {{Classical mechanics|cTopic=Branches}} | ||
सातत्यक प्रतिरूप मानता है कि | सातत्यक प्रतिरूप मानता है कि पदार्थ का तत्त्व उस स्थान को भरता है जो उसके पास होता है। इस तरह से प्रतिरूपण वस्तुएं इस तथ्य को नजरअंदाज करती हैं कि पदार्थ परमाणुओं से बना है,और इसलिए निरंतर नहीं है। हालांकि,अंतर-परमाणु दूरी की तुलना में लंबाई के तराजू पर, ऐसे प्रतिरूपण अत्यधिक सटीक होते हैं । इन प्रतिरूपण का उपयोग अंतर समीकरणों को प्राप्त करने के लिए किया जा सकता है जो भौतिक कानूनों का उपयोग करके ऐसी वस्तुओं के व्यवहार का वर्णन करते हैं, जैसे कि बड़े पैमाने पर संरक्षण, गति संरक्षण और ऊर्जा संरक्षण,और सामग्री के बारे में कुछ जानकारी संवैधानिक संबंधों द्वारा प्रदान की जाती है। | ||
सातत्यक यांत्रिकी ठोस और तरल पदार्थों के भौतिक गुणों से संबंधित है जो किसी भी विशेष समन्वय प्रणाली से स्वतंत्र हैं जिसमें वे देखे जाते हैं। इन् भौतिक गुणों को टेंसर्स द्वारा दर्शाया जाता है,जो गणितीय वस्तुएं हैं। समन्वय प्रणाली इन टेंसरों को गणितीय रूप से व्यक्त करने की अनुमति देती है। | सातत्यक यांत्रिकी ठोस और तरल पदार्थों के भौतिक गुणों से संबंधित है जो किसी भी विशेष समन्वय प्रणाली से स्वतंत्र हैं जिसमें वे देखे जाते हैं। इन् भौतिक गुणों को टेंसर्स द्वारा दर्शाया जाता है,जो गणितीय वस्तुएं हैं। समन्वय प्रणाली इन टेंसरों को गणितीय रूप से व्यक्त करने की अनुमति देती है। | ||
| Line 12: | Line 12: | ||
'''<big><u>सातत्यकता की अवधारणा</u></big>''' | '''<big><u>सातत्यकता की अवधारणा</u></big>''' | ||
रिक्त स्थान अणुओं को अलग करता है जो ठोस, तरल पदार्थ और गैसों को बनाते हैं। पदार्थ में एक सूक्ष्म स्तर पर दरारें और अनिरंतरता होती हैं। हालांकि,भौतिक घटनाओं कि | रिक्त स्थान अणुओं को अलग करता है जो ठोस, तरल पदार्थ और गैसों को बनाते हैं। पदार्थ में एक सूक्ष्म स्तर पर दरारें और अनिरंतरता होती हैं। हालांकि,भौतिक घटनाओं कि प्रतिरूपणता की जा सकती है यदि सामग्री एक निरंतरता के रूप में मौजूद है, जिसका अर्थ है कि पात्र में पदार्थ लगातार वितरित किया जाता है और पूरे रिक्त स्थान को भरता है। निरंतरता एक ऐसा गुण है जिसे लगातार उप-विभाजित किया जाता है,जो विस्तृत सामग्री के गुणों के साथ अतिसूक्ष्म तत्वों में उप-विभाजित हो सकता है। | ||
सातत्यक धारणा की वैधता को एक सैद्धांतिक विश्लेषण द्वारा साबित किया जा सकता है, जिसमें या तो कुछ स्पष्ट अवधि की पहचान की जाती है या सांख्यिकीय समरूपता और सूक्ष्म संरचना की क्षुद्रता मौजूद है। विशेष रूप से,सातत्यक धारणा एक प्रारंभिक प्रतिनिधि परिमाण की अवधारणाओं और हिल-मेडेल स्थिति के स्तर विभाजन पर टिका हुआ है। यह स्थिति संवैधानिक समीकरणों (रैखिक और अरैखिक इलास्टिक/इनलेस्टिक या युग्मित क्षेत्रों) के साथ -साथ सूक्ष्म संरचना के स्थानिक और सांख्यिकीय औसत का एक तरीका है। | सातत्यक धारणा की वैधता को एक सैद्धांतिक विश्लेषण द्वारा साबित किया जा सकता है, जिसमें या तो कुछ स्पष्ट अवधि की पहचान की जाती है या सांख्यिकीय समरूपता और सूक्ष्म संरचना की क्षुद्रता मौजूद है। विशेष रूप से,सातत्यक धारणा एक प्रारंभिक प्रतिनिधि परिमाण की अवधारणाओं और हिल-मेडेल स्थिति के स्तर विभाजन पर टिका हुआ है। यह स्थिति संवैधानिक समीकरणों (रैखिक और अरैखिक इलास्टिक/इनलेस्टिक या युग्मित क्षेत्रों) के साथ -साथ सूक्ष्म संरचना के स्थानिक और सांख्यिकीय औसत का एक तरीका है। | ||
| Line 19: | Line 19: | ||
== '''<u>एक परिचयात्मक उदाहरण के रूप में कार यातायात</u>''' == | == '''<u>एक परिचयात्मक उदाहरण के रूप में कार यातायात</u>''' == | ||
सरल उदाहरण ,सिर्फ एक लेन के साथ,एक राजमार्ग पर कार यातायात पर विचार करें। सातत्य यांत्रिकी प्रभावी रूप से कारों के घनत्व के लिए आंशिक अंतर समीकरण (पीडीई) के माध्यम से कारों के आंदोलन को प्रभावशाली रूप से | सरल उदाहरण ,सिर्फ एक लेन के साथ,एक राजमार्ग पर कार यातायात पर विचार करें। सातत्य यांत्रिकी प्रभावी रूप से कारों के घनत्व के लिए आंशिक अंतर समीकरण (पीडीई) के माध्यम से कारों के आंदोलन को प्रभावशाली रूप से प्रतिरूपण करता है। इस स्थिति की परिचितता हमें सामान्य रूप से सातत्य यांत्रिकी के अंतर्निहित सातत्य-अशुद्धि द्विभक्तीकरण को समझने के लिए सशक्त बनाती है। | ||
प्रतिरूपण शुरू करने के लिए परिभाषित करें: <math>x</math> माप की दूरी (किमी में) राजमार्ग के साथ; <math>t</math> समय है (मिनटों में); <math>\rho(x,t)</math> राजमार्ग पर कारों का घनत्व है (लेन में कारों/किमी में);तथा <math>u(x,t)</math> उन कारों का [[ प्रवाह वेग |प्रवाह वेग]] (औसत वेग) 'स्थिति पर है <math>x</math> | |||
'''<u>संरक्षण एक पीडीई ( आंशिक अंतर समीकरण ) प्राप्त करता है</u>''' | '''<u>संरक्षण एक पीडीई ( आंशिक अंतर समीकरण ) प्राप्त करता है</u>''' | ||
| Line 44: | Line 44: | ||
=== '''<big><u>अवलोकन समस्या को बंद कर देता है</u></big>''' === | === '''<big><u>अवलोकन समस्या को बंद कर देता है</u></big>''' === | ||
पुर्व PDE दो अज्ञात के साथ एक समीकरण है,इसलिए एक अच्छी तरह से पोजिक समस्या बनाने के लिए एक और समीकरण की आवश्यकता होती है। इस तरह का एक अतिरिक्त समीकरण आमतौर पर सातत्य यांत्रिकी में आवश्यक होता है और ये प्रयोगों से आता है। कार यातायात के संदर्भ में यह अच्छी तरह से प्रमाणित है कि कारें आमतौर पर घनत्व के आधार पर गति से यात्रा करती हैं, <math>u=V(\rho)</math> कुछ प्रयोगात्मक रूप से निर्धारित कार्य के लिए <math>V</math> यह घनत्व का एक घटता कार्य है। उदाहरण के लिए, [[ लिंकन टनल | लिंकन टनल]] में प्रयोगों में पाया गया कि एक अच्छा फिट (कम घनत्व को छोड़कर) प्राप्त किया जाता है <math>u=V(\rho)=27.5\ln(142/\rho)</math> (कारों/किमी में घनत्व के लिए किमी/घंटा)।{{sfn|Roberts|1994}}इस प्रकार कार यातायात के लिए मूल निरंतरता | पुर्व PDE दो अज्ञात के साथ एक समीकरण है,इसलिए एक अच्छी तरह से पोजिक समस्या बनाने के लिए एक और समीकरण की आवश्यकता होती है। इस तरह का एक अतिरिक्त समीकरण आमतौर पर सातत्य यांत्रिकी में आवश्यक होता है और ये प्रयोगों से आता है। कार यातायात के संदर्भ में यह अच्छी तरह से प्रमाणित है कि कारें आमतौर पर घनत्व के आधार पर गति से यात्रा करती हैं, <math>u=V(\rho)</math> कुछ प्रयोगात्मक रूप से निर्धारित कार्य के लिए <math>V</math> यह घनत्व का एक घटता कार्य है। उदाहरण के लिए, [[ लिंकन टनल | लिंकन टनल]] में प्रयोगों में पाया गया कि एक अच्छा फिट (कम घनत्व को छोड़कर) प्राप्त किया जाता है <math>u=V(\rho)=27.5\ln(142/\rho)</math> (कारों/किमी में घनत्व के लिए किमी/घंटा)।{{sfn|Roberts|1994}}इस प्रकार कार यातायात के लिए मूल निरंतरता प्रतिरूपण पीडीई है | ||
:<math>\frac{\partial\rho}{\partial t}+ \frac{\partial}{\partial x}[\rho V(\rho)]=0</math> | :<math>\frac{\partial\rho}{\partial t}+ \frac{\partial}{\partial x}[\rho V(\rho)]=0</math> | ||
कार घनत्व के लिए <math>\rho(x,t)</math> राजमार्ग पर। | कार घनत्व के लिए <math>\rho(x,t)</math> राजमार्ग पर। | ||
| Line 70: | Line 70: | ||
{{Anchor|}} सातत्यक यांत्रिकी,के एक अतिरिक्त क्षेत्र में नरम फोम शामिल हैं,जो एक विलक्षण अतिशयोक्तिपूर्ण-तनाव संबंध प्रदर्शित करते हैं। इलास्टोमर एक सच्चा सातत्यक है,लेकिन रिक्तियों का एक सजातीय वितरण इसे असामान्य गुण देता है।{{sfn|Dienes|Solem|1999|pp=155–162}} | {{Anchor|}} सातत्यक यांत्रिकी,के एक अतिरिक्त क्षेत्र में नरम फोम शामिल हैं,जो एक विलक्षण अतिशयोक्तिपूर्ण-तनाव संबंध प्रदर्शित करते हैं। इलास्टोमर एक सच्चा सातत्यक है,लेकिन रिक्तियों का एक सजातीय वितरण इसे असामान्य गुण देता है।{{sfn|Dienes|Solem|1999|pp=155–162}} | ||
== ''' | == '''प्रतिरूपण का निर्माण''' == | ||
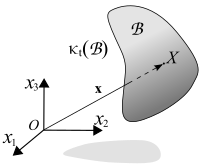
[[Image:Continuum body.svg|200px|right|thumb|चित्रा 1. एक निरंतर पदार्थ का विन्यास]] | [[Image:Continuum body.svg|200px|right|thumb|चित्रा 1. एक निरंतर पदार्थ का विन्यास]] | ||
सातत्यक यांत्रिकी प्रतिरूप भौतिक निकाय के लिए त्रि-विमीय [[ यूक्लिडियन स्पेस |यूक्लिडियन स्पेस]] में एक क्षेत्र को नियुक्त करके शुरू करते हैं <math>\mathcal B</math> | सातत्यक यांत्रिकी प्रतिरूप भौतिक निकाय के लिए त्रि-विमीय [[ यूक्लिडियन स्पेस |यूक्लिडियन स्पेस]] में एक क्षेत्र को नियुक्त करके शुरू करते हैं <math>\mathcal B</math> प्रतिरूपण किया जा रहा है। इस क्षेत्र के भीतर के बिंदुओं को कण या सामग्री बिंदु कहा जाता है। पदार्थ के विभिन्न विन्यास या अवस्था यूक्लिडियन स्पेस में विभिन्न क्षेत्रों के अनुरूप हैं। समय पर पदार्थ के विन्यास के अनुरूप क्षेत्र <math>t</math> अंकित किया गया है <math>\kappa_t(\mathcal B)</math>। | ||
एक विशेष विन्यास में पदार्थ के भीतर एक विशेष कण एक पद वेक्टर<br /> द्वारा विवरण है ; | एक विशेष विन्यास में पदार्थ के भीतर एक विशेष कण एक पद वेक्टर<br /> द्वारा विवरण है ; | ||
| Line 83: | Line 83: | ||
* प्रत्येक क्षण वैश्विक स्तर पर विपरीत कार्य करता है, ताकि पदार्थ खुद को बदल ना सके, | * प्रत्येक क्षण वैश्विक स्तर पर विपरीत कार्य करता है, ताकि पदार्थ खुद को बदल ना सके, | ||
* <small>अभिविन्यास-संरक्षण के अन्तर्गत् परिवर्तन के रूप में जो दर्पण प्रतिबिंबों का उत्पादन करते हैं वो प्रकृति में संभव नहीं हैं।</small> | * <small>अभिविन्यास-संरक्षण के अन्तर्गत् परिवर्तन के रूप में जो दर्पण प्रतिबिंबों का उत्पादन करते हैं वो प्रकृति में संभव नहीं हैं।</small> | ||
प्रतिरूपण के गणितीय सूत्रीकरण के लिए, <math>\kappa_t(\cdot)</math> भी [[ लगातार अलग -अलग |निरंतर दो बार भिन्न]] माना जाता है, ताकि गति का वर्णन करने वाले अंतर समीकरणों को तैयार किया जा सके। | |||
== '''सातत्यकता बल्''' == | == '''सातत्यकता बल्''' == | ||
| Line 217: | Line 217: | ||
:<math>\mathbf U(\mathbf x,t) = \mathbf x - \mathbf X(\mathbf x,t) \qquad \text{or}\qquad U_J = \delta_{Ji}x_i - X_J </math> | :<math>\mathbf U(\mathbf x,t) = \mathbf x - \mathbf X(\mathbf x,t) \qquad \text{or}\qquad U_J = \delta_{Ji}x_i - X_J </math> | ||
== ''' | == '''परिचातित समीकरण''' == | ||
सातत्यक यांत्रिकी उन सामग्रियों के व्यवहार से संबंधित है जिन्हें कुछ लंबाई और समय के पैमाने के लिए निरंतर के रूप में अनुमानित किया जा सकता है। ऐसी सामग्रियों के यांत्रिकी को नियंत्रित करने वाले समीकरणों में द्रव्यमान के संरक्षण, गति के संरक्षण और ऊर्जा के संरक्षण के लिए संतुलित कानून शामिल हैं। | सातत्यक यांत्रिकी उन सामग्रियों के व्यवहार से संबंधित है जिन्हें कुछ लंबाई और समय के पैमाने के लिए निरंतर के रूप में अनुमानित किया जा सकता है। ऐसी सामग्रियों के यांत्रिकी को नियंत्रित करने वाले समीकरणों में द्रव्यमान के संरक्षण, गति के संरक्षण और ऊर्जा के संरक्षण के लिए संतुलित कानून शामिल हैं। परिचातित समीकरणों की प्रणाली को पूरा करने के लिए [[ गतिकी |गतिकी]] संबंध और संवैधानिक समीकरणों की आवश्यकता होती है। संवैधानिक संबंधों के रूप में भौतिक प्रतिबंधों को लागू किया जा सकता है कि सभी शर्तों के तहत थर्मोडायनामिक्स के दूसरे कानून को संतुष्ट किया जाए। ठोस पदार्थों के निरंतर यांत्रिकी में,थर्मोडायनामिक्स का दूसरा नियम संतुष्ट है यदि क्लॉसियस -दुहम असमानता का रूप संतुष्ट है। | ||
संतुलन कानून इस विचार को व्यक्त करते हैं कि किसी मात्रा की परिवर्तन दर तीन कारणों (द्रव्यमान, गति, ऊर्जा) से उत्पन्न होनी चाहिए: | संतुलन कानून इस विचार को व्यक्त करते हैं कि किसी मात्रा की परिवर्तन दर तीन कारणों (द्रव्यमान, गति, ऊर्जा) से उत्पन्न होनी चाहिए: | ||
| Line 322: | Line 322: | ||
</math> | </math> | ||
=== <u>क्लॉसियस -दुहम असमानता</u> === | === <u>क्लॉसियस -दुहम असमानता</u> === | ||
क्लॉज़ियस-दुहम असमानता का उपयोग लचीला प्लास्टिक सामग्रियों के लिए | क्लॉज़ियस-दुहम असमानता का उपयोग लचीला प्लास्टिक सामग्रियों के लिए ऊष्मप्रवैगिकी के दूसरे नियम को व्यक्त करने के लिए किया जा सकता है। यह असमानता प्राकृतिक प्रक्रियाओं की अपरिवर्तनीयता से संबंधित एक बयान है, खासकर जब ऊर्जा अपव्यय शामिल है। | ||
पिछले भाग में संतुलन कानूनों की तरह, हम मानते हैं कि एक मात्रा का प्रवाह,मात्रा का एक स्रोत है,और प्रति यूनिट द्रव्यमान की मात्रा का एक आंतरिक घनत्व है। इस मामले में रूचि की मात्रा एन्ट्रापी है। इस प्रकार,हम मानते हैं कि रूचि के क्षेत्र में एक एन्ट्रापी प्रवाह,एक एन्ट्रापी स्रोत,एक आंतरिक द्रव्यमान घनत्व है <math>\rho</math> और एक आंतरिक विशिष्ट एन्ट्रापी (यानी प्रति यूनिट द्रव्यमान एन्ट्रापी) <math>\eta</math> है। | पिछले भाग में संतुलन कानूनों की तरह, हम मानते हैं कि एक मात्रा का प्रवाह,मात्रा का एक स्रोत है,और प्रति यूनिट द्रव्यमान की मात्रा का एक आंतरिक घनत्व है। इस मामले में रूचि की मात्रा एन्ट्रापी है। इस प्रकार,हम मानते हैं कि रूचि के क्षेत्र में एक एन्ट्रापी प्रवाह,एक एन्ट्रापी स्रोत,एक आंतरिक द्रव्यमान घनत्व है <math>\rho</math> और एक आंतरिक विशिष्ट एन्ट्रापी (यानी प्रति यूनिट द्रव्यमान एन्ट्रापी) <math>\eta</math> है। | ||
| Line 336: | Line 336: | ||
\int_{\partial \Omega} \bar{q}~\text{dA} + \int_{\Omega} \rho~r~\text{dV}. | \int_{\partial \Omega} \bar{q}~\text{dA} + \int_{\Omega} \rho~r~\text{dV}. | ||
</math> | </math> | ||
अदिश एन्ट्रापी प्रवाह संबंध द्वारा सतह पर वेक्टर प्रवाह से संबंधित हो सकता है <math>\bar{q} = -\boldsymbol{\psi}(\mathbf{x})\cdot\mathbf{n}</math>। वृद्धिशील रूप से समतापीय स्थितियों की धारणा के तहत, हमारे पास है | |||
:<math> | :<math> | ||
\boldsymbol{\psi}(\mathbf{x}) = \cfrac{\mathbf{q}(\mathbf{x})}{T} ~;~~ r = \cfrac{s}{T} | \boldsymbol{\psi}(\mathbf{x}) = \cfrac{\mathbf{q}(\mathbf{x})}{T} ~;~~ r = \cfrac{s}{T} | ||
</math> | </math> | ||
जहां पर <math>\mathbf{q}</math> हीट | जहां पर <math>\mathbf{q}</math> हीट प्रवाह वेक्टर है,<math>s</math> प्रति यूनिट द्रव्यमान में एक ऊर्जा स्रोत है,और <math>T</math> एक सामग्री बिंदु का पूर्ण तापमान है <math>\mathbf{x}</math> समय पर <math>t</math>। | ||
फिर हमारे पास अभिन्न रूप में क्लॉज़ियस -दुहम असमानता है: | फिर हमारे पास अभिन्न रूप में क्लॉज़ियस -दुहम असमानता है: | ||
Revision as of 17:41, 20 December 2022
| Part of a series on |
| सातत्यक यांत्रिकी |
|---|
सातत्यक यांत्रिकी, यांत्रिकी की एक शाखा है जो अनिरन्तर् कण के बजाय एक निरंतर द्रव्यमान के रूप में बनायी गई सामग्री के यांत्रिक व्यवहार से संबंधित है। सातत्यक यांत्रिकी को निरंतर यांत्रिकी भी कहते है ।19वीं शताब्दी में इस तरह के प्रतिरूपण को तैयार करने वाले पहले फ्रांसीसी गणितज्ञ ऑगस्टिन-लुइस कॉची थे।
स्पष्टीकरण
| Part of a series on |
| चिरसम्मत यांत्रिकी |
|---|
सातत्यक प्रतिरूप मानता है कि पदार्थ का तत्त्व उस स्थान को भरता है जो उसके पास होता है। इस तरह से प्रतिरूपण वस्तुएं इस तथ्य को नजरअंदाज करती हैं कि पदार्थ परमाणुओं से बना है,और इसलिए निरंतर नहीं है। हालांकि,अंतर-परमाणु दूरी की तुलना में लंबाई के तराजू पर, ऐसे प्रतिरूपण अत्यधिक सटीक होते हैं । इन प्रतिरूपण का उपयोग अंतर समीकरणों को प्राप्त करने के लिए किया जा सकता है जो भौतिक कानूनों का उपयोग करके ऐसी वस्तुओं के व्यवहार का वर्णन करते हैं, जैसे कि बड़े पैमाने पर संरक्षण, गति संरक्षण और ऊर्जा संरक्षण,और सामग्री के बारे में कुछ जानकारी संवैधानिक संबंधों द्वारा प्रदान की जाती है।
सातत्यक यांत्रिकी ठोस और तरल पदार्थों के भौतिक गुणों से संबंधित है जो किसी भी विशेष समन्वय प्रणाली से स्वतंत्र हैं जिसमें वे देखे जाते हैं। इन् भौतिक गुणों को टेंसर्स द्वारा दर्शाया जाता है,जो गणितीय वस्तुएं हैं। समन्वय प्रणाली इन टेंसरों को गणितीय रूप से व्यक्त करने की अनुमति देती है।
सातत्यकता की अवधारणा
रिक्त स्थान अणुओं को अलग करता है जो ठोस, तरल पदार्थ और गैसों को बनाते हैं। पदार्थ में एक सूक्ष्म स्तर पर दरारें और अनिरंतरता होती हैं। हालांकि,भौतिक घटनाओं कि प्रतिरूपणता की जा सकती है यदि सामग्री एक निरंतरता के रूप में मौजूद है, जिसका अर्थ है कि पात्र में पदार्थ लगातार वितरित किया जाता है और पूरे रिक्त स्थान को भरता है। निरंतरता एक ऐसा गुण है जिसे लगातार उप-विभाजित किया जाता है,जो विस्तृत सामग्री के गुणों के साथ अतिसूक्ष्म तत्वों में उप-विभाजित हो सकता है।
सातत्यक धारणा की वैधता को एक सैद्धांतिक विश्लेषण द्वारा साबित किया जा सकता है, जिसमें या तो कुछ स्पष्ट अवधि की पहचान की जाती है या सांख्यिकीय समरूपता और सूक्ष्म संरचना की क्षुद्रता मौजूद है। विशेष रूप से,सातत्यक धारणा एक प्रारंभिक प्रतिनिधि परिमाण की अवधारणाओं और हिल-मेडेल स्थिति के स्तर विभाजन पर टिका हुआ है। यह स्थिति संवैधानिक समीकरणों (रैखिक और अरैखिक इलास्टिक/इनलेस्टिक या युग्मित क्षेत्रों) के साथ -साथ सूक्ष्म संरचना के स्थानिक और सांख्यिकीय औसत का एक तरीका है।
जब तराजू का पृथक्करण नहीं होता है,या जब कोई प्रतिनिधि मात्रा तत्व (RVE) के आकार की तुलना में एक सूक्ष्म संकल्प की निरंतरता स्थापित करना चाहता है,तो एक सांख्यिकीय मात्रा तत्व (SVE) कार्यरत होता है,]जिसके परिणामस्वरूप यादृच्छिक निरंतरता वाले क्षेत्र होते हैं। उसके बाद वाला तब स्टोकेस्टिक परिमित तत्वों (SFE) के लिए एक माइक्रोमैकेनिक्स आधार प्रदान करता है। SVE और RVE के स्तर नियंत्रण यांत्रिकी को सांख्यिकीय यांत्रिकी से जोड़ते है। प्रयोगात्मक रूप से, RVE का मूल्यांकन केवल तभी किया जा सकता है जब संवैधानिक प्रतिक्रिया स्थानिक रूप से समरूप हो।
एक परिचयात्मक उदाहरण के रूप में कार यातायात
सरल उदाहरण ,सिर्फ एक लेन के साथ,एक राजमार्ग पर कार यातायात पर विचार करें। सातत्य यांत्रिकी प्रभावी रूप से कारों के घनत्व के लिए आंशिक अंतर समीकरण (पीडीई) के माध्यम से कारों के आंदोलन को प्रभावशाली रूप से प्रतिरूपण करता है। इस स्थिति की परिचितता हमें सामान्य रूप से सातत्य यांत्रिकी के अंतर्निहित सातत्य-अशुद्धि द्विभक्तीकरण को समझने के लिए सशक्त बनाती है।
प्रतिरूपण शुरू करने के लिए परिभाषित करें: माप की दूरी (किमी में) राजमार्ग के साथ; समय है (मिनटों में); राजमार्ग पर कारों का घनत्व है (लेन में कारों/किमी में);तथा उन कारों का प्रवाह वेग (औसत वेग) 'स्थिति पर है
संरक्षण एक पीडीई ( आंशिक अंतर समीकरण ) प्राप्त करता है
माना की कारें दिखाई नहीं देती हैं और गायब नहीं होती हैं। कारों के किसी भी समूह पर विचार करें: पर स्थित समूह के पीछे विशेष कार से सामने स्थित विशेष कार के लिए । इस समूह में कारों की कुल संख्या । चूंकि कारों को संरक्षित किया जाता है (यदि ओवरटेकिंग है, तो 'आगे / पीछे कार' एक अलग कार बन सकती है) । लेकिन लेइब्निज़ अभिन्न नियम के माध्यम से
यह अविभाज्य शून्य है, सभी समूहों के लिए,अर्थात सभी अंतरालों के लिए । सभी अंतरालों के लिए एक अभिन्न रूप से शून्य हो सकता है,यदि सभी के लिए अविभाज्य शून्य है । नतीजतन,संरक्षण का पहला क्रम अरैखिक संरक्षण PDE प्राप्त करता है
राजमार्ग पर सभी श्रेणी के लिए।
यह संरक्षण पीडीई न केवल कार यातायात पर,बल्कि तरल पदार्थ,ठोस,भीड़ पशु पौधे, बुशफायर,वित्तीय व्यापारियों पर भी लागू होता है।
अवलोकन समस्या को बंद कर देता है
पुर्व PDE दो अज्ञात के साथ एक समीकरण है,इसलिए एक अच्छी तरह से पोजिक समस्या बनाने के लिए एक और समीकरण की आवश्यकता होती है। इस तरह का एक अतिरिक्त समीकरण आमतौर पर सातत्य यांत्रिकी में आवश्यक होता है और ये प्रयोगों से आता है। कार यातायात के संदर्भ में यह अच्छी तरह से प्रमाणित है कि कारें आमतौर पर घनत्व के आधार पर गति से यात्रा करती हैं, कुछ प्रयोगात्मक रूप से निर्धारित कार्य के लिए यह घनत्व का एक घटता कार्य है। उदाहरण के लिए, लिंकन टनल में प्रयोगों में पाया गया कि एक अच्छा फिट (कम घनत्व को छोड़कर) प्राप्त किया जाता है (कारों/किमी में घनत्व के लिए किमी/घंटा)।[1]इस प्रकार कार यातायात के लिए मूल निरंतरता प्रतिरूपण पीडीई है
कार घनत्व के लिए राजमार्ग पर।
प्रमुख क्षेत्र
| सातत्य यांत्रिकीनिरंतर सामग्री के भौतिकी का अध्ययन | ठोस यांत्रिकी
परिभाषित स्थिर आकार के साथ निरंतर सामग्री के भौतिकी का अध्ययन। |
लोच
उन सामग्रियों का वर्णन करता है जो लागू तनावों को हटा दिए जाने के बाद अपने आराम के आकार में लौट आते हैं। | |
| प्लास्टिसिटी
उन सामग्रियों का वर्णन करती है जो पर्याप्त लागू तनाव के बाद स्थायी रूप से विकृत हो जाती हैं। |
रियोलॉजी
ठोस और तरल दोनों विशेषताओं वाली सामग्रियों का अध्ययन है। | ||
| द्रव यांत्रिकी
निरंतर सामग्री के भौतिकी का अध्ययन जो बल के अधीन होने पर विकृत हो जाता है। |
गैर-न्यूटोनियन द्रव
लागू कतरनी तनाव के आनुपातिक तनाव दर से नहीं गुजरते हैं। | ||
| न्यूटोनियन तरल पदार्थ लागू कतरनी तनाव के अनुपात में तनाव दर से गुजरते हैं। | |||
सातत्यक यांत्रिकी,के एक अतिरिक्त क्षेत्र में नरम फोम शामिल हैं,जो एक विलक्षण अतिशयोक्तिपूर्ण-तनाव संबंध प्रदर्शित करते हैं। इलास्टोमर एक सच्चा सातत्यक है,लेकिन रिक्तियों का एक सजातीय वितरण इसे असामान्य गुण देता है।[2]
प्रतिरूपण का निर्माण
सातत्यक यांत्रिकी प्रतिरूप भौतिक निकाय के लिए त्रि-विमीय यूक्लिडियन स्पेस में एक क्षेत्र को नियुक्त करके शुरू करते हैं प्रतिरूपण किया जा रहा है। इस क्षेत्र के भीतर के बिंदुओं को कण या सामग्री बिंदु कहा जाता है। पदार्थ के विभिन्न विन्यास या अवस्था यूक्लिडियन स्पेस में विभिन्न क्षेत्रों के अनुरूप हैं। समय पर पदार्थ के विन्यास के अनुरूप क्षेत्र अंकित किया गया है ।
एक विशेष विन्यास में पदार्थ के भीतर एक विशेष कण एक पद वेक्टर
द्वारा विवरण है ;
जहां पर समस्या के लिए चुने गए संदर्भ के कुछ ढांचे में समन्वय वैक्टर हैं (चित्र 1 देखें)। इस वेक्टर को कण स्थिति के एक फ़ंक्शन (गणित) के रूप में व्यक्त किया जा सकता है कुछ संदर्भ विन्यास में, उदाहरण के लिए प्रारंभिक समय में विन्यास, जो है
इस फ़ंक्शन में विभिन्न गुणों की आवश्यकता होती है ताकि मॉडल भौतिक समझ बनाए। इसके लिए आवश्यकता है
- समय में निरंतरता,ताकि पदार्थ एक तरह से बदल जाए जो यथार्थवादी हो,
- प्रत्येक क्षण वैश्विक स्तर पर विपरीत कार्य करता है, ताकि पदार्थ खुद को बदल ना सके,
- अभिविन्यास-संरक्षण के अन्तर्गत् परिवर्तन के रूप में जो दर्पण प्रतिबिंबों का उत्पादन करते हैं वो प्रकृति में संभव नहीं हैं।
प्रतिरूपण के गणितीय सूत्रीकरण के लिए, भी निरंतर दो बार भिन्न माना जाता है, ताकि गति का वर्णन करने वाले अंतर समीकरणों को तैयार किया जा सके।
सातत्यकता बल्
नियंत्रण यांत्रिकी कठोर निकायों के विपरीत,विकृत निकायों से संबंधित है। ठोस अवस्था एक विकृत पदार्थ है जिसमें कतरनी शक्ति,एससी है। एक ठोस पदार्थ कतरनी बलों का समर्थन कर सकता है (सामग्री की सतह के समानांतर बल जिस पर वे कार्य करते हैं)। दूसरी ओर,तरल पदार्थ कतरनी बलों को बनाए नहीं रखते हैं। ठोस और तरल पदार्थों के यांत्रिक व्यवहार के अध्ययन के लिए इन्हें निरंतर निकाय माना जाता है,जिसका अर्थ है कि यह पदार्थ के पूरे रिक्त क्षेत्र को भरता है, इस तथ्य के बावजूद कि पदार्थ रिक्त है,असतत है और परमाणुओं से बना है। इसलिए,जब सातत्यक यांत्रिकी एक निरंतर पदार्थ में एक बिंदु या कण को संदर्भित करता है, तो यह भिन्नता स्थान या परमाणु कण में एक बिंदु का वर्णन नहीं करता है,बल्कि पदार्थ का एक आदर्श हिस्सा है जो उस बिंदु पर आधिपत्य करता है।
आइजैक न्यूटन और लियोनहार्ड यूलर की शास्त्रीय गतिशीलता के बाद,एक भौतिक निकाय की गति बाहरी रूप से लागू बलों की कार्रवाई द्वारा निर्मित होती है जो दो प्रकार की होती हैं: सतह बल और पदार्थ बल .[3] इस प्रकार, कुल बल एक पदार्थ पर या पदार्थ के एक हिस्से पर लागू किया जा सकता है:
सतह बल
सतह बल या संपर्क बल, प्रति यूनिट क्षेत्र बल के रूप में व्यक्त किया जाता है, यह बल या तो पदार्थ की सीमित सतह पर कार्य कर सकता है या अन्य निकायों के साथ यांत्रिक संपर्क के परिणामस्वरूप, या काल्पनिक आंतरिक सतहों पर पदार्थ की सीमा सतह पर कार्य कर सकता है, जिसके परिणामस्वरूप पदार्थ के कुछ हिस्सों को बाध्य किया जा सकता है। यूलर-कोची का दबाव सिद्धांत के आधार पर सतह के दोनो हिस्सों के बीच यांत्रिक परस्पर क्रिया हो सकती है। जब किसी निकाय पर बाहरी संपर्क बलों द्वारा कार्य किया जाता है,तो आंतरिक संपर्क बलों को न्यूटन के प्रस्ताव के सिद्धांत के अनुसार,अपनी कार्रवाई को संतुलित करने के लिए पदार्थ के एक बिंदु से दुसरे बिंदु तक प्रेषित किया जाता है। निरंतर निकायों के लिए इन कानूनों को यूलर के कानून कहा जाता है। आंतरिक संपर्क बल संवैधानिक समीकरणों के माध्यम से पदार्थ के विरूपण से संबंधित हैं। आंतरिक संपर्क बलों को गणितीय रूप से वर्णित किया जा सकता है कि वे पदार्थ की गति से संबंधित, पदार्थ की भौतिक संरचना से कैसे संबंधित हैं।[4]पदार्थ के पूरे आयतन मे आंतरिक संपर्क बलों के वितरण को निरंतर माना जाता है। इसलिए,एक संपर्क बल घनत्व या कॉची कर्षण क्षेत्र मौजूद है[5] जहां पर एक निश्चित समय पर पदार्थ के एक विशेष विन्यास में इस वितरण का प्रतिनिधित्व करता है यह एक वेक्टर क्षेत्र नहीं है क्योंकि यह न केवल स्थिति पर निर्भर करता है एक विशेष सामग्री बिंदु,लेकिन सतह तत्व के स्थानीय अभिविन्यास पर भी इसके सामान्य वेक्टर द्वारा परिभाषित किया गया .[6]कोई अंतर क्षेत्र सामान्य वेक्टर के साथ किसी दिए गए आंतरिक सतह क्षेत्र का , पदार्थ के एक हिस्से को बाध्य करना,एक संपर्क बल का अनुभव करता है प्रत्येक तरफ पदार्थ के दोनों हिस्सों के बीच संपर्क से उत्पन्न होता है ,और इसके द्वारा दिया गया है;
जहां पर सतह कर्षण है,[7] जिसे दबाव वेक्टर,[8] संकर्षण[9]या कर्षण वेक्टर भी कहा जाता है।[10] दवाब वेक्टर एक फ्रेम-निष्पक्ष वेक्टर है।
विशेष आंतरिक सतह पर कुल संपर्क बल तब सभी अंतर सतहों पर संपर्क बलों के योग (सतह अभिन्न) के रूप में व्यक्त किया जाता है :
सातत्यक यांत्रिकी में एक निकाय को दबाव-मुक्त माना जाता है यदि मौजूद एकमात्र बल उन अंतर-परमाणु बलों (आयनिक बॉन्ड,धात्विक बंधन,और वैन डेर वाल्स बलों) को पदार्थ में एक साथ रखने और गुरुत्वाकर्षण आकर्षण सहित सभी बाहरी प्रभाव की अनुपस्थिति में अपना आकार बनाए रखने के लिए आवश्यक हैं। ।[10][11] पदार्थ के एक विशेष निर्माण के दौरान उत्पन्न दबाव को एक पदार्थ में दबाव पर विचार करते समय भी बाहर रखा जाता है। इसलिए, निरन्तर यांत्रिकी में माना जाने वाला दबाव केवल पदार्थ के विरूपण एससी द्वारा उत्पादित होता है। दबाव में केवल सापेक्ष परिवर्तन पर विचार किया जाता है,दबाव के पूर्ण मूल्य पर नहीं।
पदार्थ बल
पदार्थ बल पदार्थ के बाहरी स्रोतों से उत्पन्न होने वाले बल हैं[12] वह पदार्थ की आयतन पर कार्य करता है। यह मानते हुए कि पदार्थ का बल बाहरी स्रोतों के कारण होता हैं, इसका तात्पर्य है कि पदार्थ के विभिन्न हिस्सों (आंतरिक बलों) के बीच परस्पर क्रिया केवल संपर्क बलों के माध्यम से प्रकट होती है।[7]ये बल क्षेत्रों में पदार्थ की उपस्थिति से उत्पन्न होते हैं जैसेगुरुत्वाकर्षण क्षेत्र या विद्युत चुम्बकीय क्षेत्र,या काल्पनिक बल से जब पदार्थ गति में होते हैं। चूंकि एक निरंतर पदार्थ के द्रव्यमान को लगातार वितरित किया जाता है,इसलिए द्रव्यमान से उत्पन्न होने वाले किसी भी बल को भी लगातार वितरित किया जाता है। इस प्रकार,पदार्थ बलों को वेक्टर क्षेत्रों द्वारा निर्दिष्ट किया जाता है, जिन्हें पदार्थ की पूरी मात्रा पर निरंतर माना जाता है,[13]यानी इसमें हर बिंदु पर कार्य करना होता हैं। पदार्थ बल को पदार्थ बल घनत्व द्वारा दर्शाया जाता है (द्रव्यमान की प्रति यूनिट),जो एक ढांचा निरपेक्ष सदिश क्षेत्र है।
गुरुत्वाकर्षण बलों के मामले में,बल की तीव्रता द्रव्यमान घनत्व पर निर्भर करती है, इसलिए ये सामग्री के द्रव्यमान घनत्व से समानुपातिक है, ,और यह प्रति यूनिट द्रव्यमान बल के संदर्भ में निर्दिष्ट है () या प्रति यूनिट मात्रा ()। ये दो विनिर्देश समीकरण द्वारा सामग्री घनत्व के माध्यम से संबंधित हैं । इसी तरह, विद्युत चुम्बकीय बलों की तीव्रता विद्युत चुम्बकीय क्षेत्र के सामर्थ्य(आवेश) पर निर्भर करती है।
एक निरंतर पदार्थ पर लागू कुल पदार्थ बल को व्यक्त किया जाता है
पदार्थ पर काम करने वाले पदार्थ बल और संपर्क बल किसी दिए गए बिंदु के सापेक्ष बल के संगत क्षणों को जन्म देते हैं। इस प्रकार, कुल लागू टोक़ मूल के बारे में द्वारा दिया गया है
कुछ स्थितियों में,सामान्य तौर पर सामग्री के यांत्रिक व्यवहार के विश्लेषण में नहीं माना जाता है, दो अन्य प्रकार के बलों को शामिल करना आवश्यक हो जाता है: ये युगल दबाव हैंCite error: Invalid <ref> tag; refs with no name must have content[15] (सतह जोड़े,[12]टोरसे से संपर्क करें)[13]और पदार्थ के क्षण है। युगल तनाव एक सतह पर लागू प्रति यूनिट क्षेत्र के क्षण हैं। पदार्थ के क्षण,या पदार्थ के जोड़े, प्रति यूनिट मात्रा या प्रति यूनिट द्रव्यमान पदार्थ की मात्रा पर लागू होते हैं। दोनों एक विद्युत क्षेत्र की कार्रवाई के तहत सामग्री जहां आणविक संरचना को ध्यान में रखा जाता है (जैसे हड्डियों), बाहरी चुंबकीय क्षेत्र की कार्रवाई के तहत ठोस पदार्थ,और अव्यवस्था सिद्धांतधातु।[8][9][12] एक ध्रुवीकृत ढांकता हुआ ठोस के दबाव के विश्लेषण मे महत्वपूर्ण हैं,।[8][9][12]
सामग्री जो पदार्थ के जोड़ों और युगल को प्रदर्शित करती है, विशेष रूप से बलों द्वारा उत्पादित क्षणों के अलावा दबाव को प्रदर्शित करती है ध्रुवीय सामग्री कहलाती है।[9][13] गैर-ध्रुवीय पदार्थ वो पदार्थ है जो जिनमे केवल बलों का क्षण होता है। सातत्यक यांत्रिकी की शास्त्रीय शाखाओं में तनाव के सिद्धांत का विकास गैर-ध्रुवीय सामग्रियों पर आधारित है।
इस प्रकार,पदार्थ में सभी लागू बलों और टोरों (समन्वय प्रणाली की उत्पत्ति के संबंध में) का योग दिया जा सकता है
किनेमेटिक्स: गति और विरूपण
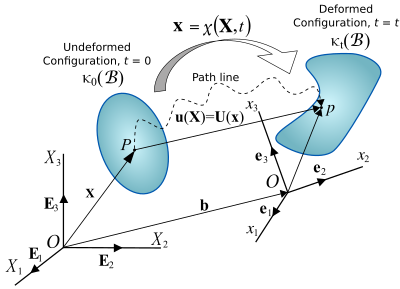
एक निरंतर पदार्थ के विन्यास में परिवर्तन के परिणाम स्वरूप विस्थापन होता है। एक पदार्थ के विस्थापन में दो घटक होते हैं: एक कठोर-पदार्थ विस्थापन और एक विरूपण (यांत्रिकी)। एक कठोर-पदार्थ विस्थापन में बिना आकार को बदले एक साथ अनुवाद और पदार्थ का रोटेशन होता है। विरूपण का तात्पर्य एक प्रारंभिक या अनिर्धारित विन्यास से पदार्थ के आकार में परिवर्तन है एक वर्तमान या विकृत विन्यास के लिए (चित्र 2)।
एक निरंतर पदार्थ की गति विस्थापन का एक निरंतर समय अनुक्रम है। इस प्रकार, भौतिक निकाय अलग -अलग समय पर अलग -अलग विन्यास पर अधिकार कर लेगा ताकि एक कण किसी स्थान में बिंदुओं की एक श्रृंखला पर नियंत्रण कर ले जो एक पथ रेखा का वर्णन करता है।
इस अर्थ में एक निरंतर पदार्थ की गति या विरूपण के दौरान निरंतरता है:
- एक बंद वक्र बनाने वाले भौतिक बिंदु हमेशा किसी भी क्षण में एक बंद वक्र ही बनाएंगे।
- एक बंद सतह बनाने वाले भौतिक बिंदु हमेशा किसी भी क्षण में एक बंद सतह ही बनायेंगे और उसका तत्व हमेशा बंद सतह के भीतर ही रहेगा।
यह एक संदर्भ विन्यास प्रारंभिक स्थिति की पहचान करने के लिए सुविधाजनक है, जिसे बाद के सभी विन्यास से संदर्भित किया जाता है। संदर्भ विन्यास को ऐसा नहीं होना चाहिए जिसपर कोई भी पदार्थ कभी भी नियंत्रण कर ले। अक्सर,विन्यास पर संदर्भ विन्यास माना जाता है, ।अवयव स्थिति वेक्टर की एक कण, संदर्भ विन्यास के संबंध में लिया गया, सामग्री या संदर्भ निर्देशांक कहा जाता है।
ठोस पदार्थों की गति या विरूपण (यांत्रिकी), या तरल पदार्थों के द्रव यांत्रिकी का विश्लेषण करते समय,पूरे समय में विन्यास के अनुक्रम या विकास का वर्णन करना आवश्यक है। गति के लिए एक विवरण सामग्री या संदर्भ निर्देशांक के संदर्भ में किया जाता है, जिसे सामग्री विवरण या लैग्रैन्जियन विवरण कहा जाता है।
लैग्रेंजियन विवरण
लैग्रैन्जियन विवरण में कणों की स्थिति और भौतिक गुणों को सामग्री या संदर्भ निर्देशांक और समय के संदर्भ में वर्णित किया गया है। इस मामले में संदर्भ विन्यास है । संदर्भ के फ्रेम में खड़ा एक पर्यवेक्षक स्थिति और भौतिक गुणों में परिवर्तन को देखता है क्योंकि समय आगे बढ़ने के साथ भौतिक पदार्थ अंतरिक्ष में चलता है। प्राप्त परिणाम प्रारंभिक समय और संदर्भ विन्यास की चयन से स्वतंत्र हैं, । यह विवरण सामान्य रूप से ठोस यांत्रिकी में उपयोग किया जाता है।
लैग्रैन्जियन विवरण में,निरंतरतर पदार्थ की गति मानचित्रण कार्य द्वारा व्यक्त की जाती है (चित्र 2),
जो प्रारंभिक विन्यास का नक्शा है मौजूदा विन्यास पर , उनके बीच एक रेखागणितीय सामंजस्य देता है, अर्थात् स्थिति सदीश देना कि एक कण , एक स्थिति वेक्टर के साथ अपरिचित या संदर्भ विन्यास में , वर्तमान या विकृत विन्यास में अधिकार कर लेगा समय पर अवयव स्थानिक निर्देशांक कहा जाता है।
भौतिक और गतिज गुण , यानी उष्मागतिक गुण और प्रवाह वेग,जो भौतिक पदार्थ की विशेषताओं का वर्णन या चिह्नित करते हैं, को स्थिति और समय के निरंतर कार्यों के रूप में व्यक्त किया जाता है, अर्थात्। ।
किसी भी गुण का सामग्री व्युत्पन् एक निरंतरता, जो एक सदिश, अदिश या टेंसर हो सकता है, गतिमान एवम तंत्र पदार्थ के कणों के एक विशिष्ट समूह के लिए उस गुण के परिवर्तन की समय दर है। सामग्री व्युत्पन्न को पर्याप्त व्युत्पन्न, या सहचालित व्युत्पन्न, या संवहन व्युत्पन्न के रूप में भी जाना जाता है। यह उस दर के रूप में विचार किया सकता है जिस पर विशेषताए बदल जाती है तब कणों के उस समूह के साथ यात्रा करने वाले पर्यवेक्षक द्वारा मापा जाता है।
लैग्रैन्जियन विवरण में, सामग्री व्युत्पन्न बस समय के संबंध में आंशिक व्युत्पन्न है, और स्थिति वेक्टर इसे स्थिर रखा जाता है क्योंकि यह समय के साथ नहीं बदलता है। इस प्रकार, हमारे पास है
तात्कालिक स्थिति एक कण की एक विशेषता है,और इसकी सामग्री व्युत्पन्न तात्कालिक प्रवाह वेग है कण का। इसलिए, निरंतरता का प्रवाह वेग क्षेत्र द्वारा दिया जाता है
इसी तरह, गतिव्रद्धि द्वारा दिया जाता है
लैग्रैन्जियन विवरण में निरंतरता को सामग्री बिंदुओं के संदर्भ विन्यास से वर्तमान विन्यास तक संदर्भ विन्यास से मैपिंग के स्थानिक और अस्थायी निरंतरता द्वारा व्यक्त किया जाता है। निरंतरता की विशेषता वाले सभी भौतिक मात्रा इस तरह से वर्णित हैं। इस अर्थ में, कार्य तथा एकल-महत्त्वपूर्ण और निरंतर हैं, जो निरंतर व्युत्पन्न के साथ स्थान और समय के संबंध मे दूसरे या तीसरे में जो भी आदेश की आवश्यकता होती है।
यूलरियन विवरण
पीछे की ओर ट्रेस करने के लिए जहां वर्तमान में स्थित कण प्रारंभिक या संदर्भित विन्यास मे स्थित था इस निरंतरता के व्युत्क्रम के लिए अनुमति देता है इस मामले में गति का विवरण स्थानिक निर्देशांक के संदर्भ में किया जाता है इस स्थिति में स्थानिक विवरण या यूलरियन विवरण कहा जाता है,अर्थात वर्तमान विन्यास को संदर्भ विन्यास के रूप में लिया जाता है।
डी अलेंब्रत द्वारा पेश किया गया यूलरियन विवरण, वर्तमान विन्यास पर केंद्रित है , अंतरिक्ष में एक निश्चित बिंदु पर क्या हो रहा है, इस पर ध्यान देना, जैसे -जैसे समय आगे बढ़ता है,व्यक्तिगत कणों पर ध्यान देने के बजाय वे अंतरिक्ष और समय के माध्यम से चलते हैं। यह दृष्टिकोण तरल यांत्रिकी के अध्ययन में आसानी से लागू होता है,जहां सबसे बड़ी रुचि की कीनेमेटिक संपत्ति वह दर है जिस पर एक संदर्भ समय में द्रव के पदार्थ के आकार के बजाय परिवर्तन हो रहा है।[16]
गणितीय रूप से,यूलरियन विवरण का उपयोग करके एक निरंतरता की गति मानचित्रण कार्य द्वारा व्यक्त की जाती है
जो कण का एक अनुरेखण प्रदान करता है जो अब स्थिति पर काबू कर लेता है वर्तमान विन्यास में इसकी मूल स्थिति के लिए प्रारंभिक विन्यास में ।
इस व्युत्क्रम कार्य के अस्तित्व के लिए एक आवश्यक और पर्याप्त स्थिति यह है कि जैकबियन मैट्रिक्स और निर्धारक, जिसे अक्सर केवल जैकबियन के रूप में संदर्भित किया जाता है,शून्य से अलग होना चाहिए। इस प्रकार,
यूलरियन विवरण में,भौतिक गुण के रूप में व्यक्त किए जाते हैं
जहां कार्यात्मक रूप लैग्रैन्जियन विवरण में के रूप में समान नहीं है यूलरियन विवरण में।
सामग्री व्युत्पन्न , चैन नियम का उपयोग करके, तो है
इस समीकरण के दाईं ओर पहला शब्द विशेषताओं के परिवर्तन की स्थानीय दर देता है जिसकी स्थिति है । दाहिने तरफ का दूसरा शब्द परिवर्तन की संवहन दर है और अंतरिक्ष (गति) में कण बदलने की स्थिति के योगदान को व्यक्त करता है।
यूलरियन विवरण में प्रवाह वेग की भिन्नता स्थानिक निरंतरता और अस्थायी निरंतरता द्वारा व्यक्त की जाती है। सदिश स्थिति के परिणाम के रूप मे वर्तमान विन्यास में,समय के प्रत्येक क्षण मे सभी भौतिक मात्राओं को इस तरह से परिभाषित किया जाता है ।
विस्थापन क्षेत्र
एक कण की स्थिति को जोड़ने वाला वेक्टर अविकृत विन्यास और विकृत विन्यास को विस्थापन (वेक्टर) कहा जाता है , लैग्रैन्जियन विवरण में, या , यूलरियन विवरण में।
एक विस्थापन क्षेत्र पदार्थ के सभी कणों के लिए सभी विस्थापन वैक्टर का एक वेक्टर क्षेत्र है, जो अवांछनीय विन्यास के साथ विकृत विन्यास से संबंधित है।विस्थापन क्षेत्र के संदर्भ में एक निरंतर पदार्थ की विरूपण या गति का विश्लेषण करना सुविधाजनक है, सामान्य रूप से, विस्थापन क्षेत्र को सामग्री निर्देशांक के रूप में व्यक्त किया जाता है
या स्थानिक निर्देशांक के संदर्भ में
जहां पर, यूनिट वैक्टर के साथ सामग्री और स्थानिक समन्वय प्रणालियों के बीच दिशा कोसाइन हैं तथा , क्रमश।इस प्रकार
और के बीच संबंध तथा द्वारा तब दिया जाता है
जानते हुए भी
फिर
अवांछित और विकृत विन्यास के लिए समन्वय प्रणालियों को अध्यारोपित करना सामान्य है, जिसके परिणामस्वरूप , होता है और दिशा कोसाइन्स क्रोनकर डेल्टास, बनाते हैं, अर्थात्
इस प्रकार, हमारे पास है
या स्थानिक निर्देशांक के संदर्भ में
परिचातित समीकरण
सातत्यक यांत्रिकी उन सामग्रियों के व्यवहार से संबंधित है जिन्हें कुछ लंबाई और समय के पैमाने के लिए निरंतर के रूप में अनुमानित किया जा सकता है। ऐसी सामग्रियों के यांत्रिकी को नियंत्रित करने वाले समीकरणों में द्रव्यमान के संरक्षण, गति के संरक्षण और ऊर्जा के संरक्षण के लिए संतुलित कानून शामिल हैं। परिचातित समीकरणों की प्रणाली को पूरा करने के लिए गतिकी संबंध और संवैधानिक समीकरणों की आवश्यकता होती है। संवैधानिक संबंधों के रूप में भौतिक प्रतिबंधों को लागू किया जा सकता है कि सभी शर्तों के तहत थर्मोडायनामिक्स के दूसरे कानून को संतुष्ट किया जाए। ठोस पदार्थों के निरंतर यांत्रिकी में,थर्मोडायनामिक्स का दूसरा नियम संतुष्ट है यदि क्लॉसियस -दुहम असमानता का रूप संतुष्ट है।
संतुलन कानून इस विचार को व्यक्त करते हैं कि किसी मात्रा की परिवर्तन दर तीन कारणों (द्रव्यमान, गति, ऊर्जा) से उत्पन्न होनी चाहिए:
- भौतिक मात्रा स्वयं सतह के माध्यम से बहती है जो मात्रा को बाधित करती है,
- वॉल्यूम की सतह पर भौतिक मात्रा का एक स्रोत है, या/और,
- वॉल्यूम के भीतर भौतिक मात्रा का एक स्रोत है।
माना की पदार्थ हो (यूक्लिडियन स्पेस का एक खुला सबसेट) और इसकी सतह हो ।
पदार्थ P में सामग्री बिंदुओं की गति को मानचित्र द्वारा वर्णित किया जाता हैा
जहां पर प्रारंभिक विन्यास में एक बिंदु की स्थिति है और विकृत विन्यास में एक ही बिंदु का स्थान है।
विरूपण प्रवणता द्वारा दिया जाता है
संतुलित कानून
माना की एक भौतिक मात्रा है जो पदार्थ के माध्यम से बह रही हो। माना की पदार्थ की सतह का स्रोत है और पदार्थ के अंदर का स्रोत है। माना की बाहरी सतह के लिए सामान्य इकाई हो । माना की भौतिक कणों का प्रवाह वेग है जो भौतिक मात्रा को ले जाते हैं। इसके अत्तिरिक्त, उस गति को दें जिस पर सीमित सतह चल रहा है (दिशा में )।
फिर, संतुलित कानूनों को सामान्य रूप में व्यक्त किया जा सकता है
फंक्शन , , तथा भौतिक मात्रा के आधार पर जो संतुलन समीकरण से संबंधित अदिश, वेक्टर या टेंसर महत्वपूर्ण हो सकता है - । यदि पदार्थ में आंतरिक सीमाएं हैं, तो वृद्धि के कारण भी संतुलन कानूनों में निर्दिष्ट करने की आवश्यकता है।
यदि हम प्रवाह क्षेत्र के दृष्टिकोण से लैग्रैन्जियन और यूलरियन विनिर्देश लेते हैं, तो यह दिखाया जा सकता है कि एक ठोस के लिए द्रव्यमान,गति और ऊर्जा के संतुलन कानूनों को इस प्रकार लिखा जा सकता है (स्रोत शब्द को मानते हुए द्रव्यमान और कोणीय के लिए शून्य है।गति समीकरण)
उपरोक्त समीकरणों में द्रव्यमान घनत्व (वर्तमान) है, की सामग्री समय व्युत्पन्न है , कण वेग है, की सामग्री समय व्युत्पन्न है , कॉची तनाव टेंसर है, पदार्थ बल घनत्व है, प्रति यूनिट द्रव्यमान की आंतरिक ऊर्जा है, की सामग्री समय व्युत्पन्न है , ऊष्मा अभिवाह वेक्टर है, और प्रति यूनिट द्रव्यमान में एक ऊर्जा स्रोत है।
संदर्भ विन्यास (लैग्रैन्जियन दृष्टिकोण) के संबंध में,संतुलन कानूनों को लिखा जा सकता है
ऊपरोक्त में, पहला पिओला-किरचॉफ तनाव टेन्सर है,और संदर्भ विन्यास में द्रव्यमान घनत्व है। पहला पिओला-किरचॉफ तनाव टेंसर कॉची तनाव टेंसर से संबंधित है
हम वैकल्पिक रूप से नाममात्र तनाव टेंसर को परिभाषित कर सकते हैं जो पहले पियोल-किरचॉफ तनाव टेंसर का स्थानान्तर है
तब संतुलन कानून बन जाते हैं
उपरोक्त समीकरणों में ऑपरेटरों को इस तरह परिभाषित किया गया है
जहां पर एक वेक्टर क्षेत्र है, एक दूसरे क्रम के टेंसर क्षेत्र है, और वर्तमान विन्यास में एक ऑर्थोनॉर्मल आधार के घटक हैं। और भी ,
जहां पर एक वेक्टर क्षेत्र है, एक दूसरे क्रम के टेंसर क्षेत्र है,और संदर्भ विन्यास में एक ऑर्थोनॉर्मल आधार के घटक हैं।
आंतरिक उत्पाद को परिभाषित किया गया है
क्लॉसियस -दुहम असमानता
क्लॉज़ियस-दुहम असमानता का उपयोग लचीला प्लास्टिक सामग्रियों के लिए ऊष्मप्रवैगिकी के दूसरे नियम को व्यक्त करने के लिए किया जा सकता है। यह असमानता प्राकृतिक प्रक्रियाओं की अपरिवर्तनीयता से संबंधित एक बयान है, खासकर जब ऊर्जा अपव्यय शामिल है।
पिछले भाग में संतुलन कानूनों की तरह, हम मानते हैं कि एक मात्रा का प्रवाह,मात्रा का एक स्रोत है,और प्रति यूनिट द्रव्यमान की मात्रा का एक आंतरिक घनत्व है। इस मामले में रूचि की मात्रा एन्ट्रापी है। इस प्रकार,हम मानते हैं कि रूचि के क्षेत्र में एक एन्ट्रापी प्रवाह,एक एन्ट्रापी स्रोत,एक आंतरिक द्रव्यमान घनत्व है और एक आंतरिक विशिष्ट एन्ट्रापी (यानी प्रति यूनिट द्रव्यमान एन्ट्रापी) है।
माना कि ऐसा क्षेत्र बनें और को इसकी सीमा होने दे। तब थर्मोडायनामिक्स के दूसरे नियम में कहा गया है कि आंतरिक एन्ट्रापी घनत्व का परिवर्तन क्षेत्र के अंदर और बाहर बहने वाली सामग्री के कारण वृद्धि की दर इस क्षेत्र में उस आपूर्ति के योग से अधिक या बराबर है ।
माना कि को एक प्रवाह वेग के साथ स्थानांतरित करें और कणों को अंदर जाने दें वेग है । सतह के लिए सामान्य इकाई बाहर की ओर हो और को क्षेत्र में पदार्थ का घनत्व होने दे, सतह पर एन्ट्रापी प्रवाह बने,और प्रति यूनिट द्रव्यमान में एन्ट्रापी स्रोत बनें।
तब एन्ट्रापी असमानता के रूप में लिखा जा सकता है
अदिश एन्ट्रापी प्रवाह संबंध द्वारा सतह पर वेक्टर प्रवाह से संबंधित हो सकता है । वृद्धिशील रूप से समतापीय स्थितियों की धारणा के तहत, हमारे पास है
जहां पर हीट प्रवाह वेक्टर है, प्रति यूनिट द्रव्यमान में एक ऊर्जा स्रोत है,और एक सामग्री बिंदु का पूर्ण तापमान है समय पर ।
फिर हमारे पास अभिन्न रूप में क्लॉज़ियस -दुहम असमानता है:
हम दिखा सकते हैं कि एन्ट्रापी असमानता को भिन्नता के रूप में लिखा जा सकता है
कॉची तनाव और आंतरिक ऊर्जा के संदर्भ में,क्लॉसियस -दुहम असमानता के रूप में लिखा जा सकता है
अनुप्रयोग
- सातत्यक यांत्रिकी
- ठोस यांत्रिकी
- तरल यांत्रिकी
- अभियांत्रिकी
यह भी देखें
- बर्नौली का सिद्धांत
- Cauchy लोचदार सामग्री
- विन्यास यांत्रिकी
- Curvilinear निर्देशांक
- स्थिति के समीकरण
- परिमित विरूपण टेनर्स
- परिमित तनाव सिद्धांत
- अतिवृद्धि सामग्री
- प्रवाह क्षेत्र के लैग्रैन्जियन और यूलरियन विनिर्देशन
- चल सेलुलर ऑटोमेटन
- पेरिडिनैमिक्स (एक गैर-स्थानीय निरंतरता सिद्धांत जो अभिन्न समीकरणों के लिए अग्रणी है)
- तनाव (भौतिकी)
- तनाव के उपाय
- टेंसर कैलकुलस
- टेंसर व्युत्पन्न (सातत्य यांत्रिकी)
- लोच का सिद्धांत
व्याख्यात्मक नोट्स
1-मैक्सवेल ने बताया कि चुंबकीय क्षेत्र में चुम्बक में और ध्रुवीकरण के विभिन्न तलों के साथ विद्युत क्षेत्र में परावैद्युत पदार्थ में गैर-विलुप्त होने वाले भौतिक क्षण मौजूद होते हैं। [13]
2-कपल स्ट्रेस और बॉडी कपल्स को सबसे पहले वोइगट और कोसेराट द्वारा खोजा गया था, और बाद में 1960 में माइंडलिन द्वारा शुद्ध क्वार्ट्ज क्रिस्टल पर बेल लैब्स के लिए अपने काम पर फिर से प्रस्तुत किया गया।
संदर्भ
उद्धरण
1-रॉबर्ट्स 1994 ।
2-डायनेस एंड सोलेम 1999 , पीपी। 155-162।
3-स्मिथ 1993 , पृ. 97.
4- स्मिथ 1993 ।
5-लुब्लिनेर 2008 ।
6-लियू 2002 ।
7-वू 2004
8-फंग 1977 ।
9-मास 1970 ।
10-अटानाकोविक और गुरन 2000 ।
11-इरगेंस 2008 ।
12-चाडविक 1999 ।
13-फंग 1977 , पृ. 76.
14-स्पेंसर 1980 , पृ. 83.
उद्धृत कार्य
- एटानाकोविक, टेओडोर एम.; गुरन, अर्देशिर (16 जून 2000)। वैज्ञानिकों और इंजीनियरों के लिए लोच का सिद्धांत । भौतिकी पर डोवर किताबें। स्प्रिंगर साइंस एंड बिजनेस मीडिया। आईएसबीएन 978-0-8176-4072-9.
- चाडविक, पीटर (1 जनवरी 1999)। सातत्य यांत्रिकी: संक्षिप्त सिद्धांत और समस्याएं । कूरियर निगम। आईएसबीएन 978-0-486-40180-5.
- डायनेस, जेके; सोलेम, जे.सी. (1999)। "कुछ हाइड्रोस्टैटिकली स्ट्रेस्ड आइसोट्रोपिक इलास्टोमेरिक फोम्स का नॉनलाइनियर बिहेवियर" । एक्टा मैकेनिक । 138 (3–4): 155–162। डीओआई : 10.1007/बीएफ01291841 । एस 2 सीआईडी 120320672 .
- फंग, वाईसी (1977)। कॉन्टिनम मैकेनिक्स में पहला कोर्स (दूसरा संस्करण)। प्रेंटिस-हॉल, इंक. आईएसबीएन 978-0-13-318311-5.
- इरगेंस, फ्रिड्जोव (10 जनवरी 2008)। सातत्य यांत्रिकी । स्प्रिंगर साइंस एंड बिजनेस मीडिया। आईएसबीएन 978-3-540-74298-2.
- लियू, आई-शिह (28 मई 2002)। सातत्य यांत्रिकी । स्प्रिंगर साइंस एंड बिजनेस मीडिया। आईएसबीएन 978-3-540-43019-3.
- ल्यूबलिनर, जैकब (2008)। प्लास्टिसिटी थ्योरी (पीडीएफ) (संशोधित संस्करण)। डोवर प्रकाशन। आईएसबीएन 978-0-486-46290-5. 31 मार्च 2010 को मूल (पीडीएफ) से संग्रहीत ।
- ओस्टोजा-स्टारजेवस्की, एम। (2008)। "7-10" । सामग्री के यांत्रिकी में माइक्रोस्ट्रक्चरल यादृच्छिकता और स्केलिंग । सीआरसी प्रेस। आईएसबीएन 978-1-58488-417-0.
- स्पेंसर, एजेएम (1980)। सातत्य यांत्रिकी । लॉन्गमैन ग्रुप लिमिटेड (लंदन)। पी। 83. आईएसबीएन 978-0-582-44282-5.
- रॉबर्ट्स, एजे (1994)। कॉन्टिनम मैकेनिक्स का एक आयामी परिचय । विश्व वैज्ञानिक।
- स्मिथ, डोनाल्ड आर. (1993). "2" । ट्रूसेडेल और नोल के बाद सातत्य यांत्रिकी का परिचय । ठोस यांत्रिकी और इसके अनुप्रयोग। वॉल्यूम। 22. स्प्रिंगर साइंस एंड बिजनेस मीडिया। आईएसबीएन 978-90-481-4314-6.
- वू, हान-चिन (20 दिसंबर 2004)। सातत्य यांत्रिकी और प्लास्टिसिटी । टेलर और फ्रांसिस। आईएसबीएन 978-1-58488-363-0.
सामान्य संदर्भ
- बत्रा, आरसी (2006)। सातत्य यांत्रिकी के तत्व । रेस्टन, वीए: एआईएए।
- बर्ट्रम, अल्ब्रेक्ट (2012)। बड़े विकृतियों की लोच और प्लास्टिसिटी - एक परिचय (तीसरा संस्करण)। स्प्रिंगर। डीओआई : 10.1007/978-3-642-24615-9 . आईएसबीएन 978-3-642-24615-9. एस 2 सीआईडी 116496103 .
- चंद्रमौली, पीएन (2014)। सातत्य यांत्रिकी । यस डी पब्लिशिंग प्राइवेट लिमिटेड आईएसबीएन 9789380381398.
- एरिंगन, ए. केमल (1980)। कॉन्टिनुआ के यांत्रिकी (दूसरा संस्करण)। क्राइगर पब कंपनी आईएसबीएन 978-0-88275-663-9.
- चेन, यूपिंग; जेम्स डी. ली; अजीम एस्कंदेरियन (2009)। सॉलिड मैकेनिक्स में मेशलेस मेथड्स (पहला संस्करण)। स्प्रिंगर न्यूयॉर्क। आईएसबीएन 978-1-4419-2148-2.
- डिल, एलिस हेरोल्ड (2006)। कॉन्टिनम मैकेनिक्स: लोच, प्लास्टिसिटी, विस्कोइलास्टिसिटी । जर्मनी: सीआरसी प्रेस। आईएसबीएन 978-0-8493-9779-0.
- दिमित्रिंको, यूरी (2011)। नॉनलाइनियर कॉन्टिनम मैकेनिक्स एंड लार्ज इनलेस्टिक डिफॉर्मेशन । जर्मनी: स्प्रिंगर. आईएसबीएन 978-94-007-0033-8.
- हटर, कोलम्बन; क्लाउस जॉनक (2004)। भौतिक मॉडलिंग के सातत्य तरीके । जर्मनी: स्प्रिंगर. आईएसबीएन 978-3-540-20619-4.
- गुरटिन, एमई (1981)। कॉन्टिनम मैकेनिक्स का एक परिचय । न्यूयॉर्क: अकादमिक प्रेस।
- लाइ, डब्ल्यू माइकल; डेविड रुबिन; एरहार्ड क्रेम्प्ल (1996)। कॉन्टिनम मैकेनिक्स का परिचय (तीसरा संस्करण)। एल्सेवियर, इंक. आईएसबीएन 978-0-7506-2894-5. मूल से 6 फरवरी 2009 को पुरालेखित।
- लुबार्डा, व्लादो ए. (2001). इलास्टोप्लास्टिक सिद्धांत । सीआरसी प्रेस। आईएसबीएन 978-0-8493-1138-3.
- मैल्वर्न, लॉरेंस ई. (1969)। एक सतत माध्यम के यांत्रिकी का परिचय । न्यू जर्सी: प्रेंटिस-हॉल, इंक।
- मेस, जॉर्ज ई. (1970). सातत्य यांत्रिकी । मैकग्रा-हिल प्रोफेशनल। आईएसबीएन 978-0-07-040663-6.
- मेस, जी. थॉमस; जॉर्ज ई. मेस (1999). इंजीनियर्स के लिए कॉन्टिनम मैकेनिक्स (दूसरा संस्करण)। सीआरसी प्रेस। आईएसबीएन 978-0-8493-1855-9.
- मौगिन, जीए (1999)। गैर-रैखिक अपरिवर्तनीय व्यवहार के थर्मोमैकेनिक्स: एक परिचय । सिंगापुर: विश्व वैज्ञानिक।
- नेमत-नासिर, सिया (2006)। प्लास्टिसिटी: ए ट्रीटीज ऑन फाइनिट डिफॉर्मेशन ऑफ हेटेरोजेनियस इनलेस्टिक मैटेरियल्स । कैम्ब्रिज: कैम्ब्रिज यूनिवर्सिटी प्रेस। आईएसबीएन 978-0-521-83979-2.
- ओस्टोजा-स्टारजेवस्की, मार्टिन (2008)। सामग्री के यांत्रिकी में माइक्रोस्ट्रक्चरल रैंडमनेस और स्केलिंग । बोका रैटन, FL: चैपमैन एंड हॉल/सीआरसी प्रेस। आईएसबीएन 978-1-58488-417-0.
- रीस, डेविड (2006)। बेसिक इंजीनियरिंग प्लास्टिसिटी - इंजीनियरिंग और विनिर्माण अनुप्रयोगों के साथ एक परिचय । बटरवर्थ-हेनीमैन। आईएसबीएन 978-0-7506-8025-7.
- राइट, TW (2002)। एडियाबेटिक शियर बैंड्स का भौतिकी और गणित । कैम्ब्रिज, यूके: कैम्ब्रिज यूनिवर्सिटी प्रेस।
बाहरी संबंध
- "शास्त्रीय सातत्य यांत्रिकी में वस्तुनिष्ठता: गति, यूलेरियन और लैग्रैंगियन फ़ंक्शंस; विरूपण ढाल; लाइ डेरिवेटिव; वेग-जोड़ सूत्र, कोरिओलिस; ऑब्जेक्टिविटी" गाइल्स लेबोर्गने द्वारा, 7 अप्रैल, 2021: "भाग IV वेग-जोड़ सूत्र और वस्तुनिष्ठता"
- ↑ Roberts 1994.
- ↑ Dienes & Solem 1999, pp. 155–162.
- ↑ Smith, p. 97.
- ↑ Slaughter.
- ↑ Smith.
- ↑ Lubliner 2008.
- ↑ Jump up to: 7.0 7.1 Liu.
- ↑ Jump up to: 8.0 8.1 8.2 Wu.
- ↑ Jump up to: 9.0 9.1 9.2 9.3 Fung 1977.
- ↑ Jump up to: 10.0 10.1 Mase.
- ↑ Atanackovic.
- ↑ Jump up to: 12.0 12.1 12.2 12.3 Irgens.
- ↑ Jump up to: 13.0 13.1 13.2 Chadwick.
- ↑ Richards, p. 55.
- ↑ Couple stresses and body couples were first explored by Voigt and Cosserat, and later reintroduced by Mindlin in 1960 on his work for Bell Labs on pure quartz crystals.[14]
- ↑ Spencer 1980, p. 83.