सातत्यक यांत्रिकी

कॉन्टिनम मैकेनिक्स यांत्रिकी की एक शाखा है जो असतत कणों के बजाय एक निरंतर द्रव्यमान के रूप में मॉडलिंग की गई सामग्री के यांत्रिक व्यवहार से संबंधित है।19 वीं शताब्दी में इस तरह के मॉडलों को तैयार करने वाले फ्रांसीसी गणितज्ञ ऑगमेंसियन ऑगस्टिन-लुई कॉची पहले थे।

स्पष्टीकरण

एक निरंतरता मॉडल मानता है कि ऑब्जेक्ट का पदार्थ उस स्थान को भरता है जो उसके पास होता है।इस तरह से मॉडलिंग वस्तुएं इस तथ्य को नजरअंदाज करती हैं कि मामला परमाणुओं से बना है, और इसलिए निरंतर नहीं है;हालांकि, अंतर-परमाणु दूरी की तुलना में लंबाई के तराजू पर, ऐसे मॉडल अत्यधिक सटीक हैं।इन मॉडलों का उपयोग अंतर समीकरणों को प्राप्त करने के लिए किया जा सकता है जो भौतिक कानूनों का उपयोग करके ऐसी वस्तुओं के व्यवहार का वर्णन करते हैं, जैसे कि बड़े पैमाने पर संरक्षण, गति संरक्षण और ऊर्जा संरक्षण, और सामग्री के बारे में कुछ जानकारी संवैधानिक संबंधों द्वारा प्रदान की जाती है। कॉन्टिनम यांत्रिकी ठोस और तरल पदार्थों के भौतिक गुणों से संबंधित है जो किसी भी विशेष समन्वय प्रणाली से स्वतंत्र हैं जिसमें वे देखे जाते हैं।भौतिक गुणों को तब टेंसर्स द्वारा दर्शाया जाता है, जो कि समन्वय प्रणालियों से स्वतंत्र होने की संपत्ति के साथ गणितीय वस्तुएं हैं।समन्वय प्रणाली इन टेंसरों को कम्प्यूटेशनल रूप से व्यक्त करने की अनुमति देती है।

एक निरंतरता की अवधारणा

अंतरिक्ष अणुओं को अलग करता है जो ठोस, तरल पदार्थ और गैसों को बनाते हैं। सामग्री में एक सूक्ष्म स्तर पर दरारें और असंतोष होते हैं। भौतिक घटना, हालांकि, मॉडलिंग की जा सकती है यदि सामग्री एक निरंतरता के रूप में मौजूद है, जिसका अर्थ है कि शरीर में मामला लगातार वितरित किया जाता है और पूरे स्थान को भरता है जो उस पर कब्जा करता है। एक निरंतरता एक ऐसा शरीर है जिसे लगातार उप-विभाजित किया जा सकता है, जो कि बल्क सामग्री के गुणों के साथ अनंत तत्वों में उप-विभाजित हो सकता है। निरंतरता धारणा की वैधता को एक सैद्धांतिक विश्लेषण द्वारा सत्यापित किया जा सकता है, जिसमें या तो कुछ स्पष्ट आवधिकता की पहचान की जाती है या सांख्यिकीय समरूपता और माइक्रोस्ट्रक्चर की एर्गोडिसिटी मौजूद है। अधिक विशेष रूप से, निरंतरता परिकल्पना/धारणा एक प्रतिनिधि प्राथमिक मात्रा की अवधारणाओं पर टिका है और पहाड़ी -मेडेल स्थिति के आधार पर तराजू के पृथक्करण है। यह स्थिति संवैधानिक समीकरणों (रैखिक और नॉनलाइनियर इलास्टिक/इनलेस्टिक या युग्मित क्षेत्रों) के साथ -साथ माइक्रोस्ट्रक्चर के स्थानिक और सांख्यिकीय औसत का एक तरीका है। जब तराजू का पृथक्करण नहीं होता है, या जब कोई प्रतिनिधि मात्रा तत्व (RVE) के आकार की तुलना में एक महीन संकल्प की निरंतरता स्थापित करना चाहता है, तो एक सांख्यिकीय मात्रा तत्व (SVE) कार्यरत होता है, जिसके परिणामस्वरूप यादृच्छिक निरंतरता वाले क्षेत्र होते हैं। बाद वाला तब स्टोकेस्टिक परिमित तत्वों (SFE) के लिए एक माइक्रोमैकेनिक्स आधार प्रदान करता है। SVE और RVE के स्तर सांख्यिकीय यांत्रिकी के लिए निरंतर यांत्रिकी लिंक। प्रयोगात्मक रूप से, आरवीई का मूल्यांकन केवल तभी किया जा सकता है जब संवैधानिक प्रतिक्रिया स्थानिक रूप से समरूप हो

एक परिचयात्मक उदाहरण के रूप में कार यातायात

सादगी के लिए सिर्फ एक लेन के साथ, एक राजमार्ग पर कार यातायात पर विचार करें। कुछ हद तक आश्चर्यजनक रूप से, और इसकी प्रभावशीलता के लिए एक श्रद्धांजलि में, सातत्य यांत्रिकी प्रभावी रूप से कारों के घनत्व के लिए आंशिक अंतर समीकरण (पीडीई) के माध्यम से कारों के आंदोलन को प्रभावी ढंग से मॉडल करता है। इस स्थिति की परिचितता हमें सामान्य रूप से कॉन्टिनम मॉडलिंग के अंतर्निहित निरंतरता-अशुद्धि डाइकोटॉमी को समझने के लिए सशक्त बनाती है।

मॉडलिंग शुरू करने के लिए परिभाषित करें: $x$ माप की दूरी (किमी में) राजमार्ग के साथ; $t$ समय है (मिनटों में); $\rho (x,t)$ राजमार्ग पर कारों का घनत्व है (लेन में कारों/किमी में);तथा $u(x,t)$ उन कारों का प्रवाह वेग (औसत वेग) 'स्थिति पर है $x$।

=== संरक्षण एक पीडीई (आंशिक अंतर समीकरण) === प्राप्त करता है कारें दिखाई नहीं देती हैं और गायब नहीं होती हैं। कारों के किसी भी समूह पर विचार करें: पर स्थित समूह के पीछे विशेष कार से $x=a(t)$ सामने स्थित विशेष कार के लिए $x=b(t)$। इस समूह में कारों की कुल संख्या ${\textstyle N=\int _{a(t)}^{b(t)}\rho (x,t)\,dx}$। चूंकि कारों को संरक्षित किया जाता है (यदि ओवरटेकिंग है, तो 'सामने / पीछे की कार' एक अलग कार बन सकती है) $dN/dt=0$। लेकिन Leibniz अभिन्न नियम के माध्यम से

${\begin{aligned}{}{\frac {dN}{dt}}&={\frac {d}{dt}}\int _{a(t)}^{b(t)}\rho (x,t)\,dx\\&=\int _{a}^{b}{\frac {\partial \rho }{\partial t}}\,dx+\rho (b,t){\frac {db}{dt}}-\rho (a,t){\frac {da}{dt}}\\&=\int _{a}^{b}{\frac {\partial \rho }{\partial t}}\,dx+\rho (b,t)u(b,t)-\rho (a,t)u(a,t)\\&=\int _{a}^{b}\left[{\frac {\partial \rho }{\partial t}}+{\frac {\partial }{\partial x}}(\rho u)\right]dx\end{aligned}}$

यह इंटीग्रल शून्य है, सभी समूहों के लिए, अर्थात्, सभी अंतरालों के लिए $[a,b]$। सभी अंतरालों के लिए एक अभिन्न रूप से शून्य हो सकता है, यदि सभी के लिए इंटीग्रैंड शून्य है $x$। नतीजतन, संरक्षण पहला आदेश nonlinear संरक्षण PDE प्राप्त करता है

${\frac {\partial \rho }{\partial t}}+{\frac {\partial }{\partial x}}(\rho u)=0$

राजमार्ग पर सभी पदों के लिए।

यह संरक्षण पीडीई न केवल कार यातायात पर, बल्कि तरल पदार्थ, ठोस, भीड़, जानवर, पौधे, बुशफायर, वित्तीय व्यापारियों, और इतने पर भी लागू होता है।

अवलोकन समस्या को बंद कर देता है

पिछला PDE दो अज्ञात के साथ एक समीकरण है, इसलिए एक अच्छी तरह से पोजिक समस्या बनाने के लिए एक और समीकरण की आवश्यकता होती है।इस तरह के एक अतिरिक्त समीकरण को आमतौर पर सातत्य यांत्रिकी में आवश्यक होता है और आमतौर पर प्रयोगों से आता है।कार यातायात के लिए यह अच्छी तरह से स्थापित है कि कारें आमतौर पर घनत्व के आधार पर गति से यात्रा करती हैं, $u=V(\rho )$ कुछ प्रयोगात्मक रूप से निर्धारित कार्य के लिए $V$ यह घनत्व का एक घटता कार्य है।उदाहरण के लिए, लिंकन टनल में प्रयोगों में पाया गया कि एक अच्छा फिट (कम घनत्व को छोड़कर) द्वारा प्राप्त किया जाता है $u=V(\rho )=27.5\ln(142/\rho )$ (कारों/किमी में घनत्व के लिए किमी/घंटा)। इस प्रकार कार यातायात के लिए मूल निरंतरता मॉडल पीडीई है

${\frac {\partial \rho }{\partial t}}+{\frac {\partial }{\partial x}}[\rho V(\rho )]=0$

कार घनत्व के लिए $\rho (x,t)$ राजमार्ग पर।

प्रमुख क्षेत्र

Continuum mechanics The study of the physics of continuous materials	Solid mechanics The study of the physics of continuous materials with a defined rest shape.	Elasticity Describes materials that return to their rest shape after applied stresses are removed.
		Plasticity Describes materials that permanently deform after a sufficient applied stress.	Rheology The study of materials with both solid and fluid characteristics.
	Fluid mechanics The study of the physics of continuous materials which deform when subjected to a force.	Non-Newtonian fluid Do not undergo strain rates proportional to the applied shear stress.
		Newtonian fluids undergo strain rates proportional to the applied shear stress.

कॉन्टिनम मैकेनिक्स के एक अतिरिक्त क्षेत्र में इलास्टोमेरिक फोम शामिल हैं, जो एक जिज्ञासु हाइपरबोलिक तनाव-तनाव संबंध प्रदर्शित करते हैं।इलास्टोमर एक सच्चा निरंतरता है, लेकिन voids का एक सजातीय वितरण इसे असामान्य गुण देता है।

मॉडल का निर्माण

चित्रा 1. एक निरंतर शरीर का विन्यास

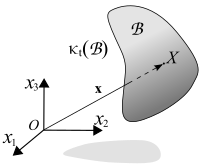
कॉन्टिनम मैकेनिक्स मॉडल भौतिक निकाय के लिए त्रि-आयामी यूक्लिडियन स्थान में एक क्षेत्र को असाइन करके शुरू करते हैं ${\mathcal {B}}$ मॉडलिंग किया जा रहा है।इस क्षेत्र के भीतर के बिंदुओं को कण या सामग्री बिंदु कहा जाता है।शरीर के विभिन्न विन्यास या राज्य यूक्लिडियन अंतरिक्ष में विभिन्न क्षेत्रों के अनुरूप हैं।समय पर शरीर के विन्यास के अनुरूप क्षेत्र $t$ लेबल किया गया है $\kappa _{t}({\mathcal {B}})$।

एक विशेष कॉन्फ़िगरेशन में शरीर के भीतर एक विशेष कण एक स्थिति वेक्टर
द्वारा विशेषता है

$\mathbf {x} =\sum _{i=1}^{3}x_{i}\mathbf {e} _{i},$

कहाँ पे $\mathbf {e} _{i}$ समस्या के लिए चुने गए संदर्भ के कुछ फ्रेम में समन्वय वैक्टर हैं (चित्र 1 देखें)।इस वेक्टर को कण स्थिति के एक समारोह के रूप में व्यक्त किया जा सकता है $\mathbf {X}$ कुछ संदर्भ कॉन्फ़िगरेशन में, उदाहरण के लिए प्रारंभिक समय पर कॉन्फ़िगरेशन, ताकि

$\mathbf {x} =\kappa _{t}(\mathbf {X} ).$

इस फ़ंक्शन में विभिन्न गुणों की आवश्यकता होती है ताकि मॉडल भौतिक समझ बनाए। $\kappa _{t}(\cdot )$ होने की जरूरत:

• समय में निरंतर, ताकि शरीर एक तरह से बदल जाए जो यथार्थवादी हो,
• हर समय विश्व स्तर पर उल्टा, ताकि शरीर खुद को काट न सके,
• अभिविन्यास-संरक्षण, परिवर्तन के रूप में जो दर्पण प्रतिबिंबों का उत्पादन करते हैं, प्रकृति में संभव नहीं हैं।

मॉडल के गणितीय सूत्रीकरण के लिए, $\kappa _{t}(\cdot )$ यह भी दो बार लगातार अलग -अलग माना जाता है, ताकि गति का वर्णन करने वाले अंतर समीकरणों को तैयार किया जा सके।

एक निरंतरता में बल

See also: Stress (mechanics) and Cauchy stress tensor

कॉन्टिनम मैकेनिक्स कठोर निकायों के विपरीत, विकृत निकायों से संबंधित है।एक ठोस एक विकृत शरीर है जिसमें कतरनी शक्ति, एससी है।एक ठोस कतरनी बलों का समर्थन कर सकता है (सामग्री की सतह के समानांतर बल जिस पर वे कार्य करते हैं)।दूसरी ओर, तरल पदार्थ कतरनी बलों को बनाए नहीं रखते हैं।ठोस और तरल पदार्थों के यांत्रिक व्यवहार के अध्ययन के लिए इन्हें निरंतर निकाय माना जाता है, जिसका अर्थ है कि यह मामला अंतरिक्ष के पूरे क्षेत्र को भरता है, इस तथ्य के बावजूद कि मामला परमाणुओं से बना है, voids है, और असतत है।इसलिए, जब कॉन्टिनम मैकेनिक्स एक निरंतर शरीर में एक बिंदु या कण को संदर्भित करता है, तो यह अंतर -अंतरिक्ष या परमाणु कण में एक बिंदु का वर्णन नहीं करता है, बल्कि शरीर का एक आदर्श हिस्सा उस बिंदु पर कब्जा करता है।

न्यूटन और यूलर की शास्त्रीय गतिशीलता के बाद, एक भौतिक निकाय की गति बाहरी रूप से लागू बलों की कार्रवाई द्वारा निर्मित होती है, जिन्हें दो प्रकार की माना जाता है: सतह बल $\mathbf {F} _{C}$ और शरीर बल $\mathbf {F} _{B}$. इस प्रकार, कुल बल ${\mathcal {F}}$ एक शरीर पर या शरीर के एक हिस्से पर लागू किया जा सकता है:

${\mathcal {F}}=\mathbf {F} _{C}+\mathbf {F} _{B}$

सतह बल

सतह बलों या संपर्क बलों, प्रति यूनिट क्षेत्र बल के रूप में व्यक्त किया जाता है, या तो शरीर की बाउंडिंग सतह पर कार्य कर सकता है, अन्य निकायों के साथ यांत्रिक संपर्क के परिणामस्वरूप, या काल्पनिक आंतरिक सतहों पर जो शरीर के बाध्य भागों पर, परिणामस्वरूप, परिणामस्वरूप सतह के दोनों ओर शरीर के हिस्सों के बीच यांत्रिक बातचीत (यूलर-कोची का तनाव सिद्धांत)। जब किसी निकाय पर बाहरी संपर्क बलों द्वारा कार्य किया जाता है, तो आंतरिक संपर्क बलों को न्यूटन के प्रस्ताव के कानून के अनुसार, अपनी कार्रवाई को संतुलित करने के लिए शरीर के अंदर बिंदु से बिंदु तक प्रेषित किया जाता है। निरंतर निकायों के लिए इन कानूनों को यूलर के कानून कहा जाता है। यूलर के गति के समीकरण)। आंतरिक संपर्क बल संवैधानिक समीकरणों के माध्यम से शरीर के विरूपण से संबंधित हैं। आंतरिक संपर्क बलों को गणितीय रूप से वर्णित किया जा सकता है कि वे शरीर की गति से संबंधित, शरीर के सामग्री मेकअप से कैसे संबंधित हैं। शरीर की मात्रा में आंतरिक संपर्क बलों के वितरण को निरंतर माना जाता है।इसलिए, एक संपर्क बल घनत्व या कॉची कर्षण क्षेत्र मौजूद है $\mathbf {T} (\mathbf {n} ,\mathbf {x} ,t)$ यह एक निश्चित समय पर शरीर के एक विशेष कॉन्फ़िगरेशन में इस वितरण का प्रतिनिधित्व करता है $t\,\!$।यह एक वेक्टर फ़ील्ड नहीं है क्योंकि यह न केवल स्थिति पर निर्भर करता है $\mathbf {x}$ एक विशेष सामग्री बिंदु, लेकिन सतह तत्व के स्थानीय अभिविन्यास पर भी इसके सामान्य वेक्टर द्वारा परिभाषित किया गया $\mathbf {n}$. कोई अंतर क्षेत्र $dS\,\!$ सामान्य वेक्टर के साथ $\mathbf {n}$ किसी दिए गए आंतरिक सतह क्षेत्र का $S\,\!$, शरीर के एक हिस्से को बाध्य करना, एक संपर्क बल का अनुभव करता है $d\mathbf {F} _{C}\,\!$ प्रत्येक तरफ शरीर के दोनों हिस्सों के बीच संपर्क से उत्पन्न होता है $S\,\!$, और यह द्वारा दिया गया है

$d\mathbf {F} _{C}=\mathbf {T} ^{(\mathbf {n} )}\,dS$

कहाँ पे $\mathbf {T} ^{(\mathbf {n} )}$ सतह कर्षण है, जिसे स्ट्रेस वेक्टर भी कहा जाता है, संकर्षण, या कर्षण वेक्टर। तनाव वेक्टर एक फ्रेम-इन अलग-अलग वेक्टर (यूलर-कोची तनाव सिद्धांत के लिए) है। विशेष आंतरिक सतह पर कुल संपर्क बल $S\,\!$ तब सभी अंतर सतहों पर संपर्क बलों की राशि (सतह अभिन्न) के रूप में व्यक्त किया जाता है $dS\,\!$:

$\mathbf {F} _{C}=\int _{S}\mathbf {T} ^{(\mathbf {n} )}\,dS$

कॉन्टिनम मैकेनिक्स में एक निकाय को तनाव-मुक्त माना जाता है यदि मौजूद एकमात्र बल उन अंतर-परमाणु बलों (आयनिक, धातु, और वैन डेर वाल्स बलों) को शरीर को एक साथ रखने और सभी बाहरी प्रभावों की अनुपस्थिति में अपना आकार रखने के लिए आवश्यक हैं।, गुरुत्वाकर्षण आकर्षण सहित। शरीर में शरीर के निर्माण के दौरान उत्पन्न तनाव को एक शरीर में तनावों पर विचार करते समय भी बाहर रखा जाता है।इसलिए, कॉन्टिनम मैकेनिक्स में विचार किए गए तनाव केवल शरीर के विरूपण द्वारा उत्पादित होते हैं, एससी।तनाव में केवल सापेक्ष परिवर्तन पर विचार किया जाता है, न कि तनाव के पूर्ण मूल्य।

बॉडी फोर्स

शरीर बल शरीर के बाहर स्रोतों से उत्पन्न होने वाले बल हैं वह शरीर की मात्रा (या द्रव्यमान) पर कार्य करता है।यह कहते हुए कि शरीर बल बाहरी स्रोतों के कारण हैं, इसका तात्पर्य है कि शरीर के विभिन्न हिस्सों (आंतरिक बलों) के बीच बातचीत अकेले संपर्क बलों के माध्यम से प्रकट होती है। ये बल बल क्षेत्रों में शरीर की उपस्थिति से उत्पन्न होते हैं, उदा।गुरुत्वाकर्षण क्षेत्र (गुरुत्वाकर्षण बल) या विद्युत चुम्बकीय क्षेत्र (विद्युत चुम्बकीय बल), या जब शरीर गति में होता है तो जड़त्वीय बलों से।चूंकि एक निरंतर शरीर के द्रव्यमान को लगातार वितरित किया जाता है, इसलिए द्रव्यमान से उत्पन्न होने वाले किसी भी बल को भी लगातार वितरित किया जाता है।इस प्रकार, शरीर बलों को वेक्टर क्षेत्रों द्वारा निर्दिष्ट किया जाता है, जिन्हें शरीर की पूरी मात्रा पर निरंतर माना जाता है, यानी इसमें हर बिंदु पर अभिनय करना।बॉडी फोर्स को बॉडी फोर्स डेंसिटी द्वारा दर्शाया जाता है $\mathbf {b} (\mathbf {x} ,t)$ (द्रव्यमान की प्रति यूनिट), जो एक फ्रेम-इंडिफ़रेंट वेक्टर फ़ील्ड है।

गुरुत्वाकर्षण बलों के मामले में, बल की तीव्रता निर्भर करती है, या आनुपातिक है, द्रव्यमान घनत्व $\mathbf {\rho } (\mathbf {x} ,t)\,\!$ सामग्री की, और यह प्रति यूनिट द्रव्यमान बल के संदर्भ में निर्दिष्ट है ($b_{i}\,\!$) या प्रति यूनिट वॉल्यूम ($p_{i}\,\!$)।ये दो विनिर्देश समीकरण द्वारा सामग्री घनत्व के माध्यम से संबंधित हैं $\rho b_{i}=p_{i}\,\!$।इसी तरह, विद्युत चुम्बकीय बलों की तीव्रता विद्युत चुम्बकीय क्षेत्र की ताकत (इलेक्ट्रिक चार्ज) पर निर्भर करती है।

एक निरंतर शरीर पर लागू कुल शरीर बल को व्यक्त किया जाता है

$\mathbf {F} _{B}=\int _{V}\mathbf {b} \,dm=\int _{V}\rho \mathbf {b} \,dV$

शरीर पर काम करने वाले शरीर बल और संपर्क बल किसी दिए गए बिंदु के सापेक्ष बल (टॉर्क्स) के संगत क्षणों को जन्म देते हैं।इस प्रकार, कुल लागू टोक़ ${\mathcal {M}}$ मूल के बारे में द्वारा दिया गया है

${\mathcal {M}}=\mathbf {M} _{C}+\mathbf {M} _{B}$

कुछ स्थितियों में, आमतौर पर सामग्री के यांत्रिक व्यवहार के विश्लेषण में नहीं माना जाता है, दो अन्य प्रकार के बलों को शामिल करना आवश्यक हो जाता है: ये युगल तनाव हैं (सतह जोड़े, टोरसे से संपर्क करें) और शरीर के क्षण।युगल तनाव एक सतह पर लागू प्रति यूनिट क्षेत्र के क्षण हैं।शरीर के क्षण, या शरीर के जोड़े, प्रति यूनिट मात्रा या प्रति यूनिट द्रव्यमान शरीर की मात्रा पर लागू होते हैं।दोनों एक विद्युत क्षेत्र, सामग्री की कार्रवाई के तहत एक ध्रुवीकृत ढांकता हुआ ठोस के लिए तनाव के विश्लेषण में महत्वपूर्ण हैं, जहां आणविक संरचना को ध्यान में रखा जाता है (जैसे हड्डियों), बाहरी चुंबकीय क्षेत्र की कार्रवाई के तहत ठोस, और अव्यवस्था सिद्धांतधातु। सामग्री जो शरीर के जोड़ों और युगल को प्रदर्शित करती है, विशेष रूप से बलों द्वारा उत्पादित क्षणों के अलावा तनाव को ध्रुवीय सामग्री कहा जाता है। गैर-ध्रुवीय सामग्री तब बलों के केवल क्षणों के साथ वे सामग्री हैं।कॉन्टिनम मैकेनिक्स की शास्त्रीय शाखाओं में तनाव के सिद्धांत का विकास गैर-ध्रुवीय सामग्रियों पर आधारित है।

इस प्रकार, शरीर में सभी लागू बलों और टोरों (समन्वय प्रणाली की उत्पत्ति के संबंध में) का योग द्वारा दिया जा सकता है

${\mathcal {F}}=\int _{V}\mathbf {a} \,dm=\int _{S}\mathbf {T} \,dS+\int _{V}\rho \mathbf {b} \,dV$

${\mathcal {M}}=\int _{S}\mathbf {r} \times \mathbf {T} \,dS+\int _{V}\mathbf {r} \times \rho \mathbf {b} \,dV$

किनेमेटिक्स: गति और विरूपण

चित्रा 2. एक निरंतर शरीर की गति।

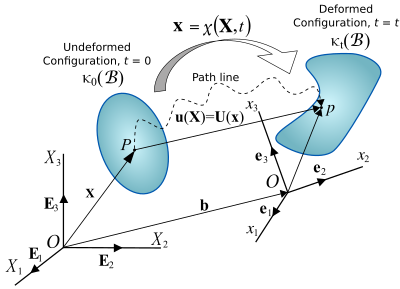
एक निरंतरता शरीर के विन्यास में परिवर्तन एक विस्थापन में परिणाम होता है।एक शरीर के विस्थापन में दो घटक होते हैं: एक कठोर-शरीर विस्थापन और एक विरूपण।एक कठोर-शरीर विस्थापन में एक साथ अनुवाद और शरीर का रोटेशन होता है, इसके आकार या आकार को बदले बिना।विरूपण का तात्पर्य एक प्रारंभिक या अनिर्धारित कॉन्फ़िगरेशन से शरीर के आकार और/या आकार में परिवर्तन है $\kappa _{0}({\mathcal {B}})$ एक वर्तमान या विकृत कॉन्फ़िगरेशन के लिए $\kappa _{t}({\mathcal {B}})$ (चित्र 2)।

एक निरंतर शरीर की गति विस्थापन का एक निरंतर समय अनुक्रम है।इस प्रकार, भौतिक निकाय अलग -अलग समय पर अलग -अलग कॉन्फ़िगरेशन पर कब्जा कर लेगा ताकि एक कण अंतरिक्ष में बिंदुओं की एक श्रृंखला पर कब्जा कर ले जो एक पथ रेखा का वर्णन करता है।

इस अर्थ में एक निरंतर शरीर की गति या विरूपण के दौरान निरंतरता है:

• किसी भी पल में एक बंद वक्र बनाने वाली सामग्री बिंदु हमेशा किसी भी समय में एक बंद वक्र बनाएंगे।
• किसी भी पल में एक बंद सतह बनाने वाली सामग्री बिंदु हमेशा किसी भी समय में एक बंद सतह बनाएगी और बंद सतह के भीतर का मामला हमेशा भीतर रहेगा।

यह एक संदर्भ कॉन्फ़िगरेशन या प्रारंभिक स्थिति की पहचान करने के लिए सुविधाजनक है, जिसे बाद के सभी कॉन्फ़िगरेशन से संदर्भित किया जाता है।संदर्भ कॉन्फ़िगरेशन को एक ऐसा नहीं होना चाहिए जो शरीर कभी भी कब्जा कर लेगा।अक्सर, कॉन्फ़िगरेशन पर $t=0$ संदर्भ विन्यास माना जाता है, $\kappa _{0}({\mathcal {B}})$।अवयव $X_{i}$ स्थिति वेक्टर की $\mathbf {X}$ एक कण, संदर्भ कॉन्फ़िगरेशन के संबंध में लिया गया, सामग्री या संदर्भ निर्देशांक कहा जाता है।

ठोस पदार्थों की गति या विरूपण, या तरल पदार्थों के प्रवाह का विश्लेषण करते समय, पूरे समय विन्यास के अनुक्रम या विकास का वर्णन करना आवश्यक है।गति के लिए एक विवरण सामग्री या संदर्भ निर्देशांक के संदर्भ में किया जाता है, जिसे सामग्री विवरण या लैग्रैन्जियन विवरण कहा जाता है।

Lagrangian विवरण

लैग्रैन्जियन विवरण में कणों की स्थिति और भौतिक गुणों को सामग्री या संदर्भ निर्देशांक और समय के संदर्भ में वर्णित किया गया है।इस मामले में संदर्भ कॉन्फ़िगरेशन कॉन्फ़िगरेशन है $t=0$।संदर्भ के फ्रेम में खड़ा एक पर्यवेक्षक स्थिति और भौतिक गुणों में परिवर्तन को देखता है क्योंकि समय आगे बढ़ने के साथ भौतिक शरीर अंतरिक्ष में चलता है।प्राप्त परिणाम प्रारंभिक समय और संदर्भ कॉन्फ़िगरेशन की पसंद से स्वतंत्र हैं, $\kappa _{0}({\mathcal {B}})$।यह विवरण सामान्य रूप से ठोस यांत्रिकी में उपयोग किया जाता है।

लैग्रैन्जियन विवरण में, एक निरंतरता शरीर की गति मानचित्रण फ़ंक्शन द्वारा व्यक्त की जाती है $\chi (\cdot )$ (चित्र 2),

$\mathbf {x} =\chi (\mathbf {X} ,t)$

जो प्रारंभिक कॉन्फ़िगरेशन की मैपिंग है $\kappa _{0}({\mathcal {B}})$ वर्तमान कॉन्फ़िगरेशन पर $\kappa _{t}({\mathcal {B}})$, उनके बीच एक ज्यामितीय पत्राचार देना, अर्थात् स्थिति वेक्टर देना $\mathbf {x} =x_{i}\mathbf {e} _{i}$ कि एक कण $X$, एक स्थिति वेक्टर के साथ $\mathbf {X}$ अपरिचित या संदर्भ विन्यास में $\kappa _{0}({\mathcal {B}})$, वर्तमान या विकृत कॉन्फ़िगरेशन में कब्जा कर लेगा $\kappa _{t}({\mathcal {B}})$ समय पर $t$।अवयव $x_{i}$ स्थानिक निर्देशांक कहा जाता है।

भौतिक और गतिज गुण $P_{ij\ldots }$, यानी थर्मोडायनामिक गुण और प्रवाह वेग, जो भौतिक शरीर की विशेषताओं का वर्णन या चिह्नित करते हैं, को स्थिति और समय के निरंतर कार्यों के रूप में व्यक्त किया जाता है, अर्थात्। $P_{ij\ldots }=P_{ij\ldots }(\mathbf {X} ,t)$।

किसी भी संपत्ति की सामग्री व्युत्पन्न $P_{ij\ldots }$ एक निरंतरता, जो एक स्केलर, वेक्टर या टेंसर हो सकता है, चलती सातत्य शरीर के कणों के एक विशिष्ट समूह के लिए उस संपत्ति के परिवर्तन की समय दर है।सामग्री व्युत्पन्न को पर्याप्त व्युत्पन्न, या कोमोविंग व्युत्पन्न, या संवहन व्युत्पन्न के रूप में भी जाना जाता है।यह उस दर के रूप में सोचा जा सकता है जिस पर संपत्ति बदल जाती है जब कणों के उस समूह के साथ यात्रा करने वाले पर्यवेक्षक द्वारा मापा जाता है।

लैग्रैन्जियन विवरण में, सामग्री व्युत्पन्न $P_{ij\ldots }$ बस समय के संबंध में आंशिक व्युत्पन्न है, और स्थिति वेक्टर $\mathbf {X}$ इसे स्थिर रखा जाता है क्योंकि यह समय के साथ नहीं बदलता है।इस प्रकार, हमारे पास है

${\frac {d}{dt}}[P_{ij\ldots }(\mathbf {X} ,t)]={\frac {\partial }{\partial t}}[P_{ij\ldots }(\mathbf {X} ,t)]$

तात्कालिक स्थिति $\mathbf {x}$ एक कण की एक संपत्ति है, और इसकी सामग्री व्युत्पन्न तात्कालिक प्रवाह वेग है $\mathbf {v}$ कण का।इसलिए, निरंतरता का प्रवाह वेग क्षेत्र द्वारा दिया जाता है

$\mathbf {v} ={\dot {\mathbf {x} }}={\frac {d\mathbf {x} }{dt}}={\frac {\partial \chi (\mathbf {X} ,t)}{\partial t}}$

इसी तरह, त्वरण क्षेत्र द्वारा दिया जाता है

$\mathbf {a} ={\dot {\mathbf {v} }}={\ddot {\mathbf {x} }}={\frac {d^{2}\mathbf {x} }{dt^{2}}}={\frac {\partial ^{2}\chi (\mathbf {X} ,t)}{\partial t^{2}}}$

लैग्रैन्जियन विवरण में निरंतरता को संदर्भ कॉन्फ़िगरेशन से मैपिंग के स्थानिक और अस्थायी निरंतरता द्वारा सामग्री बिंदुओं के वर्तमान कॉन्फ़िगरेशन तक व्यक्त किया जाता है।निरंतरता की विशेषता वाले सभी भौतिक मात्रा इस तरह से वर्णित हैं।इस अर्थ में, कार्य $\chi (\cdot )$ तथा $P_{ij\ldots }(\cdot )$ एकल-मूल्यवान और निरंतर हैं, जो निरंतर डेरिवेटिव के साथ अंतरिक्ष और समय के संबंध में जो भी आदेश की आवश्यकता होती है, आमतौर पर दूसरे या तीसरे के लिए।

यूलरियन विवरण

निरंतरता के व्युत्क्रम के लिए अनुमति देता है $\chi (\cdot )$ पीछे की ओर ट्रेस करने के लिए जहां वर्तमान में स्थित कण $\mathbf {x}$ प्रारंभिक या संदर्भित कॉन्फ़िगरेशन में स्थित था $\kappa _{0}({\mathcal {B}})$।इस मामले में गति का विवरण स्थानिक निर्देशांक के संदर्भ में किया जाता है, जिस स्थिति में स्थानिक विवरण या यूलरियन विवरण कहा जाता है, अर्थात वर्तमान कॉन्फ़िगरेशन को संदर्भ कॉन्फ़िगरेशन के रूप में लिया जाता है।

D'Alembert द्वारा पेश किया गया Eulerian विवरण, वर्तमान कॉन्फ़िगरेशन पर केंद्रित है $\kappa _{t}({\mathcal {B}})$, अंतरिक्ष में एक निश्चित बिंदु पर क्या हो रहा है, इस पर ध्यान देना, जैसे -जैसे समय आगे बढ़ता है, व्यक्तिगत कणों पर ध्यान देने के बजाय वे अंतरिक्ष और समय के माध्यम से चलते हैं।इस दृष्टिकोण को तरल प्रवाह के अध्ययन में आसानी से लागू किया जाता है, जहां सबसे बड़ी रुचि की कीनेमेटिक संपत्ति वह दर है जिस पर एक संदर्भ समय में द्रव के शरीर के आकार के बजाय परिवर्तन हो रहा है। गणितीय रूप से, यूलरियन विवरण का उपयोग करके एक निरंतरता की गति मानचित्रण फ़ंक्शन द्वारा व्यक्त की जाती है

$\mathbf {X} =\chi ^{-1}(\mathbf {x} ,t)$

जो कण का एक अनुरेखण प्रदान करता है जो अब स्थिति पर कब्जा कर लेता है $\mathbf {x}$ वर्तमान विन्यास में $\kappa _{t}({\mathcal {B}})$ इसकी मूल स्थिति के लिए $\mathbf {X}$ प्रारंभिक विन्यास में $\kappa _{0}({\mathcal {B}})$।

इस व्युत्क्रम फ़ंक्शन के अस्तित्व के लिए एक आवश्यक और पर्याप्त स्थिति यह है कि जैकबियन मैट्रिक्स के निर्धारक को अक्सर जैकबियन के रूप में संदर्भित किया जाता है, शून्य से अलग होना चाहिए।इस प्रकार,

$J=\left|{\frac {\partial \chi _{i}}{\partial X_{J}}}\right|=\left|{\frac {\partial x_{i}}{\partial X_{J}}}\right|\neq 0$

यूलरियन विवरण में, भौतिक गुण $P_{ij\ldots }$ के रूप में व्यक्त किए जाते हैं

$P_{ij\ldots }=P_{ij\ldots }(\mathbf {X} ,t)=P_{ij\ldots }[\chi ^{-1}(\mathbf {x} ,t),t]=p_{ij\ldots }(\mathbf {x} ,t)$

जहां कार्यात्मक रूप $P_{ij\ldots }$ लैग्रैन्जियन विवरण में के रूप में समान नहीं है $p_{ij\ldots }$ यूलरियन विवरण में।

की सामग्री व्युत्पन्न $p_{ij\ldots }(\mathbf {x} ,t)$, चेन नियम का उपयोग करना, तब है

${\frac {d}{dt}}[p_{ij\ldots }(\mathbf {x} ,t)]={\frac {\partial }{\partial t}}[p_{ij\ldots }(\mathbf {x} ,t)]+{\frac {\partial }{\partial x_{k}}}[p_{ij\ldots }(\mathbf {x} ,t)]{\frac {dx_{k}}{dt}}$

इस समीकरण के दाईं ओर पहला शब्द संपत्ति के परिवर्तन की स्थानीय दर देता है $p_{ij\ldots }(\mathbf {x} ,t)$ स्थिति में होने वाली स्थिति $\mathbf {x}$।दाहिने हाथ का दूसरा शब्द परिवर्तन की संवहन दर है और अंतरिक्ष (गति) में कण बदलने की स्थिति के योगदान को व्यक्त करता है।

यूलरियन विवरण में निरंतरता स्थानिक और अस्थायी निरंतरता और प्रवाह वेग क्षेत्र की निरंतर भिन्नता द्वारा व्यक्त की जाती है।सभी भौतिक मात्राओं को इस तरह से परिभाषित किया जाता है, प्रत्येक तत्काल में, वर्तमान कॉन्फ़िगरेशन में, वेक्टर स्थिति के एक समारोह के रूप में $\mathbf {x}$।

विस्थापन क्षेत्र

एक कण की स्थिति में शामिल होने वाला वेक्टर $P$ अनिर्धारित कॉन्फ़िगरेशन में और विकृत कॉन्फ़िगरेशन को विस्थापन वेक्टर कहा जाता है $\mathbf {u} (\mathbf {X} ,t)=u_{i}\mathbf {e} _{i}$, लैग्रैन्जियन विवरण में, या $\mathbf {U} (\mathbf {x} ,t)=U_{J}\mathbf {E} _{J}$, यूलरियन विवरण में।

एक विस्थापन क्षेत्र शरीर के सभी कणों के लिए सभी विस्थापन वैक्टर का एक वेक्टर क्षेत्र है, जो अवांछनीय कॉन्फ़िगरेशन के साथ विकृत कॉन्फ़िगरेशन से संबंधित है।विस्थापन क्षेत्र के संदर्भ में एक निरंतरता शरीर की विरूपण या गति का विश्लेषण करना सुविधाजनक है, सामान्य रूप से, विस्थापन क्षेत्र को सामग्री निर्देशांक के रूप में व्यक्त किया जाता है

$\mathbf {u} (\mathbf {X} ,t)=\mathbf {b} +\mathbf {x} (\mathbf {X} ,t)-\mathbf {X} \qquad {\text{or}}\qquad u_{i}=\alpha _{iJ}b_{J}+x_{i}-\alpha _{iJ}X_{J}$

या स्थानिक निर्देशांक के संदर्भ में

$\mathbf {U} (\mathbf {x} ,t)=\mathbf {b} +\mathbf {x} -\mathbf {X} (\mathbf {x} ,t)\qquad {\text{or}}\qquad U_{J}=b_{J}+\alpha _{Ji}x_{i}-X_{J}\,$

कहाँ पे $\alpha _{Ji}$ यूनिट वैक्टर के साथ सामग्री और स्थानिक समन्वय प्रणालियों के बीच दिशा कोसाइन हैं $\mathbf {E} _{J}$ तथा $\mathbf {e} _{i}$, क्रमश।इस प्रकार

$\mathbf {E} _{J}\cdot \mathbf {e} _{i}=\alpha _{Ji}=\alpha _{iJ}$

और के बीच संबंध $u_{i}$ तथा $U_{J}$ तब द्वारा दिया जाता है

$u_{i}=\alpha _{iJ}U_{J}\qquad {\text{or}}\qquad U_{J}=\alpha _{Ji}u_{i}$

जानते हुए भी

$\mathbf {e} _{i}=\alpha _{iJ}\mathbf {E} _{J}$

फिर

$\mathbf {u} (\mathbf {X} ,t)=u_{i}\mathbf {e} _{i}=u_{i}(\alpha _{iJ}\mathbf {E} _{J})=U_{J}\mathbf {E} _{J}=\mathbf {U} (\mathbf {x} ,t)$

अवांछित और विकृत कॉन्फ़िगरेशन के लिए समन्वय प्रणालियों को सुपरइम्पोज करने के लिए यह आम है, जिसके परिणामस्वरूप होता है $\mathbf {b} =0$, और दिशा कोसाइन्स क्रोनकर डेल्टास बन जाते हैं, अर्थात्

$\mathbf {E} _{J}\cdot \mathbf {e} _{i}=\delta _{Ji}=\delta _{iJ}$

इस प्रकार, हमारे पास है

$\mathbf {u} (\mathbf {X} ,t)=\mathbf {x} (\mathbf {X} ,t)-\mathbf {X} \qquad {\text{or}}\qquad u_{i}=x_{i}-\delta _{iJ}X_{J}$

या स्थानिक निर्देशांक के संदर्भ में

$\mathbf {U} (\mathbf {x} ,t)=\mathbf {x} -\mathbf {X} (\mathbf {x} ,t)\qquad {\text{or}}\qquad U_{J}=\delta _{Ji}x_{i}-X_{J}$

<!-

गवर्निंग समीकरण

कॉन्टिनम मैकेनिक्स उन सामग्रियों के व्यवहार से संबंधित है जिन्हें कुछ लंबाई और समय के तराजू के लिए निरंतर के रूप में अनुमानित किया जा सकता है। ऐसी सामग्रियों के यांत्रिकी को नियंत्रित करने वाले समीकरणों में द्रव्यमान, गति और ऊर्जा के लिए संतुलन कानून शामिल हैं। गवर्निंग समीकरणों की प्रणाली को पूरा करने के लिए कीनेमेटिक संबंध और संवैधानिक समीकरणों की आवश्यकता है। संवैधानिक संबंधों के रूप में शारीरिक प्रतिबंधों को लागू किया जा सकता है कि सभी शर्तों के तहत थर्मोडायनामिक्स के दूसरे कानून को संतुष्ट किया जाए। ठोस पदार्थों के निरंतर यांत्रिकी में, थर्मोडायनामिक्स का दूसरा नियम संतुष्ट है यदि क्लॉसियस -दुहम असमानता | एंट्रॉपी असमानता का क्लॉसियस -दयूम रूप संतुष्ट है।

संतुलन कानून इस विचार को व्यक्त करते हैं कि मात्रा में मात्रा (द्रव्यमान, गति, ऊर्जा) के परिवर्तन की दर तीन कारणों से उत्पन्न होनी चाहिए:

1. भौतिक मात्रा स्वयं सतह के माध्यम से बहती है जो मात्रा को बाधित करती है,
2. वॉल्यूम की सतह पर भौतिक मात्रा का एक स्रोत है, या/और,
3. वॉल्यूम के अंदर भौतिक मात्रा का एक स्रोत है।

होने देना $\Omega$ शरीर हो (यूक्लिडियन स्पेस का एक खुला सबसेट) और चलो $\partial \Omega$ इसकी सतह हो (की सीमा) $\Omega$)।

शरीर में सामग्री बिंदुओं की गति को मानचित्र द्वारा वर्णित किया जाए

$\mathbf {x} ={\boldsymbol {\chi }}(\mathbf {X} )=\mathbf {x} (\mathbf {X} )$

कहाँ पे $\mathbf {X}$ प्रारंभिक कॉन्फ़िगरेशन में एक बिंदु की स्थिति है और $\mathbf {x}$ विकृत कॉन्फ़िगरेशन में एक ही बिंदु का स्थान है।

विरूपण ढाल द्वारा दिया जाता है

${\boldsymbol {F}}={\frac {\partial \mathbf {x} }{\partial \mathbf {X} }}=\nabla \mathbf {x} ~.$

संतुलन कानून

होने देना $f(\mathbf {x} ,t)$ एक भौतिक मात्रा हो जो शरीर के माध्यम से बह रही हो।होने देना $g(\mathbf {x} ,t)$ शरीर की सतह पर स्रोत बनें और जाने दें $h(\mathbf {x} ,t)$ शरीर के अंदर स्रोत बनें।होने देना $\mathbf {n} (\mathbf {x} ,t)$ सतह के लिए बाहरी इकाई सामान्य हो $\partial \Omega$।होने देना $\mathbf {v} (\mathbf {x} ,t)$ भौतिक कणों का प्रवाह वेग बनें जो भौतिक मात्रा को ले जाते हैं।इसके अलावा, उस गति को दें जिस पर बाउंडिंग सतह $\partial \Omega$ चल रहा है $u_{n}$ (दिशा में $\mathbf {n}$)।

फिर, संतुलन कानूनों को सामान्य रूप में व्यक्त किया जा सकता है

${\cfrac {d}{dt}}\left[\int _{\Omega }f(\mathbf {x} ,t)~{\text{dV}}\right]=\int _{\partial \Omega }f(\mathbf {x} ,t)[u_{n}(\mathbf {x} ,t)-\mathbf {v} (\mathbf {x} ,t)\cdot \mathbf {n} (\mathbf {x} ,t)]~{\text{dA}}+\int _{\partial \Omega }g(\mathbf {x} ,t)~{\text{dA}}+\int _{\Omega }h(\mathbf {x} ,t)~{\text{dV}}~.$

कार्य $f(\mathbf {x} ,t)$, $g(\mathbf {x} ,t)$, तथा $h(\mathbf {x} ,t)$ स्केलर मूल्यवान हो सकता है, वेक्टर मूल्यवान, या टेंसर मूल्यवान हो सकता है - भौतिक मात्रा के आधार पर जो संतुलन समीकरण से संबंधित है।यदि शरीर में आंतरिक सीमाएं हैं, तो कूदने के कारण भी संतुलन कानूनों में निर्दिष्ट करने की आवश्यकता है।

यदि हम यूलरियन दृष्टिकोण लेते हैं, तो यह दिखाया जा सकता है कि एक ठोस के लिए द्रव्यमान, गति, और ऊर्जा के संतुलन कानूनों को लिखा जा सकता है (यह मानते हुए कि स्रोत शब्द द्रव्यमान और कोणीय गति समीकरणों के लिए शून्य है)

${\begin{aligned}{\dot {\rho }}+\rho ({\boldsymbol {\nabla }}\cdot \mathbf {v} )&=0&&\qquad {\text{Balance of Mass}}\\\rho ~{\dot {\mathbf {v} }}-{\boldsymbol {\nabla }}\cdot {\boldsymbol {\sigma }}-\rho ~\mathbf {b} &=0&&\qquad {\text{Balance of Linear Momentum (Cauchy's first law of motion)}}\\{\boldsymbol {\sigma }}&={\boldsymbol {\sigma }}^{T}&&\qquad {\text{Balance of Angular Momentum (Cauchy's second law of motion)}}\\\rho ~{\dot {e}}-{\boldsymbol {\sigma }}:({\boldsymbol {\nabla }}\mathbf {v} )+{\boldsymbol {\nabla }}\cdot \mathbf {q} -\rho ~s&=0&&\qquad {\text{Balance of Energy.}}\end{aligned}}$

उपरोक्त समीकरणों में $\rho (\mathbf {x} ,t)$ द्रव्यमान घनत्व (वर्तमान) है, ${\dot {\rho }}$ की सामग्री समय व्युत्पन्न है $\rho$, $\mathbf {v} (\mathbf {x} ,t)$ कण वेग है, ${\dot {\mathbf {v} }}$ की सामग्री समय व्युत्पन्न है $\mathbf {v}$, ${\boldsymbol {\sigma }}(\mathbf {x} ,t)$ कॉची तनाव टेंसर है, $\mathbf {b} (\mathbf {x} ,t)$ शरीर बल घनत्व है, $e(\mathbf {x} ,t)$ प्रति यूनिट द्रव्यमान की आंतरिक ऊर्जा है, ${\dot {e}}$ की सामग्री समय व्युत्पन्न है $e$, $\mathbf {q} (\mathbf {x} ,t)$ हीट फ्लक्स वेक्टर है, और $s(\mathbf {x} ,t)$ प्रति यूनिट द्रव्यमान में एक ऊर्जा स्रोत है।

संदर्भ कॉन्फ़िगरेशन (Lagrangian दृष्टिकोण) के संबंध में, संतुलन कानूनों को लिखा जा सकता है

${\begin{aligned}\rho ~\det({\boldsymbol {F}})-\rho _{0}&=0&&\qquad {\text{Balance of Mass}}\\\rho _{0}~{\ddot {\mathbf {x} }}-{\boldsymbol {\nabla }}_{\circ }\cdot {\boldsymbol {P}}^{T}-\rho _{0}~\mathbf {b} &=0&&\qquad {\text{Balance of Linear Momentum}}\\{\boldsymbol {F}}\cdot {\boldsymbol {P}}^{T}&={\boldsymbol {P}}\cdot {\boldsymbol {F}}^{T}&&\qquad {\text{Balance of Angular Momentum}}\\\rho _{0}~{\dot {e}}-{\boldsymbol {P}}^{T}:{\dot {\boldsymbol {F}}}+{\boldsymbol {\nabla }}_{\circ }\cdot \mathbf {q} -\rho _{0}~s&=0&&\qquad {\text{Balance of Energy.}}\end{aligned}}$

ऊपरोक्त में, ${\boldsymbol {P}}$ पहला पिओला-किरचॉफ स्ट्रेस टेंसर है, और $\rho _{0}$ संदर्भ कॉन्फ़िगरेशन में द्रव्यमान घनत्व है।पहला पिओला-किरचॉफ स्ट्रेस टेंसर कॉची स्ट्रेस टेंसर से संबंधित है

${\boldsymbol {P}}=J~{\boldsymbol {\sigma }}\cdot {\boldsymbol {F}}^{-T}~{\text{where}}~J=\det({\boldsymbol {F}})$

हम वैकल्पिक रूप से नाममात्र तनाव टेंसर को परिभाषित कर सकते हैं ${\boldsymbol {N}}$ जो पहले पियोल-किरचॉफ स्ट्रेस टेंसर का ट्रांसपोज़ है

${\boldsymbol {N}}={\boldsymbol {P}}^{T}=J~{\boldsymbol {F}}^{-1}\cdot {\boldsymbol {\sigma }}~.$

तब संतुलन कानून बन जाते हैं

${\begin{aligned}\rho ~\det({\boldsymbol {F}})-\rho _{0}&=0&&\qquad {\text{Balance of Mass}}\\\rho _{0}~{\ddot {\mathbf {x} }}-{\boldsymbol {\nabla }}_{\circ }\cdot {\boldsymbol {N}}-\rho _{0}~\mathbf {b} &=0&&\qquad {\text{Balance of Linear Momentum}}\\{\boldsymbol {F}}\cdot {\boldsymbol {N}}&={\boldsymbol {N}}^{T}\cdot {\boldsymbol {F}}^{T}&&\qquad {\text{Balance of Angular Momentum}}\\\rho _{0}~{\dot {e}}-{\boldsymbol {N}}:{\dot {\boldsymbol {F}}}+{\boldsymbol {\nabla }}_{\circ }\cdot \mathbf {q} -\rho _{0}~s&=0&&\qquad {\text{Balance of Energy.}}\end{aligned}}$

उपरोक्त समीकरणों में ऑपरेटरों को इस तरह परिभाषित किया गया है

${\boldsymbol {\nabla }}\mathbf {v} =\sum _{i,j=1}^{3}{\frac {\partial v_{i}}{\partial x_{j}}}\mathbf {e} _{i}\otimes \mathbf {e} _{j}=v_{i,j}\mathbf {e} _{i}\otimes \mathbf {e} _{j}~;~~{\boldsymbol {\nabla }}\cdot \mathbf {v} =\sum _{i=1}^{3}{\frac {\partial v_{i}}{\partial x_{i}}}=v_{i,i}~;~~{\boldsymbol {\nabla }}\cdot {\boldsymbol {S}}=\sum _{i,j=1}^{3}{\frac {\partial S_{ij}}{\partial x_{j}}}~\mathbf {e} _{i}=\sigma _{ij,j}~\mathbf {e} _{i}~.$

कहाँ पे $\mathbf {v}$ एक वेक्टर क्षेत्र है, ${\boldsymbol {S}}$ एक दूसरे क्रम के टेंसर क्षेत्र है, और $\mathbf {e} _{i}$ वर्तमान कॉन्फ़िगरेशन में एक ऑर्थोनॉर्मल आधार के घटक हैं।भी,

${\boldsymbol {\nabla }}_{\circ }\mathbf {v} =\sum _{i,j=1}^{3}{\frac {\partial v_{i}}{\partial X_{j}}}\mathbf {E} _{i}\otimes \mathbf {E} _{j}=v_{i,j}\mathbf {E} _{i}\otimes \mathbf {E} _{j}~;~~{\boldsymbol {\nabla }}_{\circ }\cdot \mathbf {v} =\sum _{i=1}^{3}{\frac {\partial v_{i}}{\partial X_{i}}}=v_{i,i}~;~~{\boldsymbol {\nabla }}_{\circ }\cdot {\boldsymbol {S}}=\sum _{i,j=1}^{3}{\frac {\partial S_{ij}}{\partial X_{j}}}~\mathbf {E} _{i}=S_{ij,j}~\mathbf {E} _{i}$

कहाँ पे $\mathbf {v}$ एक वेक्टर क्षेत्र है, ${\boldsymbol {S}}$ एक दूसरे क्रम के टेंसर क्षेत्र है, और $\mathbf {E} _{i}$ संदर्भ कॉन्फ़िगरेशन में एक ऑर्थोनॉर्मल आधार के घटक हैं।

आंतरिक उत्पाद को परिभाषित किया गया है

${\boldsymbol {A}}:{\boldsymbol {B}}=\sum _{i,j=1}^{3}A_{ij}~B_{ij}=\operatorname {trace} ({\boldsymbol {A}}{\boldsymbol {B}}^{T})~.$

क्लॉसियस -दुहम असमानता

क्लॉज़ियस-दुहम असमानता का उपयोग लोचदार-प्लास्टिक सामग्रियों के लिए थर्मोडायनामिक्स के दूसरे नियम को व्यक्त करने के लिए किया जा सकता है।यह असमानता प्राकृतिक प्रक्रियाओं की अपरिवर्तनीयता से संबंधित एक बयान है, खासकर जब ऊर्जा अपव्यय शामिल है।

पिछले खंड में संतुलन कानूनों की तरह, हम मानते हैं कि एक मात्रा का प्रवाह, मात्रा का एक स्रोत, और प्रति यूनिट द्रव्यमान की मात्रा का एक आंतरिक घनत्व है।इस मामले में ब्याज की मात्रा एन्ट्रापी है।इस प्रकार, हम मानते हैं कि एक एन्ट्रापी प्रवाह, एक एन्ट्रापी स्रोत, एक आंतरिक द्रव्यमान घनत्व है $\rho$ और एक आंतरिक विशिष्ट एन्ट्रापी (यानी प्रति यूनिट द्रव्यमान एन्ट्रापी) $\eta$ ब्याज के क्षेत्र में।

होने देना $\Omega$ ऐसा क्षेत्र बनें और जाने दें $\partial \Omega$ इसकी सीमा हो।तब थर्मोडायनामिक्स के दूसरे नियम में कहा गया है कि की वृद्धि की दर $\eta$ इस क्षेत्र में उस आपूर्ति के योग से अधिक या बराबर है $\Omega$ (एक प्रवाह के रूप में या आंतरिक स्रोतों से) और आंतरिक एन्ट्रापी घनत्व का परिवर्तन $\rho \eta$ क्षेत्र के अंदर और बाहर बहने वाली सामग्री के कारण।

होने देना $\partial \Omega$ एक प्रवाह वेग के साथ स्थानांतरित करें $u_{n}$ और कणों को अंदर जाने दें $\Omega$ वेग है $\mathbf {v}$।होने देना $\mathbf {n}$ सतह के लिए सामान्य इकाई बाहर की ओर हो $\partial \Omega$।होने देना $\rho$ क्षेत्र में पदार्थ का घनत्व हो, ${\bar {q}}$ सतह पर एन्ट्रापी प्रवाह हो, और $r$ प्रति यूनिट द्रव्यमान में एन्ट्रापी स्रोत बनें। तब एन्ट्रापी असमानता के रूप में लिखा जा सकता है

${\cfrac {d}{dt}}\left(\int _{\Omega }\rho ~\eta ~{\text{dV}}\right)\geq \int _{\partial \Omega }\rho ~\eta ~(u_{n}-\mathbf {v} \cdot \mathbf {n} )~{\text{dA}}+\int _{\partial \Omega }{\bar {q}}~{\text{dA}}+\int _{\Omega }\rho ~r~{\text{dV}}.$

स्केलर एन्ट्रापी फ्लक्स संबंध द्वारा सतह पर वेक्टर फ्लक्स से संबंधित हो सकता है ${\bar {q}}=-{\boldsymbol {\psi }}(\mathbf {x} )\cdot \mathbf {n}$।वृद्धिशील रूप से आइसोथर्मल स्थितियों की धारणा के तहत, हमारे पास है

${\boldsymbol {\psi }}(\mathbf {x} )={\cfrac {\mathbf {q} (\mathbf {x} )}{T}}~;~~r={\cfrac {s}{T}}$

कहाँ पे $\mathbf {q}$ हीट फ्लक्स वेक्टर है, $s$ प्रति यूनिट द्रव्यमान में एक ऊर्जा स्रोत है, और $T$ एक सामग्री बिंदु का पूर्ण तापमान है $\mathbf {x}$ समय पर $t$।

फिर हमारे पास अभिन्न रूप में क्लॉज़ियस -दुहम असमानता है:

${{\cfrac {d}{dt}}\left(\int _{\Omega }\rho ~\eta ~{\text{dV}}\right)\geq \int _{\partial \Omega }\rho ~\eta ~(u_{n}-\mathbf {v} \cdot \mathbf {n} )~{\text{dA}}-\int _{\partial \Omega }{\cfrac {\mathbf {q} \cdot \mathbf {n} }{T}}~{\text{dA}}+\int _{\Omega }{\cfrac {\rho ~s}{T}}~{\text{dV}}.}$

हम दिखा सकते हैं कि एन्ट्रापी असमानता को अंतर के रूप में लिखा जा सकता है

${\rho ~{\dot {\eta }}\geq -{\boldsymbol {\nabla }}\cdot \left({\cfrac {\mathbf {q} }{T}}\right)+{\cfrac {\rho ~s}{T}}.}$

Cauchy तनाव और आंतरिक ऊर्जा के संदर्भ में, क्लॉसियस -दुहम असमानता के रूप में लिखा जा सकता है

${\rho ~({\dot {e}}-T~{\dot {\eta }})-{\boldsymbol {\sigma }}:{\boldsymbol {\nabla }}\mathbf {v} \leq -{\cfrac {\mathbf {q} \cdot {\boldsymbol {\nabla }}T}{T}}.}$

अनुप्रयोग

• सातत्यक यांत्रिकी
  • ठोस यांत्रिकी
  • तरल यांत्रिकी
• अभियांत्रिकी
  • असैनिक अभियंत्रण
  • मैकेनिकल इंजीनियरिंग
  • अंतरिक्ष इंजिनीयरिंग
  • जैवचिकित्सा अभियांत्रिकी
  • केमिकल इंजीनियरिंग

यह भी देखें

• बर्नौली का सिद्धांत
• Cauchy लोचदार सामग्री
• विन्यास यांत्रिकी
• Curvilinear निर्देशांक
• स्थिति के समीकरण
• परिमित विरूपण टेनर्स
• परिमित तनाव सिद्धांत
• हाइपरलास्टिक सामग्री
• प्रवाह क्षेत्र के लैग्रैन्जियन और यूलरियन विनिर्देशन
• चल सेलुलर ऑटोमेटन
• पेरिडिनैमिक्स (एक गैर-स्थानीय निरंतरता सिद्धांत जो अभिन्न समीकरणों के लिए अग्रणी है)
• तनाव (भौतिकी)
• तनाव के उपाय
• टेंसर कैलकुलस
• टेंसर व्युत्पन्न (सातत्य यांत्रिकी)
• लोच का सिद्धांत

संदर्भ

वर्क्स का हवाला दिया गया

• Dienes, J. K.; Solem, J. C. (1999). "Nonlinear behavior of some hydrostatically stressed isotropic elastomeric foams". Acta Mechanica. 138 (3–4): 155–162. doi:10.1007/BF01291841. S2CID 120320672.
• Fung, Y. C. (1977). A First Course in Continuum Mechanics (2nd ed.). Prentice-Hall, Inc. ISBN 978-0-13-318311-5.
• Lubliner, Jacob (2008). Plasticity Theory (PDF) (Revised ed.). Dover Publications. ISBN 978-0-486-46290-5. Archived from the original (PDF) on 31 March 2010.
• Ostoja-Starzewski, M. (2008). "7-10". Microstructural randomness and scaling in mechanics of materials. CRC Press. ISBN 978-1-58488-417-0.
• Spencer, A. J. M. (1980). Continuum Mechanics. Longman Group Limited (London). p. 83. ISBN 978-0-582-44282-5.
• Roberts, A. J. (1994). A One-Dimensional Introduction to Continuum Mechanics. World Scientific.
• Smith, Donald R. (1993). "2". An introduction to continuum mechanics-after Truesdell and Noll. Solids mechanics and its applications. Vol. 22. Springer Science & Business Media. ISBN 978-90-481-4314-6.

सामान्य संदर्भ

• Batra, R. C. (2006). Elements of Continuum Mechanics. Reston, VA: AIAA.
• Bertram, Albrecht (2012). Elasticity and Plasticity of Large Deformations - An Introduction (Third ed.). Springer. doi:10.1007/978-3-642-24615-9. ISBN 978-3-642-24615-9. S2CID 116496103.
• Chandramouli, P.N (2014). Continuum Mechanics. Yes Dee Publishing Pvt Ltd. ISBN 9789380381398.
• Eringen, A. Cemal (1980). Mechanics of Continua (2nd ed.). Krieger Pub Co. ISBN 978-0-88275-663-9.
• Chen, Youping; James D. Lee; Azim Eskandarian (2009). Meshless Methods in Solid Mechanics (First ed.). Springer New York. ISBN 978-1-4419-2148-2.
• Dill, Ellis Harold (2006). Continuum Mechanics: Elasticity, Plasticity, Viscoelasticity. Germany: CRC Press. ISBN 978-0-8493-9779-0.
• Dimitrienko, Yuriy (2011). Nonlinear Continuum Mechanics and Large Inelastic Deformations. Germany: Springer. ISBN 978-94-007-0033-8.
• Hutter, Kolumban; Klaus Jöhnk (2004). Continuum Methods of Physical Modeling. Germany: Springer. ISBN 978-3-540-20619-4.
• Gurtin, M. E. (1981). An Introduction to Continuum Mechanics. New York: Academic Press.
• Lai, W. Michael; David Rubin; Erhard Krempl (1996). Introduction to Continuum Mechanics (3rd ed.). Elsevier, Inc. ISBN 978-0-7506-2894-5. Archived from the original on 6 February 2009.
• Lubarda, Vlado A. (2001). Elastoplasticity Theory. CRC Press. ISBN 978-0-8493-1138-3.
• Malvern, Lawrence E. (1969). Introduction to the mechanics of a continuous medium. New Jersey: Prentice-Hall, Inc.
• Mase, George E. (1970). Continuum Mechanics. McGraw-Hill Professional. ISBN 978-0-07-040663-6.
• Mase, G. Thomas; George E. Mase (1999). Continuum Mechanics for Engineers (Second ed.). CRC Press. ISBN 978-0-8493-1855-9.
• Maugin, G. A. (1999). The Thermomechanics of Nonlinear Irreversible Behaviors: An Introduction. Singapore: World Scientific.
• Nemat-Nasser, Sia (2006). Plasticity: A Treatise on Finite Deformation of Heterogeneous Inelastic Materials. Cambridge: Cambridge University Press. ISBN 978-0-521-83979-2.
• Ostoja-Starzewski, Martin (2008). Microstructural Randomness and Scaling in Mechanics of Materials. Boca Raton, FL: Chapman & Hall/CRC Press. ISBN 978-1-58488-417-0.
• Rees, David (2006). Basic Engineering Plasticity - An Introduction with Engineering and Manufacturing Applications. Butterworth-Heinemann. ISBN 978-0-7506-8025-7.
• Wright, T. W. (2002). The Physics and Mathematics of Adiabatic Shear Bands. Cambridge, UK: Cambridge University Press.

बाहरी संबंध

• "Objectivity in classical continuum mechanics: Motions, Eulerian and Lagrangian functions; Deformation gradient; Lie derivatives; Velocity-addition formula, Coriolis; Objectivity" by Gilles Leborgne, April 7, 2021: "Part IV Velocity-addition formula and Objectivity"