मैक्सवेल के समीकरण

For thermodynamic relations, see Maxwell relations.

मैक्सवेल के समीकरण, या मैक्सवेल-हेविसाइड समीकरण, युग्मित आंशिक विभेदक समीकरणों का एक संग्रह हैं, जो लोरेंत्ज़ बल सिद्धांत के साथ शास्त्रीय विद्युत चुंबकत्व, शास्त्रीय प्रकाशिकी और विद्युत परिपथों की नींव बनाते हैं। समीकरण इलेक्ट्रिक, ऑप्टिकल और रेडियो तकनीकों के लिए एक गणितीय प्रतिरूप प्रदान करते हैं, जैसे कि बिजली उत्पादन, बिजली का आवेश, तार रहित संचार, लेंस, रडार आदि। वे वर्णन करते हैं कि विद्युत और चुंबकीय क्षेत्र कैसे आवेशों, विद्युत धाराओं और क्षेत्रों के परिवर्तनों द्वारा उत्पन्न होते हैं। समीकरणों का नाम भौतिक विज्ञानी और गणितज्ञ जेम्स क्लर्क मैक्सवेल के नाम पर रखा गया है, जिन्होंने 1861 और 1862 में, समीकरणों का एक प्रारंभिक रूप प्रकाशित किया जिसमें लोरेंत्ज़ बल सिद्धांत शामिल था। मैक्सवेल ने सबसे पहले समीकरणों का उपयोग यह प्रस्तावित करने के लिए किया कि प्रकाश एक विद्युत चुम्बकीय घटना है। उनके सबसे सामान्य सूत्रीकरण में समीकरणों के आधुनिक रूप का श्रेय ओलिवर हीविसाइड को दिया जाता है।

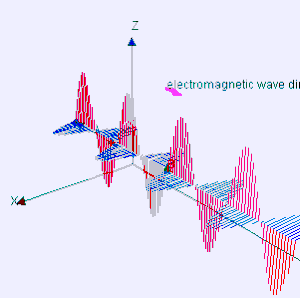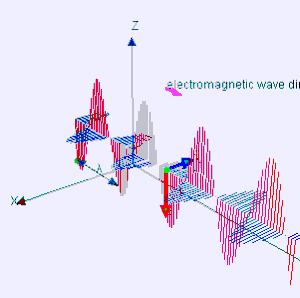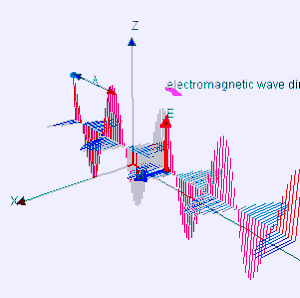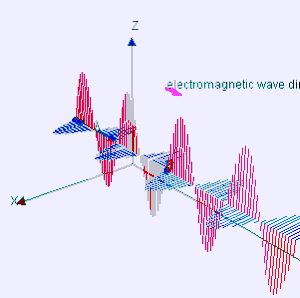
मैक्सवेल के समीकरणों को यह प्रदर्शित करने के लिए संयोजित किया जा सकता है कि कैसे विद्युत चुम्बकीय क्षेत्रों (तरंगों) में उतार-चढ़ाव निर्वात में एक स्थिर गति से फैलता है, प्रकाश की गति (299792458 m/s). विद्युत चुम्बकीय विकिरण के रूप में जाना जाता है, ये तरंगें रेडियो तरंगों से गामा किरणों तक विकिरण के एक वर्णक्रम का उत्पादन करने के लिए विभिन्न तरंग दैर्ध्य पर होती हैं।

समीकरणों के दो प्रमुख रूप हैं। सूक्ष्म समीकरणों में सार्वभौमिक प्रयोज्यता होती है लेकिन सामान्य गणनाओं के लिए बोझिल होते हैं। वे विद्युत और चुंबकीय क्षेत्र को कुल आवेश और कुल धारा से संबंधित करते हैं, जिसमें परमाणु मापक पर सामग्री में जटिल आवेश और धाराएँ शामिल हैं। मैक्रोस्कोपिक समीकरण दो नए सहायक क्षेत्रों को परिभाषित करते हैं जो पदार्थ के बड़े मापक पर व्यवहार का वर्णन करते हैं बिना परमाणु-मापक के शुल्क और चक्रण जैसी क्वांटम घटनाओं पर विचार किए बिना। हालांकि, उनके उपयोग के लिए सामग्री के विद्युत चुम्बकीय प्रतिक्रिया के घटनात्मक विवरण के लिए प्रयोगात्मक रूप से निर्धारित प्राचल की आवश्यकता होती है। "मैक्सवेल के समीकरण" शब्द का प्रयोग प्रायः वैकल्पिक योगों के लिए भी किया जाता है। विद्युत और चुंबकीय स्केलर क्षमता के आधार पर मैक्सवेल के समीकरणों के संस्करणों को सीमा मूल्य समस्या, विश्लेषणात्मक यांत्रिकी के रूप में हल करने लिए पसंद किया जाता है। सहपरिवर्ती सूत्रीकरण (अलग-अलग स्थान और समय के बजाय स्पेसटाइम पर) विशेष सापेक्षता प्रकट के साथ मैक्सवेल के समीकरणों की अनुकूलता बनाता है। आमतौर पर उच्च-ऊर्जा और गुरुत्वाकर्षण भौतिकी में उपयोग किए किए जाने वाले, घुमावदार स्पेसटाइम में मैक्सवेल के समीकरण, सामान्य सापेक्षता के साथ संगत होते हैं। वास्तव में, अल्बर्ट आइंस्टीन ने प्रकाश की अपरिवर्तनीय गति को समायोजित करने के लिए विशेष और सामान्य सापेक्षता विकसित की, मैक्सवेल के समीकरणों का एक परिणाम, इस सिद्धांत के साथ कि केवल सापेक्ष गति के भौतिक परिणाम होते हैं।

समीकरणों के प्रकाशन ने पहले अलग-अलग वर्णित घटनाओं के लिए एक सिद्धांत के एकीकरण (भौतिकी) को चिह्नित किया: चुंबकत्व, बिजली, प्रकाश और संबद्ध विकिरण। 20वीं शताब्दी के मध्य से, यह समझा गया है कि मैक्सवेल के समीकरण विद्युत चुंबकीय घटना का सटीक विवरण नहीं देते हैं, बल्कि क्वांटम इलेक्ट्रोडायनामिक्स के अधिक सटीक सिद्धांत की शास्त्रीय क्षेत्र सिद्धांत सीमा हैं।

समीकरणों का इतिहास

Main article: History of Maxwell's equations

वैचारिक विवरण

गॉस का सिद्धांत

Main article: Gauss's law

गॉस का सिद्धांत एक स्थिर विद्युत क्षेत्र और विद्युत आवेशों के बीच के संबंध का वर्णन करता है: एक स्थिर विद्युत क्षेत्र सकारात्मक आवेशों से ऋणात्मक आवेशों की ओर इशारा करता है, और एक बंद सतह के माध्यम से विद्युत क्षेत्र का शुद्ध बहिर्वाह बाध्य आवेश सहित संलग्न आवेश के समानुपाती होता है, सामग्री के ध्रुवीकरण के कारण अनुपात का गुणांक मुक्त स्थान की पारगम्यता है।

चुम्बकत्व के लिए गॉस का सिद्धांत

Main article: Gauss's law for magnetism

चुंबकत्व के लिए गॉस का सिद्धांत: चुंबकीय क्षेत्र रेखाएं न तो कभी शुरू होती हैं और न ही समाप्त होती हैं, लेकिन लूप बनाती हैं या अनंत तक विस्तारित होती हैं, जैसा कि वर्तमान की अंगूठी के कारण चुंबकीय क्षेत्र के साथ यहां दिखाया गया है।

चुंबकत्व के लिए गॉस का सिद्धांत कहता है कि विद्युत आवेशों का कोई चुंबकीय एनालॉग नहीं होता है, जिन्हें चुंबकीय मोनोपोल कहा जाता है; अलगाव में कोई उत्तर या दक्षिण चुंबकीय ध्रुव मौजूद नहीं है। इसके बजाय, एक सामग्री के चुंबकीय क्षेत्र को एक द्विध्रुवीय के लिए जिम्मेदार ठहराया जाता है, और एक बंद सतह के माध्यम से चुंबकीय क्षेत्र का शुद्ध बहिर्वाह शून्य होता है। चुंबकीय द्विध्रुव को समान और विपरीत "चुंबकीय आवेशों" के वर्तमान या अविभाज्य युग्मों के परिपथ के रूप में दर्शाया जा सकता है। संक्षेप में, गॉसियन सतह के माध्यम से कुल चुंबकीय प्रवाह शून्य है, और चुंबकीय क्षेत्र एक सोलेनोइडल वेक्टर क्षेत्र है।

फैराडे का सिद्धांत

Main article: Faraday's law of induction

एक भू-चुंबकीय तूफान में, आवेशित कणों के प्रवाह में उछाल अस्थायी रूप से पृथ्वी के चुंबकीय क्षेत्र को बदल देता है, जो पृथ्वी के वायुमंडल में विद्युत क्षेत्रों को प्रेरित करता है, जिससे विद्युत शक्ति ग्रिड में वृद्धि होती है। (बड़े मापक पर नहीं।)

फैराडे के प्रेरण के सिद्धांत का मैक्सवेल-फैराडे संस्करण यह बताता है कि कैसे एक समय-भिन्न चुंबकीय क्षेत्र एक विद्युत क्षेत्र के कर्ल से मेल खाता है। अभिन्न रूप में, यह बताता है कि एक बंद परिपथ के चारों ओर प्रभार को स्थानांतरित करने के लिए आवश्यक प्रति यूनिट प्रभार का कार्य संलग्न सतह के माध्यम से चुंबकीय प्रवाह के परिवर्तन की दर के बराबर होता है।

मैक्सवेल के जोड़ के साथ एम्पीयर का सिद्धांत

Main article: Ampère's circuital law

चुंबकीय-कोर मेमोरी (1954) एम्पीयर के सिद्धांत का एक अनुप्रयोग है। प्रत्येक चुंबकीय कोर एक अंश डेटा संग्रहीत करता है।

एम्पीयर का मूल सिद्धांत बताता है कि चुंबकीय क्षेत्र विद्युत प्रवाह से संबंधित हैं। मैक्सवेल के जोड़ में कहा गया है कि वे बदलते विद्युत क्षेत्रों से भी संबंधित हैं, जिसे मैक्सवेल ने विस्थापन धारा कहा है। अभिन्न रूप बताता है कि विद्युत और विस्थापन धाराएं किसी भी संलग्न वक्र के साथ आनुपातिक चुंबकीय क्षेत्र से जुड़ी होती हैं।

एम्पीयर के सिद्धांत में मैक्सवेल का जुड़ाव महत्वपूर्ण है क्योंकि एम्पीयर और गॉस के सिद्धांतों को अन्यथा स्थिर क्षेत्रों के लिए समायोजित किया जाना चाहिए। परिणामस्वरूप, यह भविष्यवाणी करता है कि एक घूर्णन चुंबकीय क्षेत्र होता है। एक और परिणाम स्व-स्थायी विद्युत चुम्बकीय तरंगों का अस्तित्व है जो खाली जगह से यात्रा करता है।

विद्युत चुम्बकीय तरंगों के लिए गणना की गई गति, जिसकी भविष्यवाणी आवेशों और धाराओं पर किए गए प्रयोगों से की जा सकती है, प्रकाश की गति से मेल खाती है; वास्तव में, प्रकाश विद्युत चुम्बकीय विकिरण का एक रूप है (जैसे एक्स-रे, रेडियो तरंगें और अन्य)। मैक्सवेल ने 1861 में विद्युत चुम्बकीय तरंगों और प्रकाश के बीच संबंध को समझा, जिससे विद्युत चुंबकत्व और प्रकाशिकी के सिद्धांतों को एकीकृत किया गया।

विद्युत और चुंबकीय क्षेत्र के संदर्भ में सूत्रीकरण (सूक्ष्म या निर्वात संस्करण में)

विद्युत और चुंबकीय क्षेत्र के सूत्रीकरण में चार समीकरण हैं जो दिए गए आवेश और वर्तमान वितरण के लिए क्षेत्र निर्धारित करते हैं। प्रकृति का एक अलग सिद्धांत, लोरेंत्ज़ बल सिद्धांत, वर्णन करता है कि कैसे, इसके विपरीत, विद्युत और चुंबकीय क्षेत्र आवेशित कणों और धाराओं पर कार्य करते हैं। मैक्सवेल द्वारा इस सिद्धांत के एक संस्करण को मूल समीकरणों में शामिल किया गया था, लेकिन परंपरा के अनुसार अब इसे शामिल नहीं किया गया है। ओलिवर हीविसाइड का कार्य नीचे वेक्टर कलन औपचारिकता, मानक बन गया है। यह प्रकट रूप से घूर्णन अपरिवर्तनीय है, और इसलिए एक्स, वाई, जेड घटकों में मैक्सवेल के मूल 20 समीकरणों की तुलना में गणितीय रूप से अधिक पारदर्शी है। सापेक्षवादी योग और भी अधिक सममित और स्पष्ट रूप से लोरेंत्ज़ अपरिवर्तनीय हैं। टेंसर कैलकुलस या डिफरेंशियल फॉर्म का उपयोग करके व्यक्त किए गए समान समीकरणों के लिए, § वैकल्पिक फॉर्मूलेशन देखें।

अवकलन और समाकलन सूत्रीकरण गणितीय रूप से समतुल्य हैं; दोनों उपयोगी हैं। अभिन्न सूत्रीकरण अंतरिक्ष के एक क्षेत्र के भीतर क्षेत्रों को सीमा पर क्षेत्रों से संबंधित करता है और अक्सर शुल्क और धाराओं के सममित वितरण से फ़ील्ड को सरल और सीधे गणना करने के लिए उपयोग किया जा सकता है। दूसरी ओर, अंतर समीकरण पूरी तरह से स्थानीय हैं और अधिक जटिल (कम सममित) स्थितियों में क्षेत्रों की गणना के लिए एक अधिक प्राकृतिक प्रारंभिक बिंदु हैं, उदाहरण के लिए परिमित तत्व विश्लेषण का उपयोग करना।

अंकन की कुंजी

बोल्ड में प्रतीक वेक्टर (ज्यामितीय) मात्रा का प्रतिनिधित्व करते हैं, और 'इटैलिक' में प्रतीक स्केलर (भौतिकी) मात्रा का प्रतिनिधित्व करते हैं, जब तक कि अन्यथा संकेत न दिया जाए। समीकरण विद्युत क्षेत्र का परिचय देते हैं, E, एक सदिश क्षेत्र, और चुंबकीय क्षेत्र, B, एक pseudovector क्षेत्र, प्रत्येक में आम तौर पर समय और स्थान पर निर्भरता होती है। सूत्र हैं

• कुल विद्युत आवेश घनत्व (कुल आवेश प्रति इकाई आयतन), ρ, और
• कुल विद्युत प्रवाह घनत्व (कुल वर्तमान प्रति इकाई क्षेत्र), J.

समीकरणों में दिखाई देने वाले सार्वभौमिक स्थिरांक (पहले दो स्पष्ट रूप से केवल SI इकाइयों के निर्माण में) हैं:

• मुक्त स्थान की पारगम्यता, ε₀, और
• मुक्त स्थान की पारगम्यता, μ₀, और
• प्रकाश की गति, $c={\frac {1}{\sqrt {\varepsilon _{0}\mu _{0}}}}$

विभेदक समीकरण

अवकल समीकरणों में,

• नबला प्रतीक, ∇, त्रि-आयामी ढाल ऑपरेटर, की को दर्शाता है,
• द ∇⋅ प्रतीक (उच्चारण डेल डॉट) विचलन ऑपरेटर को दर्शाता है,
• द ∇× प्रतीक (उच्चारण डेल क्रॉस) कर्ल (गणित) ऑपरेटर को दर्शाता है।

इंटीग्रल समीकरण

अभिन्न समीकरणों में,

• Ω बंद सीमा (टोपोलॉजी) सतह वाला कोई आयतन है ∂Ω, और
• Σ बंद सीमा वक्र वाली कोई भी सतह है ∂Σ,

समय-स्वतंत्र सतहों और संस्करणों के साथ समीकरणों की व्याख्या करना थोड़ा आसान है। समय-स्वतंत्र सतहें और आयतन निश्चित होते हैं और एक निश्चित समय अंतराल में नहीं बदलते हैं। उदाहरण के लिए, चूंकि सतह समय-स्वतंत्र है, हम फैराडे के सिद्धांत में अभिन्न चिह्न के तहत भिन्नता ला सकते हैं:

$${\frac {\mathrm {d} }{\mathrm {d} t}}\iint _{\Sigma }\mathbf {B} \cdot \mathrm {d} \mathbf {S} =\iint _{\Sigma }{\frac {\partial \mathbf {B} }{\partial t}}\cdot \mathrm {d} \mathbf {S} \,,$$

मैक्सवेल के समीकरणों को संभवतः समय-निर्भर सतहों और संस्करणों के साथ विभेदक संस्करण का उपयोग करके और गॉस और स्टोक्स सूत्र का उचित उपयोग करके तैयार किया जा सकता है।

• ${\scriptstyle \partial \Omega }$ सीमा सतह पर एक सतह अभिन्न है ∂Ω, लूप के साथ इंगित करता है कि सतह बंद है
• $\iiint _{\Omega }$ वॉल्यूम पर मात्रा अभिन्न है Ω,
• $\oint _{\partial \Sigma }$ सीमा वक्र के चारों ओर एक रेखा अभिन्न है ∂Σ, वक्र के बंद होने का संकेत देने वाले लूप के साथ।
• $\iint _{\Sigma }$ सतह पर एक सतह अभिन्न है Σ,
• कुल विद्युत आवेश Q में संलग्न है Ω वॉल्यूम इंटीग्रल ओवर है Ω आवेश घनत्व ρ (नीचे मैक्रोस्कोपिक सूत्रीकरण अनुभाग देखें):
  $$Q=\iiint _{\Omega }\rho \ \mathrm {d} V,$$
  कहाँ dV मात्रा तत्व है।
• शुद्ध विद्युत प्रवाह I विद्युत प्रवाह घनत्व का सतही अभिन्न अंग है J एक निश्चित सतह से गुजरना, Σ:
  $$I=\iint _{\Sigma }\mathbf {J} \cdot \mathrm {d} \mathbf {S} ,$$
  कहाँ dS सतह क्षेत्र के अंतर सदिश क्षेत्र को दर्शाता है S, सतह पर सामान्य (ज्यामिति)। Σ. (वेक्टर क्षेत्र को कभी-कभी द्वारा निरूपित किया जाता है A इसके बजाय S, लेकिन यह चुंबकीय सदिश क्षमता के लिए संकेतन के साथ संघर्ष करता है)।

एसआई इकाइयों के सम्मेलन में सूत्रीकरण

Name	Integral equations	Differential equations
Gauss's law	${\scriptstyle \partial \Omega }$ $\mathbf {E} \cdot \mathrm {d} \mathbf {S} ={\frac {1}{\varepsilon _{0}}}\iiint _{\Omega }\rho \,\mathrm {d} V$	$\nabla \cdot \mathbf {E} ={\frac {\rho }{\varepsilon _{0}}}$
Gauss's law for magnetism	${\scriptstyle \partial \Omega }$ $\mathbf {B} \cdot \mathrm {d} \mathbf {S} =0$	$\nabla \cdot \mathbf {B} =0$
Maxwell–Faraday equation (Faraday's law of induction)	$\oint _{\partial \Sigma }\mathbf {E} \cdot \mathrm {d} {\boldsymbol {\ell }}=-{\frac {\mathrm {d} }{\mathrm {d} t}}\iint _{\Sigma }\mathbf {B} \cdot \mathrm {d} \mathbf {S}$	$\nabla \times \mathbf {E} =-{\frac {\partial \mathbf {B} }{\partial t}}$
Ampère's circuital law (with Maxwell's addition)	${\begin{aligned}\oint _{\partial \Sigma }&\mathbf {B} \cdot \mathrm {d} {\boldsymbol {\ell }}=\mu _{0}\left(\iint _{\Sigma }\mathbf {J} \cdot \mathrm {d} \mathbf {S} +\varepsilon _{0}{\frac {\mathrm {d} }{\mathrm {d} t}}\iint _{\Sigma }\mathbf {E} \cdot \mathrm {d} \mathbf {S} \right)\\\end{aligned}}$	$\nabla \times \mathbf {B} =\mu _{0}\left(\mathbf {J} +\varepsilon _{0}{\frac {\partial \mathbf {E} }{\partial t}}\right)$

गाऊसी इकाइयों के सम्मेलन में सूत्रीकरण

Main article: Gaussian units

के आयामी विश्लेषण कारकों को अवशोषित करके सैद्धांतिक गणना को सरल बनाने के लिए चार्ज, विद्युत क्षेत्र और चुंबकीय क्षेत्र की परिभाषाओं को बदला जा सकता है। ε₀ और μ₀ परिपाटी द्वारा गणना की इकाइयों में। लोरेंत्ज़ बल सिद्धांत के लिए सम्मेलन में एक समान परिवर्तन के साथ यह समान भौतिकी उत्पन्न करता है, अर्थात आवेशित कणों के प्रक्षेपवक्र, या कार्य (भौतिकी) एक विद्युत मोटर द्वारा किया जाता है। इन परिभाषाओं को अक्सर सैद्धांतिक और उच्च ऊर्जा भौतिकी में पसंद किया जाता है, जहां विद्युत और चुंबकीय क्षेत्र को समान इकाइयों के साथ लेना स्वाभाविक है, विद्युत चुम्बकीय टेंसर की उपस्थिति को सरल बनाने के लिए: लोरेंत्ज़ सहसंयोजक वस्तु विद्युत और चुंबकीय क्षेत्र को एकीकृत करने के बाद घटकों के साथ होगी समान इकाई और आयाम। इस तरह की संशोधित परिभाषाएँ पारंपरिक रूप से गॉसियन (सेंटीमीटर ग्राम सेकेंड सिस्टम ऑफ यूनिट्स#अल्टरनेट डेरिवेशन्स ऑफ सीजीएस यूनिट्स इन इलेक्ट्रोमैग्नेटिज्म) यूनिट्स के साथ उपयोग की जाती हैं। गॉसियन इकाइयों में बोलचाल की भाषा में इन परिभाषाओं और परिपाटियों का उपयोग करते हुए, मैक्सवेल समीकरण बन जाते हैं:

Name	Integral equations	Differential equations
Gauss's law	${\scriptstyle \partial \Omega }$ $\mathbf {E} \cdot \mathrm {d} \mathbf {S} =4\pi \iiint _{\Omega }\rho \,\mathrm {d} V$	$\nabla \cdot \mathbf {E} =4\pi \rho$
Gauss's law for magnetism	${\scriptstyle \partial \Omega }$ $\mathbf {B} \cdot \mathrm {d} \mathbf {S} =0$	$\nabla \cdot \mathbf {B} =0$
Maxwell–Faraday equation (Faraday's law of induction)	$\oint _{\partial \Sigma }\mathbf {E} \cdot \mathrm {d} {\boldsymbol {\ell }}=-{\frac {1}{c}}{\frac {\mathrm {d} }{\mathrm {d} t}}\iint _{\Sigma }\mathbf {B} \cdot \mathrm {d} \mathbf {S}$	$\nabla \times \mathbf {E} =-{\frac {1}{c}}{\frac {\partial \mathbf {B} }{\partial t}}$
Ampère's circuital law (with Maxwell's addition)	${\begin{aligned}\oint _{\partial \Sigma }&\mathbf {B} \cdot \mathrm {d} {\boldsymbol {\ell }}={\frac {1}{c}}\left(4\pi \iint _{\Sigma }\mathbf {J} \cdot \mathrm {d} \mathbf {S} +{\frac {\mathrel {\mathrm {d} } }{\mathrm {d} t}}\iint _{\Sigma }\mathbf {E} \cdot \mathrm {d} \mathbf {S} \right)\end{aligned}}$	$\nabla \times \mathbf {B} ={\frac {1}{c}}\left(4\pi \mathbf {J} +{\frac {\partial \mathbf {E} }{\partial t}}\right)$

जब प्रकाश की गति में मात्राओं की एक प्रणाली को चुना जाता है, तो समीकरण थोड़ा सा सरल हो जाता है, c, का उपयोग गैर-आयामीकरण के लिए किया जाता है, ताकि, उदाहरण के लिए, सेकंड और लाइटसेकंड विनिमेय हों, और c = 1।

आगे के परिवर्तन, जिन्हें युक्तिकरण कहा जाता है, के कारकों को अवशोषित करके संभव है 4π, कूलम्ब के सिद्धांत या गॉस के सिद्धांत में ऐसा कारक शामिल है (मुख्य रूप से कण भौतिकी में उपयोग की जाने वाली हीविसाइड-लोरेंत्ज़ इकाइयां देखें)।

अंतर और अभिन्न योगों के बीच संबंध

अंतर और अभिन्न योगों की समानता विचलन प्रमेय और केल्विन-स्टोक्स प्रमेय का एक परिणाम है।

प्रवाह और विचलन

आयतन Ω और इसकी बंद सीमा ∂Ω, एक स्रोत युक्त (क्रमशः संलग्न)। (+) और डूबो (−) सदिश क्षेत्र का F. यहाँ, F हो सकता है E स्रोत विद्युत आवेशों के साथ क्षेत्र, लेकिन नहीं B क्षेत्र, जिसमें दिखाए गए अनुसार कोई चुंबकीय आवेश नहीं है। बाहरी इकाई सामान्य n है।

(विशुद्ध रूप से गणितीय) विचलन प्रमेय के अनुसार, के माध्यम से विद्युत प्रवाह

समरूपता (गणित) ∂Ω के रूप में फिर से लिखा जा सकता है

${\scriptstyle \partial \Omega }$ $\mathbf {E} \cdot \mathrm {d} \mathbf {S} =\iiint _{\Omega }\nabla \cdot \mathbf {E} \,\mathrm {d} V$

गॉस के समीकरण का अभिन्न संस्करण इस प्रकार फिर से लिखा जा सकता है

$$\iiint _{\Omega }\left(\nabla \cdot \mathbf {E} -{\frac {\rho }{\varepsilon _{0}}}\right)\,\mathrm {d} V=0$$

तब से Ω मनमाना है (उदाहरण के लिए मनमाना केंद्र के साथ एक मनमाना छोटी गेंद), यह संतुष्ट है अगर और केवल अगर इंटीग्रैंड हर जगह शून्य है। यह है गॉस समीकरण के अवकल समीकरण सूत्रीकरण को तुच्छ पुनर्व्यवस्था तक।

इसी प्रकार चुम्बकत्व के लिए गॉस के सिद्धांत में चुम्बकीय फ्लक्स को समाकलित रूप में पुनः लिखने से प्राप्त होता है

${\scriptstyle \partial \Omega }$ $\mathbf {B} \cdot \mathrm {d} \mathbf {S} =\iiint _{\Omega }\nabla \cdot \mathbf {B} \,\mathrm {d} V=0.$

जो सभी के लिए संतुष्ट है Ω अगर और केवल अगर $\nabla \cdot \mathbf {B} =0$ हर जगह।

सर्कुलेशन और कर्ल

सतह Σ बंद सीमा के साथ ∂Σ. F हो सकता है E या B खेत। दोबारा, n इकाई सामान्य है। (वेक्टर क्षेत्र का कर्ल वास्तव में परिसंचरण की तरह नहीं दिखता है, यह एक अनुमानी चित्रण है।)

स्टोक्स प्रमेय द्वारा | केल्विन-स्टोक्स प्रमेय हम बंद सीमा वक्र के आसपास के क्षेत्रों के लाइन इंटीग्रल को फिर से लिख सकते हैं ∂Σ खेतों के संचलन के एक अभिन्न अंग के लिए (यानी उनके कर्ल (गणित) एस) एक सतह पर यह सीमा होती है, यानी।

$$\oint _{\partial \Sigma }\mathbf {B} \cdot \mathrm {d} {\boldsymbol {\ell }}=\iint _{\Sigma }(\nabla \times \mathbf {B} )\cdot \mathrm {d} \mathbf {S} ,$$

इसलिए संशोधित एम्पीयर सिद्धांत को अभिन्न रूप में फिर से लिखा जा सकता है

$$\iint _{\Sigma }\left(\nabla \times \mathbf {B} -\mu _{0}\left(\mathbf {J} +\varepsilon _{0}{\frac {\partial \mathbf {E} }{\partial t}}\right)\right)\cdot \mathrm {d} \mathbf {S} =0.$$

तब से Σ मनमाने ढंग से चुना जा सकता है, उदा। एक मनमाना छोटा, मनमाना उन्मुख, और मनमाना केंद्रित डिस्क के रूप में, हम निष्कर्ष निकालते हैं कि इंटीग्रैंड शून्य है अगर और केवल अगर एम्पीयर के संशोधित सिद्धांत अंतर समीकरणों के रूप में संतुष्ट हैं। फैराडे के सिद्धांत की अंतर और अभिन्न रूप में समानता इसी तरह होती है।

लाइन इंटीग्रल और कर्ल शास्त्रीय द्रव गतिकी में मात्रा के अनुरूप होते हैं: द्रव का संचलन (द्रव गतिकी) एक बंद लूप के चारों ओर तरल पदार्थ के प्रवाह वेग क्षेत्र का अभिन्न रेखा है, और तरल पदार्थ की vorticity वेग का कर्ल है। मैदान।

चार्ज संरक्षण

आवेश के व्युत्क्रम को मैक्सवेल के समीकरणों के परिणाम के रूप में प्राप्त किया जा सकता है। संशोधित एम्पीयर के सिद्धांत के बाईं ओर वेक्टर कैलकुलस आइडेंटिटी द्वारा शून्य विचलन है # कर्ल का डायवर्जेंस शून्य है। डिव-कर्ल पहचान। दाहिने हाथ के विचलन का विस्तार करना, डेरिवेटिव का आदान-प्रदान करना और गॉस के सिद्धांत को लागू करना:

$$0=\nabla \cdot (\nabla \times \mathbf {B} )=\nabla \cdot \left(\mu _{0}\left(\mathbf {J} +\varepsilon _{0}{\frac {\partial \mathbf {E} }{\partial t}}\right)\right)=\mu _{0}\left(\nabla \cdot \mathbf {J} +\varepsilon _{0}{\frac {\partial }{\partial t}}\nabla \cdot \mathbf {E} \right)=\mu _{0}\left(\nabla \cdot \mathbf {J} +{\frac {\partial \rho }{\partial t}}\right)$$

अर्थात।,

$${\frac {\partial \rho }{\partial t}}+\nabla \cdot \mathbf {J} =0.$$

गॉस डाइवर्जेंस प्रमेय द्वारा, इसका मतलब है कि एक निश्चित मात्रा में आवेश के परिवर्तन की दर सीमा के माध्यम से बहने वाली शुद्ध धारा के बराबर होती है:

${\frac {d}{dt}}Q_{\Omega }={\frac {d}{dt}}\iiint _{\Omega }\rho \mathrm {d} V=-$ ${\scriptstyle \partial \Omega }$ $\mathbf {J} \cdot {\rm {d}}\mathbf {S} =-I_{\partial \Omega }.$

विशेष रूप से, एक पृथक प्रणाली में कुल आवेश संरक्षित होता है।

निर्वात समीकरण, विद्युत चुम्बकीय तरंगें और प्रकाश की गति

Further information: Electromagnetic wave equation, Inhomogeneous electromagnetic wave equation, Sinusoidal plane-wave solutions of the electromagnetic wave equation, and Helmholtz equation

यह 3डी आरेख एक विमान को रैखिक रूप से ध्रुवीकृत लहर दिखाता है जो बाएं से दाएं फैलता है, जिसे परिभाषित किया गया है E = E₀ sin(−ωt + k ⋅ r) और B = B₀ sin(−ωt + k ⋅ r) झिलमिलाहट बिंदु पर दोलनशील क्षेत्रों का पता लगाया जाता है। क्षैतिज तरंग दैर्ध्य λ है। E₀ ⋅ B₀ = 0 = E₀ ⋅ k = B₀ ⋅ k

बिना शुल्क वाले क्षेत्र में (ρ = 0) और कोई धारा नहीं (J = 0), जैसे निर्वात में, मैक्सवेल के समीकरण कम हो जाते हैं:

$${\begin{aligned}\nabla \cdot \mathbf {E} &=0,&\nabla \times \mathbf {E} &=-{\frac {\partial \mathbf {B} }{\partial t}},\\\nabla \cdot \mathbf {B} &=0,&\nabla \times \mathbf {B} &=\mu _{0}\varepsilon _{0}{\frac {\partial \mathbf {E} }{\partial t}}.\end{aligned}}$$

कर्ल लेना (∇×) कर्ल समीकरणों का, और वेक्टर कैलकुलस आइडेंटिटी का उपयोग करके # कर्ल का कर्ल हम प्राप्त करते हैं

$${\begin{aligned}\mu _{0}\varepsilon _{0}{\frac {\partial ^{2}\mathbf {E} }{\partial t^{2}}}-\nabla ^{2}\mathbf {E} =0,\\\mu _{0}\varepsilon _{0}{\frac {\partial ^{2}\mathbf {B} }{\partial t^{2}}}-\nabla ^{2}\mathbf {B} =0.\end{aligned}}$$

मात्रा $\mu _{0}\varepsilon _{0}$ (समय/लंबाई) का आयाम है2</उप>। परिभाषित $c=(\mu _{0}\varepsilon _{0})^{-1/2}$, उपरोक्त समीकरणों में मानक तरंग समीकरणों का रूप है

$${\begin{aligned}{\frac {1}{c^{2}}}{\frac {\partial ^{2}\mathbf {E} }{\partial t^{2}}}-\nabla ^{2}\mathbf {E} =0,\\{\frac {1}{c^{2}}}{\frac {\partial ^{2}\mathbf {B} }{\partial t^{2}}}-\nabla ^{2}\mathbf {B} =0.\end{aligned}}$$

पहले से ही मैक्सवेल के जीवनकाल के दौरान, यह ज्ञात मान पाया गया था $\varepsilon _{0}$ और $\mu _{0}$ देना $c\approx 2.998\times 10^{8}~{\text{m/s}}$, तो पहले से ही मुक्त स्थान में प्रकाश की गति के रूप में जाना जाता है। इसने उन्हें यह प्रस्तावित करने के लिए प्रेरित किया कि प्रकाश और रेडियो तरंगें विद्युत चुम्बकीय तरंगों का प्रचार कर रही थीं, क्योंकि इसकी काफी पुष्टि हुई थी। इकाइयों की एसआई प्रणाली में, के मान $\mu _{0}=4\pi \times 10^{-7}$ और $c=299\,792\,458~{\text{m/s}}$ परिभाषित स्थिरांक हैं, (जिसका अर्थ है कि परिभाषा के अनुसार $\varepsilon _{0}=8.854...\times 10^{-12}~{\text{F/m}}$) जो एम्पीयर और मीटर को परिभाषित करता है। नई एसआई प्रणाली में, केवल c अपना परिभाषित मान रखता है, और इलेक्ट्रॉन आवेश को एक परिभाषित मान मिलता है।

सापेक्ष पारगम्यता वाली सामग्रियों में, ε_r, और पारगम्यता (विद्युत चुंबकत्व) # सापेक्ष पारगम्यता और चुंबकीय संवेदनशीलता, μ_r, प्रकाश का कला वेग बन जाता है

$$v_{\text{p}}={\frac {1}{\sqrt {\mu _{0}\mu _{\text{r}}\varepsilon _{0}\varepsilon _{\text{r}}}}},$$

जो आमतौर पर है से कम c.

इसके साथ ही, E और B एक दूसरे के लंबवत हैं और तरंग प्रसार की दिशा में हैं, और एक दूसरे के साथ चरण (तरंगों) में हैं। एक ज्यावक्रीय समतल तरंग इन समीकरणों का एक विशेष हल है। मैक्सवेल के समीकरण बताते हैं कि कैसे ये तरंगें अंतरिक्ष के माध्यम से भौतिक रूप से फैल सकती हैं। फैराडे के प्रेरण के सिद्धांत | फैराडे के सिद्धांत के माध्यम से बदलते चुंबकीय क्षेत्र एक बदलते विद्युत क्षेत्र का निर्माण करते हैं। बदले में, वह विद्युत क्षेत्र एम्पीयर के सर्किट सिद्धांत के माध्यम से एक बदलते चुंबकीय क्षेत्र बनाता है | मैक्सवेल के एम्पीयर के सिद्धांत के अतिरिक्त। यह सतत चक्र इन तरंगों को अनुमति देता है, जिसे अब विद्युत चुम्बकीय विकिरण के रूप में जाना जाता है, वेग से अंतरिक्ष में जाने के लिए c.

मैक्रोस्कोपिक फॉर्मूलेशन

उपरोक्त समीकरण मैक्सवेल के समीकरणों के सूक्ष्म संस्करण हैं, जो विद्युत और चुंबकीय क्षेत्रों को (संभवतः परमाणु-स्तर) आवेशों और धाराओं के संदर्भ में व्यक्त करते हैं। इसे कभी-कभी सामान्य रूप कहा जाता है, लेकिन नीचे दिया गया मैक्रोस्कोपिक संस्करण समान रूप से सामान्य है, अंतर बहीखाता पद्धति का है।

सूक्ष्म संस्करण को कभी-कभी निर्वात में मैक्सवेल के समीकरण कहा जाता है: यह इस तथ्य को संदर्भित करता है कि भौतिक माध्यम समीकरणों की संरचना में निर्मित नहीं है, लेकिन केवल आवेश और वर्तमान शर्तों में प्रकट होता है। लोरेंत्ज़ द्वारा सूक्ष्म संस्करण पेश किया गया था, जिन्होंने इसके सूक्ष्म घटकों से थोक पदार्थ के स्थूल गुणों को प्राप्त करने के लिए इसका उपयोग करने की कोशिश की।

मैक्सवेल के मैक्रोस्कोपिक समीकरण, जिन्हें पदार्थ में मैक्सवेल के समीकरण के रूप में भी जाना जाता है, मैक्सवेल द्वारा प्रस्तुत किए गए समीकरणों के समान ही हैं।

Name	Integral equations (SI convention)	Differential equations (SI convention)	Differential equations (Gaussian convention)
Gauss's law	${\scriptstyle \partial \Omega }$ $\mathbf {D} \cdot \mathrm {d} \mathbf {S} =\iiint _{\Omega }\rho _{\text{f}}\,\mathrm {d} V$	$\nabla \cdot \mathbf {D} =\rho _{\text{f}}$	$\nabla \cdot \mathbf {D} =4\pi \rho _{\text{f}}$
Ampère's circuital law (with Maxwell's addition)	${\begin{aligned}\oint _{\partial \Sigma }&\mathbf {H} \cdot \mathrm {d} {\boldsymbol {\ell }}=\\&\iint _{\Sigma }\mathbf {J} _{\text{f}}\cdot \mathrm {d} \mathbf {S} +{\frac {d}{dt}}\iint _{\Sigma }\mathbf {D} \cdot \mathrm {d} \mathbf {S} \\\end{aligned}}$	$\nabla \times \mathbf {H} =\mathbf {J} _{\text{f}}+{\frac {\partial \mathbf {D} }{\partial t}}$	$\nabla \times \mathbf {H} ={\frac {1}{c}}\left(4\pi \mathbf {J} _{\text{f}}+{\frac {\partial \mathbf {D} }{\partial t}}\right)$
Gauss's law for magnetism	${\scriptstyle \partial \Omega }$ $\mathbf {B} \cdot \mathrm {d} \mathbf {S} =0$	$\nabla \cdot \mathbf {B} =0$	$\nabla \cdot \mathbf {B} =0$
Maxwell–Faraday equation (Faraday's law of induction)	$\oint _{\partial \Sigma }\mathbf {E} \cdot \mathrm {d} {\boldsymbol {\ell }}=-{\frac {d}{dt}}\iint _{\Sigma }\mathbf {B} \cdot \mathrm {d} \mathbf {S}$	$\nabla \times \mathbf {E} =-{\frac {\partial \mathbf {B} }{\partial t}}$	$\nabla \times \mathbf {E} =-{\frac {1}{c}}{\frac {\partial \mathbf {B} }{\partial t}}$

मैक्रोस्कोपिक समीकरणों में, बाउंड चार्ज का प्रभाव Q_b और बाउंड करंट I_b विद्युत विस्थापन क्षेत्र में शामिल है D और चुंबकीय क्षेत्र H, जबकि समीकरण केवल निःशुल्क शुल्कों पर निर्भर करते हैं Q_f और मुक्त धाराएँ I_f. यह कुल विद्युत आवेश Q और वर्तमान I (और उनके घनत्व) के विभाजन को दर्शाता है ρ और J) मुक्त और बाध्य भागों में:

$${\begin{aligned}Q&=Q_{\text{f}}+Q_{\text{b}}=\iiint _{\Omega }\left(\rho _{\text{f}}+\rho _{\text{b}}\right)\,\mathrm {d} V=\iiint _{\Omega }\rho \,\mathrm {d} V,\\I&=I_{\text{f}}+I_{\text{b}}=\iint _{\Sigma }\left(\mathbf {J} _{\text{f}}+\mathbf {J} _{\text{b}}\right)\cdot \mathrm {d} \mathbf {S} =\iint _{\Sigma }\mathbf {J} \cdot \mathrm {d} \mathbf {S} .\end{aligned}}$$

इस बंटवारे की लागत अतिरिक्त फ़ील्ड है D और H इन क्षेत्रों को विद्युत क्षेत्र से संबंधित परिघटना संबंधी घटक समीकरणों के माध्यम से निर्धारित करने की आवश्यकता है E और चुंबकीय क्षेत्र B, बाउंड चार्ज और करंट के साथ।

सूक्ष्म समीकरणों के बीच अंतर के विस्तृत विवरण के लिए नीचे देखें, कुल चार्ज और सामग्री योगदान सहित वर्तमान, हवा/वैक्यूम में उपयोगी; और मैक्रोस्कोपिक समीकरण, फ्री चार्ज और करंट से निपटने के लिए, सामग्री के भीतर उपयोग करने के लिए व्यावहारिक।

बाउंड चार्ज और करंट

Main articles: Current density, Bound charge, and Bound current

बायां: ऊपर और नीचे दिखाए गए अनुसार सूक्ष्म द्विध्रुवों की एक असेंबली विपरीत सतह के आवेशों का निर्माण कैसे करती है, इसका एक योजनाबद्ध दृश्य। दाएं: माइक्रोस्कोपिक करंट लूप की असेंबली कैसे मैक्रोस्कोपिक रूप से सर्कुलेटिंग करंट लूप बनाने के लिए एक साथ जुड़ती है। सीमाओं के अंदर, व्यक्तिगत योगदान रद्द करने की प्रवृत्ति होती है, लेकिन सीमाओं पर कोई रद्दीकरण नहीं होता है।

जब एक विद्युत क्षेत्र को एक परावैद्युत पर लागू किया जाता है तो इसके अणु सूक्ष्म विद्युत द्विध्रुव बनाकर प्रतिक्रिया करते हैं - उनके परमाणु नाभिक क्षेत्र की दिशा में एक छोटी दूरी की ओर बढ़ते हैं, जबकि उनके इलेक्ट्रॉन विपरीत दिशा में थोड़ी दूरी पर चलते हैं। यह सामग्री में मैक्रोस्कोपिक बाउंड चार्ज पैदा करता है, भले ही इसमें शामिल सभी चार्ज अलग-अलग अणुओं से बंधे हों। उदाहरण के लिए, यदि प्रत्येक अणु समान प्रतिक्रिया करता है, जैसा कि चित्र में दिखाया गया है, तो आवेश के ये छोटे-छोटे संचलन सामग्री के एक तरफ सकारात्मक बाउंड चार्ज # बाउंड चार्ज की एक परत और दूसरी तरफ नकारात्मक चार्ज की एक परत का निर्माण करने के लिए गठबंधन करते हैं। ओर। बाउंड चार्ज को ध्रुवीकरण घनत्व के संदर्भ में सबसे आसानी से वर्णित किया गया है P पदार्थ का, इसका द्विध्रुव आघूर्ण प्रति इकाई आयतन। अगर P एकसमान है, आवेश का एक मैक्रोस्कोपिक पृथक्करण केवल उन सतहों पर उत्पन्न होता है जहाँ P सामग्री में प्रवेश करता है और छोड़ता है। गैर-वर्दी के लिए P, बल्क में एक चार्ज भी उत्पन्न होता है।

कुछ इसी तरह, सभी सामग्रियों में घटक परमाणु चुंबकीय क्षण प्रदर्शित करते हैं # चुंबकीय क्षणों के उदाहरण जो आंतरिक रूप से परमाणुओं के घटकों के जाइरोमैग्नेटिक अनुपात से जुड़े होते हैं, विशेष रूप से उनके इलेक्ट्रॉन। चुंबकीय क्षेत्र#चुंबकीय द्विध्रुव सूक्ष्मदर्शी धारा लूपों के समुच्चयन की तस्वीर सुझाते हैं। सामग्री के बाहर, इस तरह के सूक्ष्म वर्तमान लूपों की एक असेंबली सामग्री की सतह के चारों ओर घूमते हुए एक मैक्रोस्कोपिक वर्तमान से अलग नहीं है, इस तथ्य के बावजूद कि कोई व्यक्तिगत चार्ज बड़ी दूरी की यात्रा नहीं कर रहा है। इन बाउंड करंट#आकर्षण संस्कार करंट को मैग्नेटाइजेशन का उपयोग करके वर्णित किया जा सकता है M. इसलिए, बहुत जटिल और दानेदार बाउंड चार्ज और बाउंड करंट को मैक्रोस्कोपिक स्केल पर प्रदर्शित किया जा सकता है P और M, जो इन आवेशों और धाराओं को पर्याप्त रूप से बड़े मापक पर औसत करते हैं ताकि व्यक्तिगत परमाणुओं की ग्रैन्युलैरिटी न दिखें, लेकिन यह भी पर्याप्त रूप से छोटा है कि वे सामग्री में स्थान के साथ भिन्न होते हैं। इस प्रकार, मैक्सवेल के मैक्रोस्कोपिक समीकरण एक अच्छे मापक पर कई विवरणों को अनदेखा करते हैं जो कुछ उपयुक्त मात्रा में औसत क्षेत्रों की गणना करके सकल मापक पर मामलों को समझने के लिए महत्वहीन हो सकते हैं।

सहायक क्षेत्र, ध्रुवीकरण और चुंबकीयकरण

विद्युत चुंबकत्व समीकरणों की सूची # सहायक क्षेत्रों की परिभाषाएँ हैं:

$${\begin{aligned}\mathbf {D} (\mathbf {r} ,t)&=\varepsilon _{0}\mathbf {E} (\mathbf {r} ,t)+\mathbf {P} (\mathbf {r} ,t),\\\mathbf {H} (\mathbf {r} ,t)&={\frac {1}{\mu _{0}}}\mathbf {B} (\mathbf {r} ,t)-\mathbf {M} (\mathbf {r} ,t),\end{aligned}}$$

कहाँ P ध्रुवीकरण घनत्व क्षेत्र है और M चुंबकत्व क्षेत्र है, जिसे क्रमशः सूक्ष्म बाध्य आवेशों और बाध्य धाराओं के रूप में परिभाषित किया गया है। मैक्रोस्कोपिक बाउंड चार्ज घनत्व ρ_b और बाध्य वर्तमान घनत्व J_b ध्रुवीकरण घनत्व के संदर्भ में P और चुंबकीयकरण M को तब परिभाषित किया जाता है

$${\begin{aligned}\rho _{\text{b}}&=-\nabla \cdot \mathbf {P} ,\\\mathbf {J} _{\text{b}}&=\nabla \times \mathbf {M} +{\frac {\partial \mathbf {P} }{\partial t}}.\end{aligned}}$$

अगर हम टोटल, बाउंड और फ्री चार्ज और करंट डेंसिटी को परिभाषित करते हैं

$${\begin{aligned}\rho &=\rho _{\text{b}}+\rho _{\text{f}},\\\mathbf {J} &=\mathbf {J} _{\text{b}}+\mathbf {J} _{\text{f}},\end{aligned}}$$

और खत्म करने के लिए उपरोक्त परिभाषित संबंधों का उपयोग करें D, और H, मैक्रोस्कोपिक मैक्सवेल के समीकरण सूक्ष्म समीकरणों को पुन: उत्पन्न करते हैं।

संवैधानिक संबंध

Main article: Constitutive equation § Electromagnetism

'मैक्सवेल के स्थूल समीकरण' को लागू करने के लिए, विद्युत विस्थापन क्षेत्र के बीच संबंधों को निर्दिष्ट करना आवश्यक है D और विद्युत क्षेत्र E, साथ ही चुंबकीय क्षेत्र #H- क्षेत्र और चुंबकीय सामग्री क्षेत्र H और चुंबकीय क्षेत्र B. समतुल्य रूप से, हमें ध्रुवीकरण की निर्भरता को निर्दिष्ट करना होगा P (इसलिए बाउंड चार्ज) और मैग्नेटाइजेशन M (इसलिए बाध्य वर्तमान) लागू विद्युत और चुंबकीय क्षेत्र पर। इस प्रतिक्रिया को निर्दिष्ट करने वाले समीकरणों को संवैधानिक संबंध कहा जाता है। वास्तविक दुनिया की सामग्रियों के लिए, संवैधानिक संबंध शायद ही कभी सरल होते हैं, सिवाय लगभग, और आमतौर पर प्रयोग द्वारा निर्धारित किए जाते हैं। पूर्ण विवरण के लिए संवैधानिक संबंधों पर मुख्य लेख देखें।

ध्रुवीकरण और चुंबकीयकरण के बिना सामग्री के लिए, संवैधानिक संबंध हैं (परिभाषा के अनुसार)

$$\mathbf {D} =\varepsilon _{0}\mathbf {E} ,\quad \mathbf {H} ={\frac {1}{\mu _{0}}}\mathbf {B} ,$$

कहाँ ε₀ मुक्त स्थान की पारगम्यता है और μ₀ मुक्त स्थान की पारगम्यता (विद्युत चुंबकत्व)। चूँकि कोई बाउंड चार्ज नहीं है, कुल और फ्री चार्ज और करंट बराबर हैं।

सूक्ष्म समीकरणों पर एक वैकल्पिक दृष्टिकोण यह है कि वे मैक्रोस्कोपिक समीकरण हैं, साथ ही इस कथन के साथ कि वैक्यूम अतिरिक्त ध्रुवीकरण और चुंबकीयकरण के बिना एक पूर्ण रैखिक सामग्री की तरह व्यवहार करता है। अधिक आम तौर पर, रैखिक सामग्रियों के लिए संवैधानिक संबंध होते हैं

$$\mathbf {D} =\varepsilon \mathbf {E} ,\quad \mathbf {H} ={\frac {1}{\mu }}\mathbf {B} ,$$

कहाँ ε परमिटिटिविटी है और μ सामग्री की पारगम्यता (विद्युत चुंबकत्व)। विस्थापन क्षेत्र के लिए D रैखिक सन्निकटन आमतौर पर उत्कृष्ट होता है क्योंकि प्रयोगशाला (उच्च शक्ति स्पंदित लेज़रों) में प्राप्त होने वाले सबसे चरम विद्युत क्षेत्रों या तापमानों के अलावा सभी के लिए 10 के क्रम की सामग्री के अंतर-विद्युत क्षेत्र¹¹ वी/एम बाहरी क्षेत्र की तुलना में बहुत अधिक है। चुम्बकीय क्षेत्र के लिए $\mathbf {H}$हालांकि, रैखिक सन्निकटन लोहे जैसी सामान्य सामग्रियों में टूट सकता है, जिससे हिस्टैरिसीस जैसी घटनाएं हो सकती हैं। हालाँकि, रैखिक मामले में भी विभिन्न जटिलताएँ हो सकती हैं।

• सजातीय सामग्री के लिए, ε और μ पूरी सामग्री में स्थिर हैं, जबकि विषम सामग्री के लिए वे सामग्री के भीतर स्थिति सदिश (और शायद समय) पर निर्भर करते हैं।
• आइसोट्रोपिक सामग्री के लिए, ε और μ अदिश हैं, जबकि अनिसोट्रोपिक सामग्री के लिए (उदाहरण के लिए क्रिस्टल संरचना के कारण) वे टेन्सर हैं।
• सामग्री आम तौर पर फैलाव (प्रकाशिकी) होती है, इसलिए ε और μ किसी भी घटना EM तरंगों की आवृत्ति पर निर्भर करता है।

इससे भी अधिक आम तौर पर, गैर-रेखीय सामग्री के मामले में (उदाहरण के लिए गैर-रैखिक प्रकाशिकी देखें), D और P आवश्यक रूप से आनुपातिक नहीं हैं E, इसी तरह H या M आवश्यक रूप से आनुपातिक नहीं है B. सामान्य रूप में D और H दोनों पर निर्भर है E और B, स्थान और समय पर, और संभवतः अन्य भौतिक राशियों पर।

अनुप्रयोगों में किसी को यह भी वर्णन करना होगा कि मुक्त धाराएं और आवेश घनत्व किस प्रकार व्यवहार करते हैं E और B संभवतः दबाव, और द्रव्यमान, संख्या घनत्व, और चार्ज करने वाले कणों के वेग जैसी अन्य भौतिक मात्राओं से जुड़ा हुआ है। उदाहरण के लिए, मैक्सवेल द्वारा दिए गए मूल समीकरण (मैक्सवेल के समीकरणों का इतिहास देखें) में ओम का सिद्धांत शामिल है

$$\mathbf {J} _{\text{f}}=\sigma \mathbf {E} .$$

वैकल्पिक फॉर्मूलेशन

For an overview, see Mathematical descriptions of the electromagnetic field.

For the equations in quantum field theory, see Quantum electrodynamics.

माइक्रोस्कोपिक मैक्सवेल के समीकरणों को लिखने के लिए कई अन्य गणितीय औपचारिकताओं का सारांश निम्नलिखित है, जिसमें कॉलम दो सजातीय मैक्सवेल समीकरणों को चार्ज और करंट से जुड़े दो विषम समीकरणों से अलग करते हैं। प्रत्येक फॉर्मूलेशन में विद्युत और चुंबकीय क्षेत्र के संदर्भ में प्रत्यक्ष रूप से और अप्रत्यक्ष रूप से विद्युत क्षमता के संदर्भ में संस्करण होते हैं φ और वेक्टर क्षमता A. सजातीय समीकरणों को हल करने के लिए संभावितों को एक सुविधाजनक तरीके के रूप में पेश किया गया था, लेकिन यह सोचा गया था कि सभी अवलोकन योग्य भौतिकी विद्युत और चुंबकीय क्षेत्रों (या सापेक्षिक रूप से, फैराडे टेंसर) में समाहित थी। हालांकि, क्षमताएं क्वांटम यांत्रिकी में एक केंद्रीय भूमिका निभाती हैं, और जब विद्युत और चुंबकीय क्षेत्र गायब हो जाते हैं (अहरोनोव-बोहम प्रभाव) तब भी देखने योग्य परिणामों के साथ यांत्रिक रूप से कार्य करते हैं।

प्रत्येक तालिका एक औपचारिकता का वर्णन करती है। प्रत्येक सूत्रीकरण के विवरण के लिए विद्युत चुम्बकीय क्षेत्र का गणितीय विवरण देखें। एसआई इकाइयों का उपयोग हर जगह किया जाता है।

Vector calculus

Formulation	Homogeneous equations	Inhomogeneous equations
Fields 3D Euclidean space + time	$\nabla \cdot \mathbf {B} =0$ $\nabla \times \mathbf {E} +{\frac {\partial \mathbf {B} }{\partial t}}=\mathbf {0}$	$\nabla \cdot \mathbf {E} ={\frac {\rho }{\varepsilon _{0}}}$ $\nabla \times \mathbf {B} -{\frac {1}{c^{2}}}{\frac {\partial \mathbf {E} }{\partial t}}=\mu _{0}\mathbf {J}$
Potentials (any gauge) 3D Euclidean space + time	$\mathbf {B} =\mathbf {\nabla } \times \mathbf {A}$ $\mathbf {E} =-\mathbf {\nabla } \varphi -{\frac {\partial \mathbf {A} }{\partial t}}$	$-\nabla ^{2}\varphi -{\frac {\partial }{\partial t}}\left(\mathbf {\nabla } \cdot \mathbf {A} \right)={\frac {\rho }{\varepsilon _{0}}}$ $\left(-\nabla ^{2}+{\frac {1}{c^{2}}}{\frac {\partial ^{2}}{\partial t^{2}}}\right)\mathbf {A} +\mathbf {\nabla } \left(\mathbf {\nabla } \cdot \mathbf {A} +{\frac {1}{c^{2}}}{\frac {\partial \varphi }{\partial t}}\right)=\mu _{0}\mathbf {J}$
Potentials (Lorenz gauge) 3D Euclidean space + time	$\mathbf {B} =\mathbf {\nabla } \times \mathbf {A}$ $\mathbf {E} =-\mathbf {\nabla } \varphi -{\frac {\partial \mathbf {A} }{\partial t}}$ $\mathbf {\nabla } \cdot \mathbf {A} =-{\frac {1}{c^{2}}}{\frac {\partial \varphi }{\partial t}}$	$\left(-\nabla ^{2}+{\frac {1}{c^{2}}}{\frac {\partial ^{2}}{\partial t^{2}}}\right)\varphi ={\frac {\rho }{\varepsilon _{0}}}$ $\left(-\nabla ^{2}+{\frac {1}{c^{2}}}{\frac {\partial ^{2}}{\partial t^{2}}}\right)\mathbf {A} =\mu _{0}\mathbf {J}$

Tensor calculus

Formulation	Homogeneous equations	Inhomogeneous equations
Fields space + time spatial metric independent of time	${\begin{aligned}&\partial _{[i}B_{jk]}=\\&\qquad \nabla _{[i}B_{jk]}=0\\&\partial _{[i}E_{j]}+{\frac {\partial B_{ij}}{\partial t}}=\\&\qquad \nabla _{[i}E_{j]}+{\frac {\partial B_{ij}}{\partial t}}=0\end{aligned}}$	${\begin{aligned}&{\frac {1}{\sqrt {h}}}\partial _{i}{\sqrt {h}}E^{i}=\\&\qquad \nabla _{i}E^{i}={\frac {\rho }{\varepsilon _{0}}}\\&{-}{\frac {1}{\sqrt {h}}}\partial _{i}{\sqrt {h}}B^{ij}-{\frac {1}{c^{2}}}{\frac {\partial }{\partial t}}E^{j}=\\&\qquad {-}\nabla _{i}B^{ij}-{\frac {1}{c^{2}}}{\frac {\partial E^{j}}{\partial t}}=\mu _{0}J^{j}\end{aligned}}$
Potentials space (with § topological restrictions) + time spatial metric independent of time	${\begin{aligned}B_{ij}&=\partial _{[i}A_{j]}\\&=\nabla _{[i}A_{j]}\end{aligned}}$ ${\begin{aligned}E_{i}&=-{\frac {\partial A_{i}}{\partial t}}-\partial _{i}\varphi \\&=-{\frac {\partial A_{i}}{\partial t}}-\nabla _{i}\varphi \\\end{aligned}}$	${\begin{aligned}&{-}{\frac {1}{\sqrt {h}}}\partial _{i}{\sqrt {h}}\left(\partial ^{i}\varphi +{\frac {\partial A^{i}}{\partial t}}\right)=\\&\qquad -\nabla _{i}\nabla ^{i}\varphi -{\frac {\partial }{\partial t}}\nabla _{i}A^{i}={\frac {\rho }{\varepsilon _{0}}}\\&{-}{\frac {1}{\sqrt {h}}}\partial _{i}\left({\sqrt {h}}h^{im}h^{jn}\partial _{[m}A_{n]}\right)+{\frac {1}{c^{2}}}{\frac {\partial }{\partial t}}\left({\frac {\partial A^{j}}{\partial t}}+\partial ^{j}\varphi \right)=\\&\qquad {-}\nabla _{i}\nabla ^{i}A^{j}+{\frac {1}{c^{2}}}{\frac {\partial ^{2}A^{j}}{\partial t^{2}}}+R_{i}^{j}A^{i}+\nabla ^{j}\left(\nabla _{i}A^{i}+{\frac {1}{c^{2}}}{\frac {\partial \varphi }{\partial t}}\right)=\mu _{0}J^{j}\end{aligned}}$
Potentials (Lorenz gauge) space (with topological restrictions) + time spatial metric independent of time	${\begin{aligned}B_{ij}&=\partial _{[i}A_{j]}\\&=\nabla _{[i}A_{j]}\end{aligned}}$ ${\begin{aligned}E_{i}&=-{\frac {\partial A_{i}}{\partial t}}-\partial _{i}\varphi \\&=-{\frac {\partial A_{i}}{\partial t}}-\nabla _{i}\varphi \end{aligned}}$ $\nabla _{i}A^{i}=-{\frac {1}{c^{2}}}{\frac {\partial \varphi }{\partial t}}$	$-\nabla _{i}\nabla ^{i}\varphi +{\frac {1}{c^{2}}}{\frac {\partial ^{2}\varphi }{\partial t^{2}}}={\frac {\rho }{\varepsilon _{0}}}$ $-\nabla _{i}\nabla ^{i}A^{j}+{\frac {1}{c^{2}}}{\frac {\partial ^{2}A^{j}}{\partial t^{2}}}+R_{i}^{j}A^{i}=\mu _{0}J^{j}$

Differential forms

Formulation	Homogeneous equations	Inhomogeneous equations
Fields any space + time	$dB=0$ $dE+{\frac {\partial B}{\partial t}}=0$	$d{\star }E={\frac {\rho }{\varepsilon _{0}}}$ $d{\star }B-{\frac {1}{c^{2}}}{\frac {\partial {\star }E}{\partial t}}=\mu _{0}J$
Potentials (any gauge) any space (with § topological restrictions) + time	$B=dA$ $E=-d\varphi -{\frac {\partial A}{\partial t}}$	$-d{\star }\!\left(d\varphi +{\frac {\partial A}{\partial t}}\right)={\frac {\rho }{\varepsilon _{0}}}$ $d{\star }dA+{\frac {1}{c^{2}}}{\frac {\partial }{\partial t}}{\star }\!\left(d\varphi +{\frac {\partial A}{\partial t}}\right)=\mu _{0}J$
Potential (Lorenz Gauge) any space (with topological restrictions) + time spatial metric independent of time	$B=dA$ $E=-d\varphi -{\frac {\partial A}{\partial t}}$ $d{\star }A=-{\star }{\frac {1}{c^{2}}}{\frac {\partial \varphi }{\partial t}}$	${\star }\!\left(-\Delta \varphi +{\frac {1}{c^{2}}}{\frac {\partial ^{2}}{\partial t^{2}}}\varphi \right)={\frac {\rho }{\varepsilon _{0}}}$ ${\star }\!\left(-\Delta A+{\frac {1}{c^{2}}}{\frac {\partial ^{2}A}{\partial ^{2}t}}\right)=\mu _{0}J$

सापेक्षतावादी सूत्रीकरण

For the equations in special relativity, see Classical electromagnetism and special relativity and Covariant formulation of classical electromagnetism.

For the equations in general relativity, see Maxwell's equations in curved spacetime.

मैक्सवेल समीकरणों को स्पेसटाइम-जैसे मिन्कोवस्की अंतरिक्ष पर भी तैयार किया जा सकता है जहां अंतरिक्ष और समय को समान स्तर पर माना जाता है। प्रत्यक्ष स्पेसटाइम योगों से पता चलता है कि मैक्सवेल समीकरण सापेक्ष रूप से अपरिवर्तनीय हैं। इस समरूपता के कारण, विद्युत और चुंबकीय क्षेत्रों को समान स्तर पर माना जाता है और फैराडे टेंसर के घटकों के रूप में पहचाना जाता है। यह चार मैक्सवेल समीकरणों को दो तक कम कर देता है, जो समीकरणों को सरल करता है, हालांकि अब हम परिचित वेक्टर सूत्रीकरण का उपयोग नहीं कर सकते हैं। वास्तव में अंतरिक्ष + समय सूत्रीकरण में मैक्सवेल समीकरण गैलीलियन परिवर्तन नहीं हैं और एक छिपी हुई समरूपता के रूप में लोरेंत्ज़ का आक्रमण है। यह सापेक्षता सिद्धांत के विकास के लिए प्रेरणा का एक प्रमुख स्रोत था। वास्तव में, यहां तक ​​​​कि सूत्रीकरण जो अंतरिक्ष और समय को अलग-अलग व्यवहार करता है, एक गैर-सापेक्षवादी सन्निकटन नहीं है और केवल चर का नाम बदलकर समान भौतिकी का वर्णन करता है। इस कारण सापेक्षवादी अपरिवर्तनीय समीकरणों को आमतौर पर मैक्सवेल समीकरण भी कहा जाता है।

नीचे दी गई प्रत्येक तालिका एक औपचारिकता का वर्णन करती है।

Tensor calculus

Formulation	Homogeneous equations	Inhomogeneous equations
Fields Minkowski space	$\partial _{[\alpha }F_{\beta \gamma ]}=0$	$\partial _{\alpha }F^{\alpha \beta }=\mu _{0}J^{\beta }$
Potentials (any gauge) Minkowski space	$F_{\alpha \beta }=2\partial _{[\alpha }A_{\beta ]}$	$2\partial _{\alpha }\partial ^{[\alpha }A^{\beta ]}=\mu _{0}J^{\beta }$
Potentials (Lorenz gauge) Minkowski space	$F_{\alpha \beta }=2\partial _{[\alpha }A_{\beta ]}$ $\partial _{\alpha }A^{\alpha }=0$	$\partial _{\alpha }\partial ^{\alpha }A^{\beta }=\mu _{0}J^{\beta }$
Fields any spacetime	${\begin{aligned}&\partial _{[\alpha }F_{\beta \gamma ]}=\\&\qquad \nabla _{[\alpha }F_{\beta \gamma ]}=0\end{aligned}}$	${\begin{aligned}&{\frac {1}{\sqrt {-g}}}\partial _{\alpha }({\sqrt {-g}}F^{\alpha \beta })=\\&\qquad \nabla _{\alpha }F^{\alpha \beta }=\mu _{0}J^{\beta }\end{aligned}}$
Potentials (any gauge) any spacetime (with §topological restrictions)	$F_{\alpha \beta }=2\partial _{[\alpha }A_{\beta ]}$	${\begin{aligned}&{\frac {2}{\sqrt {-g}}}\partial _{\alpha }({\sqrt {-g}}g^{\alpha \mu }g^{\beta \nu }\partial _{[\mu }A_{\nu ]})=\\&\qquad 2\nabla _{\alpha }(\nabla ^{[\alpha }A^{\beta ]})=\mu _{0}J^{\beta }\end{aligned}}$
Potentials (Lorenz gauge) any spacetime (with topological restrictions)	$F_{\alpha \beta }=2\partial _{[\alpha }A_{\beta ]}$ $\nabla _{\alpha }A^{\alpha }=0$	$\nabla _{\alpha }\nabla ^{\alpha }A^{\beta }-R^{\beta }{}_{\alpha }A^{\alpha }=\mu _{0}J^{\beta }$

Differential forms

Formulation	Homogeneous equations	Inhomogeneous equations
Fields any spacetime	$\mathrm {d} F=0$	$\mathrm {d} {\star }F=\mu _{0}J$
Potentials (any gauge) any spacetime (with topological restrictions)	$F=\mathrm {d} A$	$\mathrm {d} {\star }\mathrm {d} A=\mu _{0}J$
Potentials (Lorenz gauge) any spacetime (with topological restrictions)	$F=\mathrm {d} A$ $\mathrm {d} {\star }A=0$	${\star }\Box A=\mu _{0}J$

• टेन्सर कैलकुलस फॉर्मूलेशन में, इलेक्ट्रोमैग्नेटिक टेंसर F_αβ एक विषम सहसंयोजक क्रम 2 टेन्सर है; चार संभावित, A_α, एक सहपरिवर्ती सदिश है; द करेंट, J^α, एक वेक्टर है; चौकोर कोष्ठक, [ ], रिक्की कैलकुलस#सममित और असममित भागों को दर्शाता है; ∂_α निर्देशांक के संबंध में आंशिक व्युत्पन्न है, x^α. मिन्कोवस्की अंतरिक्ष निर्देशांक में एक जड़त्वीय फ्रेम के संबंध में चुना जाता है; (x^α) = (ct, x, y, z), ताकि सूचकांकों को बढ़ाने और घटाने के लिए इस्तेमाल किया जाने वाला मीट्रिक टेंसर है η_αβ = diag(1, −1, −1, −1). Minkowski अंतरिक्ष पर डी'अलेम्बर्ट ऑपरेटर है ◻ = ∂_α∂^α वेक्टर फॉर्मूलेशन के रूप में। सामान्य स्पेसटाइम में, समन्वय प्रणाली x^α मनमाना है, सहसंयोजक व्युत्पन्न ∇_α, रिक्की टेन्सर, R_αβ और सूचकांकों को ऊपर उठाना और घटाना लोरेंत्ज़ियन मीट्रिक द्वारा परिभाषित किया गया है, g_αβ और d'Alembert ऑपरेटर के रूप में परिभाषित किया गया है ◻ = ∇_α∇^α. टोपोलॉजिकल प्रतिबंध यह है कि अंतरिक्ष का दूसरा वास्तविक सह-समरूपता समूह गायब हो जाता है (विवरण के लिए विभेदक फॉर्म फॉर्म्युलेशन देखें)। मिन्कोव्स्की अंतरिक्ष के लिए एक रेखा को हटाकर इसका उल्लंघन किया जाता है, जो रेखा के पूरक पर बिंदु-जैसे मोनोपोल के साथ एक (फ्लैट) अंतरिक्ष-समय को प्रतिरूप कर सकता है।
• मनमाना स्थान समय पर विभेदक रूप सूत्रीकरण में, F = 1/2F_αβdx^α ∧ dx^β इलेक्ट्रोमैग्नेटिक टेंसर है जिसे 2-फॉर्म माना जाता है, A = A_αdx^α संभावित 1-रूप है, $J=-J_{\alpha }{\star }\mathrm {d} x^{\alpha }$ वर्तमान 3-रूप है, d बाहरी व्युत्पन्न है, और ${\star }$ स्पेसटाइम के लोरेंत्ज़ियन मीट्रिक द्वारा परिभाषित रूपों पर हॉज स्टार है (इसके अभिविन्यास तक, यानी इसका संकेत)। F, हॉज स्टार जैसे 2-रूपों के विशेष मामले में ${\star }$ केवल स्थानीय मापक के लिए मीट्रिक टेन्सर पर निर्भर करता है. इसका मतलब यह है कि, जैसा कि तैयार किया गया है, विभेदक रूप क्षेत्र समीकरण अनुरूप ज्यामिति हैं, लेकिन लॉरेंज गेज की स्थिति अनुरूप आक्रमण को तोड़ती है। परिचालक $\Box =(-{\star }\mathrm {d} {\star }\mathrm {d} -\mathrm {d} {\star }\mathrm {d} {\star })$ लाप्लास-बेल्ट्रामी संचालिका है|डी'अलेम्बर्ट-लाप्लास-बेल्ट्रामी संचालिका 1-रूपों पर एक स्वेच्छित छद्म-रीमैनियन मैनिफोल्ड#लोरेंट्ज़ियन मैनिफोल्ड पर है। टोपोलॉजिकल स्थिति फिर से है कि दूसरा वास्तविक कोहोलॉजी समूह 'तुच्छ' है (जिसका अर्थ है कि इसका रूप एक परिभाषा से होता है)। दूसरे डॉ कहलमज गर्भाशय के साथ आइसोमोर्फिज्म द्वारा इस स्थिति का अर्थ है कि प्रत्येक बंद 2-फॉर्म सटीक है।

अन्य औपचारिकताओं में ज्यामितीय बीजगणित#स्पेसटाइम प्रतिरूप और मैक्सवेल के समीकरणों का एक मैट्रिक्स प्रतिनिधित्व शामिल है। ऐतिहासिक रूप से, एक चतुर्धातुक सूत्रीकरण प्रयोग किया गया।

समाधान

मैक्सवेल के समीकरण आंशिक अंतर समीकरण हैं जो विद्युत और चुंबकीय क्षेत्रों को एक दूसरे से और विद्युत आवेशों और धाराओं से संबंधित करते हैं। अक्सर, आवेश और धाराएँ स्वयं लोरेंत्ज़ बल और #संवैधानिक संबंधों के माध्यम से विद्युत और चुंबकीय क्षेत्रों पर निर्भर होते हैं। ये सभी युग्मित आंशिक अंतर समीकरणों का एक संग्रह बनाते हैं जिन्हें हल करना अक्सर बहुत मुश्किल होता है: समाधान शास्त्रीय विद्युत चुंबकत्व की सभी विविध घटनाओं को शामिल करते हैं। कुछ सामान्य टिप्पणियाँ अनुसरण करती हैं।

किसी भी अंतर समीकरण के लिए, सीमा की स्थिति और प्रारंभिक शर्तें एक विद्युत चुंबकत्व अद्वितीयता प्रमेय के लिए आवश्यक हैं। उदाहरण के लिए, यहां तक ​​​​कि अंतरिक्ष-समय में कहीं भी कोई शुल्क नहीं है और कोई धारा नहीं है, ऐसे स्पष्ट समाधान हैं जिनके लिए ई और बी शून्य या स्थिर हैं, लेकिन विद्युत चुम्बकीय तरंगों के अनुरूप गैर-तुच्छ समाधान भी हैं। कुछ मामलों में, मैक्सवेल के समीकरणों को पूरे अंतरिक्ष में हल किया जाता है, और सीमा की स्थिति अनंत पर स्पर्शोन्मुख सीमा के रूप में दी जाती है। अन्य मामलों में, मैक्सवेल के समीकरण अंतरिक्ष के एक परिमित क्षेत्र में हल किए जाते हैं, उस क्षेत्र की सीमा पर उपयुक्त स्थितियों के साथ, उदाहरण के लिए पूरी तरह से मेल खाने वाली परत शेष ब्रह्मांड का प्रतिनिधित्व करती है, या आवधिक सीमा की स्थिति, या दीवारें जो एक छोटे से क्षेत्र को बाहरी दुनिया से अलग करती हैं (जैसा कि वेवगाइड या कैविटी गुंजयमान यंत्र के साथ)। जेफिमेंको के समीकरण (या निकटता से संबंधित लीनार्ड-विचर्ट क्षमताएं) विद्युत और चुंबकीय क्षेत्रों के लिए मैक्सवेल के समीकरणों का स्पष्ट समाधान हैं जो किसी दिए गए शुल्क और धाराओं के वितरण द्वारा बनाए गए हैं। यह तथाकथित मंदित समाधान प्राप्त करने के लिए विशिष्ट प्रारंभिक स्थितियों को मानता है, जहां केवल वही क्षेत्र मौजूद होते हैं जो आवेशों द्वारा निर्मित होते हैं। हालांकि, जेफिमेंको के समीकरण उन स्थितियों में मददगार नहीं होते हैं, जब आरोप और धाराएं उनके द्वारा बनाए गए क्षेत्रों से स्वयं प्रभावित होते हैं।

संख्यात्मक आंशिक अंतर समीकरणों का उपयोग मैक्सवेल के समीकरणों के अनुमानित समाधान की गणना करने के लिए किया जा सकता है जब सटीक समाधान असंभव हो। इनमें परिमित तत्व विधि और परिमित-अंतर समय-डोमेन विधि शामिल हैं। अधिक जानकारी के लिए, कम्प्यूटेशनल इलेक्ट्रोमैग्नेटिक्स देखें।

मैक्सवेल के समीकरणों का अधिनिर्धारण

मैक्सवेल के समीकरण अतिनिर्धारित प्रणाली प्रतीत होते हैं, जिसमें वे छह अज्ञात (तीन घटक) शामिल करते हैं E और B) लेकिन आठ समीकरण (दो गॉस के सिद्धांतों में से प्रत्येक के लिए एक, फैराडे और एम्पीयर के सिद्धांतों के लिए तीन वेक्टर घटक)। (धाराएं और शुल्क अज्ञात नहीं हैं, चार्ज संरक्षण के अधीन स्वतंत्र रूप से निर्दिष्ट किए जा सकते हैं।) यह मैक्सवेल के समीकरणों में एक निश्चित सीमित प्रकार की अतिरेक से संबंधित है: यह सिद्ध किया जा सकता है कि फैराडे के सिद्धांत और एम्पीयर के सिद्धांत को संतुष्ट करने वाली कोई भी प्रणाली स्वचालित रूप से दोनों को भी संतुष्ट करती है। गॉस के सिद्धांत, जब तक सिस्टम की प्रारंभिक स्थिति होती है, और चार्ज के संरक्षण और चुंबकीय मोनोपोल के अस्तित्व को मानते हैं। यह स्पष्टीकरण पहली बार 1941 में जूलियस एडम्स स्ट्रैटन द्वारा पेश किया गया था। हालांकि एक संख्यात्मक एल्गोरिथम (प्रारंभिक स्थितियों के अलावा) में गॉस के दो सिद्धांतों को आसानी से अनदेखा करना संभव है, गणनाओं की अपूर्ण सटीकता उन सिद्धांतों के लगातार बढ़ते उल्लंघन का कारण बन सकती है। इन उल्लंघनों को चित्रित करने वाले डमी चरों को पेश करने से, चार समीकरण अतिनिर्धारित नहीं होते हैं। परिणामी सूत्रीकरण से अधिक सटीक एल्गोरिदम हो सकते हैं जो सभी चार सिद्धांतों को ध्यान में रखते हैं। दोनों की पहचान $\nabla \cdot \nabla \times \mathbf {B} \equiv 0,\nabla \cdot \nabla \times \mathbf {E} \equiv 0$, जो आठ समीकरणों को घटाकर छह स्वतंत्र कर देता है, अतिनिर्धारण का सही कारण हैं। समतुल्य रूप से, अतिनिर्धारण को विद्युत और चुंबकीय आवेश के संरक्षण के रूप में देखा जा सकता है, क्योंकि वे ऊपर वर्णित व्युत्पत्ति में आवश्यक हैं लेकिन दो गॉस के सिद्धांतों द्वारा निहित हैं।

रैखिक बीजगणितीय समीकरणों के लिए, समीकरणों और अज्ञात को फिर से लिखने के लिए कोई 'अच्छे' सिद्धांत बना सकता है। समीकरण रैखिक रूप से निर्भर हो सकते हैं। लेकिन विभेदक समीकरणों में, और विशेष रूप से पीडीई में, किसी को उपयुक्त सीमा स्थितियों की आवश्यकता होती है, जो समीकरणों पर इतने स्पष्ट तरीके से निर्भर नहीं करते हैं। इससे भी अधिक, यदि कोई उन्हें वेक्टर और स्केलर क्षमता के संदर्भ में फिर से लिखता है, तो गेज फिक्सिंग के कारण समीकरणों को कम करके आंका जाता है।

== मैक्सवेल के समीकरण क्यूईडी == की शास्त्रीय सीमा के रूप में मैक्सवेल के समीकरण और लोरेंत्ज़ बल सिद्धांत (बाकी शास्त्रीय विद्युत चुंबकत्व के साथ) विभिन्न प्रकार की घटनाओं की व्याख्या और भविष्यवाणी करने में असाधारण रूप से सफल हैं। हालांकि वे क्वांटम प्रभावों के लिए जिम्मेदार नहीं हैं और इसलिए उनकी प्रयोज्यता का क्षेत्र सीमित है। मैक्सवेल के समीकरणों को क्वांटम इलेक्ट्रोडायनामिक्स (QED) की शास्त्रीय सीमा के रूप में माना जाता है।

कुछ देखी गई विद्युत चुम्बकीय घटनाएं मैक्सवेल के समीकरणों के साथ असंगत हैं। इनमें फोटॉन-फोटॉन स्कैटरिंग और फोटॉन या आभासी कण, गैर-शास्त्रीय प्रकाश और विद्युत चुम्बकीय क्षेत्रों के क्वांटम उलझाव से संबंधित कई अन्य घटनाएं शामिल हैं (क्वांटम प्रकाशिकी देखें)। उदा. मैक्सवेल सिद्धांत द्वारा क्वांटम क्रिप्टोग्राफी का वर्णन नहीं किया जा सकता है, लगभग भी नहीं। मैक्सवेल के समीकरणों की अनुमानित प्रकृति अत्यधिक मजबूत क्षेत्र व्यवस्था (यूलर-हाइजेनबर्ग लैग्रैंगियन देखें) या बहुत छोटी दूरी पर जाने पर अधिक से अधिक स्पष्ट हो जाती है।

अंत में, मैक्सवेल के समीकरण किसी भी घटना की व्याख्या नहीं कर सकते हैं, जिसमें प्रकाश विद्युत प्रभाव, प्लैंक का सिद्धांत, डुआन-हंट सिद्धांत, और सिंगल-फोटॉन हिमस्खलन डायोड | सिंगल-फोटॉन लाइट डिटेक्टर जैसे क्वांटम पदार्थ के साथ बातचीत करने वाले व्यक्तिगत फोटॉन शामिल हैं। हालांकि, इस तरह की कई घटनाओं को शास्त्रीय विद्युत चुम्बकीय क्षेत्र के साथ युग्मित क्वांटम पदार्थ के आधे रास्ते के सिद्धांत का उपयोग करके अनुमानित किया जा सकता है, या तो बाहरी क्षेत्र के रूप में या मैक्सवेल के समीकरणों के दाहिने हाथ की ओर चार्ज वर्तमान और घनत्व के अपेक्षित मूल्य के साथ।

रूपांतर

विद्युतचुंबकीय क्षेत्र के शास्त्रीय सिद्धांत के रूप में मैक्सवेल समीकरणों पर लोकप्रिय बदलाव अपेक्षाकृत दुर्लभ हैं क्योंकि मानक समीकरण समय की कसौटी पर उल्लेखनीय रूप से खरे उतरे हैं।

चुंबकीय एकाधिकार

Main article: Magnetic monopole

मैक्सवेल के समीकरण बताते हैं कि ब्रह्मांड में विद्युत आवेश है, लेकिन कोई चुंबकीय आवेश (जिसे चुंबकीय मोनोपोल भी कहा जाता है) नहीं है। दरअसल, व्यापक खोजों के बावजूद चुंबकीय आवेश कभी नहीं देखा गया है, और मौजूद नहीं हो सकता है। यदि वे मौजूद थे, तो चुंबकत्व के लिए गॉस के सिद्धांत और फैराडे के सिद्धांत दोनों को संशोधित करने की आवश्यकता होगी, और परिणामी चार समीकरण विद्युत और चुंबकीय क्षेत्रों के आदान-प्रदान के तहत पूरी तरह से सममित होंगे।

यह भी देखें

• Algebra of physical space
• Fresnel equations
• Gravitoelectromagnetism
• Interface conditions for electromagnetic fields
• Moving magnet and conductor problem
• Riemann–Silberstein vector
• Spacetime algebra
• Wheeler–Feynman absorber theory

अग्रिम पठन

See also: List of textbooks in electromagnetism

• Imaeda, K. (1995), "Biquaternionic Formulation of Maxwell's Equations and their Solutions", in Ablamowicz, Rafał; Lounesto, Pertti (eds.), Clifford Algebras and Spinor Structures, Springer, pp. 265–280, doi:10.1007/978-94-015-8422-7_16, ISBN 978-90-481-4525-6

ऐतिहासिक प्रकाशन

• फैराडे की बल की रेखाओं पर – 1855/56। मैक्सवेल का पहला पेपर (भाग 1 और 2) - ब्लेज़ लैब्स रिसर्च (पीडीएफ) द्वारा संकलित।
• बल की भौतिक रेखाओं पर – 1861।
• जेम्स क्लर्क मैक्सवेल, विद्युत चुम्बकीय क्षेत्र का एक गतिशील सिद्धांत, फिलोसोफिकल ट्रांजैक्शन ऑफ़ द रॉयल सोसाइटी ऑफ़ लंदन '155', 459–512 (1865)। (यह लेख मैक्सवेल द्वारा रॉयल सोसाइटी के लिए 8 दिसंबर, 1864 की प्रस्तुति के साथ था।)
  • विद्युत चुम्बकीय का एक गतिशील सिद्धांत फील्ड - 1865। मैक्सवेल का 1865 का पेपर उनके 20 समीकरणों का वर्णन करता है, Google पुस्तकें से लिंक।
• जे. क्लर्क मैक्सवेल (1873), बिजली और चुंबकत्व पर एक ग्रंथ :
  • मैक्सवेल, जे.सी., बिजली और चुंबकत्व पर एक ग्रंथ - खंड 1 - 1873 - पॉस्नर मेमोरियल संग्रह - कार्नेगी मेलन विश्वविद्यालय।
  • मैक्सवेल, जे.सी., बिजली और चुंबकत्व पर एक ग्रंथ - खंड 2 - 1873 - पॉस्नर मेमोरियल संग्रह - कार्नेगी मेलन विश्वविद्यालय।

सापेक्षता से पहले के घटनाक्रम:

• Larmor Joseph (1897). "On a dynamical theory of the electric and luminiferous medium. Part 3, Relations with material media" . Phil. Trans. R. Soc. 190: 205–300.
• Lorentz Hendrik (1899). "Simplified theory of electrical and optical phenomena in moving systems". Proc. Acad. Science Amsterdam. I: 427–443.
• Lorentz Hendrik (1904). "Electromagnetic phenomena in a system moving with any velocity less than that of light". Proc. Acad. Science Amsterdam. IV: 669–678.
• हेनरी पोंकारे (1900) लोरेंत्ज़ सिद्धांत और प्रतिक्रिया सिद्धांत (in French), डच अभिलेखागार, 'वी', 253-278।
• हेनरी पोंकारे (1902) विज्ञान और परिकल्पना (in French).
• हेनरी पोंकारे (1905) इलेक्ट्रॉन की गतिशीलता पर (in French), विज्ञान अकादमी की कार्यवाही, '140', 1504-1508।
• कैट, वाल्टन और डेविडसन। वर्तमान विस्थापन का इतिहास Archived 2008-05-06 at the Wayback Machine. वायरलेस वर्ल्ड, मार्च 1979।

बाहरी संबंध

• "Maxwell equations", Encyclopedia of Mathematics, EMS Press, 2001 [1994]
• maxwells-equations.com — An intuitive tutorial of Maxwell's equations.
• The Feynman Lectures on Physics Vol. II Ch. 18: The Maxwell Equations
• Wikiversity Page on Maxwell's Equations

आधुनिक उपचार

• इलेक्ट्रोमैग्नेटिज्म (अध्याय 11), बी. क्रोवेल, फुलर्टन कॉलेज
• व्याख्यान श्रृंखला: सापेक्षता और विद्युत चुंबकत्व, आर। फिट्ज़पैट्रिक, ऑस्टिन में टेक्सास विश्वविद्यालय
• मैक्सवेल के समीकरणों से विद्युत चुम्बकीय तरंगें प्रोजेक्ट PHYSNET पर।
• MIT वीडियो व्याख्यान श्रृंखला (36 × 50 मिनट के व्याख्यान) (.mp4 प्रारूप में) - विद्युत और चुंबकत्व प्रोफेसर वाल्टर लेविन द्वारा पढ़ाया जाता है।

अन्य

• Silagadze, Z. K. (2002). "मैक्सवेल समीकरणों और अतिरिक्त आयामों की फेनमैन की व्युत्पत्ति". Annales de la Fondation Louis de Broglie. 27: 241–256. arXiv:hep-ph/0106235. Bibcode:2001hep.ph....6235S.
• प्रकृति मील के पत्थर: फोटॉन – मील का पत्थर 2 (1861) मैक्सवेल के समीकरण

श्रेणी:मैक्सवेल के समीकरण श्रेणी:विद्युत चुंबकत्व श्रेणी:भौतिकी के समीकरण श्रेणी:अंतरिक्ष और समय के कार्य श्रेणी:जेम्स क्लर्क मैक्सवेल श्रेणी:आंशिक अवकल समीकरण श्रेणी:वैज्ञानिक सिद्धांत